Определение синуса угла, представленного на графике — «Шпаргалка ЕГЭ»
Чему равен синус угла AOB?
1) 2) 3) 4)
Решение задачи
Данный урок показывает, как, используя понятие синуса угла: синус угла – это отношение противоположного катета прямоугольного треугольника к его гипотенузе – определить синус произвольного угла изображенного на рисунке. Для решения задачи необходимо провести перпендикуляр через одну из сторон данного угла, тем самым получив прямоугольный треугольник. Используя клеточки на изображенном рисунке можно с легкостью определить длину одного из катетов. После этого можно найти дину гипотенузы (чаще всего для этого используется длина второго катета и теорема Пифагора). После того как длина гипотенузы была определена арифметические вычисления приводят к получению итогового ответа.
Решение данной задачи рекомендовано для учащихся 7-х классов при изучении тем «Треугольники» («Треугольники»), «Соотношение между сторонами и углами треугольника» («Виды треугольников», «Основные свойства прямоугольных треугольников»), для учащихся 8-х классов при изучении темы «Подобные треугольники» («Синус, косинус и тангенс острого угла прямоугольного треугольника»), «Площадь» («Теорема Пифагора»), для учащихся 9-х классов при изучении темы «Соотношение между сторонами и углами треугольника.
Рекомендуем
Отзывы учеников
- Светлана Иванова
К ЕГЭ по математике я готовилась сама, без репетитора. Ничего сверхъестественного я не делала: зубрила формулы и решала задачи на сайте ШпаргалкаЕГЭ.
Вообще к части В я готовилась в основном в конце 10-го класса, в 11-ом я занималась только частью С. Мой результат — 75 баллов.
- Влад Долгорукий
Большое спасибо! Сервис нереально помог. К ЕГЭ готовился с репетитором. На занятиях использовали сайт для закрепления навыков решения различных типов задач, особенно части С.
Всем рекомендую Генератор Вариантов. - Александр Шпик
Hello People. Я продвигаю свою идеологию «Втопку книжки». Зайди в ВК или на сайт ShpargalkaEGE смотри ролики по задачам. Все, что не знаешь, включая самые мелочи конспектируй и учи. Не ленись закреплять результат. Мои баллы ЕГЭ — 82.
Всем рекомендую Генератор Вариантов.тригонометрия — Нахождение синуса угла в градусах без $\pi$
Задай вопрос
спросил
Изменено 6 лет, 10 месяцев назад
Просмотрено 2к раз
$\begingroup$
9{n-1}$$
Проблема для меня в том, что у меня есть мера угла в градусах, но $x$ выше в радианах.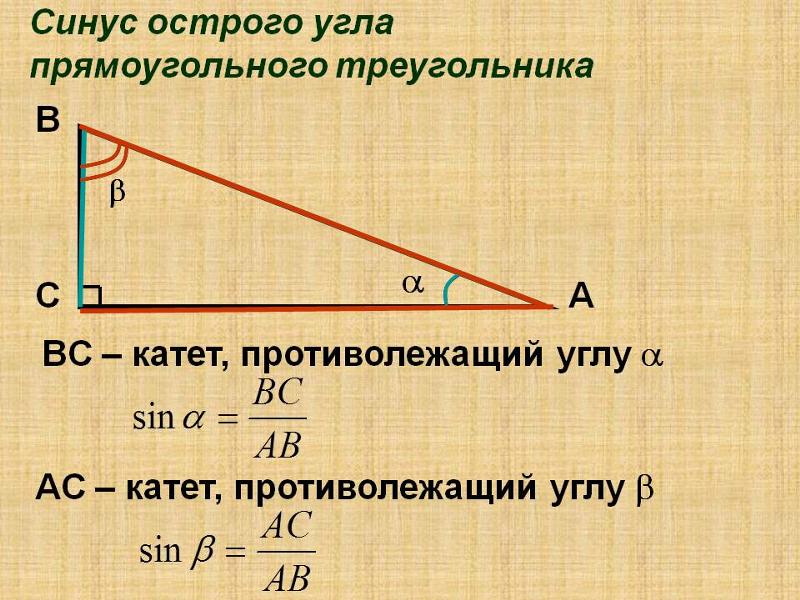
o$ вообще без участия $\pi$? 9о)$ без использования $\pi$?
Чтобы было ясно, я не ищу ничего, что включает приближения или бесконечные ряды, которые не могут быть полностью выражены в конечном объеме пространства (например, приведенный выше ряд Тейлора подходит, потому что он может быть выражен в сигма-нотации).
- тригонометрия
- Пи
$\endgroup$
5
$\begingroup$
Как отмечено в комментарии, есть уравнения, которые вы можете написать для тригонометрические функции рациональных частей прямого угла (и, следовательно, для синуса любого рационального числа степеней) без использования $\pi$ или каких-либо тригонометрических функций. Однако реальное использование этих уравнений может оказаться несколько громоздким. 9м}\справа)}{2}}. $$
Вы можете найти значение для любого $k$, начав с $m=1$ и применив
формула половинного угла повторно для $m=2,3,\ldots,k$:
\начать{выравнивать}
\Cos\left(\frac{180}{2}\right) &= \Cos(90) = 0,\\
\Cos\влево(\frac{180}{4}\вправо) &=
\ sqrt {\ гидроразрыва {1 + \ Cos \ влево (\ гидроразрыва {180} {2} \ вправо)} {2}}
= \ sqrt {\ frac {1 + 0} {2}} = \ frac {1} {\ sqrt 2}, \\
\Cos\влево(\frac{180}{8}\вправо) &=
\ sqrt {\ гидроразрыва {1 + \ Cos \ влево (\ гидроразрыва {180} {4} \ справа)} {2}}
= \ sqrt {\ frac {1 + \ frac {1} {\ sqrt 2}} {2}}
= \ sqrt {\ frac {\ sqrt 2 + 1} {2 \ sqrt 2}}, \\
\Cos\влево(\frac{180}{16}\вправо) &=
\ sqrt {\ гидроразрыва {1 + \ Cos \ влево (\ гидроразрыва {180} {8} \ вправо)} {2}}
= \ sqrt {\ frac {1 + \ sqrt {\ frac {\ sqrt 2 + 1} {2 \ sqrt 2}}} {2}}
= \ sqrt {\ frac {\ sqrt {2 \ sqrt 2} + \ sqrt {\ sqrt 2 + 1}} {2 \ sqrt {2 \ sqrt 2}}}, \\
\end{выравнивание}
и так далее, чтобы получить $\Cos\left(\frac{180}{2^k}\right)$
для любого $k$.
2}.
$$
$\endgroup$
5
$\begingroup$
В связи с ответом Дэвида К. я также отмечаю одну небольшую проблему:
$$\sin(\frac x2)=\pm\sqrt{\frac{1-\cos(x)}2}$$
Очевидно, что $\sin(\frac x2)$ может быть отрицательным.
Однако мы знаем, что при $0\le x\le\pi$ $\sin(x)>0$, другими словами, положительно.
На интервале от $-\frac{\pi}2\le x\le\frac{\pi}2$, $\cos(x)>0$.
Итак, мы можем начать с $\cos(1)\приблизительно 0,540302306$.
У нас есть $$\cos(0,5)\приблизительно 0,877581562$$
$$\cos(0,25)\приблизительно 0,968912422$$
$$\cos(0,125)\приблизительно 0,992197667$$
2 и т.д. (эти значения были получены по формуле половины угла)
Аналогично имеем: (используя формулу половины угла)
$$\sin(1)\приблизительно0,841470985$$
$$\sin(0.5)\ приблизительно0,479425539$$
$$\sin(0,25)\приблизительно0,247403959$$
$$\sin(0,125)\приблизительно0,124674733$$
и т.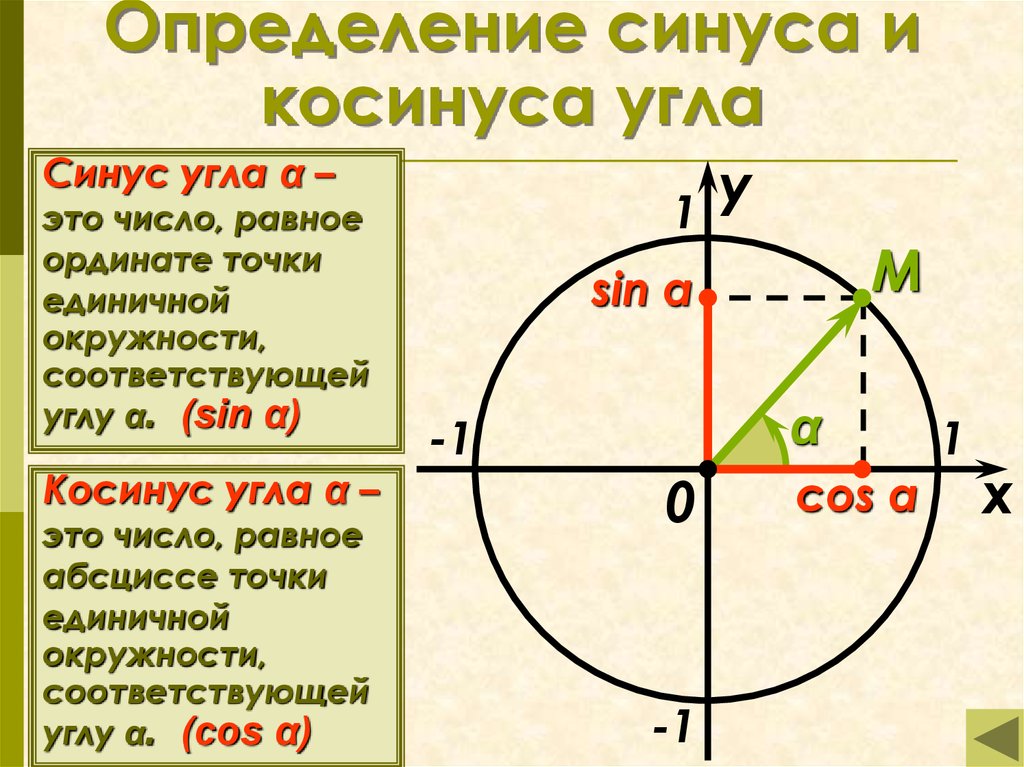
д.
Теперь, зная наши тригонометрические тождества, можно использовать формулу суммы углов для аппроксимации желаемого значения с желаемой точностью.
$\endgroup$
Использование функции синуса для нахождения угла (Ключевой этап 3)
Урок
Функция синуса связывает заданный угол с противолежащей стороной и гипотенузой прямоугольного треугольника. Угол (обозначенный θ) определяется по следующей формуле:
В этой формуле θ — угол прямоугольного треугольника, противоположная сторона — длина стороны, противоположной углу, а гипотенуза — длина наибольшей стороны. sin −1 — функция обратного синуса (см. , примечание ). На изображении ниже показано, что мы имеем в виду:
Как использовать функцию синуса для нахождения угла прямоугольного треугольника
Найти угол прямоугольного треугольника легко, если мы знаем противоположную сторону и гипотенузу.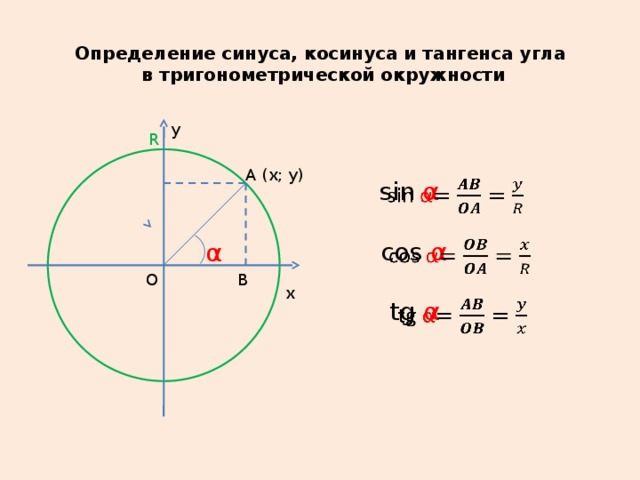
Чему равен угол прямоугольного треугольника, изображенного ниже?
Пошагово:
Начните с формулы:
θ = sin −1 (противоположное / гипотенуза)
Не забывайте: sin −1 — функция обратного синуса (применяется ко всему в скобках) и / означает ÷
Подставляем в формулу длину противоположной стороны и длину гипотенузы. В нашем примере наоборот 2 см, а гипотенуза 4 см.
θ = sin −1 (2/4) θ = sin −1 (2 ÷ 4) θ = sin −1 (0,5) θ = 30°
Ответ:
Угол прямоугольного треугольника с противоположным катетом 2 см и гипотенузой 4 см равен 30°.
Вспоминая формулу
Часто самая сложная часть поиска неизвестного угла — это вспомнить, какую формулу использовать.
Всякий раз, когда у вас есть прямоугольный треугольник, в котором вы знаете две стороны и должны найти неизвестный угол… ……подумайте о тригонометрии… ……………подумайте о синусе, косинусе или тангенсе… …………………………..думаю СОХ КАН ТОА .
Глядя на приведенный выше пример, мы знаем O pposite и H ypotenuse.
Две буквы, которые мы ищем, — это OH , которые входят в SOH в SOH CAH TOA. Это напоминает нам уравнение:
S in θ = O pposite / H ypotenuse
Нам нужен угол θ, а не синус угла, sin θ. Для этого нам нужно взять арксинус, sin -1 (см. Примечание ).
θ = S в −1 ( O pposite / H ypotenuse)
Слайды урока
Ползунок ниже дает еще один пример нахождения угла прямоугольного треугольника (если известны гипотенуза и противоположная сторона).
Откройте слайдер в новой вкладкеИнтерактивный виджет
Вот интерактивный виджет, который поможет вам узнать о синусоидальной функции прямоугольного треугольника.
Что такое функция обратного синуса?
Функция обратного синуса является противоположностью функции синуса. Функция синуса принимает угол и дает отношение, противоположное гипотенузе:
Функция обратного синуса, sin −1 , работает в другом направлении. Он берет отношение, противоположное гипотенузе, и дает угол:
Поменять стороны, инвертировать синус
Вы можете увидеть функцию синуса в уравнении:
Чтобы сделать θ предметом уравнения, возьмите арксинус обеих частей. Обратный синус компенсирует синус слева от стороны равенства, поэтому уравнение выглядит следующим образом:
При сравнении двух уравнений синус переместился с одной стороны знака равенства на другую и изменился с sin на sin −1 .