Сравнение чисел при решении уравнений, неравенств и задач с модулями
При решении уравнений и неравенств, а также задач с модулями требуется расположить найденные корни на числовой прямой.
Как ты знаешь, найденные корни могут быть разными.
Они могут быть такими: \( 4\), \( -3\), \( 8\), \( 125\).
А могут быть и вот такими: \( \sqrt{6}\), \( \left( 4-\sqrt{3} \right)\), \( \frac{\sqrt[6]{6}}{\sqrt{13}+\frac{4}{13}}\).
Если числа не рациональные, а иррациональные, или представляют собой сложные математические выражения, то расположить их на числовой прямой весьма проблематично.
Для этого нужно уметь их сравнивать.
Калькуляторами на экзамене пользоваться нельзя, а приближенный подсчет не дает 100% гарантий, что одно число меньше другого (вдруг разница между сравниваемыми числами \( 0,000001\)?).
Что делать?
Прочитай эту статью и все поймешь!
Например, нам необходимо сравнить две дроби: \( 1,6\) и \( 1\frac{6}{13}\).
Давай разберем каждый вариант
Вариант 1. Сравнение дробей с помощью приведения к общему знаменателю
Запишем \( 1,6\) в виде обыкновенной дроби:
\( 1,6=1\frac{6}{10}=1\frac{3}{5}\) – (как ты видишь, я также сократила на \( 2\) числитель и знаменатель).
Теперь нам необходимо сравнить дроби:
\( 1\frac{3}{5}\) и \( 1\frac{6}{13}\)
Сейчас мы можем продолжить сравнивать также двумя способами. Мы можем:
Способ 1. Числитель больше знаменателя
Просто приведите все к общему знаменателю, представив обе дроби как неправильные (числитель больше знаменателя):
\( \frac{8}{5}\vee \frac{19}{13}\)
\( \frac{8\cdot 13}{5\cdot 13}\vee \frac{19\cdot 5}{13\cdot 5}\)
\( \frac{104}{65}\vee \frac{95}{65}\)
Какое число больше? Правильно, то, у которого числитель больше, то есть первое.
\( 1,6>1\frac{6}{13}\)
Способ 2.
Отбросьте единицу«Отбросьте» \( 1\) (считай, что мы из каждой дроби вычли единицу, и соотношение дробей друг с другом, соответственно, не изменилось) и будем сравнивать дроби:
\( \frac{3}{5}\vee \frac{6}{13}\)
Приводим их также к общему знаменателю:
\( \frac{3\cdot 13}{13\cdot 5}\vee \frac{6\cdot 5}{13\cdot 5}\)
Заметь, в принципе мы можем
\( \frac{39}{13\cdot 5}\vee \frac{30}{13\cdot 5}\)
Мы получили абсолютно точно такой же результат, как и в предыдущем случае – первое число больше, чем второе:
\( 1,6>1\frac{6}{13}\)
Проверим также, правомерно ли мы вычли единицу? Посчитаем разницу в числителе при первом расчете и втором:
1) \( 104-95=9\)
2) \( 39-30=9\)
Итак, мы рассмотрели, как сравнивать дроби, приводя их к общему знаменателю.
Перейдем к другому методу – сравнение дробей приводя их к общему… числителю.
Вариант 2. Сравнение дробей с помощью приведения к общему числителю
Да, да. Это не опечатка. В школе редко кому рассказывают этот метод, но очень часто он весьма удобен. Чтобы ты быстро понял его суть, задам тебе только один вопрос – «в каких случаях значение дроби наибольшее?»
Конечно, ты скажешь «когда числитель максимально большой, а знаменатель максимально маленький».
Например, ты же точно скажешь, что \( \frac{8}{13}<\frac{12}{13}\) Верно?
А если нам надо сравнить такие дроби: \( \frac{6}{13}\vee \frac{6}{28}\)?
Думаю, ты тоже сразу верно поставишь знак, ведь в первом случае \( 6\) делят на \( 13\) частей, а во втором на целых \( 28\), значит, во втором случае кусочки получаются совсем маленькие, и соответственно: \( \frac{6}{13}>\frac{6}{28}\).
Как ты видишь, знаменатели здесь разные, а вот числители одинаковы.
Однако, для того, чтобы сравнить эти две дроби, тебе не обязательно искать общий знаменатель. Хотя… найди его и посмотри, вдруг знак сравнения все же неправильный?
\( \frac{6\cdot 28}{13\cdot 28}>\frac{6\cdot 13}{28\cdot 13}\)
\( \frac{168}{364}>\frac{78}{364}\)
А знак-то тот же.
Вернемся к нашему изначальному заданию – сравнить \( 1\frac{3}{5}\)и \( 1\frac{6}{13}\). Будем сравнивать \( \frac{3}{5}\) и \( \frac{6}{13}\).
Приведем данные дроби не к общему знаменателю, а к общему числителю.
Для этого просто числитель и знаменатель первой дроби умножим на \( 2\). Получим:
\( \frac{6}{10}\) и \( \frac{6}{13}\).
Какая дробь больше? Правильно, первая.
Вариант 3. Сравнение дробей с помощью вычитания
Как сравнивать дроби с помощью вычитания? Да очень просто.
Мы из одной дроби вычитаем другую. Если результат получается положительным, то первая дробь (уменьшаемое) больше второй (вычитаемое), а если отрицательным, то наоборот.
В нашем случае попробуем из второй вычесть первую дробь: \( 1\frac{6}{13}-1,6\).
Как ты уже понял, мы так же переводим \( 1,6\) в обыкновенную дробь и получаем тот же результат – \( 1\frac{3}{5}\) .
Наше выражение приобретает вид:
\( 1\frac{6}{13}-1\frac{3}{5}\)
Далее нам все равно придется прибегнуть к приведению к общему знаменателю.
Вопрос как: первым способом, преобразуя дроби в неправильные, или вторым, как бы «убирая» единицу? Кстати, это действие имеет вполне математическое обоснование. Смотри:
\( \left( 1+\frac{6}{13} \right)-\left( 1+\frac{3}{5} \right)=1+\frac{6}{13}-1-\frac{3}{5}=\frac{6}{13}-\frac{3}{5}\)
Мне больше нравится второй вариант, так как перемножение в числителе при приведении к общему знаменателю становится в разы проще.
Приводим к общему знаменателю:
\( \frac{6}{13}-\frac{3}{5}=\frac{6\cdot 5}{13\cdot 5}-\frac{3\cdot 13}{5\cdot 13}=\frac{30}{13\cdot 5}-\frac{39}{5\cdot 13}=-\frac{9}{5\cdot 13}\)
Здесь главное не запутаться, какое число и откуда мы отнимали.
Внимательно посмотреть ход решения и случайно не перепутать знаки. Мы отнимали от второго числа первое и получили отрицательный ответ, значит?..
Правильно, первое число больше второго.
\( 1,6>1\frac{6}{13}\)
Вариант 5. Сравнение дробей с помощью деления
Да, да. И так тоже можно.
Логика проста: когда мы делим большее число на меньшее, в ответе у нас получается число, больше единицы, а если мы делим меньшее число на большее, то ответ приходится на промежуток от \( 0\) до \( 1\).
Чтобы запомнить это правило, возьми для сравнения любые два простых числа, например, \( 6\) и \( 4\). Ты же знаешь, что \( 6\) больше \( 4\)?
Теперь разделим \( 6\) на \( 4\). Наш ответ – \( 1,5\). Соответственно, теория верна.
Если мы разделим \( \displaystyle 4\) на \( 6\), что мы получим \( 0,\left( 6 \right)\) – меньше единицы, что в свою очередь подтверждает, что \( \displaystyle 4\) на самом деле меньше \( 6\).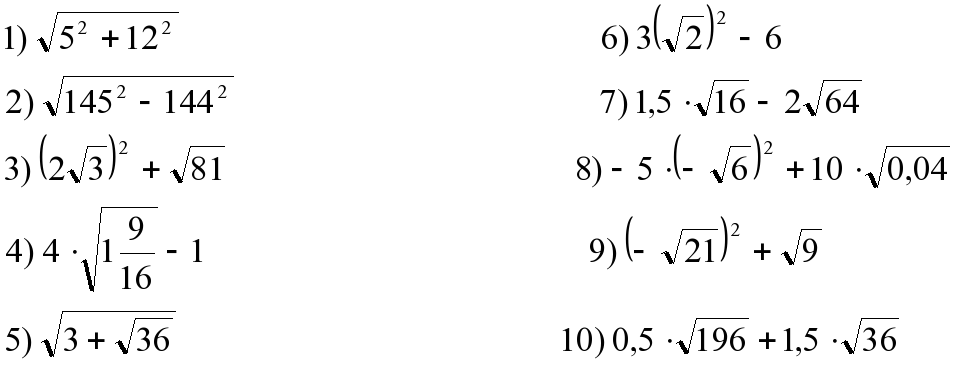
{3}}=6\)
А что больше? \( y\) или \( x\)? Это ты, конечно, сравнишь без всякого труда. Чем большее число мы возводим в степень, тем больше будет значение.
Итак. Выведем правило.
Если показатели степени корней одинаковы (в нашем случае это \( 3\)), то необходимо сравнивать подкоренные выражения (\( 4\) и \( 6\)) – чем больше подкоренное число, тем больше значение корня при равных показателях.
Сложно запомнить? Тогда просто держи в голове пример \( \sqrt{16}\) и \( \sqrt{4}\). Что больше?
\( \sqrt{16}=4\)
\( \sqrt{4}=2\)
\( 4\) больше \( 2\).
Показатели степени корней одинаковы, так как корень квадратный. Подкоренное выражение одного числа (\( 16\)) больше другого (\( 4\)), значит, правило действительно верное.
А что, если подкоренные выражения одинаковые, а вот степени корней разные? Например: \( \sqrt[4]{6}\vee \sqrt[3]{6}\).
Тоже вполне понятно, что при извлечении корня большей степени получится меньшее число.
{6}}=12\)
Ты без труда видишь, что в данных уравнениях \( a\) должно быть больше \( b\), следовательно:
\( \sqrt[3]{12}>\sqrt[6]{12}\).
Если подкоренные выражения одинаковы (в нашем случае \( 12\)), а показатели степени корней различны
(в нашем случае это \( 3\) и \( 6\)), то необходимо сравнивать показатели степени (\( 3\) и \( 6\)) – чем больше показатель, тем меньше данное выражение.
Изначально, обрати внимание на основание логарифма. Ты помнишь, что:
Если основание логарифма меньше \( 1\), то функция убывает, а если больше, то возрастает.
Именно на этом будет основаны наши суждения. Рассмотрим сравнение логарифмов, которые уже приведены к одинаковому основанию, либо аргументу.
Для начала упростим задачу: пусть в сравниваемых логарифмах равные основания.
Тогда:
Функция \( y={{\log }_{a}}x\), при \( a>0\) возрастает на промежутке от \( \left( 0;\ +\infty \right)\), значит по определению \( {{x}_{1}}<{{x}_{2}}\), то \( {{y}_{1}}<{{y}_{2}}\) («прямое сравнение»)
Пример: \( {{\log }_{3}}6\vee {{\log }_{3}}\frac{18}{21}\) – основания одинаковы, \( a>0\) ,соответственно сравниваем аргументы: \( 6>\frac{18}{21}\), следовательно: \( {{\log }_{3}}6>{{\log }_{3}}\frac{18}{21}\)
Функция \( y={{\log }_{a}}x\), при \( 0<a<1\), убывает на промежутке от \( \left( 0;\ +\infty \right)\), значит по определению \( {{x}_{1}}<{{x}_{2}}\), то \( {{y}_{1}}>{{y}_{2}}\) («обратное сравнение»).
\( {{\log }_{\frac{1}{3}}}12\vee {{\log }_{\frac{1}{3}}}24\) – основания одинаковы.
\( 0<a<1\), соответственно сравниваем аргументы: \( 12<24\). Однако, знак у логарифмов будет «обратный», так как функция убывает: \( {{\log }_{\frac{1}{3}}}12>{{\log }_{\frac{1}{3}}}24\).
Запишем все в общем табличном виде:
| \( a>1\), при этом \( {{a}_{1}}<{{a}_{2}}\) | \( 0<a<1\), при этом \( {{a}_{1}}>{{a}_{2}}\) |
| \( x>1\) | \( {{\log }_{{{a}_{1}}}}x>{{\log }_{{{a}_{2}}}}x\) |
| \( 0<x<1\) | \( {{\log }_{{{a}_{1}}}}x<{{\log }_{{{a}_{2}}}}x\) |
Соответственно, как ты уже понял, при сравнении логарифмов нам необходимо привести к одинаковому основанию, либо аргументу.
К одинаковому основанию мы приходим, используя формулу перехода от одного основания к другому.
Можно также сравнивать логарифмы с третьим числом и на основании этого делать вывод о том, что меньше, а что больше.
Например, подумай, как сравнить вот эти два логарифма?
\( {{\log }_{3}}5\vee {{\log }_{8}}26\)
Небольшая подсказка – для сравнения тебе очень поможет логарифм, аргумент которого будет равен \( 25\).
Подумал? Давай решать вместе.
Мы легко сравним с тобой эти два логарифма:
\( {{\log }_{8}}26\vee {{\log }_{8}}25\)
Не знаешь как? Смотри выше. Мы только что это разбирали. Какой знак там будет? Правильно:
\( {{\log }_{8}}26\vee {{\log }_{8}}25\)
\( {{\log }_{3}}5={{\log }_{9}}25\). Согласен?
Сравним между собой:
\( {{\log }_{8}}25\vee {{\log }_{9}}25\)
У тебя должно получиться следующее:
\( {{\log }_{8}}25>{{\log }_{9}}25\)
А теперь соедини все наши выводы в один. Получилось?
\( \left. \begin{array}{l}lo{{g}_{8}}26>{{\log }_{8}}25\\{{\log }_{8}}25>{{\log }_{3}}5\end{array} \right|\Rightarrow {{\log }_{8}}26>{{\log }_{3}}5\)
Как избавляться от логарифмов
Как избавляться от логарифмов, подробно описано в теме «Логарифмические неравенства».
b}\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \) или \( {\log _a}x \vee {\log _a}y{\rm{ }} \Leftrightarrow {\rm{ }}\left[ {\begin{array}{*{20}{l}}{x \vee y\;{\rm{при}}\;a > 1}\\{x \wedge y\;{\rm{при}}\;0 < a < 1}\end{array}} \right. \)
Также можем добавить правило про логарифмы с разными основаниями и одинаковым аргументом:
\( \displaystyle \begin{array}{l}a>b>1\ \ \Leftrightarrow \ \ {{\log }_{a}}x<{{\log }_{b}}x\\1>a>b>0\ \ \Leftrightarrow \ \ {{\log }_{a}}x>{{\log }_{b}}x\end{array}\)
Объяснить его можно так: чем больше основание, тем в меньшую степень его придется возвести, чтобы получить один и тот же \( x\). Если же основание меньше \( 1\), то все наоборот, так как соответствующая функция монотонно убывающая.
Пример.
Сравните числа: \( {{\log }_{3}}5\) и \( {{\log }_{8}}26\).
Решение:
Согласно вышеописанным правилам:
\( \displaystyle \left. \begin{array}{l}{{\log }_{8}}26>{{\log }_{8}}25\\{{\log }_{8}}25>{{\log }_{9}}25={{\log }_{3}}5\text{ }\end{array} \right|\Rightarrow \text{ }{{\log }_{8}}26>{{\log }_{3}}5\)
А теперь формула для продвинутых.
{2}14<2,25}}\end{array}\)
Сравнение тригонометрических выражений
Что такое синус, косинус, тангенс, котангенс? Для чего нужна единичная тригонометрическая окружность и как на ней найти значение тригонометрических функций?
Если ты не знаешь ответы на эти вопросы, очень рекомендую тебе прочитать теорию по этой теме. А если знаешь, то сравнить тригонометрические выражения между собой для тебя не составляет труда!
Немного освежим память.
Нарисуем единичную тригонометрическую окружность и вписанный в нее треугольник. Справился?
Теперь отметь, по какой стороне у нас откладывается косинус, а по какой синус, используя стороны треугольника. (ты, конечно помнишь, что синус, это отношение противолежащей стороны к гипотенузе, а косинус прилежащей?). Нарисовал? Отлично!
Последний штрих – проставь, где у нас будет \( 0{}^\circ \) , где \( 90{}^\circ \)и так далее.
\circ }}\)
Как ты теперь понимаешь, сравнение котангенсов – то же самое, только наоборот: мы смотрим, как относятся друг к другу отрезки, определяющие косинус и синус.
Повторяем и систематизируем школьный курс алгебры и начал анализа
Повторяем и систематизируем школьный курс алгебры и начал анализа
ОглавлениеПРЕДИСЛОВИЕГЛАВА I.  § 1. НАТУРАЛЬНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ § 2. СЛОЖЕНИЕ И ЗАКОНЫ СЛОЖЕНИЯ § 3. ВЫЧИТАНИЕ § 4. УМНОЖЕНИЕ И ЗАКОНЫ УМНОЖЕНИЯ § 5. ДЕЛЕНИЕ § 6. ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ § 7. ПОНЯТИЕ МНОЖЕСТВА § 8. ОПЕРАЦИИ НАД МНОЖЕСТВАМИ § 9. ВЗАИМНО ОДНОЗНАЧНОЕ СООТВЕТСТВИЕ § 10. ПРОСТЫЕ И СОСТАВНЫЕ ЧИСЛА § 11. НАИБОЛЬШИЙ ОБЩИЙ ДЕЛИТЕЛЬ § 12. НАИМЕНЬШЕЕ ОБЩЕЕ КРАТНОЕ Контрольные вопросы ГЛАВА II § 1. ОБЫКНОВЕННЫЕ ДРОБИ § 2. ПРАВИЛЬНЫЕ И НЕПРАВИЛЬНЫЕ ДРОБИ § 3. ОСНОВНОЕ СВОЙСТВО ДРОБИ § 4. СЛОЖЕНИЕ И ВЫЧИТАНИЕ ДРОБЕЙ § 5. УМНОЖЕНИЕ ДРОБЕЙ § 6. ДЕЛЕНИЕ ДРОБЕЙ § 7. ДЕСЯТИЧНЫЕ ДРОБИ § 8. ОБРАЩЕНИЕ ДЕСЯТИЧНОЙ ДРОБИ В ОБЫКНОВЕННУЮ И ОБЫКНОВЕННОЙ В ДЕСЯТИЧНУЮ. ПЕРИОДИЧЕСКИЕ ДРОБИ § 9. ОТНОШЕНИЕ. ПРОПОРЦИЯ § 10. СВОЙСТВА ПРОПОРЦИИ § 11. ПРОЦЕНТ. ОСНОВНЫЕ ЗАДАЧИ НА ПРОЦЕНТЫ § 12. ДЕЛЕНИЕ ЧИСЛА НА ЧАСТИ, ПРЯМО И ОБРАТНО ПРОПОРЦИОНАЛЬНЫЕ ДАННЫМ ЧИСЛАМ Контрольные вопросы ГЛАВА III § 1. КООРДИНАТНАЯ ПРЯМАЯ § 2.  МНОЖЕСТВО ЦЕЛЫХ ЧИСЕЛ§ 3. МНОЖЕСТВО РАЦИОНАЛЬНЫХ ЧИСЕЛ § 4. МОДУЛЬ ЧИСЛА § 5. СРАВНЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 6. СЛОЖЕНИЕ И ВЫЧИТАНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 7. УМНОЖЕНИЕ И ДЕЛЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ § 8. ВОЗВЕДЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ В СТЕПЕНЬ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА IV § 1. СВОЙСТВА СТЕПЕНИ С НАТУРАЛЬНЫМ ПОКАЗАТЕЛЕМ § 2. ЧИСЛОВЫЕ ВЫРАЖЕНИЯ § 3. ВЫРАЖЕНИЯ С ПЕРЕМЕННЫМИ § 4. ТОЖДЕСТВЕННО РАВНЫЕ ВЫРАЖЕНИЯ § 5. ОДНОЧЛЕНЫ § 6. МНОГОЧЛЕНЫ § 7. ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ МНОГОЧЛЕНОВ § 8. УМНОЖЕНИЕ МНОГОЧЛЕНА НА ОДНОЧЛЕН И МНОГОЧЛЕНА НА МНОГОЧЛЕН § 9. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ВЫНЕСЕНИЯ ОБЩЕГО МНОЖИТЕЛЯ ЗА СКОБКИ § 10. РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ § 11. ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ Контрольные вопросы ГЛАВА V § 1. ДРОБЬ § 2. ЦЕЛЫЕ И ДРОБНЫЕ ВЫРАЖЕНИЯ § 3. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ СУММЫ И РАЗНОСТИ ДВУХ ДРОБЕЙ § 4. ТОЖДЕСТВЕННОЕ ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ И ЧАСТНОГО ДВУХ ДРОБЕЙ § 5.  СТЕПЕНЬ ДРОБИКонтрольные вопросы ГЛАВА VI § 1. ПОНЯТИЕ ОБ ИРРАЦИОНАЛЬНОМ ЧИСЛЕ § 2. РАЗВИТИЕ ПОНЯТИЯ О ЧИСЛЕ. МНОЖЕСТВО ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ § 3. КОРЕНЬ СТЕПЕНИ ИЗ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА § 4. АЛГОРИТМ ИЗВЛЕЧЕНИЯ КВАДРАТНОГО КОРНЯ ИЗ ЧИСЛА § 5. АРИФМЕТИЧЕСКИЕ ДЕЙСТВИЯ С ДЕЙСТВИТЕЛЬНЫМИ ЧИСЛАМИ § 6. ПРЕОБРАЗОВАНИЯ АРИФМЕТИЧЕСКИХ КОРНЕЙ § 7. СТЕПЕНЬ С ЦЕЛЫМ И ДРОБНЫМ ПОКАЗАТЕЛЕМ Контрольные вопросы ГЛАВА VII § 1. УРАВНЕНИЯ С ОДНОЙ ПЕРЕМЕННОЙ § 2. ПОНЯТИЕ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 3. СВОЙСТВА ЧИСЛОВЫХ РАВЕНСТВ И ТЕОРЕМЫ О РАВНОСИЛЬНОСТИ УРАВНЕНИЙ § 4. ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙ, СОДЕРЖАЩЕЕ ПАРАМЕТР Контрольные вопросы ГЛАВА VIII § 1. ПОНЯТИЕ ФУНКЦИИ § 2. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ § 3. МОНОТОННОСТЬ ФУНКЦИИ § 4. ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ СПРАВОЧНЫЙ МАТЕРИАЛ § 5. ПЕРИОДИЧЕСКИЕ ФУНКЦИИ § 6. ПРОМЕЖУТКИ ЗНАКОПОСТОЯНСТВА И КОРНИ ФУНКЦИИ Контрольные вопросы ГЛАВА IX § 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ § 2.  ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК§ 3. КВАДРАТИЧНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК § 4. ФУНКЦИЯ y=k/x И ЕЕ ГРАФИК § 5. ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ И ЕЕ ГРАФИК Контрольные вопросы ГЛАВА X § 1. КВАДРАТНЫЕ УРАВНЕНИЯ § 2. ТЕОРЕМА ВИЕТА § 3. ГРАФИЧЕСКИЙ СПОСОБ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ § 4. УРАВНЕНИЕ СО МНОГИМИ ПЕРЕМЕННЫМИ § 5. СИСТЕМЫ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XI § 1. НЕРАВЕНСТВА § 2. ОСНОВНЫЕ СВОЙСТВА НЕРАВЕНСТВ § 3. ДЕЙСТВИЯ С НЕРАВЕНСТВАМИ § 4. ДОКАЗАТЕЛЬСТВА НЕРАВЕНСТВ § 5. НЕРАВЕНСТВА, СОДЕРЖАЩИЕ ПЕРЕМЕННУЮ § 6. РЕШЕНИЕ ЛИНЕЙНЫХ И КВАДРАТНЫХ НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XII § 1. СИСТЕМЫ И СОВОКУПНОСТИ НЕРАВЕНСТВ § 2. НЕРАВЕНСТВА И СИСТЕМЫ НЕРАВЕНСТВ С ДВУМЯ ПЕРЕМЕННЫМИ § 3. РЕШЕНИЕ НЕРАВЕНСТВ, СОДЕРЖАЩИХ ПЕРЕМЕННУЮ ПОД ЗНАКОМ МОДУЛЯ § 4. РЕШЕНИЕ РАЦИОНАЛЬНЫХ НЕРАВЕНСТВ МЕТОДОМ ПРОМЕЖУТКОВ Контрольные вопросы ГЛАВА XIII § 1. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ § 2. АРИФМЕТИЧЕСКАЯ ПРОГРЕССИЯ § 3.  ГЕОМЕТРИЧЕСКАЯ ПРОГРЕССИЯ§ 4. СУММА БЕСКОНЕЧНОЙ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ ПРИ |q|Контрольные вопросы ГЛАВА XIV § 1. ГРАДУСНОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 2. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВЫХ ВЕЛИЧИН § 3. СИНУС И КОСИНУС ЧИСЛОВОГО АРГУМЕНТА § 4. ТАНГЕНС И КОТАНГЕНС ЧИСЛОВОГО АРГУМЕНТА. СЕКАНС И КОСЕКАНС ЧИСЛА а § 5. ОСНОВНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ТОЖДЕСТВА § 6. ДОПОЛНИТЕЛЬНЫЕ СВОЙСТВА ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XV § 1. ФОРМУЛЫ ПРИВЕДЕНИЯ § 2. ФОРМУЛЫ СЛОЖЕНИЯ § 3. ФОРМУЛЫ ДВОЙНОГО УГЛА СПРАВОЧНЫЙ МАТЕРИАЛ § 4. ПРЕОБРАЗОВАНИЕ ПРОИЗВЕДЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ В СУММУ § 5. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ПОЛОВИННОГО АРГУМЕНТА § 7. ВЫРАЖЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ ЧЕРЕЗ ТАНГЕНС ПОЛОВИННОГО АРГУМЕНТА Контрольные вопросы ГЛАВА XVI § 1. СВОЙСТВА ФУНКЦИИ y = sin(x) И ЕЕ ГРАФИК § 2. СВОЙСТВА ФУНКЦИ И у = cos(x) И ЕЕ ГРАФИК § 3.  СВОЙСТВА ФУНКЦИ И у=tg(x) И ЕЕ ГРАФИК§ 4. СВОЙСТВА ФУНКЦИ И y=ctg(x) И ЕЕ ГРАФИК § 5. НАХОЖДЕНИЕ ПЕРИОДОВ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XVII § 1. АРКСИНУС И АРККОСИНУС § 2. АРКТАНГЕНС И АРККОТАНГЕНС Контрольные вопросы ГЛАВА XVIII § 1. РЕШЕНИЕ УРАВНЕНИЙ ВИДА cos(x)=а § 2. РЕШЕНИЕ УРАВНЕНИЙ ВИДА sin(x)=a § 3. РЕШЕНИЕ УРАВНЕНИЙ ВИДА tg(х)=а § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ, ПРИВОДИМЫХ К КВАДРАТНОМУ § 5. РЕШЕНИЕ ОДНОРОДНЫХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ § 6. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ, РЕШАЕМЫЕ С ПОМОЩЬЮ ФОРМУЛ СЛОЖЕНИЯ, ПОНИЖЕНИЯ СТЕПЕНИ § 7. РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ Контрольные вопросы ГЛАВА XIX § 1. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА sin(х) > а, sin(х) § 2. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА cos(x) > a, cos(x) § 3. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ВИДА tg(х) > a, tg(х) § 4. РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ НЕРАВЕНСТВ ГЛАВА XX § 1. ПРИРАЩЕНИЕ АРГУМЕНТА И ПРИРАЩЕНИЕ ФУНКЦИИ § 2.  ПРЕДЕЛ ФУНКЦИИ§ 3. НЕПРЕРЫВНОСТЬ ФУНКЦИИ § 4. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ § 5. ПРОИЗВОДНАЯ СУММЫ, ПРОИЗВЕДЕНИЯ, ЧАСТНОГО § 6. ПРОИЗВОДНАЯ СТЕПЕННОЙ И СЛОЖНОЙ ФУНКЦИИ § 7. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ Контрольные вопросы ГЛАВА XXI § 1. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ПРОМЕЖУТКОВ МОНОТОННОСТИ ФУНКЦИИ § 2. КРИТИЧЕСКИЕ ТОЧКИ ФУНКЦИИ, ЕЕ МАКСИМУМЫ И МИНИМУМЫ § 3. ОБЩАЯ СХЕМА ИССЛЕДОВАНИЯ ФУНКЦИИ § 4. ЗАДАЧИ НА НАХОЖДЕНИЕ НАИМЕНЬШЕГО И НАИБОЛЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ Контрольные вопросы ГЛАВА XXII § 1. ФОРМУЛЫ ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ СПРАВОЧНЫЙ МАТЕРИАЛ § 2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ § 3. СКОРОСТЬ И УСКОРЕНИЕ В ДАННЫЙ МОМЕНТ ВРЕМЕНИ § 4. ГРАФИКИ ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ Контрольные вопросы ГЛАВА XXIII § 1. ПОТЕРЯННЫЕ И ПОСТОРОННИЕ КОРНИ ПРИ РЕШЕНИИ УРАВНЕНИЙ (НА ПРИМЕРАХ) § 2. ПОСТОРОННИЕ КОРНИ ИРРАЦИОНАЛЬНОГО УРАВНЕНИЯ (НА ПРИМЕРАХ) § 3. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ УРАВНЕНИЙ § 4. РЕШЕНИЕ ИРРАЦИОНАЛЬНЫХ НЕРАВЕНСТВ СПРАВОЧНЫЙ МАТЕРИАЛ Контрольные вопросы ГЛАВА XXIV § 1.  ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК§ 2. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ § 3. ПОКАЗАТЕЛЬНЫЕ НЕРАВЕНСТВА § 4. СИСТЕМЫ ПОКАЗАТЕЛЬНЫХ УРАВНЕНИЙ И НЕРАВЕНСТВ Контрольные вопросы ГЛАВА XXV § 1. ОБРАТНАЯ ФУНКЦИЯ § 2. ПОНЯТИЕ ЛОГАРИФМА § 3. СВОЙСТВА ЛОГАРИФМОВ § 4. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ, ЕЕ СВОЙСТВА И ГРАФИК § 5. ТЕОРЕМЫ О ЛОГАРИФМЕ ПРОИЗВЕДЕНИЯ, ЧАСТНОГО И СТЕПЕНИ. ФОРМУЛА ПЕРЕХОДА К НОВОМУ ОСНОВАНИЮ § 6. ДЕСЯТИЧНЫЕ ЛОГАРИФМЫ И ИХ СВОЙСТВА § 7. ЛОГАРИФМИРОВАНИЕ И ПОТЕНЦИРОВАНИЕ Контрольные вопросы ГЛАВА XXVI § 1. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ § 2. ЛОГАРИФМИЧЕСКИЕ НЕРАВЕНСТВА § 3. СИСТЕМЫ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ § 4. ПРОИЗВОДНЫЕ ЛОГАРИФМИЧЕСКОЙ И ПОКАЗАТЕЛЬНОЙ ФУНКЦИЙ. ЧИСЛО e Контрольные вопросы ГЛАВА XXVII § 1. ПОНЯТИЕ ПЕРВООБРАЗНОЙ ФУНКЦИИ § 2. ОСНОВНОЕ СВОЙСТВО ПЕРВООБРАЗНОЙ ФУНКЦИИ § 3. ТРИ ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ § 4. КРИВОЛИНЕЙНАЯ ТРАПЕЦИЯ И ЕЕ ПЛОЩАДЬ Контрольные вопросы ГЛАВА XXVIII § 1.  ФОРМУЛА НЬЮТОНА—ЛЕЙБНИЦА§ 2. ОСНОВНЫЕ ПРАВИЛА ИНТЕГРИРОВАНИЯ § 3. ВЫЧИСЛЕНИЕ ПЛОЩАДЕЙ С ПОМОЩЬЮ ИНТЕГРАЛА § 4. МЕХАНИЧЕСКИЕ И ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА ПРИЛОЖЕНИЕ Введение 1. Задачи на движение 2. Задачи на совместную работу 3. Задачи на планирование 4. Задачи на зависимость между компонентами арифметических действий 5. Задачи на проценты 6. Задачи на смеси (сплавы) 7. Задачи на разбавление |
Как извлекать квадратные корни
Объяснение:
Самый сложный элемент этой задачи — уметь правильно упростить каждый из квадратных корней. Это означает, что мы начнем с нашего первого участника . Существует несколько различных методов упрощения квадратных корней, каждый из которых имеет свои преимущества. Кроме того, некоторые калькуляторы, разрешенные в ACT, могут сделать это за вас (возможно, стоит изучить).
Но для тех из нас, кому не так повезло, вот один конкретный метод, в котором используется то, что называется деревом факторов.
Начните с написания числа внутри квадратного корня, в нашем случае 45. И найдите два множителя (числа, которые при умножении равны) 45 кроме 1 и самого числа. В нашем случае есть две возможности: 9 и 5 или 3 и 15. Оба будут работать, но мы выберем последнюю пару. Посмотрите на каждый из двух факторов, чтобы увидеть, можно ли повторить тот же процесс. Глядя на число 3, мы понимаем, что оно простое, а это означает, что дополнительных множителей не существует. Поэтому оставляем 3 как есть. Однако число 15 можно далее разбить на факторы 5 и 3, что мы можем проиллюстрировать, как показано на рисунке. Затем мы пытаемся повторить процесс со следующим уровнем чисел, но вскоре понимаем, что и 5, и 3 — простые числа. Следовательно, мы не можем идти дальше, и наше дерево факторов готово.
Но что нам теперь делать? Ищем пары. Для каждой пары чисел, находящихся под радикалом, мы помещаем одно число вне квадратного корня.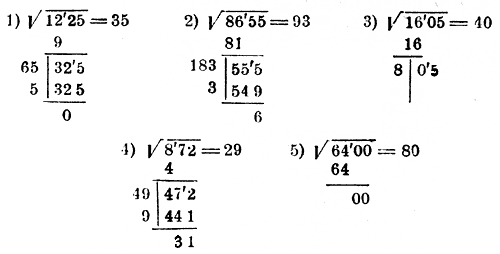
Это означает, что одна 3 выходит за пределы квадратного корня. Для каждого под радикалом без пары мы помещаем это число в квадратный корень, что означает, что одна 5 входит в квадратный корень. Это дает окончательный ответ .
Затем мы повторяем процесс со вторым участником, . Факторное дерево для 180 может иметь несколько разных путей, но любой правильный (включая приведенный ниже пример) должен заканчиваться одними и теми же числами под радикалом. Хотя, возможно, не в том же порядке, числа под корнем должны включать две двойки, две тройки и одну пятерку. Мы видим, что пара двоек и пара троек должны дать нам одну двойку и одну тройку на внешней стороне корешка. квадратный корень, а безпарная 5 должна быть внутри. Каждый раз, когда несколько чисел оказываются либо внутри, либо снаружи, мы просто умножаем эти числа.
Следовательно, получаем .
Затем мы завершаем процесс еще раз с нашим последним участником, 125.
Это неизменно дает следующее дерево факторов.
Проблема в данном случае в том, что у нас не пара, а три пятерки. В этом случае мы просто соединяем две из них, оставляя одну из пяти нечетных.
Наш окончательный ответ для этого участника: .
Подстановка наших упрощенных квадратных корней вместо оригиналов дает нам новое выражение
. Отсюда лучше всего думать о яблоке. В первом семестре у меня 3 «яблока». Затем я вычитаю или убираю 6 «яблок». Наконец, я добавляю обратно 5 «яблок». Сколько у меня яблок?
. У меня есть 2 яблока, или другими словами .
Видео-урок: Прибавление и вычитание квадратных корней
Стенограмма видео
В этом видео мы рассмотрим
некоторые выражения, которые добавляют или вычитают радикальные или поверхностные термины. Мы будем рассматривать выражения
где эти термины могут быть собраны как похожие термины, так что выражения могут быть
упрощенный.
Радикальный или сурд, термины, которые не
упростить можно комбинировать или собирать в алгебраические выражения почти таким же образом
что вы будете собирать переменные термины, такие как три 𝑥 и пять 𝑥 или два 𝑦 и семь
𝑦 и так далее.
Глядя на этот пример, упростите квадратный корень из семи плюс квадратный корень из семи.
А теперь представим, что мы позволили 𝑥 равный корень семь. Тогда мы могли бы выразить корень семь плюс корень семь по-другому. Это будет 𝑥 плюс 𝑥. Теперь, если бы вы увидели 𝑥 плюс 𝑥, вы бы вполне счастливо собрать те, как термины. Вы бы добавили один 𝑥 к другому 𝑥 и у вас будет два 𝑥s. И так как мы только что сказали здесь, что 𝑥 было равно квадратному корню из семи, два 𝑥 означает удвоенный квадратный корень из семь, которую мы пишем так, два корня семь.
Теперь важно помнить
что большая двойка перед этим означает, что это в два раза больше квадратного корня из
Семь.
И вы должны быть осторожны, чтобы не
спутать это с этим выражением, которое представляет собой маленькую двойку в этом знаке квадратного корня,
что означает квадратный корень из семи.
Вот еще пример.
Упростите кубический корень из трех плюс два раза кубический корень из трех плюс три раза кубический корень из трех.
И первый член, просто куб корень из трех, значит, у нас есть один из них. Таким образом, мы могли бы сказать, что это один раз кубический корень из трех. Итак, у нас есть один из кубических корней из троек. У нас есть еще два кубических корня из троек. И затем, у нас есть еще три на кроме того, эти кубический корень из троек. Итак, в сумме один плюс два равно три плюс три будет шесть. У нас их шесть, шесть раз кубический корень из трех. Итак, это наш ответ.
Теперь нам нужно упростить
квадратный корень из восьми плюс три раза квадратный корень из двух минус четыре раза
квадратный корень из двух.
Вот эти вторые два термина явно похожи на термины. У нас есть три участка площади корень из двух, а затем мы отнимаем четыре лота от квадратного корня из двух. Итак, если у нас есть три из них, и мы убери четыре, у нас останется отрицательный один из них, или мы просто запишем отрицательный корень два. Итак, это становится корнем восемь минус корень два. Но подождите, восемь имеет квадрат фактор. Четыре — это квадратное число, и это множитель восемь, поэтому корень восемь можно записать как квадратный корень из четырех раз два. И это можно записать как квадратный корень из четырех, умноженный на квадратный корень из двух.
Квадратный корень из четырех равен
два. Итак, квадратный корень из четырех раз
квадратный корень из двух равен удвоенному корню из двух, или, как мы обычно пишем, всего два
корень два.
Итак, корень восемь минус корень два может
можно переписать как два корня два минус один корень два. И два корня два минус один корень два
всего один корень два. Хотя, очевидно, мы бы не
потрудитесь написать единицу перед ним, так что это просто квадратный корень из двух.
Теперь у нас есть немного больше сложное выражение с корнем 11, а также просто некоторые нормальные числа, не с участием радикалов или сурдов. Таким образом, шесть и минус три являются нормальные номера. И четыре корня 11 и два корня 11 похожи на термины, потому что оба они содержат квадратный корень из 11. Они радикальные или поверхностные. Итак, мы собрали похожие термины и теперь мы можем объединить их. Шесть убери, три будет три. И четыре корневых 11 плюс еще два root 11s дает мне шесть root 11s. Итак, это наш ответ.
Итак, вот еще один пример, этот
время со скобками.
Упростить два плюс шесть корень пять плюс девять плюс восемь корень пять.
Здесь скобки не действительно есть эффект. Они говорят вам сделать расчеты в определенном порядке, а операции все сложения. А из-за ассоциативности Кроме того, не будет никакой разницы, если вы сделаете их в другом порядке. Итак, мы просто удалим скобки пока, а потом будем собирать подобные термины. Ну, два и девять являются рациональными числа, а шесть корней пять и восемь корней пять являются радикальными или поверхностными терминами.
Итак, лайк собрали условия, мы можем их комбинировать. А два и девять дают 11. А потом шесть корней пятерок плюс еще восемь корневых пятерок дают нам 14 корневых пятерок. Так это упрощенная версия нашего исходного выражения.
Итак, давайте посмотрим на наш последний пример затем.
Упростить корень семь минус два минус
пять минус три корень семь.
Здесь скобки важный. Первый сет на самом деле не имеет эффект, потому что установить корень семь минус два эффективно уже оценено, так что вы не может упростить это дальше. Но второй набор скобок очень важны. Итак, мы можем удалить первый набор круглые скобки. Но этот отрицательный знак, мы убираем пять, и мы убираем минус три из корня семь. Итак, это выглядит так. Теперь, если мы убираем негатив три корня семь, это то же самое, что добавить три корня семь.
Итак, сейчас мы находимся в ситуации, когда
мы можем определить подобные термины. Итак, это те, у кого
радикалы, коренные семерки или сурды. А это как раз нормальные
рациональное число. Итак, у нас есть один корень семь плюс
еще три корневых семерки дают нам четыре корневых семерки. И у нас есть два отрицательных дубля
прочь еще пять, что составляет минус семь.