Решить системы линейных уравнений методом гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Решение систем линейных уравнений методом Гаусса

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Решение систем линейных уравнений методом Гаусса

2. Метод Гаусса – это метод последовательного исключения переменных

• Систему уравнений приводят к
эквивалентной ей системе с
треугольной матрицей. Это называется
прямым ходом.
• Из полученной треугольной системы
переменные находят с помощью
последовательных подстановок. Это
называется обратным ходом.

3. При выполнении прямого хода используют следующие преобразования:

1. Умножение или деление коэффициентов
свободных членов на одно и то же число;
2. Сложение и вычитание уравнений;
3. Перестановка уравнений системы;
4. Исключение из системы уравнений, в
которых все коэффициенты при
неизвестных и свободные члены равны
нулю.

4. Решить систему уравнений методом Гаусса

x y 5
2 x y 7
Нужно записать расширенную матрицу системы
1 1 5
2 1 7
Вертикальная черта внутри матрицы не несёт
никакого математического смысла – это
просто отчеркивание для удобства
оформления.
Матрица системы – это матрица,
составленная только из
коэффициентов при неизвестных.
Расширенная матрица системы – это
та же матрица системы плюс
столбец свободных членов, в
данном случае.

6. Решение. Умножим первую строку на (-2)

1 1 5
2 1 7
2 2 10
2 1 7

7.

ко второй строке прибавим первую строку умноженную на -21 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7

8. Разделим опять первую строку на (-2)

1 1 5
2 1 7
2 2 10
0 3 3
2 2 10
2 1 7
1 1 5
0 3 3
строка, которую ПРИБАВЛЯЛИ – не изменилась.
Всегда меняется строка, К КОТОРОЙ ПРИБАВЛЯЮТ.

9. Цель элементарных преобразований –

Цель элементарных преобразований
–
привести матрицу к ступенчатому виду.
Сам термин «ступенчатый вид» не
вполне теоретический, в научной и
учебной литературе он часто
называется трапециевидный
вид или треугольный

10. В результате элементарных преобразований получена эквивалентная исходной система уравнений

В результате элементарных преобразований
получена эквивалентная исходной система уравнений
x y 5
2 x y 7
x y 5
y 1
Выполняем обратный ход, т.е. подстановку в первое
уравнение вместо у,
х =-5+у
х=-5+1
х=-4
Ответ: (-4; 1)

11.

Решить систему уравнений методом Гаусса3 x 2 y z 4
2 x y 3z 9
x 2 y 2z 3
Решение.
Переставим третье уравнение на место первого и запишем расширенную
матрицу:
x 2 y 2z 3
3 x 2 y z 4
2 x y 3z 9
1 2 2 3
3 2 1 4
2 1 3 9

12. Чтобы в первом столбце получить а2=а3=0, умножим 1-ю строку сначала на 3, а затем на 2 и вычтем результаты из 2-й и 3-й строк

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 8 7 5
0 3 1 3

13. Разделим 2-ю строку на 8, полученные результаты умножим на 3 и вычтем из 3-й строки

1 2 2 3
3 2 1 4
2 1 3 9
1 2 2 3
0 1 7 5
8 8
0 3 1 3
1 2 2 3
0 8 7 5
0 3 1 3
1 2 2 3
0 3 21 15
8
8
0 3 1 3
1 2 2
3
21
15
0
3
8
8
39
0 0 13
8
8

14. Запишем новую эквивалентную систему с учетом расширенной матрицы

x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
x 2 y 2z 3
7
5
y z
8
8
13
39
z
8
8
Выполняем обратный ход, с помощью
последовательных подстановок находим
неизвестные
13
39
z
z 3
8
8
7
5
5 21 16
y 3
y
2
8
8
8 8
8
x 2 2 2 3 3 x 3 4 6 1
Ответ: (1; 2; 3)

English     Русский Правила

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)



Образовательные онлайн сервисы: теория и практика

• Главная
• Примеры
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
• Видео-уроки
  • Математический анализ
  • Векторная алгебра и Аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование.
    Методы оптимизации
• Готовые работы
  • Математический анализ
  • Векторная алгебра и аналитическая геометрия
  • Линейная алгебра
  • Теория вероятностей и математическая статистика
  • Математическое программирование
    Методы оптимизации
  • Математика в экономике
    Экономическая статистика
  • Другое
• Контакты

Полезные материалы:

• Учебники
• Справочники
• Онлайн калькуляторы

• Помощь в решении
• Онлайн занятия в Zoom

Решение системы линейных уравнений методом Жордана-Гаусса (метод прямоугольников)

Видеоурок: Метод Жордана-Гаусса (метод прямоугольников)

Пример из видеоурока в рукописном виде:

Пример 2.

Запишем систему в виде:

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
-2	4	-4	-2	-2	1	1
-1	1	0	-1	1	1	-2

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника: НЭ = СЭ — (А*В)/РЭ, где РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

1	-2	2	-1	-1	2	4
0	-1	1	3	-1	2	-2
0	0	0	-4	-4	5	9
0	-1	2	-2	0	3	2

Разрешающий элемент равен (-1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	-1	-3	1	-2	2
0	0	0	-4	-4	5	9
0	0	1	-5	1	1	4

 

Разрешающий элемент равен (1). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	-7	1	-2	8
0	1	0	-8	2	-1	6
0	0	1	-5	1	1	4
0	0	0	-4	-4	5	9

Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

1	0	0	0	8	-10.75	-7.75
0	1	0	0	10	-11	-12
0	0	1	0	6	-5. 25	-7.25
0	0	0	1	1	-1.25	-2.25

Теперь исходную систему можно записать как:
x1 = -7.75 — 8×5 — 10.75×6
x2 = -12 — 10×5 — 11×6
x3 = -7.25 — 6×5 — 5.25×6
x4 = -2.25 — x5 — 1.25×6
Необходимо переменные x5,x6 принять в качестве свободных переменных и через них выразить остальные переменные.
Приравняем переменные x5,x6 к 0
x1 = -7.75
x2 = -12
x3 = -7.25
x4 = -2.25
Среди базисных переменных есть отрицательные значения. Следовательно, данное решение не опорное.



Задать вопрос
Заказать помощь

Отзывы

+7-911-7987704

vk. com/id286009794

Написать в Whatsapp

Написать в Viber

@matem96

Skype: matem96.ru



Общее решение системы линейных уравнений методом исключения Гаусса

  Исследование  Математика

Этот онлайн-калькулятор решает систему линейных алгебраических уравнений методом исключения Гаусса. Он дает результат независимо от того, есть ли у вас уникальное решение, бесконечное количество решений или нет решения. Он также выводит результат в формате с плавающей запятой и дроби.

На сайте уже есть один калькулятор, решающий СЛАУ (систему линейных алгебраических уравнений) методом исключения Гаусса-Жордана (также известного как исключение Гаусса) — исключения Гаусса. Он даже показывает решение шаг за шагом.

Однако у него есть некоторые недостатки, которые решит новый калькулятор из этой статьи:

• предыдущий калькулятор дает решение в формате с плавающей запятой, тогда как во многих задачниках ответ обычно дается в виде дроби.
• предыдущий калькулятор только определяет факт наличия бесконечного числа решений, но не дает общего решения.
• предыдущий калькулятор работает только в том случае, когда количество уравнений равно количеству неизвестных, и поэтому не может решать недоопределенные (количество неизвестных больше количества уравнений) и переопределенные системы (количество неизвестных равно меньше, чем количество уравнений).

Что касается второго и третьего пунктов, то универсальность метода исключения Гаусса–Жордана делает его пригодным для систем линейных уравнений с любым количеством уравнений и неизвестных.

Описание самого метода исключения Гаусса можно посмотреть по ссылке выше, а под калькулятором мы смотрим разные системы линейных уравнений: с одним решением, с бесконечным числом решений, без решения и с недоопределенными и сверхдетерминированные системы.

Калькулятор находит единственное решение, если оно существует, или общее решение, если существует бесконечное число решений. Приведенные ниже данные по умолчанию являются примером системы с бесконечным числом решений:

Метод Гаусса для системы линейных уравнений с любым количеством переменных.

1 2 -3 5 1 1 3 -13 22 -1 3 5 1 -2 5 2 3 4 -7 4

Матрица уравнений

Количество решений

 

Коэффициенты решения

 

Файл очень большой. Во время загрузки и создания может происходить замедление работы браузера.

1. Система линейных уравнений, имеющая единственное решение

Пример: система линейных уравнений:

После приведения матрицы к трапецеидальному виду методом Гаусса получаем:

С помощью обратной подстановки находим единственное решение:

Система непротиворечива и определена.

2. Система линейных уравнений, имеющая бесконечное число решений

Пример: система линейных уравнений:

После приведения матрицы к трапецеидальному виду методом Гаусса получаем:

В итоге получаем систему:

Последние два уравнения верны для любых значений переменных:

поэтому их можно отбросить.

Чтобы найти решения оставшихся двух уравнений, x1 и x2 должны быть выражены через x3 и x4.

При этом сами x3 и x4 могут принимать любые значения

Полученная система недоопределена. Формулы:

для произвольных x3 и x4 описывают бесконечное множество решений этой системы.

3. Система линейных уравнений, не имеющая решений

Пример: система линейных уравнений:

После приведения матрицы к трапецеидальному виду методом Гаусса получаем:

Полученная система несовместна, так как последнее уравнение:

не может удовлетворяться никакими значениями неизвестных.

Эта система несовместна, то есть не имеет решения.

4. Переопределенная система линейных уравнений (количество неизвестных меньше числа уравнений)

Пример: система линейных уравнений:

Приведя матрицу к трапецеидальному виду методом Гаусса, получим

Как видите, в этом случае «лишнее» уравнение можно просто отбросить и задача сводится к случаям 1 или 2.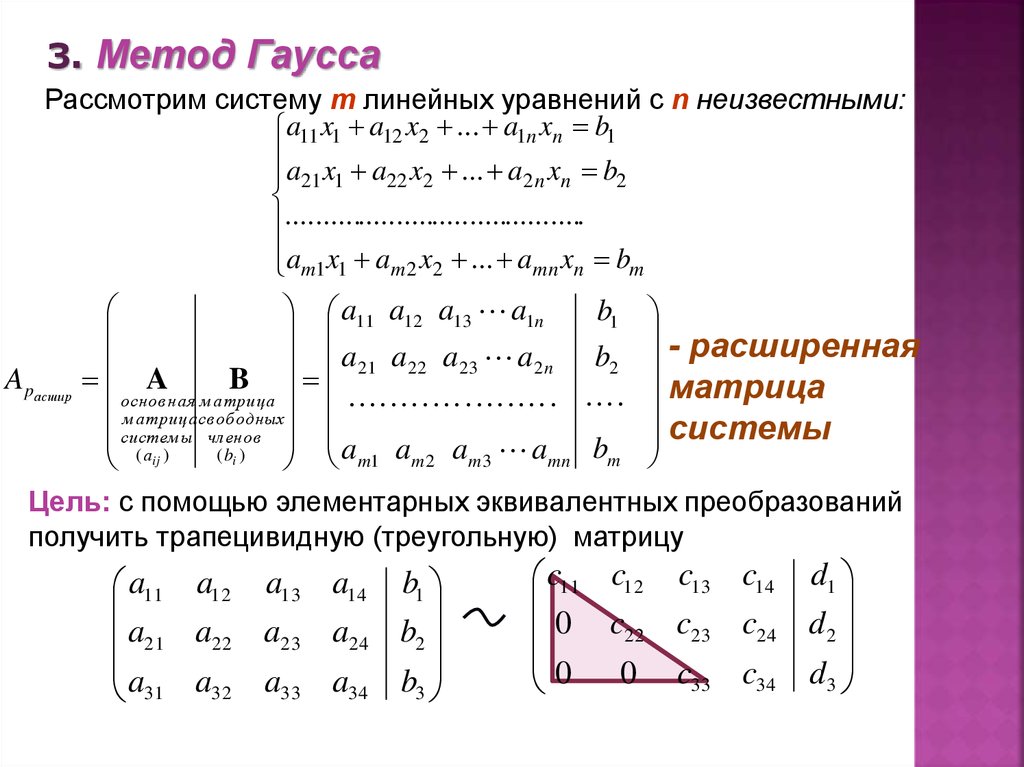 Также в результате преобразований можно получить те же уравнения, «лишнее» из которых тоже можно отбросить — и опять задача сводится к случаям 1 или 2.

5. Недоопределенная система линейных уравнений (количество неизвестных больше числа уравнений)

Пример: система линейных уравнений:

Приведя матрицу к трапецеидальному виду методом Гаусса, получим :

Полученная эквивалентная система имеет вид:

Как видите, в ней нет уравнений, дающих однозначные значения для х3 и х4, что эквивалентно уравнениям:

, которые можно отбросить .

Таким образом, этот случай сводится к случаю 2 с бесконечным множеством решений, которые описываются следующими формулами:

URL скопирован в буфер обмена

Аналогичные калькуляторы

• • Исключение Гаусса с дробями
• • Решение неоднородная система линейных уравнений с использованием обратной матрицы
• • Исключение Гаусса
• • Правило Крамера
• • Балансировщик химических уравнений
• • Математический раздел (304 калькулятора)

 дроби Гаусс Система линейных уравнений Метод Гаусса Математическая система линейных уравнений недоопределенная система

  003  Тимур  2022-10-06 12:28:47

Дифференциальные уравнения — Обзор: Системы уравнений

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / Системы ЦЭ / Обзор : Системы уравнений

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Уведомление для мобильных устройств

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы наверное на мобильном телефоне). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5.1: Обзор: Системы уравнений

Поскольку мы будем работать почти исключительно с системами уравнений, в которых количество неизвестных равно количеству уравнений, мы ограничим наш обзор системами такого типа.

Все, что мы будем здесь делать, можно легко распространить на системы с большим количеством неизвестных, чем уравнений, или с большим количеством уравнений, чем неизвестных, если это необходимо.

Начнем со следующей системы \(n\) уравнений с \(n\) неизвестными, \(x_{1}\), \(x_{2}\),…, \(x_{n} \).

\[\begin{equation}\begin{aligned}{a_{11}}{x_1} + {a_{12}}{x_2} + \cdots + {a_{1n}}{x_n} & = {b_1}\ \ {a_{21}}{x_1} + {a_{22}}{x_2} + \cdots + {a_{2n}}{x_n} & = {b_2}\\ \vdots \hspace{0,8in} & \ \ {a_{n1}}{x_1} + {a_{n2}}{x_2} + \cdots + {a_{nn}}{x_n} & = {b_n}\end{выровнено}\label{eq:eq1} \конец{уравнение}\]

Обратите внимание, что в нижних индексах коэффициентов в этой системе \(a_{ij}\) \(i\) соответствует уравнению, в котором находится коэффициент, а \(j\) соответствует неизвестному, что умножается на коэффициент.

Чтобы использовать линейную алгебру для решения этой системы, мы сначала запишем расширенную матрицу для этой системы. Расширенная матрица — это просто все коэффициенты системы и числа для правой части системы, записанные в матричной форме. Вот расширенная матрица для этой системы.

\[\left( {\begin{array}{*{20}{r}}{{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1n}}}& {{b_1}}\\{{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2n}}}&{{b_2}}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\{{a_{n1}}}&{{a_{n2}}}& \cdots &{{a_{nn}}}&{{b_n}}\end{массив} } \верно)\]

Чтобы решить эту систему, мы будем использовать элементарные операции со строками (которые мы определим чуть позже), чтобы переписать расширенную матрицу в треугольной форме. Матрица будет иметь треугольную форму, если все элементы ниже главной диагонали (диагональ, содержащая \(a_{11}\), \(a_{22}\), …, \(a_{nn}\)) равны нулю .

После этого мы можем вспомнить, что каждая строка в расширенной матрице соответствует уравнению. Затем мы преобразуем нашу новую расширенную матрицу обратно в уравнения, и на этом этапе решение системы станет очень простым.

Прежде чем работать с примером, давайте сначала определим элементарные операции со строками. Их три.

1. Поменяйте местами два ряда. Это именно то, что он говорит. Мы поменяем местами строку \(i\) на строку \(j\). Обозначение, которое мы будем использовать для обозначения этой операции: \({R_i} \leftrightarrow {R_j}\)
2. Умножить строку \(i\) на константу \(c\). Это означает, что каждая запись в строке \(i\) будет умножена на константу \(c\). Обозначение этой операции: \(c{R_i}\)
3. Добавить число, кратное строке \(i\), к строке j. В уме мы умножим строку \(i\) на соответствующую константу, а затем добавим результат к строке \(j\) и поместим новую строку обратно в строку \(j\), оставив строку \(i\) в матрица без изменений. Обозначение этой операции: \(c{R_i} + {R_j}\)

Всегда немного легче понять эти операции, если мы увидим их в действии. Итак, давайте решим пару систем.

Пример 1. Решите следующую систему уравнений. \[\begin{align*} — 2{x_1} + {x_2} — {x_3} & = 4\\ {x_1} + 2{x_2} + 3{x_3} & = 13\\ 3{x_1} + { x_3} & = — 1\конец{выравнивание*}\]

Показать решение

Первый шаг — записать расширенную матрицу для этой системы. Не забывайте, что коэффициенты отсутствующих членов равны нулю.

\[\require{color} \left( {\begin{array}{*{20}{r}}{\color{Red} — 2}&1&{- 1}&4\\1&{\color{Red} 2 }&3&{13}\\3&0&{\color{Red} 1}&{ — 1}\end{массив}} \right)\]

Теперь мы хотим, чтобы записи ниже главной диагонали были равны нулю. Главная диагональ окрашена в красный цвет, чтобы мы могли следить за ней в этом первом примере. По причинам, которые со временем станут очевидными, мы бы предпочли, чтобы все элементы главной диагонали также были единицами.

Мы можем получить единицу в самом верхнем месте, заметив, что если мы поменяем местами первый и второй ряд, мы получим единицу в самом верхнем месте бесплатно. Итак, давайте сделаем это.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} — 2}&1&{- 1}&4\\1&{\color{Red} 2 }&3&{13}\\3&0&{\color{Red} 1}&{ — 1}\end{array}} \right)\begin{array}{*{20}{c}}{{R_1} \leftrightarrow {R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\{ — 2}& {\color{Red} 1}&{ — 1}&4\\3&0&{\color{Red} 1}&{- 1}\end{array}} \right)\]

Теперь нам нужно, чтобы две последние записи (-2 и 3) в первом столбце были равны нулю. Мы можем сделать это, используя операцию третьей строки. Обратите внимание, что если мы возьмем первую строку в 2 раза и добавим ее во вторую строку, мы получим ноль во второй записи в первом столбце, а если мы возьмем -3 раза первую строку в третью строку, мы получим 3 в быть нулем. Мы можем выполнить обе эти операции одновременно, так что давайте сделаем это.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\{ — 2}&{\color{Red} 1}&{ — 1}&4\\3&0&{\color{Red} 1}&{ — 1}\end{array}} \right)\begin{array}{*{20}{c}}{2{ R_1} + {R_2}}\\{ — 3{R_1} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color {Красный} 1}&2&3&{13}\\0&{\color{Красный} 5}&5&{30}\\0&{ — 6}&{\color{Красный} — 8}&{ — 40}\end{массив }} \верно)\]

Прежде чем перейти к следующему шагу, убедитесь, что вы выполнили то, что мы только что сделали. Давайте посмотрим на первую операцию, которую мы выполнили. Эта операция требует умножить запись в строке 1 на 2 и добавить ее к соответствующей записи в строке 2, а затем заменить старую запись в строке 2 этой новой записью. Ниже приведены четыре отдельные операции, которые мы выполнили для этого.

\[\begin{align*}2\left( 1 \right) + \left( { — 2} \right) & = 0\\ 2\left( 2 \right) + 1 & = 5\\ 2\left ( 3 \right) + \left( { — 1} \right) & = 5\\ 2\left( {13} \right) + 4 & = 30\end{align*}\]

Ладно, следующий шаг необязателен, но опять же его удобно делать. Технически 5 во втором столбце можно оставить. Тем не менее, это облегчит нашу жизнь в будущем, если это будет 1. Мы можем использовать операцию второй строки, чтобы позаботиться об этом. Мы можем разделить всю строку на 5. Это даст

. \[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 5}&5&{ 30}\\0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\begin{array}{*{20}{c}}{\frac {1}{5}{R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\ \0&{\color{Red} 1}&1&6\\0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\]

Следующим шагом будет использование операции с третьей строкой, чтобы преобразовать -6 во втором столбце в ноль.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&{ — 6}&{\color{Red} — 8}&{ — 40}\end{array}} \right)\begin{array}{*{20}{c}}{6{R_2} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{ Красный} 1}&1&6\\0&0&{\color{Красный} — 2}&{ — 4}\end{массив}} \right)\]

Итак, официально мы закончили, но опять же, удобно разместить все единицы на главной диагонали, поэтому мы сделаем последний шаг.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&0&{\color{Red} — 2}&{ — 4}\end{array}} \right)\begin{array}{*{20}{c}}{ — \frac{1}{2}{ R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red } 1}&1&6\\0&0&{\color{Red} 1}&2\end{массив}} \right)\]

Теперь мы можем вернуться к уравнениям.

\[\require{color}\left( {\begin{array}{*{20}{r}}{\color{Red} 1}&2&3&{13}\\0&{\color{Red} 1}&1&6\ \0&0&{\color{Red} 1}&2\end{массив}} \right)\hspace{0,25in} \Rightarrow \hspace{0,25in}\begin{aligned}{x_1} + 2{x_2} + 3{ x_3} &= 13\\{x_2} + {x_3} &= 6\\{x_3} &= 2\end{выровнено}\]

На данный момент решить довольно просто. Мы получаем \(x_{3}\) бесплатно, и как только мы получаем это, мы можем подставить это во второе уравнение и получить \(x_{2}\). Затем мы можем использовать первое уравнение, чтобы получить \(x_{1}\). Обратите также внимание, что наличие единиц вдоль главной диагонали несколько помогло в этом процессе.

Решение этой системы уравнений:

\[{x_1} = — 1\hspace{0,25 дюйма}\hspace{0,25 дюйма}{x_2} = 4\hspace{0,25 дюйма}\hspace{0,25 дюйма}{x_3} = 2\]

Процесс, используемый в этом примере, называется Исключение Гаусса . Давайте посмотрим на другой пример.

Пример 2. Решите следующую систему уравнений. \[\begin{align*}{x_1} — 2{x_2} + 3{x_3} & = — 2\\ — {x_1} + {x_2} — 2{x_3} & = 3\\ 2{x_1} — {x_2} + 3{x_3} & = 1\конец{выравнивание*}\]

Показать решение

Сначала запишите расширенную матрицу.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3&1 \конец{массив}} \справа)\]

Мы не будем вводить столько слов при работе с этим примером. Вот работа для этой расширенной матрицы.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3&1 \end{array}} \right)\begin{array}{*{20}{c}}{{R_1} + {R_2}}\\{ — 2{R_1} + {R_3}}\\ \to \ конец {массив} \ left( {\ begin {массив} {* {20} {r}} 1 & { — 2} & 3 & { — 2} \\ 0 & { — 1} & 1 & 1 \\ 0 & 3 & { — 3} & 5 \ конец {массив}} \справа)\] \[\begin{array}{*{20}{r}}{ — {R_2}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}1& { — 2}&3&{ — 2}\\0&1&{ — 1}&{ — 1}\\0&3&{ — 3}&5\end{массив}} \right)\begin{массив}{*{20}{c }}{ — 3{R_2} + {R_3}}\\ \to \end{array}\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2} \\0&1&{ — 1}&{ — 1}\\0&0&0&8\end{массив}} \right)\]

В этом примере мы не будем идти дальше. Вернемся к уравнениям, чтобы понять, почему.

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&8\end{массив} } \right) \Rightarrow \begin{align}{x_1} — 2{x_2} + 3{x_3} & = — 2\\{x_2} — {x_3} & = — 1\\0 & = 8\end{ выровнено}\]

Последнее уравнение должно вызвать некоторое беспокойство. Тут один из трех вариантов. Во-первых, нам каким-то образом удалось доказать, что 0 равно 8, и мы знаем, что это невозможно. Во-вторых, мы допустили ошибку, но, проанализировав нашу работу, не видно, что мы допустили ошибку.

Остается третий вариант. Когда мы получаем что-то вроде третьего уравнения, которое просто не имеет смысла, мы сразу понимаем, что решения нет. Другими словами, не существует набора из трех чисел, который одновременно делает все три уравнения верными.

Давайте рассмотрим еще один пример. Мы собираемся получить систему для этого нового примера, внеся очень небольшое изменение в систему по сравнению с предыдущим примером.

Пример 3. Решите следующую систему уравнений. \[\begin{align*}{x_1} — 2{x_2} + 3{x_3} & = — 2\\ — {x_1} + {x_2} — 2{x_3} & = 3\\ 2{x_1} — {x_2} + 3{x_3} & = — 7\end{align*}\]

Показать решение

Итак, единственная разница между этой системой и системой из второго примера в том, что мы заменили 1 справа от знака равенства в третьем уравнении на -7.

Теперь запишите расширенную матрицу для этой системы.

\[\left( {\begin{array}{*{20}{r}}1&{ — 2}&3&{ — 2}\\{ — 1}&1&{ — 2}&3\\2&{ — 1}&3& { — 7}\end{массив}} \right)\]

Шаги для этой задачи идентичны шагам для второй проблемы, поэтому мы не будем их все записывать. Выполнив те же действия, мы придем к следующей матрице.

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив} } \верно)\]

На этот раз последнее уравнение сокращается до

\[0 = 0\]

и в отличие от второго примера это не проблема. Ноль на самом деле равен нулю!

Мы могли бы остановиться здесь и вернуться к уравнениям, чтобы получить решение, и в этом случае решение есть. Однако, если мы сделаем еще один шаг и получим ноль над единицей во втором столбце, а также под ней, наша жизнь станет немного проще. Выполнение этого дает,

\[\left( {\begin{array}{*{20}{r}}1&{- 2}&3&{- 2}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив} } \right)\begin{array}{*{20}{c}}{2{R_2} + {R_1}}\\ \Rightarrow \end{array}\left( {\begin{array}{*{20 }{r}}1&0&1&{ — 4}\\0&1&{ — 1}&{ — 1}\\0&0&0&0\end{массив}} \right)\]

Если мы теперь вернемся к уравнению, мы получим следующие два уравнения.

\[\left( {\begin{array}{*{20}{r}}1&0&1&{- 4}\\0&1&{- 1}&{- 1}\\0&0&0&0\end{массив}} \right)\ hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}\begin{array}{*{20}{r}}{{x_1} + {x_3} = — 4}\\{{x_2} — {x_3} = — 1}\\{}\конец{массив}\]

У нас есть два уравнения и три неизвестных. Это означает, что мы можем решить для двух переменных с точки зрения оставшейся переменной. Поскольку \(x_{3}\) входит в оба уравнения, мы будем решать с их помощью.

\[\begin{align*}{x_1} & = — {x_3} — 4\\ {x_2} & = {x_3} — 1\end{align*}\]

Это решение означает, что мы можем выбрать значение \(x_{3}\) как угодно, а затем найти значения \(x_{1}\) и \(x_{2} \). В этих случаях мы обычно записываем решение следующим образом:

. \[\begin{align*}{x_1} & = — t — 4\\ {x_2} & = t — 1\hspace{0.25in}\hspace{0.25in}t = {\mbox{любое действительное число}} \\ & {x_3} = t\end{align*}\]

Таким образом, мы получаем бесконечное число решений, по одному для каждого значения \(t\).

Эти три примера подводят нас к интересному факту о системах уравнений.

Факт

Учитывая систему уравнений, \(\eqref{eq:eq1}\), у нас будет одна из трех возможностей для количества решений.

1. Нет решения.
2. Ровно одно решение.
3. Бесконечно много решений.

Прежде чем перейти к следующему разделу, нам нужно рассмотреть еще одну ситуацию. Система уравнений в \(\eqref{eq:eq1}\) называется неоднородной системой, если хотя бы одно из b _i ’ s не равно нулю.