Онлайн калькулятор определитель второго порядка: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Содержание

Калькулятор определителя — вычислить определитель матрицы

Онлайн-калькулятор определителя поможет вам вычислить определитель матрицы заданных входных элементов. Калькулятор определяет значение определителя матрицы до размера матрицы 5 × 5. Он рассчитывается путем умножения его основных диагональных элементов и приведения матрицы к форме эшелона строк. У нас есть подробная информация о том, как рассчитать его вручную, определение, формулы и много других полезных данных, связанных с определителем матрицы. Наш калькулятор определяет результат с помощью следующих различных методов расчета:

Развернуть по столбцу.
Разверните по строке.
Формула Лейбница.
Правило треугольника.
Правило Сарруса.

Но давайте начнем с основ.

Читать дальше!

Что такое детерминант?

Это скалярное значение, которое получается из элементов квадратной матрицы и имеет определенные свойства линейного преобразования, описываемого матрицей. определитель матрицы калькулятор положительный или отрицательный, в зависимости от того, сохраняет ли линейное преобразование ориентацию векторного пространства или меняет ее на обратное. Это помогает нам найти обратную матрицу, а также то, что полезно в системах линейных уравнений, исчислении и многом другом. Он обозначается как det (A), det A или | A |.

Заметка:

Матрицы заключены в квадратные скобки, а определители обозначены вертикальными чертами. Матрица – это массив чисел, но определитель – одно число.

Как найти определитель матрицы онлайн вручную (шаг за шагом):

Определитель матриц можно вычислить разными методами. Здесь мы приводим подробные формулы для разного порядка матрицы, чтобы найти определитель разными методами:

Для умножения матриц 2×2:

Независимо от того, какой метод вы выбрали для расчетов, определитель матрицы онлайн A = (aij) 2 × 2 определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix} \\
\)

\(det⁡ A = ad-bc \)

Пример:
Найти определитель матрицы калькулятор 2×2 A

\(
det A =
\begin{vmatrix}
4 & 12 \\
2 & 7
\end{vmatrix} \\
\)

Решение:

\(
det A =
\begin{vmatrix}
a & b \\
c & d
\end{vmatrix} \\
\)

\(|A| = (7)(4) – (2)(12)\)
\(|A| = 28 – 24\)
\(|A| = 4\)

Для умножения матрицы 3×3:

Здесь обсуждаются расчеты для матриц 3×3 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 3 × 3 из разложения столбца определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
e & f \\h & i\end{vmatrix} – d\begin{vmatrix}b & c \\h & i\end{vmatrix}+g\begin{vmatrix}b & c \\e & f\end{vmatrix} \)

Пример:
найти

\(
det A =
\begin{vmatrix}
2 & 0 & 3\\1 & 4 & 1 \\0 & 4 & 7
\end{vmatrix} \\
\)?

Решение:

\(det⁡ A= 2\begin{vmatrix}
4 & 1 \\4 & 7\end{vmatrix} – 1\begin{vmatrix}0 & 3 \\4 & 7\end{vmatrix}+0\begin{vmatrix}0 & 3 \\4 & 1\end{vmatrix} \)

\( det⁡ A = 2[(7)(4)-(4)(1)]-1[(4)(3)-(7)(0)]+ 0[(4)(3)-(1)(0)] \)

\( det⁡ A = 2[28-4]-1[12-0]+ 0[12-0] \)

\( det⁡ A = 2[24]-1[12]+ 0[12] \)

\( det⁡ A = 48-12+ 0 \)

\( det⁡ A = 36 \)

Развернуть по строке:

Для вычислений матрица A = (aij) 3 × 3 из разложения строки определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
e & f \\h & i\end{vmatrix} – b\begin{vmatrix}d & f \\g & i\end{vmatrix}+c\begin{vmatrix}d & e \\g & h\end{vmatrix} \)

Пример:

найти

\(
det A =
\begin{vmatrix}
3 & 0 & 2\\1 & 4 & 1 \\7 & 0 & 4
\end{vmatrix} \\
\)?

Решение:

\(det⁡ A= 3\begin{vmatrix}
4 & 1 \\0 & 4\end{vmatrix} – 0\begin{vmatrix}1 & 1 \\7 & 4\end{vmatrix}+2\begin{vmatrix}1 & 4 \\7 & 0\end{vmatrix} \)

\(det⁡ A = 3[(4)(4)-(0)(1)]-0[(4)(1)-(7)(1)]+ 2[(0)(1)-(7)(4)]\)
\(det⁡ A = 3[16-0]-0[4-7]+ 2[0-28]\)
\(det⁡ A = 3[16]-0[-3]+ 2[-28]\)
\(det⁡ A = 48+0- 56\)
\(det⁡ A = -8\)

Формула Лейбница:

Для расчетов матрица A = (aij) 3 × 3 по формуле Лейбница определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
\)

\(det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) \)

Пример:

найти

\(
det A =
\begin{vmatrix}
2 & 3 & 8\\6 & 1 & 2 \\5 & 8 & 9
\end{vmatrix} \\
\)?

Решение:

\(
det A =
\begin{vmatrix}
2 & 3 & 8\\6 & 1 & 2 \\5 & 8 & 9
\end{vmatrix} \\
\)
\(det⁡ A = 2*1*9-2*2*8-3*6*9+3*2*5+8*6*8-8*1*5\)

\(det A =198\)

Правило треугольника:

Для расчетов матрица A = (aij) 3 × 3 из правила Треугольника определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
\)

Image

\(det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) \)

Пример:

найти

\(
det A =
\begin{vmatrix}
4 & 5 & 8\\0 & 4 & 9 \\1 & 2 & 3
\end{vmatrix} \\
\)?

Решение:

\(
det A =
\begin{vmatrix}
4 & 5 & 8\\0 & 4 & 9 \\1 & 2 & 3
\end{vmatrix} \\
\)
\(det⁡ A = 4*4*3+5*9*1+8*0*2-1*4*8-2*9*4-3*0*5\)

\(det A =-11\)

Правило Сарруса:

Для расчетов матрица A = (aij) 3 × 3 по правилу Сарруса определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c\\d & e & f \\g & h & i
\end{vmatrix} \\
\)

Image

\(det⁡ A =(a*e*i)-(a*f*h)-(b*d*i)+(b*f*g)+(c*d*h)-(c*e*g) \)

Пример:

найти

\(
det A =
\begin{vmatrix}
9 & 5 & 1\\3 & 5 & 7 \\4 & 8 & 6
\end{vmatrix} \\
\)?

Решение:

\(
det A =
\begin{vmatrix}
9 & 5 & 1\\3 & 5 & 7 \\4 & 8 & 6
\end{vmatrix} \\
\)

\(det⁡ A = 9*5*6+5*7*4+1*3*8-4*5*1-8*7*9-6*3*5\)

\(det A = -180\)

Для матричного умножения 4×4:

Здесь обсуждаются расчеты для матриц 4х4 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 4 × 4 из разложения столбца определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
f & g & h\\j & k & l\\n & o & p\end{vmatrix} – e\begin{vmatrix}b & c & d\\j & k & l\\ n & o & p\end{vmatrix}+i\begin{vmatrix}b & c & d \\f & g & h\\n & o & p\end{vmatrix}-m\begin{vmatrix}b & c & d\\f & g & h\\j & k & l\end {vmatrix}\)

Затем просто определите определитель 3×3, используя приведенную выше формулу 3×3.

Пример:

найти

\(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
\)?

Решение:

\(det⁡ A= 1\begin{vmatrix}4 & 3 & 8\\4 & 3 & 2\\4 & 9 & 6\end{vmatrix} – 2\begin{vmatrix}8 & 7 & 2\\4 & 3 & 2\\ 4 & 9 & 6\end{vmatrix}+1\begin{vmatrix}8 & 7 & 2 \\4 & 3 & 8\\4 & 9 & 6\end{vmatrix}-1\begin{vmatrix}8 & 7 & 2\\4 & 3 & 8\\4 & 3 & 2\end {vmatrix}\)

\(det⁡ A=1( 4\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+8\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -2( 8\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 7\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) +1( 8\begin{vmatrix}3 & 8 \\9 & 6\end{vmatrix} – 7\begin{vmatrix}4 & 8 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -1( 8\begin{vmatrix}
3 & 8 \\3 & 2\end{vmatrix} – 7\begin{vmatrix}4 & 8 \\4 & 6\end{vmatrix}+2\begin{vmatrix}4 & 3 \\4 & 3\end{vmatrix})\)

\(det⁡ A = 1[4(18-18)-3(24-8)+ 8(36-12)]-2[ 8(18-18)-7(24-8)+ 2(36-12)]+ 1[ 8(18-72)-7(24-32)+ 2(36-12)] -1[8(6-24)-7(8-32)+ 2(12-12)]\)

\(det⁡ A = 1[4(0)-3(16)+ 8(24)]-2[ 8(0)-7(16)+ 2(24)]+ 1[ 8(-54)-7(-8)+ 2(24)]-1[8(-18)-7(-24)+ 2(0)]\)

\(det⁡ A = 1[0-48+192]-2[0-112+48]+ 1[ -432+56+48]-1[-144+168+0]\)

\(det⁡ A = 1[144]-2[-64]+ 1[-328]-1[24]\)

\(det⁡ A = 144+128-328- 24\)

\(det⁡ A = -80\)

Развернуть по строке:

Для вычислений матрица A = (aij) 4 × 4 из разложения строки определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
f & g & h\\j & k & l\\n & o & p\end{vmatrix} – b\begin{vmatrix}e & g & h\\i & k & l\\ m & o & p\end{vmatrix}+c\begin{vmatrix}e & f & h \\i & j & l\\m & n & p\end{vmatrix}-d\begin{vmatrix}e & f & g\\i & j & k\\m & n & o\end {vmatrix}\)

Затем просто определите определитель 3×3, используя приведенную выше формулу 3×3.
Пример:
найти

\(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
\)?
Решение:

\(det⁡ A= 1\begin{vmatrix}4 & 3 & 8\\4 & 3 & 2\\4 & 9 & 6\end{vmatrix} – 8\begin{vmatrix}2 & 3 & 8\\1 & 3 & 2\\ 1 & 9 & 6\end{vmatrix}+7\begin{vmatrix}2 & 4 & 8 \\1 & 4 & 2\\1 & 4 & 6\end{vmatrix}-2\begin{vmatrix}2 & 4 & 3\\1 & 4 & 3\\1 & 4 & 9\end {vmatrix}\)

\(det⁡ A=1( 4\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}4 & 2 \\4 & 6\end{vmatrix}+8\begin{vmatrix}4 & 3 \\4 & 9\end{vmatrix}) -8( 2\begin{vmatrix}
3 & 2 \\9 & 6\end{vmatrix} – 3\begin{vmatrix}1 & 2 \\1 & 6\end{vmatrix}+8\begin{vmatrix}1 & 3 \\1 & 9\end{vmatrix}) +7( 2\begin{vmatrix}
4 & 2 \\4 & 6\end{vmatrix} – 4\begin{vmatrix}1 & 2 \\1 & 6\end{vmatrix}+8\begin{vmatrix}1 & 4 \\1 & 4\end{vmatrix}) -2( 2\begin{vmatrix}
4 & 3 \\4 & 9\end{vmatrix} – 4\begin{vmatrix}1 & 3 \\1 & 9\end{vmatrix}+3\begin{vmatrix}1 & 4 \\1 & 4\end{vmatrix})\)

\(det⁡ A = 1[4(18-18)-3(24-8)+ 8(36-12)]-8[ 2(18-18)-3(6-2)+ 8(9-3)]+ 7[ 2(24-8)-4(6-2)+ 8(4-4)]-2[2(36-12)-4(9-3)+ 3(4-4)] \)
\(det⁡ A = 1[4(0)-3(16)+ 8(24)]-8[ 2(0)-3(4)+ 8(6)]+ 7[ 2(16)-4(4)+ 8(0)]-2[2(24)-4(6)+ 3(0)]\)
\(det A = 1[0-48+192]-8[0-12+48]+ 7[ 32-16+0]-2[48-24+0]\)
\(det⁡ A = 1[144]-8[36]+ 7[16]-2[24]\)
\(det A = 144-288+112- 48 \)
\(det⁡ A = -80\)

Формула Лейбница:

Для расчетов матрица A = (aij) 4 × 4 по формуле Лейбница определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c & d\\e & f & g &h \\i & j & k & l \\ m & n & o & p
\end{vmatrix} \\
\)

\(det A = a*f*k*p + a*j*o*h + a*n*g*l + e*b*o*l + e*j*c*p + e*n*k*d + i*b*g*p + i*f*o*d + i*n*c*h+ m*b*k*h + m*f*c*l + m*j*g*d − a*f*o*l – a*j*g*p – a*n*k*h − e*b*k*p – e*j*o*d -e*n*c*l− i*b*o*h – i*f*c*p – i*n*g*d − m*b*g*l – m*f*k*d – m*j*c*h\)

Пример:
Find \(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
\)?

Решение:

\(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2\\2 & 4 & 3 &8 \\1 & 4 & 3 & 2 \\ 1 & 4 & 9 & 6
\end{vmatrix} \\
\)
\(1*4*3*6-1*4*2*9-1*3*4*6+1*3*2*4+1*8*4*9-1*8*3*4-8*2*3*6+8*2*2*9+8*3*1*6-8*3*2*1-8*8*1*9+8*8*3*1+7*2*4*6-7*2*2*4-7*4*1*6+7*4*2*1+7*8*1*4-7*8*4*1-2*2*4*9+2*2*3*4+2*4*1*9-2*4*3*1-2*3*1*4+2*3*4*1\)
\(=-80\)

Для умножения матрицы 5×5:

Здесь обсуждаются расчеты для матриц 5×5 разными методами:

Развернуть по столбцу:

Для расчетов матрица A = (aij) 5 × 5 из разложения столбца определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c & d & e\\f & g & h & i & j\\k & l & m & n & o \\ p & q & r & s & t \\ u & v & w & x & y
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
g & h & i & j\\l & m & n & o\\q & r & s & t\\v & w & x & y\end{vmatrix} – f\begin{vmatrix}b & c & d & e\\l & m & n & o\\ q & r & s & t\\ v & w & x & y\end{vmatrix}+k\begin{vmatrix}b & c & d & e \\g & h & i & j\\q & r & s & t\\v & w & x & y\end{vmatrix}-p\begin{vmatrix}b & c & d & e\\g & h & i & j\\l & m & n & o\\q & r & s & t\end {vmatrix}\)

Затем просто определите определитель 4×4, используя приведенную выше формулу 4×4.

Развернуть по строке:

Для расчетов матрица A = (aij) 5 × 5 из разложения строки определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a & b & c & d & e\\f & g & h & i & j\\k & l & m & n & o \\ p & q & r & s & t \\ u & v & w & x & y
\end{vmatrix} \\
\)

\(det⁡ A= a\begin{vmatrix}
g & h & i & j\\l & m & n & o\\q & r & s & t\\v & w & x & y\end{vmatrix} – b\begin{vmatrix}g & h & i & j\\k & m & n & o\\ p & r & s & t\\ u & w & x & y\end{vmatrix}+c\begin{vmatrix}f & g & i & j \\k & l & n & o\\p & q & s & t\\u & v & x & y\end{vmatrix}-d\begin{vmatrix}f & g & h & j\\k & l & m & o\\p & q & r & t\\u & v & w & y\end {vmatrix}+e\begin{vmatrix}f & g & h & i\\k & l & m & n\\p & q & r & s\\u & v & w & x\end {vmatrix}\)

Затем просто определите определитель 4×4, используя приведенную выше формулу 4×4.

Формула Лейбница:

Для расчетов матрица A = (aij) 5 × 5 по формуле Лейбница определяется по следующей формуле:

\(
det A =
\begin{vmatrix}
a11 & a12 & a13 & a14 & a15\\a21 & a22 & a23 & a24 & a25\\a31 & a32 & a33 & a34 & a35 \\ a41 & a42 & a43 & a44 & a45 \\ a51 & a52 & a53 & a54 & a55
\end{vmatrix} \\
\)

Образ

Пример:
Find \(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2 & 8\\2 & 4 & 3 &8 & 3\\1 & 4 & 3 & 2 &1\\ 1 & 4 & 9 & 6 & 2 \\ 1 & 5 & 7 & 3 & 4
\end{vmatrix} \\
\)?
Решение:
\(
det A =
\begin{vmatrix}
1 & 8 & 7 & 2 & 8\\2 & 4 & 3 &8 & 3\\1 & 4 & 3 & 2 &1\\ 1 & 4 & 9 & 6 & 2 \\ 1 & 5 & 7 & 3 & 4
\end{vmatrix} \\
\)
\( =1*4*3*6*4-1*4*3*2*3-1*4*2*9*4+1*4*2*2*7+1*4*1*9*3-1*4*1*6*7-1*3*4*6*4+1*3*4*2*3+1*3*2*4*4-1*3*2*2*5-1*3*1*4*3+1*3*1*6*5+1*8*4*9*4-1*8*4*2*7-1*8*3*4*4+1*8*3*2*5+1*8*1*4*7-1*8*1*9*5-1*3*4*9*3+1*3*4*6*7+1*3*3*4*3-1*3*3*6*5-1*3*2*4*7+1*3*2*9*5-8*2*3*6*4+8*2*3*2*3+8*2*2*9*4-8*2*2*2*7-8*2*1*9*3+8*2*1*6*7+8*3*1*6*4-8*3*1*2*3-8*3*2*1*4+8*3*2*2*1+8*3*1*1*3-8*3*1*6*1-8*8*1*9*4+8*8*1*2*7+8*8*3*1*4-8*8*3*2*1-8*8*1*1*7+8*8*1*9*1+8*3*1*9*3-8*3*1*6*7-8*3*3*1*3+8*3*3*6*1+8*3*2*1*7-8*3*2*9*1+7*2*4*6*4-7*2*4*2*3-7*2*2*4*4+7*2*2*2*5+7*2*1*4*3-7*2*1*6*5-7*4*1*6*4+7*4*1*2*3+7*4*2*1*4-7*4*2*2*1-7*4*1*1*3+7*4*1*6*1+7*8*1*4*4-7*8*1*2*5-7*8*4*1*4+7*8*4*2*1+7*8*1*1*5-7*8*1*4*1-7*3*1*4*3+7*3*1*6*5+7*3*4*1*3-7*3*4*6*1-7*3*2*1*5+7*3*2*4*1-2*2*4*9*4+2*2*4*2*7+2*2*3*4*4-2*2*3*2*5-2*2*1*4*7+2*2*1*9*5+2*4*1*9*4-2*4*1*2*7-2*4*3*1*4+2*4*3*2*1+2*4*1*1*7-2*4*1*9*1-2*3*1*4*4+2*3*1*2*5+2*3*4*1*4-2*3*4*2*1-2*3*1*1*5+2*3*1*4*1+2*3*1*4*7-2*3*1*9*5-2*3*4*1*7+2*3*4*9*1+2*3*3*1*5-2*3*3*4*1+8*2*4*9*3-8*2*4*6*7-8*2*3*4*3+8*2*3*6*5+8*2*2*4*7-8*2*2*9*5-8*4*1*9*3+8*4*1*6*7+8*4*3*1*3-8*4*3*6*1-8*4*2*1*7+8*4*2*9*1+8*3*1*4*3-8*3*1*6*5-8*3*4*1*3+8*3*4*6*1+8*3*2*1*5-8*3*2*4*1-8*8*1*4*7+8*8*1*9*5+8*8*4*1*7-8*8*4*9*1-8*8*3*1*5+8*8*3*4*1\)
\( =-248\)

Заметка:

Правило Треугольника и Правило Сарруса применимо только к матрице до 3×3. Наш онлайн-калькулятор определителей матриц использует все эти формулы для точных вычислений определителей. Просто вы можете использовать наш онлайн-математический калькулятор, который поможет вам легко выполнять различные математические операции за короткий промежуток времени.

Как использовать этот онлайн-калькулятор определителя матрицы:

Наш онлайн-калькулятор помогает найти определитель матрицы калькулятор размером до 5×5 пятью различными методами. Просто следуйте пунктам для получения точных результатов.
Читать дальше!

Входы:

Прежде всего, выберите порядок матрицы из выпадающего списка калькулятора.
Затем введите значения матрицы в соответствующие поля.
Затем выберите метод, с помощью которого вы найдете определитель.
Наконец, нажмите кнопку “Рассчитать”.

Заметка:

Есть поле «номер столбца или строки», в которое вы вводите номер строки или номер столбца, которые необходимо развернуть. Кроме того, в нем есть поля для создания матрицы и очистки матрицы, он автоматически сгенерирует матрицу и очистит все значения из матрицы соответственно.

Выходы:

После заполнения всех полей калькулятор показывает:

Определитель матрицы.
Пошаговые расчеты.

Заметка:

Независимо от того, какой метод вы выберете для расчетов, онлайн-калькулятор определителя покажет вам результаты в соответствии с выбранным вариантом.

Детерминантные свойства:

Поскольку детерминанты обладают многими полезными свойствами, но здесь мы перечислили некоторые из их важных свойств:

Определитель произведения чисел равен произведению определителей чисел.
Если мы поменяем местами две строки и два столбца матрицы, то определитель останется тем же, но с противоположным знаком.
определитель матрицы онлайн равен транспонированной матрице.
определитель матрицы калькулятор 5 × 5 полезен в расширении Лапласа.
Если мы добавим те же две копии первой строки в любую строку (столбцы в любой столбец), то определитель не изменится.

Часто задаваемые вопросы (FAQ):

Для чего используются детерминанты?

Определитель полезен при определении решения линейных уравнений, фиксируя, как линейное преобразование изменяет объем или площадь и изменяет переменные в интегралах. Он отображается как функция, вход которой представляет собой квадратную матрицу, а выход представляет собой одно число.

Что означает определитель 0?

Определитель 0 означает, что объем равен нулю (0). Это может произойти только тогда, когда один вектор перекрывает один другой.

Может ли определитель быть отрицательным?

Поскольку это действительное число, а не матрица. Значит, это может быть отрицательное число. Определитель существует только для квадратных матриц (2 × 2, 3 × 3, … n × n).

Конечное примечание:

К счастью, вы узнали о детерминантах, о том, как их найти вручную, и о различных приложениях в математике, включая решение линейных уравнений; определить изменение объема или площади при линейном преобразовании и т. д. Когда дело доходит до решения определителя для матрицы более высокого порядка, это очень сложная задача. Просто попробуйте этот онлайн-калькулятор определителя, который позволяет вам найти определитель матриц с помощью различных методов расчета с полным расчетом. Как правило, студенты и профессионалы используют этот калькулятор определителя матрицы для решения своих математических задач.

Other languages: Determinant Calculator, Determinant Hesaplama, Kalkulator Wyznacznika Macierzy, Kalkulator Penentu Matriks, Determinanten Rechner, 行列式計算, 행렬식 계산기, Determinant Kalkulačka, Calculadora De Determinantes, Calcul Déterminant Matrice, Calculadora De Determinantes, Calcolo Determinante, حساب محدد, Determinantti laskin, Determinantberegner.

Определитель матрицы. Онлайн калькулятор

0
AC		+/-	÷
7	8	9	×
4	5	6	—
1	2	3	+
0	00	,	=

Данный калькулятор позволит вам легко найти определитель матрицы, а так же получить подробное решение.

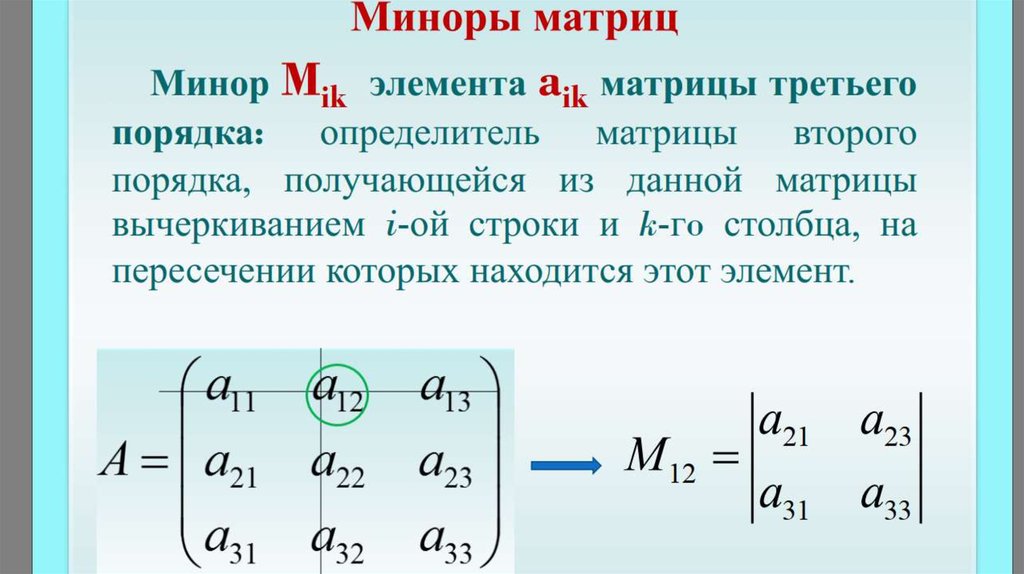
Калькулятор вычисляет определитель для матриц размерности от 1 × 1 до 9 × 9

Матрица размерности m × n – это таблица чисел у которой m строк и n столбцов. Элементы матрицы обозначаются как a_ij, где i – номер строки, j – номер столбца.
Определитель квадратной матрицы – это число, ставящееся в соответствие матрице и которое может быть вычислено по ее элементам.

Как найти определитель матрицы

Определитель квадратной матрицы – это число, скалярная величина характеризующее данную матрицу. Также вместо термина определитель, используют слово – детерминант.

Вычислить определитель можно только для квадратной матрицы.

Квадратная матрицы – это матрица у которой число строк совпадает с числом столбцов.

Определитель матрицы A может обозначатся как: det(A), |A| или Δ(A).

Как найти определитель матрицы размерности 2 × 2

Для матрицы 2 × 2 определитель вычисляется по формуле:

Приведем пример, вычислим определитель для матрицы A.

A =

1	2
3	4

Исходя из формулы получим:
det A = ad – bc = 1 ⋅ 4 — 3 ⋅ 2 = -2

det A =

1	2
3	4

= -2

Как найти определитель матрицы размерности 3 × 3

Для матрицы 3 × 3 определитель вычисляется по формуле:

det A =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

= a₁₁^{a₂₂ a₂₃
a₃₂ a₃₃} — a₁₂^{a₂₁ a₂₃
a₃₁ a₃₃} + a₁₃^{a₂₁ a₂₂
a₃₁ a₃₂} = a₁₁

a₂₂a₃₃ — a₁₁a₂₃a₃₂ — a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ — a₁₃a₂₂a₃₁

Приведем пример, вычислим определитель для матрицы A.

A =

1	2	3
5	7	0
9	0	-3

A =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

где,

a₁₁ = 1
a₁₂ = 2
a₁₃ = 3
a₂₁ = 5
a₂₂ = 7
a₂₃ = 0
a₃₁ = 9
a₃₂ = 0
a₃₃ = -3

Исходя из формулы получим:
det A = a₁₁a₂₂a₃₃ — a₁₁a₂₃a₃₂ — a₁₂a₂₁a₃₃ + a₁₂a₂₃a₃₁

+ a₁₃a₂₁a₃₂ — a₁₃a₂₂a₃₁ = (1 ⋅ 7 ⋅ (-3)) — (1 ⋅ 0 ⋅ 0) — (2 ⋅ 5 ⋅ (-3)) + (2 ⋅ 0 ⋅ 9) + (3 ⋅ 5 ⋅ 0) — (3 ⋅ 7 ⋅ 9) = -180

det A =

1	2	3
5	7	0
9	0	-3

= -180

Как найти определитель матрицы размерности 4 × 4

Для матрицы 4 × 4, как и для любой матрицы n × n определитель вычисляется по формуле разложения по строке:

Приведем пример, вычислим определитель для матрицы A.

det A =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

A =

a₁₁	a₁₂	a₁₃	a₁₄
a₂₁	a₂₂	a₂₃	a₂₄
a₃₁	a₃₂	a₃₃	a₃₄
a₄₁	a₄₂	a₄₃	a₄₄

где,

a₁₁ = 1
a₁₂ = 3
a₁₃ = 7
a₁₄ = 0
a₂₁ = 5
a₂₂ = -3
a₂₃ = 0
a₂₄ = 8
a₃₁ = 0
a₃₂ = 4
a₃₃ = -3
a₃₄ = 2
a₄₁ = 1
a₄₂ = 2
a₄₃ = 0
a₄₄ = 9

Для матрицы размерности n × n значение определителя вычисляется по формуле

M_1j — дополнительный минор к элементу a_1j, получаемый из исходной матрицы А путем вычеркивания первой строки и j-го столбца

Значение n = 4, поэтому необходимо найти 4 дополнительных минора путем вычеркивания первой строки и j-го столбца

M₁₁ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

= ^{^{^{-3 0 8
4 -3 2
2 0 9}}} = 129

M₁₂ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

= ^{^{^{5 0 8
0 -3 2
1 0 9}}} = -111

M₁₃ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

= ^{^{^{5 -3 8
0 4 2
1 2 9}}} = 122

M₁₄ =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

= ^{^{^{5 -3 0
0 4 -3
1 2 0}}} = 39

Исходя из приведенной выше формулы, распишем сумму

det A = (-1)¹ ⋅ a₁₁ ⋅ M₁₁ + (-1)² ⋅ a₁₂ ⋅ M₁₂ + (-1)³ ⋅ a₁₃ ⋅ M₁₃ + (-1)⁴ ⋅ a₁₄ ⋅ M₁₄

det A = (-1)¹ ⋅ 1 ⋅ det

-3	0	8
4	-3	2
2	0	9

+ (-1)² ⋅ 3 ⋅ det^{^{^{5 0 8
0 -3 2
1 0 9}}} + (-1)³ ⋅ 7 ⋅ det^{^{^{5 -3 8
0 4 2
1 2 9}}} + (-1)⁴ ⋅ 0 ⋅ det^{^{^{5 -3 0
0 4 -3
1 2 0}}} = (-1)¹ ⋅ 1 ⋅ 129 + (-1)² ⋅ 3 ⋅ (-111) + (-1)³ ⋅ 7 ⋅ 122 + (-1)⁴ ⋅ 0 ⋅ 39 = 1316

det A = (-1)¹ ⋅ 1 ⋅ 129 + (-1)² ⋅ 3 ⋅ (-111) + (-1)³ ⋅ 7 ⋅ 122 + (-1)⁴ ⋅ 0 ⋅ 39 = 1316

det A =

1	3	7	0
5	-3	0	8
0	4	-3	2
1	2	0	9

= 1316

Вам могут также быть полезны следующие сервисы

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка.

Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Determinant Calculator: Wolfram|Alpha

WolframAlpha

Take the determinant of matrices with Wolfram|Alpha

123321213

Math Input

Vectors & Matrices

Больше, чем просто онлайн-калькулятор определителей

Wolfram|Alpha — идеальный ресурс для вычисления определителей матриц. Он также может вычислять матричные произведения, ранг, недействительность, сокращение строк, диагонализацию, собственные значения, собственные векторы и многое другое.

Узнайте больше о:

Детерминанты »

Советы по вводу запросов

Для ввода запросов используйте простой английский или общепринятый математический синтаксис. Чтобы ввести матрицу, разделяйте элементы запятыми, а строки — фигурными скобками, скобками или круглыми скобками.

определитель {{2, 3}, {4, 7}}
определитель {{1, 2, 3}, {4, 5, 6}, {7, 8, 9}}
найти определитель матрицы ((а, 3), (5, -7))

|{{2/3, -5/7}, {-3, 4/9}}|
определитель [[2, 3], [5, 6]]

Просмотреть другие примеры »

Доступ к средствам мгновенного обучения

Получите немедленную обратную связь и рекомендации с помощью пошаговых решений и Генератора проблем Wolfram

Узнайте больше о:

Пошаговые решения »
Генератор задач Wolfram »

База знаний об определителях

Определитель — это свойство квадратной матрицы.

Значение определителя имеет много значений для матрицы. Определитель, равный 0, означает, что матрица сингулярна и, следовательно, необратима. Систему линейных уравнений можно решить, создав матрицу из коэффициентов и взяв определитель; этот метод называется правилом Крамера и может использоваться только в том случае, если определитель не равен 0. Геометрически определитель представляет собой площадь параллелограмма со знаком, образованную векторами-столбцами, принятыми в качестве декартовых координат.

Существует множество методов вычисления определителя. Определения некоторых матриц, таких как диагональные или треугольные матрицы, можно вычислить, взяв произведение элементов на главной диагонали. Для матрицы 2 на 2 определитель вычисляется путем вычитания обратной диагонали из главной диагонали, что известно как формула Лейбница. Определитель произведения матриц равен произведению определителей этих матриц, поэтому может быть полезно разложить матрицу на более простые матрицы, вычислить отдельные определители, а затем умножить результаты. Некоторые полезные методы разложения включают QR, LU и разложение Холецкого. Для более сложных матриц для вычисления определителя необходимо использовать формулу Лапласа (разложение кофакторов), исключение Гаусса или другие алгоритмы.

Онлайн-калькулятор для расчета определителя 5×5

Онлайн-калькулятор вычисляет значение определителя матрицы 5×5 с помощью разложения Лапласа по строке или столбцу и алгоритма Гаусса.

Определитель 5х5

det A=|a11a12a13a14a15a21a22a23a24a25a31a32a33a34a35a41a42a43a44a45a51a52a53a54a55|

Введите коэффициенты

₁₁ =

а ₁₂ =

а ₁₃ =

а ₁₄ =

а ₁₅ =

а ₂₁ =

а ₂₂ =

а ₂₃ =

а ₂₄ =

а ₂₅ =

₃₁ =

а ₃₂ =

а ₃₃ =

а ₃₄ =

а ₃₅ =

а ₄₁ =

а ₄₂ =

а ₄₃ =

а ₄₄ =

а ₄₅ =

а ₅₁ =

а ₅₂ =

₅₃ =

а ₅₄ =

а ₅₅ =

Вычисление значения определителя с помощью расширения Лапласа

Вы можете выбрать строку или столбец, которые будут использоваться для расширения.

Расчет с помощью алгоритма Гаусса

Примечание:

Если ведущие коэффициенты равны нулю, то столбцы или строки меняются местами соответственно, чтобы было возможно деление на старший коэффициент. Значение определителя правильное, если после преобразований нижняя треугольная матрица равна нулю, а все элементы главной диагонали равны 1.

Объяснение методов

Теорема разложения Лапласа

Теорема развития Лапласа предлагает метод вычисления определителя, в котором определитель развивается после строки или столбца. Размерность уменьшается и может быть уменьшена далее шаг за шагом до скаляра.

det A=∑i=1n-1i+j⋅aijdetAij ( Расширение по j-му столбцу )

det A=∑j=1n-1i+j⋅aijdetAij ( Разложение по i-й строке )

где A _ij , подматрица матрицы A, возникающая при удалении i-й строки и j-го столбца.

Пример разложения Лапласа по первой строке матрицы 3×3.

det A=|a11a12a13a21a22a23a31a32a33|

Первый элемент задается коэффициентом a ₁₁ и субдетерминантом, состоящим из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a11|a22a23a32a33|

Второй элемент определяется коэффициентом a ₁₂ и субдетерминант, состоящий из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a12|a21a23a31a33|

Третий элемент задается коэффициентом a ₁₃ и субдетерминантом, состоящим из элементов с зеленым фоном.

|a11a12a13a21a22a23a31a32a33|=>a13|a21a22a31a32|

С тремя элементами определитель может быть записан как сумма определителей 2×2.

Важно учитывать, что знаки элементов чередуются следующим образом.

|+-+-+-+-+|

Метод Гаусса

В методе Гаусса определитель преобразуется таким образом, что элементы нижней матрицы треугольника становятся равными нулю. Для этого вы используете правила коэффициента строки и добавление строк. Добавление строк не меняет значения определителя. Факторы ряда должны рассматриваться как множители перед определителем.

Калькулятор определителя — вычислить определитель матрицы

Определитель матрицы. Онлайн калькулятор

Данный калькулятор позволит вам легко найти определитель матрицы, а так же получить подробное решение.

Как найти определитель матрицы

Как найти определитель матрицы размерности 2 × 2

Как найти определитель матрицы размерности 3 × 3

Как найти определитель матрицы размерности 4 × 4

Determinant Calculator: Wolfram|Alpha

Take the determinant of matrices with Wolfram|Alpha

Больше, чем просто онлайн-калькулятор определителей

Советы по вводу запросов

Доступ к средствам мгновенного обучения

База знаний об определителях

Определитель — это свойство квадратной матрицы.

Онлайн-калькулятор для расчета определителя 5×5

Онлайн-калькулятор для расчета определителя 5×5

Определитель 5х5

Введите коэффициенты

Вычисление значения определителя с помощью расширения Лапласа

Расчет с помощью алгоритма Гаусса

Объяснение методов

Теорема разложения Лапласа

Пример разложения Лапласа по первой строке матрицы 3×3.

Метод Гаусса

Добавить комментарий Отменить ответ