Вычитание векторов онлайн калькулятор: Онлайн калькулятор. Сложение и вычитание двух векторов

Содержание

Сложение и вычитание двух векторов — онлайн калькулятор

В результате сложения двух векторов a и b получается вектор с, все элементы которого равны попарной сумме соответствующих элементов слагаемых векторов. При вычитании тех же векторов все элементы результирующего вектора с равны попарной разности соответствующих элементов.

Нахождение суммы и разности векторов онлайн позволяет обойтись без самостоятельного проведения расчетов. Нужно просто задать векторы (точками или координатами), выбрать действие (сложение или вычитание) и нажать кнопку «рассчитать». После этого онлайн-калькулятор выдаст результат вместе с подробными промежуточными выкладками

Как сложить и вычесть векторы с помощью онлайн-калькулятора

Чтобы сложить или вычесть векторы при помощи онлайн калькулятора, достаточно лишь задать необходимые векторы. Для этого:

Опеделитесь, с какими векторами вы хотите работать. Это могут быть векторы на плоскости или векторы в пространстве.
В рассматриваемом примере, оставим размерность «2». То есть, мы работаем с векторами на плоскости.
Теперь нужно выбрать форму представления векторов: их можно задать координатами либо точками:
Для наглядности, зададим один вектор точками, а второй – координатами.
Теперь в поле «Значение вектора» нужно ввести соответствующие значения. Зададим векторы произвольным образом:
Осталось нажать «Рассчитать» и получить ответ. Отметим, что складываемые и вычитаемые векторы можно также умножать на число. Для наглядности, умножим первый вектор a на 3 и сложим результат с вектором b:

Материалы, которые помогут вам лучше разобраться в теме:

Векторы на плоскости и в пространстве — основные определения
Операции над векторами и их свойства: сложение и умножение
Координаты вектора в декартовой системе координат (ДСК)
Нахождение координат вектора через координаты точек
Векторное произведение — определения, свойства, формулы, примеры и решения
Операции над векторами в прямоугольной системе координат

Ответ:

Решение

Ответ:

list» :key=»`error-${eIdx}`» v-html=»e»/>

Похожие калькуляторы:

Длина вектора. Модуль вектора
Векторное произведение векторов
Умножение вектора на число
Угол между векторами
Смешанное произведение векторов
Скалярное произведение векторов
Определение вектора по двум точкам
Разложение вектора по базису

Проверить являются ли вектора базисом
Ортогональность векторов
Компланарность векторов
Коллинеарность векторов

Проекция вектора на вектор
Площадь треугольника, построенного на векторах
Площадь параллелограмма, построенного на векторах

Как найти сумму и разность векторов без онлайн-калькулятора

Рассмотрим пример с применением формулы для суммы векторов на плоскости. Пусть нужно сложить два вектора: a(3; 5) и b(4; 3). Произведем вычисления:

c→=a→+b→=(ax+bx;ay+by)a→+b→=(3+4;5+3)=(7;8)

Правильность решения можно проверить с помощью онлайн-калькулятора.

Данный сервис будет полезен школьникам и студентам при самостоятельной подготовке к экзаменам и контрольным по векторной алгебре.

Понравился калькулятор? Поделись с друзьями!

Калькулятор сложения и вычитания векторов

Укажите размерность пространства 23

Укажите форму представления первого вектора

Координаты точек начала и конца первого вектораКоординаты первого вектора

Укажите форму представления второго вектора
Координаты точек начала и конца второго вектораКоординаты второго вектора

Задайте координаты первого вектора
a̅ = { ; }

Задайте координаты второго вектора
b̅ = { ; }

+ —

Как сложить или вычесть два вектора

Сложение векторов по правилу треугольника

Чтобы сложить два вектора a и b по правилу треугольника, необходимо:

1. Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с концом другого.

2. Из начала вектора a в конец вектора b провести вектор c.

Вектор c – есть сумма векторов a и b

a + b = c

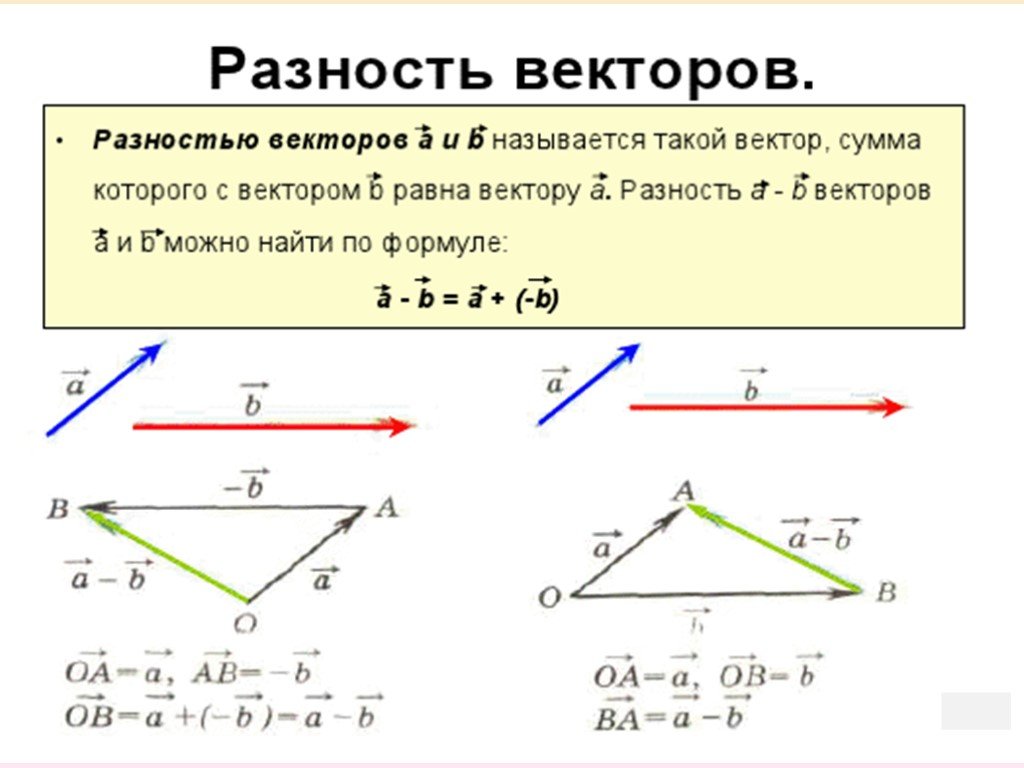
Вычитание векторов по правилу треугольника

Чтобы вычесть два вектора a и b по правилу треугольника, необходимо:

1. Параллельно перенести векторы a и b, так чтобы начало одного из векторов совпадало с началом другого.
2. Из конца вектора b в конец вектора a провести вектор c.

Вектор c – есть разность векторов a и b

a − b = c

Как сложить два вектора, координаты которых заданы точками

Найдем сумму векторов плоскости.

Координаты обоих векторов заданны точками:

Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов AB и CD будет вектор c

Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x; B_y — A_y} = {-2 — 5 ; 11 — 9} = {-7 ; 2}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x; D_y — C_y} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
c = AB + CD = {AB_x + CD_x ; AB_y + CD_y} = {-7 + (-3) ; 2 + (-11)} = {-10 ; -9}

c = AB + CD

Как вычесть два вектора, координаты которых заданы точками

Пример. Найдем разность векторов пространства. Координаты обоих векторов заданны точками.

Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов AB и CD будет вектор c.

Вычислим координаты первого вектора по двум точкам A и B:

AB = {B_x — A_x; B_y — A_y; B_z — A_z} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}

Вычислим координаты второго вектора по двум точкам C и D:

CD = {D_x — C_x; D_y — C_y; D_z — C_z} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}

c = AB — CD = {AB_x — CD_x ; AB_y — CD_y ; AB_z — CD_z} = {-8 — 7 ; -1/5 — 6 ; -275/4 — 7} = {-15 ; -31/5 ; -303/4}= {-15 ; -6. 2 ; -75.75}

Вычитание векторов в координатном представлении

Найдем разность векторов плоскости.

Координаты вектора a: (5 ; 9)
Координаты вектора b: (-1 ; 7)

Для того, чтобы вычесть два вектора необходимо вычесть их координаты. Результатом вычитания векторов a и b будет вектор c

c = a — b = {a_x — b

x ; a_y — b_y} = {5 — (-1) ; 9 — 7} = {6 ; 2}

c = a — b

Сложение векторов в координатном представлении

Пример. Найдем сумму векторов пространства.

Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)

Для того, чтобы сложить два вектора необходимо сложить их координаты. Результатом сложения векторов a и b будет вектор c

c = a + b = {a_x + b_x ; a_y + b_y ; a_z + b_z} = {5 + 2 ; 1 + 4 ; 7 + 6} = {7 ; 5 ; 13}

Калькулятор вычитания векторов

Онлайн-калькулятор для вычитания одного вектора из другого с указанием компонентов равнодействующей, ее величины и направления. .

Пусть u и v — два вектора, заданные в компонентной форме формулой
u = 1 , u ₂ > и v = 1 , v ₂ >
Вычитание вектора v из вектора u определяется формулой
и — v = < и ₁ — в ₁ , у ₂ — в ₂ >

Использование калькулятора векторов вычитания

Есть два калькулятора, которые можно использовать для вычитания одного вектора из другого в зависимости от того, знаете ли вы компоненты или величину и направление вычитаемых векторов.

1 — Введите компоненты u ₁ , u ₂ и v ₁ , v ₂ двух векторов u и v соответственно как действительные числа и нажмите «Вычесть два вектора». Выходами являются компоненты вектора u — v, его величина и направление в градусах.
2 — Введите величины (неотрицательные вещественные числа) и направления двух векторов u и v соответственно как действительные числа и нажмите «Вычесть два вектора». Выходами являются компоненты вектора u — v, его величина и направление в градусах.

Дополнительные ссылки

Найдите величину и направление векторов.

векторные калькуляторы
Сложение векторов и скалярное умножение.

сообщите об этом объявлении

Двухмерный векторный калькулятор сложения и вычитания с графиками

Калькулятор сложения векторов вычисляет сложение и вычитание до пяти двумерных векторов. Сложение и вычитание векторов графически нарисован в системе координат x-y. Формат вектора может быть выбран как величина и угол направления или компоненты.

Формулы сложения и вычитания векторов, которые используются в этом калькуляторе, приведены ниже.

Калькулятор сложения и вычитания векторов:

ВХОДНЫЕ ПАРАМЕТРЫ
Векторный формат:			Компоненты (x,y)Величина/угол
КОМПОНЕНТЫ ВЕКТОРА

Вектор


ВЕЛИЧИНЫ И УГЛЫ ВЕКТОРОВ

Вектор
Магнитуда
Угол (°)

РЕЗУЛЬТАТИВНЫЙ ВЕКТОР
		+-		+-		+-		+-

Примечание.