Как правильно умножать отрицательные числа?
Поможем понять и полюбить математику
Начать учиться
В 6 классе каждый школьник знает отличие между положительным и отрицательным числом и правила умножения. В этой статье объединим эти две темы и попрактикуемся в умножении отрицательных чисел.
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают.
То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента.
Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
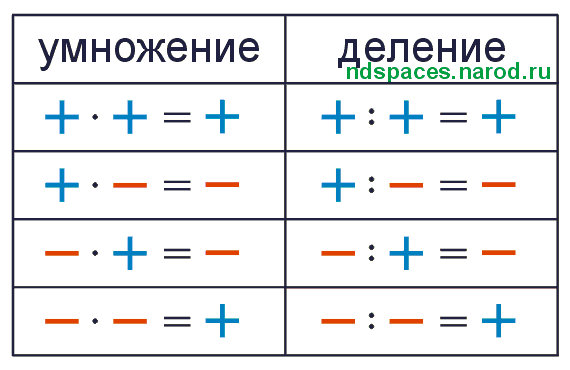
Умножение отрицательных чисел
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули.
- (-а) * (-b) = a * b
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3.
Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6. - Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Шпаргалки для родителей по математике
Все формулы по математике под рукой
Лидия Казанцева
Автор Skysmart
К предыдущей статье
104.
6K
Как найти координаты точки?
К следующей статье
Признаки равенства треугольников
Получите план обучения, который поможет понять и полюбить математику
На вводном уроке с методистом
Выявим пробелы в знаниях и дадим советы по обучению
Расскажем, как проходят занятия
Подберём курс
§ Вычитание отрицательных чисел. Вычитание рациональных чисел
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Как известно вычитание — это действие, противоположное сложению.
Если «a» и «b» — положительные числа,
то вычесть из числа «a» число «b», значит
найти такое число «c», которое при сложении
«с» числом «b» даёт число «a».
a − b = с или с + b = a
Определение вычитания сохраняется для всех рациональных чисел. То есть вычитание положительных и отрицательных чисел можно заменить сложением.
Запомните!
Чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число противоположное вычитаемому.
Или по другому можно сказать, что вычитание числа «b» — это тоже самое сложение, но с числом противоположным числу «b».
a − b = a + (−b)
Пример.
6 − 8 = 6 + (− 8) = −2
Пример.
0 − 2 = 0 + (−2) = −2
Запомните!
Стоит запомнить выражения ниже.
0 − a = − a
a − 0 = a
a − a = 0
Как видно из примеров выше вычитание числа «b» — это сложение с числом противоположным числу «b».
Это правило сохраняется не только при вычитании из бóльшего числа меньшего, но
и позволяет из меньшего числа вычесть большее число, то есть всегда можно найти
разность двух чисел.
Разность может быть положительным числом, отрицательным числом или числом ноль.
Примеры вычитания отрицательных и положительных чисел.
- −3 − (+ 4) = −3 + (−4) = −7
- −6 − (−7) = −6 + (+ 7) = 1
- 5 − (−3) = 5 + (+ 3) = 8
Удобно запомнить правило знаков, которое позволяет уменьшить количество скобок.
Знак «плюс» не изменяет знака числа, поэтому, если перед скобкой стоит плюс, то знак в скобках не меняется.
+ (−a) = −a
Знак «минус» перед скобками меняет знак числа в скобках на противоположный.
−(+ a) = − a
−(−a) = + a
Из равенств видно, что если перед и внутри скобок стоят одинаковые знаки, то получаем «+», а если знаки разные, то получаем «−».
(−6) + (+ 2) − (−10) − (− 1) + (− 7) = −6 + 2 + 10 + 1 − 7 = − 13 + 13 = 0
Правило знаков сохраняется и в том случае, если в скобках не одно число, а
алгебраическая сумма чисел.
a − (− b + c) + (d − k + n) = a + b − c + d − k + n
Обратите внимание, если в скобках стоит несколько чисел и перед скобками стоит знак «минус», то должны меняться знаки перед всеми числами в этих скобках.
Чтобы запомнить правило знаков можно составить таблицу определения знаков числа.
Правило знаков для чисел
| + (+) = + | + (−) = − |
| − (−) = + | − (+) = − |
Или выучить простое правило.
Запомните!
Минус на минус даёт плюс.
Плюс на минус даёт минус.
Координатная прямая Координаты точек на числовой оси Сложение отрицательных чисел Вычитание отрицательных чисел Умножение отрицательных чисел Деление отрицательных чисел
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».
Оставить комментарий:
| Отправить |
Основные правила для положительных и отрицательных чисел
Описание
Правила для добавления и вычитания двух чисел положительных и отрицательных
Источник
, созданный Кариной Гото для вашего вашего YourDictionary
Числа больше нуля называются положительными числами, а числа меньше нуля — отрицательными числами. Это означает, что они падают по обе стороны от числовой прямой. Однако то, что они находятся на одной линии, не означает, что они следуют одним и тем же правилам! Продолжайте читать список основных правил использования положительных и отрицательных чисел в математике.
При использовании положительных и отрицательных чисел используются правила для чисел со знаком (числа с положительными или отрицательными знаками перед ними).
Эти шаги, также известные как операции над числами со знаком, помогут вам избежать путаницы и решить математические задачи как можно быстрее и правильнее.
Следуйте этим правилам, чтобы определить лучший способ сложения, вычитания, умножения и деления положительных и отрицательных чисел. Помните, что если нет знака + или -, число положительное.
Реклама
Дополнение: одинаковые знаки, добавьте числа
Когда вы складываете два числа вместе, и они имеют одинаковый знак (два положительных или два отрицательных числа), сложите числа и сохраните знак. Например:
- 1 + 1 = 2
- 51 + 32 = 83
- -14 + (-6) = -20
- -196 + (-71) = -267
Обратите внимание, что уравнения с двумя положительные суммы имеют положительные суммы, а уравнения с двумя отрицательными числами имеют отрицательные суммы. Если вы используете числовую прямую для решения задачи, добавление двух положительных чисел приведет к положительной стороне, а добавление двух отрицательных чисел приведет к отрицательной стороне.
Сложение: разные знаки, вычитание чисел
Если вы складываете положительные и отрицательные числа вместе, вычтите меньшее число из большего и используйте знак из большего числа. Например:
- 6 + (-5) = 1
- -17 + 22 = 5
- -100 + 54 = -45
- 299 + (-1) = 298
Как видите, сложив числа с разными знаками на самом деле является формой вычитания. При использовании числовой прямой ваша сумма будет ближе к нулю.
Реклама
Вычитание: Переключиться на сложение
Вычитание положительных и отрицательных чисел означает, что вы складываете противоположные числа или добавите обратное. Замените знак вычитания на сложение, а следующий за ним знак измените на противоположный. Затем следуйте инструкциям по добавлению. Например:
- -3 — (+5) становится -3 + (-5) = -8
- 9 — (-7) становится 9 + (+7) = 16
- -14 — (+8) становится -14 + (-8) = -22
- 25 — (-90) становится 25 + (+90) = 115
Хороший совет: всякий раз, когда вы видите знак минус и знак минус вместе, например, в 9 — (-7), немедленно превращайте их в положительные знаки.
Отрицательные знаки компенсируют друг друга, и уравнение становится задачей на сложение.
Умножение и деление: один и тот же знак, положительный результат
Кажется, что умножение и деление сложнее, чем сложение и вычитание, но на самом деле они намного проще. Правило умножения положительных и отрицательных чисел с одинаковым знаком (два положительных или два отрицательных) состоит в том, что произведение всегда будет положительным. Например:
- 8 x 4 = 32
- (-8) x (-4) = 32
- 10 x 9 = 90
- (-10) x (-9) = 90
То же правило применяется для деления . При делении числа на другое число с тем же знаком частное (ответ) положительно. Например:
- 12 ÷ 6 = 2
- -12 ÷ (-6) = 2
- 100 ÷ 5 = 20
- -100 ÷ (-5) = 20
числа всегда равны положительному числу? Подобно вычитанию отрицательных чисел, эти операции превращают отрицательные числа в противоположные (обратные).
По сути, вы вычитаете отрицательное число несколько раз — и, как показано выше, вычитание отрицательных чисел приводит к положительному уравнению.
Реклама
Описание
Правила для умножения и деления двух чисел положительные и отрицательные
ИСТОЧНИК
Созданы Кариной Гото для вашего. Умножение и деление: обратный знак, отрицательный результат
При умножении положительного и отрицательного числа произведение всегда будет отрицательным. Неважно, в каком порядке стоят знаки. Например:
- 6 х (-7) = -42
- -7 х 6 = -42
- 12 х (-11) = -132
- -11 х 12 = -132
Во всех этих случаях вам сначала нужно умножить или разделить числа. Затем решите, является ли произведение или частное положительным (два положительных или два отрицательных в уравнении) или отрицательным (один положительный и один отрицательный в уравнении).
Еще один способ подумать о сложении положительных и отрицательных чисел — посмотреть на знаки подряд.
Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:- 7 + (+2) = 9 (++ похожи на знаки, поэтому уравнение представляет собой сложение)
- 9 + (-8) = 1 (+- не являются знаками, поэтому уравнение представляет собой вычитание)
- 11 — (+13) = 2 (-+ разные знаки, поэтому уравнение представляет собой вычитание)
- 15 — (-10) = 25 (— похожи на знаки, поэтому уравнение представляет собой сложение)
Этот метод следует те же правила, что и выше, но они могут помочь вам решить проблему быстрее, если вы предпочитаете работать над знаками заранее. Как только вы концептуально поймете положительные и отрицательные числа, вы сможете решить, какой метод лучше всего подходит для вас.
Объявление
Понимание основ математики
Как только вы познакомитесь с основами математики и ее правилами, перед вами откроется весь математический мир.
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.Сложение и вычитание положительных и отрицательных чисел
Числа могут быть положительными или отрицательными
Это номер строки:
Отрицательные числа (-) Положительные числа (+) «-» — отрицательный знак. «+» — положительный знак Отсутствие знака означает положительный результат
Если в числе без знака это обычно означает, что это положительное число .
Пример: 5 на самом деле +5
Играй!
На числовой прямой положительный идет вправо, а отрицательный — влево.
Попробуйте использовать ползунки ниже и посмотрите, что произойдет:
числа/изображения/номер-линия-add.js?sub=n
Воздушные шары и гири
Давайте представим числа как шарики (положительные) и веса (отрицательные):
К этой корзине привязаны воздушные шары и грузы:
- Воздушные шары подтягиваются ( положительный )
- И гири тянутся вниз ( отрицательный )
Добавление положительного числа
Добавление положительных чисел — это простое сложение.
Мы можем добавить воздушные шары (мы добавляем положительное значение )
корзина поднимается вверх (положительный результат)
Пример: 2 + 3 = 5
на самом деле говорит
«Положительное 2 плюс положительное 3 равно положительному 5»
Мы могли бы записать это как (+2) + (+3) = (+5)
Вычитание положительного числа
Вычитание положительных чисел — это простое вычитание.
Мы можем забрать воздушные шары (мы вычитаем положительное значение )
корзина тянется вниз (негатив)
Пример: 6 − 3 = 3
на самом деле говорит
«Положительные 6 минус Положительные 3 равно Положительным 3»
Мы могли бы записать это как (+6) — (+3) = (+3)
Добавление отрицательного числа
Теперь давайте посмотрим, как выглядит сложение и вычитание отрицательных чисел:
Мы можем добавлять веса (мы добавляем отрицательные значения )
корзина тянется вниз (негатив)
Пример: 6 + (−3) = 3
на самом деле означает
«Положительные 6 плюс отрицательные 3 равны положительным 3»
Мы могли бы записать это как (+6) + (−3) = (+3)
Последние два примера показали нам, что удаление воздушных шаров (вычитание положительного значения) или добавление веса (добавление отрицательного значения) приводит к тому, что корзина опускается.
Таким образом, они имеют одинаковый результат :
.- (+6) — (+3) = (+3)
- (+6) + (-3) = (+3)
Другими словами вычитание положительного аналогично добавлению отрицательного .
Вычитание отрицательного числа
Наконец, мы можем убрать веса (мы вычитаем отрицательные значения )
корзина поднимается вверх (положительный результат)
Пример: чему равно 6 − (−3) ?
6−(−3) = 6 + 3 = 9
Да, действительно! Вычитание минуса – это то же самое, что добавление!
Два минуса дают плюс
Что мы нашли?
Добавление положительного числа — это простое сложение…
Добавление положительного Добавление
Положительное и отрицательное вместе…
Вычитание положительного
или
Добавление отрицательного
равно
ВычитаниеПример: Сколько будет 6 − (+3) ?
6−(+3) = 6 − 3 = 3
Пример: Сколько будет 5 + (−7) ?
5+(-7) = 5 — 7 = -2
Вычитание отрицательного значения.
..Вычитание минуса аналогично Сложение
Пример: чему равно 14 − (−4) ?
14−(−4) = 14 + 4 = 18
Правила:
Все это можно поместить в два правила :
Правило Пример +(+) Два одинаковых знака становятся положительным знаком 3+(+2) = 3 + 2 = 5 −(−) 6−(−3) = 6 + 3 = 9 +(-) Два разных знака становятся отрицательным знаком 7+(−2) = 7 − 2 = 5 −(+) 8−(+2) = 8 − 2 = 6 Они «подобны знакам», когда они похожи друг на друга (другими словами: одинаковы).
Итак, все, что вам нужно запомнить, это:
Два похожих на знака становятся положительным знаком
Два не похожих на знака становятся отрицательным знаком
Пример: Что такое 5+(−2) ?
+(-) — это в отличие от знаков (они не одинаковы), поэтому они становятся отрицательным знаком .
5+(−2) = 5 − 2 = 3
Пример: чему равно 25−(−4) ?
−(−) равно подобны знакам , поэтому они становятся положительным знаком .
25−(−4) = 25+4 = 29
Начальный отрицательный результат
Что, если мы начнем с отрицательного числа?
Использование числовой линии может помочь:
Пример: чему равно −3+(+2) ?
+(+) — это , как и знаков, поэтому они становятся положительным знаком .
-3+(+2) = -3 + 2
Начните с -3 на числовой прямой,
сдвиньте вперед 2 и вы окажетесь на -1−3+(+2) = −3 + 2 = −1
Пример: чему равно −3+(−2) ?
+(-) являются в отличие от знаков, поэтому они становятся отрицательным знаком .
-3+(-2) = -3 — 2
Начните с -3 на числовой прямой,
переместитесь назад на 2, и вы окажетесь на -5-3+(-2) = — 3 − 2 = −5
А теперь поиграй!
Попробуйте сыграть в Casey Runner, вам нужно знать правила положительного и отрицательного, чтобы добиться успеха! Объяснение здравого смысла
И есть объяснение «здравого смысла»:
Если я скажу «Ешь!» Я призываю вас есть (положительно)
Если я скажу «Не есть!» Я говорю обратное (отрицательно).
Теперь, если я скажу « НЕ НЕ ЕШЬ!», я говорю, что не ем. хочу, чтобы вы голодали, поэтому я снова говорю: «Ешьте!» (положительно).
Итак, два минуса дают плюс, и если вас это устраивает, то вы сделали!
Другое объяснение здравого смысла
Друг +, враг —
+ + ⇒ + друг друга мой друг + — ⇒ — друг врага мой враг — + ⇒ — враг друга мой враг − − ⇒ + враг врага мой друг Пример банка
Пример: В прошлом году банк по ошибке списал с вашего счета 10 долларов, и они хотят это исправить.
Итак, банк должен забрать минус 10 долларов .
Допустим, ваш текущий баланс составляет 80 долларов США, поэтому у вас будет:
80 долларов США − (− 10 долларов США) = 80 долларов США + 10 долларов США = 90 долларов США
Таким образом, вы получите 10 долларов США еще в вашем аккаунте.
Длинный пример, который может вам понравиться
Очки союзников
Элли может быть озорной или милой. Итак, родители Элли сказали
«Если ты будешь хорошим, мы добавим 3 балла (+3).
Если ты будешь непослушным, мы уменьшим 3 балла (−3).
Когда ты наберешь 30 баллов, ты получишь игрушку.»Союзник начинает день с 9 очками: 9 Мама Элли обнаруживает пролитое молоко: 9 − 3 = 6 Потом папа признается, что пролил молоко и пишет «отменить».
Как нам «отменить» минус 3?
Мы добавляем 3 обратно!Итак, мама считает: 6 — (-3) = 6 + 3 = 9 Таким образом, когда мы вычитаем отрицательное значение, мы получаем 90 149 очков (т. е. то же самое, что и сложение очков).
Таким образом, вычитание отрицательного значения равно . Сложение
.Несколько дней спустя. У Элли 12 очков. Мама добавляет 3 балла, потому что в комнате Элли чисто. 12 + 3 = 15 Папа говорит: «Я убрал эту комнату» и пишет «отменить» на графике. Мама считает: 15 — (+3) = 12 Папа видит, как Элли расчесывает собаку. Пишет «+3» на графике. Мама считает: 12 + (+3) = 15 Элли бросает камень в окно. Папа пишет «-3» на графике.
Два одинаковых знака подряд (++ или —) означают, что вы складываете числа, а два разных знака подряд (+- или —) означают, что вы вычитаете. Например:
В отличие от других предметов, в математике нет нюансов или интерпретаций — она просто такая, какая есть! Для дополнительной математической практики ознакомьтесь с инструкциями по решению задач на деление в длину (с примерами). Вы также можете просмотреть различные типы чисел в математике перед следующим заданием по математике.
..
