Перевод градусов в радианы и обратно: понятие, взаимосвязь, примеры
Оглавление
Время чтения: 6 минут
1 391
Основное понятие градуса и радиана и их взаимосвязь
В математике, такое определение, как угол принято измерять градусами и радианами.
Эти два измерения угла имеют взаимосвязь и необходимо четко понимать в чем она заключается.
В данном материале, мы постараемся разобраться и вывести
основную формулу для вычисления градусов в значение радиан, и соответственно в обратном порядке.
Определение
Радиан — это угол, который образуется окружной дугой, ее длина, следовательно, равняется радиусу данной окружности.
Радианная мера — угловое значение,где за единицу берется угол в 1 радиан. А именно, вышеупомянутая мера любого угла — это соотношение принятого угла к радиану. Из этого следует, что величина полного значения угла равняется \[2 \cdot \pi\] радиан.
Определяем длину окружности, по стандартной формуле:
\[ l=2 \cdot \pi \cdot r \]
Чтобы определить полный угол в радианах проводим следующие действие: \[\frac{l}{r}=\frac{2 \cdot \pi \cdot r}{r}=2 \cdot \pi\] , соответственно в градусах значение будет равно 360.
{\circ}}{2 \cdot \pi} \cdot 3600 \approx 206280\].
\[ 1 \text { радиан }=\left(\frac{180}{\pi}\right) \text { градусов. } \]
\[ 1 \text { градус }=\left(\frac{\pi}{180}\right) \text { рад. } \]
Рассмотрим на конкретном примере:
\[1 \text { радиан }=\left(\frac{180}{\pi}\right)=\left(\frac{180}{3,14}\right)=57,324\] следовательно в 1 радиане 57 градусов.
\[1 \text { градус }=\left(\frac{\pi}{180}\right) \text { радиан }=\left(\frac{3,14}{180}\right)=0,017\] радиан (сокращенно рад.).
\[\text { х радиан }=\left(\frac{\chi \cdot 180}{\pi}\right)\], дословно будет звучать как: 180 * умножить на числовое значение угла и раздели.
Соответствие градусов и радиан принято, для удобства решения сводить в таблицу.
Пример, приведен в таблице 1.
Таблица 1. Соотношение значений.
| Числовые значения в градусах | Соответствующие данные радиан |
| 1° | 0,018 |
| 2° | 0,035 |
Как мы видим изученная тема не очень сложная.
{\circ}=\left(\frac{\pi}{180}\right) \cdot 60 \text { радиан }=1 \text { рад } \]
Ответ: 1 рад.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |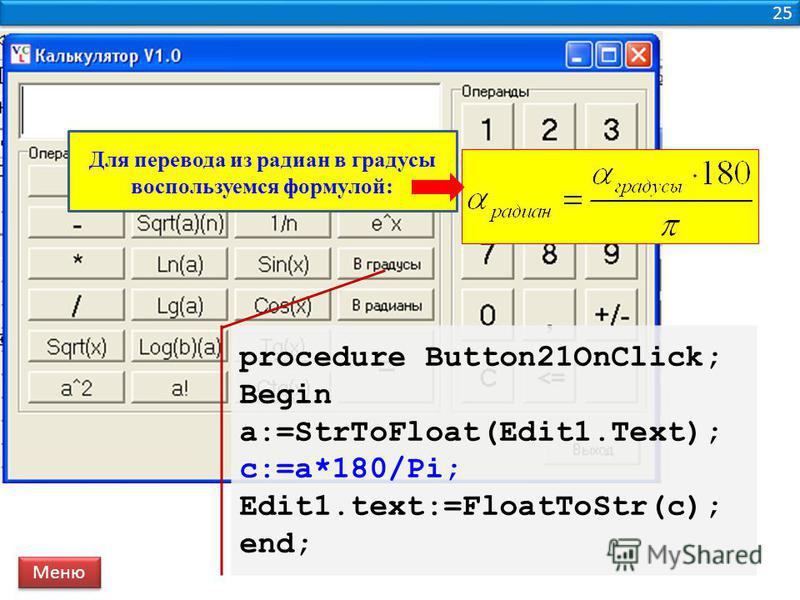
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | cos(pi/2) | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |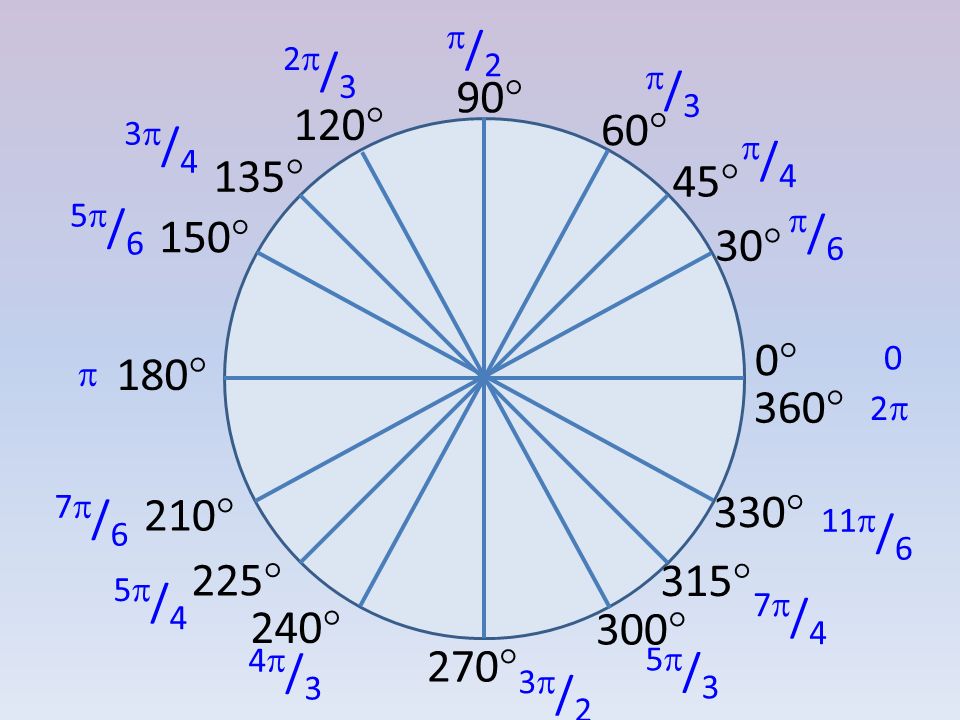
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | arcsin(-1/2) | ||
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |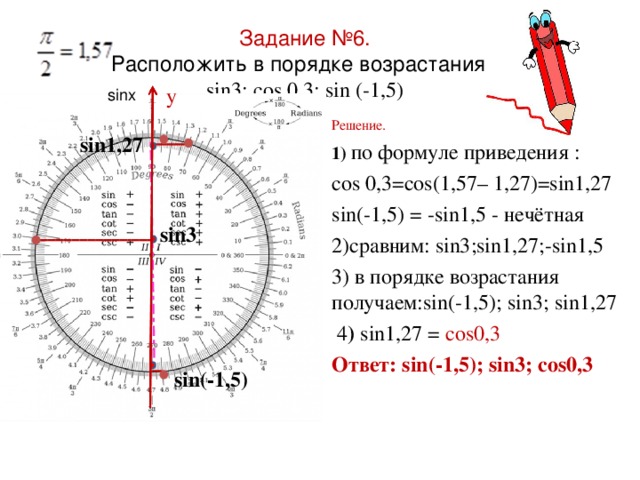
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
радиан в градусы — преобразование, формула, примеры
радианы в градусы — это форма преобразования, используемая для преобразования измерения углов в геометрии. Для измерения угла существуют две разные измерительные системы.
Двумя единицами измерения угла являются радианы и градусы. Единица радианы используется в основном в концепции тригонометрии. Меру углов можно преобразовать из радианов в градусы с помощью формулы. Чтобы понять эту формулу и преобразование радианов в градусы, мы поймем значение каждой единицы угла. В этой статье мы также увидим таблицу преобразования радианов в градусы.
| 1. | Радианы в градусы Преобразование |
| 2. | Радиан в Градус Формула |
| 3. | Как преобразовать радианы в градусы? |
| 4. | Радианы в градусы Таблица преобразования |
| 5. | Часто задаваемые вопросы по преобразованию радианов в градусы |
Радиан в градус Преобразование
Существуют две разные единицы измерения угла: радианы и градусы. Следовательно, для нас важно уметь переводить угловые единицы, то есть радианы в градусы и градусы в радианы.
Когда мы берем радиус круга и вращаем его, мы начинаем строить угол, который можно измерить в радианах или градусах. Давайте посмотрим, что означает каждая единица угла и как измерить угол.
Радианы
Когда мы полностью поворачиваем радиус вокруг окружности, он завершает один оборот. Угол, образуемый радиусом в центре круга после одного полного оборота, равен 2π радиан. Угол в радианах, образуемый радиусом в центре окружности, представляет собой отношение длины дуги к длине радиуса. Когда длина дуги становится равной длине радиуса, угол, образуемый в центре, становится равным 1 радиану. Обозначим единицу радиан как рад. радиан — единица измерения углов в системе СИ.
Градусы
Углы измеряются в градусах. Один оборот делится на 360 равных частей и каждая часть называется градусом. Угол, образовавшийся в центре окружности после одного полного оборота радиуса, равен 360°. Символ градусов обозначается как «°». Градусы не являются единицей СИ для измерения углов, но это общепринятая единица измерения.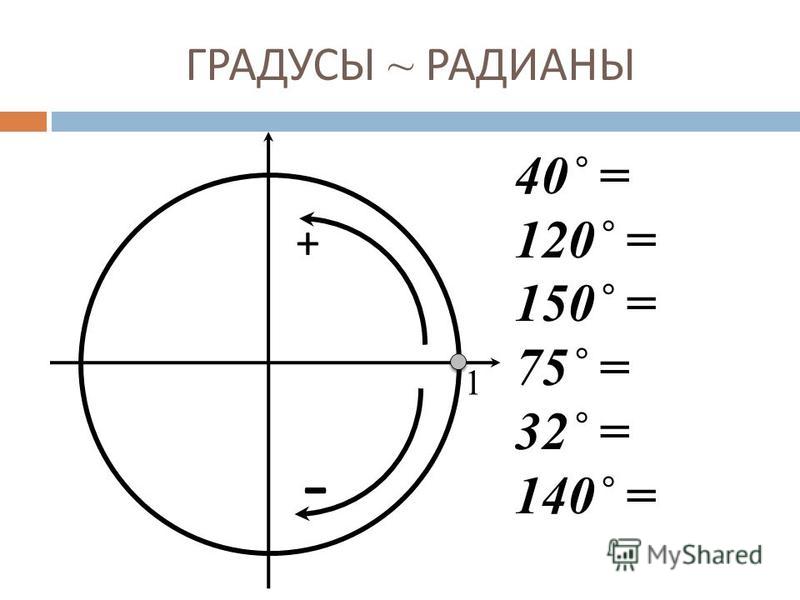
Следовательно, при решении задач предпочтительно переводить единицу измерения угла из радианов в градусы, чтобы лучше понять ее. Инструментом для измерения угла в градусах является транспортир.
Сравнивая меры угла для полного оборота, мы наблюдаем,
- 360 градусов = 2π радиан
- 180 градусов = π радиан
Радиан в Градус Формула
Формула преобразования радианов в градусы используется для преобразования радианов в градусы. Чтобы преобразовать радианы в градусы, нам нужно умножить радианы на 180°/π радиан. Когда мы измеряем углы, мы используем два типа единиц измерения: градусы и радианы, 1 градус записывается как 1°. А 1 радиан записывается как 1 (или) 1c т.е. если после меры угла нет единицы, значит она в радианах. Один оборот по окружности делится на 360 равных частей и каждая часть называется градусом. Один полный оборот против часовой стрелки в радианах составляет 2π, а в градусах — 360°. Таким образом, градусная мера и радианная мера связаны.
Формула для преобразования угла в радианах в градусы:
Угол в радианах × 180°/π = Угол в градусах
Формула перевода радиан в градусы
Один полный оборот вокруг окружности дает 2π радиан, что эквивалентно 360°. Следовательно, у нас есть 2π радиан = 360°. Теперь, чтобы вывести формулу перевода радианов в градусы, упростим это уравнение.
2π радиан = 360°
π радиан = 360°/2
π радиан = 180°
1 радиан = 180°/π
Следовательно, угол в градусах получается путем умножения угла в 180 радиан / π. то есть
Угол в радианах × 180°/π = угол в градусах
Таким образом, была получена формула преобразования радианов в градусы.
Таким образом, чтобы преобразовать радианы в градусы, используйте эту формулу = мера в радианах × (180°/π). Конечная единица измерения будет (°). 1 рад равен 57,296°.
Как преобразовать радианы в градусы?
Радианы и градусы — это две единицы измерения углов.
2π радиан эквивалентны 360°, полученным после одного полного оборота окружности. Преобразование радианов в градусы можно выполнить по формуле «Угол в радианах × 180°/π = угол в градусах». Любой угол, указанный в радианах, можно преобразовать в градусы, используя следующие шаги:
- Запишите величину угла, указанную в радианах.
- Мы знаем, что 1 радиан = 180°/π. Итак, чтобы преобразовать угол, указанный в радианах, в градусы, мы умножаем его на 180°/π.
Угол в градусах = угол в радианах × 180°/π - Упростите значения и выразите ответ в градусах (°).
Давайте разберемся с этим на примере.
Рассмотрим угол π / 6 радиан. Теперь нам нужно преобразовать радианы в градусы для этого угла, используя формулу преобразования.
(π / 6) × (180°/π) = (Угол в градусах)
Угол в градусах = 180°/6 = 30°
Следовательно, π / 6 радиан равно 30°.
Радианы в градусы Таблица преобразования
Теперь сопоставим перевод конкретных углов из радиан в градусы, которые чаще всего используются при решении задач.
В приведенной ниже таблице показаны значения радиана для соответствующих мер угла в градусах:
Радианы в Градусы Диаграмма
Мы также можем обратиться к следующей таблице из радианов в градусы, чтобы увидеть измерение любого угла в градусах по отношению к его измерению в радианах. Мы знаем, что для единичного круга длина окружности будет равна 2π, что аналогично вращению на 360º, как показано ниже.
☛Важные замечания по преобразованию радианов в градусы
Вот несколько важных моментов, которые следует учитывать при преобразовании радианов в градусы:
- Углы измеряются с использованием двух основных единиц измерения: градусов и радианов. .
- Один полный оборот против часовой стрелки равен 2π рад в радианах.
- 1° равен 0,017453 радиана, а 1 рад равен 57,2958°.
- Чтобы преобразовать угол из радианов в градусы, мы умножаем его на 180°/π.
- Чтобы преобразовать угол из градусов в радианы, мы умножаем его на π/180°.
☛Похожие темы
Ознакомьтесь с еще несколькими интересными темами, тесно связанными с преобразованием радианов в градусы.
- Калькулятор радианов в градусы
- Формула для поворота на 180 градусов
- радиан
- Градусов
- Калькулятор радианов в градусы
Радианы в Градусы Примеры
Пример 1: Преобразуйте угол π/5 рад в градусы, используя формулу радианов в градусы.
Решение: Формула для преобразования радианов в градусы:
Угол в радианах × 180°/π = Угол в градусах
(π/5) × (180°/π )= Угол в градусах
Угол в градусах = 180°/5
Угол в градусах = 36°
Следовательно, π/5 рад равно 36°, если использовать формулу преобразования радианов в градусы.
Ответ: π/5 рад = 36°
Пример 2: В окружности с центром О точки А и В лежат на окружности.
∠AOB имеет меру π/4 рад. Преобразование меры угла ∠AOB из радианов в градусы.Решение: Дано: ∠AOB = π/4 рад
Нам нужно преобразовать π/4 рад в градусы, используя формулу радианы в градусы.
Требуется следующая формула: Угол в радианах × 180°/π = Угол в градусах
π/4 рад × (180°/π ) = (Угол в градусах)
Угол в градусах = 180°/4
Угол в градусах = 45°
Следовательно, мера ∠AOB равна 45° в градусах.
Ответ: ∠AOB = 45°
Пример 3: Мать Эми дала ей (1/5) th круглого торта и спросила ее об угле, образуемом ломтиком в центре торта. Можете ли вы помочь Эми определить угол среза в радианах и градусах?
Решение: Порция торта, полученная Эми = (1/5) -й части всего торта. Поскольку форма торта круглая, а угол полного круга = 360°, мы можем заключить, что:
Угол полного торта = 2π рад
Угол для (1/5) -го среза = 2π/5 рад
Мы знаем,
Значение этого угла в градусах = угол в радианах × (180°/π)
= (2π /5) × (180°/π) = 72°
Таким образом, угол среза Эми в радианах равен 2π/5 рад, а при переводе из радиан в градусы его мера равна 72°.
Ответ: Срез Эми в радианах равен 2π/5 рад, а в градусах равен 72°.
∠AOB имеет меру π/4 рад. Преобразование меры угла ∠AOB из радианов в градусы.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы по радианам в градусы
Что означает преобразование радианов в градусы в геометрии?
В геометрии есть две единицы измерения углов: радианы и градусы. Радианы — это единица СИ для измерения углов. Один полный оборот окружности равен 2π радианам, что эквивалентно 360° в градусах. Следовательно, 2π радиан = 360°, что подразумевает 1 радиан = (180°/π) градусов. Поэтому, когда единица измерения углов преобразуется из радианов в градусы с помощью формулы, это называется преобразованием радианов в градусы.
Как преобразовать радианы в градусы?
Преобразование величины угла из радианов в градусы можно выполнить по следующей формуле: Угол в радианах × 180°/π = Угол в градусах.
Например, рассмотрим угол π/9 рад. Теперь, используя формулу преобразования радианов в градусы, мы имеем π/9 рад × 180°/π = (угол в градусах).
Угол в градусах = 180°/9 = 20°
Следовательно, используя формулу, π/9 рад равно 20°
Какая формула используется для преобразования радианов в градусы?
Мы знаем, что 2π радиан равно 360° в градусах, то есть 2π радиан = 360°. Упрощая это уравнение, мы можем получить формулу для перевода радианов в градусы.
2π радиан = 360°
1 радиан = 360°/2π
1 радиан = 180°/π
Следовательно, необходимая формула: Угол в радианах × 180°/π = Угол в градусах
В чем разница между радианами и градусами?
Радианы и градусы являются единицами измерения углов. Радиан — это единица СИ, а градус — нет, но это общепринятая единица измерения углов. Радианы измеряют углы по пройденному расстоянию, тогда как градусы измеряют углы по наклону.
Для чего используется калькулятор радианов в градусы?
Калькулятор радианов в градусы — это онлайн-инструмент, который помогает конвертировать радианы в градусы для заданного значения.
Это поможет вам преобразовать радианы в градусы за несколько секунд. Чтобы преобразовать угол, указанный в радианах, в градусы, нам просто нужно умножить угол на 180 ° / π.
Что такое радиан в 1 градус?
Один полный оборот окружности равен 2π радианам, что эквивалентно 360°, следовательно, мы имеем уравнение:
2π рад = 360°
1° = 2π/360 рад
1° = π/180 рад
Следовательно, 1 градус равен π/180 радиан.
Какое выражение преобразует pi/4 радианы в градусы?
Используя формулу преобразования радианов в градусы, градусы = радианы × 180 / π
Y° = (180/π) × π/4 90 106
Y°= 45 градусов
Как перевести радианы в градусы, минуты и секунды?
Чтобы преобразовать радианы в градусы, мы разделим на π, а затем умножим на 180. Доли градуса можно преобразовать в минуты, умножив дробь на 60, чтобы получить количество минут. Точно так же любая часть оставшихся минут будет умножена на 60, чтобы получить количество секунд.
Можно ли преобразовать отрицательные значения радиана в градусы, используя формулу радиана в градусы?
Да, мы можем преобразовать отрицательные значения радиана в градусы, используя формулу радиан-градус.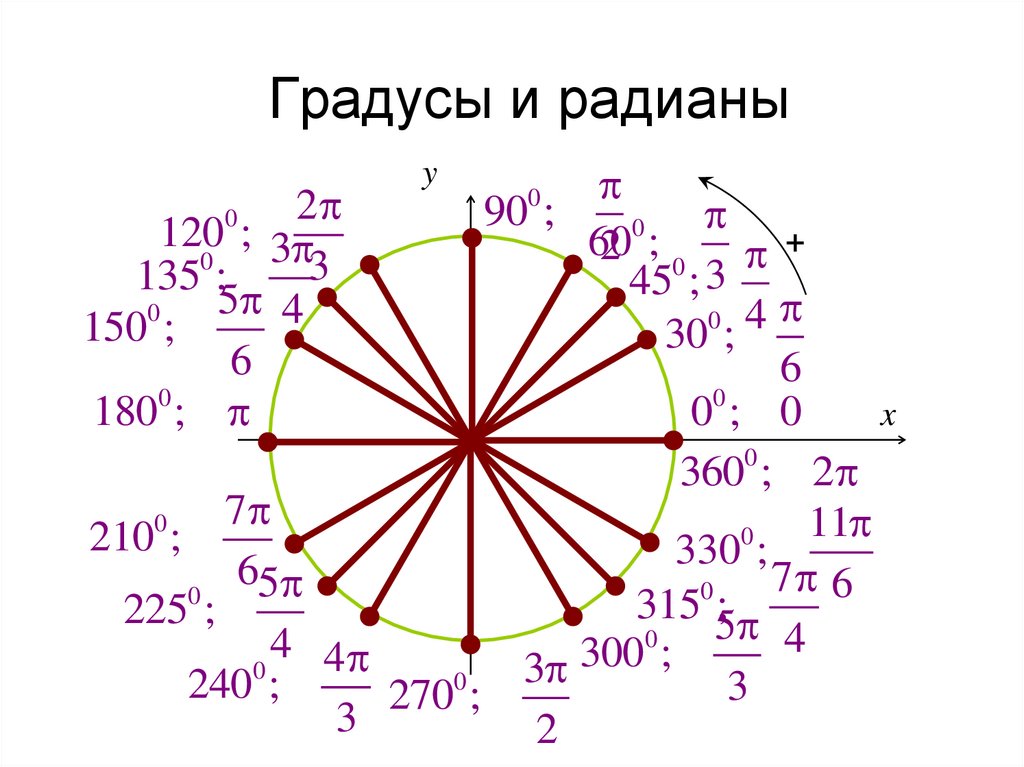
Формула градусы = радианы × 180 / π, и ее можно использовать как для положительных, так и для отрицательных значений.
Какое выражение переводит 8π радиан в градусы?
Используя формулу преобразования радианов в градусы, градусы = радианы × 180 / π
Z° = (180/π) × 8π
Z°= 1440 градусов
Как преобразовать 6π в градусы, используя формулу радиан в градусы?
Используя формулу преобразования радианов в градусы, градусы = радианы × 180 / π
X° = (180/π) × 6π 90 106
X°= 180 × 6 90 106
X°= 1080°
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по измерению углов
Радианы в градусы — преобразование, формулы, примеры решений и часто задаваемые вопросы
Радианы в градусы — это тип преобразования, используемый в геометрии для преобразования угловых измерений. Существует два альтернативных метода измерения угла. Радианы и градусы — это две единицы измерения углов. Радиан — наиболее часто используемая единица измерения в тригонометрии.
Различные типы углов измеряются в радианах, а затем преобразуются в градусы по формуле. Эта формула обсуждается ниже.
Для измерения углов используются два отдельных способа. Прямой угол делится на 90 равных частей, которые в шестидесятеричной системе называются градусами. Каждый градус делится на 60 равных частей, называемых минутами, которые далее делятся на 60 равных частей, называемых секундами. Преобразование градусов в радианы также можно узнать здесь.
- 60” = 1 минута (1’)
- 90° = 1 прямой угол
Радианы
Угол, образуемый радиусом с центром окружности после полного оборота, называется 2π радиан. Угол в радианах, образованный радиусом в центре окружности, представляет собой отношение длины дуги к длине радиуса. Если длина дуги равна длине радиуса, угол, образуемый в центре, называется 1 радианом. Единицей радиана является рад . Радиан — это единица измерения углов в системе СИ.
Градусы
Углы также можно измерять в градусах. Один оборот делит окружность на 360 равных частей, каждая из которых равна градусу. Таким образом, угол, образовавшийся в центре окружности после одного полного оборота, равен 360°. Для обозначения градусов используется символ «°». Градус не является единицей СИ для измерения угла, но это наиболее часто используемая единица измерения угла.
Путем сравнения мер угла для полного оборота
- 360 градусов = 2π радиан
- 180 градусов = π радиан
Как преобразовать градусы в радианы?
Значение 180° равно π радианам. Для преобразования заданного угла из градусов в радианы мы умножаем значение угла в градусах на коэффициент π/180.
Где значение π = 22/7 или 3,14
Шаги, показанные ниже, используются для преобразования угла в градусах в радианы.
Шаг 1: Отметьте значение заданного угла в градусах
Шаг 2: Умножьте полученное на предыдущем шаге значение на π/180
Шаг 3: Решите выражение и объясните ответ
Шаг 4: Полученный результат является мерой угла в радианах
Пример: Преобразование 60 градусов в радианы.
Решение:
Данный угол равен 60 градусов
Угол в радианах = Угол в градусах x (π/180) 2 Следовательно, 60 градусов равны π/3 в радианах.
Формула радианов в градусы
Формула радианов в градусы преобразует значение угла в радианах в градусы. Чтобы преобразовать угол в радианах в градусы, мы умножаем значение в радианах на 180°/π. Углы используются в двух единицах: градусах и радианах, 1 градус выражается как 1°, тогда как 1 радиан выражается 1 c или 1, т. е. ни одна единица измерения также не используется для выражения угла в радианах. Формула преобразования угла в радианах в градусы:
Угол в радианах × 180°/π = Угол в градусах
2π радиан = 360°
π 8 радиан = 1080 02 1 радиан = 180/π градусов = 57,296 градусов
Таблица преобразования радианов в градусы
В приведенной ниже таблице показаны значения угла в радианах и соответствующие им значения в градусах.
| Угол в радианах | Угол в градусах | |
| 0 | 0° | 30° |
| π/4 | 45° | |
| π/3 | 60° | |
| π/2 | 90° | |
| π | 1007688 (3π)/2 | 270º |
| 2π | 360º |
Решенные примеры для R Перевод
адианов в градусыПример 1. Преобразование 9π/5 радиан в градусы.
Решение:
Поскольку π радиан = 180° или 1 радиан = 1c = (180/π)°
Следовательно, (9π/5) c = (9π/5 × 180 )° = 324°
Таким образом, (9π/5) c = 324 o
Пример 2: Преобразование −5π/6 радиан в градусы.
Решение:
Мы знаем, что π радиан = 180° или 1 радиан = 1c = (180/π)°
Следовательно, (−5π/6) c = (−5π/6 × 180/π)° = −150 °
Таким образом, (9π/5) c = −150°
Пример 3: Преобразование 18π/5 в градусы.
Решение:
Мы знаем, что π радиан = 180° или 1 радиан = 1c = (180/π)°
Следовательно, (18π/5) c = (18π/5 × 18π/5 × 18π/5 π)° = 648°
Таким образом, (18π/5) c = 648°
Пример 4: Преобразовать −3 радиана в градусы.
Решение:
Мы знаем, что π радиан = 180° или 1 радиан = 1c = (180/π)°
Следовательно, (−3) c = (−3 × 180/π) ° = (180 × 7 × −3/22)° = (−1719/11) = −171°(9 × 60/11)’ = −171°49’5”
Таким образом, (−3) c = −171 o 49 футов 5 дюймов
Пример 5: Преобразование 11 радиан в градусы.
Решение:
Мы знаем, что π радиан = 180° или 1 радиан = 1 c = (180/π)°
Следовательно, (11) c = (11 × 180/π)° = (11 × 180 × 7 /22) = 630°
Таким образом, (11) c = 630°
Пример 6: Преобразовать 1 радиан в градусы.
Решение:
Мы знаем, что π радиан = 180° или 1 радиан = 1 c = (180/π)°
Следовательно, (1) c
0 )° = (180 × 7/22) = 57°(3 × 60/11) = 57°16′(4 × 60/11)” = 57°16’21”Таким образом, (1) c = 57 o 16’21”
Часто задаваемые вопросы о преобразовании радианов в градусы
Вопрос 1: В чем разница между радианами и градусами?
Ответ:
Радианы и градусы — это единицы измерения углов. Радиан — это единица СИ для измерения угла, тогда как градус — это общая единица, используемая для измерения углов. Отношение между ними равно π рад = 180°
Вопрос 2: Чему равен радиан 1 градуса?
Ответ:
Полный оборот окружности равен 2π радианам, что эквивалентно 360°, то есть 2π рад = 360°
Таким образом, 1° = 2π/360 рад 901 равно π/180 радиан.
