12. Уравнения, содержащие модуль. Рациональные уравнения
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯ
Уравнения, содержащие модуль
Если в уравнении некоторые выражения, содержащие неизвестное, стоят по знаком модуля, то решение исходного уравнения ищется отдельно на каждом из промежутков знакопостоянства этих выражений.Пример 1
Решить уравнение |3x-6|=x+2.
Решение:
Рассмотрим первый случай: 3х-6≥0, тогда 3х-6=х+2, 2х=8, х=4.
Рассмотрим второй случай: 3х-6<0, тогда 3х-6=-(х+2), 4х=4, х=1.
Ответ: 1; 4.
Пример 2
Решить уравнение |x-2| — 3|x-1| + 4|x-3| = 5.
Отметим на координатной прямой точки:
х-2=0 х-1=0 х-3=0х=2 х=1 х=3
Рассмотрим решения уравнения на промежутках (-∞; 1]; (1; 2]; (2; 3] и (3; +∞).
При х≤1: -(х-2) + 3(х-1) -4(х-3)=5, -х+2+3х-3-4х+12=5, -2х=-6, х=3. Ответ не принадлежит промежутку, следовательно нет решений.
При 1<х≤2: -(х-2) — 3(х-1) -4(х-3)=5, -х+2-3х+3-4х+12=5, -8х=-12, х=1,5. Ответ принадлежит промежутку.
При 2<х≤3: х-2 — 3(х-1) -4(х-3)=5, х-2-3х+3-4х+12=5, -6х=-8, х=4/3. Ответ не принадлежит промежутку, следовательно нет решений.
При х>3: х-2 — 3(х-1) +4(х-3)=5, х-2-3х+3+4х-12=5, 2х=16, х=8. Ответ принадлежит промежутку.
Ответ: 1,5; 8.
Рациональные уравнения Рациональным уравнением называется уравнение вида
где P(x), Q(x) — многочлены.
Решение уравнения сводится к решению системы:Пример
Решить уравнение
Решение:
x2-4=0, х-2≠0,x2=4, х≠ 2.
х=-2 или х=2.
Число 2 не может быть корнем.
Ответ: -2.
УПРАЖНЕНИЯ 1.
 Из данных уравнений выберите те, которые не имеют корней:
Из данных уравнений выберите те, которые не имеют корней:а) |x|+4=1; |x-5|=2; |x+3|=-6. б) |1+x|=3; |1-x|=-4; 8+|x|=2.
Решение:
а) |x|+4=1 не имеет корней, т.к. |x|=-3 и модуль не может быть отрицательным числом; |x-5|=2 имеет корни; |x+3|=-6 не имеет корней, т.к. модуль не может быть отрицательным числом.
Ответ: |x|+4=1; |x+3|=-6.
2. Решите уравнение:
а) |5x|=15; б) |2x|=16.
Решение:
а) |5x|=15;
|5||x|=15;
5|x|=15;
|x|=3;
x=3 или x=-3.
3. Решите уравнение:
а) |5x+1|=5; б) |2x-1|=10.
а) |5x+1|=5;
Ответ: -1,2; 0,8.
4. Решите уравнение:
а) |5x2+3x-1|=-x2-36; б) |3x2-5x-4|=-4x2-23.
Решение:
а) |5x2+3x-1|=-x2-36. Рассмотрим выражение -x2-36, оно принимает отрицательные значения при любых значениях х, следовательно уравнение |5x2+3x-1|=-x2-36 не имеет корней.
Ответ: нет корней
5. Решите уравнение: Решение:
Ответ: -1/3.
6. Решите уравнение:
Решение:
14х2-5x-1=0,
7. Решите уравнение:
Решение:
8. Решите уравнение: Решение:
х ≠3.
Ответ: -4; 1.
9. Найдите, при каком значении переменной значение выражения
равно: а) -6; б) 6.
 Решение:
Решение:10. Решите уравнение:
Решение:
а) Разложим знаменатели на множители:
х2-36=(x-6)(x+6).
108-24x+х2=(x-6)(x-18).
2x-36=2(x-18).
11. Решите уравнение:
а) х2-6|x|=0; б) х2+4|x|=0.
а) х2-6|x|=0;
х≥0: х2-6x=0; х(х-6)=0, x1=0, x2=6.
x<0: х2+6x=0; х(х+6)=0, x1=0, x2=-6.
Ответ: -6; 0; 6.
12.Решите уравнение:
а) х2-3|x|+2=0; б) х2-2|x|+1=0.
Решение:а) х2-3|x|+2=0.
х≥0: х2-3x+2=0; D=9-8=1, x1=2, x2=1.
x<0: х2+3x+2=0; D=9-8=1, x1=-2, x2=-1.

Ответ: -2; -1; 1; 2.
13. Решите уравнение:
а) |x-2|+|x-4|=5; б) |x-1|-|x-4|=6.
Решение:а) |x-2|+|x-4|=5.
x≤2: -(x-2)-(x-4)=5, -x+2-x+4=5, x=0,5.
2<x≤4: x+2-(x-4)=5, x-2-x+4=5, 2=5 — нет решений.
x>4: x-2+x-4=5, 2x=11, x=5,5.
Ответ: 0,5; 5,5.
14.Решите уравнение:
а) |3- |4- |x|||=5; б) 8-|2 -|x|||=3.
Решение:а) |3- |4- |x|||=5;
3- |4- |x||=5 или 3- |4- |x||=-5;
|4-|x||=-2 — нет решений |4-|x||=8
4-|x|=8 или 4-|x|=-8
|x|=-4 — нет решений |x|=12
х=12 или х=-12.

Ответ: -12; 12.
15. Решите уравнение:
Решение:
а)
3x-7≥0: х2
3x-7<0: х2-3x-10=0; D=9+40=49, x1=5, x2=-2.
3x-7≠0, x≠7/3.
Ответ: -2; 5.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ 1. Какие из чисел -4; -1; 2; 1,5; 2,5 являются корнями уравнения:
а) |3x-1|=5; б) |4-2x|=1?
2. Решите уравнение:
а) |3x|=21; б) |2x|=-12.
3. Решите уравнение:
а) |2x-5|=1; б) |3x+6|=18.
4. Решите уравнение:
5. Решите уравнение:
6. Решите уравнение:
7. Решите уравнение:
8. Решите уравнение:
9. Решите уравнение:
а) 3(x-1) = |2x-1|; б) |5-2x|=|x+4|.
10. Решите уравнение:
а) |х2+x|=12; б) |х2-3x|=10. 2+3x-10=0`;
2+3x-10=0`;
`D=9-4*(-10)=49`;
`x=(-3+7)/2=2`;`x=(-3-7)/2=-5`.
б) Отберем корни, принадлежащие отрезку `[-6; -4]`.
Сразу видно, что `2` не входит в данный отрезок, а `-5` входит.
`(-1-sqrt(65))/2=` `-sqrt(1/4)-sqrt(65/4)=` `-sqrt(66/4)=` `-sqrt(16,5)`;
`(-1+sqrt(65))/2=` `-sqrt(1/4)+sqrt(65/4)=` `sqrt(64/4)=` `sqrt(16)`;
`-6=-sqrt(36)`;
`-4=-sqrt(16)`.
Теперь видно, что `-6
Получились следующие корни: `-5; (-1-sqrt(65))/2`.Решение №2 (скан):
$IMAGE2$Ответ: а) `(-1+-sqrt(65))/2; -5; 2`;
б) `-5; (-1-sqrt(65))/2`.
Различные методы решения уравнений
I. Линейные уравнения
II. Квадратные уравнения
ax2 + bx + c = 0, a ≠ 0, иначе уравнение становится линейным
Корни квадратного уравнения можно вычислять различными способами, например:
Мы хорошо умеем решать квадратные уравнения.
III. Уравнения, приводимые к квадратным.
замена переменной: а) биквадратное уравнение ax2n + bxn + c = 0, a ≠ 0, n ≥ 2
2) симметрическое уравнение 3 степени – уравнение вида
3) симметрическое уравнение 4 степени – уравнение вида
ax4 + bx3 + cx2 + bx + a = 0, a ≠ 0, коэффициенты a b c b a или
ax4 + bx3 + cx2 – bx + a = 0, a ≠ 0, коэффициенты a b c (–b) a
Т.к. x = 0 не
является корнем уравнения, то возможно деление обеих частей уравнения на x2, тогда получаем:
.
Произведя замену решаем квадратное уравнение a(t2 – 2) + bt + c = 0
Например, решим уравнение x4 – 2x3 – x2 – 2x + 1 = 0, делим обе части на x2,
, после замены получаем уравнение t2 – 2t – 3 = 0
– уравнение не имеет корней.
Ответ:
4) Уравнение вида (x – a)(x – b)(x – c)(x – d) = Ax2, коэффициенты ab = cd
Например, (x + 2)(x +3)(x + 8)(x + 12) = 4x2. Перемножив 1–4 и 2–3 скобки, получим (
имеем (t + 14)(t + 11 ) = 4.
5) Однородное уравнение 2 степени – уравнение вида Р(х,у) = 0, где Р(х,у) – многочлен, каждое слагаемое которого имеет степень 2.
Ответ: -2; -0,5; 0
IV. Все приведенные уравнения узнаваемы и типичны, а как быть с уравнениями произвольного вида?
Пусть дан многочлен Pn(x) = anxn + an-1xn-1 + …+a1x + a0 , где an≠ 0
Рассмотрим метод понижения степени уравнения.
Известно, что, если коэффициенты a являются
целыми числами и an = 1 , то целые
корни уравнения Pn(x) = 0
находятся среди делителей свободного члена a0.
Например, x4 + 2x3 – 2x2
– 6x + 5 = 0, делителями числа 5 являются числа 5;
–5; 1; –1. Тогда
P4(1) = 0, т.е.
x = 1 является корнем уравнения. Понизим
степень уравнения P4(x) = 0 с
помощью деления “уголком” многочлена на множитель х –1,
получаем
Тогда
P4(1) = 0, т.е.
x = 1 является корнем уравнения. Понизим
степень уравнения P4(x) = 0 с
помощью деления “уголком” многочлена на множитель х –1,
получаем
P4(x) = (x – 1)(x3 + 3x2 + x – 5).
Аналогично, P3(1) = 0, тогда P4(x) = (x – 1)(x – 1)(x2 + 4x +5), т.е. уравнение P4(x) = 0 имеет корни x1 = x2 = 1. Покажем более короткое решение этого уравнения (с помощью схемы Горнера).
| 1 | 2 | –2 | –6 | 5 | |
| 1 | 1 | 3 | 1 | –5 | 0 |
| 1 | 1 | 4 | 5 | 0 |
значит, x1 = 1 значит,
x2 = 1.
Итак, (x – 1)2(x2 + 4x + 5) = 0
Что мы делали? Понижали степень уравнения.
V. Рассмотрим симметрические уравнения 3 и 5 степени.
а) ax3 + bx2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.
б) ax5 + bx4 + cx3 + cx2 + bx + a = 0, очевидно, x = –1 корень уравнения, далее понижаем степень уравнения до двух.
Например, покажем решение уравнения 2x5 + 3x4 – 5x3 – 5x2 + 3x + = 0
| 2 | 3 | –5 | –5 | 3 | 2 | |
| –1 | 2 | 1 | –6 | 1 | 2 | 0 |
| 1 | 2 | 3 | –3 | –2 | 0 | |
| 1 | 2 | 5 | 2 | 0 |
x = –1
x = 1
x = 1
Получаем (x – 1)2(x + 1)(2x2
+ 5x + 2) = 0. Значит, корни уравнения: 1; 1; –1;
–2; –0,5.
Значит, корни уравнения: 1; 1; –1;
–2; –0,5.
VI. Приведем список различных уравнений для решения в классе и дома.
Предлагаю читателю самому решить уравнения 1–7 и получить ответы…
Уравнения в целых числах (диофантовы уравнения) / math5school.ru
Немного теории
Уравнения в целых числах – это алгебраические уравнения с двумя или более неизвестными переменными и целыми коэффициентами. Решениями такого уравнения являются все целочисленные (иногда натуральные или рациональные) наборы значений неизвестных переменных, удовлетворяющих этому уравнению. Такие уравнения ещё называют диофантовыми, в честь древнегреческого математика Диофанта Александрийского, который исследовал некоторые типы таких уравнений ещё до нашей эры.
Современной постановкой диофантовых задач мы обязаны французскому математику Ферма.
Именно он поставил перед европейскими математиками вопрос о решении неопределённых уравнений только в целых числах. Наиболее известное уравнение в
целых числах – великая теорема Ферма: уравнение
Наиболее известное уравнение в
целых числах – великая теорема Ферма: уравнение
xn + yn = zn
не имеет ненулевых рациональных решений для всех натуральных n > 2.
Теоретический интерес к уравнениям в целых числах достаточно велик, так как эти уравнения тесно связаны со многими проблемами теории чисел.
В 1970 году ленинградский математик Юрий Владимирович Матиясевич доказал, что общего способа, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения, не существует и быть не может. Поэтому следует для разных типов уравнений выбирать собственные методы решения.
При решении уравнений в целых и натуральных числах можно условно выделить следующие методы:
способ перебора вариантов;
применение алгоритма Евклида;
представление чисел в виде непрерывных (цепных) дробей;
разложения на множители;
решение уравнений в целых числах как квадратных (или иных) относительно какой-либо переменной;
метод остатков;
метод бесконечного спуска.

Задачи с решениями
1. Решить в целых числах уравнение x2 – xy – 2y2 = 7.
РешениеЗапишем уравнение в виде (x – 2y)(x + y) = 7.
Так как х, у – целые числа, то находим решения исходного уравнения, как решения следующих четырёх систем:
1) x – 2y = 7, x + y = 1;
2) x – 2y = 1, x + y = 7;
3) x – 2y = –7, x + y = –1;
4) x – 2y = –1, x + y = –7.
Решив эти системы, получаем решения уравнения: (3; –2), (5; 2), (–3; 2) и (–5; –2).
Ответ: (3; –2), (5; 2), (–3; 2), (–5; –2).
2. Решить в целых числах уравнение:
а) 20х + 12у = 2013;
б) 5х + 7у = 19;
в) 201х – 1999у = 12.
Решениеа) Поскольку при любых целых значениях х и у левая часть уравнения делится на два, а правая является нечётным числом, то уравнение не имеет решений в целых числах.
Ответ: решений нет.
б) Подберём сначала некоторое конкретное решение. В данном случае, это просто, например,
В данном случае, это просто, например,
x0 = 1, y0 = 2.
Тогда
5x0 + 7y0 = 19,
откуда
5(х – x0) + 7(у – y0) = 0,
5(х – x0) = –7(у – y0).
Поскольку числа 5 и 7 взаимно простые, то
х – x0 = 7k, у – y0 = –5k.
Значит, общее решение:
х = 1 + 7k, у = 2 – 5k,
где k – произвольное целое число.
Ответ: (1+7k; 2–5k), где k – целое число.
в) Найти некоторое конкретное решение подбором в данном случае достаточно сложно. Воспользуемся алгоритмом Евклида для чисел 1999 и 201:
НОД(1999, 201) = НОД(201, 190) = НОД(190, 11) = НОД(11, 3) = НОД(3 , 2) = НОД(2, 1) = 1.
Запишем этот процесс в обратном порядке:
1 = 2 – 1 = 2 – (3 – 2) = 2·2 – 3 = 2· (11 – 3·3) – 3 = 2·11 – 7·3 = 2·11 – 7(190 – 11·17) =
= 121·11 – 7·190 = 121(201 – 190) – 7·190 = 121·201 – 128·190 =
= 121·201 – 128(1999 – 9·201) = 1273·201 – 128·1999.
Значит, пара (1273, 128) является решением уравнения 201х – 1999у = 1. Тогда пара чисел
x0 = 1273·12 = 15276, y0 = 128·12 = 1536
является решением уравнения 201х – 1999у = 12.
Общее решение этого уравнения запишется в виде
х = 15276 + 1999k, у = 1536 + 201k, где k – целое число,
или, после переобозначения (используем, что 15276 = 1283 + 7·1999, 1536 = 129 + 7·201),
х = 1283 + 1999n, у = 129 + 201n, где n – целое число.
Ответ: (1283+1999n, 129+201n), где n – целое число.
3. Решить в целых числах уравнение:
а) x3 + y3 = 3333333;
б) x3 + y3 = 4(x2y + xy2 + 1).
Решениеа) Так как x3 и y3 при делении на 9 могут давать только остатки 0, 1 и 8 (смотрите таблицу в разделе «Делимость целых чисел и остатки»), то x3 + y3
может давать только остатки 0, 1, 2, 7 и 8. Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Но число 3333333 при делении на 9 даёт остаток 3. Поэтому исходное уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
б) Перепишем исходное уравнение в виде (x + y)3 = 7(x2y + xy2) + 4. Так как кубы целых чисел при делении на 7 дают остатки 0, 1 и 6, но не 4, то уравнение не имеет решений в целых числах.
Ответ: целочисленных решений нет.
4. Решить
а) в простых числах уравнение х2 – 7х – 144 = у2 – 25у;
б) в целых числах уравнение x + y = x2 – xy + y2.
Решениеа) Решим данное уравнение как квадратное относительно переменной у. Получим
у = х + 9 или у = 16 – х.
Поскольку при нечётном х число х + 9 является чётным, то единственной парой простых чисел, которая удовлетворяет первому равенству, является (2; 11).
Так как х, у – простые, то из равенства у = 16 – х имеем
2 х 16, 2 у 16.
С помощью перебора вариантов находим остальные решения: (3; 13), (5; 11), (11; 5), (13; 3).
Ответ: (2; 11), (3; 13), (5; 11), (11; 5), (13; 3).
б) Рассмотрим данное уравнение как квадратное уравнение относительно x:
x2 – (y + 1)x + y2 – y = 0.
Дискриминант этого уравнения равен –3y2 + 6y + 1. Он положителен лишь для следующих значений у: 0, 1, 2. Для каждого из этих значений из исходного уравнения получаем квадратное уравнение относительно х, которое легко решается.
Ответ: (0; 0), (0; 1), (1; 0), (1; 2), (2; 1), (2; 2).
5. Существует ли бесконечное число троек целых чисел x, y, z таких, что x2 + y2 + z2 = x3 + y3 + z3 ?
РешениеПопробуем подбирать такие тройки, где у = –z. Тогда y3 и z3 будут всегда взаимно уничтожаться, и наше уравнение будет иметь вид
x2 + 2y2 = x3
или, иначе,
x2(x–1) = 2y2.
Чтобы пара целых чисел (x; y) удовлетворяла этому условию, достаточно, чтобы число x–1 было удвоенным квадратом целого числа. Таких чисел бесконечно много, а именно, это все числа вида 2n2+1. Подставляя в x2(x–1) = 2y2 такое число, после несложных преобразований получаем:
y = xn = n(2n2+1) = 2n3+n.
Все тройки, полученные таким образом, имеют вид (2n2+1; 2n3+n; –2n3– n).
Ответ: существует.
6. Найдите такие целые числа x, y, z, u, что x2 + y2 + z2 + u2 = 2xyzu.
РешениеЧисло x2 + y2 + z2 + u2 чётно, поэтому среди чисел x, y, z, u чётное число нечётных чисел.
Если все четыре числа x, y, z, u нечётны, то x2 + y2 + z2 + u2 делится на 4, но при этом 2xyzu не делится
на 4 – несоответствие.
Если ровно два из чисел x, y, z, u нечётны, то x2 + y2 + z2 + u2 не делится на 4, а 2xyzu делится на 4 – опять несоответствие.
Поэтому все числа x, y, z, u чётны. Тогда можно записать, что
x = 2x1, y = 2y1, z = 2z1, u = 2u1,
и исходное уравнение примет вид
x12 + y12 + z12 + u12 = 8x1y1z1u1.
Теперь заметим, что (2k + 1)2 = 4k(k + 1) + 1 при делении на 8 даёт остаток 1. Поэтому если все числа x1, y1,
z1, u1 нечётны, то x12 + y12 + z12 +
u12 не делится на 8. А если ровно два из этих чисел нечётно, то x12 + y12 +
z12 + u12 не делится даже на 4. Значит,
Значит,
x1 = 2x2, y1 = 2y2, z1 = 2z2, u1 = 2u2,
и мы получаем уравнение
x22 + y22 + z22 + u22 = 32x2y2z2u2.
Снова повторив те же самые рассуждения, получим, что x, y, z, u делятся на 2n при всех натуральных n, что возможно лишь при x = y = z = u = 0.
Ответ: (0; 0; 0; 0).
7. Докажите, что уравнение
(х – у)3 + (y – z)3 + (z – x)3 = 30
не имеет решений в целых числах.
РешениеВоспользуемся следующим тождеством:
(х – у)3 + (y – z)3 + (z – x)3 = 3(х – у)(y – z)(z – x).
Тогда исходное уравнение можно записать в виде
(х – у)(y – z)(z – x) = 10.
Обозначим a = x – y, b = y – z, c = z – x и запишем полученное равенство в виде
abc = 10.
Кроме того очевидно, a + b + c = 0. Легко убедиться, что с точностью до перестановки из равенства abc = 10 следует, что числа |a|, |b|, |c| равны либо 1, 2, 5, либо 1, 1, 10. Но во всех этих случаях при любом выборе знаков a, b, c сумма a + b + c отлична от нуля. Таким образом, исходное уравнение не имеет решений в целых числах.
8. Решить в целых числах уравнение 1! + 2! + . . . + х! = у2.
РешениеОчевидно, что
если х = 1, то у2 = 1,
если х = 3, то у2 = 9.
Этим случаям соответствуют следующие пары чисел:
х1 = 1, у1 = 1;
х2 = 1, у2 = –1;
х3 = 3, у3 = 3;
х4 = 3, у4 = –3.
Заметим, что при х = 2 имеем 1! + 2! = 3, при х = 4 имеем 1! + 2! + 3! + 4! = 33 и ни 3, ни 33 не являются квадратами целых чисел. Если же х > 5, то, так как
5! + 6! + . . . + х! = 10n,
. . + х! = 10n,
можем записать, что
1! + 2! + 3! + 4! + 5! + . . . + х! = 33 + 10n.
Так как 33 + 10n – число, оканчивающееся цифрой 3, то оно не является квадратом целого числа.
Ответ: (1; 1), (1; –1), (3; 3), (3; –3).
9. Решите следующую систему уравнений в натуральных числах:
a3 – b3 – c3 = 3abc, a2 = 2(b + c).
РешениеТак как
3abc > 0, то a3 > b3 + c3;
таким образом имеем
b
Складывая эти неравенства, получим, что
b + c
С учётом последнего неравенства, из второго уравнения системы получаем, что
a2
Но второе уравнение системы также показывает, что а – чётное число. Таким образом, а = 2, b = c = 1.
Ответ: (2; 1; 1)
10. Найти все пары целых чисел х и у, удовлетворяющих уравнению х2 + х = у4 + у3 + у2 + у.
Разложив на множители обе части данного уравнения, получим:
х(х + 1) = у(у + 1)(у2 + 1),
или
х(х + 1) = (у2 + у)(у2 + 1)
Такое равенство возможно, если левая и правая части равны нулю, или представляют собой произведение двух последовательных целых чисел. Поэтому, приравнивая к нулю те или иные множители, получим 4 пары искомых значений переменных:
х1 = 0, у1 = 0;
х2 = 0, у2 = –1;
х3 = –1, у3 = 0;
х4 = –1, у4 = –1.
Произведение (у2 + у)(у2 + 1) можно рассматривать как произведение двух последовательных целых чисел, отличных от нуля, только при у = 2. Поэтому х(х + 1) = 30, откуда х5 = 5, х6 = –6. Значит, существуют ещё две пары целых чисел, удовлетворяющих исходному уравнению:
х5 = 5, у5 = 2;
х6 = –6, у6 = 2.
Ответ: (0; 0), (0; –1), (–1; 0), (–1; –1), (5; 2), (–6; 2.)
Задачи без решений
1. Решить в целых числах уравнение:
а) ху = х + у + 3;
б) х2 + у2 = х + у + 2.
2. Решить в целых числах уравнение:
а) х3 + 21у2 + 5 = 0;
б) 15х2 – 7у2 = 9.
3. Решить в натуральных числах уравнение:
а) 2х + 1 = у2;
б) 3·2х + 1 = у2.
4. Доказать, что уравнение х3 + 3у3 + 9z3 = 9xyz в рациональных числах имеет единственное решение
x = y = z = 0.
5. Доказать, что уравнение х2 + 5 = у3 в целых числах не имеет решений.
X-20 Dyna-Soar. Невзошедшая звезда / Блог компании Timeweb / Хабр
Космос – дело тонкое. Если это пилотируемый космос, то тонкое вдвойне, а уж с крылатыми аппаратами всё совсем сложно. И пусть дело происходит на заре нового века человечества, но ведь сильнейшей сверхдержаве с гигантским научным потенциалом (как своим, так и трофейным) по силам освоить даже самые трудные и сложные задачи, особенно если за них берутся лучшие коллективы. Проект многоразового космического корабля Dyna-Soar прямо говорит об обратном. Перспективная машина не пошла дальше макетов, и если бы не её наследие, то быть бы ей забытой. Однако так вышло, что без неё не было бы SpaceShuttle, а значит, вероятно, и отечественных «Спирали» и «Бурана», так что нельзя говорить об советском крылатом космосе, не затронув Dyna-Soar.
И пусть дело происходит на заре нового века человечества, но ведь сильнейшей сверхдержаве с гигантским научным потенциалом (как своим, так и трофейным) по силам освоить даже самые трудные и сложные задачи, особенно если за них берутся лучшие коллективы. Проект многоразового космического корабля Dyna-Soar прямо говорит об обратном. Перспективная машина не пошла дальше макетов, и если бы не её наследие, то быть бы ей забытой. Однако так вышло, что без неё не было бы SpaceShuttle, а значит, вероятно, и отечественных «Спирали» и «Бурана», так что нельзя говорить об советском крылатом космосе, не затронув Dyna-Soar.
Предтечи с немецкими корнями
Как известно, американцы после войны получили в своё распоряжение большую часть немецкой ракетной программы. Это касается в том числе и интеллектуального потенциала. Так, Вернер фон Браун оказался в США уже в 1945, а Вальтер Дорнбергер – ещё один ключевой немецкий ракетчик – попал в Америку в 1947 году после британского расследования использования труда заключенных концлагерей при производстве V-2. Дорнбергер в Штатах времени зря не терял. Он стал советником президента США и консультантом ВВС по управляемым ракетам, участвовал в разработке гиперзвукового аппарата Х-15, а в 1950 году стал консультантом фирмы Bell.
Дорнбергер в Штатах времени зря не терял. Он стал советником президента США и консультантом ВВС по управляемым ракетам, участвовал в разработке гиперзвукового аппарата Х-15, а в 1950 году стал консультантом фирмы Bell.
Американские учёные также ознакомились и со значительным объёмом документации по «Серебряной птице» Эйгена Зенгера. Хотя идея их очень заинтересовала, идти по советскому пути и глубоко прорабатывать на свой лад эту машину они не стали. Тем не менее, в своих первых наработках по крылатому космическому аппарату фирма Bell на Silbervogel оглядывалась, а Дорнбергер даже пытался (хотя и неудачно) переманить её авторов – Эйгена Зенгера и Ирену Бредт.
Модель BoMi (чёрный) c cамолётом-разгонщиком
Так или иначе, но в 1952 году белловцы представили военным проект пилотируемого аппарата BoMi (от англ. BOmber-MIssile–- бомбардировщик-ракета). Это была двухступенчатая машина, фактически состоящая из двух ракетных самолётов общей стартовой массой в 363 тонны, из которых 1,8 тонн – боевая нагрузка. Первая ступень – двухместный самолёт-разгонщик, оснащённый пятью ракетными двигателями. Длина аппарата составляла 37 метров, а размах крыла – 18 метров. Фюзеляж её должен был изготовляться из алюминия, а подверженные особому нагреву кромки крыла – из титана. Разгонщик должен был набирать нужную скорость в течение двух минут, после чего отделялась вторая ступень, пока сам самолёт планировал обратно на базу.
Первая ступень – двухместный самолёт-разгонщик, оснащённый пятью ракетными двигателями. Длина аппарата составляла 37 метров, а размах крыла – 18 метров. Фюзеляж её должен был изготовляться из алюминия, а подверженные особому нагреву кромки крыла – из титана. Разгонщик должен был набирать нужную скорость в течение двух минут, после чего отделялась вторая ступень, пока сам самолёт планировал обратно на базу.
Вторая ступень также была пилотируемой, причём предполагалось два её варианта. Первый, суборбитальный, представлял собой цельнотитановый аппарат длиной 18,3 метра и с размахом крыла 10,7 метра. Эта ступень уже была маршевой и должна была донести полезную нагрузку до цели, достигнув в процессе высоты в 30 км и скорости в 4 Маха (4,8 тыс. км/ч), причём большая часть полёта также должна была пройти в планировании. Интересно, что уже здесь принялось крыло типа «двойная дельта», в отличие от относительно простого трапецевидного крыла «Серебряной птицы». Орбитальный вариант включал в себя цельнотитановый 44-метровый разгонщик и 23-метровую маршевую ступень, способную доставить до цели 34 тонны бомб.
Дельтавидное, или треугольное, крыло обладает рядом достоинств, критичных для высокоскоростных самолётов, и особенно для космопланов. Оно легче и жёстче, а следовательно, и тоньше, чем прямое или стреловидное, упрощает передачу нагрузки на фюзеляж. Именно поэтому его (а также различные его вариации) применяют на очень быстрых самолётах
Такое крыло называют «крыло двойная дельта». Оно позволяет добиться относительно безболезненного увеличения площади крыла, повышая подъёмную силу. А в случае применения схемы «бесхвостка», как на этом Saab 35, наплыв ещё и позволяет отнести управляющие поверхности максимально далеко назад, избавляясь от горизонтальных стабилизаторов. К тому же снижается вес планера и сопротивление воздуха
И вот как раз крыло BoMi — это крыло «двойная дельта», а сам аппарат выполнен по схеме «бесхвостка»
Сравните с небольшим крылом Серебряной птицы
Bell представили проект Главному исследовательскому центру ВВС на базе Райт (WrightAirDevelopmentCenter, WADC), где в целом остались скорее недовольны, но в то же время заинтересованы. BoMi позволял обогатить имеющиеся скромные знания о поведении подобных машин в космосе. Вместе с тем военные сомневались, что белловцы вообще смогут реализовать проект, справедливо указывая на недооценку проблем охлаждения и слишком оптимистические оценки аэродинамического качества (коэффициент, показывающий, сколько километров самолёт без тяги способен пролететь, потеряв один километр высоты).
BoMi позволял обогатить имеющиеся скромные знания о поведении подобных машин в космосе. Вместе с тем военные сомневались, что белловцы вообще смогут реализовать проект, справедливо указывая на недооценку проблем охлаждения и слишком оптимистические оценки аэродинамического качества (коэффициент, показывающий, сколько километров самолёт без тяги способен пролететь, потеряв один километр высоты).
Bell, тем не менее, получили в 1954 году годовой контракт на дальнейшую проработку своих идей. В процессе ушел самолёт-разгонщик, и BoMi должен был выводиться на заданную высоту благодаря ракете-носителю. Однако постепенно военные пришли к тому, что BoMi гораздо лучше подойдёт роль разведчика. Так появился BrassBell – проект разведчика с дальностью до 18,5 тыс. км, выводимого в космос с помощью ракеты-носителя. Впрочем, бомбардировочные задачи также не забывались. В конце 1955 года ВВС предложили отрасли проработать пилотируемый гиперзвуковой аппарат с полезной нагрузкой до 11,3 тонн, ускоряемый ракетой, способный провести бомбардировку или выполнить разведку. В 1956 году тема получила официальный индекс SR-126 RoBo (от англ. Rocket-Bomber – ракета-бомбардировщик, фантазия у американцев зашкаливала). RoBo должен был совмещать в себе наработки BoMi и BrassBell. На предложение откликнулись Boeing, Bell, NAA, Convair, Douglas и ряд других фирм, составлявших весь цвет авиастроительной отрасли США. Тема их заинтересовала, и в дополнение к $860 тыс. компании в общей сложности к концу 1957 фискального года израсходовали $3,2 млн, включая собственные средства. 20 июня 1957 года началась многодневная конференция, в ходе которой участники представили свои идеи.
В 1956 году тема получила официальный индекс SR-126 RoBo (от англ. Rocket-Bomber – ракета-бомбардировщик, фантазия у американцев зашкаливала). RoBo должен был совмещать в себе наработки BoMi и BrassBell. На предложение откликнулись Boeing, Bell, NAA, Convair, Douglas и ряд других фирм, составлявших весь цвет авиастроительной отрасли США. Тема их заинтересовала, и в дополнение к $860 тыс. компании в общей сложности к концу 1957 фискального года израсходовали $3,2 млн, включая собственные средства. 20 июня 1957 года началась многодневная конференция, в ходе которой участники представили свои идеи.
Различные варианты RoBo. Условно финальным является нижний, с огромными законцовками крыла, исполняющими роль килей
Он же, но по версии моделистов
Компании Bell и Douglas выбрали трехступенчатый аппарат типа ракетоплана (третья ступень – тот самый RoBo – фактически должна была бы просто планировать – прим. А.С.), Convair – аппарат с третьей ступенью, оснащенной комбинированной двигательной установкой с ракетным и турбореактивным двигателями.NorthAmerican предложила достаточно традиционный двухступенчатый аппарат, Boeing – беспилотный ракетоплан, названный планирующим управляемым снарядом» (glide-missile), а фирма Republic хотела построить малый беспилотный летательный аппарат, напоминающий перехватчик проекта XF -103 с маршевым гиперзвуковым ПВРД, стартующий с помощью некоего нового трехступенчатого ускорителя
(Вадим Лукашевич, Игорь Афанасьев —-«Космические крылья»)
Комиссия ВВС, изучив проекты, отметила, что в целом создание подобного аппарата возможно, однако существовал ряд нерешённых на тот момент проблем. Например, необходимо было бы разработать специальную систему наведения, учитывающую вращение Земли, ракетные двигатели тогда ещё не обладали достаточной надёжностью, чтобы использовать их для пилотируемых полётов, не хватает данных о гиперзвуковых полётах и т.д. В конце концов, стоимость такого проекта должна была быть чрезвычайно высокой. И, тем не менее, военные сочли, что прототип сможет полететь в 1965 году, а полноценная боевая система RoBo – в 1974 году.
Параллельно ВВС США в ноябре 1956 года запустили НИР HYWARDS (Hypersonic Weapons Reseaгchand Development Supporting System – Вспомогательная система для НИОКР по гиперзвуковому оружию). Этот проект фокусировался на сборе данных по аэродинамике, возможностям пилотирования человеком и на других проблемах, возникающих на этапе возвращения космоплана в атмосферу. На этом участке аппарат идёт на скорости порядка 15 Махов (17,9 тыс. км/ч) и подвергается довольно специфичным нагрузкам. Машина должна была совершать первые полёты после воздушного запуска с бомбардировщика, а затем перейти к стартам при помощи модифицированной в носитель баллистической ракеты.
К работе по HYWARDS привлекли Национальный консультативный комитет по воздухоплаванию NACA (далее NASA, хотя таковым бюро стало только с июля 1958 года), а именно два исследовательских центра. Такой синтез позволил армейцам получить доступ к серьёзным научным учреждениям. В СССР, например, ВВС по ряду причин (об этом в другой раз как-нибудь) с космическими учреждениями взаимодействовали куда менее активно.
Лаборатория им. Эймса предложила среднеплан с дальностью 3,2 тыс. км. Компоновка машины обеспечивала относительно высокое аэродинамическое качество, однако расплачиваться приходилось переусложнением. Дело в том, что на заданных скоростях, а особенно в условиях спуска с орбиты, аппарат оказывается в зоне очень высокого нагрева — фактически в плазме. Проект Лаборатории им. Эймса вынужден был в эту зону заходить всем фюзеляжем, что вынуждало устанавливать дополнительные системы охлаждения конструкции, тем самым сжирались все преимущества высокой «летучести».
В Лаборатории аэронавтики им. Лэнгли поступили иначе. Там спроектировали низкоплан с дельтавидным крылом и плоской нижней частью фюзеляжа. В такой компоновке можно было вывести большую часть конструкции машины из зоны сверхвысокой температуры, по факту превратив низ в щит. Это, в свою очередь, значительно упрощало всю теплозащиту, а с ней и весь аппарат. Более того, в Лаборатории им. Лэнгли предложили поднять скорость до 18 Махов (21,5 тыс. км/ч), чтобы снизить аэродинамический нагрев на большей высоте, тем самым ещё чуть облегчив жизнь теплозащиты. Конечно, такой вариант проигрывал проекту Лаборатории им. Эймса по аэродинамическому качеству, но зато достигал большей дальности (5,2 тыс. км). Фактически, учёные из Лаборатории им. Лэнгли впервые доказали, что аэродинамика может снизить нагрев и нагрузки на гиперзвуковых скоростях.
км/ч), чтобы снизить аэродинамический нагрев на большей высоте, тем самым ещё чуть облегчив жизнь теплозащиты. Конечно, такой вариант проигрывал проекту Лаборатории им. Эймса по аэродинамическому качеству, но зато достигал большей дальности (5,2 тыс. км). Фактически, учёные из Лаборатории им. Лэнгли впервые доказали, что аэродинамика может снизить нагрев и нагрузки на гиперзвуковых скоростях.
HYWARDS от Лаборатории им. Лэнгли
В общем, работы по крылатым космическим аппаратам, которые должны были выводиться на орбиту с помощью ракет, постепенно продвигались. И хотя их стоимость явно должна была быть очень высокой, но всё-таки преимущества казались очевидными, а превосходство над СССР – неоспоримым и непреодолимым. Казалось, американцам не о чем волноваться и можно постепенно развивать свой проект.
И тут на орбиту вышел «Спутник».
Зачатие «Динозавра»
10 октября 1957 года Командование ВВС США по исследованиям и разработкам (ARDC) своим решением объединило проекты BrassBell, RoBo и HYWARDS в один, получивший официальное обозначение System 464L или Dyna-Soar. Этот акроним образован от английского словосочетания dynamic soaring (динамическое планирование) и возник из-за использования в схеме полёта волнообразной траектории подобной той, что для своего проекта использовал Зенгер. Такая траектория позволяла упростить охлаждение машины—, очень важный пункт для космопланов.
Этот акроним образован от английского словосочетания dynamic soaring (динамическое планирование) и возник из-за использования в схеме полёта волнообразной траектории подобной той, что для своего проекта использовал Зенгер. Такая траектория позволяла упростить охлаждение машины—, очень важный пункт для космопланов.
о динозавре
По произношению оригинальный акроним очень близок к слову «динозавр», а потому в русскоязычной литературе авторы с этим часто играются, но в англоязычных источниках (по крайней мере в тех, с которыми я ознакомился) почему-то это не особо используется.
После ряда консультаций и договора ВВС и NASA о совместной реализации проекта как продолжения аппаратов Х-1 (первый ракетный самолёт, преодолевший звуковой барьер) и Х-15 (первый гиперзвуковой пилотируемый полёт) 21 декабря 1957 года ARDC выпустила директиву об этапах разработки Dyna-Soar. На первом этапе предполагалось построить экспериментальный одноместный демонстратор технологий, способный достичь скорости около 19,8 тыс. км/ч и высоты в 52 км. На втором —необходимо было достичь целей программы BrassBell. Двухступенчатый ускоритель должен был доставить машину на высоту в 107 км и разогнать до 24,1 тыс. км/ч, после чего машине требовалось спланировать на дальность 9,3 тыс. км, по пути проведя высокодетальное фотографирование и радиолокационную разведку целей, а по возможности и отбомбиться. Наконец, на третьем этапе необходимо было создать боевой многоцелевой аппарат уровня RoBo, способный выполнить следующие задачи:
км/ч и высоты в 52 км. На втором —необходимо было достичь целей программы BrassBell. Двухступенчатый ускоритель должен был доставить машину на высоту в 107 км и разогнать до 24,1 тыс. км/ч, после чего машине требовалось спланировать на дальность 9,3 тыс. км, по пути проведя высокодетальное фотографирование и радиолокационную разведку целей, а по возможности и отбомбиться. Наконец, на третьем этапе необходимо было создать боевой многоцелевой аппарат уровня RoBo, способный выполнить следующие задачи:
- осуществление разведывательно-ударных миссий;
- инспектирование спутников;
- выполнение спасательных работ;
- транспортировка грузов;
- выполнение функций космического командного пункта по управлению наземными войсковыми операциями.
Во всех случаях система состояла из одно- или многоступенчатого ракетного ускорителя, созданного на базе существующих или перспективных баллистических ракет или ракет-носителей, а также из ракетоплана в качестве финальной боевой ступени.
Первое полугодие 1958 года ушло на проработку концепций и на разработку проектов Dyna-Soar первого этапа основными подрядчиками (Republic, Lockheed, NorthAmericaп, Convair, Douglas, McDonnell, Northrop, а также совместные проекты Bell – Martin и Boeing- –Vought). К концу июня работы Bell–Martin и Boeing–Vought были взяты в детальную проработку, им выделили по $9 млн. Следующие полтора года ушли на согласования, переработки и битву за финансирование.
Представленный Bell–Martin проект…
…и проект Boeing–Vought. Далековато от того, что получилось в итоге
В конце концов, к 9 ноября 1959 года всё было утверждено, были выставлены сроки. Так, уже в апреле 1962 года предполагалось начать серию лётных испытаний, в рамках которых прототип должен был сбрасываться с самолёта; в июле 1963 года предполагался первый беспилотный, а с мая 1964 года должны были начаться пилотируемые суброрбитальные полёты. Наконец, первый пилотируемый орбитальный полёт должен был состояться в августе 1965 года. Предполагалось, что к этому моменту суммарные расходы составят $493,6 млн. Победителем конкурса стал проект Boeing–-Vought, а Martin получили заказ на разработку ракетного ускорителя на базе МБР Titan. Bell, которые были первыми на этой поляне, которые вложили миллионы собственных средств, которые даже предложили, как казалось, более удачную схему (настолько, что изначально заметно отличающийся проект Boeing к концу эволюционировал в почти неотличимую машину) остались не у дел.
Предполагалось, что к этому моменту суммарные расходы составят $493,6 млн. Победителем конкурса стал проект Boeing–-Vought, а Martin получили заказ на разработку ракетного ускорителя на базе МБР Titan. Bell, которые были первыми на этой поляне, которые вложили миллионы собственных средств, которые даже предложили, как казалось, более удачную схему (настолько, что изначально заметно отличающийся проект Boeing к концу эволюционировал в почти неотличимую машину) остались не у дел.
Компания Bell рассматривалась ВВС скорее как разработчик прототипов. Во время Второй мировой войны они занимались производством истребителей для отправки в Советский Союз по ленд-лизу. Хотя они построили первый американский реактивный самолет и X-1, первый самолет, преодолевший звуковой барьер, они не выигрывали полномасштабный контракт на разработку пилотируемого самолета с 1955 года. Boeing, с другой стороны, был ведущим изготовителем бомбардировщиков B-52 и МБР Minuteman для стратегического командования ВВС США.Чтобы компенсировать проигрыш в конкурсе на B-70 (его выиграла компания NorthAmerican со своей знаменитой Валькирией –- прим. А.С.) в конце 1957 года, было логично, что компания будет строить следующий крупный проект.
(Марк Уэйд, Аstronautix.com)
Суперсплавы и носители
А в итоге спроектировали что-то такое
Следующие три с лишним года превратились в классический для новейших систем кошмар разработки. Dyna-Soar был принципиально новым аппаратом, а значит, вторгался в неизведанные доселе зоны науки и техники. Неудивительно, что и различных вариантов космоплана было много, а учитывая, что он был секретным и, ко всему прочему, не дошёл до лётных испытаний, то приходится говорить о некоем усреднённом варианте конструкции.
Что ожидаемо, серьёзные проблемы создала теплозащита, а точнее поиск и подбор подходящих материалов. Многие материалы не производились никогда в нужных количествах или в необходимом для деталей машины виде. Также необходимо было разработать новые технологии для сверки, ковки, резки и крепления таких элементов, потому что сплавы оказались одновременно прочными и хрупкими.
Вообще применялись различные сплавы и суперсплавы (то есть способные выдерживать особо жёсткие нагрузки) на основе никеля и молибдена. Для большинства элементов конструкции, в частности несущей пространственной фермы и прикрывающих её панелей, использовался материал Rene 41 (хром 18-20%, кобальт 12%, молибден 9-10.5%, титан 3.0-3.3%, алюминий 1.4-1.6%, остальное – никель), также использованный для капсул программы Mercury и отлично себя зарекомендовавший. Сверху на эти панели наносился войлок из кварцитового волокна, позже ставший важным элементом теплозащиты SpaceShuttle. Поверх войлока использовался ниобиевый сплав D-36. Из него же, кстати, сделали сбрасываемый защитный экран для остекления. Дело в том, что конструкция предполагала три лобовых окна, и защитить их от деформации при нагреве не получилось. Пришлось ставить экран и специально отрабатывать полёты для ситуаций, когда сбросить его не получалось.
Dyna-Soar проходит через атмосферу в воображении художника. Хорошо виден сбрасываемый экран на одном из лобовых окон
Хорошо виден сбрасываемый экран на одном из лобовых окон
С более горячими зонами пришлось повозиться гораздо дольше. Так, для передних кромок крыла, где температура должна была достигать 1565 градусов Цельсия, использовали титаново-молибденовый сплав TZM. Проблема этого материала состояла, однако, в том, что молибден при меньших температурах (порядка 1450 градусов Цельсия) начинал окисляться, что приводило к оплавлению и разрушению изготовленных из него деталей. Boeing пришлось повозиться порядка двух лет, прежде чем решение было выработано. Им стало специальное покрытие под названием дизил. Оно значительно укрепляло молибден, предотвращая окисление и механические повреждения, к тому же красило машину в чёрный цвет. Однако его необходимо было менять после каждого полёта, что значительно удорожало конструкцию. Самое же горячее место – носовой конус с ожидаемой температурой до 2010 градусов Цельсия –- защитили графитовой оболочкой с кремниевым покрытием и циркониевыми плитками снаружи.
По пути приходилось вносить изменения в конструкцию под новые, скорректированные задачи. Так, изначально рассчитанный на один виток космоплан пришлось адаптировать для многовитковых полётов. Понадобилась установка тормозного двигателя для схода с орбиты и даже добавка специальной ступени Transtage для того, чтобы можно было менять орбиты и инспектировать спутники. Также пришлось частично отказаться от водных стенок внутри корпуса, которые должны были обеспечивать более равномерное распределение тепла. Они остались только в самых важных зонах, для защиты пилота.
Модель Dyna-Soar со ступенью Transtage
Теоретически, Dyna-Soar была одноместной машиной, однако прорабатывались варианты с экипажем до пяти человек. По всей видимости, это был вариант использования космоплана в качестве космического такси, доставляющего набитых в тесную кабину астронавтов на орбитальную станцию. Самое интересное, что речи о стыковочном узле не шло:– слишком уж маленьким оказывался аппарат. Астронавты должны были перебираться на станцию через открытый космос. Также было непонятно, как обеспечить безопасность людей. Пилот хотя бы имел катапультируемое кресло, так что он мог спастись, будучи в атмосфере, а вот что предстояло бы делать пассажирам – вопрос. Помимо катапультируемого кресла, безопасность обеспечивалась благодаря собственной небольшой силовой установке на твердотопливных ракетных двигателях, которая должна была отвести космоплан от терпящей бедствие ракеты-носителя. Но в ситуации, когда корабль находится в космосе или же в плазме на этапе спуска в атмосфере, пилоту деться было некуда: от специальной спасательной капсулы, в которой он бы размещался, отказались для экономии веса.
Астронавты должны были перебираться на станцию через открытый космос. Также было непонятно, как обеспечить безопасность людей. Пилот хотя бы имел катапультируемое кресло, так что он мог спастись, будучи в атмосфере, а вот что предстояло бы делать пассажирам – вопрос. Помимо катапультируемого кресла, безопасность обеспечивалась благодаря собственной небольшой силовой установке на твердотопливных ракетных двигателях, которая должна была отвести космоплан от терпящей бедствие ракеты-носителя. Но в ситуации, когда корабль находится в космосе или же в плазме на этапе спуска в атмосфере, пилоту деться было некуда: от специальной спасательной капсулы, в которой он бы размещался, отказались для экономии веса.
Dyna-Soar в пассажирском варианте
Садиться машина должна была на асфальтовые или бетонные ВПП или, что представляется несколько более вероятным, на дно солёных озёр (вроде того, на котором размещается авиабаза ВВС США «Эдвардс»). Для этого Dyna-Soar оснащалась трёхопорным лыжным шасси. От колёс отказались, поскольку такая конструкция бы не выдержала сверхвысоких температур. При этом посадочная скорость машины находилась в диапазоне от 148 до 426 км/ч. Однако траектория снижения оказывалась довольно крутой, да и вообще считалось, что управление аппаратом будет очень непростым, поэтому пилот получил в своё распоряжение множество электронных вспомогательных систем, а также полноценную автоматическую систему управления.
От колёс отказались, поскольку такая конструкция бы не выдержала сверхвысоких температур. При этом посадочная скорость машины находилась в диапазоне от 148 до 426 км/ч. Однако траектория снижения оказывалась довольно крутой, да и вообще считалось, что управление аппаратом будет очень непростым, поэтому пилот получил в своё распоряжение множество электронных вспомогательных систем, а также полноценную автоматическую систему управления.
Посадочная конфигурация, видно выпущенное лыжное шасси
Пока Boeing возился с проектированием космоплана, компания Martin занималась выбором и подготовкой ракеты-носителя. К моменту окончания конкурса она Martinуже подготовила МБР Titan, совершившую первый полёт в феврале 1959 года. Эта ракета подходила для запуска Dyna-Soar по суборбитальной траектории, однако со значительными ограничениями по грузоподъёмности. В январе 1961 года основным носителем стала значительно более мощная, но ещё не летавшая ракета Titan II. Её первый полёт состоялся в марте 1962 года, и считалось, что спустя год (когда планировался первый полёт Dyna-Soar) она уже будет полностью готова. Однако в мае 61-го Boeing предложили сократить программу и отказаться от суборбитальных полётов, а для вывода космоплана на орбиту силёнок у Titan II уже не хватало.
Однако в мае 61-го Boeing предложили сократить программу и отказаться от суборбитальных полётов, а для вывода космоплана на орбиту силёнок у Titan II уже не хватало.
Различные варианты носителей для Dyna-Soar
ВВС предложили Titan II модернизировать, добавив к нему два твердотопливных ускорителя. Такой вариант изначально получил наименование Soltan (SOLidTitAN – твердотопливный титан), а позднее получил имя Titan III. Однако внезапно во внутренний проект ВВС и NASA влезли армейцы — управление баллистических ракет армии США. Там руководил Вернер фон Браун, команда которого трудилась над ракетой-носителем Saturn I. По сравнению с Soltan эта ракета обладала более высокой грузоподъёмностью и могла вывести на низкую околоземную орбиту без малого 10 тонн против 8 у Soltan в штатной конфигурации. Правда, при форсировании Soltan мог вывести 9 тонн, но всё равно Saturn I был привлекательнее. Тем не менее, ВВС всё-таки добились того, что их ракета стала носителем, оставив фон Брауна не у дел. Сложно сказать, что здесь сыграло большую роль:– сложные взаимоотношения между родами войск (при этом ВВС курировали и Titan, и Dyna-Soar), дешевизна Soltan относительно Saturn I или же относительная готовность Soltan. Так или иначе, выбранный Soltan пришлось доработать, добавив ещё одну ступень (третью) – Transtage. Благодаря ей получившаяся новая ракета, наречённая Titan IIIC, могла вывести на орбиту уже 11,3 тонны. Transtage должна была довыводить космоплан на орбиту, а также помогать в маневрировании и сходе с неё.
Сложно сказать, что здесь сыграло большую роль:– сложные взаимоотношения между родами войск (при этом ВВС курировали и Titan, и Dyna-Soar), дешевизна Soltan относительно Saturn I или же относительная готовность Soltan. Так или иначе, выбранный Soltan пришлось доработать, добавив ещё одну ступень (третью) – Transtage. Благодаря ей получившаяся новая ракета, наречённая Titan IIIC, могла вывести на орбиту уже 11,3 тонны. Transtage должна была довыводить космоплан на орбиту, а также помогать в маневрировании и сходе с неё.
Макнамара возражает и выигрывает
Разработка Dyna-Soar очень быстро превратилась в борьбу за военный бюджет. И перспективы будущей машины на этом фронте были далеко не безоблачными. Проблема состояла в том, что в рамках одного проекта необходимо было построить две сильно различающихся машины – для испытательных и боевых полётов. При этом на оба проекта возлагались не только практические, но, в первую очередь, исследовательские задачи. Высокая стоимость для по сути научного проекта с неясными перспективами и расплывчато сформулированными задачами была огромным недостатком.
Мало этого, так в ВВС параллельно вели проработку других пилотируемых многоразовых машин, только уже концептуально иных. Одной из них являлся аппарат, получивший индекс SAINT. Его целевое назначение – инспектор (а при необходимости и истребитель) спутников, отсюда и название:SAtelliteINspecTor. «Святой» (а именно так и переводится акроним), в отличие от Dyna-Soar, обладал так называемым несущим корпусом: то есть именно корпус создавал подъёмную силу в отличие от конкурента, где на это работало крыло. Благодаря этому можно было сэкономить на массе, увеличив боевую нагрузку. К тому же «Динозавр» требовал сложной и дорогой системы теплозащиты, а «Святой» мог довольствоваться более простой уносимой, аналогичной классическим спускаемым аппаратам типа советских «Востоков» или «Союзов». При этом SAINT-II точно также мог маневрировать на этапе спуска, совершая так называемый боковой манёвр, как и наш герой. Ко всему прочему инспектор мог спокойно выйти на орбиту на РН Titan-II с доп. ступенью Chariot.
При сравнимой цене SAINT-II становился значимым конкурентом Dyna-Soar. Предполагалось, что за три года (1962-1965 гг.) на конкурента будет потрачено порядка $413 млн, после чего он сможет поступить на вооружение. Общие же затраты на Dyna-Soar оценивались уже тогда в районе $1-1,5 млрд. Видя подобные оценки, защитники «Динозавра» раскритиковали «Святого», акцентируя внимание ВВС на том, что заданные оценки бюджета и количества испытательных полётов нереалистичны. Руководство ВВС прислушалось, и в октябре 1961 года закрыло проект, запретив использовать даже само обозначение SAINT.
Однако от этого бед у Dyna-Soar не убавилось. В ноябре того же 1961 года программа окончательно стала сугубо исследовательской, а в январе 1962 года ВВС отменили работы по боевому орбитальному кораблю, оставив только испытательный, «полуготовый» аппарат, способный лишь в ограниченном объеме выполнять разведку, инспекцию спутников, транспортные операции и бомбардировку с орбиты. К этому моменту Boeing уже предложили, а ВВС утвердили отказ от суборбитальных полётов. Это сокращало и удешевляло программу испытаний.
Это сокращало и удешевляло программу испытаний.
ВВС и NASA рассчитывали, что испытательные полёты позволят понять, как использовать космическое пространство в военных целях, а также развить программу пилотируемых полётов и проверить использование боевых систем в космосе. Однако такой подход не устраивал Минобороны США.
Роберт Макнамара
Министр обороны США Роберт Макнамара де-факто отменил выделение Конгрессом США дополнительных $514,5 млн, из которых $85,5 млн должны были пойти на Dyna-Soar. Корпорации Boeing пришлось продолжать разработку на собственные средства. 23 февраля 1962 года Макнамара утвердил окончательное переориентирование Dyna-Soar, которая теперь была нужна только для того, чтобы проверить возможность выполнения пилотируемым орбитальным планером маневрирования при входе в атмосферу и точной посадки на ВПП в заданном месте Земли.
В 1962 году был собран и представлен публике макет корабля. Кроме того, официально объявлено об идущей уже два года работе с будущими астронавтами проекта. К этому времени в отряде уже успел побывать и даже выйти из него Нил Армстронг.
К этому времени в отряде уже успел побывать и даже выйти из него Нил Армстронг.
Макет Dyna-Soar и его астронавты
К началу 1963 года в Минобороны решили сравнить Dyna-Soar и готовящиеся к полётам корабли типа Gemini, чтобы понять, какой из проектов лучше подойдёт для обеспечения военного присутствия в космосе. А NASA и ВВС договорились о том, что на Gemini полетят и военные лётчики. Очень быстро стало понятно, что Gemini обладали огромным преимуществом. Они позволяли испытывать военные системы в ходе длительных полётов (Dyna-Soar годился только для полётов на несколько витков), были банально дешевле и легче, могли маневрировать на орбите и нести большую полезную нагрузку. На этом фоне такие преимущества «Динозавра», как способность маневрировать на спуске и более быстрый возврат, а также потенциальная возможность (это ещё предстояло доказать) выполнять полноценные боевые задачи, в основном нивелировались.
Gemini
И хотя Boeing получили $358 млн на продолжение разработки и подготовку к испытаниям, включавшую в себя сбросы прототипа с модифицированного бомбардировщика B-52, дни проекта были сочтены. Дело в том, что заместитель министра обороны Гарольд Браун предложил создать обслуживаемую кораблями Gemini военную космическую станцию, которая могла выполнять, наверное, все основные задачи Dyna-Soar. Вплоть до конца 1963 года ВВС боролись за проект, предлагая различные варианты его модернизации, однако это были уже конвульсии. Пока военные подгоняли задачи под проект, Минобороны приняло решение. 10 декабря 1963 года Макнамара поручил закрыть проект, а оставшиеся средства передать на другие разработки.
Дело в том, что заместитель министра обороны Гарольд Браун предложил создать обслуживаемую кораблями Gemini военную космическую станцию, которая могла выполнять, наверное, все основные задачи Dyna-Soar. Вплоть до конца 1963 года ВВС боролись за проект, предлагая различные варианты его модернизации, однако это были уже конвульсии. Пока военные подгоняли задачи под проект, Минобороны приняло решение. 10 декабря 1963 года Макнамара поручил закрыть проект, а оставшиеся средства передать на другие разработки.
Основными причинами закрытия программы были:
- нечеткость целевого назначения;
- чрезмерные затраты времени и финансовых ресурсов на разработку, без гарантии успешного завершения проекта;
- отсутствие ярко выраженных преимуществ перед космическими кораблями капсульного типа, за исключением более высокой маневренности при спуске в атмосфере и меньших затрат на поисково-спасательные операции.
(Вадим Лукашевич, Игорь Афанасьев — «Космические крылья»)
На Dyna-Soar потратили $410 млн, и эти траты не были напрасными. Да, от самого проекта остался только макет, а многие разработанные системы были утилизированы. Но, во-первых, США получили отличную ракету-носитель Titan III, а во-вторых… Во-вторых, очень многие наработки, оставшиеся с «Динозавра», очень пригодились как при дальнейших работах над кораблями с несущим корпусом, так и над Space Shuttle. Особенно это касается вопросов теплозащиты и аэродинамики. Так что, несмотря на бесславный конец, Dyna-Soar записала своё имя в историю.
Да, от самого проекта остался только макет, а многие разработанные системы были утилизированы. Но, во-первых, США получили отличную ракету-носитель Titan III, а во-вторых… Во-вторых, очень многие наработки, оставшиеся с «Динозавра», очень пригодились как при дальнейших работах над кораблями с несущим корпусом, так и над Space Shuttle. Особенно это касается вопросов теплозащиты и аэродинамики. Так что, несмотря на бесславный конец, Dyna-Soar записала своё имя в историю.
Вадим Лукашевич, Игорь Афанасьев — «Космические крылья»;
Clarence Geiger — «History of the X-20A Dyna-Soar» Vol. 1: AFSC Historical Publications Series 63-50-I, Document ID ASD-TR-63-50-I. Wright Patterson AFB, Ohio: Aeronautical Systems Division Information Office, 1963
Марк Уэйд — интернет-ресурс
www.astronautix.comСергей Собянин отменил систему обязательных QR-кодов для посещения ресторанов и кафе в Москве
Обязательные QR-коды для посещения московских ресторанов отменят с понедельника, 19 июля. Об этом сообщил мэр столицы Сергей Собянин в ходе заседания президиума Координационного совета при правительстве РФ по борьбе с COVID-19.
Об этом сообщил мэр столицы Сергей Собянин в ходе заседания президиума Координационного совета при правительстве РФ по борьбе с COVID-19.
«Второе решение — с 19 числа мы отменяем обязательные QR-коды в общепите. Это важное решение. У меня было много обращений от бизнеса, общественных организаций, партийных организаций, в частности, от Федерации рестораторов и отельеров, от «Единой России», — заявил Сергей Собянин.
Столичный градоначальник также выразил благодарность московским рестораторам за помощь в борьбе с пандемией.
«Хотел поблагодарить московский бизнес за ответственное отношение к тем мерам, которые мы предпринимали, совместная работа позволила сделать дальнейшие шаги по нормализации обстановки и нормальной работе экономики. Тем не менее мы должны понимать, мы находимся еще в зоне риска, в зоне эпидемии, которая продолжается, конечно, должны выполнять все сантребования и, конечно, обеспечить в дальнейшем массовую вакцинацию населения, и всем нам соблюдать требования и беречь себя и своих родных», — сказал Сергей Собянин.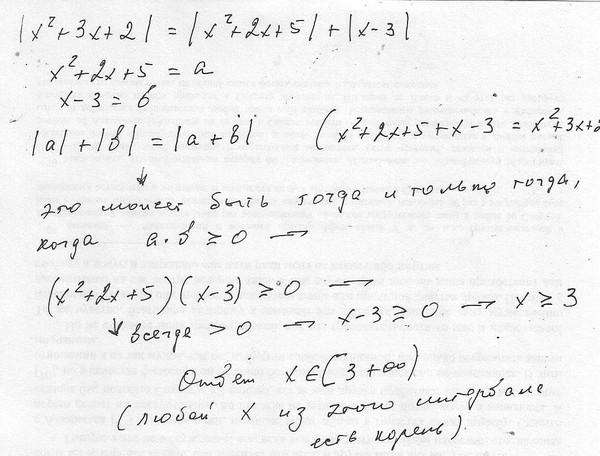
Кроме того, мэр Москвы поблагодарил москвичей за активное участие в мероприятиях, направленных по снижению заболеваемости.
По словам главы города, за минувший месяц более 2 млн человек сделали прививку от коронавируса.
«После тех решений, которые по согласованию с правительством мы приняли, за предыдущие шесть месяцев было привито первым компонентом 1,7 млн человек, а за последний месяц, за один месяц — более 2 млн человек», — сказал столичный градоначальник.
Ранее мэр Москвы сообщал, что около 110 тыс. человек в день делают прививку от коронавирусной инфекции в столице.
Важно также отметить, как сказал мэр Москвы, количество случаев госпитализации в столице снизилось на треть.
«Ситуация в Москве продолжает оставаться сложной, но тем не менее уже четвертую неделю видим улучшение основных показателей. От пика заболеваемости почти в два раза снизилось количество ежедневно выявляемых заболевших ковидом. На треть снизилось количество госпитализаций. Конечно, это стало возможным благодаря ограничительным мерам, которые были введены», — сказал Собянин.
Мэр добавил, что первым компонентом вакцины от коронавируса в Москве привились более 3,8 млн человек.
Более 6 тыс. коек выведут из ковидного фонда в Москве.
«На сегодняшний день в Москве привиты первым компонентом 3,8 млн человек. Вторым, полный цикл — больше 2 млн человек. В связи с улучшением ситуации и хорошей динамикой вакцинации мы приняли ряд серьезных решений: во-первых, мы видим, что у нас заполняемость коечного фонда снизилась, поэтому мы приняли решение о выводе из ковидной группировки более 6 тыс. коек, и они в ближайшее время начнут работу», — сказал Собянин.
Вместе с тем, Сергей Собянин подчеркнул, что ситуация в Москве продолжает оставаться сложной.
Lenovo выпустила моноблоки ideacentre AIO 3 и AIO 5
Компания Lenovo представила на украинском рынке стильные, компактные и высокопроизводительные моноблоки ideacentre AIO 3 и 3i, а также ideacentre AIO 5i для развлечений и работы. Устройства оборудованы мощными процессорами Intel Core i7 10-го поколения, а ideacentre AIO 3 можно выбрать еще и с процессором AMD Ryzen 7. Широкий экран на изящной эргономичной подставке впишется в любой интерьер и не займет много места на рабочем столе.
Стильные устройства “все в одном” для любых задач
Моноблоки ideacentre All-in-One 3 и 3i оснащены практически безрамочными дисплеями с разрешением Full HD (1920×1080 пикселей), что обеспечивает четкую и реалистичную картинку. Пользователь может выбрать оптимальный размер экрана для своих потребностей из трех доступных вариантов: 27, 23.8 и 21.5 дюйма. Благодаря широким углам обзора, устройство идеально подходит для отдыха с близкими за просмотром кинофильмов или сериалов.
Ideacentre AIO 3 и 3i можно опционально приобрести с сенсорным экраном и интуитивно управлять приложениями, просматривать и сразу редактировать изображения, перетаскивать файлы на дисплее. Интерактивное взаимодействие с моноблоком поможет по-новому проживать теплые моменты с родными, создавая семейные коллажи из архивных фотографий.
Элегантный дизайн All-in-One устройства скрывает в себе мощность процессоров 10-го поколения Intel Core i7 или высокопроизводительного AMD Ryzen 7. Кроме процессора, эффективную работу обеспечивают 16 ГБ оперативной памяти. Пользователь также может выбрать конфигурацию с дискретной видеокартой и комбинированным дисковым пространством, например, твердотельный накопитель на 1 ТБ в сочетании с SSD-накопителем на 256 ГБ.
Эргономичное решение для комфортного пользования
Моноблок ассоциируется с кучей проводов, которые неряшливо лежат на столе, раздражают и мешают? Инженеры Lenovo решили эту проблему – в подставку AIO-устройств встроен кабельный коллектор. Он собирает все провода и помогает освободить пространство для важных гаджетов или приятных мелочей. На диване с попкорном или за столом в творческом процессе – ideacentre AIO 3 и 3i подстроится под любое положение пользователя благодаря возможности наклонять подставку моноблока.
Экран и звучание, которые достойны внимания
На новом 27-дюймовом моноблоке ideacentre AIO 5i можно наслаждаться еще более реалистичным изображением. Экран с разрешением Quad HD (2560×1440 пикселей) позволяет сфокусироваться на мельчайших деталях и получить максимальное удовольствие от просмотра видео или игрового процесса. Дисплей с соотношением экрана к корпусу в 93% и тонкими рамками дает больше пространства для работы в видео и фоторедакторах. Ideacentre AIO 5i доступен также с диагональю 23,8 дюйма и разрешением Full HD (1920×1080 пикселей). Как и ideacentre AIO 3 и 3i, старшее поколение устройств можно выбрать с опциональным сенсорным дисплеем.
Для максимального погружения в мир развлечений важно не только изображение, но и качественное звучание. Аудиосистема ideacentre AIO 5i – безоговорочный плюс новинки. Сертифицированные динамики JBL от Harman, премиум-технология Dolby Audio, два высокочастотных и один низкочастотный динамики прекрасно синхронизируются, обеспечивая объемный и чистый звук.
Продуманные детали для полного погружения
Оснащенный процессором Intel Core i7 10-го поколения (в максимальной конфигурации), ideacentre AIO 5i справится с большинством рабочей нагрузки. Моноблок быстро реагирует на запросы пользователя и стабильно работает при воспроизведении «тяжелого» программного обеспечения. Это делает владельца устройства более продуктивным и позволяет креативить без задержек. К тому же моноблоки ideacentre AIO 5i, а также ideacentre AIO 3 и 3i имеют все необходимые порты и разъемы для подключения дополнительных аксессуаров, в том числе второго монитора.
Важно, чтобы мобильный телефон был всегда рядом с компьютером, но мешают провода подзарядки? Достаточно просто положить смартфон на основу Lenovo ideacentre AIO 5i и гаджет будет заряжаться. Инфракрасная камера и технология Windows Hello позволяют автоматически войти в систему за несколько секунд.
Чтобы владелец был уверен в своей конфиденциальности, моноблоки ideacentre AIO 5i, а также ideacentre AIO 3 и 3i оснащены шторкой TrueBlock Privacy Shutter. Достаточно нажать кнопку в верхней части экрана и шторка закроет веб-камеру, пока та не нужна.
Цены и доступность
Новые All-in-One устройства от Lenovo доступны по цене:
- Моноблоки Lenovo ideacentre AIO 3 и 3i – от 17 999 грн.
- Моноблоки Lenovo ideacentre AIO 5i – от 25 999 грн.
Технические характеристики Lenovo ideacentre AIO 3 и 3i
- Процессор: Intel Core i7 (в максимальной конфигурации) или AMD Ryzen 7 (в максимальной конфигурации)
- Операционная система: Windows 10 Home (в максимальной конфигурации)
- Дисплей: 27″/23.8″/21.5″ Full HD (1920×1080 пикселей), IPS, опциональный сенсорный экран, яркость до 250 нит
- Графика: для устройств на базе Intel: интегрированная Intel UHD Graphics или Intel Iris Plus Graphics, дискретная AMD Radeon 625 (опционально). Для устройств на базе AMD: интегрированная AMD Radeon
- Оперативная память: до 16 ГБ
- Накопитель: PCIe SSD до 512 ГБ (в максимальной конфигурации), HDD до 1 ТБ (опционально)
- Аудиосистема: два стереодинамика мощностью по 3 Вт
- Порты: 2 x USB 2.0, 2 x USB 3.1, кардридер “3-в-1” (SD, SDHC, SDXC), RJ45, комбинированный разъем для наушников и микрофона, разъем питания, HDMI-выход, оптический привод (опционально)
- Сеть: 2 x 2 WiFi 802.11 ac, Bluetooth 5.0 combo с картой WiFi
- Габариты: в зависимости от диагонали экрана: 27″ – 613.1x185x485.2мм, 23.8″ – 541.04x185x447.36 мм, 21.5″ – 490.5x185x418.88 мм
- Вес: 5.5 кг
- Цвет: черный (Business Black), белый (Foggy White)
Технические характеристики Lenovo ideacentre AIO 5i
- Процессор: Intel Core i7 (в максимальной конфигурации)
- Операционная система: Windows 10 Home (в максимальной конфигурации)
- Дисплей: 27″ Quad HD (2560×1440 пикселей), 23,8″ Full HD (1920×1080 пикселей), IPS, опциональный сенсорный экран, яркость до 250 нит
- Графика: интегрированная Intel UHD Graphics 630, дискретная NVIDIA GeForce GTX1650
- Оперативная память: до 16 ГБ
- Накопитель: PCIe SSD до 1 ТБ, HDD до 2 ТБ (в максимальной конфигурации)
- Аудиосистема: два ВЧ-динамики JBL от Harman мощностью по 3 Вт, один НЧ-динамик 5 Вт, технология Dolby Audio Premium
- Порты: USB-C, 2 x USB 3.1, 2 x USB 2.0, кардридер “3-в-1” (SD, SDHC, SDXC), RJ45, комбинированный разъем для наушников и микрофона, HDMI. Беспроводная зарядка для смартфона в основе моноблока
- Сеть: 2 x 2 WiFi 802.11 ac, Bluetooth 5.0 combo с картой WiFi
- Габариты: в зависимости от диагонали экрана: 27″ – от 614.8×476.43×25.5 мм, 23,8″ – 541.04x185x447.36 мм
- Вес: 7.25 кг
- Цвет: черный (Black), серый (Mineral Grey)
Читайте больше новостей о Lenovo
Читайте обзоры:уравнений абсолютных значений
уравнений абсолютных значений Уравнения абсолютных значенийВыполните следующие действия, чтобы найти абсолютное значение равенства который содержит одно абсолютное значение:
- Выделите абсолютное значение на одной стороне уравнения.
- Число на другой стороне уравнения отрицательное? Если вы ответили утвердительно, то уравнение не имеет решения. Если вы ответили нет, переходите к шагу 3.
- Напишите два уравнения без абсолютных значений.Первое уравнение установит количество внутри столбцов, равное количеству на другом сторона знака равенства; второе уравнение установит количество внутри столбцы равны противоположному числу на другой стороне.
- Решите два уравнения.
Выполните следующие действия, чтобы найти равенство абсолютного значения
который содержит два абсолютных значения (по одному с каждой стороны уравнения):
- Напишите два уравнения без абсолютных значений.Первое уравнение установит количество внутри столбцов с левой стороны равным количество внутри полос с правой стороны. Второе уравнение установит количество внутри столбцов с левой стороны равным противоположному количества внутри полос с правой стороны.
- Решите два уравнения.
Давайте рассмотрим несколько примеров.
Пример 1: Решить | 2x — 1 | + 3 = 6
| Шаг 1: Изолировать абсолютное значение | | 2x — 1 | + 3 = 6 | 2x — 1 | = 3 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 3, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 2x — 1 = 3 | 2х — 1 = -3 |
| Шаг 4: Решить оба уравнения | 2x — 1 = 3 2x = 4 х = 2 | 2х — 1 = -3 2x = -2 х = -1 |
Пример 2: Решить | 3x — 6 | — 9 = -3
| Шаг 1: Изолировать абсолютное значение | | 3х — 6 | — 9 = -3 | 3x — 6 | = 6 | |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Нет, это положительное число, 6, так что продолжайте шаг 3 | |
| Шаг 3: Запись два уравнения без столбцов абсолютных значений | 3х — 6 = 6 | 3х — 6 = -6 |
| Шаг 4: Решить оба уравнения | 3x — 6 = 6 3x = 12 х = 4 | 3х — 6 = -6 3x = 0 х = 0 |
Пример 3: Решить | 5x + 4 | + 10 = 2
| Шаг 1: Изолировать абсолютное значение | | 5x + 4 | + 10 = 2 | 5x + 4 | = -8 |
| Шаг 2: Is число на другой стороне уравнения отрицательное? | Да, это отрицательное число, -8.Нет решения к этой проблеме. |
Пример 4: Решить | x — 7 | = | 2x — 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 7 = 2х — 2 | х — 7 = — (2х — 2) |
| Шаг 4: Решить оба уравнения | х — 7 = 2х — 2 -x — 7 = -2 -x = 5 х = -5 | х — 7 = -2x + 2 3x — 7 = 2 3x = 9 х = 3 |
Пример 5: Решить | x — 3 | = | x + 2 |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = х + 2 | х — 3 = — (х + 2) |
| Шаг 4: Решить оба уравнения | х — 3 = х + 2 — 3 = -2 ложное заявление Нет решения из этого уравнения | х — 3 = -x — 2 2x — 3 = -2 2x = 1 х = 1/2 |
Итак, единственное решение этой проблемы — x = 1/2
Пример 6: Решить | x — 3 | = | 3 — x |
| Шаг 1: Запись два уравнения без столбцов абсолютных значений | х — 3 = 3 — х | х — 3 = — (3 — х) |
| Шаг 4: Решить оба уравнения | х — 3 = 3 — х 2x — 3 = 3 2x = 6 х = 3 | х — 3 = — (3 — х) х — 3 = -3 + х -3 = -3 Все действительные числа являются решениями этого уравнения |
Так как 3 входит в набор действительных чисел, мы просто скажем, что решение этого уравнения — все действительные числа
Решение квадратных уравнений: выбор метода
Purplemath
Когда вы решаете квадратные уравнения в своем домашнем задании, вы часто можете получить «подсказку» относительно лучшего метода, основанного на теме и заголовке раздела.Например, если вы работаете над домашним заданием в разделе «Решение с помощью факторинга», то вы знаете, что должны решать с помощью факторинга. Но в обзоре главы и на тесте вы не знаете, из какого раздела вашего учебника была взята та или иная квадратичная диаграмма. Какой метод лучше использовать?
Вы можете использовать квадратичную формулу для всего, но формула может занять много времени.
Например:
MathHelp.com
Решить (
x + 1) ( x — 3) = 0.
Чтобы решить это квадратное уравнение, я мог бы перемножить выражение в левой части, упростить поиск коэффициентов, вставить эти значения коэффициентов в квадратную формулу и перейти к ответу.
Но зачем мне это? Я имею в виду, ради всего святого, это факторинг, и они уже учли его и установили для меня равным нулю. Хотя квадратичная формула определенно дала бы мне правильный ответ, зачем с ней возиться?
Вместо этого я сразу решу два фактора, которые они мне дали:
( x + 1) ( x — 3) = 0
x + 1 = 0, x — 3 = 0
x = –1, x = 3
Это было быстро! И мой ответ:
Кстати, строгого порядка решений нет.Да, я обычно размещаю свои решения в числовом порядке, поэтому в приведенном выше случае отрицательный ответ предшествовал положительному. Но, если ваш инструктор ничего не сказал (и я был бы удивлен, если бы это было так), приведенный выше ответ был бы столь же правильным, если бы он был написан как « x = 3, –1».
Квадратичное выражение в левой части знака «равно» не учитывается.
(Как я очень быстро это узнал? Чтобы факторизовать, должны быть целые множители ac = (1) (- 4) = –4, что в сумме дает b = 1.Я вижу, что их нет.)
Эта квадратичная величина не была предоставлена мне в «(переменная часть) 2 равно (некоторое число)», поэтому решение путем извлечения квадратных корней невозможно.
Я мог бы решить это уравнение, заполнив квадрат, но это утомительно и чревато ошибками. Я мог бы попытаться решить, построив график, но лучшее, что я смогу сделать, это получить десятичное приближение из моего «программного обеспечения» (то есть моего графического калькулятора).
Чтобы получить точный и быстрый ответ, я воспользуюсь квадратичной формулой:
Поскольку в инструкциях ничего не упоминается о десятичных приближениях, я оставлю свой ответ в форме квадратного корня:
Решить
x 2 — 3 x — 4 = 0.
Это уравнение не настроено для меня как готовое к извлечению квадратного корня, и я никогда не буду использовать завершение квадрата, если они специально не скажут мне об этом. Однако, прежде чем применять квадратичную формулу, я сначала быстро проверю, можно ли факторизовать выражение в левой части этого уравнения.
Существуют ли целые множители ac = (1) (- 4) = –4, которые в сумме дают –3? Да: –4 и +1.Таким образом, эта квадратичная величина факторизуема, и я уже нашел числа, которые можно использовать для ее разложения (поскольку ведущий коэффициент равен 1):
x 2 — 3 x — 4 = 0
( x + 1) ( x — 4) = 0
x + 1 = 0, x — 4 = 0
x = –1, x = 4
И я закончил, просто так быстро.Мой ответ:
Квадратичное выражение в левой части этого уравнения состоит всего из двух членов, и ни один из них не вычитается, поэтому я не буду использовать простые методы разложения на множители. Но я замечаю, что это разница квадратов, и я знаю, что могу множить разницу квадратов.
x 2 — 4 = 0
( x + 2) ( x — 2) = 0
x + 2 = 0, x — 2 = 0
x = –2, x = 2
Тогда мой ответ:
Примечание: я мог бы переместить 4 в правую часть уравнения, а затем извлечь квадратный корень из любой стороны x 2 = 4.Этот метод дал бы мне тот же ответ, что и приведенный выше факторинг. Если не указано иное, вы должны использовать тот метод, который вам больше нравится.
Решить 6
x 2 + 11 x — 35 = 0.
Ик.
Квадратичное выражение в левой части этого уравнения может быть множителем , но похоже, что поиск факторизации, если таковая имеется, будет неприятным объемом работы.Сейчас я чувствую себя немного бездумным и ленивым, поэтому я воспользуюсь квадратичной формулой. Во время работы мне нужно не забывать ставить ± перед радикалом и ставить черту дроби под всем числителем, представляющим собой целую часть « b 2 ± (корень квадратный)»:
Значения решения представляют собой дроби без радикалов, что означает, что квадратичное могло быть разложено на множители . Но теперь у меня есть ответ, поэтому меня больше не волнует факторизация.
Это квадратное выражение состоит из двух членов и ничего не вычитает, так что либо это разница квадратов (которую я могу разложить на множители), либо ее можно отформатировать как «(переменная часть) 2 равно (число)», чтобы я мог квадратный корень с обеих сторон. Поскольку 48 не является квадратом, я не могу применить формулу разности квадратов. Вместо этого мне придется извлекать квадратный корень из обеих частей:
Итак, мой точный ответ:
Примечание. Если вам специально не сказано предоставлять десятичное приближение для решений, которые включают радикалы, вы должны предположить, что они хотят, чтобы вы дали «точную» форму ответа; то есть они хотят видеть эти квадратные корни.
В этом квадратичном выражении есть два члена, которые легко множить:
x 2 -7 x = 0
x ( x -7) = 0
x = 0, x — 7 = 0
x = 0, x = 7
Мой ответ:
Найдите решения квадратичного уравнения, представленного в таблице ниже:
x -значение | –1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|
y -значение | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 |
Прежде чем я паникую, я думаю об одном методе «решения», который не включает в себя фактическое квадратное уравнение: решение с помощью построения графиков.
Когда они хотят, чтобы я решил квадратное уравнение с помощью построения графиков, они на самом деле просят меня найти точки пересечения x соответствующей квадратичной функции . И под словом «найти» они подразумевают «с красивой картинки». Но дело в том, что они хотят, чтобы я отметил связь между ними и предоставил затем значения x , когда y = 0.
Я могу сделать это по картинке или по Т-образной диаграмме значений.В данном случае вместо графика мне дали таблицу. Есть две точки, у которых одна из координат равна нулю; а именно (0, 9) и (3, 0). Что из этого я хочу? Тот, у которого y = 0, это вторая из двух точек. И мое решение — соответствующее значение x .
Скорее всего, вы не увидите много, а может быть, и совсем другое упражнение этого последнего вида.
Кстати, если вам интересно, почему было только одно решение этой квадратичной, это потому, что (предполагаемое и лежащее в основе) уравнение было ( x — 3) 2 = 0.Итак, одно решение было «повторено».
При решении квадратных уравнений в целом сначала перенесите все на одну сторону от знака «равно» (что уже было сделано в приведенных выше примерах). Затем сначала проверьте, есть ли очевидное факторинг или очевидное извлечение квадратного корня, которое вы можете сделать. Если нет, то обычно лучше прибегать к квадратичной формуле. Но не используйте квадратичную формулу для всего; хотя он всегда даст вам ответ — в конечном итоге — это не всегда самый быстрый метод.А скорость может иметь большое значение в ходе тестов по времени.
URL: https://www.purplemath.com/modules/solvquad6.htm
Решение квадратных уравнений с факторингом
Purplemath
Этот урок охватывает множество способов решения квадратичных вычислений, таких как извлечение квадратного корня, вычисление квадрата и использование квадратичной формулы.Но начнем с решения по факторингу.
(Прежде чем перейти к решению квадратных уравнений, вы уже должны знать, как разложить квадратные выражения на множители. Если нет, сначала просмотрите, как разложить квадратичные уравнения на множители.)
Вы уже разложили квадратные выражения на множители. Новым здесь является то, что квадратное выражение является частью уравнения, и вам предлагается найти значения переменной, которые делают уравнение истинным. Вот как это работает:
MathHelp.com
Решите (
x — 3) ( x — 4) = 0 путем факторизации.
Хорошо, эта квадратичная для меня уже учтена.Но как мне использовать эту факторизацию для решения уравнения?
Для решения квадратичных вычислений путем факторинга мы используем то, что называется «Свойство нулевого произведения». Это свойство говорит о том, что кажется довольно очевидным, но только после того, как нам на это указали; а именно:
Свойство нулевого произведения: если мы умножаем две (или более) вещи вместе и результат равен нулю, то мы знаем, что по крайней мере одна из тех вещей, которые мы умножили, также должны быть равны нулю.Другими словами, единственный способ получить ноль при умножении двух (или более) множителей состоит в том, чтобы один из множителей был равен нулю.
Итак, если мы умножаем два (или более) множителя и получаем нулевой результат, то мы знаем, что по крайней мере один из множителей сам был равен нулю. В частности, мы можем установить каждый из факторов равным нулю и решить полученное уравнение для одного решения исходного уравнения.
Мы можем сделать полезный вывод о множителях (а именно, что один из этих множителей должен был быть равен нулю, поэтому мы можем установить множители равными нулю), только если сам продукт равен нулю.Если произведение множителей равно на все , отличное от нуля, то мы не можем сделать никаких утверждений о значениях факторов.
Следовательно, при решении квадратных уравнений путем факторизации мы должны всегда иметь уравнение в форме «(квадратное выражение) равно (нулю)», прежде чем предпринимать какие-либо попытки решить квадратное уравнение путем факторизации.
Возвращение к упражнению:
Принцип нулевого фактора говорит мне, что хотя бы один из факторов должен быть равен нулю.Поскольку хотя бы один из коэффициентов должен быть равен нулю, я могу установить , каждые коэффициентов равны нулю:
x — 3 = 0 или x — 4 = 0
Это дает мне простые линейные уравнения, которые легко решить:
И эти два значения — решение, которое они ищут:
Обратите внимание, что « x = 3, 4» означает то же самое, что и « x = 3 или x = 4»; единственная разница — это форматирование.Формат « x = 3, 4» является более распространенным.
Решите
x 2 + 5 x + 6 = 0 и проверьте.
Это уравнение уже имеет форму «(квадратичное) равно (нулю)», но, в отличие от предыдущего примера, оно еще не учтено. Я ДОЛЖЕН сначала разложить на множители квадратичный, потому что только когда я УМНОЖДАЮ и получаю ноль, я могу что-либо сказать о факторах и решениях.Я не могу сделать никаких выводов об отдельных членах квадратичной функции без учета фактора (например, 5 x или 6), потому что я могу добавить много всего, что в сумме равно нулю.
Итак, первое, что мне нужно сделать, это фактор:
x 2 + 5 x + 6 = ( x + 2) ( x + 3)
Теперь я могу переформулировать исходное уравнение в виде произведения факторов, при этом произведение равно нулю:
Теперь я могу решить каждый фактор, установив каждый из них равным нулю и решив получившиеся линейные уравнения:
x + 2 = 0 или x + 3 = 0
x = –2 или x = — 3
Эти два значения являются решением исходного квадратного уравнения.Итак, мой ответ:
Однако я еще не закончил, потому что в исходном упражнении мне предлагалось «проверить», что означает, что мне нужно вставить свои ответы обратно в исходное уравнение и убедиться, что оно получилось правильным. В этом случае я буду вставлять выражение в левой части исходного уравнения и проверять, что я получаю правую часть; а именно с 0:
проверка x = –3:
[–3] 2 + 5 [–3] + 6
9–15 + 6
9 + 6–15
15–15
0
проверка x = –2:
[–2] 2 + 5 [–2] + 6
4–10 + 6
4 + 6 — 10
10–10
0
Когда в упражнении указано, что вы должны решить «и проверить» вышеуказанное «plug-n-chug», они ищут вас, чтобы показать, что вы включили свой ответ в исходное упражнение и получили что-то, что сработало правильно.Выше, где я показал свои чеки, все, что им нужно. Но делайте свою работу аккуратно!
Между прочим, вы можете использовать эту технику «проверки», чтобы проверить свои ответы на любое «решающее» упражнение. Так, например, если вы не уверены в своем ответе на вопрос «фактор и решение» в следующем тесте, попробуйте включить свои ответы в исходное уравнение и убедиться, что ваши решения приводят к истинным утверждениям.
Это уравнение не в форме «(квадратичное) равно (нулю)», поэтому я пока не могу его решить.Первое, что мне нужно сделать, это перебрать все термины с одной стороны, а с другой стороны — ноль. Только тогда я могу разложить на множители и решить:
x 2 — 3 = 2 x
x 2 — 2 x — 3 = 0
( x — 3) ( x + 1) = 0
x — 3 = 0, x + 1 = 0
x = 3, x = –1
Тогда мое решение:
Решите (
x + 2) ( x + 3) = 12.
Студенты часто видят уравнения такого типа и говорят:
«Круто! Это уже учтено! Я установлю множители равными 12 и решу, чтобы получить x = 10 и x = 9. Это было легко!»
Да, это было легко; это тоже было неправильно. Очень-очень неправильно.
Помимо того факта, что ни (10 + 2) (10 + 3), ни (9 + 2) (9 + 3) не равно 12, мы никогда не должны забывать, что мы должны иметь «(квадратичное) равно (нулю)», прежде чем мы сможем решить по факторингу.
Возвращение к упражнению:
Каким бы заманчивым это ни казалось, я не могу приравнять каждый из множителей в левой части уравнения к другой части уравнения и решить. В противном случае я бы получил совершенно неправильную путаницу.
Вместо этого я сначала должен умножить и упростить левую часть, затем вычесть 12 из левой и повторно разложить на множители. Только тогда я смогу решить.
( x + 2) ( x + 3) = 12
x 2 + 5 x + 6 = 12
x 2 + 5 x — 6 = 0
( x + 6) ( x — 1) = 0
x + 6 = 0, x — 1 = 0
x = –6, x = 1
Тогда мое решение:
Эту двухчленную квадратичную легче разложить на множители, чем предыдущие квадратичные: я сразу вижу, что могу вычесть x из обоих членов, взяв x вперед.Это дает мне:
Очень распространенная ошибка, которую делают ученики на этом этапе, — это «решить» уравнение для « x + 5 = 0» путем деления на x . Но это неверный шаг. Почему? Потому что мы не можем делить на ноль. Как это здесь играет роль?
При делении на коэффициент x делается неявное предположение, что x не равно нулю.Для такого предположения нет абсолютно никаких оснований! И такое предположение привело бы к потере половины нашего решения этого уравнения.
Возвращение к упражнению:
Мне нужно помнить, что фактор может содержать только переменную без добавления к другим терминам; в частности, « x » — вполне допустимый коэффициент. Мне нужно установить и коэффициентов равными нулю, а затем решить два результирующих линейных уравнения:
x ( x + 5) = 0
x = 0, x + 5 = 0
x = 0, x = –5
Тогда мое решение:
В предыдущем примере было два члена, и его было легко разложить на множители.Есть еще один случай двухчленной квадратичной системы, который мы можем разложить на множители. Это только немного сложнее:
Это уравнение имеет форму «(квадратичное) равно (нулю)», поэтому я могу решить его путем факторизации. Но как это учесть? Заметив, что это разница квадратов. Применим формулу разности квадратов, которую выучил:
x 2 — 4 = 0
( x — 2) ( x + 2) = 0
x — 2 = 0, x + 2 = 0
x = 2, x = –2
Тогда мое решение:
Примечание. Приведенное выше решение также можно отформатировать как « x = ± 2».Это произносится как « x равно плюс или минус 2».
В последнем примере, приведенном выше, на следующей странице показано, как решить, извлекая квадратный корень.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в решении квадратных уравнений путем факторизации. Попробуйте выполнить указанное упражнение или введите свое собственное. Затем нажмите кнопку и выберите «Решить с учетом факторинга», чтобы сравнить свой ответ с ответом Mathway. (Или перейдите к следующей странице.)
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.)
URL: https://www.purplemath.com/modules/solvquad.htm
Математическая сцена — Уравнения III — Урок 2
Математическая сцена — Уравнения III — Урок 2 — Квадратные уравнения| 2008 Rasmus ehf и Jhann sak Ptursson | Уравнения III |
Урок 2 Уравнения кубической и четвертой степени
Как мы можем решить такие уравнения, как кубическое уравнение показано здесь?
x 3 — x 2 4x + 4 = 0
Существует чрезвычайно сложная формула решения кубические уравнения.Некоторые калькуляторы имеют встроенную формулу и поэтому могут использоваться для решения кубических уравнений.
Мы собираемся узнать, как эти уравнения могут быть решены с помощью факторизация. Если уравнение имеет решения, которые являются целыми числами a, b и c, то мы можем разложить уравнение на множители следующим образом:
x 3 — x 2 4x + 4 = (x — а) (х — б) (х — в) = 0
Умножая скобки, видим, что константа член 4 должен быть числом, которое мы получаем, когда мы умножаем a, b и c вместе.
abc = 4
Все решения a, b и c должны быть множителями 4, поэтому не так много целых чисел, которые нам нужно учитывать.
У нас есть только следующие возможности:
1, 2 и 4
Хорошо изучите каждое из этих чисел, чтобы найти, какие из них являются решениями уравнения.
f (1) = 1 3 — 1 2 4 × 1 + 4 = 0 1 — решение
f (-1) = (-1) 3 — (-1) 2 4 × (-1) + 4 = 6
f (2) = 2 3 -2 2 4 × 2 + 4 = 0 2 — решение
f (−2) = (−2) 3 — (−2) 2 4 × (−2) + 4 = 0 −2 — решение
Мы нашли три решения, поэтому нам не нужно попробуйте 4 и −4 как кубический уравнение имеет максимум три решения.
Эти три числа дают нам значения a, b и c и мы можем факторизовать уравнение.
x 3 — x 2 4x + 4 = (x — 1) (х — 2) (х + 2) = 0
Этот метод включает поиск целых чисел, которые являются множителями
(можно разделить на) постоянный член, а затем проверить, действительно ли эти
целые числа являются решениями уравнения.
К сожалению, мы не можем предполагать, что решения уравнения третьей степени являются
все целые числа.
Однако, если мы можем найти одно целочисленное решение, допустим, что это x = a, тогда по
Теорема остатка, мы знаем, что (x — a) является фактором уравнения. Мы
можно найти другой множитель, квадратичный множитель, путем деления. Затем мы можем решить квадратное уравнение, используя
формула решения квадратиков.
Пример 1
Решите уравнение x 3 — 3x 2 2x + 4 = 0
Ставим числа, кратные 4 в уравнение, чтобы проверить, верны ли какие-либо из них.
f (1) = 1 3 — 3 × 1 2 2 × 1 + 4 = 0 1 — решение
f (−1) = (−1) 3 — 3 × (−1) 2 2 × (-1) + 4 = 2
f (2) = 2 3 — 3 × 2 2 2 × 2 + 4 = −4
f (−2) = (−2) 3 — 3 × (−2) 2 2 × (−2) + 4 = −12
f (4) = 4 3 — 3 × 4 2 2 × 4 + 4 = 12
f (−4) = (−4) 3 — 3 × (−4) 2 2 × (−4) + 4 = −100
Единственное целочисленное решение — x = 1.Когда мы нашли одно решение, нам действительно не нужно проверять другие числа, потому что теперь мы можем решить уравнение, разделив на (x — 1) и попытавшись решить квадратичный получаем из деления.
Теперь мы можем разложить наши выражение следующим образом:
x 3 — 3x 2 2x + 4 = (х — 1) (х 2 — 2х — 4) = 0
Теперь нам остается решить квадратичную уравнение.
x 2 — 2x — 4 = 0
Используем формулу квадратиков с a = 1, b = −2 и c = −4.
Мы нашли все три решения уравнение x 3 — 3x 2 2x + 4 = 0. Это: эфтирфаранди:
.х = 1
х = 1 + 5
x = 1 — 5
Пример 2
Мы можем легко использовать тот же метод для решения уравнение четвертой степени или уравнения еще более высокой степени.Решите уравнение f (x) = x 4 — x 3 — 5x 2 + 3x + 2 = 0.
Сначала мы находим целые множители постоянный член, 2. Целочисленные множители 2 равны 1 и 2.
f (1) = 1 4 — 1 3 — 5 × 1 2 + 3 × 1 + 2 = 0 1 — решение
f (−1) = (−1) 4 — (−1) 3 — 5 × (−1) 2 + 3 × (−1) + 2 = −4
f (2) = 2 4 — 2 3 — 5 × 2 2 + 3 × 2 + 2 = −4
f (−2) = (−2) 4 — (−2) 3 — 5 × (−2) 2 + 3 × (−2) + 2 = 0 ср. нашли вторую решение.
Два найденных нами решения 1 и −2 означают, что мы можем разделить на x —
1 и x + 2 и остатка не будет. Сделайте это в два этапа.
Сначала разделим на x + 2
Теперь разделите полученный кубический коэффициент по x — 1.
Теперь мы разложили на множители
f (x) = x 4 — x 3 — 5x 2 + 3x + 2 в
f (x) = (x + 2) (x — 1) (x 2 — 2x — 1) и только
Осталось решить квадратное уравнение
x 2 — 2x — 1 = 0.Мы используем формула с a = 1, b = −2 и c = −1.
Всего найдено четыре решения. Их:
х = 1
х = -2
х = 1 +
х = 1 —
Иногда мы можем решить уравнение третьей степени, заключив в скобки члены два на два и найдя множитель что у них общего.Давайте посмотрим на это на примере.
Пример 3.
Решите уравнение x 3 — 2x 2 — 4x + 8 = 0
x 3 — 2x 2 — 4x + 8 = 0 (x 3 — 2x 2 ) — (4x — 8) = 0 [x 2 (x — 2) — 4 (x — 2)] = 0 (x — 2) [x 2 — 4] = 0 (х — 2) (х — 2) (х + 2) = 0 | Здесь скобка (x — 2) является общим множителем и может быть вынесена за пределы общая скобка. |
Обратите внимание, что скоба (x — 2) происходит дважды, когда мы закончили факторизацию. x = 2 — это поэтому двойное решение, и у нас есть только два разных. Это:
x = 2 и x = −2 .Лауснир: x = 2 og x = −2 .
Примеры, которые мы рассмотрели до сих пор, являются уравнения, в которых член с наибольшей степенью имеет коэффициент 1.
Как мы иметь дело с уравнениями, где этот коэффициент — какое-то другое число?
Общая форма — f (x) = ax 3 + bx 2 + cx + d, где a, b, c и d — целые числа.
Мы можем искать целочисленные решения в том же как и раньше, проверяя множители постоянного члена d. Если мы найдем целочисленное решение, тогда мы можем разделить и найти другие решения, как и раньше.
Если ни один из факторов d не дает нам решения
затем мы ищем решения, которые являются дробями.
Предположим, есть дробное решение, и назовем его
решение x = t / n.
Это означает, что x — t / n является фактором f (x), или, если мы умножаем на n, то xn — t является множителем.
Теперь предположим, что мы разделили f (x) на xn.
— t и нашли квадратичный множитель, мы можем назвать его
Ax 2 + Bx + C.
Теперь у нас есть результат
ax 3 + bx 2 + cx + d = (xn — t) (Ax 2 + Bx + C)
сравнивая коэффициенты x 3 на
обе стороны уравнения мы видим, что a = nA и, следовательно, n должно быть множителем
а.
Аналогично, сравнивая постоянные члены, мы видим, что
d = −tC и, следовательно, t является множителем d.
Мы заключаем, что любая дробь является решением кубическое уравнение ax 3 + bx 2 + cx + d должен иметь вид t / n, где t — множитель числа d, а n — фактор числа a.
Обобщение для функции степени n:
ф (х) = a n x n + a n − 1 x n − 1 + × × × × + а 1 х + 0
с коэффициентами а 0 , а 1 , а 2 , × × × × × а n − 2 , n − 1 и n .
Если эта функция имеет рациональное решение, скажем, t / n, тогда t — коэффициент 0 , а n — коэффициент n .
Пример 4
Решите уравнение f (x) = 2x 3 — 7x 2 + 4x + 3 = 0.
Возможные целые корни f (x) — это делители 3, это 1 и 3. Дроби, которые могут быть корнями, — это эти четыре числа, разделенные на множители 2.Итак, полный список рациональных чисел, которые нам нужно рассмотреть, — это , 1, 3 / 2 и 3.Сразу видно, что нам не нужно рассмотрите любые отрицательные значения, поскольку все они будут давать отрицательные значения для f (x), а не 0.
Теперь попробуем другие возможностиf () = 2 () 3 — 7 () 2 + 4 × + 3 = 3
f (1) = 2 × 1 3 — 7 × 2 + 4 × 1 + 3 = 2
ф ( 3 / 2 ) = 2 ( 3 / 2 ) 3 — 7 ( 3 / 2 ) 2 + 4 × 3 / 2 + 3 = 0, поэтому мы нашли решение.
x = 3 / 2 — это решение, поэтому (x — 3 / 2 ) является множителем. Разделить на (x — 3 / 2 ) может быть сложно. Поэтому мы умножаем на 2 и вместо этого делим на (2x — 3). Если (x — 3 / 2 ) является фактор
, тогда (2x — 3).
Теперь нам нужно решить уравнение x 2 — 2x — 1 = 0.Мы уже решили это уравнение в примере 2. Решения: 1 + 2 og 1 — 2.
Итак, мы нашли три решения. Их:
х = 3 / 2 = 1
х = 1 + 2
х = 1 — 2
Попробуйте выполнить тест 2 по уравнениям III.
Не забудьте использовать контрольный список для следите за своей работой.
Решение уравнений абсолютных значений — Подготовка к оценке TSI
Решение уравнений типа абсолютных значений |
x | = к .Уравнения абсолютного значения полезны при определении расстояния и измерения ошибок.
Мы рассмотрим следующие примеры:
| x | = 3
| x — 6 | = 4
| 2 x — 3 | = 9
| х + 7 | = — 2
| x + 8 | = | 3 x — 4 |
Пример 1 : Решить для x : | x | = 3
Решение.
Это уравнение просит нас найти все числа x , которые равны 3 единиц от нуля на числовой прямой.
Мы должны рассматривать числа как справа, так и слева от нуля на числовой прямой.
Обратите внимание, что 3 и -3 — это три единицы от нуля.
Решение: x = 3 или x = −3 .
Пример 1 предлагает правило, которое мы можем использовать при решении уравнений абсолютных значений.
Если c — положительное число, то | x | = c эквивалентно x = c или x = — c.
Пример 2 : Решить для x : | x — 6 | = 4
Решение.
Шаг 1. Разбейте уравнение на два эквивалентных уравнения, используя правило: Если | x | = c , затем x = c или x = — c .
| x — 6 | = 4 эквивалентно x — 6 = 4 или x — 6 = — 4
Шаг 2. Решите каждое уравнение .
x — 6 + 6 = 4 + 6
x = 10
х — 6 + 6 = — 4 + 6
x = 2
Шаг 3 . Проверьте решения.
| 10 — 6 | = | 4 | = 4
| 2 — 6 | = | — 4 | = 4
Решения: x = 10 и x = 2 .
Пример 3 : Решить относительно x : | 2 x — 3 | = 9
Решение.
Шаг 1.
Разбейте уравнение на два эквивалентных уравнения, используя правило: Если | x | = c , затем x = c или x = — c .
| 2 x — 3 | = 9 эквивалентно 2 x — 3 = 9 или 2 x — 3 = -9
Шаг 2. Решите каждое уравнение .
2 x — 3 = 9 или 2 x — 3 = -9
2 x — 3 + 3 = 9 + 3 или 2 x — 3 + 3 = -9 + 3
2 x = 12 или 2 x = -6
2 x ÷ 2 = 12 ÷ 2 или 2 x ÷ 2 = -6 ÷ 2
x = 6 или x = -3
Шаг 3 . Проверьте решения.
x = 6: | 2 (6) — 3 | = | 12 — 3 | = | 9 | = 9
x = -3: | 2 (-3) — 3 | = | -6 — 3 | = | -9 | = 9
Решения: x = 6 и x = -3 .
Пример 4 : Решить для x : | x + 7 | = — 2
Решение.
Абсолютное значение числа никогда не бывает отрицательным. У этого уравнения нет решения .
Решение уравнений типа абсолютных значений |
x | = | y |.Если абсолютные значения двух выражений равны, то либо два выражения равны, либо они противоположны.
Если x и y представляют алгебраические выражения, | x | = | y | эквивалентно x = y или x = — y.
Пример 5 : Решить для x : | x + 8 | = | 3 x — 4 |
Решение.
Шаг 1. Разбейте уравнение на два эквивалентных уравнения .
| x + 8 | = | 3 x — 4 | эквивалентно x + 8 = 3 x — 4 или x + 8 = — (3 x — 4)
Шаг 2.Решите каждое уравнение.
x + 8 = 3 x — 4 или x + 8 = — (3 x — 4)
x + 8 = 3 x — 4 или x + 8 = — 3 x + 4
x + 8- x = 3 x -4- x или x + 8 + 3 x = -3 x + 4 + 3 x
8 = 2 x — 4 или 4 x + 8 = 4
8 + 4 = 2 x — 4 + 4 или 4 x + 8-8 = 4-8
12 = 2 x или 4 x = — 4
12 ÷ 2 = 2 x ÷ 2 или 4 x ÷ 4 = — 4 ÷ 4
6 = x или x = — 1
Шаг 3 . Проверьте решения.
x = 6: | 6 + 8 | = | 3 (6) — 4 |
| 14 | = | 18 — 4 |
| 14 | = | 14 |
14 = 14
x = — 1: | — 1 + 8 | = | 3 ( — 1) — 4 |
| 7 | = | — 3-4 |
| 7 | = | — 7 |
7 = — 7
Решения: x = 6 и x = — 1 .
Решение уравнения абсолютных значений
Далее мы узнаем, как решить уравнение абсолютного значения . Чтобы решить такое уравнение, как [latex] | 2x — 6 | = 8 [/ latex], мы замечаем, что абсолютное значение будет равно 8, если количество внутри столбцов абсолютного значения равно [latex] 8 [/ latex] или [латекс] -8 [/ латекс]. Это приводит к двум различным уравнениям, которые мы можем решить независимо.
[латекс] \ begin {array} {lll} 2x — 6 = 8 \ hfill & \ text {или} \ hfill & 2x — 6 = -8 \ hfill \\ 2x = 14 \ hfill & \ hfill & 2x = — 2 \ hfill \\ x = 7 \ hfill & \ hfill & x = -1 \ hfill \ end {array} [/ latex]
Полезно знать, как решать проблемы, связанные с функциями абсолютного значения.Например, нам может потребоваться определить числа или точки на линии, которые находятся на заданном расстоянии от заданной контрольной точки.
Общее примечание: уравнения абсолютных значений
Абсолютное значение x записывается как [latex] | x | [/ latex]. Он имеет следующие свойства:
[латекс] \ begin {array} {l} \ text {If} x \ ge 0, \ text {then} | x | = x. \ Hfill \\ \ text {If} x <0, \ text {тогда } | x | = -x. \ hfill \ end {array} [/ latex]
Для действительных чисел [латекс] A [/ латекс] и [латекс] B [/ латекс], уравнение вида [латекс] | A | = B [/ латекс] с [латексом] B \ ge 0 [/ latex], будут решения, когда [latex] A = B [/ latex] или [latex] A = -B [/ latex].Если [latex] B <0 [/ latex], уравнение [latex] | A | = B [/ latex] не имеет решения.
Уравнение абсолютного значения в форме [latex] | ax + b | = c [/ latex] имеет следующие свойства:
[латекс] \ begin {array} {l} \ text {If} c <0, | ax + b | = c \ text {не имеет решения}. \ Hfill \\ \ text {If} c = 0, | ax + b | = c \ text {имеет одно решение}. \ hfill \\ \ text {If} c> 0, | ax + b | = c \ text {имеет два решения}. \ hfill \ end {array} [ / латекс]
Как: решить уравнение абсолютного значения.
- Изолировать выражение абсолютного значения с одной стороны от знака равенства.
- Если [latex] c> 0 [/ latex], запишите и решите два уравнения: [latex] ax + b = c [/ latex] и [latex] ax + b = -c [/ latex].
Пример 8: Решение уравнений абсолютных значений
Решите следующие уравнения абсолютных значений:
а. [латекс] | 6x + 4 | = 8 [/ латекс]
б. [латекс] | 3x + 4 | = -9 [/ латекс]
c. [латекс] | 3x — 5 | -4 = 6 [/ латекс]
d. [латекс] | -5x + 10 | = 0 [/ латекс]
Решение
а. [латекс] | 6x + 4 | = 8 [/ латекс]
Напишите два уравнения и решите каждое:
[латекс] \ begin {array} {ll} 6x + 4 \ hfill & = 8 \ hfill & 6x + 4 \ hfill & = — 8 \ hfill \\ 6x \ hfill & = 4 \ hfill & 6x \ hfill & = — 12 \ hfill \\ x \ hfill & = \ frac {2} {3} \ hfill & x \ hfill & = — 2 \ hfill \ end {array} [/ latex]
Два решения: [латекс] x = \ frac {2} {3} [/ latex], [latex] x = -2 [/ latex].
г. [латекс] | 3x + 4 | = -9 [/ латекс]
Нет решения, так как абсолютное значение не может быть отрицательным.
г. [латекс] | 3x — 5 | -4 = 6 [/ латекс]
Выделите выражение абсолютного значения и запишите два уравнения.
[латекс] \ begin {array} {lll} \ hfill & | 3x — 5 | -4 = 6 \ hfill & \ hfill \\ \ hfill & | 3x — 5 | = 10 \ hfill & \ hfill \\ \ hfill & \ hfill & \ hfill \\ 3x — 5 = 10 \ hfill & \ hfill & 3x — 5 = -10 \ hfill \\ 3x = 15 \ hfill & \ hfill & 3x = -5 \ hfill \\ x = 5 \ hfill & \ hfill & x = — \ frac {5} {3} \ hfill \ end {array} [/ latex]
Есть два решения: [latex] x = 5 [/ latex], [latex] x = — \ frac {5} {3} [/ latex].
г. [латекс] | -5x + 10 | = 0 [/ латекс]
Уравнение устанавливается равным нулю, поэтому нам нужно написать только одно уравнение.
[латекс] \ begin {array} {l} -5x + 10 \ hfill & = 0 \ hfill \\ -5x \ hfill & = — 10 \ hfill \\ x \ hfill & = 2 \ hfill \ end {array} [/ latex ]
Есть одно решение: [латекс] х = 2 [/ латекс].
Попробуй 7
Решите уравнение абсолютного значения: [latex] | 1 — 4x | + 8 = 13 [/ latex].
Решение
Распределительная собственность — ChiliMath
Распределительное свойство умножения над сложением позволяет нам исключить символ группировки, обычно в форме круглых скобок.Следующая диаграмма иллюстрирует основной шаблон или формулу, как ее применять.
Основная «формула» распределительной собственности
Несколько заметок:
- Это делается путем умножения внешнего члена на каждый член в скобках.
- Таким образом, возьмите член a, который находится вне скобок, и распределите его по каждому члену внутри скобок.
- Обратите внимание, что ab означает a, умноженное на b.
- Точно так же ac означает a, умноженное на c.
Объединение одинаковых терминов с использованием свойства распределения
Пример 1: Распространить, а затем упростить приведенное ниже выражение.
Можно ли сразу скомбинировать x-члены? Не так быстро! Член 2x находится внутри скобок, а 3x — снаружи. Мы не можем объединить их, потому что они находятся в разных местах.
Что нам нужно сделать, так это сначала удалить символ круглой скобки, прежде чем мы сможем объединить похожие термины, которые могут возникнуть при сложении или вычитании.Вот где полезность этого свойства вступает в игру.
На этом этапе скобки опускаются, и все x-члены можно комбинировать. Я бы переставил их, поместив похожие термины рядом, прежде чем выполнять требуемую операцию.
Пример 2: Распределить, а затем упростить приведенное ниже выражение.
Поскольку здесь две круглые скобки, мы должны применить свойство дважды. Это должно избавить нас от символов группировки и позволить нам комбинировать похожие термины.
После удаления двух круглых скобок теперь можно комбинировать похожие термины. Перед выполнением необходимой операции сложения или вычитания убедитесь, что вы переставили термины таким образом, чтобы похожие термины располагались рядом.
Пример 3: Распределить, а затем упростить приведенное ниже выражение.
Я надеюсь, что теперь вы видите закономерность. Имея три круглые скобки, мы также должны применить его трижды.
Поскольку все термины теперь находятся за пределами круглых скобок, продолжайте комбинировать похожие термины.
Пример 4: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Пример 5: Распространить, а затем упростите приведенное ниже выражение.
Решение:
Пример 6: Распределить, а затем упростить приведенное ниже выражение.
Решение:
Сначала примените свойство распределения к внутренним скобкам и объедините похожие термины.Наконец, избавьтесь от символа квадратной скобки, распределив еще раз.
Вы также можете использовать свойство распределения при решении уравнений .
Решение линейных уравнений с использованием распределительного свойства
Пример 7: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Как видите, внешнее число 3, находящееся непосредственно слева от круглой скобки, предполагает, что мы можем применить свойство для удаления символа группировки.
- Возьмите это число 3 и умножьте на каждый член в скобках.
- После этого символ скобки должен исчезнуть. Затем мы можем перейти к обычным шагам решения уравнения. В этом примере мы выделим переменную «x» слева от уравнения. После распределения вычтите обе части на 3 и разделите на — \, 6 с обеих сторон уравнения, чтобы прийти к окончательному ответу.
Пример 8: Решите приведенное ниже линейное уравнение, используя свойство распределения.
Наличие двух круглых скобок в левой части уравнения означает, что мы должны распределить дважды.
Избавившись от символов группировки, теперь мы можем комбинировать одинаковые термины и изолировать переменную в левой части уравнения.
Пример 9: Используйте свойство распределения для решения уравнения.
Решение:
Начните с распределения 4 в первые скобки, а затем — 1 во вторую скобку.Затем объедините похожие термины, которые возникают после исключения скобок. Наконец, решите x, выделив его слева.
Пример 10: Используйте свойство распределения для решения уравнения.
Решение:
Здесь мы видим две круглые скобки, что означает, что мы распределяем дважды, по одной с каждой стороны уравнения, чтобы исключить символы группировки. Затем решите линейное уравнение как обычно. 😀
.

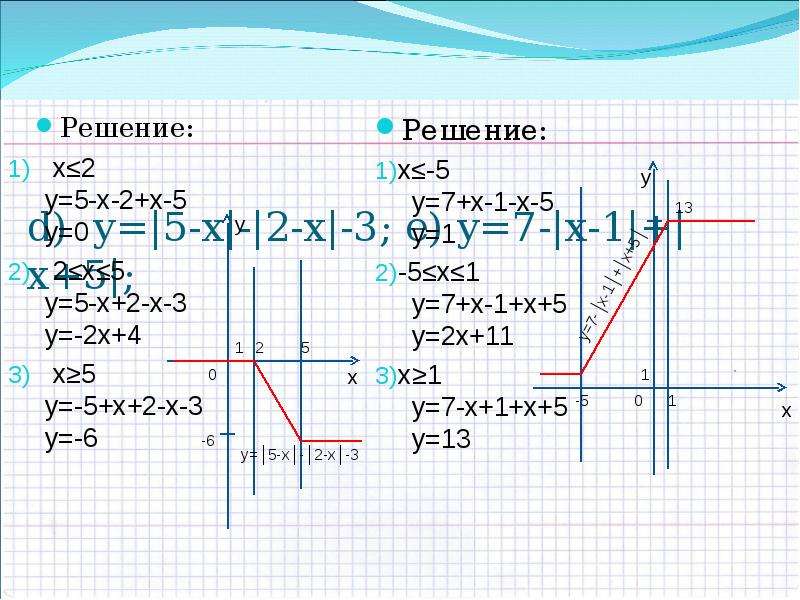 NorthAmerican предложила достаточно традиционный двухступенчатый аппарат, Boeing – беспилотный ракетоплан, названный планирующим управляемым снарядом» (glide-missile), а фирма Republic хотела построить малый беспилотный летательный аппарат, напоминающий перехватчик проекта XF -103 с маршевым гиперзвуковым ПВРД, стартующий с помощью некоего нового трехступенчатого ускорителя
NorthAmerican предложила достаточно традиционный двухступенчатый аппарат, Boeing – беспилотный ракетоплан, названный планирующим управляемым снарядом» (glide-missile), а фирма Republic хотела построить малый беспилотный летательный аппарат, напоминающий перехватчик проекта XF -103 с маршевым гиперзвуковым ПВРД, стартующий с помощью некоего нового трехступенчатого ускорителя Чтобы компенсировать проигрыш в конкурсе на B-70 (его выиграла компания NorthAmerican со своей знаменитой Валькирией –- прим. А.С.) в конце 1957 года, было логично, что компания будет строить следующий крупный проект.
Чтобы компенсировать проигрыш в конкурсе на B-70 (его выиграла компания NorthAmerican со своей знаменитой Валькирией –- прим. А.С.) в конце 1957 года, было логично, что компания будет строить следующий крупный проект.