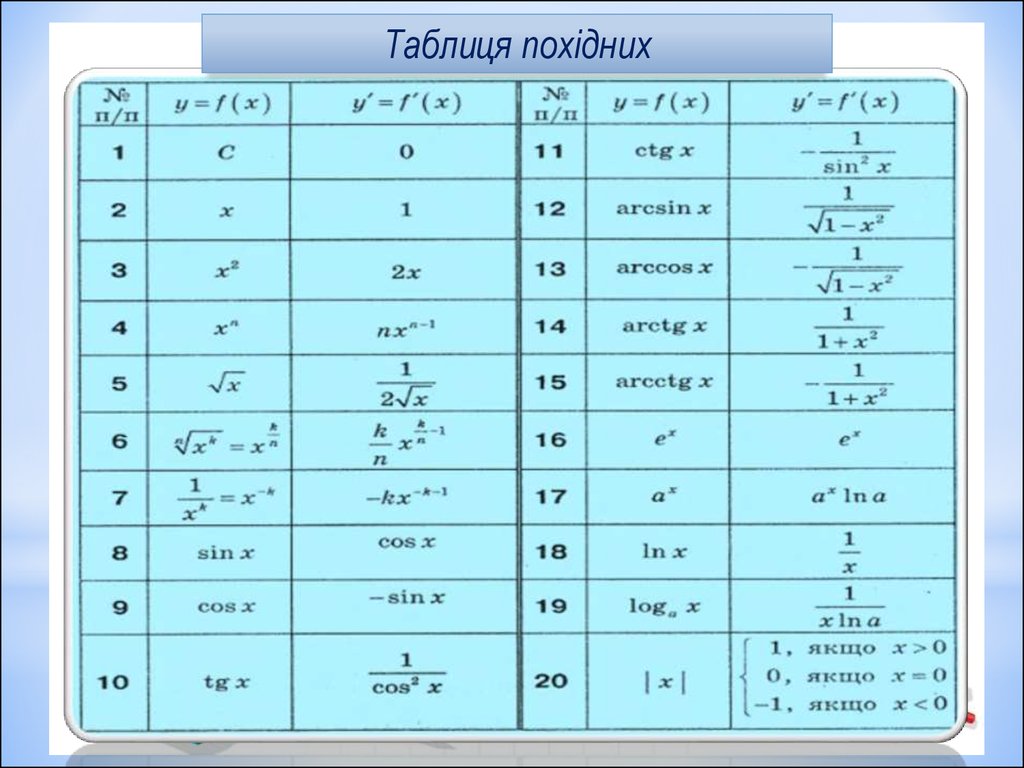
46. Теорема сложной функции
Пусть сложная функция у = f(x) = g(v(x)) такова, что функция у = v(x) определена на промежутке U , а функция u = v(x) определена на промежутке Х и множество всех её значений входит в промежуток U. Пусть функция u = v(x) имеет производную в каждой точке внутри промежутка Х , а функция y = g(u) имеет производную в каждой точке внутри промежутка U. Тогда функция y = f(x) имеет производную в каждой точке внутри промежутка Х , вычисляемую по формуле
y’x = y’u • u’x.
Формулу читают так: производная y по x равна производной y по u, умноженной на производную u по x.
Формулу записывают ещё так:
f’ (x) = g’ (u) v’ (x).
Доказательство.
В
точке х
Х зададим
приращение аргумента
,
(х+
х)
Х. Тогда
функция u = v(x) получит приращение
, а
функция y = g(u) получит приращение y. Надо
учесть, что, так как функция u=v(x) в
точке x имеет производную, то она
непрерывна в этой точке и
при
.
Если функция u(x) дифференцируема в точке x0, а функция y = f(u) дифференцируема в точке u0 = f(x0), то сложная функция F(x) = f(u(x)) дифференцируема в точке x0, причем:
| F ‘(x0) = f ‘(u(x0))u’ (x0). |
Производная степенной функции с любым действительным показателем |
Известно,
что (xn)’ = nxn-1 для натурального n.
Пусть теперь n любое действительное
число и х>0. Справедливо тождество xn =
enlnx. Тогда у = enlnx – сложная
функция и ее производная вычисляется
следующим образом: y’ = (enlnx)’ =
enlnx(nlnx)’ =
enlnx =
xn =
nxn-1. Итак, при любом действительном
n и х>0 верна формула (xn)’ = nxn-1. Можно
показать, что эта формула справедлива и
при х<0, еслипри этом функция y
= xn определена. |
47. Производные высших порядков явно заданной функции
Производная у’=ƒ'(х) функции у=ƒ(х) есть также функция от х и называется производной первого порядка.
Если функция ƒ'(х) дифференцируема, то ее производная называется производной второго порядка и обозначается у»
Итак, у»=(у’)’.
Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается у'» (или ƒ'»(х)). Итак, у'»=(y»)’
Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:
y(n)=(y(n-1)) .
Производные порядка выше первого называются производными высших порядков.
Примеры:
y’ = (x4)’ = 4×3 y» = (y’)’ = (4×3)’ = 12×2
48 Понятие дифференциала функции
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную.
Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых ƒ'(х)•∆х и а•∆х, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
Поэтому первое слагаемое ƒ'(х) ∆х называют главной частью приращения функции ∆у.
Дифференциалом функции у=ƒ(х) в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается dу (или dƒ(х)):
dy=ƒ'(х)•∆х.
Дифференциал dу называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции у=х.
Так как у’=х’=1, то, согласно формуле (24.1), имеем dy=dx=∆x, т. е. дифференциал независимой переменной равен приращению этой переменной: dх=∆х.
Поэтому формулу (24.1) можно записать так:
dy=ƒ'(х)dх,
(24.
2)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (24.2) следует равенство dy/dx=ƒ'(х). Теперь обозначение
производной dy/dx можно рассматривать как отношение дифференциалов dy и dх.
Теорема существования и дифференцируемости функции, заданной неявно
Теорема 1. Пусть функция F(x,y) удовлетворяет условиям
F(x0,y0) = 0 ;
частные производные F’x и F’y непрерывны в некоторой окрестности точки (x0,y0) ;
F’y(x0,y0) ≠ 0 .
Тогда
уравнение F(x,y) = 0 определяет неявно в некоторой окрестности точки x0 единственную непрерывную функцию y(x) , удовлетворяющую условию y(x0) = y0 .
функция y(x) имеет производную, непрерывную в окрестности точки x0 .
Выясним смысл условий теоремы.
Существование непрерывной неявной функции y = f(x) в окрестности точки (x0, y0) следует из теоремы существования, так как:
условие 1 гарантирует существование точки, координаты которой удовлетворяют уравнению F(x,y) = 0 ;
из
условия 2 следует непрерывность
функции F(x,y) в окрестности точки
(x0,y0) , а из условия 3 — ее монотонность
по y при каждом фиксированном x из
этой окрестности.
Следовательно, условия 1–3 обеспечивают выполнение условий существования неявной функции y(x) , удовлетворяющей условию y(x0) = y0 и непрерывной в окрестности точки x0 .
Производная функции, заданной неявно
Функция y(x) в окрестности точки x0 обращает уравнение F(x,y) = 0 в тождество, т.е.
|
Дифференцируя это тождество, получaeм dF(x, y(x)) ≡ 0, а в силу инвариантности формы полного дифференциала имеем
|
Теорема
1 обобщается для неявных функций любого
числа переменных.
Например:
Теорема 2. Пусть функция F(x,y,z) = 0 удовлетворяет условиям
F(x0,y0,z0) = 0 ;
частные производные F’x , F’y и F’z непрерывны в некоторой окрестности точки (x0,y0,z0) ;
F’z(x0,y0,z0) ≠ 0 .
Тогда
уравнение F(x,y,z) = 0 определяет неявно в некоторой окрестности точки (x0,y0) единственную непрерывную функцию z(x,y) , удовлетворяющую условию z(x0,y0) = z0 ;
функция z(x,y) имеет непрерывные частные производные в окрестности точки (x0,y0)
{n}\dbinom{a}{k}\dbinom{b}{n-k}\qquad\text{для }a\in\mathbb{N}\text{ и }b\in\mathbb{N} \end{уравнение} (см. также «Разрубить узел» страница), то вы можете легко использовать его, чтобы получить доказательство теоремы 2, применяя стандартный трюк полиномиального тождества (если два одномерных многочлена совпадают $\mathbb{N}$, то они совпадают) дважды (поскольку есть две неопределенности).Следующая личность, которая мне нужна, простая (одна из форм идентичности поглощения):
Предложение 3.
Пусть $k$ — натуральное число. Тогда в кольце многочленов $\mathbb{Q}\left[ y\right] $ (в одном неопределенном $y$) имеем \begin{уравнение} \dbinom{y}{k}=\dfrac{y}{k}\dbinom{y-1}{k-1}. \end{уравнение}
Пусть $k$ — натуральное число. Тогда в кольце многочленов
$\mathbb{Q}\left[ y\right] $ (в одном неопределенном $y$) имеем
\begin{уравнение}
\dbinom{y}{k}=\dfrac{y}{k}\dbinom{y-1}{k-1}.
\end{уравнение} Доказательство предложения 3. Определение $\dbinom{y-1}{k-1}$ дает
\начать{выравнивать*}
\dbinom{y-1}{k-1} & =\dfrac{\left(y-1\right) \left(y-2\right)
\cdots\left( \left( y-1\right) -\left( k-1\right) +1\right) }{\left(
k-1\справа) !}\\
& =\dfrac{\left(y-1\right) \left(y-2\right) \cdots\left(yk+1\right)
}{\влево( k-1\вправо) !}.
\конец{выравнивание*}
Умножая это равенство на $\dfrac{y}{k}$, находим
\начать{выравнивать*}
\dfrac{y}{k}\dbinom{y-1}{k-1} & =\dfrac{y}{k}\cdot\dfrac{\left(y-1\right)
\влево(y-2\вправо) \cdots\влево(y-k+1\вправо) }{\влево(k-1\вправо)
!}=\dfrac{y\cdot\left( y-1\right) \left( y-2\right) \cdots\left(
y-k+1\вправо) }{k\cdot\влево( k-1\вправо) !}\\
& =\dfrac{y\left( y-1\right) \cdots\left( y-k+1\right) }{k!}
\конец{выравнивание*}
(поскольку $y\cdot\left( y-1\right) \left( y-2\right) \cdots\left(
y-k+1\right) =y\left( y-1\right) \cdots\left( y-k+1\right) $ и
$k\cdot\left( k-1\right) !=k!$).
(На всякий случай: предложение 4 есть следствие 3.17 в Дарий Гринберг, Заметки об комбинаторных основах алгебры , 10 января 2019 г.)
Теперь определим странную нотацию:
Определение. Пусть $R\in\mathbb{Q}\left[ x,y\right] $ — многочлен от два неопределенных $x$ и $y$. Пусть $a\in\mathbb{Q}$. Затем, $\operatorname*{ev}\limits_{y\to a}R$ обозначает результат заменив $a$ на $y$ в $R$. Это многочлен от $\mathbb{Q}\left[ х\справа] $. 9{2}$.
Для алгебраистов в зале: если мы зафиксируем $a\in\mathbb{Q}$, то карта $\operatorname*{ev}\limits_{y\to a}$ (отправляя каждый $R\in \mathbb{Q}\left[ x,y\right] $ to $\operatorname*{ev}\limits_{y\to a}R\in\mathbb{Q}\left[ x\right] $) является $\mathbb{Q}\left[ x\right] Гомоморфизм $-алгебры, называемый гомоморфизмом вычислений .
Наконец, нам понадобится следующая формула для производной многочлена: что является алгебраическим аналогом классического аналитического определения производная:
Теорема 5. Пусть $P\in\mathbb{Q}\left[ x\right] $ — многочлен. Рассмотрим многочлен $P\left( x+y\right) \in\mathbb{Q}\left[ x,y\right] $ в двух неопределенных $x$ и $y$. Тогда многочлен $P\left( x+y\right) -P\left( x\right) \in\mathbb{Q}\left[ x,y\right] $ есть делится на $y$, и мы имеем \begin{уравнение} \dfrac{d}{dx}P=\operatorname*{ev}\limits_{y\to 0}\dfrac{P\left( х+у\вправо) -P\влево( х\вправо) }{у}.
{2}+1+1=3,
\end{уравнение}
хотя вы не можете просто заменить $1$ на 9{3}-1}{г-1}$. Так,
когда $R$ — это дробь двух полиномов, которая сама по себе является
многочлен, то $\operatorname*{ev}\limits_{y\to a}R$ действительно
что-то вроде «предел $R$, когда $y$ приближается к $a$», потому что для того, чтобы
вычислить $\operatorname*{ev}\limits_{y\to a}R$, мы должны сначала переписать
дробь как действительный многочлен и только после этого подставьте $a$ вместо $y$.