Как найти производную от $\\ln (\\sqrt x )$ ?
Последняя обновленная дата: 19 февраля 2023 г.
•
Всего просмотров: 235,8K
•
Просмотры сегодня: 4.24K
Ответ
Проверено
235.8K+ виды
HINT: 202 , у нас есть уравнение $\ln (\sqrt x )$ , и мы должны найти его производную. Одним из методов нахождения производной является использование цепного правила, и, поскольку у нас задействован квадратный корень, мы будем использовать это цепное правило для производных.
Цепное правило для производных — это правило, которое мы используем для нахождения производной функций вида $f(g(x))$ .
Полное пошаговое решение:
Цепное правило для производных имеет формулу:
$h(x) = f(g(x))$
И,
$h'(x) = f’ (g(x)).g'(x)$
Теперь, чтобы использовать цепное правило для производных, нам нужно сначала убедиться, что наше уравнение удовлетворяет требованиям этого правила, поэтому, сравнивая уравнение, мы получаем,
$ f(x) = \ln (x)$
И,
$g(x) = \sqrt x $ 9{(\dfrac{{ — 1}}{2})}}$ или $\dfrac{1}{{2\sqrt x }}$
Поскольку у нас есть производная от $\ln (x)$ как $\ dfrac{1}{x}$ , мы имеем, что $f'(x) = \dfrac{1}{x}$ , поэтому $f'(g(x)) = \dfrac{1}{{\sqrt x }}$ .
Также мы знаем, что $g'(x) = \dfrac{1}{{2\sqrt x }}$ .
Подставляя все значения в цепное правило для производных,
$ \Rightarrow f(x) = \ln (x)$
$ \Rightarrow g(x) = \sqrt x $
И,
$ \Rightarrow h(x) ) = f(g(x)) = \ln (\sqrt x )$
Теперь мы знаем, что
$ \Rightarrow h'(x) = f'(g(x)).g'(x)$
Подставляя значения $f'(g(x)) = \dfrac{1}{{\sqrt x }}$ и $g'(x) = \dfrac{1}{{2\sqrt x}} $
Следовательно,
$ \Rightarrow h'(x) = \dfrac{1}{{\sqrt x }}.\dfrac{1}{{2\sqrt x }}$
Упрощая уравнение,
$ \Rightarrow h'(x) = \dfrac{1}{{2x}}$
Производная от $\ln (\sqrt x )$ равна $\dfrac{1}{{2x}}$ .
Примечание: Цепное правило для производных в основном используется для составных функций. Составная функция — это функция, которая может быть построена как $f(g(x))$ . Мы используем его, когда нам нужно дифференцировать функцию функции. Мы используем правило произведения при дифференцировании двух функций, умноженных вместе.
Недавно обновленные страницы
Рассчитать изменение энтропии, связанное с преобразованием 11 класса химии JEE_Main
Закон, сформулированный доктором Нернстом, является первым законом термодинамики класса 11 химии JEE_Main
Для реакции при rm0rm0rmC и нормальном давлении A класса 11 химия JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC класс 11 химия JEE_Main
Для реакции rm2Clg в rmCrmlrm2rmg признаки 11 класса химии JEE_Main
Изменение энтальпии перехода жидкой воды в химический класс 11 JEE_Main
Рассчитайте изменение энтропии при переходе в химический класс 11 JEE_Main
Закон, сформулированный доктором Нернстом, представляет собой Первый закон термодинамики 11-го класса химии JEE_Main
Для реакция при rm0rm0rmC и нормальном давлении А химический класс 11 JEE_Main
Двигатель, работающий между rm15rm0rm0rmC и rm2rm5rm0rmC химический класс 11 JEE_Main
0003
Изменение энтальпии перехода жидкой воды класса 11 химии JEE_Main
Тенденции сомнения
`y = sqrt(x + sqrt(x + sqrt(x)))` Найдите производную функции.
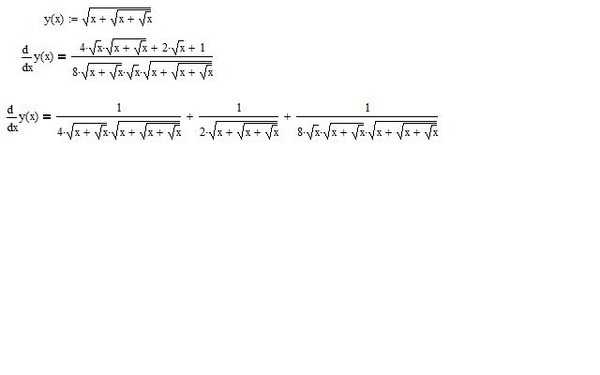 Цитата страницы
Начать эссе
значок-вопрос
Спросите репетитора
Цитата страницы
Начать эссе
значок-вопрос
Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяУкажите эту страницу следующим образом:
«`y = sqrt(x + sqrt(x + sqrt(x)))` Найдите производную функции». eNotes Editorial , 5 сентября 2015 г., https://www.enotes.com/homework-help/y-sqrt-x-sqrt-x-sqrt-x-find-derivative-function-497414. По состоянию на 19 февраля 2023 г.
`y=sqrt(x+sqrt(x+sqrt(x)))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x)))))) *d/dx ( x+sqrt(x+sqrt(x)))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x)))))) *(1+d/dxsqrt(x+sqrt (x)))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x)))) *(1+(1/(2sqrt(x+sqrt(x))) *d/dx (x+sqrt(x))))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x))))) *(1+(1/(2sqrt(x+sqrt(x)))))*(1+d /dxsqrt(x)))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x)))))) *(1+(1/(2sqrt(x+sqrt(x)) ))) *(1+1/(2sqrt(x))))`
`y’=(1/(2sqrt(x+sqrt(x+sqrt(x)))))) *(1+(1 /(2sqrt(x+sqrt(x)))) *((2sqrt(x)+1)/(2sqrt(x))))`
`y’=(1/(2sqrt(x+sqrt(x) +sqrt(x))))) *(1+(2sqrt(x)+1)/(4sqrt(x)sqrt(x+sqrt(x))))`
`y’=(1/(2sqrt (x+sqrt(x+sqrt(x))))) *((4sqrt(x)sqrt(x+sqrt(x))+2sqrt(x)+1)/(4sqrt(x)sqrt(x+sqrt (х))))`
`y’=(4sqrt(x)sqrt(x+sqrt(x))+2sqrt(x)+1)/(8sqrt(x)sqrt(x+sqrt(x))sqrt(x+sqrt(x) +квт(х))))`
Утверждено редакцией eNotes
Примечание:- 1) Если y = sqrt(x) ; тогда dy/dx = 1/2sqrt(x)
Теперь
y = sqrt[x + sqrt{(x) + sqrt(x)}]
Применим цепное правило, т.
, если y = u *в ; где u & v botyh — функции от ‘x’; затем
dy/dx = u*(dv/dx) + v*(du/dx)
Кроме того, применяйте правило внешнего к внутреннему, когда внутри функции есть подфункции.
Решение в прикрепленном файле.
Изображения:
Это изображение было помечено как неприемлемое Нажмите, чтобы снять отметку
Изображение (1 из 1)
Опубликовано
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов воспитателя
математика
Последний ответ опубликован 07 октября 2013 г. в 20:13:27.
Как определить, является ли это уравнение линейной или нелинейной функцией?
84 Ответы воспитателя
Математика
Последний ответ опубликован 09 октября 2017 г.
