Основные формулы с арксинусом, арккосинусом, арктангенсом и арккотангенсом, сумма арксинуса и арккосинуса числа, арктангенс от тангенса
Формулы с обратными тригонометрическими функциями: arcsin, arccos, arctg и arcctg
Ранее мы рассматривали обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс. Как и в случае с другими функциями, между ними существуют связи и зависимости, реализуемые в виде формул, которые можно использовать для решения задач.
Сейчас мы будем рассматривать основные формулы с использованием этих функций: какие они бывают, на какие группы их можно разделить, как их доказать и как решать задачи с их помощью.
Формулы котангенса арккотангенса, тангенса арктангенса, синуса арксинуса и косинуса арккосинуса
Для начала сгруппируем формулы, в которых содержатся основные свойства обратных тригонометрических функций. Мы уже обсуждали и доказывали их ранее, а здесь приведем, чтобы логика объяснения была более понятной и все формулы были в одной статье.
для α∈-1, 1 sin(arccis α)=α, cos(arccos α)=α,для α∈(-∞, ∞) tg(arctg α)=α, ctg(arcctg α)=α
Указанное в них легко сформулировать из самих определений обратных тригонометрических функций числа. Если вы забыли, как найти, например, тангенс арктангенса, все можно посмотреть в этой формуле.
Формулы арккотангенса котангенса, арктангенса тангенса и арксинуса синуса и арккосинуса косинуса
для -π2≤α≤π2 arcsin (sin α)=α,для 0≤α≤π arccos(cos α)=α,для -π2<α<π2 arctg (tg α)=α,для 0<α<π arcctg (ctg α)=α
Здесь все также более-менее очевидно, как и в предыдущем пункте: эти формулы можно вывести из определений арксинуса, арккосинуса и др. Единственное, на что нужно обратить пристальное внимание: они будут верны только в том случае, если a (число или угол) будут входить в указанный предел. В противном случае расчет по формуле будет ошибочен, и применять ее нельзя.
Как соотносятся между собой арксинусы, арккосинусы, арктангенсы и арккотангенсы противоположных чисел
В этом блоке мы сформулируем важное утверждение:
Определение 1Обратные тригонометрические функции отрицательного числа можно выразить через арксинус, арккосинус, арктангенс и арккотангенс противоположного ему положительного числа.
для α∈-1, 1 arccis (-α)=-arcsin α, arccos (-α)=π-arccos α,для α∈(-∞, ∞) arctg (-α)=-arctg α, arcctg (-α)=π-arcctg α
Таким образом, если в расчетах нам встречаются эти функции для отрицательных чисел, мы можем от них избавиться, преобразовав их в аркфункции положительных чисел, с которыми иметь дело проще.
Формулы суммы: арксинус + арккосинус, арктангенс + арккотангенс
Они выглядят следующим образом:
для α∈-1, 1 arccis α+arccos α=π2,для α∈(-∞, ∞) arctg α+arcctg α=π2
Из написанного видно, что арксинус некоторого числа можно вывести с помощью его арккосинуса, и наоборот. С арктангенсом и арккотангенсом аналогично – они соотносятся между собой аналогичным образом.
Формулы связи между прямыми и обратными тригонометрическими функциями
Знать связи между прямыми функциями и их аркфункциями очень важно для решения многих практических задач. Как же быть, если у нас есть необходимость вычислить, к примеру, тангенс арксинуса? Ниже приведен список основных формул для этого, которые полезно выписать себе.
| -1≤α≤1,sin (arcsin α)=α | -1≤α≤1,sin (arccos α)=1-α2 | -∞≤α≤+∞,sin (arctg α)=α1+α2 | -∞≤α≤+∞, sin (arcctg α)=11+α2 |
| -1≤α≤1,cos (arcsin α)=1-α2 | -1≤α≤1,cos (arccos α)=α | -∞≤α≤+∞,cos (arctg α)=11+α2 | -∞≤α≤+∞, cos (arcctg α)=11+α2 |
| -1<α<1,tg (arcsin α) =α1-α2 | α∈(-1, 0)∪(0, 1),tg (arccos α) =1-α2α | -∞≤α≤+∞,tg (arctg α)=α | α≠0 ,tg (arcctg α)=1α |
| α∈(-1, 0)∪(0, 1),ctg (arcsin α)=1-α2α | -1<α<1,ctg (arccos α)=α1-α2 | α≠0,ctg (arctg α)=1α | -∞≤α≤+∞, ctg (arcctg α)=α |
Теперь разберем примеры, как они применяются в задачах.
Пример 1Вычислите косинус арктангенса из 5.
Решение
У нас для этого есть подходящая формула следующего вида: cos(arctg α)=11+α2
Подставляем нужное значение: cos(arctg5)=11+(5)2=26
Пример 2Вычислить синус арккосинуса 12.
Решение
Для этого нам понадобится формула: sin (arccos α)=1-a2
Подставляем в нее значения и получаем: sin (arccos 12)=1-(12)2=32
Обратите внимание, что непосредственные вычисления приводят к аналогичному ответу: sin(arccos 12)=sin π3=32
Если вы забыли, как правильно вычислять значения прямых и обратных функций, вы всегда можете вернуться к нашим предыдущим материалам, где мы разбирали это.
Доказательства формул синусов арккосинуса, арккотангенса и арктангенса
Для того, чтобы наглядно вывести полученные формулы, нам понадобятся основные тригонометрические тождества и собственно формулы основных обратных функций — косинуса арккосинуса и др. Мы их уже выводили ранее, поэтому тратить время на их доказательства не будем. Начнем сразу с формул синусов арккосинуса, арккотангенса и арктангенса. Используя тождество, получим:
sin2α+cos2α=11+ctg2α=1sin2α
Вспомним, что tgα·ctgα=1. Из этого можно получить:
sinα=1-cos2α, 0≤α≤π sinα=tgα1+tg2α, -π2<α<π2sinα=11+ctg2α, 0<α<π
У нас получилось, что мы выразили синус через необходимые аркфункции при заданном условии.
Теперь в первой формуле вместо a мы добавим arccos a. Итог — формула синуса арккосинуса.
Далее во вторую вместо a ставим arctg a. Это формула синуса арктангенса.
Аналогично с третьей – если мы добавим в нее arcctg a, будет формула синуса арктангенса.
Все наши расчеты можно сформулировать более емко:
- sinα=1-cos2α, 0≤α≤π
Следовательно, sin(arccosα)=1-cos2(arccosα)=1-a2
- sinα=tgα1+tgα, -π2<α<π2,
Следовательно, sin(arctgα)=tg(arctgα)1+tg2(arctgα)=α1+α2
- sinα=11+ctg2α, 0<α<π
Следовательно, sin(arctgα)=11+tg2(arctgα)=11+α2
Выводим формулы косинуса арксинуса, косинуса арктангенса и косинуса арккотангенса.
Их мы выведем по имеющемуся шаблону:
- Из cosα=1-sin2α, -π2≤α≤π2 следует, что
cos(arcsin α)=1-sin2(arcsin α)=1-a2
- Из cosα=11+tg2α, -π2<α<π2 следует, что
- Из cosα=ctgα1+ctg2α, 0<α<πcos(arctgα)=11+tg2(arctgα)=11+α2
следует, что cos(arctgα)=ctg(arcctgα)1+ctg2(arcctgα)=α1+α2
Доказательства формул тангенсов арксинуса, арккосинуса и арккотангенса
- Исходим из tgα=sin α1-sin2α, -π2<α<π2.
Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1. - Исходим из tgα=1-cos2αcosα, α∈[0, π2)∪(π2, π], получаем
Получаем tg(arcsin α)=sin(arcsinα)1-sin2(arcsinα)=α1-α2 при условии, что -1<α<1.tg(arccosα)=1-cos2(arccosα)cos(arccosα)=1-α2α при условии α∈(-1, 0)∪(0, 1).
- Исходим из tgα=1ctgα, α∈(0, π2)∪(π2, π), получаем tg(arcctgα)=1ctg(arcctgα)=1α при условии, что α≠0.
Теперь нам нужны формулы котангенсов арксинуса, арккосинуса и арктангенса. Вспомним одно из тригонометрических равенств:
ctgα=1tgα
Используя его, мы можем сами вывести необходимые формулы, используя формулы тангенса арксинуса, тангенса арккосинуса и тангенса арктангенса. Для этого понадобится поменять в них местами числитель и знаменатель.
Как выразить арксинус через арккосинус, арктангенс и арккотангенс и так далее
Мы связали между собой прямые и обратные тригонометрические функции. Полученные формулы дадут нам возможность связать и одни обратные функции с другими, то есть выразить одни аркфункции через другие аркфункции.
Разберем примеры.
Здесь мы можем заменить арксинус на арккосинус, арктангенс и арккотангенс соответственно, и получить искомую формулу:
arcsinα=arccos1-α2, 0≤α≤1-arccos1-a2, -1≤α<0arcsinα=arctgα1-α2, -1<α<1arcsinα=arcctg1-α2α, 0<α≤1arcctg1-α2α-π, -1≤α≤0
А так мы выразим арккосинус через остальные обратные функции:
arccosα=arcsin1-α2, 0≤α≤1π-arcsin1-α2, -1≤α<0arccosα=arctg1-α2α, 0<α≤1π+arctg1-α2α, -1<α<0arccosα=arcctgα1-α2, -1<α<1
Формула выражения арктангенса:
arctgα=arcsinα1+α2, -∞<α<+∞arctgα=arccos11+α2, α≥0-arccos11+α2, α<0arctgα=arcctg1α, α≠0
Последняя часть – выражение арккотангенса через другие обратные функции:
arcctgα=arcsin11+α2, α≥0π-arcsin11+α2, α<0arcctgα=arccosα1+α2, -∞<α<+∞arcctgα=arctg1α, α≠0
Теперь попробуем доказать их, опираясь на основные определения обратных функций и ранее выведенных формул.
Возьмём arcsinα=arctgα1-α2, -1<α<1 и постараемся вывести доказательство.
Мы знаем, что arctgα1-α2 — это число, величина которого составляет от минус половины пи до плюс половины пи. Из формулы синуса арктангенса получим:
sin(arctgα1-α2)=α1-α21+(α1-α2)2=α1-α21+α21-α2=α1-α21+α21-α2=α1-α211-α2=α
Получается, что arctgα1-α2 при условии 1<a<1 – это и есть арксинус числа a.
Вывод: arcsina=arctga1-a2, -1<a<1
Прочие формулы доказываются по аналогии.
В завершение разберем один пример применения формул на практике.
Пример 3Условие Вычислить синус арккотангенса минус корня из 3.
Решение
Нам понадобится формула выражения арккотангенса через арксинус: arcctgα=arcsin11+a2, α≥0π-arcsin 11+a2, α<0
Подставим в нее α=-3 и получим ответ – 12. Непосредственное вычисление дало бы нам те же результаты: sin(arcctg(-3))=sin5π6=12 Для решения задачи можно взять и другую формулу, выражающую синус через котангенс: sinα=11+ctg2α, 0<α<π
В итоге у нас бы вышло: sin(arcctg(-3))=11+ctg2(arcctg(-3))=11+(-3)2=12
Или возьмем формулу синуса арккотангенса и получим тот же ответ: sin(arcctgα)=11+α2 sin(arcctg(-3))=11+(-3)2=12
Прочие формулы с обратными функциями
Мы рассмотрели самые основные формулы, которые понадобятся вам при решении задач.
Однако это не все формулы с аркфункциями: есть и ряд других, специфичных, которые употребляются нечасто, но все же их знание может быть полезно. Запоминать их особого смысла нет: проще вывести их тогда, когда они нужны.
Разберем одну из них, называемую формулой половинного угла. Она выглядит следующим образом:
sin2α2=1-cosα2
Если угол альфа при этом больше нуля, но меньше числа пи, то у нас выходит:
sinα2=1-cosα2
Учитывая данное условие, заменяем упомянутый угол на arccos. В итоге наша предварительная формула выглядит так:
sinarccosα2=1-cos(arccosα)2⇔sinarccosα2=1-α2
Отсюда мы выводим итоговую формулу, в которой арксинус выведен через арккосинус:
arccosα2=arcsin1-α2
Мы перечислили не все связи, которые имеются между обратными тригонометрическими функциями, а лишь наиболее употребляемые из них. Важно подчеркнуть, что ценность имеют не столько сами сложные формулы, что мы привели в статье: заучивать их наизусть не нужно. Гораздо важнее уметь самому делать нужные преобразования, и тогда сложные вычисления не потребуется хранить в голове.
В продолжение темы в следующей статье мы рассмотрим преобразование выражений с арксинусом, арккосинусом, арктангенсом и арккотангенсом.
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Обратная тригонометрическая функция: арктангенс
Перед изучением этого раздела рекомендуется прочитать Попытка «отменить» тригонометрические функции.
Этот раздел является копией книги «Обратная тригонометрическая функция: арксинус» с соответствующими изменениями.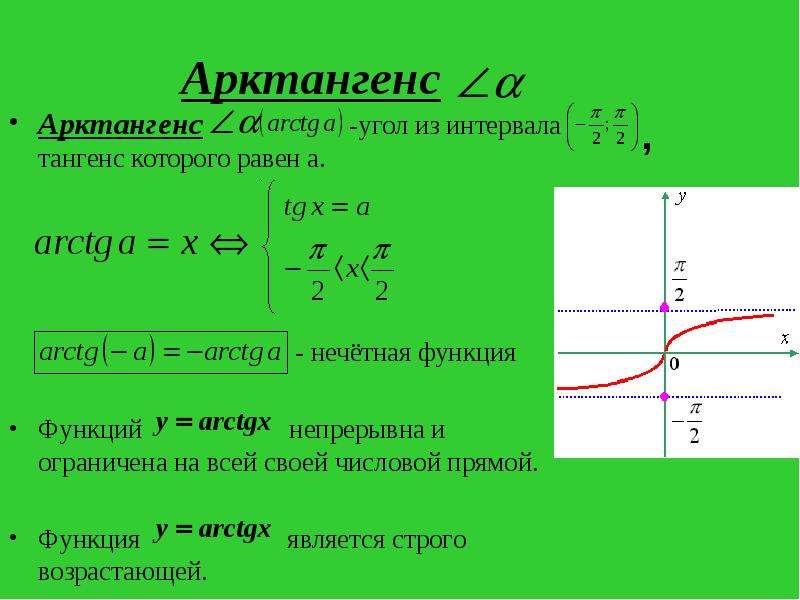
Если вы освоили секцию арксинуса, то это должно быть быстро и легко!
Функция арктангенса (точное определение ниже) — это лучшее, что мы можем сделать , пытаясь получить обратную величину
касательная функция.
Функция арктангенса на самом деле обратная зеленой фигуре, показанной выше!
Вот функциональная панель того, что происходит:
| Функция тангенса принимает действительное число
(исключая $\,\frac{\pi}{2} + k\pi\,$ для целых чисел $\,k\,$)
в качестве входа. Выводит вещественное число. Например (как показано ниже), | Когда мы пытаемся использовать поле касательной функции «назад»,
мы попадаем в беду. Результат $\,0.5\,$ мог быть | Однако,
когда мы используем зеленый кусок касательная кривая, проблема решена! Теперь есть только один вход , который работает. Обратите внимание, что $\,\color{green}{x}\,$ находится в интервале $\,( -\frac{\pi}2,\frac{\pi}2)\,.$ |
Это немного неправильное название, но функция арктангенса (точное определение ниже) часто упоминается как
как «функция арктангенса».
Лучшее название было бы что-то вроде «обратная функция тангенса с соответствующими ограничениями».
(Неудивительно, однако, что люди не говорят что-то такое длинное и громоздкое.)
Итак, что же такое $\,\arctan 0.5\,$?
$\,\arctan 0,5\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\ ,0.5\,$
Что такое $\,\arctan x\,$?
В более общем случае пусть $\,x\,$ будет любым действительным числом.
Затем:
$\,\arctan x\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\ ,х\,$
В моем собственном уме (здесь говорит автор доктор Кэрол Бернс) я произношу следующие слова:
$\,\arctan x\,$ — число между $\,-\frac{\pi}{2}\,$ и $\,\frac{\pi}{2}\,$, тангенс которого $\,х\,$
Я лично знаю конечные точки не включены , так что это меня не смущает.
{-1}\,$
Пусть $\,x\,$ — действительное число.
Используя обозначение ‘$\,\arctan\,$’ для функции арктангенса: $$ \cssId{s63}{y = \arctan x}\ \ \ \ \ \cssId{s64}{\text{если и только если}}\ \ \ \ \bigl(\ \cssId{s65}{\тангенс у = х}\ \ \cssId{s66}{\text{И}}\ \ \cssId{s67}{-\frac{\pi}{2} \lt y\lt \frac{\pi}{2}}\ \bigr) $$ 9{-1} х}\ \ \ \ \ \cssId{s70}{\text{если и только если}}\ \ \ \ \bigl(\ \cssId{s71}{\тангенс у = х}\ \ \cssId{s72}{\text{И}}\ \ \cssId{s73}{-\frac{\pi}{2} \lt y\lt \frac{\pi}{2}}\ \bigr) $$
Примечания к определению функции арктангенса:
- ПОНИМАНИЕ ОПРЕДЕЛЕНИЯ:
Определение точно отвечает на вопрос: «Каково число $\,\arctan x\,$?»
Вот как:- Напомним, что «если и только если» означает то же самое, что и эквивалентно.
Эквивалентные предложения имеют одинаковые значения истинности:
если одно истинно, то верно и другое; если одно ложно, то и другое. - Таким образом, если предложение ‘$\,y = \arctan x\,$’ истинно,
, то сложное предложение ‘$\,\tan y = x\ \ \text{AND}\ \ -\frac{\pi}{2} \lt y\lt \frac{\pi}{2}\,$’ тоже должно быть правдой. - Если ‘$\,y = \arctan x\,$’ истинно, затем ‘$\,y\,$’ — это просто другое название для ‘$\,\arctan x\,$’.
- Если ‘$\,y = \arctan x\,$’ истинно,
тогда две вещи должны быть верны относительно $\,\arctan x\,$ (т. е. $\,y\,$):
9{\ text {находясь в интервале $ \ strut \, (- \ frac {\ pi} {2}, \ frac {\ pi} {2}) \, $}}} \ \ bigr)
$$
- То есть:
$\,\arctan x\,$ — число в интервале $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$, тангенс которого равен $\, х\,$
- Напомним, что «если и только если» означает то же самое, что и эквивалентно.
е. $\,y\,$):
9{\ text {находясь в интервале $ \ strut \, (- \ frac {\ pi} {2}, \ frac {\ pi} {2}) \, $}}} \ \ bigr)
$$ Ваш браузер не поддерживает аудио элементы.
ПРОЧТЕНИЕ, ЧАСТЬ 2
- ФОРМАЛЬНОЕ НАЗВАНИЕ В ОТНОШЕНИИ ОБОЗНАЧЕНИЙ ФУНКЦИИ СОКРАЩЕНИЯ:
Формальное имя функции, обсуждаемой в этом разделе, — «арктангенс».
Произносится как ARC-tangent.При использовании обозначения функции «арктангенс» сокращается как «$\,\arctan\,$».
Произносится так же, как «арктангенс».
Таким образом, ‘$\,\arctan x\,$’ читается вслух как ‘арктангенс $\,x\,$’. {-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$
Ниже этот метод используется для построения графика функции арктангенса:Вот часть касательной кривой
, которая используется для определения функции арктангенса:
домен: $\,(-\frac{\pi}{2},\frac{\pi}{2})\,$диапазон: $\,(-\infty,\infty)\,$
Вот та же кривая,
вместе с его отражением относительно линии $\,\color{red}{y = x}\,$График функции арктангенса
домен: $\,(-\infty,\infty)\,$диапазон: $\,(-\frac{\pi}{2},\frac{\pi}{ 2})\,$
Обратите внимание, что домен и область значений функции и ее обратной функции меняются местами! 9{-1}\,$ что-то делает, а $\,f\,$ отменяет действие Поскольку функции тангенса и арктангенса являются , а не истинными инверсиями друг друга,
отношения между ними немного сложнее.
9\circ\,$, тангенс которого равен $\,-\frac{1}{\sqrt 3}\,.Вот направление, в котором они делают красиво «отменяют» друг друга: начните с числа, сначала примените функцию арктангенса, затем примените функцию тангенса, и в конечном итоге там, где вы начали. Подробности:
Для всех $\,x\in \Bbb R\,$ $$ \cssId{sb65}{\tan(\arctan x) = x} $$
- начните с $\,\color{red}{x}\in \Bbb R\,$
- функция арктангенса переводит $\,\color{red}{x}\,$ в $\,\color{green}{\arctan x}\,$ в интервале $\,(-\frac{\pi} 2,\frac{\pi}2)\,$
- функция касательной переводит
$\,\color{green}{\arctan x}\,$ обратно в $\,\color{red}{x}\,$
Вот направление, в котором они не обязательно хорошо «отменяют» друг друга: начните с числа, сначала примените функцию тангенса, затем примените функцию арктангенса. Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$
тогда вы не окажетесь там, где начали!Подробности:
Для всех $\,x\in (-\frac{\pi}2,\frac{\pi}2)\,$ $$ \cssId{sb75}{\arctan(\tan x) = x} $$
(См. верхний график справа.) Для всех $\,x\,$ в области определения функции тангенса, но не в $\,(-\frac{\pi}2,\frac{\pi}2)\,$ $$ \cssId{sb78}{\arctan(\tan x) \ne x} $$
(См. нижний график справа.) $- По мере необходимости, просмотреть информацию о размере и знаке касательная функция.
- Нарисуйте единичный круг. 9\circ\,$, тангенс которого равен минус , угол находится в квадранте IV.
Поскольку нам нужен угол, тангенс которого имеет размер $\,\frac{1}{\sqrt 3} \приблизительно 0,58\,$, делаем красный сегмент имеет эту длину.
Таким образом, показанный (отрицательный) угол равен $\,\arctan(-1/\sqrt 3)\,.$- Сообщает ли нам какой-нибудь особый треугольник острый угол, тангенс которого равен $\,\frac{1}{\sqrt 3}\,$? 9\циркуляр\,.
$- Используя радианную меру, $\,\arctan(-1/\sqrt{3}) = -\frac{\pi}6\,.$
Формула, график, идентификаторы, домен, диапазон и часто задаваемые вопросы
Arctan определяется как функция, обратная тангенсу. Arctan(x) обозначается как tan -1 (x). Имеется шесть тригонометрических функций, и обратные ко всем шести функциям записываются как sin -1 x, cos -1 x, tan -1 x, cosec -1 x, sec -1 x. , и кроватка -1 х.
Arctan (tan -1 x) не похож на 1/tan x. tan -1 x обратное значение tan x, тогда как 1/ tan x обратное значение tan x.
загар -1 x используется для решения различных тригонометрических уравнений. В этой статье мы подробно изучим формулу, график, свойства и другие функции функции арктангенса.Что такое формула Арктана?
Тангенс — это тригонометрическая функция, и в прямоугольном треугольнике тангенс равен отношению перпендикуляра к основанию (перпендикуляр/основание).
Arctan — это ссылка на обратную функцию тангенса. Символически арктан представлен загаром -1 .x в тригонометрических уравнениях.
Формула арктангенса
Как обсуждалось выше, основная формула для арктангенса задается следующим образом: арктангенс (перпендикуляр/основание) = θ, где θ — угол между гипотенузой и основанием прямоугольного треугольника. Мы используем эту формулу для арктангенса, чтобы найти значение угла θ в градусах или радианах.
Предположим, тангенс угла θ равен x.
Тогда x = tan θ
θ = tan -1 x
Возьмем прямоугольный треугольник ABC с углом BCA в качестве θ.
Сторона AB перпендикулярна (p), а сторона BC является основанием (b). Теперь, когда мы изучили, что касательная равна перпендикуляру к основанию.т. е. тангенс θ = перпендикуляр/основание = p/b
И, используя приведенное выше выражение,
Арктан Идентификационные данныеθ = тангенс -1 ( р/б)
Существуют различные тождества Арктана, которые используются для решения различных тригонометрических уравнений. Некоторые важные тождества арктангенса приведены ниже:
- арктанген(-х) = -арктан(х)
- тангенс(арктан х) = х
- арктангенс(1/х) = π/2 – арктан(х)
- arctan(1/x) = -π/2 – arctan(x)
- sin(arctan x) = x/ √(1+x 2 )
- cos(arctan x) = 1/ √(1 +x 2 )
Существует также некоторая стандартная формула арктангенса для π. Эти формулы перечислены ниже.
- π/4 = 4 арктан(1/5) – арктан(1/239)
- π/4 = арктан(1/2) + арктан(1/3)
- π/4 = 2 арктан(1) /2) – арктан(1/7)
- π/4 = 2 арктан(1/3) + арктан(1/7)
- π/4 = 8 арктан(1/10) – 4 арктан(1/515 ) – арктан(1/239)
- π/4 = 3 арктан(1/4) + арктан(1/20) + арктан(1/1985)
Как применять формулу арктангенса?
Чтобы найти арктангенс заданного значения, изучите приведенный пример,
Пример: В прямоугольном треугольнике PQR, если высота треугольника составляет √3 единиц, а основание треугольника равно 1 единице.
Найдите угол. Решение:
Чтобы найти угол,
Используя формулу арктангенса,
θ = арктангенс (перпендикуляр/высота)
= arctan (√3/1)
= 60°Домен и диапазон арктангенса
Все тригонометрические функции, включая tan (x), имеют отношение «многие к одному». Однако обратная функция может существовать только в том случае, если она имеет взаимно-однозначное отношение и отношение. По этой причине домен tan x должен быть ограничен, иначе не может существовать обратное. Другими словами, тригонометрическая функция должна быть ограничена своей основной ветвью, поскольку нам нужно только одно значение.
- Домен загара x равен (-π/2, π/2)
- Диапазон tan (x) равен все действительные числа
Мы знаем, что область определения и область значений тригонометрической функции преобразуются в область значений и область значений обратной тригонометрическая функция соответственно.
Таким образом, мы можем сказать, что доменом tan-1x являются все действительные числа, а диапазон равен (-π/2, π/2). Интересно отметить, что мы можем распространить функцию арктангенса на комплексные числа. В таком случае доменом arctan будут все комплексные числа.Таблица Arctan
Любой угол, выраженный в градусах, также может быть преобразован в радианы. Для этого мы умножаем значение градуса на коэффициент π/180°. Кроме того, функция арктангенса принимает действительное число в качестве входных данных и выводит соответствующее уникальное значение угла. В приведенной ниже таблице указаны значения арктангенса для некоторых действительных чисел. Их также можно использовать при построении графика арктангенса.
Как мы выяснили выше, значение arctan может быть получено в градусах или радианах. Итак, приведенная ниже таблица иллюстрирует оценочные значения арктангенса.
x arctan(x)
(в градусах)
Arctan(x)
(в радианах) 900 03
-∞ -90° — π/2 -√3 -60° -π/3 -1 -45° -π/ 4 -1/√3 — 30° -π/6 0 0° 0 1/√3 30° π/6 1 45° π/4 9 0028 √3 60° π/3 ∞ 90° π/2 Свойства арктангенса (x)
Свойства арктангенса x используются для решения различных тригонометрических уравнений.
Существуют различные тригонометрические свойства, которые необходимо изучить для изучения тригонометрии. Некоторые важные свойства функции arctan приведены ниже в этой статье:- tan (tan -1 x) = x
- tan -1 (-x) = -tan -1 x
- tan -1 (1/x) = детская кроватка -1 x, когда x > 0
- тангенс -1 x + тангенс -1 y = тангенс -1 [(x + y)/(1 – xy)], когда xy < 1
- тангенс -1 x – tan -1 y = tan -1 [(x – y)/(1 + xy)], когда xy > -1
- tan -1 x + cot -1 х = π/2
- тангенс -1 (tan x) = x [когда x ∈ R – {x : x = (2n + 1) (π/2), где n ∈ Z}]
- tan -1 (tan x) = x [когда x НЕ является нечетным кратным π/2. иначе tan -1 (tan x) не определен.]
- 2 tan -1 x = sin -1 (2x / (1+x 2 )), когда |x| ≤ 1
- 2 тангенс -1 x = cos -1 ((1-x 2 ) / (1+x 2 )), когда x ≥ 0
- 2 тангенс 90 348 -1 х = tan-1(2x / (1-x 2 )), когда -1 < x < 1
График Arctan
График функции Arctan является бесконечным графиком.
Домен arctan равен R (действительные числа), а диапазон функции Arctan равен (-π/2, π/2). График функции Arctan обсуждается ниже на изображении ниже:График построен с использованием значения известных точек, для функции y = tan -1 (x)
- x = ∞ = > y = π/2
- x = √3 => y = π/3
- x = 1/√3 => y = π/6
- x = 0 => y = 0
- x = -1/√3 => y = -π/6
- x = -√3 => y = -π/3
- x = -∞ => y = -π/2
Производная арктангенса
Производная арктангенса очень важна для изучения математики. Производная функции арктангенса вычисляется с использованием следующей концепции:
y = арктангенс x (пусть)…(1)
Взяв тангенс обеих сторон ) = х]
тангенс у = х
Дифференцирование обеих сторон (с помощью цепного правила)
с 2 y × dy/dx = 1
dy/dx = 1 / с 2 y
dy/dx = 1 / (1 + желтовато-коричневый 2 y) {using, sec 2 y = 1 + tan 2 y}
d / dx (arctan x) = 1 / (1 + x 2 ) 9 0003
Интеграл арктангенса х
Интеграл арктангенса определяется как первообразная функции арктангенса.
Интеграция Arctan x производится с использованием концепции, приведенной ниже,Возьмем f(x) = tan -1 x и g(x) = 1
Мы знаем, что ∫f(x)g(x)dx = f(x) ∫g(x)dx – ∫[d(f(x))/dx × ∫g(x) dx] dx
подставляя значения f(x) и g(x) в приведенное выше уравнение, мы получаем,
∫tan — 1 x dx = x tan -1 x – ½ ln |1+x 2 | + C
где,
C — постоянная интегрированияТакже проверьте
- Тригонометрическая таблица
- Тригонометрические отношения
- Тригонометрические тождества
Решенные примеры на Arctan
Пример 1: вычислить тангенс -1 (1). Задано (45°)
Сейчас,
желтовато-коричневый — 1 (1) = тангенс -1 (тангенс 45°)
= 45°Пример 2: вычислить тангенс -1 (1,732).
Решение:
Учитывая
тангенс -1 (1,732)
Значение 1,732 также можно записать как
900 02 1,732 = тангенс (60°)Сейчас,
тангенс — 1 (1,732) = tan -1 ( tan 60°)
= 60°-1 1/x
Решение:
мы знаем, что tan -1 x + tan -1 y = tan -1 [(x + y)/(1 – xy)]
tan -1 x + tan -1 1/x = tan -1 [(x + 1/x)/(1 – x × 1/x)]
– x × 1/x)]
= тангенс -1 [(х + 1/х)/(0 )]
= tan -1 [∞]
= π/2
7
Решение:
мы знаем, что производное от tan — 1 x = 1 / (1 + x 2 )
d/dx (tan -1 √x) = 1 / (1 + [√x] 2 )
= 1 / (1+ x)
Таким образом, производная от d/dx (tan -1 √x) равна 1 / (1+x)
Часто задаваемые вопросы по Arctan
Вопрос 1: Что такое Arctan?Ответ:
Функция, обратная тангенсу, называется арктангенсом.
{-1}\,$
находится путем отражения графика $\,f\,$
о прямой $\,y = x\,.$ 
Если число, с которого вы начали, находится вне интервала $\,(-\frac{\pi}2,\frac{\pi}2)\,$
тогда вы не окажетесь там, где начали!
$
$
загар -1 x используется для решения различных тригонометрических уравнений. В этой статье мы подробно изучим формулу, график, свойства и другие функции функции арктангенса.
Сторона AB перпендикулярна (p), а сторона BC является основанием (b). Теперь, когда мы изучили, что касательная равна перпендикуляру к основанию.
Найдите угол. 
Таким образом, мы можем сказать, что доменом tan-1x являются все действительные числа, а диапазон равен (-π/2, π/2). Интересно отметить, что мы можем распространить функцию арктангенса на комплексные числа. В таком случае доменом arctan будут все комплексные числа.
Существуют различные тригонометрические свойства, которые необходимо изучить для изучения тригонометрии. Некоторые важные свойства функции arctan приведены ниже в этой статье:
Домен arctan равен R (действительные числа), а диапазон функции Arctan равен (-π/2, π/2). График функции Arctan обсуждается ниже на изображении ниже:
Интеграция Arctan x производится с использованием концепции, приведенной ниже,
