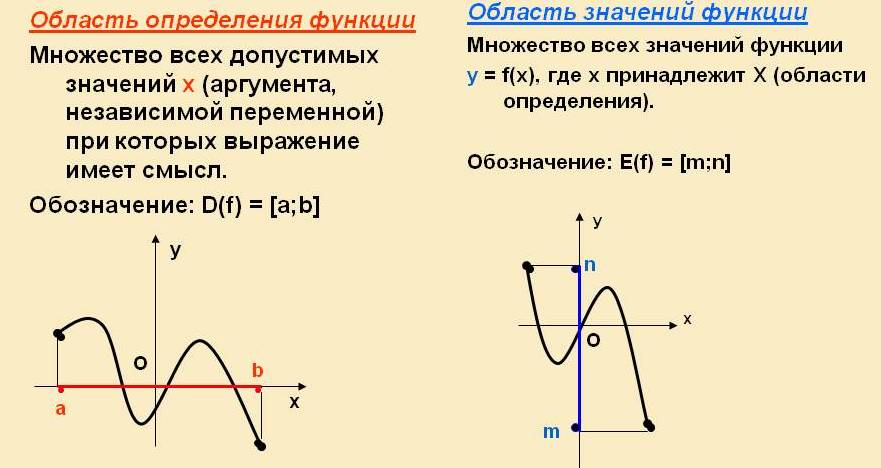
Область определения функции y(x)
Областью определения называют множество значений аргумента при котором существует значение функции и обозначают или . Областью значений называют множество чисел, которые принимает функция при прохождении аргументом всех значений из области определения.
Ее обозначают или . Графически обе области хорошо иллюстрирует следующий рисунок
Для схематической функции рассматриваемые области принимают значения
Методика нахождения области определения для всех функций одна и та же: нужно выявить точки при которых функция не существует, а затем исключить из множества действительных чисел . В результаты получим набор промежутков или интервалов, точки, которые образуют область определения.
Особенности элементарных функций
1) Если функция имеет вид полинома то ее областью определения будет вся действительная ось или . Такая функция определена повсюду.
2) Дробно рациональная функция , где – полиномы, областью определения имеет значения аргумента при которых знаменатель не превращается в ноль. Сначала находим решения уравнения, если те существуют, вырезаем из множества действительных значений. В результате получим набор интервалов
Сначала находим решения уравнения, если те существуют, вырезаем из множества действительных значений. В результате получим набор интервалов
где – корни уравнения .
3) Функция содержит корень парного степени . В таком случае областью определения будут точки , при которых подкоренная функция принимает неотрицательные значения, т.е. решения неравенства .
4) Если корень содержит знаменатель
то область определения определяют из строгого неравенства .
5) Если в знаменателе имеем корень нечетной степени
то область определения находим из условия .
5) Если является логарифмом от другой функции , то по свойству логарифма область определения находим из условия . Как правило, это будет интервал или несколько интервалов.
6) Экспонента областью определения имеет множество аргументов , для которых определена . Например, функция определена на всей действительной оси.
7) Простые тригонометрические функции (косинус и синус) определены на всем множестве действительных чисел .
8) Тангенс и котангенс областями определения имеют интервалы, граничащих между собой точками
для первой функции и
для второй, т.е.
В случаях когда при аргументах есть множители , точки в которых функция не существует следует определять из условия
Подобным образом и для котангенса
9) Следует отметить, что обратные тригонометрические функции — арксинус и арккосинус областями значений имеют отрезок . Для отыскания областей определения необходимо решить двойное неравенство
Например, для функции имеем неравенство с которого получим
При суперпозиции функций, то есть когда задана их комбинацию, нужно находить область определения каждой из функций, после чего — сечение найденных областей.
Пример.
Решение.
Область определения первого слагаемого находим из неравенства
Второй и третий дадут следующий вклад
Сечением найденных областей будет интервал
—————————————
Находите области определения по приведенной выше схеме, выключайте все лишние промежутки и точки и не допускайте ошибок. Помните, что установление областей определения — это одно из самых простых заданий при исследовании функции.
Помните, что установление областей определения — это одно из самых простых заданий при исследовании функции.
Посмотреть материалы:
- Исследования функции и построения графика
- Интервалы монотонности функции
- Наибольшее и наименьшее значение функции на отрезке
- Локальный экстремум функции. Примеры
- Выпуклость и вогнутисть графика функции
- Асимптоты функции
Помогите решить / разобраться (М)
Сообщения без ответов | Активные темы | Избранное
Правила форума
Посмотреть правила форума
| kot-obormot |
| ||
189 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| thething |
| |||
27/12/17 |
| |||
| ||||
| Someone |
| |||
23/07/05 |
| |||
| ||||
| EUgeneUS |
| ||
|
| ||
| |||
| wrest |
| ||
05/09/16 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 6 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
2.
 3 Локальные переменные и область действия функции 2.3 Локальные переменные и область действия функции
3 Локальные переменные и область действия функции 2.3 Локальные переменные и область действия функцииПРИМЕЧАНИЕ. Это заархивированная версия этих заметок 2020-21 гг., которая может быть устаревшей. Текущие студенты CSC110/111 должны посетить текущую страницу заметок, https://www.teach.cs.toronto.edu/~csc110y/fall/notes/.
Одно из ключевых назначений функций — разделить различные вычисления в программе, чтобы нам не приходилось беспокоиться о них всех сразу. Когда мы пишем наш код в отдельных функциях, мы можем сосредоточиться на работе только с одной функцией и игнорировать остальной код в других функциях.
Одним из способов, которым Python поддерживает этот способ проектирования программ, является разделение переменных в каждой функции, так что вызов функции может обращаться только к своим собственным переменным, но не к переменным, определенным в других функциях . В этом разделе мы рассмотрим, как это работает, и узнаем больше о том, как Python отслеживает вызовы функций и переменные.
Пример 1: введение области действия локальной переменной
Рассмотрим пример из предыдущего раздела:
квадрат по определению (x: число с плавающей запятой) -> число с плавающей запятой:
"""Возврат х в квадрате.
>>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
возврат х ** 2 Параметр x — это переменная , которой присваивается значение в зависимости от того, когда была вызвана функция. Поскольку эта переменная полезна только внутри тела функции, Python не позволяет сделать ее доступной снаружи тела. Мы говорим, что x — это локальная переменная из квадратных , потому что она ограничена телом функции. Вот еще один способ выразить это, используя важное новое определение. Область переменной — это места в коде, где можно получить доступ к этой переменной. Локальная переменная функции — это переменная, областью действия которой является тело этой функции.
Давайте проиллюстрируем это, сначала создав переменную в консоли Python, а затем вызвав квадрат 9.0020 .
>>> n = 10,0 >>> результат = квадрат (n + 3,5)
Мы знаем, что при вызове Square сначала вычисляется его аргумент-выражение n + 3,5 , в результате чего получается значение 13,5 , которое затем присваивается параметру x . Теперь давайте рассмотрим, как выглядит модель памяти при вычислении оператора return . Наивная диаграмма просто показала бы две переменные n и x и соответствующие им значения: мы не показываем результат , потому что ему еще не присвоено значение; это происходит только после возврата квадрат .
нет | 10,0 |
х | 13,5 |
Но это очень обманчиво! В наших диаграммах модели памяти мы группируем переменные в зависимости от того, вводятся ли они в консоли Python или внутри функции:
нет | 10,0 |
х | 13,5 |
Мы используем имя __main__ для обозначения таблицы переменных, определенных в консоли Python. Это специальное имя в Python — подробнее об этом позже. Внутри тела
Это специальное имя в Python — подробнее об этом позже. Внутри тела квадрат , единственная переменная , которую можно использовать, равна x , а снаружи в консоли Python только переменная , которую можно использовать, равна n . Поначалу это может показаться сложным, но эти диаграммы моделей памяти — хороший способ визуализировать происходящее. В момент, когда вычисляется тело квадрата, активна только таблица « квадрат » в модели памяти:
нет | 10,0 |
х | 13,5 |
Но после того, как квадрат возвращается, и мы возвращаемся к консоли Python, таблица « квадрат » больше не доступна, и активна только таблица __main__ :
нет | 10,0 |
результат | 182,25 |
х | 13,5 |
Попытка доступа к переменной x из консоли Python приводит к ошибке:
>>> n = 10,0 >>> квадрат(n + 3,5) 182,25 >>> х Traceback (последний последний вызов): Файл "", строка 1, в NameError: имя «x» не определено
Пример 2: повторяющиеся имена переменных
Принцип «отдельных таблиц» в нашей модели памяти применяется даже тогда, когда мы используем одно и то же имя переменной в двух разных местах. Предположим, мы изменили наш пример выше, чтобы использовать
Предположим, мы изменили наш пример выше, чтобы использовать x вместо n в консоли Python:
>>> х = 10,0 >>> результат = квадрат (х + 3,5)
Следуя тем же рассуждениям, что и выше, выражение аргумента x + 3,5 вычисляется для получения 13,5 , которое затем присваивается параметру x . Изменяет ли это переменную x в консоли Python? Нет! Это разные переменные, даже если они имеют одно и то же имя.
х | 10,0 |
х | 13,5 |
Мы можем подтвердить это после оценки вызова функции, проверив значение исходного x .
>>> х = 10,0 >>> результат = квадрат (х + 3,5) >>> результат 182,25 >>> х 10,0
Вот как выглядит наша модель памяти после возврата квадратов :
х | 10,0 |
результат | 182,25 |
х | 13,5 |
Пример 3: (не)доступ к переменным другой функции
Наш последний пример в этом разделе включает две функции, одна из которых вызывает другую:
квадрат по определению (x: число с плавающей запятой) -> число с плавающей запятой:
"""Возврат х в квадрате. >>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
вернуть х**2
def Square_of_sum (числа: список) -> float:
"""Вернуть квадрат суммы заданных чисел."""
итог = сумма (числа)
обратный квадрат (всего)
>>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
вернуть х**2
def Square_of_sum (числа: список) -> float:
"""Вернуть квадрат суммы заданных чисел."""
итог = сумма (числа)
обратный квадрат (всего) Давайте сначала вызовем нашу новую функцию Square_of_sum в консоли Python:
>>> числа = [1,5, 2,5] >>> результат = квадрат_суммы (числа) >>> результат 16.0
Мы можем проследить, что происходит в трех точках, когда мы вызываем Square_of_sum :
Прямо перед вызовом Square_of_sum (из консоли) | Прямо перед кв. 9Вызывается 0020 (из | Прямо перед возвратом в квадрат | ||||||||||||||||
|
|
|
Из этих диаграмм видно, как список [1. передается из консоли в  5, 2.5]
5, 2.5] Square_of_sum , и как число 4.0 передается из Square_of_sum в квадрат .
Теперь предположим, что мы хотим сделать что-то немного глупое: иметь квадратных доступа к всего вместо x . Из нашей модели памяти мы знаем, что этим переменным должно быть присвоено одно и то же значение, поэтому поведение программы не должно измениться, верно?
квадрат по определению (x: число с плавающей запятой) -> число с плавающей запятой:
"""Возврат х в квадрате.
>>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
return total ** 2 # Теперь мы используем total вместо x
def Square_of_sum (числа: список) -> float:
"""Вернуть квадрат суммы заданных чисел."""
итог = сумма (числа)
обратный квадрат (всего) Давайте посмотрим, что произойдет, когда мы попытаемся позвонить Square_of_sum в консоли Python теперь:
>>> числа = [1,5, 2,5] >>> Square_of_sum(числа) Traceback (последний последний вызов): Файл "", строка 1, вФайл "", строка 15, в square_of_sum Файл "", строка 9, в квадрате NameError: имя «всего» не определено
Произошла ошибка! Посмотрим на состояние памяти при вызове квадрата (то же самое, что и выше):
цифры | [1,5, 2,5] |
номера | [1,5, 2,5] |
Всего | 4,0 |
х | 4,0 |
Что ж, действительно есть переменная total и переменная x с одним и тем же значением, 4. . Так почему же мы получаем эту ошибку? Правило Python для локальной области видимости: локальная переменная доступна только в теле функции, она определена . Здесь оператор  0
0 return total ** 2 находится в теле квадрат , но пытается получить доступ к локальной переменной другой функции ( Square_of_sum ). Когда интерпретатор Python пытается получить значение total , он ищет только в области квадрат и не находит total , что приводит к NameError .
Несколько неинтуитивный момент в этом поведении заключается в том, что это происходит даже когда Square_of_sum все еще активен . В нашем примере Square вызывается из Square_of_sum , поэтому переменная total действительно существует в памяти Python — она просто недоступна. Хотя это может показаться ограничением языка, на самом деле это хорошо: это предотвращает случайное использование переменной из совершенно другой функции при работе с функцией.
Резюме
В этом разделе мы узнали, как Python обрабатывает локальных переменных , сделав их доступными только из той функции, в которой они определены. Хотя мы надеемся, что это интуитивно понятно, некоторые детали и диаграммы, которые мы здесь представили, носили чисто технический характер. Рекомендуем вернуться к этому разделу через несколько дней и просмотреть этот материал, возможно, объяснив своими словами, что происходит в каждом примере. Вы также можете попрактиковаться в рисовании диаграммы модели памяти в этом стиле для будущего кода, который вы пишете.
CSC110/111 Примечания к курсу ГлавнаяОбласть действия переменной в R
В R переменные — это контейнеры для хранения значений данных. Они являются ссылкой или указателем на объект в памяти, что означает, что всякий раз, когда переменная присваивается экземпляру, она сопоставляется с этим экземпляром. Переменная в R может хранить вектор, группу векторов или комбинацию многих объектов R. Пример :
Пример :
Python3
900 19 print
|
Выход:
[1] 0 1 2 3 [1] «Питон» «Р» [1] 1 2 3 4 [1] «Деби» «Сандип» «Субхам» «Шиба» [[1]] [1] 1 2 3 4 [[2]] [1] «Деби» «Сандип» «Субхам» «Шиба»
Временная сложность: O(1)
Вспомогательный пробел: O(1)
Соглашение об именах переменных
- Имя переменной в R должно состоять из буквенно-цифровых символов, за исключением символа подчеркивания ('_') и период('.
 ') , специальные символы, которые можно использовать в именах переменных.
') , специальные символы, которые можно использовать в именах переменных. - Имя переменной должно всегда начинаться с алфавита.
- Другие специальные символы, такие как ('!', '@', '#', '$') не допускаются в именах переменных.
Пример:
Python3
900 05 |
Вышеприведенный код при выполнении выдаст ошибку из-за неправильного именования переменных.
Ошибка: неожиданный символ в "2b" Выполнение остановлено
Область действия переменной
Место, где мы можем найти переменную и при необходимости получить к ней доступ, называется областью действия переменной. В основном существует два типа областей действия переменных:
- Глобальные переменные: Глобальные переменные — это те переменные, которые существуют на протяжении всего выполнения программы. Его можно изменить и получить к нему доступ из любой части программы.
- Локальные переменные: Локальные переменные — это те переменные, которые существуют только в определенной части программы, такой как функция, и освобождаются при завершении вызова функции.
Глобальная переменная
Как следует из названия, доступ к глобальным переменным можно получить из любой части программы.
- Они доступны на протяжении всего срока действия программы.
- Они объявляются в любом месте программы за пределами всех функций или блоков.

- Объявление глобальных переменных: Глобальные переменные обычно объявляются вне всех функций и блоков. Доступ к ним возможен из любой части программы.
Python3
|
Вывод:
[1] 5 [1] 10
Временная сложность: O(1)
Вспомогательное пространство: O(1)
В приведенном выше коде переменная ' global ' объявлена в верхней части программы вне всех функций, поэтому она является глобальной переменной, доступ к которой или ее обновление можно получить из любой точки программы.
Локальная переменная
Переменные, определенные внутри функции или блока, называются локальными по отношению к этим функциям.
- Локальные переменные не существуют вне блока, в котором они объявлены, т. е. к ним нельзя получить доступ или использовать их вне этого блока.
- Объявление локальных переменных: Локальные переменные объявляются внутри блока.
Пример:
Python3
9072 0 печать (возраст) |
Время Сложность: O(1)
Вспомогательное пространство: O(1)
Вывод:
Ошибка печати (возраст): объект 'возраст' не найдено
Вышеупомянутая программа выводит сообщение об ошибке «Объект «возраст» не найден». Переменная age была объявлена внутри функции func(), поэтому она является локальной для этой функции и невидима для части программы за пределами этой функции. Чтобы исправить указанную выше ошибку, нам нужно отобразить значение переменной age только из функции func(). Пример:
Переменная age была объявлена внутри функции func(), поэтому она является локальной для этой функции и невидима для части программы за пределами этой функции. Чтобы исправить указанную выше ошибку, нам нужно отобразить значение переменной age только из функции func(). Пример:
Python3
|
Вывод:
Возраст: [1] 18
Временная сложность: O(1)
Вспомогательный пробел: O(1)
Доступ к глобальным переменным
Доступ к глобальным переменным можно получить из любой точки кода, в отличие от локальных переменных, область действия которых ограничена блоком кода, в котором они созданы. Пример:
Пример:
Python3
90 019
|
Вывод:
Ошибка печати(а): объект "а" не найден
В приведенном выше коде мы видим, что мы не можем получить доступ к переменной «a» вне функции, поскольку она назначается оператором присваивания (<-) , который делает «a» локальной переменной. Для выполнения присваивания глобальным переменным используется супероператор присваивания (<<-) 9. 0004 используется. Как работает супероператор присваивания? При использовании этого оператора внутри функции выполняется поиск переменной в фрейме родительской среды, если она не найдена, продолжается поиск на следующем уровне, пока не будет достигнута глобальная среда. Если переменная все еще не найдена, она создается и назначается на глобальном уровне. Пример:
0004 используется. Как работает супероператор присваивания? При использовании этого оператора внутри функции выполняется поиск переменной в фрейме родительской среды, если она не найдена, продолжается поиск на следующем уровне, пока не будет достигнута глобальная среда. Если переменная все еще не найдена, она создается и назначается на глобальном уровне. Пример:
Python3
|
Выход:
[1] 10 [1] 10 [1] 10
Когда оператор «a <<- 10» встречается в inner_function() , он ищет переменную «a» в среде external_function() .

 10.2019, 18:43
10.2019, 18:43 

 Заметьте, что она нечётная. Посмотрите на её предел на плюс бесконечности. Далее, вот Вы получили неравенство
Заметьте, что она нечётная. Посмотрите на её предел на плюс бесконечности. Далее, вот Вы получили неравенство


 >>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
вернуть х**2
def Square_of_sum (числа: список) -> float:
"""Вернуть квадрат суммы заданных чисел."""
итог = сумма (числа)
обратный квадрат (всего)
>>> квадрат(3.0)
9,0
>>> квадрат(2,5)
6,25
"""
вернуть х**2
def Square_of_sum (числа: список) -> float:
"""Вернуть квадрат суммы заданных чисел."""
итог = сумма (числа)
обратный квадрат (всего)  ') , специальные символы, которые можно использовать в именах переменных.
') , специальные символы, которые можно использовать в именах переменных.