X y z 1 график: Построить трехмерный график онлайн

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )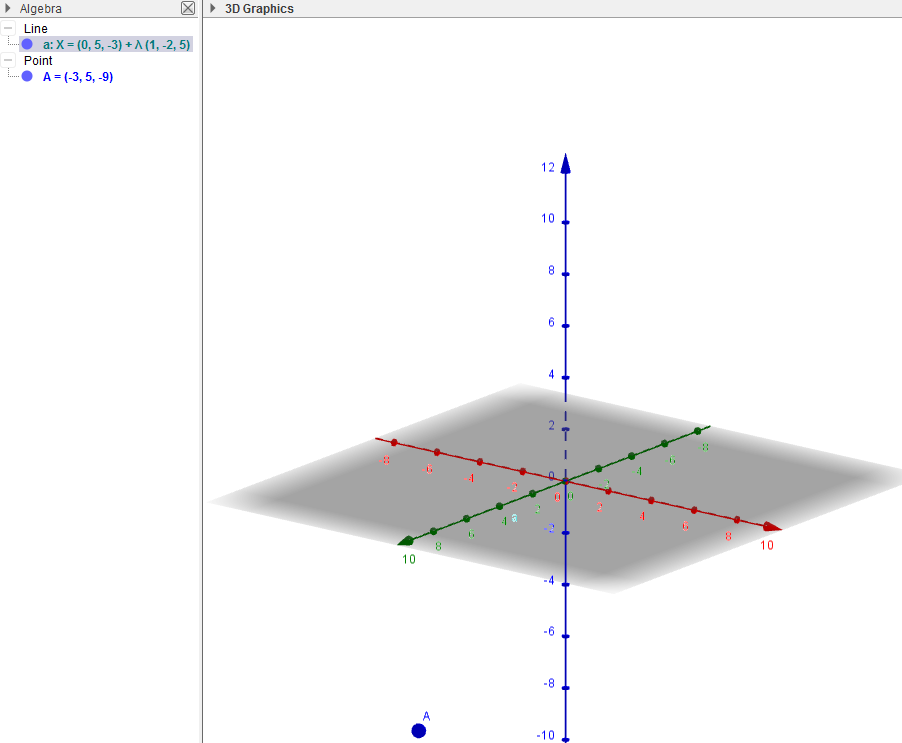
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )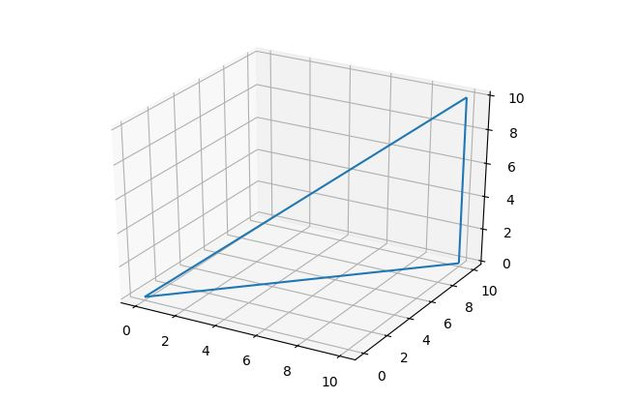
26Найти точное значениеcsc(30 град. )
27Найти точное значениеsin(0)
28Найти точное значение sin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )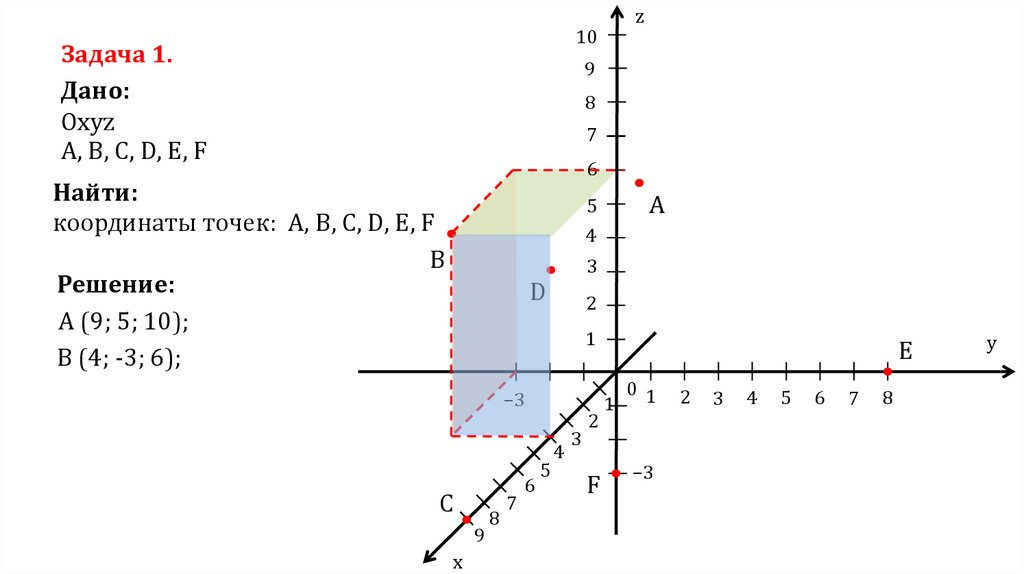
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )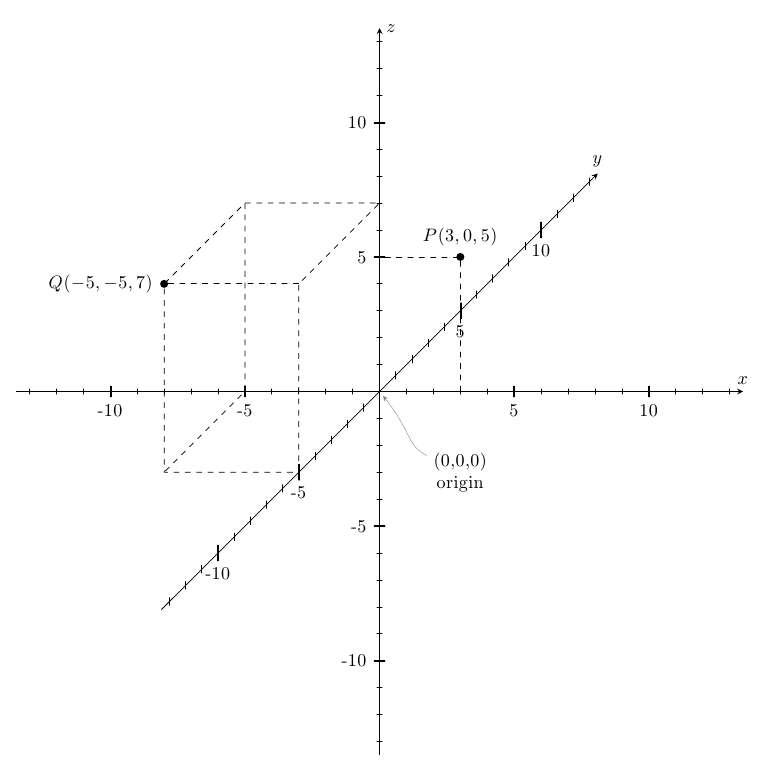
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значение tan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88 Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94Найти точное значениеarcsin(0)
95
Найти точное значение		sin(120 град. )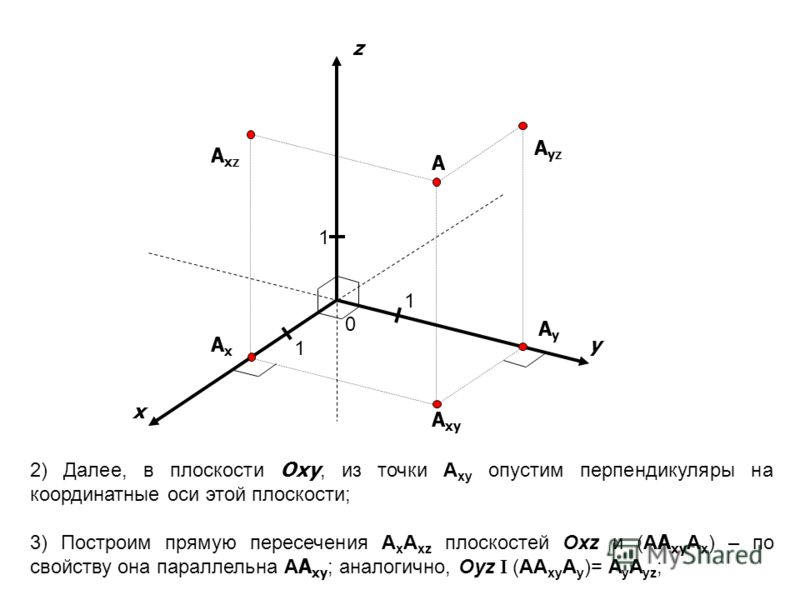
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100Преобразовать из градусов в радианы88 град.

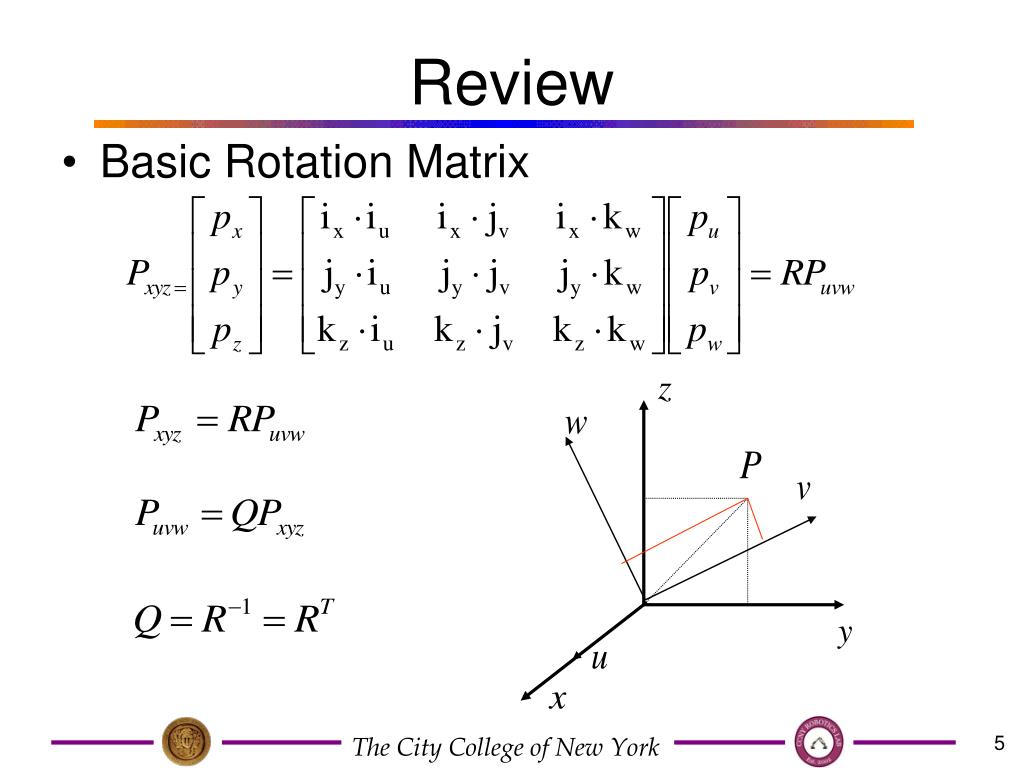
Трехмерные графики. Анимация — Решение математических задач в Maple

График поверхности, заданной явной функцией.

График функции z = f(x, y) можно нарисовать, используя команду plot3d(f(x,y), x=x1…x2, y=y1…y2, options). Параметры этой команды частично совпадают с параметрами команды plot. К часто используемым параметрам команды plot3d относится light=[angl1, angl2, c1, c2, c3] – задание подсветки поверхности, создаваемой источником света из точки со сферическими координатами (angl1, angl2). Цвет определяется долями красного (c1), зеленого (c2) и синего (c3) цветов, которые находятся в интервале [0,1]. Параметр style=opt задает стиль рисунка: POINT –точки, LINE – линии, HIDDEN – сетка с удалением невидимых линий, PATCH

– заполнитель (установлен по умолчанию), WIREFRAME – сетка с выводом невидимых линий, CONTOUR – линии уровня, PATCHCONTOUR – заполнитель и линии уровня. Параметр shading=opt задает функцию интенсивности заполнителя, его значение равно xyz – по умолчанию, NONE – без раскраски.

В качестве примера построим график функции f=sin(x)+cos(y).

График поверхности, заданной параметрически. 2=4.   

График пространственных кривых.

В пакете plot имеется команда spacecurve для построения пространственной кривой, заданной параметрически: x = x(t), y = y(t),z = z(t). Параметры команды:

> spacecurve([x(t),y(t),z(t)],t=t1..t2),

где переменная t изменяется от t1 до t2.

Построим график пространственной кривой х=sin(t), у=cos(t), z=exp(t).

Анимация.

Maple позволяет выводить на экран движущиеся изображения с помощью команд animate (двумерные) и animate3d (трехмерные) из пакета plot. Среди параметров команды animate3d есть frames – число кадров анимации (по умолчанию frames=8).

Трехмерные изображения удобнее настраивать не при помощи опций команды plot3d, а используя контекстное меню программы. Для этого следует щелкнуть правой кнопкой мыши по изображению. Тогда появится контекстное меню настройки изображения. Команды этого меню позволяют изменять цвет изображения, режимы подсветки, устанавливать нужный тип осей, тип линий и управлять движущимся изображением.

Многомерное исчисление

. Как построить график $x + y + z = 1$ без использования графических устройств?

спросил

Изменено 3 года назад

Просмотрено 53 тысячи раз

$\begingroup$

Как построить график $x + y + z = 1$ без использования графических устройств?

Я равняю $z = 0$, чтобы найти график на плоскости xy. Итак, я получил строку $y = 1-x$ Но когда я равняю 0 либо для $x$, либо для $y,$, я получаю $z = 1-y$ или $z = 1-x$, и это две разные линии под разными углами. Различные веб-сайты с графиками давали мне разные ответы…

Пожалуйста, не показывайте какие-то сумасшедшие и сложные методы построения графика. Мне просто нужны простые шаги, такие как подстановка $x,y,z$ в виде нулей и т.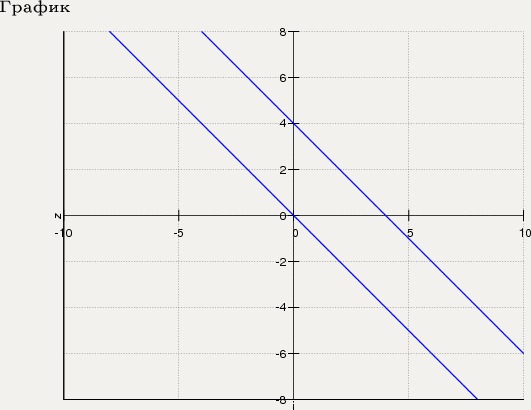 д. $\endgroup$

1

$\begingroup$

Надеюсь, вы не возражаете, если я опубликую здесь решение для тишины. Я думаю, что это говорит вам все, однако другие хорошие ответы дают вам теоретические моменты. 🙂

$\endgroup$

1

$\begingroup$

Рисовать 3D-графики вручную может быть очень сложно. Когда дело доходит до рисования простых плоскостей, мне нравится рисовать ту часть плоскости, которая равна 9.0039 только в одном октанте (например, в этом случае мы можем рассматривать только первый октант, где $x,y,z \ge 0$). Для этого находим, где плоскость пересекает каждую из 3 осей.

  • Для точки пересечения $x$ установите $y=z=0$, чтобы получить $x+0+0=1$, что дает точку $(1,0,0)$.
  • Для точки пересечения $y$ установите $x=z=0$, чтобы получить $0+y+0=1$, что дает точку $(0,1,0)$.
  • Для точки пересечения $z$ установите $x=y=0$, чтобы получить $0+0+z=1$, что дает точку $(0,0,1)$.

Наконец, нарисуйте заданный октант, содержащий эти 3 пересечения, и обозначьте каждую из этих 3 точек. Соедините эти точки, чтобы сформировать треугольник, представляющий часть плоскости внутри этого октанта.

$\endgroup$

$\begingroup$

$x+y+z=1$ образует плоскость. Этот самолет содержит все три линии, которые вы нашли (и многое другое). Но того, что вы сделали, должно быть достаточно — если вы знаете несколько точек на плоскости (в данном случае, например, вы знаете (1,0,0), (0,1,0) и (0,0, 1) и многое другое), можно зарисовать всю плоскость.

$\endgroup$

$\begingroup$

В 2D график $$\frac xa +\frac yb=1$$ — прямая, соединяющая $(a,0)$ и $(0, b)$. Это может быть легко подтверждено заменой.

Аналогично, в 3D, $$\frac xa +\frac yb+\frac zc=1$$ плоскость, проходящая через $(a,0,0), (0, b, 0), (0,0,c)$.

Вопрос выше относится к случаю, когда $a=b=c=1$.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *