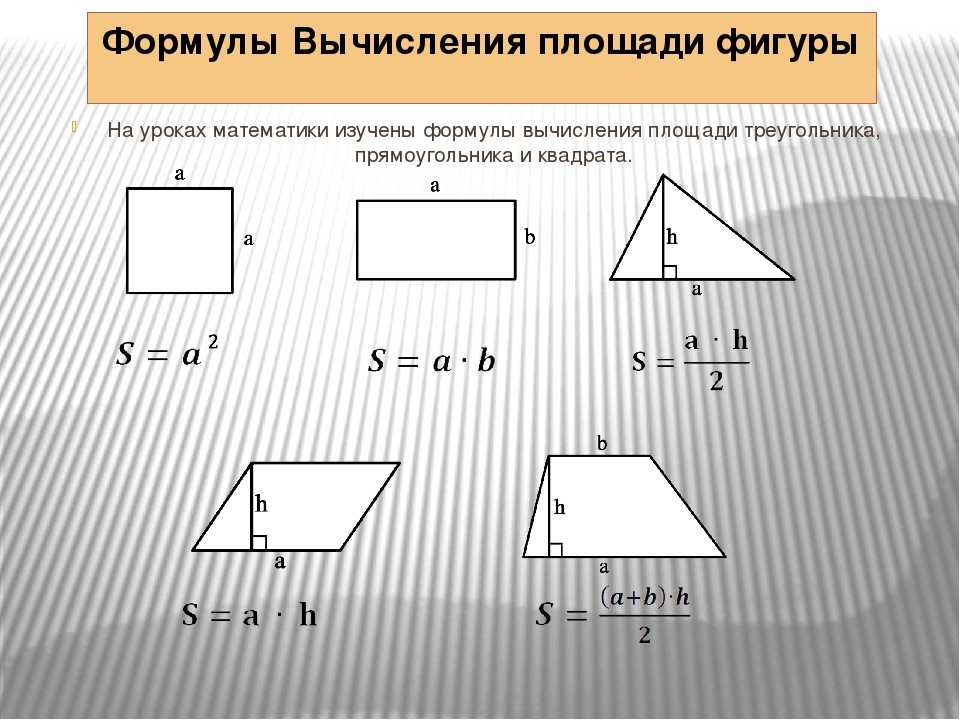
Площади фигур
Формула площади треугольника
Площадь треугольника (S):
h — высота треугольника;
a — основание.
Площадь прямоугольного треугольника по катетам
Формула площади прямоугольного треугольника, (S):
a, b — катеты треугольника.
Площадь треугольника, формула Герона
Формула (Герона) площади треугольника через полупериметр (S):
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Площадь равнобедренного треугольника
Площадь треугольника с двумя одинаковыми сторонами.
b — основание треугольника
a — равные стороны
h — высота
Формула площади треугольника через высоту h и основание b, (S):
Формула площади треугольника через, стороны a, b, (S):
Площадь равностороннего треугольника равна:
Формулы расчета, площади равностороннего треугольника.
a — сторона треугольника
h — высота
Площадь квадрата через диагональ
Как рассчитать площадь квадрата через диагональ
a — сторона квадрата
c — диагональ
Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади ромба
S = a · H
где: H — высота ромба.
a — сторона ромба
Площадь неравнобедренной трапеции :
a — нижнее основание;
b — верхнее основание;
h — высота трапеции.
Формула площади правильного многоугольника
a — сторона многоугольника
n — количество сторон
Записи по теме
Площади кругов и окружностей
Формулы площадей для кругов и окружностей: площадь круга, площадь сегмента круга, площадь кольца, площадь сектора кольца.
Площади поверхностей
Формулы площади поверхностей объёмных фигур. Формулы для расчёта площади поверхности куба, прямоугольного параллелепипеда, правильной и усечённой пирамид, усечённого конуса.
Площадь фигуры. Все формулы
Площади геометрических фигур — численные значения, характеризующие их размер в двумерном пространстве. Эта величина может измеряться в системных и внесистемных единицах. Так, например, внесистемная единица площади — сотка, гектар. Это в том случае, если измеряемой поверхностью является участок земли. Системная же единица площади — квадрат длины. В системе СИ принято считать, что единица площади плоской поверхности — это квадратный метр. В СГС единица площади выражается через квадратный сантиметр.
Геометрия и формулы площадей неразрывно связаны.
Эта связь заключается в том, что вычисление площадей плоских фигур основывается именно на их применении. Для многих фигур выведены несколько вариантов, по которым вычисляются их квадратные размеры. Опираясь на данные из условия задачи, мы можем определить максимально простой способ для решения. Тем самым облегчить расчет и свести вероятность ошибки вычисления к минимуму. Для этого рассмотрим основные площади фигур в геометрии.
Содержание
- 1 Треугольник
- 2 Прямоугольник
- 3 Квадрат
- 4 Ромб
- 5 Трапеция
- 6 Цилиндр и параллелепипед
- 7 Кольцо
- 8 Многоугольник
Треугольник
Формулы для нахождения площади любого треугольника представлены несколькими вариантами:
1) Площадь треугольника рассчитывается по основанию a и высоте h. Основанием считают сторону фигуры, на которую опущена высота. Тогда площадь треугольника:
2) Площадь прямоугольного треугольника рассчитывается точно также, если гипотенузу считать основанием.
Если же за основание принять катет, то площадь прямоугольного треугольника будет равна уменьшенному вдвое произведению катетов.
На этом формулы для вычисления площади любого треугольника не заканчиваются. Другое выражение содержит стороны a,b и синусоидальную функцию угла γ, заключенного между a и b. Значение синуса находится по таблицам. Также его можно узнать с помощью калькулятора. Тогда площадь треугольника:
По данному равенству тоже можно убедиться в том, что площадь прямоугольного треугольника определяется через длины катетов. Т.к. угол γ — прямой, поэтому площадь прямоугольного треугольника рассчитывается без умножения на функцию синуса.
3) Рассмотрим частный случай — правильный треугольник, у которого сторона a известна по условию или ее длина найдется при решении. О фигуре в задаче по геометрии больше ничего не известно. Тогда площадь как найти при этом условии? В этом случае применяется формула для площади правильного треугольника:
Прямоугольник
Как найти площадь прямоугольника и использовать при этом размеры сторон, имеющих общую вершину? Выражение для вычисления такое:
Если для вычисления площади прямоугольника требуется использовать длины диагоналей, то тогда понадобится функция синуса угла, образованного при их пересечении.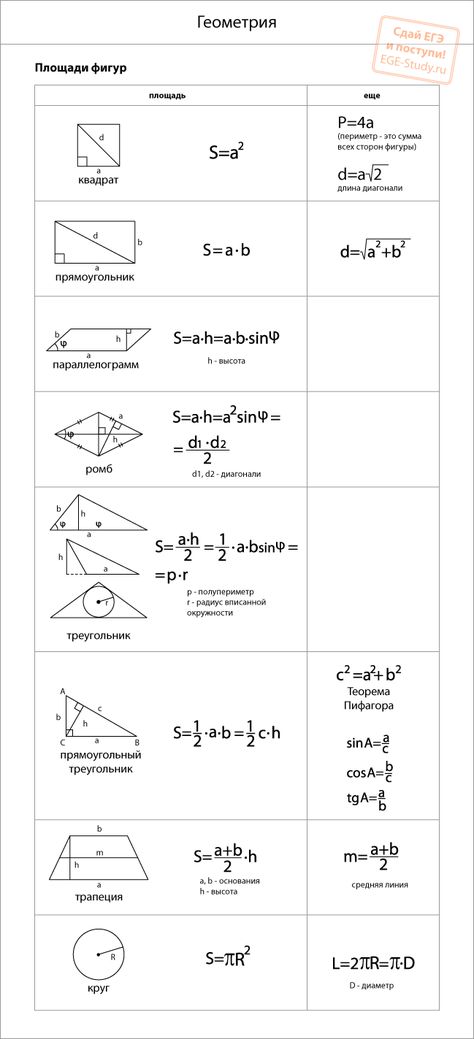
Такая формула площади прямоугольника имеет вид:
Квадрат
Площадь квадрата определяют как вторую степень длины стороны:
Доказательство вытекает из определения, согласно которому квадратом называют прямоугольник. У всех сторон, образующих квадрат, одинаковые размеры. Поэтому вычисление площади такого прямоугольника сводится к перемножению одной на другую, т. е. ко второй степени стороны. И формула для вычисления площади квадрата примет искомый вид.
Площадь квадрата можно найти другим способом, например, если использовать диагональ:
Как вычислить площадь фигуры, которая образована частью плоскости, ограниченной окружностью? Для расчета площади формулы такие:
- Через радиус окружности r. Для площади круга вычисление можно сделать следующим образом:
- Через диаметр окружности d. Найти площадь круга можно так:
Параллелограмм
Для параллелограмма формула содержит линейные размеры стороны, высоты и математическое действие — умножение.
Если же высота неизвестна, то тогда как найти площадь параллелограмма? Есть еще один способ вычисления. Потребуется определенное значение, которое примет тригонометрическая функция угла, образованного смежными сторонами, а также их длины.
Формулы площади параллелограмма таковы:
Ромб
Как найти площадь четырехугольника, называемого ромбом? Площадь ромба определяется с помощью простых математических действий с диагоналями. Доказательство опирается на тот факт, что отрезки диагоналей в d1 и d2 пересекаются под прямым углом. По таблице синусов видно, что для прямого угла данная функция равна единице. Поэтому площадь ромба рассчитывается так:
Еще площадь ромба может быть найдена другим способом. Доказать это тоже нетрудно, если учесть, что стороны его одинаковы по длине. Затем подставить их произведение в похожее выражение для параллелограмма. Ведь частным случаем именно этой фигуры является ромб. Здесь γ — внутренний угол ромба. Площадь ромба определяют так:
Трапеция
Как найти площадь трапеции через основания (a и b), если в задаче указаны их длины? Здесь без известного значения длины высоты h вычислить площадь такой трапеции не удастся.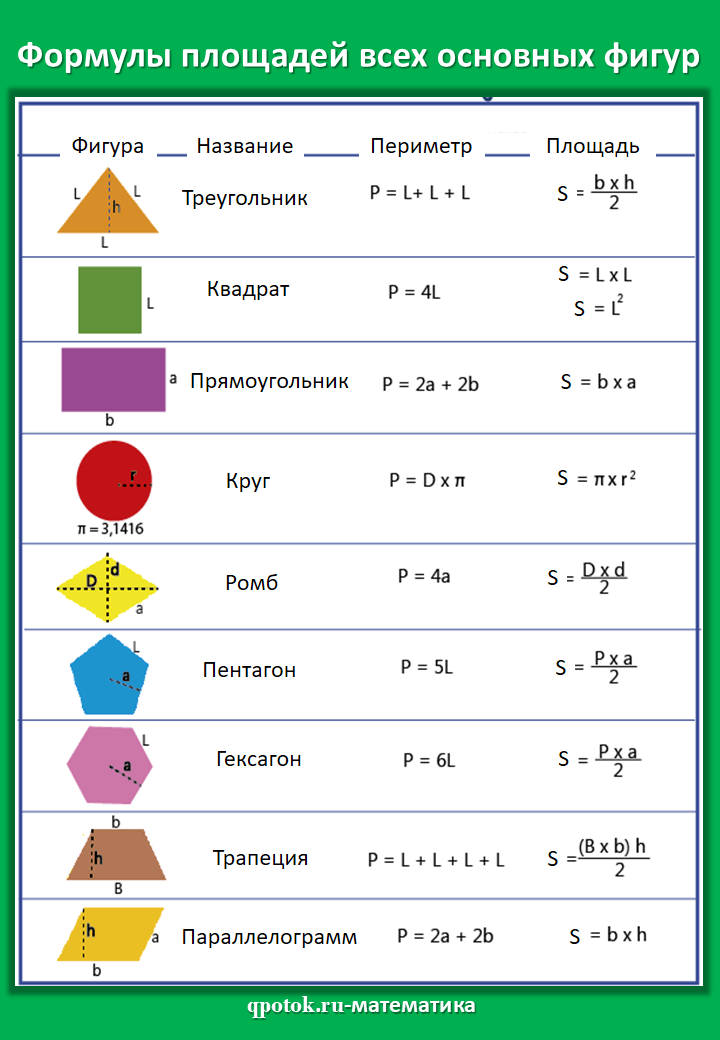
Т.к. эту величину содержит выражение для вычисления:
Квадратный размер прямоугольной трапеции тоже можно вычислить таким же способом. При этом учитывают, что в прямоугольной трапеции понятия высоты и боковой стороны объединены. Поэтому для прямоугольной трапеции нужно указывать вместо высоты длину боковой стороны.
Цилиндр и параллелепипед
Рассмотрим что нужно, чтобы рассчитать поверхность всего цилиндра. Площадь данной фигуры составляет пара кругов, называемых основаниями, и боковая поверхность. Окружности, образующие круги имеют длины радиусов, равные r. Для площади цилиндра имеет место такое вычисление:
Как найти площадь параллелепипеда, который состоит из трех пар граней? Его измерения совпадают с конкретной парой. Грани, находящиеся противоположно, имеют одинаковые параметры. Сначала находят S(1), S(2), S(3) — квадратные размеры неравных граней. Затем уже площадь поверхности параллелепипеда:
Кольцо
Две окружности с общим центром образуют кольцо.
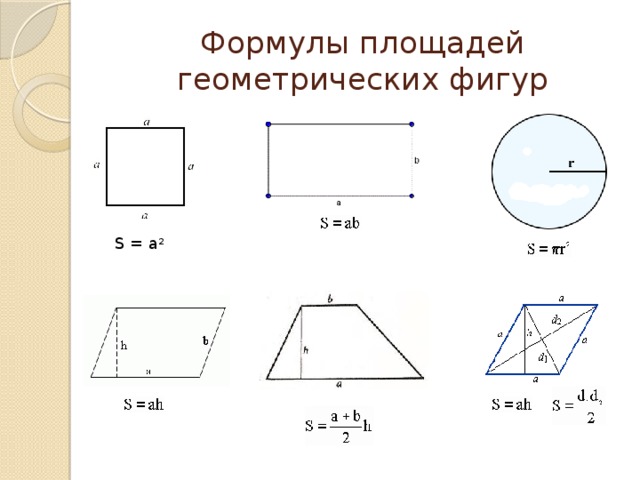Они же ограничивают площадь кольца. При этом обе расчетные формулы учитывают размеры каждой окружности. Первая из них, вычисляющая площадь кольца, содержит больший R и меньший r радиусы. Чаще их называют внешним и внутренним. Во втором выражении площадь кольца рассчитывается через больший D и меньший d диаметры. Таким образом, площадь кольца по известным радиусам рассчитывают так:Площадь кольца, с использованием длин диаметров, определяют следующим образом:
Многоугольник
Как найти площадь многоугольника, форма которого не является правильной? Общей формулы для площади таких фигур нет. Но если она изображена на координатной плоскости, например, это может быть клетчатая бумага, тогда как найти площадь поверхности в этом случае? Тут применяют способ, который не требует приблизительно измерить фигуру. Поступают так: если нашли точки, которые попадают в уголок клетки или имеют целые координаты, то учитывают только их. Чтобы затем выяснить, чему равна площадь, используют формулу, доказанную Пиком.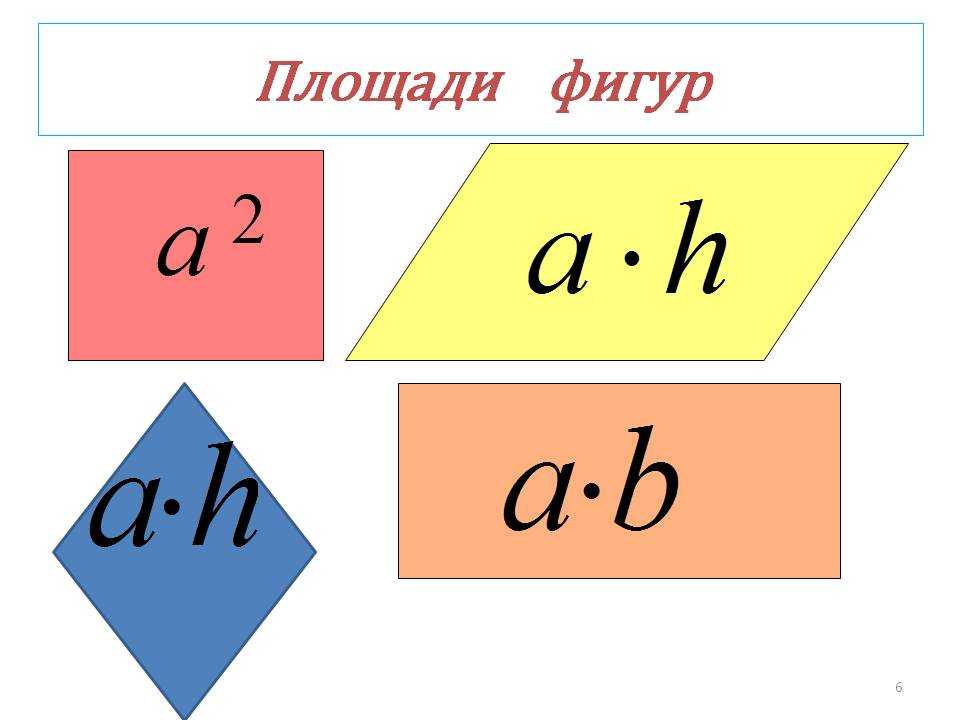
где В,Г — количество точек, расположенных внутри и на всей ломаной линии соответственно.
Поделиться с друзьями:
Area — Math Open Reference
Area — Math Open ReferenceОткрытый справочник по математике
Главная Контакт О Тематический указатель
Что такое площадь?
Площадь — это мера того, сколько места есть на плоской поверхности. Например, площадь двух листов бумаги в два раза больше площади одного листа, потому что на них вдвое больше места для записи.
Различные фигуры имеют разные способы нахождения площади.
Например, в прямоугольнике мы находим площадь, умножая длину на ширину.
В прямоугольнике выше площадь равна 2 × 4 или 8. Если вы посчитаете маленькие квадраты, вы обнаружите, что их 8.
шт.
Площадь измеряется в квадратных единицах. Например, в прямоугольнике выше, если стороны 2 и 4 метра, то площадь равна 8 квадратных метров. Если бы стороны были 2 фута и 4 фута в длину, площадь была бы 8 квадратных футов. Самое главное, что нужно помнить при расчете площади, это то, что
Обозначение
Мы говорим о прямоугольнике выше, имеющем площадь, скажем, 8 квадратных метров, но есть сокращенный способ записи. Мы пишем букву единицы с надстрочным индексом 2 после нее, вот так:
«8 квадратных метров» записывается как 8 м 2
«8 квадратных футов» записывается как 8 футов 2
Преобразование единиц
Есть много единиц площади. Например, площадь земли измеряется в таких единицах, как акры и гектары.
Самый простой способ конвертировать из одних единиц в другие — использовать поисковую систему Google.
Например, если вы введете «300 квадратных футов в квадратных метрах», вам будет сказано, что 300 квадратных футов равны 27,87 квадратных метров.
Площади плоских фигур
Для многих фигур существуют способы вычисления площади, например площадь круга. Они перечислены ниже со ссылками на страницы, которые объясняют каждую из них более подробно.
См. также
- Площадь поверхности твердых тел
| Квадрат | См. Площадь квадрата | |
| Прямоугольник | См. Площадь прямоугольника | |
| Треугольник | См. | |
| Треугольник (SAS) | См. Площадь треугольника (sas) | |
| Треугольник Даны 3 стороны | См. формулу Герона | См. формулу Герона |
| Равносторонний треугольник | См. Равносторонний участок | |
| Параллелограмм | См. область параллелограмма | |
| Трапеция | См. трапециевидную форму | |
| Ромб | 3 метода См. Площадь ромба | См. площадь ромба |
| Воздушный змей | , где D 1 , D 2 — диагонали. | См. Площадь воздушного змея |
| Правильный многоугольник | 4 метода См.  Площадь правильного многоугольника | См. Площадь правильного многоугольника |
| Круг | См. Площадь круга | |
| Эллипс | См. Площадь эллипса | |
| Сегмент круга | См. Площадь круглого сегмента. | См. Площадь круглого сегмента |
| Кольцо | См. Площадь кольца |
площадь треугольникаПлощади на координатной плоскости
Если вы знаете координаты x,y вершин фигуры, есть способы вычислить площадь по этим координатам. См. Многоугольники на координатной плоскости.
(C) 2011 Copyright Math Open Reference.
Все права защищены
Объем и площадь поверхности призмы (Видео)
vimeo.com/video/468634057?app_id=122963″ frameborder=»0″ allow=»autoplay; fullscreen; picture-in-picture» allowfullscreen=»»> TranscriptPractice
Привет! Добро пожаловать в это видео о нахождении объема и площади поверхности призмы !
Прежде чем мы перейдем к тому, как найти объем и площадь поверхности призмы, давайте рассмотрим несколько ключевых терминов, которые мы увидим в наших формулах. Первое слово, которое нам нужно определить, это base. Основания призмы — это две уникальные стороны, в честь которых названа призма. Например, если у вас есть шестиугольная призма , основаниями являются два шестиугольника на каждом конце призмы.
Другое слово, которое будет регулярно встречаться в наших формулах, — высота. Важно различать высоту, потому что она отличается от высоты, используемой в некоторых наших формулах площади. Высота призмы – это длина ребра между двумя основаниями.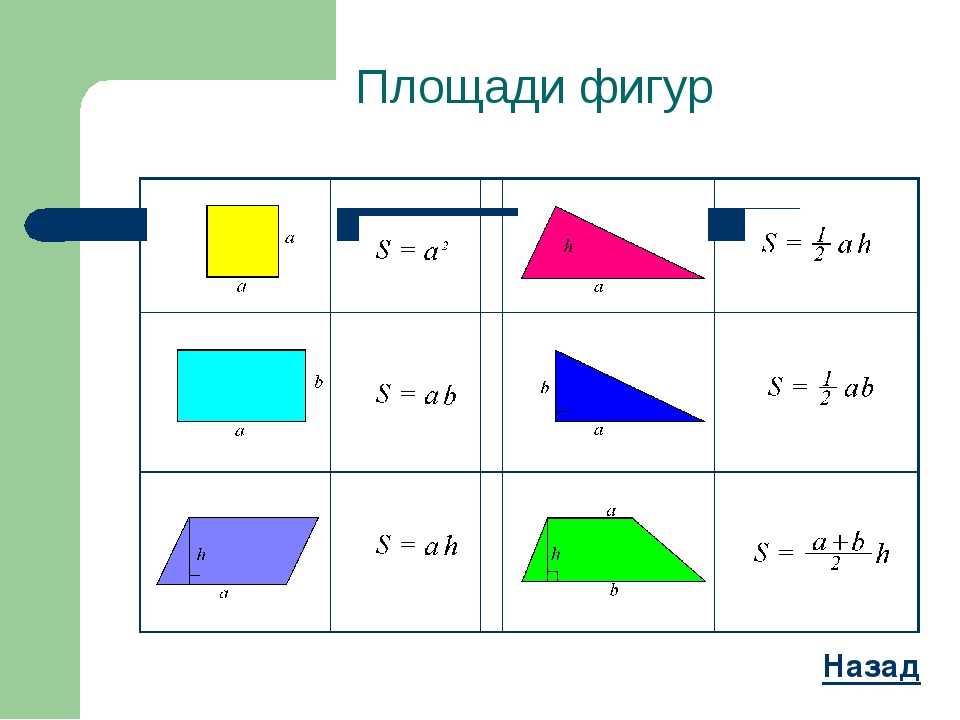
И, наконец, я хочу рассмотреть слово обычный . Помните, что правильность многоугольников означает, что каждая сторона многоугольника имеет одинаковую длину.
Теперь, когда мы рассмотрели некоторые из наших ключевых терминов, давайте посмотрим на наши две формулы.
Чтобы найти объем призмы, умножьте площадь основания призмы на ее высоту. Это записывается как \(V=Bh\). Обратите внимание, что большая буква B обозначает площадь основания. Важно, чтобы вы писали эту букву B с большой буквы, потому что в противном случае она просто означает основание. Мы видим это в формуле площади треугольника ½ bh.
Формула площади поверхности призмы \(SA=2B+ph\), где B, опять же, обозначает площадь основания, p представляет периметр основания, а h обозначает высоту призмы. призма.
Теперь, когда мы знаем, что такое формулы, давайте рассмотрим несколько примеров задач с их использованием.
Найдите объем и площадь поверхности этой прямоугольной призмы.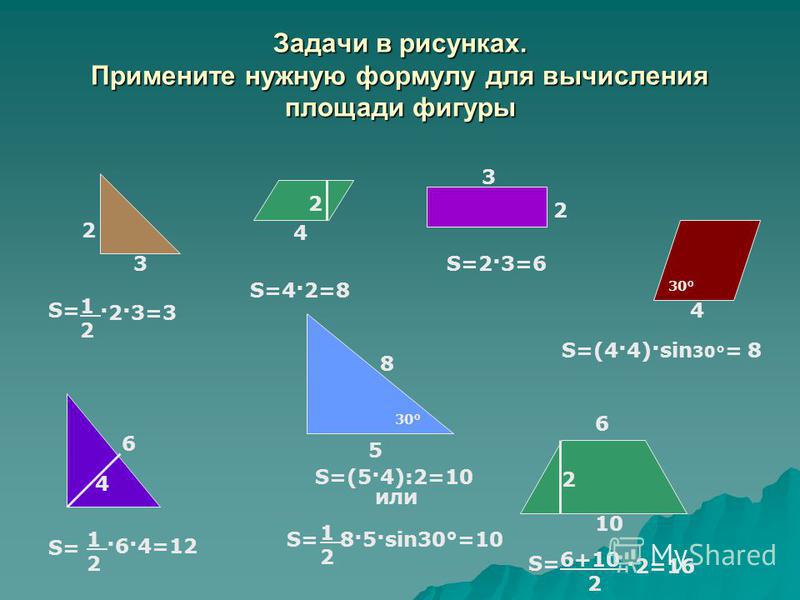
Начнем с громкости.
\(V=Bh\)
Так как большая B обозначает площадь основания, мы подставим в формулу площади прямоугольника длину, умноженную на ширину.
Формула объема прямоугольной призмы
Итак \(V=lwh\)
Теперь подставим наши значения. 93\). Помните, поскольку мы умножаем на три измерения, наши единицы измерения кубичны.
Теперь давайте посмотрим на нашу поверхность.
\(SA=2B+ph\)
Опять же, мы подставим в нашу формулу площадь прямоугольника, а также подставим в нашу формулу периметр прямоугольника.
\(SA=2lw+2l+wh\)
Теперь мы можем подставить наши известные значения.
\(SA=24\times 7+2(4+7)(13)\)
И упростим, чтобы получить ответ.
Площадь поверхности 342 квадратных метра.
Помните, что с площадью поверхности мы складываем площади каждой грани вместе, поэтому мы умножаем только на два измерения, поэтому мы возводим наши единицы в квадрат.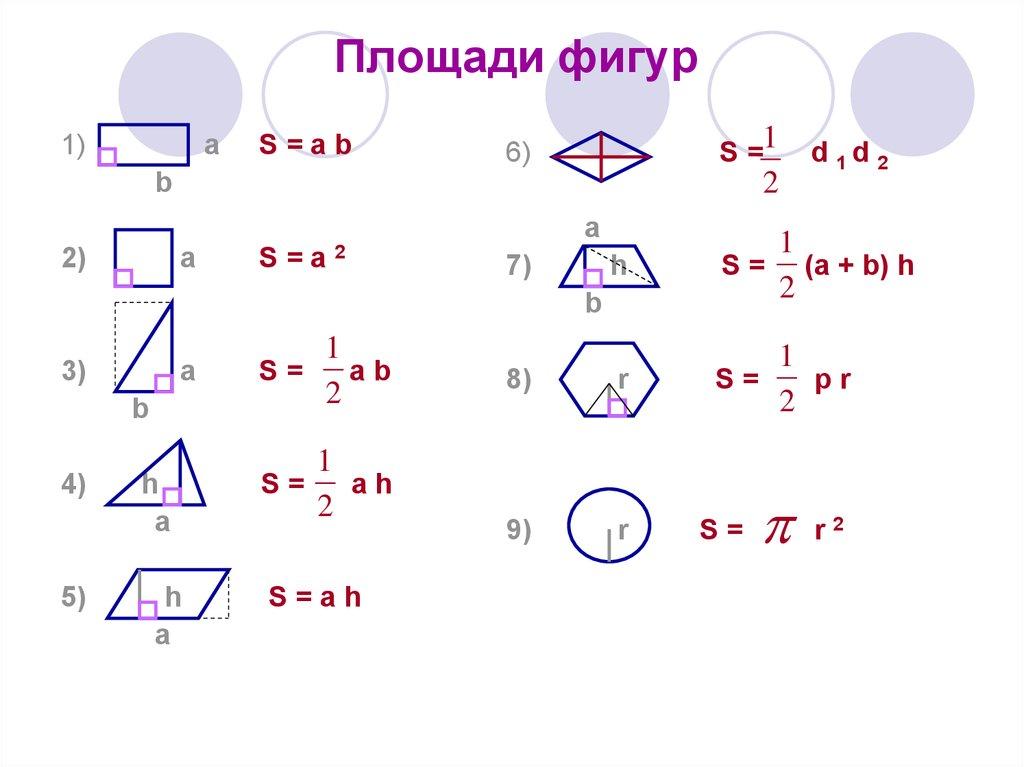
Давайте попробуем другой пример.
Найдите объем и площадь поверхности этой правильной пятиугольной призмы.
Начнем с нашего тома.
\(V=Bh\)
Мы хотим подставить в нашу формулу площадь правильного пятиугольника. Эта формула не является общепринятой, так что ничего страшного, если вам нужно ее найти.
Площадь правильного пятиугольника находится как \(V=(\frac{1}{2}pa)h\)
Теперь мы можем подставить наши значения. Помните, правильный означает, что все стороны пятиугольника конгруэнтны, поэтому мы можем найти наш периметр, умножив значение стороны на 5.
\(V=(\frac{1}{2}\times 5\times 5\ умножить на 3)(14)\)
Что, если мы умножим это, даст нам 525 кубических футов.
Теперь перейдем к площади поверхности.
\(SA=2B+ph\)
Во-первых, мы хотим произвести замену в наших формулах. 92\)
Площадь поверхности нашей призмы составляет 425 квадратных футов.
Давайте рассмотрим еще один пример, но на этот раз я хочу, чтобы вы попробовали его самостоятельно.
Найдите объем и площадь поверхности этой правильной треугольной призмы.
Поставьте видео на паузу и посмотрите, сможете ли вы найти ответы самостоятельно. Тогда сравните их с моими.
Готовы проверить?
Давайте сначала посмотрим на громкость.
\(V=Bh\)
Подставим в нашу формулу площадь треугольника. 93\)
Объем нашей треугольной призмы равен 750 кубических дюймов.
Теперь на поверхность.
\(SA=2B+ph\)
Сначала подставьте свои формулы.
\(SA=2(\frac{1}{2}bh)+(3s)h\)
Мы можем использовать 3s для периметра, потому что это правильный треугольник или равносторонний треугольник, поэтому все стороны имеют одинаковую длину.
Теперь подставим наши значения и решим.
\(SA=2(\frac{1}{2}\times 5\times 12)+(3\times 12)(25)=60+900=93\)
Показать ответ
Ответ:
| \(V=Bh\) | Чтобы найти объем призмы, используйте формулу \(V=Bh\), где \( V\) обозначает объем, \(B\) обозначает площадь основания призмы, а \(h\) обозначает ее высоту. | ||||||||||||||||||||||||||||||||
| \(V=(lw)h\) | Поскольку это прямоугольная призма, подставьте формулу площади прямоугольника вместо \(B\). Площадь основания призмы равна \(lw\), то есть длине, умноженной на ширину. 93\) Показать ответ Ответ:
Скрыть ответ Вопрос №3: Показать ответ Ответ:
Скрыть ответ Вопрос № 4: Показать ответ Ответ:
|
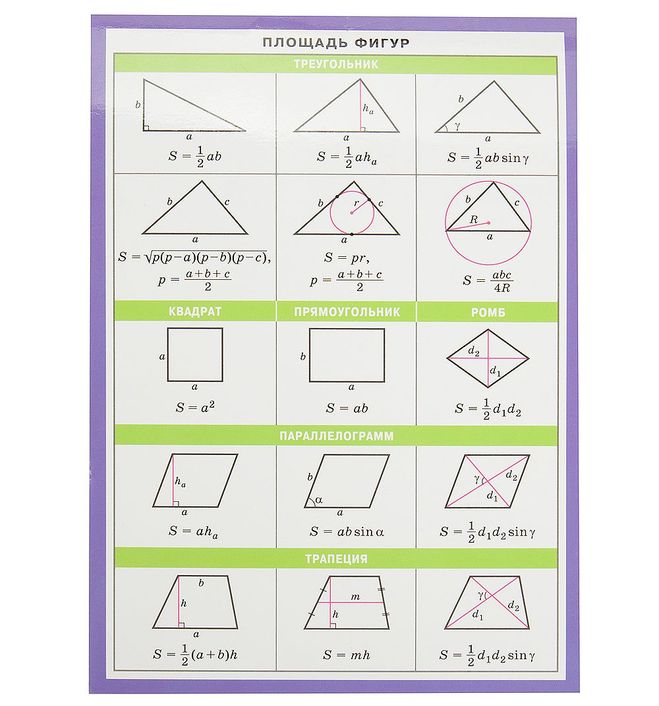
93\)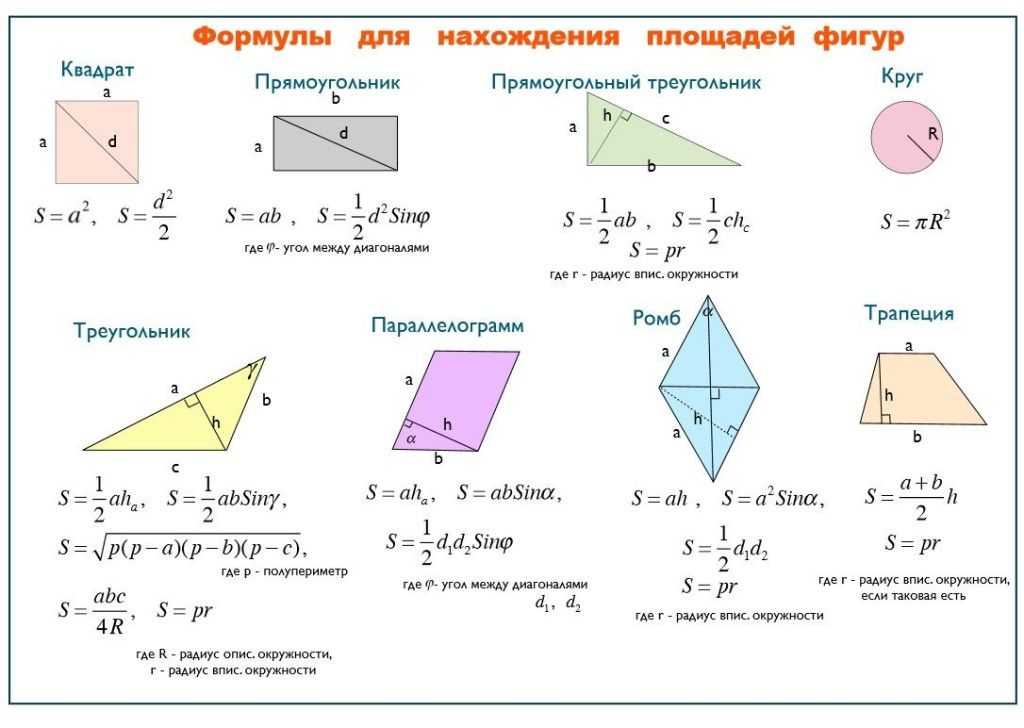
3\) 93\). Следовательно, ответ Б правильный.
Поскольку \((3\times13)=393\)