Четность, нечетность, периодичность тригонометрических функций
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
НОВЫЙ МАТЕРИАЛ
Функция
Область определения D(y)
y=sin x
Множество значений E(y)
y=cos x
y=tg x
y=ctg x
R
R
R
R
ДОМАШНЕЕ ЗАДАНИЕ
№ 1 (4,6), № 2 (4,6),
№ 3 (1,2), № 5 (2)
стр.6
РЕШЕНИЕ УПРАЖНЕНИЙ
1. Найдите область определения функции:
РЕШЕНИЕ УПРАЖНЕНИЙ
2. Найти множество значений функции:
РЕШЕНИЕ УПРАЖНЕНИЙ
3. Найдите область определения функции:
Решение
0
0
•
-1
РЕШЕНИЕ УПРАЖНЕНИЙ
3. Найдите область определения функции:
Найдите область определения функции:
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
11 класс
ДОМАШНЕЕ ЗАДАНИЕ
П.1.3
№ 18, 32(а.б.в)
Функции
Чётные
Ни чётные,
ни нечётные
Нечётные
СИММЕТРИЯ ОТНОСИТЕЛЬНО ОСИ ОУ И НАЧАЛА КООРДИНАТ
ЧЕТНЫЕ ФУНКЦИИ
- Функция y = f(x) называется четной, если для любого х из области определения функции верно равенство f(-x) = f(x).
- Чтобы узнать является ли функция четной нужно в функцию f(x) вместо переменной х поставить переменную( –x ).
ЧЕТНЫЕ ФУНКЦИИ
- Например: является ли четной функция f(x) = 3x 2 + 2
- f (-x) = 3(-x) 2 + 2 = 3x 2 + 2 = f(x) – функция четная
ЧЕТНЫЕ ФУНКЦИИ
- Проверим являются ли данные функции четными
- f( — x) = 2(-x) 4 – 3(-x) 2 = 2x 4 — 3x 2 — четная
- f ( — x) = (- x ) 3 – 2 (- x ) 2 = – x 3 – 2x 2 Не является четной
- f(x) = 2x 4 — 3x 2
- f (x) = x 3 — 2x 2
ГРАФИК ЧЕТНОЙ ФУНКЦИИ
- График четной функции симметричен относительно оси ординат (ось ОУ).

НЕЧЕТНЫЕ ФУНКЦИИ
- Функция y = f(x) называется нечетной, если для любого х из области определения функции верно равенство
f(-x) = — f(x).
- чтобы узнать является ли функция нечетной нужно в функцию f(x) вместо переменной х поставить переменную ( – x ) и получить первоначальную функцию с противоположными знаками .
НЕЧЕТНЫЕ ФУНКЦИИ
- Например: является ли нечетной функция f(x) = 3x 3 + х
- f (-x) = 3(-x) 3 + (-х) = — 3x 3 — х = -( 3x 3 + х)=
= — f(x) – функция нечетная
НЕЧЕТНЫЕ ФУНКЦИИ
- Проверим являются ли данные функции нечетными
- f ( — x) = 2(-x) 4 + 3(-x) = = 2x 4 — 3x — не является нечетной
- f ( — x) = (- x ) 3 – 2 (- x ) = – x 3 + 2x нечетная
- f(x) = 2x 4 + 3x
- f (x) = x 3 — 2x
ГРАФИК НЕЧЕТНОЙ ФУНКЦИИ
- График нечетной функции симметричен относительно начала координат.

ЧЕТНЫЕ И НЕЧЕТНЫЕ ФУНКЦИИ
- Функции могут быть как четными, нечетными , так и ни четными, ни нечетными.
Пример: y (x) = x 2 + 2x
y(-x) = (-x) 2 + 2(-x) = x 2 — 2x
Для любого значения x верны равенства :
- Sin(-x) = -Sin x Cos(-x) = Cos x
- Sin(-x) = -Sin x Cos(-x) = Cos x
- Sin(-x) = -Sin x
- Cos(-x) = Cos x
Следовательно :
y= Sin x – нечетная функция
y= Cos x – четная функция
Так как для любого значения x из области определения функции
y = tg x верно равенство
tg(-x) = -tg x ,
то y = tg x – нечетная функция.
ПРИМЕР
Выяснить, является ли функция
y = 2 + Sin 2 x четной или нечетной.
Решение :
y(-x) = 2 + Sin 2 (-x) = 2 + (-Sin x) 2 =
=2 + Sin 2 x = y(x)
y = 2 + Sin 2 x – четная функция .
Пример: определите, является ли данная функция четной или нечетной
Решение:
Определите, являются ли данные функции четными или нечетными:
Разбейте функции на три группы:
- четные
- нечетные
- не являются ни четными, ни нечетными
Проверяем ответы
четные
нечетные
1
ни чет., ни нечет.
2
4
5
3
9
10
7
6
15
8
11
14
12
13
Подведение итогов урока
- y=sinx – нечетная функция,
т.к. sin(-x)=-sinx
График функции симметричен относительно начала координат
2.
т.к. cos(-x)=cosx
График функции симметричен относительно оси Оу
ЧЕТНОСТЬ, НЕЧЕТНОСТЬ, ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
11 класс
Для любого значения x верны равенства :
- Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
- Sin (x + 2 π ) = Sin x Cos (x + 2 π ) = Cos х
- Sin (x + 2 π ) = Sin x
- Cos (x + 2 π ) = Cos х
Следовательно, значения Sin и Cos периодически повторяются при изменении аргумента на 2 π .
Такие функции называются периодическими с периодом 2 π .
Функция f(x) называется периодической , если существует такое число T ≠ 0 , что для любого x из области определения этой функции выполняется равенство
f(x – T) = f(x) = f(x + T).
Число T называется периодом функции f(x).
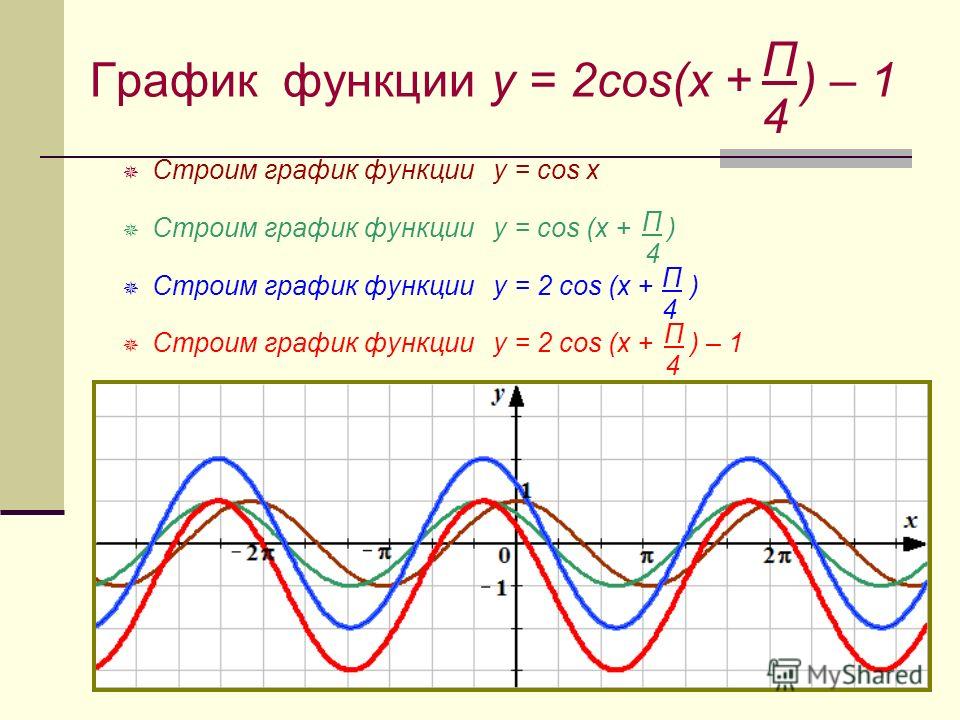
Функция y = cos x
y
y=cos x
1
-3 π /2
— π /2
π /2
π
3 π /2
0
— π
x
-1
Графиком функции у = cos x является косинусоида
- D(y) =R
- Периодическая Т=2
- Четная cos(-x)=cos x
- Нули функции:
у=0, cos x=0 при х = 1/2 n, n Z
sin(x+ /2)=cos x
32
32
ПОКАЖЕМ, ЧТО ЧИСЛО 2 Π ЯВЛЯЕТСЯ НАИМЕНЬШИМ ПОЛОЖИТЕЛЬНЫМ ПЕРИОДОМ ФУНКЦИИ Y = COS X.
Пусть Т › 0 – период косинуса, т.е. для любого x выполняется равенство
Cos (x + T) = Cos x. Положив x = 0 , получим Cos T = 1.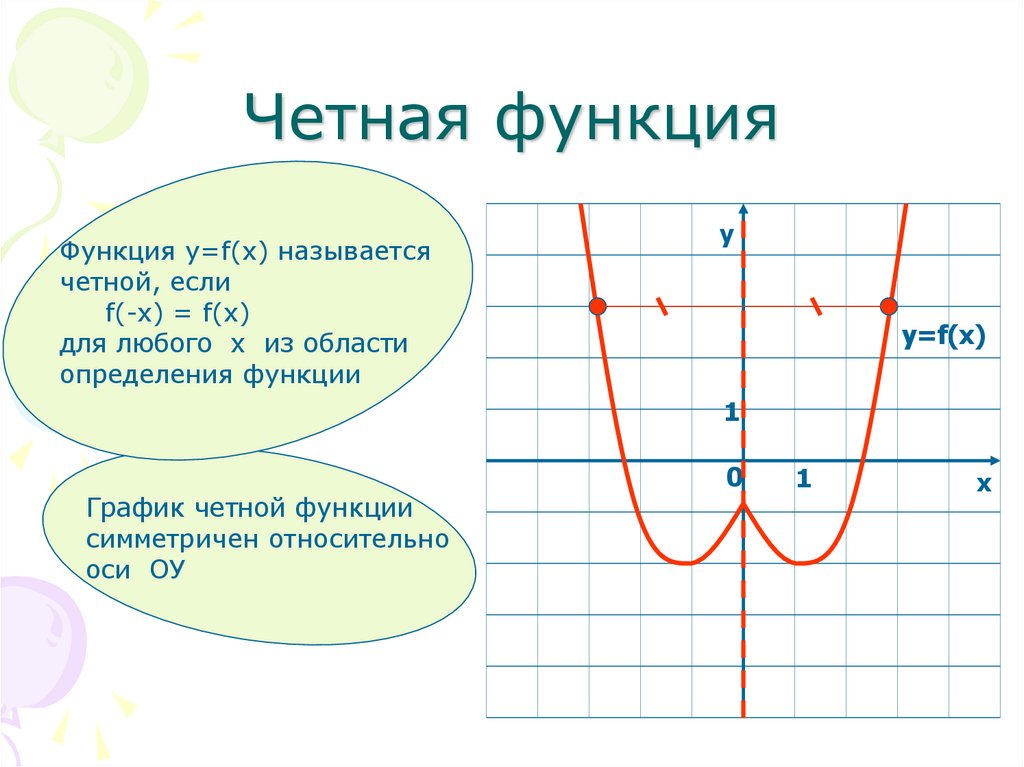 Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
Отсюда T = 2 π k, k є Ζ . Так как Т › 0, то Т может принимать значения 2 π , 4 π , 6 π , …, и поэтому период не может быть меньше 2 π .
Функция y=sin x и ее свойства
y
y=sin x
1
0
-3 π /2
3 π /2
π /2
— 2 π
2 π
— π /2
— π
π
x
-1
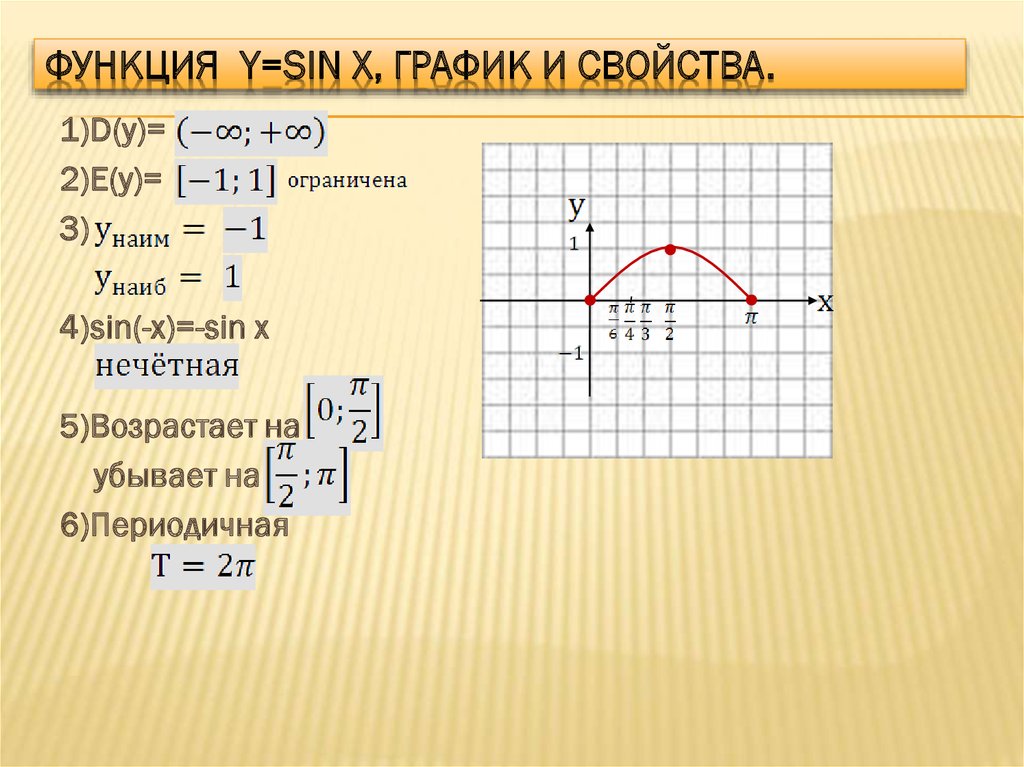
Графиком функции y=sin x является синусоида
Свойства функции:
- D(y) =R
- Периодическая (Т=2 )
- Нечетная ( sin(-x)=-sin x)
- Нули функции:
у=0, sin x=0 при х = n, n Z
34
АНАЛОГИЧНО МОЖНО ДОКАЗАТЬ, ЧТО НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = SIN X ТАКЖЕ РАВЕН 2 Π
Пример :
Доказать, что f(x) = Sin 3x – периодическая функция с периодом ( 2 π ) /3.
Доказательство :
Данная функция определена для всех x є R , поэтому достаточно показать, что для любого x верно равенство f(x + T) = f(x) .
f(x + (2 π )/3) = Sin 3(x + (2 π )/3) =
= Sin (3x + 2 π ) = Sin 3x = f(x)
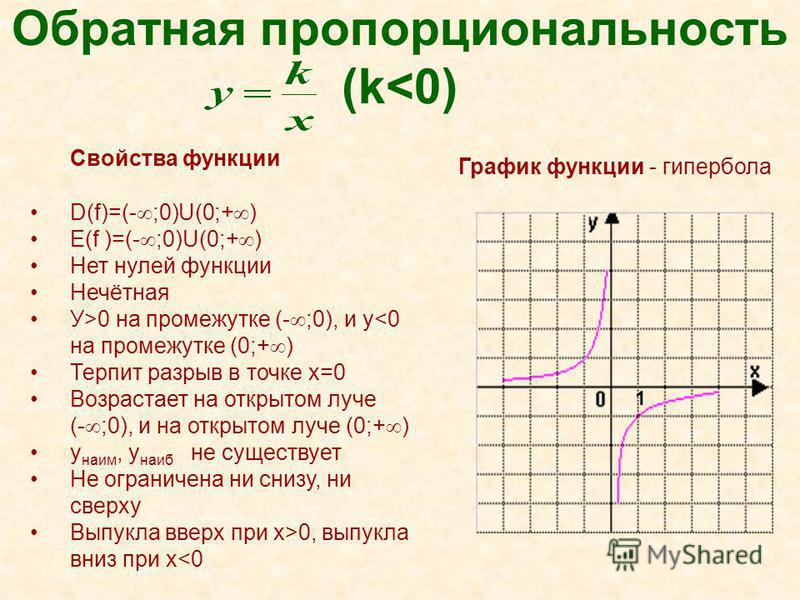
Построение графика функции у= tg x на всей бласти определения:
Функция у= tg x периодическая с периодом П, следовательно график этой функции получается на интервале от (-П/2;П/2) сдвигами вдоль оси абсцисс на П k, где
Построить график функции y = — tg (x + /2) .
у
y = ctg x
х
Т.к. — tg (x + /2) = ctg x , то построен график функции
y = ctg x .
ПОКАЖЕМ, ЧТО ФУНКЦИЯ Y= TG X ЯВЛЯЕТСЯ ПЕРИОДИЧЕСКОЙ С ПЕРИОДОМ Π .
Если x принадлежит области определения этой функции, т.е. x ≠ — π /2 + π n, n є Ζ , то по формулам приведения получаем
tg(x – π ) = -tg( π – x) = -(-tg x) = tg x
tg(x + π ) = tg x
Таким обтазом, tg(x – π ) = tg x = tg(x + π ). Следовательно, π – период функции у = tg x.
ПОКАЖЕМ, ЧТО Π – НАИМЕНЬШИЙ ПОЛОЖИТЕЛЬНЫЙ ПЕРИОД ФУНКЦИИ Y = TG X.
Пусть Т – период тангенса, тогда tg(x + T) = tg x, откуда при x = 0 получаем tg T = 0, T = k π , k є Ζ . Так как наименьшее целое положительное k равно 1, то π – наименьший положительный период функции y = tg x.
ДОКАЗАТЬ, ЧТО У = TG (X/3) – ПЕРИОДИЧЕСКАЯ ФУНКЦИЯ С ПЕРИОДОМ 3 Π .
Доказательство :
Так как tg ((x + 3 π )/3) = tg (x/3 + π ) = tg (x/3)
и
tg((x — 3 π )/3) = tg(x/3 – π ) = tg (x/3), то tg(x/3) – периодическая функция с периодом 3 π .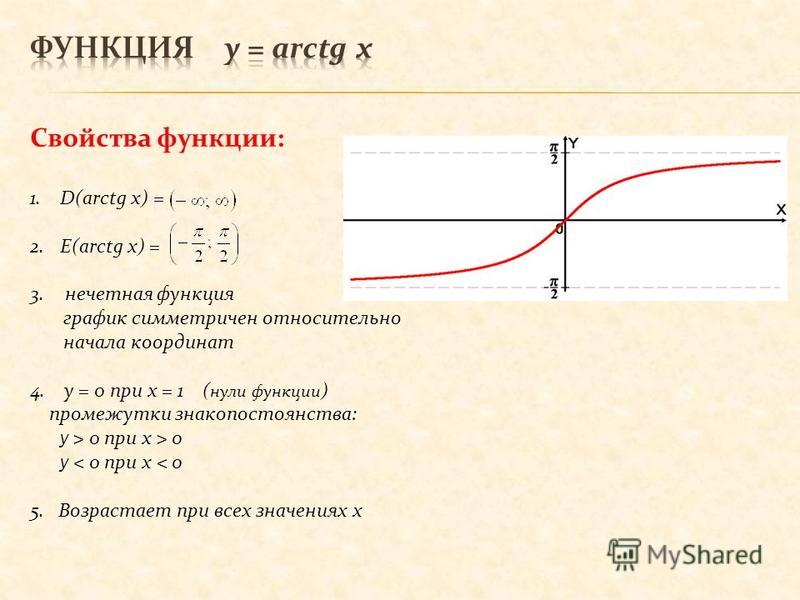
Чётность и нечётность, периодичность тригонометрических функций с изменениями
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
1. Четность, нечетность, периодичность тригонометрических функций
11 класс2. Новый материал
ФункцияОбласть
определения D(y)
Множество
значений E(y)
y=sin x
R
1 у 1
y=cos x
R
1 у 1
y=tg x
y=ctg x
х n , n Z
2
х n , n Z
R
R
3.
 Решение упражнений1. Найдите область определения функции:
Решение упражнений1. Найдите область определения функции:1
а ) у cos
х
б ) у sin x
D у ;0 0 ;
D у 0 ;
4. Решение упражнений
3. Найдите область определения функции:а ) у sin x 1
б ) у lg sin x
б ) sin x 0 ;
Решение
а ) sin x 1 0 ;
sin x 1 ;
0
0
2 πn х π 2 πn , n Z
Ответ : D у 2πn ; π 2πn , n Z
-1
D y R ;
Ответ : D y R .
5. Решение упражнений
3. Найдите область определения функции:в ) у 1 2 sin x
Решение : 1 2 sin x 0 ;
7π
6
1
sin x ;
2
7π
π
2 πn y 2 πn , n Z
6
6
π
7π
Ответ : D у
2 πn ; 2 πn , n Z
6
6
1
2
π
6
6. Четность и нечетность тригонометрических функций
11 класс7. Симметрия относительно оси Оу и начала координат
8. Четные функции
Функция y = f(x) называется четной, если длялюбого х из области определения функции
верно равенство f(-x) = f(x).
Чтобы узнать является ли функция четной нужно в
функцию f(x) вместо переменной х поставить
переменную(–x).

9. Четные функции
Например: является ли четной функцияf(x) = 3×2 + 2
f(-x) = 3(-x)2 + 2 = 3×2 + 2 = f(x) – функция
четная
10. Четные функции
Проверим являются ли данные функциичетными
f(-x) = 2(-x)4 – 3(-x)2 = 2×4 — 3×2 f(x) = 2×4 — 3×2
четная
f(x) = x3 — 2×2
f(-x) = (-x)3 – 2(-x)2 = – x3 – 2×2
Не является четной
11. График четной функции
График четной функции симметриченотносительно оси ординат (ось ОУ).
12. Нечетные функции
Функция y = f(x) называется нечетной, если длялюбого х из области определения функции верно
равенство
f(-x) = — f(x).
чтобы узнать является ли функция нечетной нужно
в функцию f(x) вместо переменной х поставить
переменную (–x) и получить первоначальную
функцию с противоположными знаками.
13. Нечетные функции
Например: является ли нечетной функцияf(x) = 3×3 + х
f(-x) = 3(-x)3 + (-х) = -3×3 — х = -(3×3 + х)=
= — f(x) – функция нечетная
14.
 Нечетные функцииПроверим являются ли данные
Нечетные функцииПроверим являются ли данныефункции нечетными
f(x) = 2×4 + 3x
f(x) = x3 — 2x
f(-x) = 2(-x)4 + 3(-x) = =2×4
— 3x — не является
нечетной
f(-x) = (-x)3 – 2(-x) = – x3
+ 2x нечетная
15. График нечетной функции
График нечетной функции симметриченотносительно начала координат.
16. Четные и нечетные функции
Функции могут быть как четными,нечетными, так и ни четными, ни нечетными.
Пример: y(x) = x2 + 2x
y(-x) = (-x)2 + 2(-x) = x2 — 2x
Для любого значения x верны равенства:
Sin(-x) = -Sin x
Cos(-x) = Cos x
Следовательно:
y= Sin x – нечетная функция
y= Cos x – четная функция
т.к. sin(-x)=-sinx
1. y=sinx – нечетная функция,
График функции симметричен относительно
начала координат
2. y=cosx – нечетная функция,
т.к. cos(-x)=cosx
График функции симметричен
относительно оси Оу
Так как для любого значения x из
области определения функции
y = tg x верно равенство
tg(-x) = -tg x,
то y = tg x – нечетная функция.

20. Пример
Выяснить, является ли функцияy = 2 + Sin2 x четной или нечетной.
Решение:
y(-x) = 2 + Sin2(-x) = 2 + (-Sin x)2 =
=2 + Sin2x = y(x)
y = 2 + Sin2x – четная функция.
Пример: определите, является ли данная
функция четной или нечетной
Решение:
Работа в тетрадях
Определите, являются ли данные функции
четными или нечетными:
Разбейте функции на три группы:
—
четные
нечетные
не являются ни четными, ни нечетными
Проверяем ответы
четные
нечетные
ни чет., ни
нечет.
1
4
2
3
5
7
9
10
11
6
8
14
15
12
13
Функция f(x) называется периодической,
если существует такое число T ≠ 0, что для
любого x из области определения этой
функции выполняется равенство
f(x – T) = f(x) = f(x + T).
Число T называется периодом функции f(x).
Для любого значения x верны равенства:
Sin (x + 2π) = Sin x
Cos (x + 2π) = Cos х
Следовательно, значения Sin и Cos периодически
повторяются при изменении аргумента на 2π.
Такие функции называются периодическими с
периодом 2π.
28. Покажем, что число 2π является наименьшим положительным периодом функции y = Cos x.
Пусть Т › 0 – период косинуса, т.е. для любого xвыполняется равенство
Cos (x + T) = Cos x. Положив x = 0, получим Cos T
= 1. Отсюда T = 2πk, k є Ζ. Так как Т › 0, то Т
может принимать значения 2π, 4π, 6π, …, и
поэтому период не может быть меньше 2π.
29. Аналогично можно доказать, что наименьший положительный период функции y = Sin x также равен 2π
Пример:Доказать, что f(x) = Sin 3x – периодическая
функция с периодом (2π)/3.
Доказательство:
Данная функция определена для всех x є R,
поэтому достаточно показать, что для любого x
верно равенство f(x + T) = f(x).
f(x + (2π)/3) = Sin 3(x + (2π)/3) =
= Sin (3x + 2π) = Sin 3x = f(x)
30. Покажем, что функция y= tg x является периодической с периодом π.
Если x принадлежит области определения этойфункции, т.
 е. x ≠ -π/2 + πn, n є Ζ, то по формулам
е. x ≠ -π/2 + πn, n є Ζ, то по формуламприведения получаем
tg(x – π) = -tg(π – x) = -(-tg x) = tg x
tg(x + π) = tg x
Таким обтазом, tg(x – π) = tg x = tg(x + π).
Следовательно, π – период функции у = tg x.
31. Покажем, что π – наименьший положительный период функции y = tg x.
Пусть Т – период тангенса, тогда tg(x + T) = tg x,откуда при x = 0 получаем tg T = 0, T = kπ, k є Ζ.
Так как наименьшее целое положительное k
равно 1, то π – наименьший положительный
период функции y = tg x.
32. Доказать, что у = tg (x/3) – периодическая функция с периодом 3π.
Доказательство:Так как tg((x + 3π)/3) = tg (x/3 + π) = tg (x/3)
и
tg((x — 3π)/3) = tg(x/3 – π) = tg (x/3), то tg(x/3)–
периодическая функция с периодом 3π.
English Русский Правила
Какая функция ни четная ни нечетная функция. Как определять четные и нечетные функции
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией.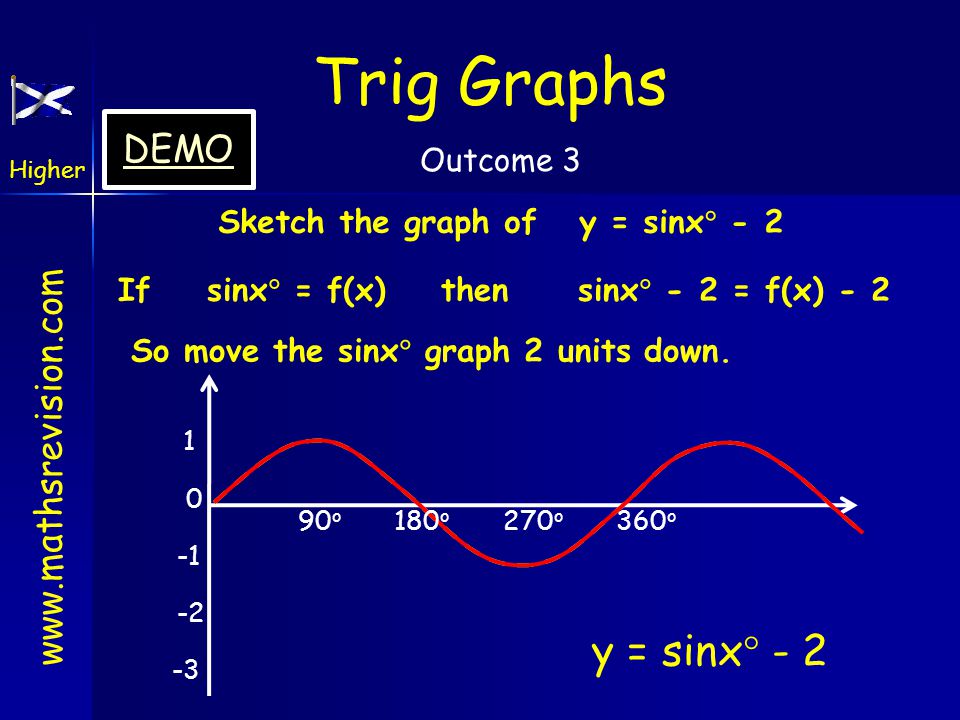 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Исследование функции.
1) D(y) – Область опрделения: множество всех тех значений переменной х. при которых алгебраические выражения f(x) и g(x) имеют смысл.
Если функция задана формулой, то область определения состоит из всех значений независимой переменной, при которых формула имеет смысл.
2) Свойства функции: четность/нечетность, периодичность:
Нечётными и чётными называются функции, графики которых обладают симметрией относительно изменения знака аргумента.
Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (симметричная относительно центра координат).
Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (симметричная относительно оси ординат).
Ни
чётная ни нечётная функция (функция
общего вида) —
функция, не обладающая симметрией.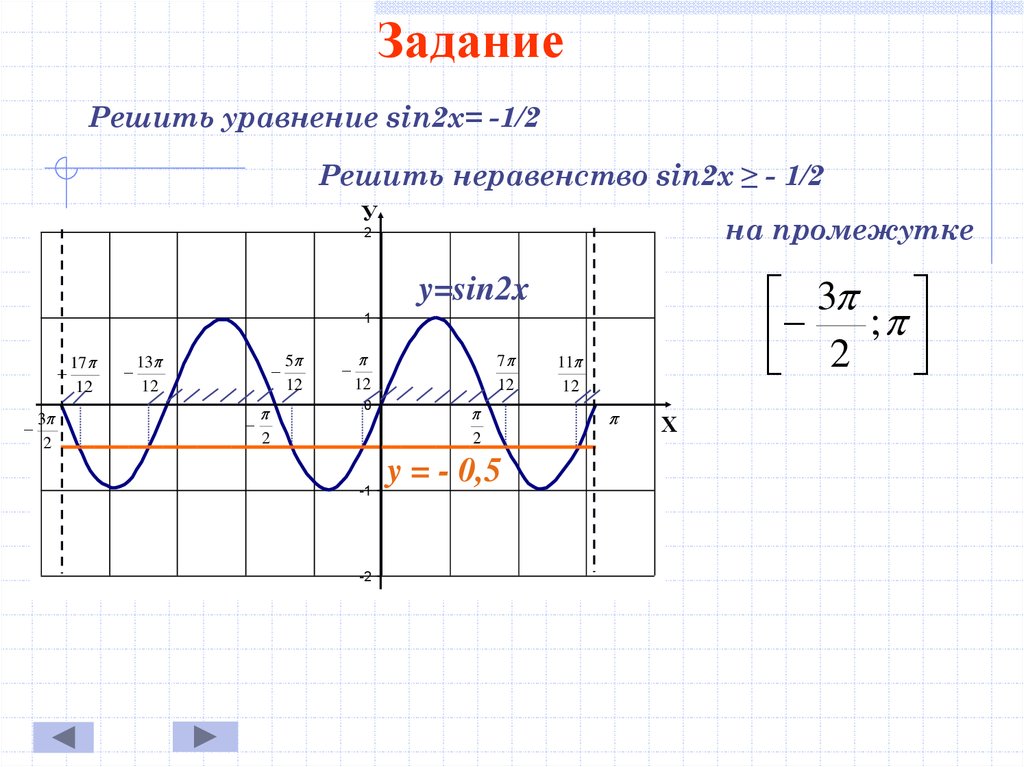 В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
В
эту категорию относят функции, не
подпадающие под предыдущие 2 категории.
Функции, не принадлежащие ни одной из категорий выше, называются ни чётными ни нечётными (или функциями общего вида).
Нечётные функции
Нечётная степень где — произвольное целое число.
Чётные функции
Чётная степень где — произвольное целое число.
Периоди́ческая фу́нкция ― функция, повторяющая свои значения через некоторый регулярный интервал аргумента, то есть не меняющая своего значения при добавлении к аргументу некоторого фиксированного ненулевого числа (пери́ода функции) на всей области определения.
3) Нули (корни) функции — точки, где она обращается в ноль.
Нахождение
точки пересечения графика с осью Oy . Для
этого нужно вычислить значение f (0).
Найти также точки пересечения графика
с осью Ox ,
для чего найти корни уравнения f (x )
= 0 (или
убедиться в отсутствии корней).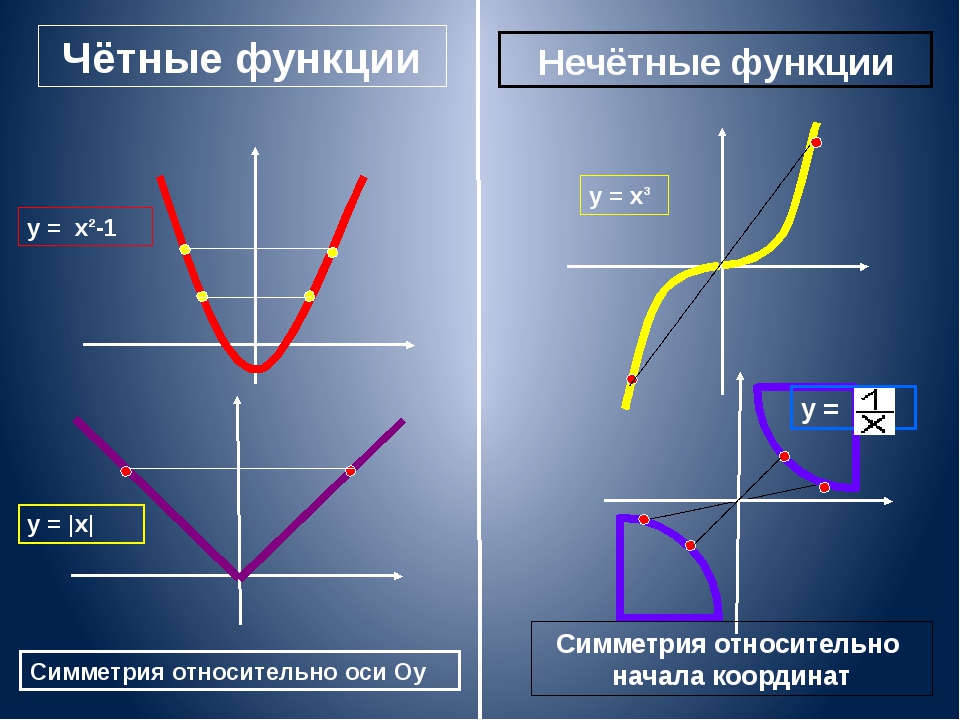
Точки, в которых график пересекает ось , называют нулями функции . Чтобы найти нули функции нужно решить уравнение , то есть найти те значения «икс» , при которых функция обращается в ноль.
4) Промежутки постоянства знаков, знаки в них.
Промежутки, где функция f(x) сохраняет знак.
Интервал знакопостоянства – это интервал, в каждой точке которого функция положительна либо отрицательна.
ВЫШЕ оси абсцисс.
НИЖЕ оси .
5) Непрерывность (точки разрыва, характер разрыва, ассимптоты).
Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
Устранимые точки разрыва
Если предел функции существует , но функция не определена в этой точке, либо предел не совпадает со значением функции в данной точке:
,
то
точка называется точкой
устранимого разрыва функции (в комплексном
анализе -устранимая
особая точка).
Если «поправить» функцию в точке устранимого разрыва и положить , то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности , что и обосновывает название точки, как точки устранимого разрыва.
Точки разрыва первого и второго рода
Если функция имеет разрыв в данной точке (то есть предел функции в данной точке отсутствует или не совпадает со значением функции в данной точке), то для числовых функций возникает два возможных варианта, связанных с существованием у числовых функций односторонних пределов :
если оба односторонних предела существуют и конечны, то такую точку называют точкой разрыва первого рода . Точки устранимого разрыва являются точками разрыва первого рода;
если
хотя бы один из односторонних пределов
не существует или не является конечной
величиной, то такую точку называют точкой
разрыва второго рода .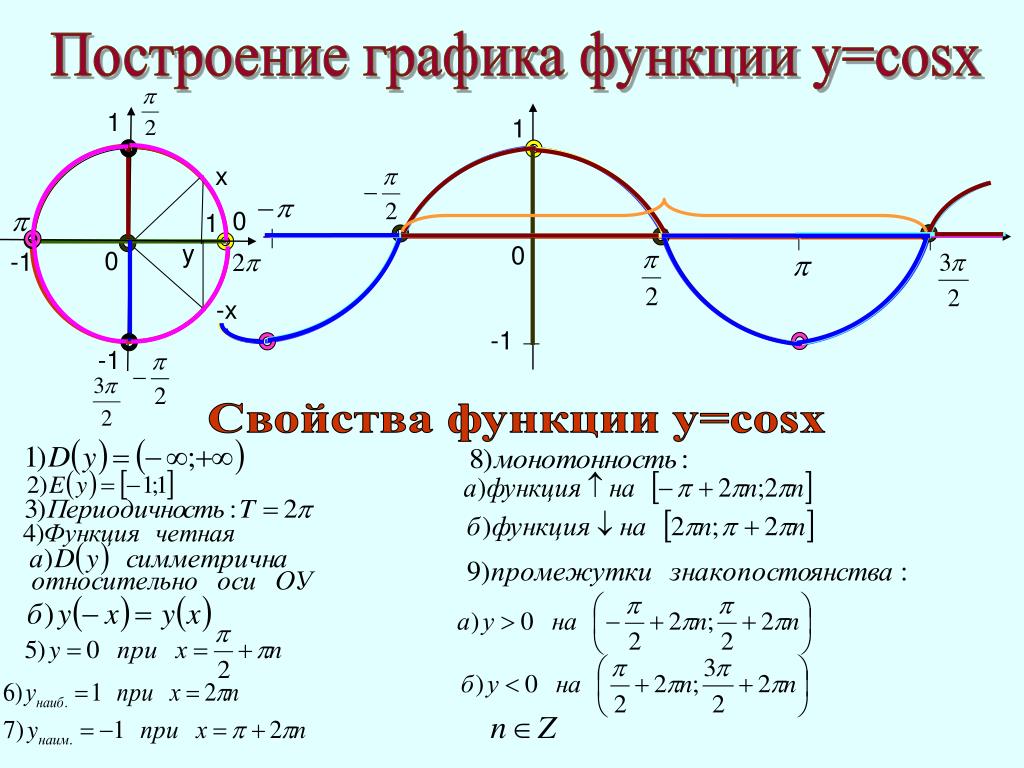
Аси́мпто́та — прямая , обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви вбесконечность.
Вертикальная
Вертикальная асимптота — прямая предела .
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная
Горизонтальная асимптота — прямая вида при условии существования предела
.
Наклонная
Наклонная асимптота — прямая вида при условии существования пределов
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует.
если в
п. 2.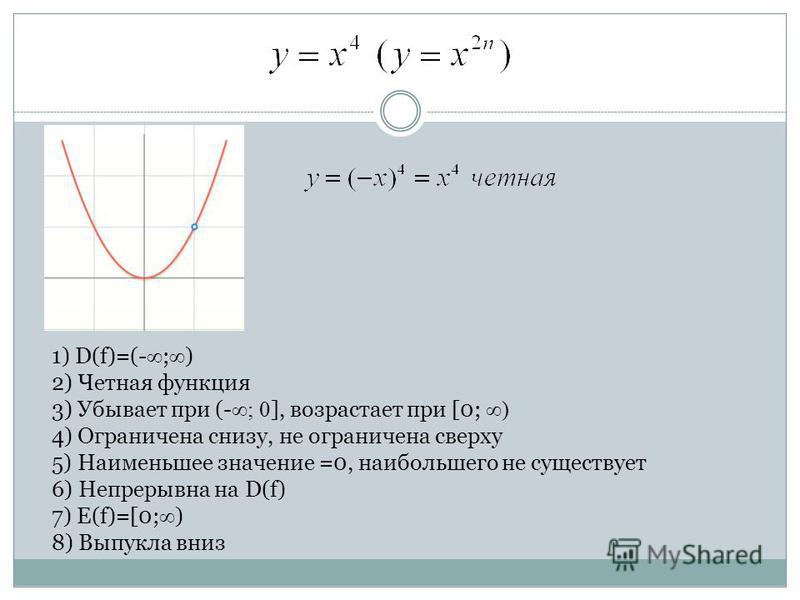 ), то ,
и предел находится
по формуле горизонтальной асимптоты, .
), то ,
и предел находится
по формуле горизонтальной асимптоты, .
6) Нахождение промежутков монотонности. Найти интервалы монотонности функции f (x )(то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f (x ). Для этого находят производную f (x ) и решают неравенство f (x )0. На промежутках, где это неравенство выполнено, функция f (x )возрастает. Там, где выполнено обратное неравенство f (x )0, функция f (x )убывает.
Нахождение
локального экстремума. Найдя
интервалы монотонности, мы можем сразу
определить точки локального экстремума
там, где возрастание сменяется убыванием,
располагаются локальные максимумы, а
там, где убывание сменяется возрастанием
— локальные минимумы. Вычислить значение
функции в этих точках. Если функция
имеет критические точки, не являющиеся
точками локального экстремума, то
полезно вычислить значение функции и
в этих точках. {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
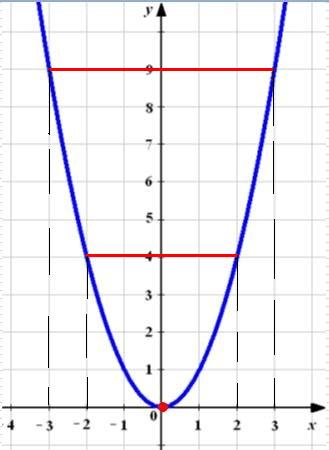
Для этого воспользуйтесь миллиметровкой или графическим калькулятором. Выберите несколько любых числовых значений независимой переменной x {\displaystyle x}
и подставьте их в функцию, чтобы вычислить значения зависимой переменной y {\displaystyle y}
. Найденные координаты точек нанесите на координатную плоскость, а затем соедините эти точки, чтобы построить график функции. {2}+1}
мы получили следующие координаты точек:
{2}+1}
мы получили следующие координаты точек:
- (1,3) и (-1,3)
- (2,9) и (-2,9)
Проверьте, симметричен ли график функции относительно начала координат. Начало координат – это точка с координатами (0,0). Симметрия относительно начала координат означает, что положительному значению y {\displaystyle y} (при положительном значении x {\displaystyle x} ) соответствует отрицательное значение y {\displaystyle y} (при отрицательном значении x {\displaystyle x} ), и наоборот. Нечетные функции обладают симметрией относительно начала координат.
- Если в функцию подставить несколько положительных и соответствующих отрицательных значений x {\displaystyle x}
, значения y {\displaystyle y}
будут различаться по знаку.
 {2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
{2}}
. Будучи записанной в такой форме, функция кажется четной, потому что присутствует четный показатель степени. Но этот пример доказывает, что вид функции нельзя быстро определить, если независимая переменная заключена в скобки. В этом случае нужно раскрыть скобки и проанализировать полученные показатели степени.
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.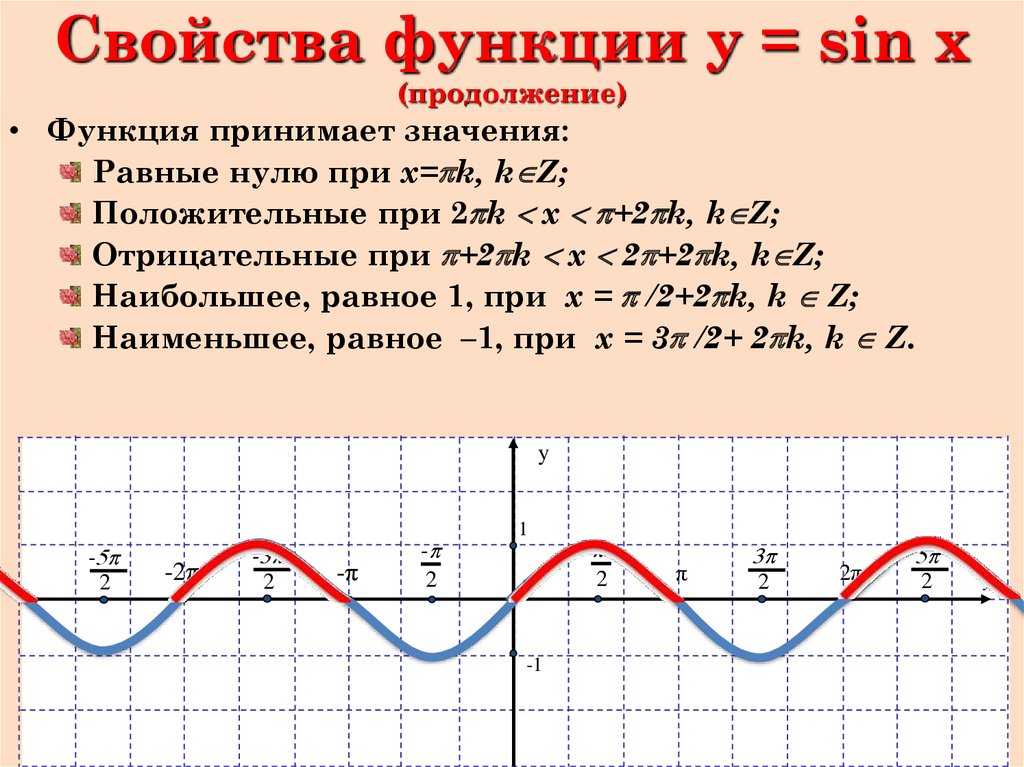 е. функция является четной.
е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции. И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
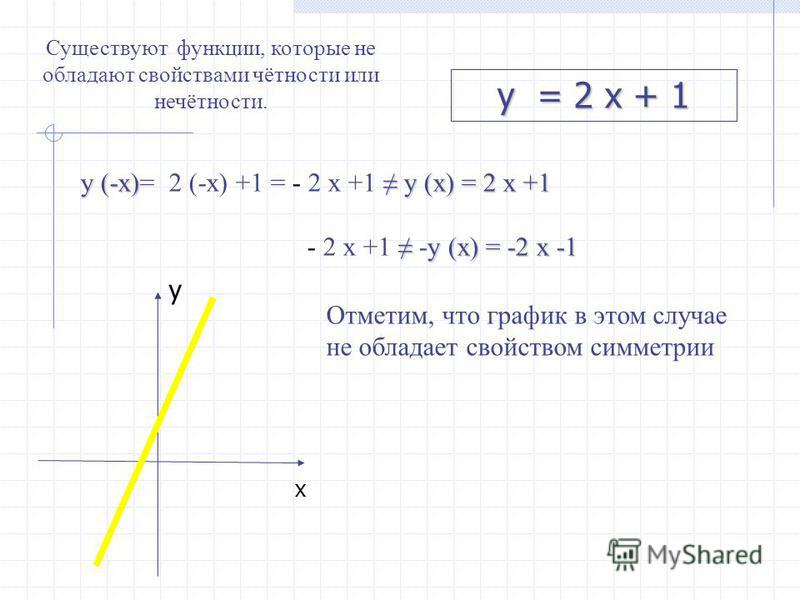
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством. Скажем, (-2, 2), [-5, 5], (-оо, +оо) — симметричные множества, в то время как }
Как выяснить четная или нечетная функция. Четность и нечетность функций. Алгоритм исследования функции на чётность
Зависимость переменной y от переменно x, при которой каждому значению х соответствует единственное значение y называется функцией. 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Функция
называется четной (нечетной), если для
любогои выполняется равенство
.
График четной
функции симметричен относительно оси
.
График нечетной функции симметричен относительно начала координат.
Пример 6.2. Исследовать на четность или нечетность функции
1)
;
2)
;
3)
.
Решение .
1) Функция определена
при
.
Найдем
.
Т.е.
.
Значит, данная функция является четной.
2) Функция определена
при
Т.е.
.
Таким образом, данная функция нечетная.
3) функция определена для , т.е. для
,
.
Поэтому функция не является ни четной,
ни нечетной. Назовем ее функцией общего
вида.
3. Исследование функции на монотонность.
Функция
называется возрастающей (убывающей) на
некотором интервале, если в этом интервале
каждому большему значению аргумента
соответствует большее (меньшее) значение
функции.
Функции возрастающие
(убывающие) на некотором интервале
называются монотонными.
Если функция
дифференцируема на интервале
и имеет положительную (отрицательную)
производную
,
то функция
возрастает (убывает) на этом интервале.
Пример 6.3 . Найти интервалы монотонности функций
1)
;
3)
.
Решение .
1) Данная функция определена на всей числовой оси. Найдем производную .
Производная равна
нулю, если
и
.
Область определения – числовая ось,
разбивается точками
,
на интервалы. Определим знак производной
в каждом интервале.
В интервале
производная отрицательна, функция на
этом интервале убывает.
В интервале
производная положительна, следовательно,
функция на этом интервале возрастает.
2) Данная функция
определена, если
или
.
Определяем знак квадратного трехчлена в каждом интервале.
Таким образом, область определения функции
Найдем производную
,
,
если
,
т.е.
,
но
.
Определим знак производной в интервалах
.
В интервале
производная отрицательна, следовательно,
функция убывает на интервале
.
В интервале
производная положительна, функция
возрастает на интервале
.
4. Исследование функции на экстремум.
Точка
называется точкой максимума (минимума)
функции
,
если существует такая окрестность точки,
что для всех
из этой окрестности выполняется
неравенство
.
Точки максимума и минимума функции называются точками экстремума.
Если функция
в точкеимеет экстремум, то производная функции
в этой точке равна нулю или не существует
(необходимое условие существования
экстремума).
Точки, в которых производная равна нулю или не существует называются критическими.
5. Достаточные условия существования экстремума.
Правило 1 .
Если при переходе (слева направо) через
критическую точку
производная
меняет знак с «+» на «–», то в точкефункция
имеет максимум; если с «–» на «+», то
минимум; если
не меняет знак, то экстремума нет.
Правило 2 .
Пусть в точке
первая производная функции
равна нулю
,
а вторая производная существует и
отлична от нуля. Если
,
то– точка максимума, если
,
то– точка минимума функции.
Пример 6.4 . Исследовать на максимум и минимум функции:
1)
;
2)
;
3)
;
4)
.
Решение.
1) Функция определена
и непрерывна на интервале
.
Найдем производную
и решим уравнение
,
т.е.
.Отсюда
– критические точки.
Определим знак
производной в интервалах
,
.
При переходе через
точки
и
производная меняет знак с «–» на «+»,
поэтому по правилу 1
– точки минимума.
При переходе через
точку
производная меняет знак с «+» на «–»,
поэтому
– точка максимума.
,
.
2) Функция определена
и непрерывна в интервале
.
Найдем производную
.
Решив уравнение
,
найдем
и
– критические точки. Если знаменатель
,
т. е.
е.
,
то производная не существует. Итак,
– третья критическая точка. Определим
знак производной в интервалах.
Следовательно,
функция имеет минимум в точке
,
максимум в точках
и
.
3) Функция определена
и непрерывна, если
,
т.е. при
.
Найдем производную
.
Найдем критические
точки:
Окрестности точек
не принадлежат области определения,
поэтому они не являются т. экстремума.
Итак, исследуем критические точки
и
.
4) Функция определена
и непрерывна на интервале
.
Используем правило 2. Найдем производную
.
Найдем критические точки:
Найдем вторую
производную
и определим ее знак в точках
В точках
функция имеет минимум.
В точках
функция имеет максимум.
В июле 2020 года NASA запускает экспедицию на Марс. Космический аппарат доставит на Марс электронный носитель с именами всех зарегистрированных участников экспедиции.
Регистрация участников открыта. Получите свой билет на Марс по этой ссылке .
Получите свой билет на Марс по этой ссылке .
Если этот пост решил вашу проблему или просто понравился вам, поделитесь ссылкой на него со своими друзьями в социальных сетях.
Один из этих вариантов кода нужно скопировать и вставить в код вашей веб-станицы, желательно между тегами
и или же сразу после тега . По первому варианту MathJax подгружается быстрее и меньше тормозит страницу. Зато второй вариант автоматически отслеживает и подгружает свежие версии MathJax. Если вставить первый код, то его нужно будет периодически обновлять. Если вставить второй код, то страницы будут загружаться медленнее, зато вам не нужно будет постоянно следить за обновлениями MathJax.
Подключить MathJax проще всего в Blogger или WordPress: в панели управления сайтом добавьте виджет, предназначенный для вставки стороннего кода JavaScript, скопируйте в него первый или второй вариант кода загрузки, представленного выше, и разместите виджет поближе к началу шаблона (кстати, это вовсе не обязательно, поскольку скрипт MathJax загружается асинхронно). Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Вот и все. Теперь изучите синтаксис разметки MathML, LaTeX и ASCIIMathML, и вы готовы вставлять математические формулы на веб-страницы своего сайта.
Очередной канун Нового Года… морозная погода и снежинки на оконном стекле… Все это побудило меня вновь написать о… фракталах, и о том, что знает об этом Вольфрам Альфа. По этому поводу есть интересная статья , в которой имеются примеры двумерных фрактальных структур. Здесь же мы рассмотрим более сложные примеры трехмерных фракталов.
Фрактал можно наглядно представить (описать), как геометрическую фигуру или тело (имея ввиду, что и то и другое есть множество, в данном случае, множество точек), детали которой имеют такую же форму, как и сама исходная фигура. То есть, это самоподобная структура, рассматривая детали которой при увеличении, мы будем видеть ту же самую форму, что и без увеличения. Тогда как в случае обычной геометрической фигуры (не фрактала), при увеличении мы увидим детали, которые имеют более простую форму, чем сама исходная фигура. {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.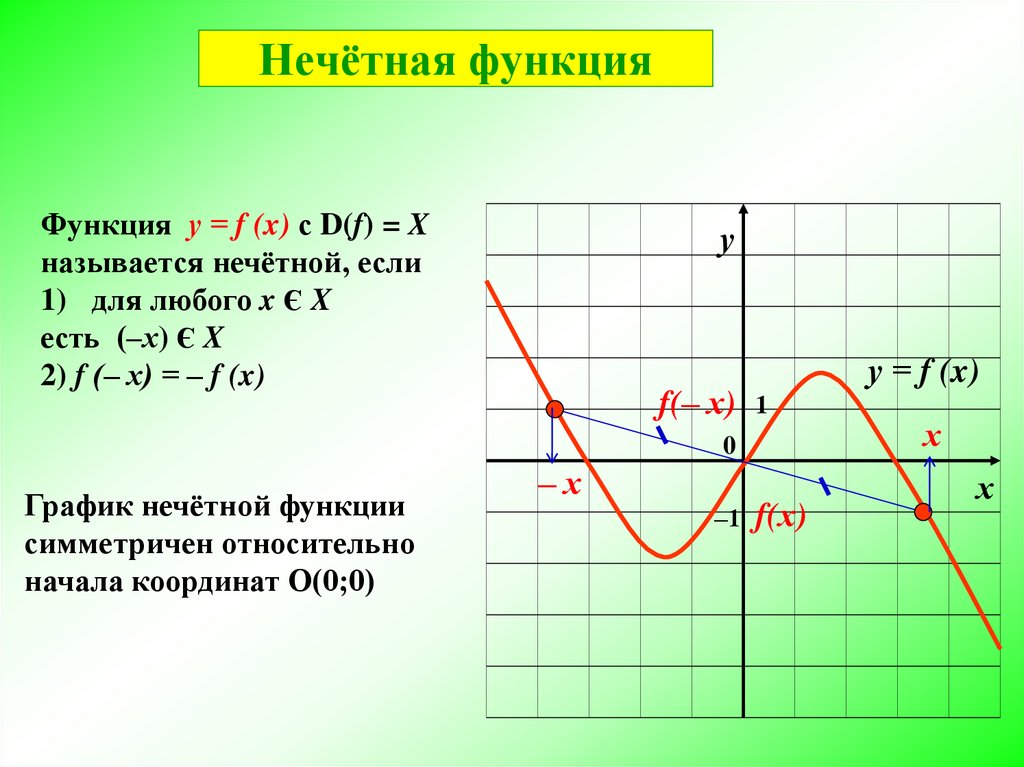
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
Которые в той или иной степени были вам знакомы. Там же было замечено, что запас свойств функций будет постепенно пополняться. О двух новых свойствах и пойдет речь в настоящем параграфе.
Определение 1.
Функцию у = f(x), х є Х, называют четной, если для любого значения х из множества X выполняется равенство f (-х) = f (х).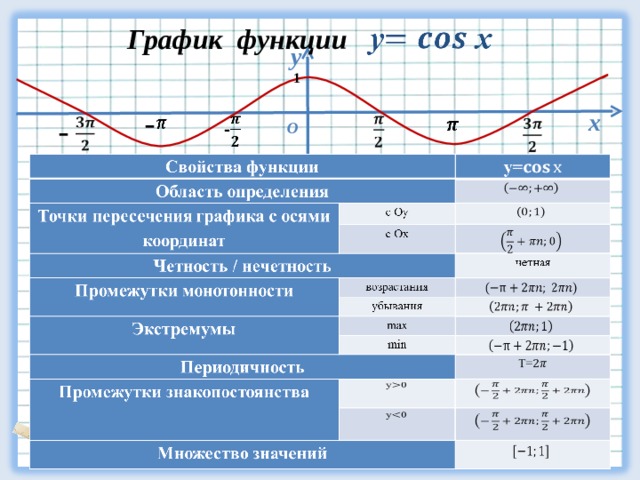
Определение 2.
Функцию у = f(x), х є X, называют нечетной, если для любого значения х из множества X выполняется равенство f (-х) = -f (х).
Доказать, что у = х 4 — четная функция.
Решение. Имеем: f(х) = х 4 , f(-х) = (-х) 4 . Но (-х) 4 = х 4 . Значит, для любого х выполняется равенство f(-х) = f(х), т.е. функция является четной.
Аналогично можно доказать, что функции у — х 2 ,у = х 6 ,у — х 8 являются четными.
Доказать, что у = х 3 ~ нечетная функция.
Решение. Имеем: f(х) = х 3 , f(-х) = (-х) 3 . Но (-х) 3 = -х 3 . Значит, для любого х выполняется равенство f (-х) = -f (х), т.е. функция является нечетной.
Аналогично можно доказать, что функции у = х, у = х 5 , у = х 7 являются нечетными.
Мы с вами не раз уже убеждались в том, что новые термины в математике чаще всего имеют «земное» происхождение, т.е. их можно каким-то образом объяснить. Так обстоит дело и с четными, и с нечетными функциями. Смотрите: у — х 3 , у = х 5 , у = х 7 — нечетные функции, тогда как у = х 2 , у = х 4 , у = х 6 — четные функции.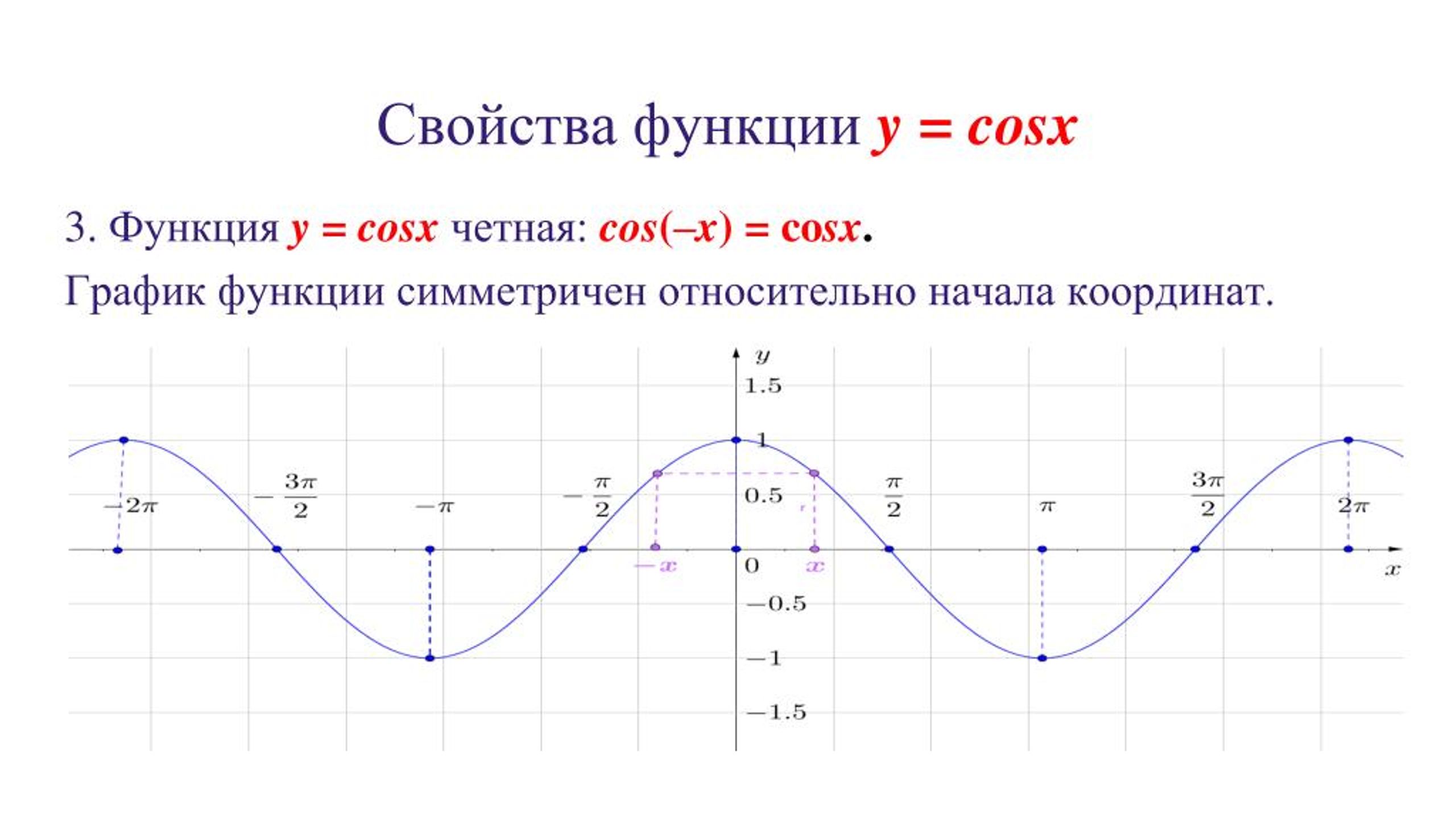 И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
И вообще для любой функции вида у = х» (ниже мы специально займемся изучением этих функций), где n — натуральное число , можно сделать вывод: если n — нечетное число, то функция у = х» — нечетная; если же n — четное число, то функция у = хn — четная.
Существуют и функции, не являющиеся ни четными, ни нечетными. Такова, например, функция у = 2х + 3. В самом деле, f(1) = 5, а f (-1) = 1. Как видите, здесь Значит, не может выполняться ни тождество f(-х) = f (х), ни тождество f(-х) = -f(х).
Итак, функция может быть четной, нечетной, а также ни той ни другой.
Изучение вопроса о том, является ли заданная функция четной или нечетной, обычно называют исследованием функции на четность.
В определениях 1 и 2 речь идет о значениях функции в точках х и -х. Тем самым предполагается, что функция определена и в точке х, и в точке -х. Это значит, что точка -х принадлежит области определения функции одновременно с точкой х. Если числовое множество X вместе с каждым своим элементом х содержит и противоположный элемент -х, то X называют симметричным множеством.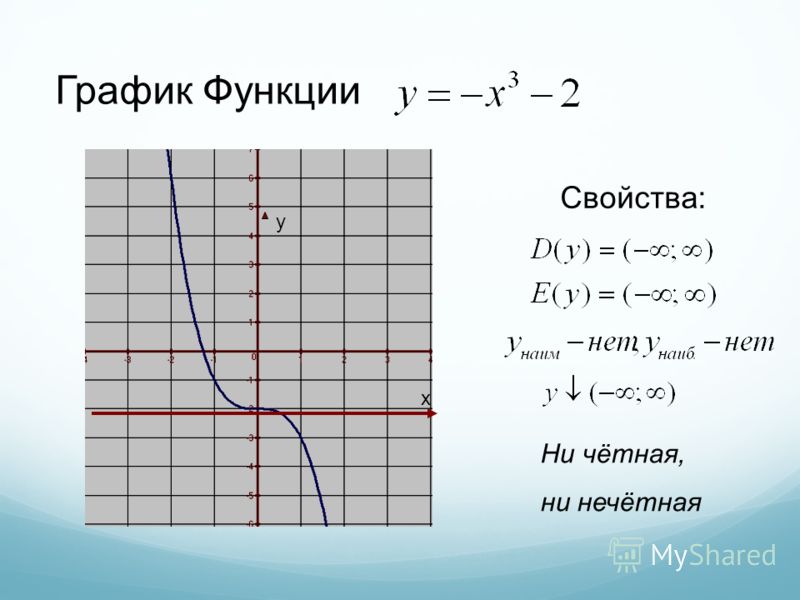 3 симметрична относительно начала координат.
3 симметрична относительно начала координат.
Графики четной и нечетной функции обладают следующими особенностями:
Если функция является четной, то ее график симметричен относительно оси ординат. Если функция является нечетной, то ее график симметричен относительно начала координат.
Пример. Построить график функции \(y=\left|x \right|\).
Решение. Рассмотрим функцию: \(f\left(x \right)=\left|x \right|\) и подставим вместо \(x \) противоположное \(-x \). В результате не сложных преобразований получим: $$f\left(-x \right)=\left|-x \right|=\left|x \right|=f\left(x \right)$$ Другими словами, если аргумент заменить на противоположный по знаку, функция не изменится.
Значит эта функция — четная, а ее график будет симметричен относительно оси ординат (вертикальной оси). График этой функции приведен на рисунке слева. Это означает что при построении графика, можно строить только половину, а вторую часть (левее вертикальной оси рисовать уже симметрично правой части). Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Определив симметричность функции перед началом построения ее графика, можно намного упростить процесс построения или исследования функции. Если сложно выполнять проверку в общем виде, можно поступить проще: подставить в уравнение одинаковые значения разных знаков. Например -5 и 5. Если значения функции получатся одинаковыми, то можно надеяться что функция будет четной. С математической точки зрения такой подход не совсем правильный, но с практической — удобный. Чтобы увеличить достоверность результата можно подставить несколько пар таких противоположных значений.
Пример. Построить график функции \(y=x\left|x \right|\).
Решение. Выполним проверку так же как в предыдущем примере: $$f\left(-x \right)=x\left|-x \right|=-x\left|x \right|=-f\left(x \right)$$ Это означает, что исходная функция является нечетной (знак функции поменялся на противоположный).
Вывод: функция симметрична относительно начала координат. Можно строить только одн половину, а вторую рисовать симметрично. 2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
2$$
В результате получим, что:
$$f\left(-x \right)\not=f\left(x \right),f\left(-x \right)\not=-f\left(x \right)$$
А это означает, что функция не является ни четной, ни нечетной.
Вывод: функция не симметрична ни относительно начала координат ни относительно центра системы координат. Это произошло потому, что она представляет собой сумму двух функций: четной и не четной. Такая же ситуация будет если вычитать две разные функции. А вот умножение или деление приведет к другому результату. Например, произведение четной и нечетной функций дает нечетную. Или частное двух нечетных приводит к четной функции.
Четность и нечетность функции являются одним из основных ее свойств, и на четность занимает внушительную часть школьного курса по математике. Она во много определяет характер поведения функции и значительно облегчает построение соответствующего графика.
Определим четность функции. Вообще говоря, исследуемую функцию считают четной, если для противоположных значений независимой переменной (x), находящихся в ее области определения, соответствующие значения y (функции) окажутся равными.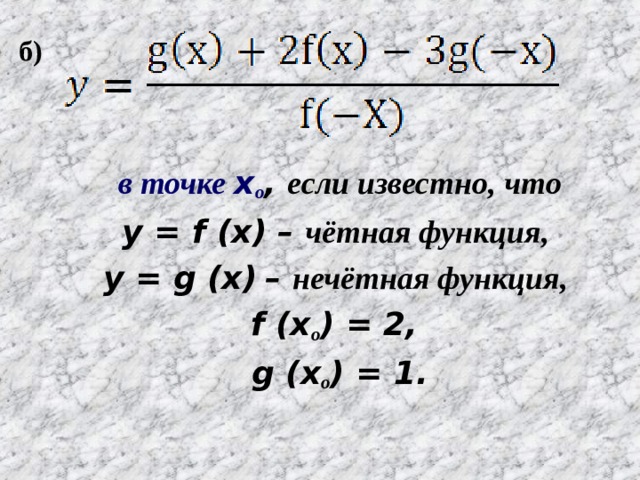 (-x))=- h(x). Следовательно, h(x) — нечетная.
(-x))=- h(x). Следовательно, h(x) — нечетная.
Кстати, следует напомнить, что есть функции, которые невозможно классифицировать по этим признакам, их называют ни четными, ни нечетными.
Четные функции обладают рядом интересных свойств:
- в результате сложения подобных функций получают четную;
- в результате вычитания таких функций получают четную;
- четной, также четная;
- в результате умножения двух таких функций получают четную;
- в результате умножения нечетной и четной функций получают нечетную;
- в результате деления нечетной и четной функций получают нечетную;
- производная такой функции — нечетная;
- если возвести нечетную функцию в квадрат, получим четную.
Четность функции можно использовать при решении уравнений.
Чтобы решить уравнение типа g(x) = 0, где левая часть уравнения представляет из себя четную функцию, будет вполне достаточно найти ее решения для неотрицательных значений переменной. Полученные корни уравнения необходимо объединить с противоположными числами.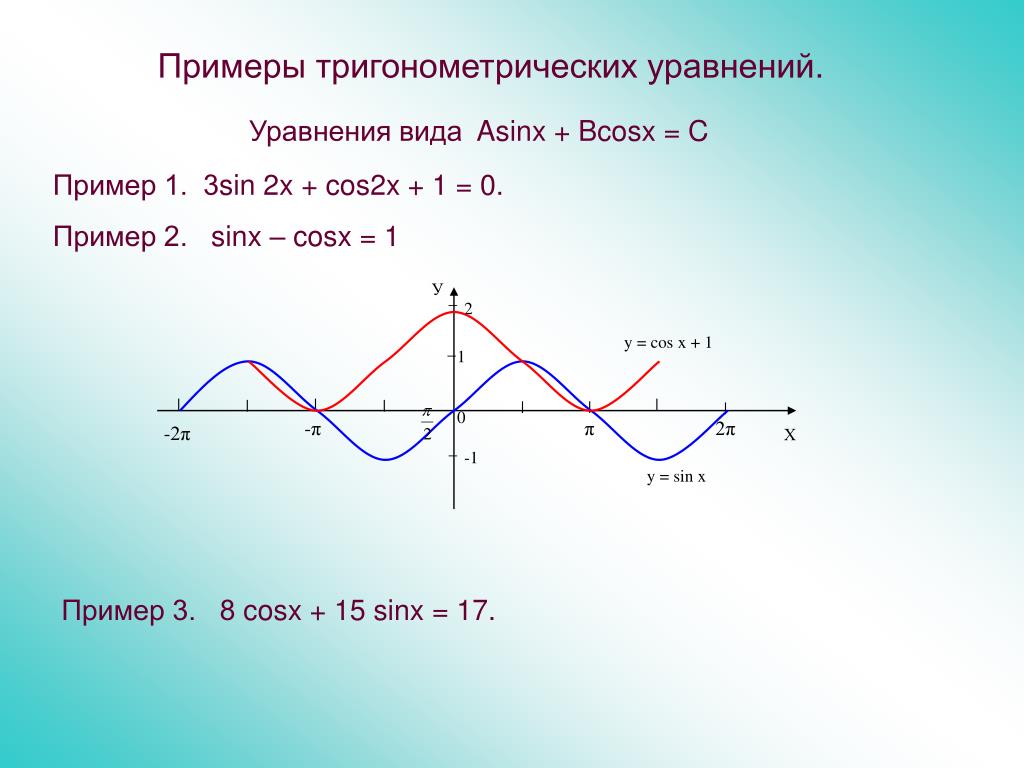 {2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
{2}-3
, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3 ; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x . Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
Функция является четной функцией , когда f(-x)=f(x)
для любого x
из области определения. Такая функция будет симметрична относительно оси Oy
. {2}} \neq 1
для любого x \in [-1;1]
.
{2}} \neq 1
для любого x \in [-1;1]
.
Ограниченной принято называть функцию y=f(x), x \in X тогда, когда существует такое число K > 0 , для которого выполняется неравенство \left | f(x) \right | \neq K для любого x \in X .
Пример ограниченной функции: y=\sin x ограничена на всей числовой оси, так как \left | \sin x \right | \neq 1 .
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1}) > y(x_{2}) .
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x) . Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2} , причем x_{1} > x_{2} , будет y(x_{1})
Корнями функции принято называть точки, в которых функция F=y(x)
пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0
).
а) Если при x > 0 четная функция возрастает, то убывает она при x
б) Когда при x > 0 четная функция убывает, то возрастает она при x
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x
г) Когда нечетная функция будет убывать при x > 0 , то она будет убывать и при x
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняться неравенство f(x) > f(x_{0}) . y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0} , у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0} ), и для них тогда будет выполняется неравенство f(x)
Необходимое условие
Согласно теореме Ферма: f»(x)=0
тогда, когда у функции f(x)
, что дифференцируема в точке x_{0}
, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0} .
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f»(x) ;
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку ;
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции , а большее — наибольшим .
| 1 | Найдите количество возможностей | 7 выбрать 3 | |||||||||||||
| 2 | Найдите количество возможностей | 8 выбрать 3 | |||||||||||||
| 3 | Найдите количество возможностей | 5 выбрать 2 | |||||||||||||
| 4 | Найдите количество возможностей | 4 выбрать 2 | |||||||||||||
| 5 | Найдите количество возможностей | 8 выбрать 4 | |||||||||||||
| 6 | Найдите количество возможностей | 10 выбрать 3 | |||||||||||||
| 7 | Найдите количество возможностей | 7 выбрать 4 | |||||||||||||
| 8 | Найдите количество возможностей | 6 выбрать 3 | |||||||||||||
| 9 | Найдите количество возможностей | 9 выбрать 3 | |||||||||||||
| 10 | Найдите количество возможностей | 3 выбрать 2 | |||||||||||||
| 11 | Найдите количество возможностей | 6 выбрать 4 | |||||||||||||
| 12 | Найдите количество возможностей | 5 выбрать 4 | |||||||||||||
| 13 | Найдите количество возможностей | 7 переставить 3 | |||||||||||||
| 14 | Найдите количество возможностей | 7 выбрать 2 | |||||||||||||
| 15 | Найдите количество возможностей | 10 выбрать 5 | |||||||||||||
| 16 | Найдите количество возможностей | 10 выбрать 6 | |||||||||||||
| 17 | Найдите количество возможностей | 13 выбрать 5 | |||||||||||||
| 18 | Найдите количество возможностей | 3 выбрать 3 | |||||||||||||
| 19 | Найдите количество возможностей | 4 выбрать 1 | |||||||||||||
| 20 | Найдите количество возможностей | 4 выбрать 4 | |||||||||||||
| 21 | Найдите количество возможностей | 5 выбрать 1 | |||||||||||||
| 22 | Найдите количество возможностей | 6 переставить 3 | |||||||||||||
| 23 | Найдите количество возможностей | 8 выбрать 5 | |||||||||||||
| 24 | Найдите количество возможностей | 9переставить 4 | |||||||||||||
| 25 | Найдите количество возможностей | 13 выбрать 3 | |||||||||||||
| 26 | Найдите количество возможностей | 12 выбрать 2 | |||||||||||||
| 27 | Найдите количество возможностей | 12 выбрать 4 | |||||||||||||
| 28 | Найдите количество возможностей | 12 выбрать 3 | |||||||||||||
| 29 | Найдите количество возможностей | 9 выбрать 5 | |||||||||||||
| 30 | Найдите количество возможностей | 9 выбрать 2 | |||||||||||||
| 31 | Найдите количество возможностей | 7 выбрать 5 | |||||||||||||
| 32 | Найдите количество возможностей | 6 переставить 6 | |||||||||||||
| 33 | Найдите количество возможностей | 8 переставить 5 | |||||||||||||
| 34 | Найдите количество возможностей | 8 переставить 3 | |||||||||||||
| 35 | Найдите количество возможностей | 7 переставить 5 | |||||||||||||
| 36 | Найдите количество возможностей | 52 выбрать 5 | |||||||||||||
| 37 | Найдите количество возможностей | 5 переставить 3 | |||||||||||||
| 38 | Найдите количество возможностей | 12 выбрать 5 | |||||||||||||
| 39 | Найдите количество возможностей | 3 выбрать 1 | |||||||||||||
| 40 | Найдите количество возможностей | 11 выбрать 5 | |||||||||||||
| 41 | Найдите количество возможностей | 10 выбрать 2 | |||||||||||||
| 42 | Найдите количество возможностей | 15 выбрать 3 | |||||||||||||
| 43 | Найдите количество возможностей | 52 выбрать 4 | |||||||||||||
| 44 | Найдите количество возможностей | 9 выбрать 4 | |||||||||||||
| 45 | Найдите количество возможностей | 9 переставить 3 | |||||||||||||
| 46 | Найдите количество возможностей | 7 переставить 4 | |||||||||||||
| 47 | Найдите количество возможностей | 7 переставить 2 | |||||||||||||
| 48 | Найдите количество возможностей | 11 выбрать 4 | |||||||||||||
| 49 | Найдите количество возможностей | 11 выбрать 2 | |||||||||||||
| 50 | Найдите количество возможностей | 11 выбрать 3 | |||||||||||||
| 51 | Найдите количество возможностей | 10 переставить 5 | |||||||||||||
| 52 | Найдите количество возможностей | 5 выбрать 5 | |||||||||||||
| 53 | Найдите количество возможностей | 6 выбрать 1 | |||||||||||||
| 54 | Найдите количество возможностей | 8 переставить 4 | |||||||||||||
| 55 | Найдите количество возможностей | 8 выбрать 6 | |||||||||||||
| 56 | Найдите количество возможностей | 13 выбрать 4 | |||||||||||||
| 57 | Оценить | и | |||||||||||||
| 58 | Найти любое уравнение, перпендикулярное прямой | -7x-5y=7 | |||||||||||||
| 59 | Найдите количество возможностей | 13 выбрать 2 | |||||||||||||
| 60 | Найдите количество возможностей | 10 переставить 2 | |||||||||||||
| 61 | Найдите количество возможностей | 10 переставить 3 | |||||||||||||
| 62 | Найдите количество возможностей | 10 выбрать 7 | |||||||||||||
| 63 | Найдите количество возможностей | 20 выбрать 4 | |||||||||||||
| 64 | Найдите количество возможностей | 6 переставить 4 | |||||||||||||
| 65 | Найдите количество возможностей | 5 переставить 4 | |||||||||||||
| 66 | Найдите количество возможностей | 6 выбрать 5 | |||||||||||||
| 67 | Найдите количество возможностей | 52 выбрать 3 | |||||||||||||
| 68 | Найдите количество возможностей | 4 выбрать 0 | |||||||||||||
| 69 | Найдите количество возможностей | 9переставить 7 | |||||||||||||
| 70 | Найдите количество возможностей | 6 выбрать 2 | |||||||||||||
| 71 | Найдите количество возможностей | 5 переставить 5 | |||||||||||||
| 72 | Найдите количество возможностей | 5 переставить 2 | |||||||||||||
| 73 | Найдите количество возможностей | 6 выбрать 6 | |||||||||||||
| 74 | Найдите количество возможностей | 7 выбрать 6 | |||||||||||||
| 75 | Найдите количество возможностей | 8 переставить 6 | |||||||||||||
| 76 | Найдите количество возможностей | 7 переставить 7 | |||||||||||||
| 77 | Найдите количество возможностей | 9 переставить 5 | |||||||||||||
| 78 | Найдите количество возможностей | 2 переставить 2 | |||||||||||||
| 79 | Найдите количество возможностей | 10 выбрать 8 | |||||||||||||
| 80 | Найдите количество возможностей | 12 выбрать 7 | |||||||||||||
| 81 | Найдите количество возможностей | 15 выбрать 5 | |||||||||||||
| 82 | Найдите обратное | [[1,0,1],[2,-2,-1],[3,0,0]] | |||||||||||||
| 83 | Найти диапазон | 1/4x-7 | |||||||||||||
| 84 | Найдите количество возможностей | 10 переставить 7 | |||||||||||||
| 85 | Найдите количество возможностей | 12 выбрать 6 | |||||||||||||
| 86 | Найдите количество возможностей | 2 выбрать 1 | |||||||||||||
| 87 | Найдите количество возможностей | 30 выбрать 3 | |||||||||||||
| 88 | Найдите количество возможностей | 9 выбрать 6 | |||||||||||||
| 89 | Найдите количество возможностей | 8 переставить 2 | |||||||||||||
| 90 | Найдите количество возможностей | 7 выбрать 1 | |||||||||||||
| 91 | Найдите количество возможностей | 6 перестановка 2 | |||||||||||||
| 92 | Найдите количество возможностей | 4 переставить 2 | |||||||||||||
| 93 | Найдите количество возможностей | 4 переставить 3 | |||||||||||||
| 94 | Найдите количество возможностей | 3 переставить 3 | |||||||||||||
| 95 | Найдите количество возможностей | 46 выбрать 6 | |||||||||||||
| 96 | Найдите количество возможностей | 5 переставить 1 | |||||||||||||
| 97 | Найдите количество возможностей | 52 выбрать 7 | |||||||||||||
| 98 | Найдите количество возможностей | 52 переставить 5 | |||||||||||||
| 99 | Найдите количество возможностей | 93 | |||||||||||||
| 6 | Решить для ? | cos(x)=1/2 | |||||||||||||
| 7 | Найти x | sin(x)=-1/2 | |||||||||||||
| 8 | Преобразование градусов в радианы | 225 | |||||||||||||
| 9 | Решить для ? | cos(x)=(квадратный корень из 2)/2 | |||||||||||||
| 10 | Найти x | cos(x)=(квадратный корень из 3)/2 | |||||||||||||
| 11 | Найти x | sin(x)=(квадратный корень из 3)/2 | 92=9 | ||||||||||||
| 14 | Преобразование градусов в радианы | 120 градусов | |||||||||||||
| 15 | Преобразование градусов в радианы | 180 | |||||||||||||
| 16 | Найти точное значение | желтовато-коричневый(195) | 92-4|||||||||||||
| 38 | Найти точное значение | грех(255) | |||||||||||||
| 39 | Оценить | лог база 27 из 36 | |||||||||||||
| 40 | Преобразовать из радианов в градусы | 2 шт.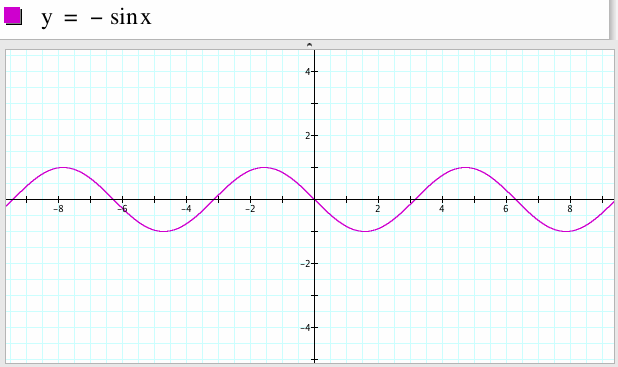 | 92-3sin(x)+1=0|||||||||||||
| 43 | Найти x | tan(x)+ квадратный корень из 3=0 | |||||||||||||
| 44 | Найти x | sin(2x)+cos(x)=0 | |||||||||||||
| 45 | Упростить | (1-cos(x))(1+cos(x)) | 92=25|||||||||||||
| 59 | График | f(x)=- натуральный логарифм x-1+3 | |||||||||||||
| 60 | Найдите значение с помощью единичного круга | угловой синус(-1/2) | |||||||||||||
| 61 | Найти домен | квадратный корень из 36-4x^2 92=0 | |||||||||||||
| 66 | Найти x | cos(2x)=(квадратный корень из 2)/2 | |||||||||||||
| 67 | График | у=3 | |||||||||||||
| 68 | График | f(x)=- логарифмическая база 3 x-1+3 | 92 | ||||||||||||
| 71 | Найти x | квадратный корень из x+4+ квадратный корень из x-1=5 | |||||||||||||
| 72 | Решить для ? | cos(2x)=-1/2 | |||||||||||||
| 73 | Найти x | логарифмическая база x из 16=4 | 9х|||||||||||||
| 75 | Упростить | (cos(x))/(1-sin(x))+(1-sin(x))/(cos(x)) | |||||||||||||
| 76 | Упростить | сек(х)sin(х) | |||||||||||||
| 77 | Упростить | кубический корень из 24 кубический корень из 18 | 92=0|||||||||||||
| 96 | Найти x | 3x+2=(5x-11)/(8г) | |||||||||||||
| 97 | Решить для ? | sin(2x)=-1/2 | |||||||||||||
| 98 | Найти x | (2x-1)/(x+2)=4/5 | 93)=\sin(u)$ |
| 1. | Что такое четные и нечетные функции? |
| 2. | Четные и нечетные функции в тригонометрии |
| 3. | Интегральные свойства четных и нечетных функций |
| 4. | График четных и нечетных функций |
| 5. | Свойства четных и нечетных функций |
| 6. | Часто задаваемые вопросы о четных и нечетных функциях |
Что такое четные и нечетные функции?
г.Обычно мы считаем вещественную функцию четной или нечетной. Чтобы определить, является ли функция четной или нечетной, мы подставляем -x вместо x в функцию f(x), то есть мы проверяем выходное значение f(-x), чтобы определить тип функции. Четные и нечетные функции симметричны. Давайте сначала разберемся с их определениями.
Четные и нечетные функции Определение
- Четная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с f(x), для всех значений x в области f функция называется четной функцией.
 Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
f(-x) = (-x) 2 = x 2 для всех значений x, поскольку квадрат отрицательного числа равен квадрату положительного значения числа. Отсюда следует f(-x) = f(x) для всех x. Следовательно, f(x) = x 2 — четная функция. Точно так же такие функции, как x 4 , x 6 , x 8 и т. д., являются четными функциями. - Нечетная функция — Для функции f(x) с действительным знаком, когда выходное значение f(-x) совпадает с отрицательным значением f(x), для всех значений x в области определения f, функция называется нечетной. Нечетная функция должна содержать следующее уравнение: f(-x) = -f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f.
 Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
f(-x) = (-x) 3 = -(x 3 ) для всех значений x, поскольку куб отрицательного числа совпадает с отрицательным значением куба положительного значения числа . Отсюда следует f(-x) = -f(x) для всех x. Следовательно, f(x) = x 3 — нечетная функция. Точно так же такие функции, как x 5 , x 7 , x 9 и т. д., являются нечетными функциями. - И четные, и нечетные функции — Вещественнозначная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет условию f(-x) = f(x) и f(-x) = -f (x) для всех значений x в области определения функции f(x). Существует только одна функция, которая одновременно является четной и нечетной, и это нулевая функция, f(x) = 0 для всех x. Мы знаем, что для нулевой функции f(-x) = -f(x) = f(x) = 0 для всех значений x.
 Следовательно, f(x) = 0 — четная и нечетная функция. г.
Следовательно, f(x) = 0 — четная и нечетная функция. г. - Ни четная, ни нечетная функция — Говорят, что функция f(x) с действительным знаком не является ни четной, ни нечетной, если она не удовлетворяет f(-x) = f(x) и f(-x) = -f (x) хотя бы для одного значения x в области определения функции f(x). Давайте рассмотрим пример, чтобы лучше понять определение. Рассмотрим f(x) = 2x 5 + 3x 2 + 1, f(-x) = 2(-x) 5 + 3(-x) 2 + 1 = -2x 5 + 3x 2 + 1, что не равно ни f(x), ни -f(x). Следовательно, f(x) = 2x 5 + 3x 2 + 1 не является ни четной, ни нечетной функцией.
Четные и нечетные функции в тригонометрии
В этом разделе мы разделим тригонометрические функции на четные и нечетные. У нас есть шесть тригонометрических отношений (синус, косинус, тангенс, котангенс, косеканс и секанс). Эти тригонометрические отношения дают положительные значения в разных квадрантах для различных мер углов.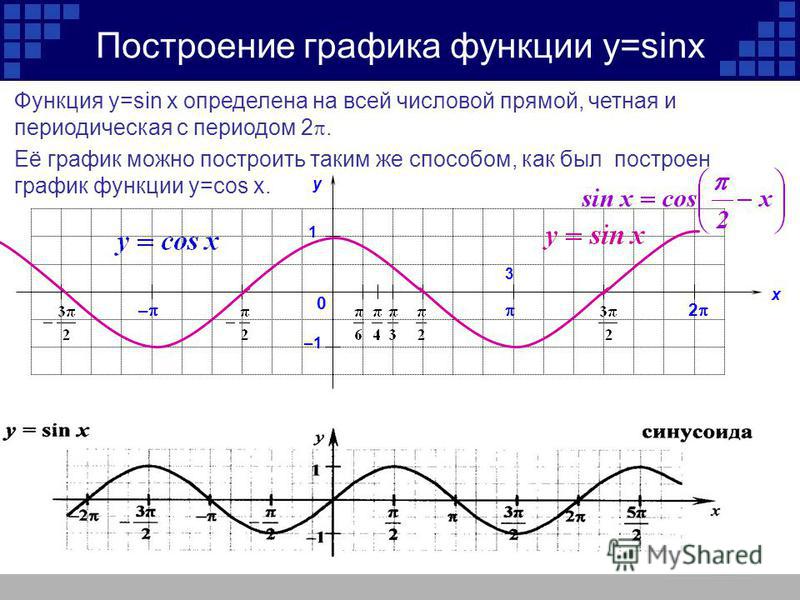
В первом квадранте (где все координаты x и y положительны) все шесть тригонометрических отношений имеют положительные значения. Во втором квадранте положительны только синус и косеканс. В третьем квадранте положительны только тангенс и котангенс. В четвертом квадранте положительны только косинус и секанс. На основании этих признаков мы разделим их на четные и нечетные функции.
Если тригонометрическое соотношение четное или нечетное, можно проверить через единичный круг. Угол, измеренный в направлении против часовой стрелки, является положительным углом, тогда как угол, измеренный в направлении по часовой стрелке, является отрицательным углом.
- sinθ = y, sin(-θ) = -y; Следовательно, sin(-θ) = -sinθ. Следовательно, sinθ — нечетная функция.
- cosθ = y, cos(-θ) = y; Следовательно, cos(-θ) = cosθ. Следовательно, cosθ — четная функция.
- tanθ = y, tan(-θ) = -y; Следовательно, tan(-θ) = -tanθ. Следовательно, tanθ — нечетная функция.
 г.
г. - cosecθ = y, cosec(-θ) = -y; Следовательно, cosec(-θ) = -cosecθ. Следовательно, cosecθ — нечетная функция.
- секθ = у, сек(-θ) = у; Следовательно, sec(-θ) = secθ. Следовательно, secθ — четная функция.
- кроватка θ = у, кроватка (-θ) = -у; Следовательно, cot(-θ) = -cotθ. Следовательно, cotθ — нечетная функция.
Интегральные свойства четных и нечетных функций
Интеграл функции дает площадь под кривой. Мы используем свойства четных и нечетных функций при решении определенных интегралов. Для этого нам нужно знать пределы интеграла и характер функции. Если функция четная или нечетная, а интервал равен [-a, a], мы можем применить следующие два правила: 9{а}\) f(x) dx = 0
График четных и нечетных функций
Теперь посмотрим, как графически ведут себя четные и нечетные функции. График четной функции симметричен относительно оси y . Другими словами, график четной функции остается прежним после отражения относительно оси у. Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Для любых двух противоположных входных значений x значение функции будет оставаться одинаковым на протяжении всей кривой.
Принимая во внимание, что график нечетной функции симметричен относительно начала координат . Другими словами, график нечетной функции находится на одном и том же расстоянии от начала координат, но в противоположных направлениях. Для любых двух противоположных входных значений x функция имеет противоположные значения y. Вот несколько примеров четных и нечетных функций.
Свойства четных и нечетных функций
- Сумма двух четных функций четна, а сумма двух нечетных функций нечетна.
- Разница между двумя четными функциями четна, а разница между двумя нечетными функциями нечетна. г.
- Сумма четной и нечетной функций не является ни четной, ни нечетной, если только одна из них не является нулевой функцией.
- Произведение двух четных функций является четным, и произведение двух нечетных функций также является четной функцией.

- Произведение четной и нечетной функций нечетно.
- Частное двух четных функций четно, и частное двух нечетных функций также является четной функцией.
- Частное четной и нечетной функций нечетно. г.
- Композиция двух четных функций четна, а композиция двух нечетных функций нечетна.
- Композиция четной и нечетной функций четна.
Важные замечания о четных и нечетных функциях
- Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f (-x) = -f(x) для всех значений x.
- В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. г.
- График четной функции симметричен относительно оси Y, а график нечетной функции симметричен относительно начала координат.
- f(x) = 0 — единственная функция, которая является четной и нечетной функцией.
Темы, связанные с четными и нечетными функциями
- Функция четности
- Нечетная функция
- Типы функций
Часто задаваемые вопросы о четных и нечетных функциях
Что такое четные и нечетные функции в математике?
Функция f(x) является четной, если f(-x) = f(x), для всех значений x в D(f), и нечетной, если f(-x) = -f(x), для все значения х. График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
График четной функции симметричен относительно оси y, а график нечетной функции симметричен относительно начала координат. Вещественная функция f(x) называется одновременно четной и нечетной, если она удовлетворяет f(-x) = f(x) и f(-x) = -f(x) для всех значений x в области функции f(x).
Как определить четные и нечетные функции алгебраически?
Чтобы проверить, является ли функция четной или нечетной алгебраически, мы проверяем, является ли f(-x) = f(x) или f(-x) = -f(x) для всех значений x соответственно. Если мы заменяем x на -x в функции и значение функции становится отрицательным, то функция называется нечетной функцией. Если мы заменим x на -x в функции и значение функции не изменится, то функция будет известна даже как функция.
Если функция f четная, то какой тип симметрии имеет график функции f?
Четные и нечетные функции демонстрируют разные типы симметрии. Даже функции имеют линейную симметрию. Линия симметрии является осью Y. Даже функции — это функции, в которых, когда мы заменяем x на -x, значение функции для этого конкретного x не меняется. График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
График четной функции ведет себя одинаково для всех точек на оси X, которые находятся как слева от начала координат, так и справа от него.
Какие тригонометрические функции являются четными и нечетными функциями?
В тригонометрии cosθ и secθ — четные функции, а sinθ, cosecθ, tanθ, cotθ — нечетные функции. Различные тригонометрические отношения имеют положительные и отрицательные значения в разных квадрантах. Следовательно, используя единичный круг, мы можем видеть, что cosθ и secθ — четные функции, а остальные четыре тригонометрических отношения — нечетные.
Как определить графически четные и нечетные функции?
График четной функции симметричен относительно оси y. График нечетной функции симметричен относительно начала координат. График четной функции остается прежним после отражения относительно оси у. График нечетной функции находится на одинаковом расстоянии от начала координат, но в противоположных направлениях. Используя те же критерии, мы можем идентифицировать четные и нечетные функции графически.
Если f и g являются четными функциями, является ли f+g четной и нечетной функцией?
Если f и g — четные функции, то f + g — четная функция. Рассмотрим функцию h(x) = f(x) + g(x). Замените x на -x в h(x), h(-x) = f(-x) + g(-x) = f(x) + g(x) = h(x). Поскольку f(x) и g(x) четные, f(-x) = f(x) и g(-x) = g(x). Следовательно, f + g — четная функция. Это не четная и нечетная функция одновременно.
Определенные интегралы четных и нечетных функций — Krista King Math
Что делать, если вы считаете, что функция четная или нечетная
Иногда мы можем упростить определенный интеграл, если узнаем, что интегрируемая функция является четной или нечетной функцией. Если функция не четная и не нечетная, то интегрируем как обычно.
Чтобы узнать, четная функция или нечетная, подставим ???-x??? в функцию для ???x???. Если мы вернем исходную функцию ???f(x)???, функция будет четной. Если мы вернем исходную функцию, умноженную на ???-1???, функция будет нечетной. Другими словами,
Другими словами,
Если ???f(-x)=f(x)???, функция четная
Если ???f(-x)=-f(x)???, функция нечетная
Если мы обнаружим, что функция четная или нечетная, следующим шагом будет проверка пределов интегрирования (интервал, по которому мы интегрируем). Чтобы использовать специальные правила четных или нечетных функций для определенных интегралов, наш интервал должен быть в форме ???[-a,a]???. Другими словами, пределы интегрирования имеют одинаковое числовое значение, но разные знаки, например ???[-1,1]??? или ???[-5,5]???. 9а_{-а}f(x)\dx=0???
Вот два видео. Первый — это обход определенного интеграла четной функции; второй — прохождение определенного интеграла нечетной функции.
Четные функции:
Нечетные функции:
Пройти курс
Хотите узнать больше об исчислении 2? У меня есть пошаговый курс для этого.
 a_0f(x)\dx??? 97+4\sin{x}\dx=0???
a_0f(x)\dx??? 97+4\sin{x}\dx=0???Получите доступ к полному курсу Calculus 2
Начать
Четная функция, нечетная функция, периодическая функция — QuantumStudy
Если f : X → Y — вещественнозначная функция такая, что для всех x ∈ D
⇒ − x ∈ D (где D = область определения f) и :
если f(− x) = f(x) для каждого x ∈ D, то f называется четной функцией
г., и если f(− x) = − f(x), то f называется нечетной функцией.
График четной функции симметричен относительно оси y (т. е. если (x , y) лежит на кривой, то (− x , y) также лежит на кривой), а график нечетной функции симметричен относительно начала координат (т. е. если (x, y) лежит на кривой , то (−x, −y) также лежит на кривой).
Примечания: ⋄ Иногда легко доказать, что f(x) − f(−x) = 0 для четных функций и f(x) + f(−x) = 0 для нечетных функций.
⋄ Функция может быть четной или нечетной или ни четной, ни нечетной.
⋄ Каждая функция, определенная в симметричном интервале D
(т.е. x∈ D ⇒ −x ∈ D), может быть выражена как сумма четной и нечетной функций.
$\large f(x) = (\frac{f(x) + f(-x)}{2}) + (\frac{f(x) — f(-x)}{2})$
Пусть $\large h(x) = (\frac{f(x) + f(-x)}{2}) \; а также \; g(x) = (\frac{f(x) – f(-x)}{2})$
Теперь легко показать, что h(x) четно, а g(x) нечетно.
⋄ Первая производная четной функции является нечетной функцией и наоборот. Это остается вам в качестве упражнения для доказательства.
⋄ Если x = 0 ∈ область определения f, то для нечетной функции f(x), непрерывной в точке x = 0, f(0) = 0, т.е. если для функции f(0) ≠ 0, то эта функция не может быть нечетным.
Отсюда следует, что для дифференцируемой четной функции f ‘(0) = 0, т. е. если для дифференцируемой функции f ‘(0) ≠ 0, то функция f не может быть четной
Иллюстрация : Какая из следующих функций ( являются) четными, нечетными или ни одним из них:
(i) f(x) = x 2 sinx
(ii) $\large f(x) = \sqrt{1 + x + x^2} – \sqrt {1 – х + х^2} $ 9x}{2}$
= f(x)
Следовательно, f(x) четно
Расширение области:
Пусть функция определена в некоторой области, которая полностью неотрицательна (или не положительна).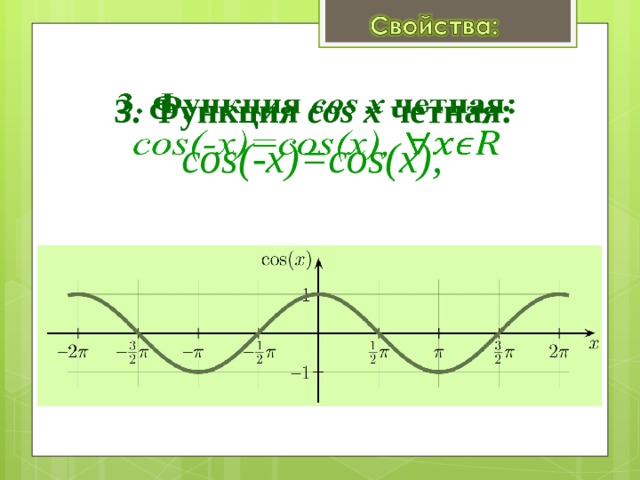 Область определения f(x) может быть расширена до множества
Область определения f(x) может быть расширена до множества
X = {−x : x∈ область определения f(x)} двумя способами:
(i) Четное расширение: Четное расширение равно получается определением новой функции f(−x) для x ∈ X, такой что f(−x) = f(x).
(ii) Нечетное расширение: 92 & \mathrm{,} \; -2 < x \le 0 \end{массив} \right. $
Периодическая функция:
Функция f: X → Y называется периодической функцией, если существует положительное действительное число p такое, что:
f(x + p) = f(x) , для все x ∈ X .
Наименьшее из всех таких положительных чисел p называется главным периодом или просто периодом f.
Все периодические функции могут быть проанализированы на интервале в один период в пределах домена, поскольку один и тот же шаблон должен повторяться во всем домене.
Пример:
sinx, cosx, secx — периодические функции с периодом 2π
tanx, cotx — периодические функции с периодом π (x) периодическая с периодом 1
(вы можете доказать это математически?).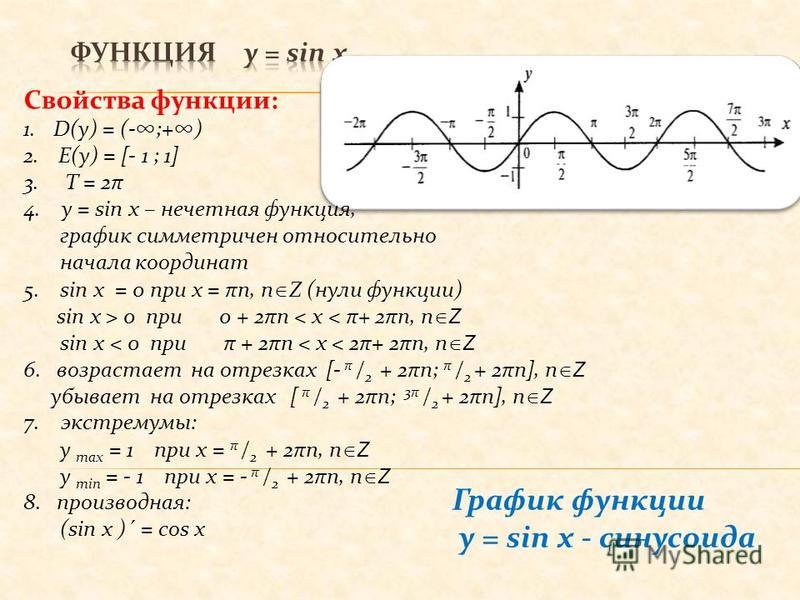
На экзамене задают два типа вопросов. Вас могут попросить проверить периодичность функции или найти период функции.
В первом случае вам просто нужно показать, что f(x + T) = f(x) для одного и того же T ( > 0), не зависящего от x, тогда как во втором вам нужно найти наименьшее положительное число T, не зависящее от x. x, для которого выполняется f(x + T)=f(x).
Следует помнить следующие моменты:Если f(x) периодична с периодом p, то af(x) +b, где a , b ∈ R (a ≠ 0), также периодична с периодом p.
∎ Если f(x) периодична с периодом p , то f(ax + b), где a, b ∈ R ( a ≠0) также периодична с периодом $\large \frac{p}{|a|} $ .
∎ Пусть f(x) имеет период p = m/n (m, n ∈ N и взаимно прост) и g(x) имеет период q = r/s (r, s ∈ N и взаимно прост) и пусть t будет НОК p и q, т.е. $\large t = \frac{LCM \; из (m , r)}{HCF \; из (r , s)}$
Тогда t будет периодом f + g при условии, что не существует положительного числа k (< t), для которого
f(k + x) + g(k + x) = f(x) + g( x), иначе k будет периодом.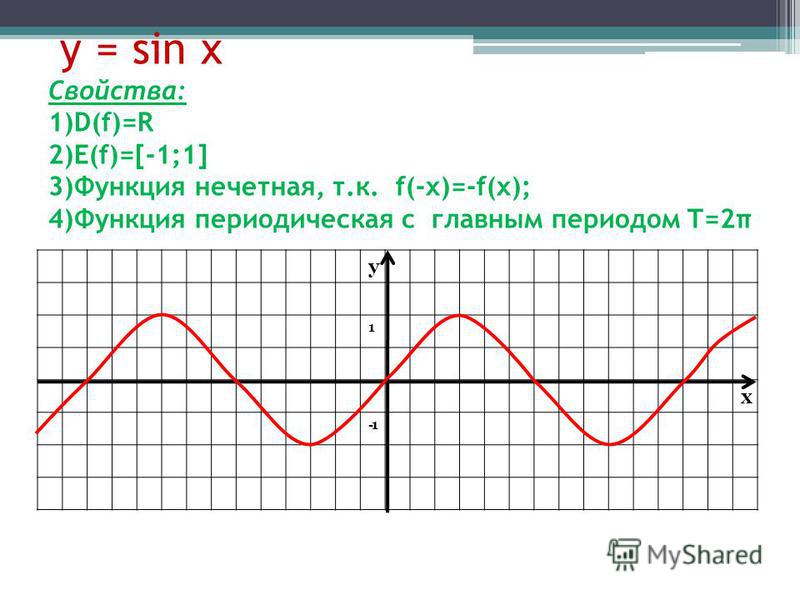
То же правило применимо для любой другой алгебраической комбинации f(x) и g(x)
Примечания:НОК p и q всегда существуют, если p/q — рациональная величина. Если p/q иррационально, то алгебраическая комбинация f и g непериодична.
∎ sin n x, cos n x, cosec n x и sec n x имеют период 2π, если n нечетно, и π, если n четно.
∎ tan n x и cot n x имеют период π независимо от того, является ли n нечетным или четным.
∎ Постоянная функция является периодической, но не имеет четко определенного периода.
∎ Если функция g является периодической, то туман всегда будет периодической функцией. Период тумана может быть, а может и не быть периодом g.
∎ Если f периодическая, а g строго монотонная (отличная от линейной), то туман непериодический. 93 x – cosec(3x-5)$
Период e lnsinx = 2π , tan 3 x = π
cosec(3x-5) = 2π/3 ; период = 2π
(ii) f(x) = x –[x-b] = b+{x –b}
⇒ период = 1
(iii) $\large f(x) = \frac{|sinx + cosx|}{|sinx| + |cosx|} $
Поскольку период |sinx + cox| = π и период |sinx| + | cosx| равно π/2.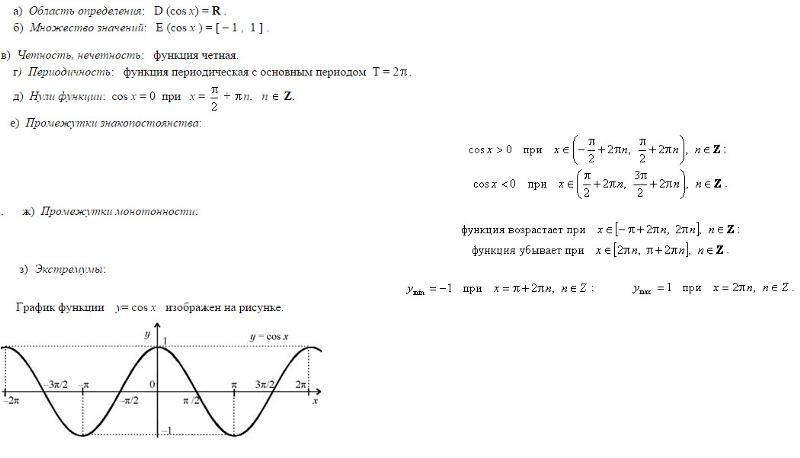


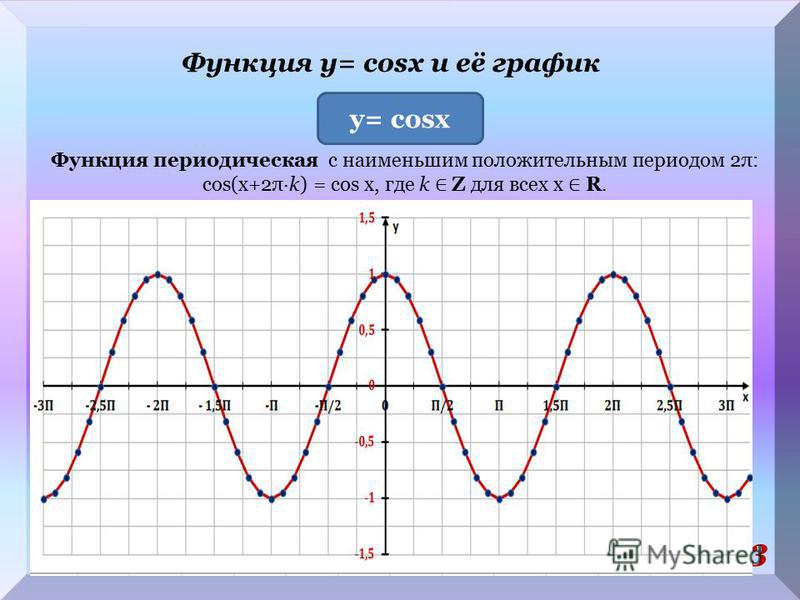
 Если кто-то может объяснить мне, что происходит, это было бы очень полезно. Спасибо.
Если кто-то может объяснить мне, что происходит, это было бы очень полезно. Спасибо.

 Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 .
Четная функция должна содержать следующее уравнение: f(-x) = f(x) для всех значений x в D(f), где D(f) обозначает область определения функции f. Другими словами, мы можем сказать, что уравнение f (-x) — f (x) = 0 выполняется для четной функции для всех x. Рассмотрим пример, f(x) = x 2 . 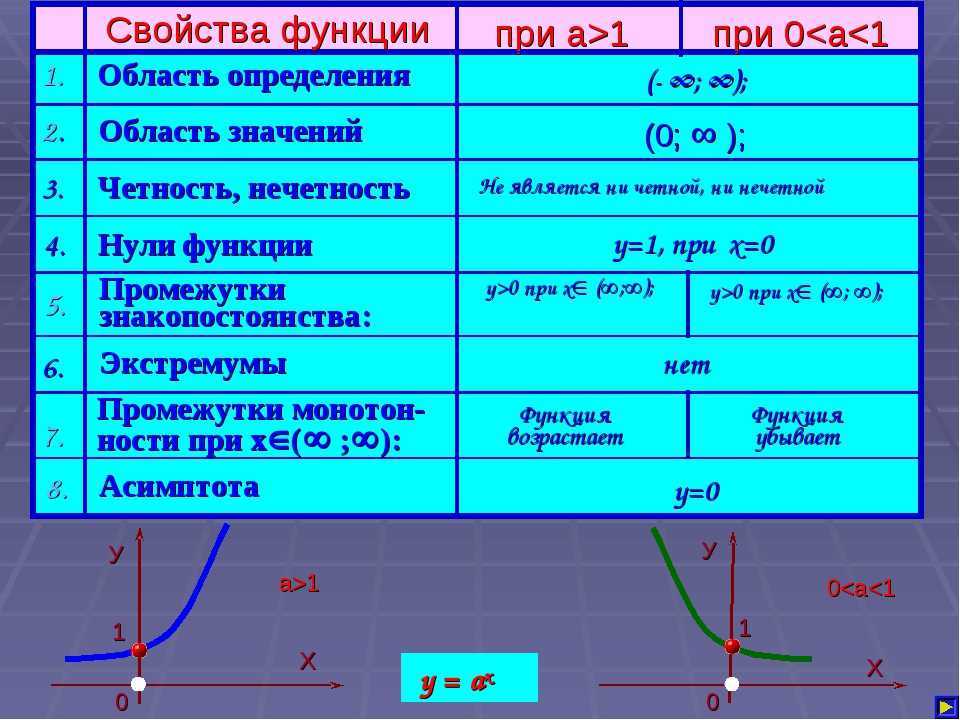 Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .
Другими словами, мы можем сказать, что уравнение f (-x) + f (x) = 0 выполняется для нечетной функции для всех x. Рассмотрим пример, f(x) = x 3 .  Следовательно, f(x) = 0 — четная и нечетная функция.
Следовательно, f(x) = 0 — четная и нечетная функция.