Векторная величина в физике. Примеры векторных величин
Векторная величина в физике. Примеры векторных величин
Физика и математика не обходятся без понятия «векторная величина». Это необходимо знать и распознавать, а также уметь управлять им. Обязательно стоит научиться, чтобы не запутаться и избежать глупых ошибок.
Содержание
- 1 Как отличить скалярную величину от векторной?
- 2 Какие действия чаще всего выполняются с векторами?
- 3 Какие векторы изучают в физике?
- 4 Первая величина — скорость
- 5 Вторая величина — сила
- 6 Третья величина — перемещение
- 7 Четвертая величина — ускорение
- 8 Пятая величина — импульс
- 9 Задача о неупругом ударе
- 10 Задача с разделением тела на части
- 11 Задача про выстрел под углом
- 12 Задача о переправе через реку
Как отличить скалярную величину от векторной?
У первого всегда есть только одна характеристика. Это его числовое значение. Большинство скаляров могут быть как положительными, так и отрицательными. Примеры включают электрический заряд, работу или температуру. Но есть скаляры, которые не могут быть отрицательными, например длина и масса.
Это его числовое значение. Большинство скаляров могут быть как положительными, так и отрицательными. Примеры включают электрический заряд, работу или температуру. Но есть скаляры, которые не могут быть отрицательными, например длина и масса.
Векторная величина, помимо числовой, всегда взятой по модулю, также характеризуется направлением. Поэтому его можно представить графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенном направлении.
При письме каждая векторная величина обозначается стрелкой на букве. Если мы говорим о числовом значении, то стрелка не пишется или берется по модулю.
Какие действия чаще всего выполняются с векторами?
Сначала противостояние. Они могут быть, а могут и не совпадать. В первом случае их модули совпадают. Но это не единственное условие. Они также должны иметь равные или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположностями. Если хотя бы одно из указанных условий не выполняется, векторы не равны.
Если хотя бы одно из указанных условий не выполняется, векторы не равны.
Затем идет добавление. Это можно сделать по двум правилам: треугольник или параллелограмм. Первый предписывает сначала отложить вектор, затем второй — от его конца. Результатом сложения будет то, что нужно нарисовать от начала первого до конца второго.
Правило параллелограмма можно использовать, когда вам нужно добавить векторные величины в физике. В отличие от первого правила, здесь их следует отложить на один балл. Затем соберите их до параллелограмма. Результатом действия нужно считать диагональ параллелограмма, проведенную из той же точки.
Если одну векторную величину вычесть из другой, они снова откладываются от точки. Только результатом будет вектор, равный вектору, проведенному от конца второго до конца первого.
Какие векторы изучают в физике?
Их столько, сколько скаляров. Вы можете только вспомнить, какие векторные величины существуют в физике. Или узнать признаки, по которым их можно вычислить. Тем, кто отдает предпочтение первому варианту, такой столик пригодится. Перечисляет основные векторные физические величины.
Тем, кто отдает предпочтение первому варианту, такой столик пригодится. Перечисляет основные векторные физические величины.
| Обозначение формулы | Имя |
| v | скорость |
| р | в движении |
| а | ускорение |
| Ф | сила |
| р | пульсировать |
| А ТАКЖЕ | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих ценностей.
Первая величина — скорость
Начать стоит, чтобы привести примеры векторных величин. Это связано с тем, что он изучается одним из первых.
Скорость определяется как характеристика движения тела в пространстве. Задайте числовое значение и направление. Итак, скорость — это векторная величина. Кроме того, его принято делить на виды. Первый — это линейная скорость. Он вводится при рассмотрении равномерного прямолинейного движения. В этом случае он оказывается равным отношению пути, пройденного телом, и времени движения.
В этом случае он оказывается равным отношению пути, пройденного телом, и времени движения.
Эту же формулу можно использовать для нерегулярных движений. Только тогда он будет средним. Кроме того, выбираемый временной интервал должен быть как можно короче. Когда временной интервал стремится к нулю, значение скорости уже мгновенное.
Если рассматривать произвольное движение, то здесь скорость всегда является векторной величиной. Ведь его нужно разложить на прямые составляющие по каждому вектору, который направляет координатные линии. Кроме того, он определяется как производная по времени от радиус-вектора.
Вторая величина — сила
Он определяет меру силы воздействия, которое приходит на тело от других тел или полей. Поскольку сила является векторной величиной, она обязательно имеет значение по величине и направлению. Поскольку он действует на тело, то здесь также важна сила. Чтобы получить визуальное представление о векторах силы, вы можете обратиться к следующей таблице.
| Власть | Пункт применения | Направление |
| строгость | центр тела | в центре земли |
| вселенская гравитация | центр тела | в центре другого тела |
| эластичность | место контакта взаимодействующих тел | от внешних воздействий |
| трение | между соприкасающимися поверхностями | в обратном направлении движения |
Кроме того, результирующая сила также является векторной величиной. Он определяется как сумма всех механических сил, действующих на тело. Для его определения необходимо провести сложение по принципу правила треугольника. Вам просто нужно отложить векторы по очереди с конца предыдущего. Результатом будет то, что связывает начало первого с концом последнего.
Третья величина — перемещение
Во время движения тело описывает определенную линию. Это называется траектория. Эта строчка может быть совершенно разной. Важнее не внешний вид, а начальная и конечная точки движения. Они соединены линией, называемой сдвигом. Это тоже векторная величина. Кроме того, он всегда направлен от начала движения к точке, где движение было остановлено. Его принято обозначать латинской буквой r.
Важнее не внешний вид, а начальная и конечная точки движения. Они соединены линией, называемой сдвигом. Это тоже векторная величина. Кроме того, он всегда направлен от начала движения к точке, где движение было остановлено. Его принято обозначать латинской буквой r.
Здесь может возникнуть вопрос: «Является ли путь векторной величиной?» В общем, это утверждение не соответствует действительности. Путь равен длине пути и не имеет определенного направления. Исключением является ситуация, когда рассматривается прямолинейное движение в одном направлении. Следовательно, величина вектора смещения совпадает по величине с траекторией, и их направление оказывается таким же. Следовательно, при рассмотрении движения по прямой без изменения направления движения, путь может быть включен в примеры векторных величин.
Четвертая величина — ускорение
это характеристика скорости изменения скорости. Кроме того, ускорение может иметь как положительные, так и отрицательные значения. При движении по прямой он направлен в сторону большей скорости. Если движение происходит по криволинейной траектории, вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
При движении по прямой он направлен в сторону большей скорости. Если движение происходит по криволинейной траектории, вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Среднее и мгновенное значения ускорения разделены. Первое следует рассчитывать как отношение изменения скорости за определенный период времени к этому времени. Когда рассматриваемый временной интервал стремится к нулю, мы говорим о мгновенном ускорении.
Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс — это векторная величина, потому что она напрямую связана со скоростью и силой, прилагаемой к телу. У них обоих есть направление и импульс.
По определению, последняя равна произведению веса тела и скорости. Используя понятие количества движения тела, вы можете иначе написать известный закон Ньютона. Оказывается, изменение количества движения равно произведению силы на временной интервал.
В физике важную роль играет закон сохранения количества движения, который гласит, что в замкнутой системе тел его полный импульс постоянен.
Мы очень кратко перечислили, какие (векторные) величины изучаются в курсе физики.
Задача о неупругом ударе
Состояние. На путях есть стационарная площадка. К вам приближается карета со скоростью 4 м / с. Вес платформы и вагона — 10 и 40 тонн соответственно. Автомобиль ударяется о платформу, происходит автоматическое сцепление. Необходимо рассчитать скорость системы платформы автомобиля после удара.
Решение. Сначала необходимо ввести следующие обозначения: скорость автомобиля до удара — v1, машина с платформой после спаривания — v, масса машины — m1, платформа — m2. В зависимости от состояния задачи необходимо знать значение скорости v.
Правила решения таких задач требуют схематического изображения системы до и после взаимодействия. Ось OX целесообразно направить по рельсам в направлении движения каретки.
В этих условиях транспортную систему можно считать закрытой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, трение о рельсы не учитывается.
Согласно закону сохранения количества движения их векторная сумма до взаимодействия между автомобилем и платформой равна общей для сцепления после удара. Сначала платформа не двигалась, поэтому ее импульс был нулевым. Переместилась только машина, ее импульс — произведение m1 и v1.
Поскольку удар был неупругим, то есть автомобиль зацепился за платформу, а затем начал катиться вместе в одном направлении, импульс системы не изменил направление. Но его значение изменилось. А именно произведением суммы массы автомобиля с платформой на требуемую скорость.
Вы можете записать это равенство: m1 * v1 = (m1 + m2) * v. Это будет верно для проекции векторов момента на выбранную ось. Легко вывести равенство, которое потребуется для вычисления желаемой скорости: v = m1 * v1 / (m1 + m2).
Согласно правилам, значения массы следует переводить из тонн в килограммы. Поэтому, когда вы подставляете их в формулу, вы должны сначала умножить известные значения на тысячу. Простые вычисления дают число 0,75 м / с.
Отвечать. Скорость вагона-платформы 0,75 м / с.
Задача с разделением тела на части
Состояние. Скорость летящей гранаты — 20 м / с. Он разделен на две части. Масса первого 1,8 кг. Продолжайте движение в том направлении, в котором летела граната, со скоростью 50 м / с. Второй осколок имеет массу 1,2 кг. Насколько это быстро?
Решение. Обозначьте массы фрагментов буквами m1 и m2. Их скорости будут v1 и v2 соответственно. Начальная скорость гранаты v. В задаче надо вычислить значение v2.
Чтобы более крупный осколок продолжал двигаться в том же направлении, что и вся граната, второй должен лететь в противоположном направлении. Если выбрать направление оси, которое было при начальном импульсе, то после разрыва большой фрагмент летит вдоль оси, а маленький — против оси.
В этой задаче допустимо использование закона сохранения количества движения в связи с тем, что взрыв гранаты происходит мгновенно. Поэтому, несмотря на то, что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его величиной по абсолютной величине.
Сумма значений вектора импульса после взрыва гранаты такая же, как и раньше. Если написать закон сохранения количества движения тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Легко выразить требуемую скорость. Он будет определяться по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м / с.
Отвечать. Скорость маленького осколка — 25 м / с.
Задача про выстрел под углом
Состояние. Пушка установлена на платформе массой M. Из нее выстреливается снаряд массой m. Он взлетает под углом α к горизонту со скоростью v (заданной относительно земли). Необходимо знать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения количества движения в проекции на ось OX. Но только в том случае, если проекция возникающих внешних сил равна нулю.
Для направления оси OX нужно выбрать сторону, по которой будет лететь пуля, и параллельную горизонтальной линии. В этом случае проекции сил тяжести и реакция опоры на OX будут равны нулю.
В этом случае проекции сил тяжести и реакция опоры на OX будут равны нулю.
Проблема будет решена в общем виде, так как конкретных данных для известных значений нет. Ответ — формула.
Импульс системы перед выстрелом был равен нулю, так как платформа и пуля были неподвижны. Пусть требуемая скорость платформы обозначается латинской буквой u. Тогда его импульс после выстрела будет определяться как произведение массы и проекции скорости. Поскольку платформа будет втягиваться (против направления оси OX), значение импульса будет со знаком минус.
Импульс снаряда является произведением его массы и проекции скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквальном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из него путем несложных преобразований получается формула ответа: u = (mv * cos α) / M.
Отвечать. Скорость платформы определяется по формуле u = (mv * cos α) / M.
Задача о переправе через реку
Состояние. Ширина реки по всей длине одинакова и равна, берега параллельны. Известны скорость потока воды в реке v1 и собственная скорость лодки v2. 1). При переправе нос лодки направлен строго на противоположный берег. Как далеко он уйдет вниз по течению? 2). Под каким углом α нужно ориентировать нос лодки так, чтобы она доходила до противоположного берега строго перпендикулярно начальной точке? Сколько времени займет такой переход?
Решение. 1). Максимальная скорость лодки — это векторная сумма двух значений. Первый из них — течение реки, которая направляется по берегам. Второй — собственная скорость лодки перпендикулярно берегу. На чертеже изображены два одинаковых треугольника. Первый формируется шириной реки и расстоянием, пройденным лодкой. Второй — из векторов скорости.
Следующая запись следует: s / l = v1 / v2. После преобразования получается формула искомого значения: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться собственный вектор скорости, равен отношению между модулями v1 и v2. Чтобы рассчитать время в пути, вам нужно разделить ширину реки на рассчитанную максимальную скорость. Величина последнего рассчитывается по теореме Пифагора.
Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться собственный вектор скорости, равен отношению между модулями v1 и v2. Чтобы рассчитать время в пути, вам нужно разделить ширину реки на рассчитанную максимальную скорость. Величина последнего рассчитывается по теореме Пифагора.
v = (v22 — v12), поэтому t = l / (√ (v22 — v12)).
Отвечать. 1) s = l * (v1 / v2), 2) sin α = v1 / v2, t = l / (√ (v22 — v12)).
Поделиться:
- Предыдущая записьРеки, вытекающие из Байкала. Единственная река, вытекающая из Байкала
- Следующая записьБалтийское море: соленость, глубина, координаты, описание
×
Рекомендуем посмотреть
Adblock
detector
Векторная величина в физике. Примеры векторных величин
Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.
Как отличить скалярную величину от векторной?
Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.
Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.
При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.
Какие действия чаще всего выполняются с векторами?
Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.
Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.
Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.
Какие векторы изучают в физике?
Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.
| Обозначение в формуле | Наименование |
| v | скорость |
| r | перемещение |
| а | ускорение |
| F | сила |
| р | импульс |
| Е | напряженность электрического поля |
| В | магнитная индукция |
| М | момент силы |
Теперь немного подробнее о некоторых из этих величин.
Первая величина — скорость
С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.
Это обусловлено тем, что ее изучают в числе первых.
Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.
Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.
Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.
Вторая величина — сила
Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.
| Сила | Точка приложения | Направление |
| тяжести | центр тела | к центру Земли |
| всемирного тяготения | центр тела | к центру другого тела |
| упругости | место соприкосновения взаимодействующих тел | против внешнего воздействия |
| трения | между соприкасающимися поверхностями | в сторону, противоположную движению |
Также еще векторной величиной является равнодействующая сила.
Третья величина — перемещение
Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.
Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении.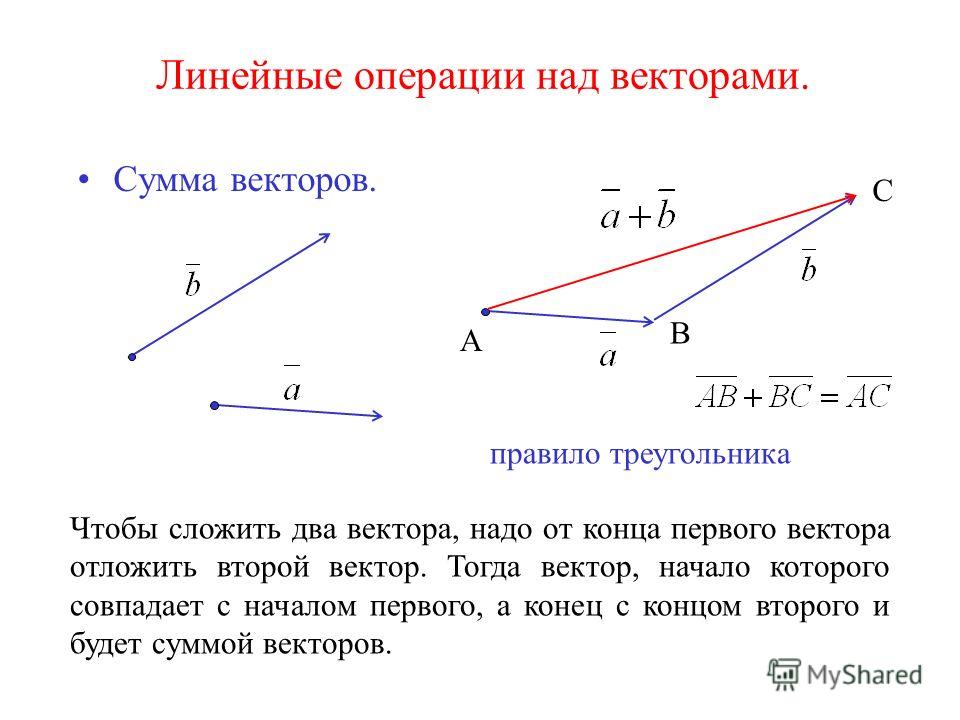 Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.
Четвертая величина — ускорение
Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.
Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.
Пятая величина — импульс
По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.
По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.
В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.
Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.
Задача о неупругом ударе
Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.
Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v1, вагона с платформой после сцепки — v, масса вагона m1, платформы — m2.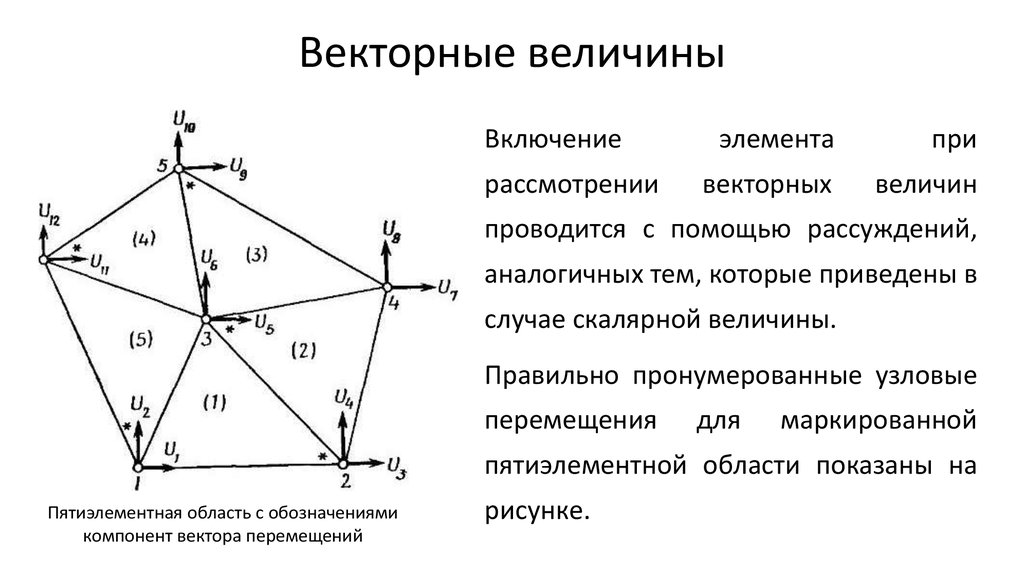 По условию задачи необходимо узнать значение скорости v.
По условию задачи необходимо узнать значение скорости v.
Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.
В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.
Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m1 и v1.
Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.
Можно записать такое равенство: m1 * v1 = (m1 + m2) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m1 * v1 / (m1 + m2).
По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.
Ответ. Скорость вагона с платформой равна 0,75 м/с.
Задача с разделением тела на части
Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?
Решение. Пусть массы осколков обозначены буквами m1 и m2. Их скорости соответственно будут v1 и v2. Начальная скорость гранаты — v. В задаче нужно вычислить значение v2.
Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.
В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.
Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m1 + m2) * v = m1 * v1 — m2 * v2. Из него просто выразить искомую скорость. Она определится по формуле: v2 = ((m1 + m2) * v — m1 * v1) / m2. После подстановки числовых значений и расчетов получается 25 м/с.
После подстановки числовых значений и расчетов получается 25 м/с.
Ответ. Скорость маленького осколка равна 25 м/с.
Задача про выстрел под углом
Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.
Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.
За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.
Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.
Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.
Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.
Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.
Задача о переправе через реку
Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v1 и собственная скорость катера v2. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?
Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.
Из них следует такая запись: s / l = v1 / v2. После преобразования получается формула для искомой величины: s = l * (v1 / v2).
2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v1 и v2. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v1 и v2. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.
v = √(v22 – v12), тогда t = l / (√(v22 – v12)).
Ответ. 1). s = l * (v1 / v2), 2). sin α = v1 / v2, t = l / (√(v22 – v12)).
PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
- 2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.
 4 Статика
4 Статика - 2.5 Механические колебания и волны
- 3 Термодинамика и МКТ
- 3.1 МКТ
- 3.2 Термодинамика
- 4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
- 5 Оптика.
 СТО
СТО- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
- 5.3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
- 6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 7 Общие темы
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.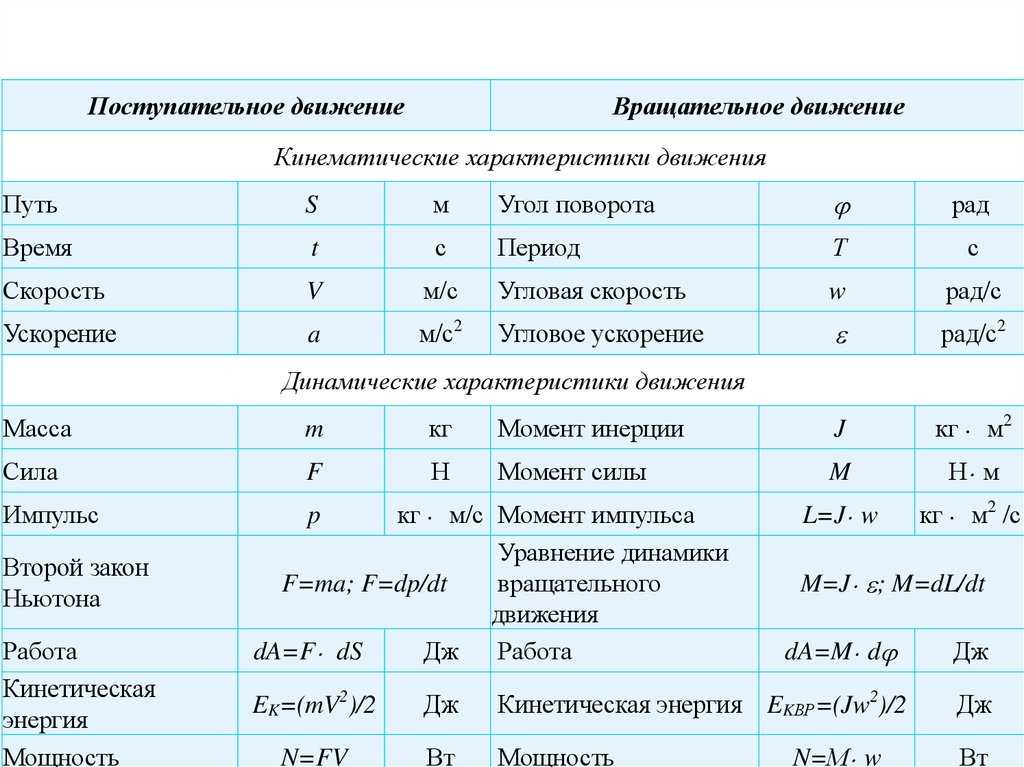
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике
Новые страницы
Запрос не дал результатов.
Что является векторной величиной?
Что является векторной величиной?
Векторная величина или вектор — это всякая величина, обладающая направлением. Скалярная величина или скаляр — это всякая величина, не обладающая направлением. Пример 1.
Скалярная величина или скаляр — это всякая величина, не обладающая направлением. Пример 1.
Что такое векторная величина в физике?
Векторная величина (вектор) – это физическая величина, которая имеет две характеристики – модуль и направление в пространстве. Примеры векторных величин: скорость, сила, ускорение, напряженность и т. д. Геометрически вектор изображается как направленный отрезок прямой линии, длина которого в масштабе – модуль вектора.
Что такое векторная величина 7 класс?
Ве́кторная величина́ — физическая величина, являющаяся вектором (тензором ранга 1). Противопоставляется с одной стороны скалярным (тензорам ранга 0), с другой — тензорным величинам (строго говоря — тензорам ранга 2 и более). Также может противопоставляться тем или иным объектам совершенно другой математической природы.
Какие из физических величин являются векторными?
Вектор — это величина, имеющая численное значение и направление. Например скорость, ускорение, сила, перемещение. 3. Скалярная величина, в отличии от векторной, не имеет направления.
Например скорость, ускорение, сила, перемещение. 3. Скалярная величина, в отличии от векторной, не имеет направления.
Что называется векторной величиной?
Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление. … Примеры — скорость, сила, перемещение (перемещением движущейся точки в данный момент времени называют вектор с началом в точке начала ее движения, и концом в точке ее расположения в этот момент.
Какую величину называют скаляром приведите примеры?
scalaris «ступенчатый») в физике — величина, каждое значение которой может быть выражено одним (как правило, действительным) числом. … К скалярным величинам относятся длина, площадь, время, температура, электрический заряд, работа, статистический вес и т. д. Скалярная величина также называется скаляром.
Что не является скалярной величиной?
Не скалярные величины — величины, имеющие направление, векторные. Векторные величины (векторы) — величины, которые кроме численного значения имеют определённое направление в пространстве. Скорость, сила,ускорение, импульс, давление, напряженность электрического поля — векторные величины.
Векторные величины (векторы) — величины, которые кроме численного значения имеют определённое направление в пространстве. Скорость, сила,ускорение, импульс, давление, напряженность электрического поля — векторные величины.
Какие величины называют векторными и скалярными приведите примеры?
Векторные величины имеют направление (примером может послужит сила «F» или ускорение «a»). … Скалярные же величины имеют лишь значение, например масса «m».
Какая физическая величина является скалярной а не векторной?
Скалярная величина (от лат. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. … К скалярным величинам относятся длина, площадь, время, температура и т.
Что такое сила сила векторная величина или скалярная?
Си́ла — физическая векторная величина, являющаяся мерой воздействия на данное тело со стороны других тел или полей. Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Приложение силы обусловливает изменение скорости тела или появление деформаций и механических напряжений.
Как складываются векторные величины?
Для того чтобы сложить векторы и , нужно поместить начало вектора в конец вектора . Тогда вектор с началом в начале и концом в конце и будет равен их сумме. Точно так же можно складывать любое число векторов.
Что такое перемещение Какая это величина?
Перемещение, так же как и путь, обозначается буквой S и измеряется в метрах. Но это две разные величины, которые необходимо различать. Величины, кроме числового значения, имеют направление, называют векторными величинами. Перемещение — это векторная величина.
Какой формулой выражается перемещение?
Перемещение s→- перемещение; вектор, соединяющий начальную и конечную точки движения. Проекция вектора перемещения на данную ось: sx = x — x0. Путь (l) — длина траектории.
Что такое перемещение?
Перемеще́ние (в кинематике) — изменение положения физического тела в пространстве с течением времени относительно выбранной системы отсчёта. — от итал. spostamento (перемещение). — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах; в системе СГС — в сантиметрах.
— от итал. spostamento (перемещение). — это модуль перемещения, в Международной системе единиц (СИ) измеряется в метрах; в системе СГС — в сантиметрах.
Что означает фраза перемещение векторная величина?
Перемещение — векторная величина! … Это вектор, который проведен из начальной точки отправления тела в конечную точку. Имеет численное значение, равное длине вектора.
Что такое траектория перемещения?
Траектория — воображаемая линия, по которой движется тело. Путь — длина траектории. Перемещение — направленный отрезок, соединяющий начальное и конечное положения тела.
Чему равно перемещение в физике?
Перемещение — направленный отрезок, соединяющий начальную точку и конечную при движении тела, но тело начало движение из той же точки, в которую вернулось, следовательно, перемещение мяча равно нулю: Δr=0.
Что такое перемещение от чего оно зависит?
Перемещение — это разница между этими точками, она не зависит от того, каким путём объект попал из первой точки во вторую. Пройденное же расстояние — это общая длина пути, пройденного объектом, пока он двигался от одной точки в другую.
Пройденное же расстояние — это общая длина пути, пройденного объектом, пока он двигался от одной точки в другую.
Что больше Путь или перемещение?
Путь всегда больше или равен модулю перемещения. Путь не может быть отрицательным. Двигаясь по окружности радиусом , материальная точка совершила половину полного оборота.
Как найти перемещение по координатам?
Перемещение тела найдем по формуле: S = х — х0. Конечную координату х можно определить, подставляя в уравнение движения время t1: х = 4 — 3t1. В общем виде формула перемещения: S = 4 — 3t1 — х0 = 4 — 3t1 — 4 = — 3t1 = -3 · 2 = — 6 м (Тело движется в отрицательном направлении оси ОХ).
Как рассчитать перемещение при равномерном движении?
Скорость равномерного прямолинейного движения прямо пропорциональна перемещению тела и обратно пропорциональна значению времени этого перемещения. v → = s → t . Можно выразить перемещение из этой формулы, умножив обе части на значение времени: s → = v → ⋅ t .
Как найти перемещение по уравнению?
Если начальная скорость тела равна нулю, то формула проекции перемещения тела имеет вид: sx = . Чтобы получить уравнение движения тела, подставим в формулу проекции перемещения ее выражение через разность координат sx = x – x0. x = x0 + v0xt + .
Как вывести формулу перемещения при равноускоренном движении?
равноускоренном движении: Sх = V0x t + ахt2/2.
Как найти ускорение при равномерном движении?
Ускорение тела при его равноускоренном движении — это величина, равная отношению изменения скорости к промежутку времени, за которое это изменение произошло: a → = v → − v 0 → t .
Как найти S при равноускоренном движении?
1. Скорость и путь при равноускоренном движении
- Рассмотрим некоторые особенности перемещения тела при прямолинейном равноускоренном движении без начальной скорости. …
- s = v 0 t + a t 2 2 , где а — это ускорение.
 2/2 выразить начальную скорость, ускорение.
2/2 выразить начальную скорость, ускорение. Как вывести формулу пути равноускоренного движения?
Формулы для равноускоренного движения v=v0+at v = v 0 + a t . Здесь v0 — начальная скорость тела, a=const a = c o n s t — ускорение. Покажем на графике, что при равноускоренном движении зависимость v(t) имеет вид прямой линии. Ускорение можно определить по углу наклона графика скорости.
Как в физике обозначается начальная скорость?
где ˉv0 – начальная скорость движения, ˉa=const .
Как определить пройденный путь?
Расчет пути при равномерном движении Чтобы определить путь, который прошло тело при равномерном движении, необходимо скорость движения тела умножить на время которое это тело двигалось. S=V*t.
Что такое путь пройденный телом?
Путь, пройденный телом— это длина траектории. А длина траектории-это линия по которой движется тело.
Скалярные и векторные величины в физике и математике
Величиной в физике и математике называют свойства физических тел, измеряемых при помощи выполнения математических операций.
 Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.
Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.Содержание
- Особенности скалярных величин
- Определение положительного скаляра и его измерения
- Особенности векторных величин
- Свойства векторов
Особенности скалярных величин
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
- Чистые скаляры. Характеризуются числовым значением, не находящимся в зависимости от осей отсчета — линий пересечения плоских поверхностей в единой системе координат.
- Псевдоскаляры. Находятся при помощи расчета числа, знак которого зависит от положительного направления осей в системе координат.
В физике в список скалярных величин входят:
- Масса — определяет величину материи и ее гравитационные свойства.
 Измеряется в килограммах и обозначается буквой латинского алфавита m.
Измеряется в килограммах и обозначается буквой латинского алфавита m. - Температура — средняя кинетическая энергия физического тела. Выражается в кельвинах или градусах Цельсия.
- Работа — мера действия силы на физическое тело или систему тел. Измеряется в Джоулях и обозначается латинской буквой A.
- Длина — величина, определяющая дистанцию между 2 концами тела в продольном направлении. Исчисляется в метрах. Особым видом длины является путь — скаляр, выражающий расстояние между начальным и конечным положением объекта, осуществляющего перемещение по заданной траектории.
- Время — продолжительность действия или события. Рассчитывается в секундах.
- Период — время совершения 1 полного колебания. Обозначается символом T и измеряется в секундах.
- Частота — величина, обратная периоду. Определяет количество полных колебаний в единицу времени. Рассчитывается в Герцах.
- Объем — скаляр, обозначающий размер пространства, ограниченного поверхностями со всех сторон.
 Измеряется в м3.
Измеряется в м3. - Напряжение — измеряет изменение потенциальной энергии тела, приходящейся на единицу заряда. Обозначается буквой U и рассчитывается в Вольтах.
- Сила тока — скаляр, показывающий число электрических зарядов, проходящих через сечение проводника в единицу времени. Обозначается символом I и рассчитывается в Амперах.
- Энергия — обозначает способность тела осуществлять работу.
Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры.
 Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).
Особенности векторных величин
Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением».
 Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.В физике и математике примерами векторных величин являются:
- Сила — мера взаимодействия физических веществ. Обозначается латинской буквой F и измеряется в Ньютонах. Три закона Исаака Ньютона составляют основу классической механики. С их помощью можно определить массу тела и его ускорение.
- Скорость — расстояние, пройденное материей за определенный временной промежуток. Маркируется символом V и рассчитывается в м/с. Скорость используется для определения пути и времени движения предмета при помощи формулы: S = V * t. Скорость, с которой тело движется по окружности, называется линейной.
- Ускорение — величина, показывающая изменение показателей скорости физического тела. Ускорение свободного падения действует на все тела, придавая им силу тяжести.
 Оно направлено к ядру Земли и равняется 9,8 м/с2
Оно направлено к ядру Земли и равняется 9,8 м/с2 - Импульс — характеризует величину движения тела. Маркируется буквой латинского алфавита p и рассчитывается в кг*м/с. С помощью этой величины человек может определить массу физического тела и скорость ее передвижения.
На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка.
 Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:- Произведение вектора на косинус между осью и направленным отрезком равен проекции вектора.
- Проекция на ось принимает значения меньше 0, если отрезок с осью образует тупой угол.
- Проекция на ось принимает значение больше 0, если отрезок с осью образует острый угол.
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.
Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината.
 Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.

С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Предыдущая
ФизикаПружинный маятник — формулы и уравнения нахождения величин
Следующая
ФизикаМатематический маятник — определение, формулы и принцип действия
Векторные величины
В физике имеются многие величины, для знания которых недостаточно знать, чему равна эта величина.
 Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления.
Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления.Физические величины, характеризуемые размером величины и ее направлением, называются векторными. Размер векторной величины чаще называется ее модулем. В отличие от векторных, величины, характеризующиеся только своим значением, называются скалярными.
 Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов.
Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов.Векторные величины на рисунках принято изображать в виде стрелок. Причем направление стрелки указывает направление векторной величины, а длина стрелки определяется ее модулем. Обозначаются векторные величины буквами. Причем на рисунках над буквой, обозначающей векторную величину рисуется стрелочка, а в печатном тексте эти буквы печатаются жирным шрифтом.
Пусть при своем движении тело переместилось из точки А в точку В. Величину изменения положения тела можно определить как расстояние от точки А до точки В.
 Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля.
Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля.Векторные величины можно складывать. Так пусть, например, тело сначала переместилось из точки А в точку В, а затем еще переместилось в точку С.
 Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника.
Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника. Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a.
Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a.Вектора можно вычитать. Для того, чтобы из вектора а вычесть вектор b надо к вектору а прибавить вектор противоположный вектору b: c = a – b = a + (-b). Заметим, что –b – это не отрицательный вектор, а вектор противоположный вектору b, то есть вектор по модулю равный вектору b, а по направлению противоположный ему.
 Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.
Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.Вектор можно умножать на скаляр. Если вектор а умножить на скаляр α, то получится вектор с = α·а, направление которого совпадает с направлением вектора а, а модуль в α раз больше.
Вектора можно скалярно умножать друг на друга. Скалярным произведением векторов а и b называется скаляр , где и — модули векторов а и b, а α – угол между ними. Замети, что результатом скалярного произведения двух векторов является скаляр. Причем знак этого произведения может быть как положительный, так и отрицательный. Это определяется знаком косинуса. Если угол между векторами острый, то их скалярное произведение положительно, а если тупой – то отрицательно.

Пусть есть вектор а и координатная ось Х. Из начала и конца вектора опустим перпендикуляры на координатную ось. Длина отрезка на координатной оси между основаниями этих перпендикуляров – ах — является проекцией вектора а на ось Х. Проекция вектора на ось – величина скалярная. При этом она может быть положительной и отрицательной. Если вектор и ось направлены преимущественно в одну сторону, то проекция вектора на ось положительна, а если вектор и ось направлены в противоположные стороны, то отрицательна. Так проекция вектора а на ось Х положительная, а проекция вектора b на ту же ось отрицательная. Если вектор и ось взаимно перпендикулярны, то проекция вектора на ось равна нулю. Если угол между вектором а и осью Х равен α, то проекция вектора на ось равна: . На рисунке изображен вектор а и система координат XY. Если угол между вектором и осью Х равен α, то угол между вектором и осью Y равен 90° — α.
 При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
.
При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
.Если , то . Аналогично в проекции на ось Y.
Скалярное произведение векторов а и b можно выразить через их проекции: .
Любой вектор можно представить в виде суммы двух или более векторов. Часто вектора представляют в виде суммы двух взаимно перпендикулярных векторов, направленных вдоль координатных осей X и Y. На рисунке представлено разложение вектора а на два взаимно перпендикулярных вектора ах и аy. Вектора ах и аy называются составляющими вектора а по направлениям Х и Y.
Скаляры и векторы
Чтобы лучше понять науку движения необходимо использовать некоторые математические идеи из векторный анализ .
 Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных:
Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных: НЕ ПАНИКУЙ! . В векторном анализе есть много сложных частей, и мы не будем их рассматривать. Мы собираемся ограничиться самыми основами. Векторы позволяют нам смотреть на сложные, многомерные проблемы как более простая группа одномерных задач. В основном нас будут интересовать определения Слова немного странные, но идеи очень мощный, как вы увидите. Если вы хотите узнать больше о векторах, вы можете скачать этот отчет о векторный анализ.
Математика и наука были изобретены людьми для описания и понимать окружающий мир. Мы живем в (по крайней мере) четырехмерном мире, управляемом течение времени и трех пространственных измерений; вверх и вниз, влево и вправо, и вперед и назад. Заметим, что существуют некоторые величины и процессы в наш мир, которые зависят от направления , в котором они происходят, и есть некоторые величины, которые не зависят по направлению.
 Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .
Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .Векторные величины имеют две характеристики: величину и направление. Скалярные величины имеют только величину. Когда сравнение две векторные величины одного и того же типа, вы должны сравнить обе величина и направление. Для скаляров вам нужно только сравнивать величина. При выполнении любой математической операции над векторной величиной (например, сложение, вычитание, умножение .
 .) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры.
.) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры.На слайде мы перечисляем некоторые из обсуждаемых физических величин в Руководство для начинающих по аэронавтике и сгруппировать их либо в векторные, либо в скалярные величины. особенно интерес, силы которые работают на летающих самолетах, масса, тяга и аэродинамические силы, все векторные величины. Результирующий движение самолета по водоизмещению, скорости и ускорения также являются векторными величинами. Эти величины можно определить, применяя законы Ньютона для векторов. Скалярные величины включают большую часть термодинамическое состояние переменные, связанные с двигательной системой, такие как плотность, давление и температура пропеллентов. энергия, Работа, а также энтропия связанные с двигателями также скалярные величины.
Векторы имеют величину и направление, скаляры имеют только величину.
 Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество».
Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество».В то время как законы Ньютона описывают результирующее движение тела, существуют специальные уравнения, описывающие движение жидкостей, газы и жидкости. Для любой физической системы масса, импульс и энергия системы необходимо сохранить.
 Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
Деятельность:
Экскурсии с гидомНавигация ..
- Домашняя страница руководства для начинающих
Примеры векторных и скалярных величин в физике
При изучении физики существует множество различных аспектов измерения и множество типов инструментов измерения. Скалярные и векторные величины являются двумя из этих типов инструментов измерения. Продолжайте читать примеры скалярной величины и примеры векторной величины в физике.

инфографические скалярные и векторные примеры
Advertisement
Определение скалярных и векторных величин
Понимание разницы между скалярными и векторными величинами является важным первым шагом в физике. Основное различие в их определениях:
- Скаляр является измерением единицы строго в величине .
- Вектор — это измерение, которое относится как к величина единицы и направление движения единицы.
Другими словами, скалярная величина имеет величину, такую как размер или длина, но не имеет определенного направления. Когда у него есть конкретное направление, это векторная величина.
Примеры скалярных величин
Скалярные величины, как указано выше, являются измерениями, строго относящимися к величине среды. В скалярной величине совершенно нет направленных составляющих — только величина среды.
 Исследуйте 10 примеров скалярных величин.
Исследуйте 10 примеров скалярных величин.Площадь
Если вы измеряете площадь поверхности участка земли или двумерного объекта, у него нет направления, только величина. Вы можете связать с ним направление, когда рассматриваемый объект является трехмерным, поскольку вы измеряете его в разных направлениях. Но площадь является скалярной, когда измерение простое и двумерное.
Плотность
Плотность объекта можно найти, разделив его массу на объем. Поскольку в этом расчете требуется только две точки, это скалярная величина. Направление не влияет на плотность объекта.
Расстояние
Сколько вы прошли? Измеряя расстояние, вы определяете величину пройденного вами пространства. Он не включает водоизмещение или скорость; скалярная величина расстояния обсуждает только то, сколько земли было пройдено.
Энергия
Как и другие скалярные величины, энергия является произведением двух факторов (в данном случае силы и перемещения). Он описывает величину использования энергии без измерения направления.

Реклама
Масса
Многие люди используют слова «вес» и «масса» как синонимы, но это не одно и то же. Масса – это количество материи, присутствующей в объекте. Это не зависит от направления; масса объекта одинакова независимо от того, в каком направлении движется объект.
Скорость
Может быть трудно понять разницу между скоростью и скоростью. Однако знание того, что скорость является скалярной величиной, может оказаться полезным, поскольку при измерении скорости направление не имеет значения.
Реклама
Температура
Когда вы измеряете температуру термометром, вы измеряете свою среднюю тепловую энергию. Поскольку вы уже знаете, что энергия является скалярной величиной, вы, вероятно, можете понять, что температура также скалярна.
Время
Скалярные величины часто относятся ко времени, которое включает в себя измерение лет, месяцев, недель, дней, часов, минут, секунд и даже миллисекунд. При измерении времени не учитывается или не измеряется направление, хотя кажется, что время всегда движется вперед.

Объем
Скалярное количество может относиться к объему среды, например, к ее объему. Все, от тонн и унций до граммов, миллилитров и микрограммов, — все это скалярные величины, если они применяются к измеряемой среде, а не к движению среды.
Работа
Работа – это энергия, переданная объекту силой. Это скалярная величина, поскольку она является произведением силы и перемещения. Работа — это не то же самое, что сила, которая является векторной величиной, потому что работа — это результат действия силы.
Примеры векторных величин
Векторные величины относятся как к направлению движения среды, так и к измерению скалярной величины. Вы можете заметить, что скалярные произведения часто являются произведениями двух векторных величин. Ознакомьтесь с этими 10 примерами векторных величин, встречающихся в вашей повседневной жизни.
Ускорение
Хотя скорость является скалярной величиной, ускорение отличается. Ускорение измеряет скорость изменения скорости объекта.
 Он учитывает период времени, а также направление, что делает его векторной величиной.
Он учитывает период времени, а также направление, что делает его векторной величиной. Реклама
Смещение
Скалярная величина расстояния измеряет землю, пройденную движением, а смещение измеряет, насколько далеко она сдвинулась от своего первоначального местоположения. Вы можете видеть, что направление и величина очень важны при измерении смещения!
Сила
Сила имеет как величину, так и направление. В отличие от скалярного количества работы, сила заставляет объект изменять свою скорость. Думайте о таких силах, как гравитация, когда решаете, является ли это векторной величиной.
Повышение/понижение температуры
Измерение температуры среды является скалярной величиной. Однако измерение повышения или понижения температуры среды является векторной величиной. У него есть направление и величина.
Магнитная поляризация
Поляризация указывает на то, что два устройства отошли друг от друга. Направление (вдали друг от друга), а также величина (насколько далеко или насколько) являются важными факторами при измерении поляризации.

Импульс
Импульс указывает, что объект находится в движении. Это произведение массы и скорости, и его можно рассчитать только в том случае, если вы знаете, как быстро движется объект (величина) и в каком направлении.
Положение
Может показаться, что фиксированное положение не имеет ни величины, ни направления. И это правильно — если вы определяете «позицию» таким образом. Вектор положения берется относительно начала системы координат; то есть он существует в конце прямой линии, которая соединяется с серединой оси. С этой точки зрения легко увидеть направление и величину.
Реклама
Тяга
Тяга — это тип силы реакции, которая также имеет величину и направление. Подумайте о том, что вас толкают или толкают по воздуху — вы определенно движетесь в направлении, имеющем огромную величину! Чаще всего он используется в механике и аэронавтике.
Скорость
Измерение скорости, с которой объект меняет положение, является векторной величиной.
 Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.
Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.Вес
Вес объекта является произведением его массы и действующего на него гравитационного ускорения. Поскольку это связано с силой тяжести, вес имеет направление (вниз), а также величину.
Реклама
Источник дополнительной технической информации в Интернете
Высокотехнические примеры и пояснения, касающиеся скалярных и векторных величин, можно найти на веб-сайте National Aeronautics and Space. Он содержит полное описание скаляров и векторов, а также примеры и способы их использования.
Физика вокруг нас
Итак, теперь у вас есть несколько примеров скалярных и векторных величин, и вы понимаете некоторые различия между ними. Для получения дополнительной информации о физике ознакомьтесь с этими примерами контактной силы, которые вы, вероятно, увидите в физическом мире.
 Вы также можете больше углубиться в законы физики с повседневными примерами инерции.
Вы также можете больше углубиться в законы физики с повседневными примерами инерции.Штатный писатель
Объяснение урока: Векторные величины | Nagwa
В этом объяснителе мы научимся описывать, как векторы используются в механике для решения задач в двух измерениях.
При моделировании реального движения с помощью математики необходимо различать векторные и скалярные величины. Скалярная величина может принимать только положительные (или нулевые) значения, указывающие на величину определенных признаков независимо от направления. Расстояние и скорость являются скалярными величинами потому что они не задают направление, а соответствующие реальные признаки имеют конкретное направление. Например, если нам говорят, что самолет летит со скоростью 200 километров в час, это говорит нам о его скорости путешествует, но не туда, куда он идет. Такие величины, как время и масса, также считаются скалярами, поскольку они по своей сути не касаются направлений и, следовательно, может принимать только положительные значения.

С другой стороны, векторная величина указывает как направление, так и величину. Перемещение и скорость являются векторными аналогами расстояние и скорость соответственно. Другими словами, расстояние — это величина смещения, а скорость — величина скорости. Поскольку скорость объекта также указывает его направление, самолет, летящий на север со скоростью 200 километров в час будет отличаться от скорости другого самолета, летящего на юг. с той же скоростью.
Рассмотрим, как задается направление в одномерном (или линейном) движении. В линейном движении есть ровно два разных варианта для направлений, поэтому направления можно указать, поставив положительный или отрицательный знак перед их скалярными аналогами. Для этого мы можем использовать следующие шаги.
Практическое руководство. Определение направлений векторных величин в линейном движении
Чтобы указать направление движения объекта по прямой линии, нам нужно
- определяют положительное направление, которое называют ориентацией движения,
- сравнивают заданное направление с положительным направлением:
- если направление совпадает с положительным направлением, перед ним ставится знак плюс (часто опускается).
 скалярный аналог;
скалярный аналог; - если направление не совпадает с положительным направлением, перед скалярным аналогом ставится знак минус.
- если направление совпадает с положительным направлением, перед ним ставится знак плюс (часто опускается).
Рассмотрим скорости самолетов из приведенного выше примера. Здесь один самолет летит на север, а другой летит на юг с той же скоростью. Мы не можем определить скорости двух плоскостей, не назначив сначала либо север, либо юг положительной стороной. направление. Если мы говорим, что север является положительным направлением, скорость первой плоскости равна +200 км/ч или просто 200 км/ч, а второй самолет имеет скорость −200 км/ч. Заметим, что единица скорости равна скорости.
Заметим, что в первом случае мы опустили положительный знак в скорости, чтобы написать 200 км/ч, что соответствует его скорости. В таких случаях мы должны будьте осторожны, чтобы отличать векторные величины от скалярных величин. Говоря, что самолет имеет скорость 200 км/ч — это не то же самое, что сказать, что он имеет скорость 200 км/ч, так как последний содержит дополнительную информацию о его направлении.
 Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую.
Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую.В нашем первом примере мы найдем скорость и смещение объекта относительно их скалярных аналогов, когда их направления указано.
Пример 1. Расчет скорости, скорости, расстояния и перемещения по прямым путям
Автомобиль движется по шоссе по указанному маршруту.
Расстояние между точками А и В составляет 60 км, а расстояние между точками B и C составляет 30 км. Автомобиль едет из А в С, проходит через В, затем возвращается в A, проходящий через B. Внутри каждого сегмента автомобиль движется с постоянной скоростью 90 км/ч. Чему равно перемещение автомобиля из С в В? Кроме того, что такое скорость этого отрезка?
Ответ
Перемещение и скорость являются векторными величинами, скалярными аналогами которых являются расстояние и скорость соответственно.
 Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.
Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.Сначала рассмотрим смещение. Скалярным аналогом смещения является расстояние. Так как мы хотим найти смещение от C до B, нам нужно сначала найти расстояние между этими двумя точками. Нам дано, что расстояние между B и C равно 30 км, что равно величине водоизмещения. Направление от С до B направлен влево, что обозначается знаком минус. Следовательно, смещение от C до B задается путем помещения отрицательного знака в фронт скалярного аналога, который составляет 30 км.
 Это дает нам
−30 км.
Это дает нам
−30 км.Далее найдем скорость. Скалярным аналогом скорости является скорость, и нам известно, что автомобиль движется с постоянной скоростью. скорость 90 км/ч; следовательно, это равно величине скорости от C в B. Направление скорости автомобиля из C в B направлено влево, что противоположно положительному направлению. Следовательно, скорость от C до B задается путем помещения знака минус перед скалярным аналогом, 90 км/ч. Это дает нам −90 км/ч.
Следовательно, перемещение и скорость автомобиля на участке от C до B определяются выражением −30,−90/.kmkmh
В предыдущем примере мы нашли смещение и скорость объекта, используя их скалярные эквиваленты. Другой важный вектор движущимися величинами являются ускорение и сила. Подобно смещению и скорости, эти величины имеют определенные направления, связанные с их в движении, на что указывают их знаки в одномерном движении. Однако их скалярные аналоги не имеют специальных имен, как расстояние и скорость, поэтому мы называем их величиной ускорения или величиной силы.
 И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже.
И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже.Vector Scalar Unit Displacement Distance m Velocity Speed m/s Acceleration Magnitude of acceleration m/ с 2 Сила Величина силы Н Мы помним, что ускорение — это скорость изменения скорости, поэтому его интерпретация тесно связана со скоростью объекта. В то время как скорость указывает направление движения, ускорение указывает, как изменяется скорость. Рассмотрим, как интерпретировать направления скорости и ускорения при прямолинейном движении.

Свойства: скорость и ускорение в линейном движении
Направления скорости и ускорения движущегося объекта связаны следующим образом:
- Если скорость и ускорение имеют один и тот же знак, то скорость объекта увеличивается.
- Если скорость и ускорение имеют разные знаки, то скорость объекта уменьшается.
Мы можем понять указанные выше свойства, рассмотрев следующую диаграмму.
На приведенной выше левой диаграмме скорость и ускорение направлены в одном направлении. Например, мы можем представить парусник, путешествующий вправо, где ветер, действующий как ускорение, дует в том направлении, в котором уже движется лодка. парусник двигаться быстрее, а это значит, что скорость лодки увеличится. Точно так же мы можем изобразить сценарий, представленный по схеме справа. В этом случае ветер дует против парусника, что замедляет движение лодки. Это приводит к скорость лодки уменьшается.
В нашем следующем примере мы рассмотрим взаимосвязь между скоростью объекта и его ускорением при линейном движении.

Пример 2. Интерпретация знаков векторных величин
Предположим, что положительное направление движения направлено вправо. Что из следующего правильно описывает движение частицы скорость которого отрицательна, а ускорение положительно?
- Частица замедляется при движении вправо.
- Частица замедляется при движении влево.
- Частица ускоряется при движении вправо.
- Частица ускоряется при движении влево.
Ответ
Напомним, что скорость и ускорение являются векторными величинами, знаки которых в контексте линейного движения указывают направление. Так как мы учитывая, что положительное направление движения направлено вправо, мы знаем, что положительный знак связан с правильным направлением, в то время как отрицательный знак означает левое направление.
Мы можем начать с определения направления скорости. Скорость частицы отрицательна; следовательно, направление его скорости равно оставил.
 Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево.
Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево.Ускорение — это скорость изменения скорости, поэтому его значение всегда связано со скоростью. Чтобы интерпретировать знак ускорения, мы вспомнить связь между направлением скорости и ускорением:
- Если скорость и ускорение имеют один и тот же знак, то скорость объекта увеличивается.
- Если скорость и ускорение имеют разные знаки, то скорость объекта уменьшается.
Обратите внимание, что в этом примере скорость и ускорение имеют противоположные знаки. Отсюда скорость частицы, равная величине скорости, уменьшается.
Это приводит к ответу B, в котором говорится, что частица замедляется, когда движется влево.
До сих пор мы рассматривали векторные величины в линейном движении. Направление в линейном движении простое, потому что есть только два варианта направление. Когда мы рассматриваем движение на плоскости, т.
 е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.
е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.Вместо знаков мы указываем направления плоскостного движения с помощью векторов. Кратко остановимся на некоторых свойствах векторов. В двоем размеры, любой вектор можно записать в терминах стандартных единичных векторов ⃑𝑖 и ⃑𝑗. Эти стандартные единичные векторы представляют собой векторы вдоль горизонтальной и вертикальной осей, величина которых равна 1.

Мы можем написать общий двумерный вектор, начинающийся с начала координат и заканчивающийся в точке (𝑎,𝑏), умножая эти стандартные единичные векторы скалярами и сложением их вместе, что приводит к выражению 𝑎⃑𝑖+𝑏⃑𝑗, как показано ниже.
Напомним, что величина вектора определяется длиной стрелки, которая определяется выражением ‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏.
Эта формула величины взята из теоремы Пифагора. Мы можем видеть это на рисунке выше, так как векторная стрелка (красная) образует гипотенуза прямоугольного треугольника в сочетании с горизонтальной и вертикальной компонентами. Следовательно, квадрат величины дается добавлением квадраты длин горизонтальной и вертикальной стрелок, равные 𝑎 и 𝑏 соответственно. Это приводит к приведенной выше формуле для величины 𝑎⃑𝑖+𝑏⃑𝑗.
Мы можем использовать векторы для представления векторных величин, таких как перемещение, скорость, ускорение и сила. Величины этих векторов соответствуют их скалярным аналогам, которые аналогичны тому, что мы обсуждали в контексте линейного движения.
 Когда мы знаем векторную величину движения, мы
можно использовать теорему Пифагора, чтобы найти ее скалярный аналог.
Когда мы знаем векторную величину движения, мы
можно использовать теорему Пифагора, чтобы найти ее скалярный аналог.В следующем примере мы найдем скорость объекта, найдя модуль скорости.
Пример 3: Расчет скорости по скорости
Скорость частицы равна 4⃑𝑖−3⃑𝑗 м/с. Найдите скорость частицы.
Ответ
Напомним, что скорость является скалярным эквивалентом скорости, которая является векторной величиной. Скорость имеет ту же единицу, что и скорость, и равна к величине скорости. В этом примере нам задана скорость частицы в виде вектора. Его скорость равна величине скорость, поэтому мы можем найти скорость, вычислив величину данного вектора.
Напомним, что величина вектора 𝑎⃑𝑖+𝑏⃑𝑗 определяется выражением ‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏.
Из нашего заданного вектора мы видим, что 𝑎=4 и 𝑏=−3. Подставляя эти значения в приведенную выше формулу, мы получить величину заданного вектора: 4+(−3)=√25=5.
Используя те же единицы измерения, что и скорость, скорость частицы равна 5 м/с.

В предыдущем примере мы рассматривали величину векторной величины, которая приводит к ее скалярному эквиваленту. С другой стороны, направление векторных величин можно понять, используя угол по отношению к любому стандартному единичному вектору. Мы можем получить такие углы, построив соответствующий прямоугольный треугольник и используя тригонометрию, как показано ниже.
Если мы знаем, что вектор принимает форму 𝑎⃑𝑖+𝑏⃑𝑗, то мы знаем, что зеленые стороны прямоугольный треугольник выше задается 𝑎 и 𝑏 соответственно. Чтобы найти отмеченный угол между диагональным вектором и стандартный единичный вектор ⃑𝑖, мы можем использовать отношение тангенсов tan𝑏𝑎.
Когда угол между векторами превышает 90∘, этот метод потребует небольшого модификация. В таких случаях мы можем нарисовать прямоугольный треугольник, содержащий остроугольную часть этого угла, опустив прямой угол в процесса, как показано на следующей диаграмме.
На приведенной выше диаграмме мы по-прежнему получаем прямоугольный треугольник, а отмеченный угол можно найти, используя отношение тангенса загар|𝑎|𝑏.
 Однако нам нужно добавить прямой угол
(90∘) к отмеченному углу, чтобы получить угол между ⃑𝑖
и 𝑎⃑𝑖+𝑏⃑𝑗.
Однако нам нужно добавить прямой угол
(90∘) к отмеченному углу, чтобы получить угол между ⃑𝑖
и 𝑎⃑𝑖+𝑏⃑𝑗.В нашем следующем примере мы найдем угол между ускорением объекта и стандартным единичным вектором.
Пример 4. Расчет направления ускорения
Ускорение частицы равно 4⃑𝑖−3⃑𝑗 м/с 2 . Найдите угол, округлив до ближайшего степени, что ускорение этой частицы делает с единичным вектором ⃑𝑖.
Ответ
Напомним, что ускорение — это векторная величина в движении, которая представляет скорость изменения скорости. В этом примере нам дается ускорение частицы как вектор. Начнем с рисования этого вектора и единичного вектора ⃑𝑖 на та самая сетка.
Мы ищем угол, который обозначен как 𝜃 на диаграмме выше. Мы видим, что вертикальные и горизонтальные стрелки вместе с диагональной стрелкой образуют прямоугольный треугольник. Две перпендикулярные стороны имеют длины 4 и 3 соответственно.
 Мы должны быть
будьте осторожны, чтобы не ошибиться, что длина вертикальной стороны равна -3, поскольку длина является скалярной величиной, которая не может быть отрицательной.
Мы должны быть
будьте осторожны, чтобы не ошибиться, что длина вертикальной стороны равна -3, поскольку длина является скалярной величиной, которая не может быть отрицательной.Сторона длины 4 примыкает к углу 𝜃, а сторона длины 3 противоположна 𝜃. Тогда отношение тангенсов этого угла определяется выражением таннапротив соседнего𝜃==34.
Мы можем найти 𝜃 из этого уравнения, применяя арктангенс: 𝜃=34=36,87….tan∘
Округляя этот ответ до ближайшего градуса, угол между ускорение объекта, а единичный вектор ⃑𝑖 равен 37∘.
Полезность векторных величин в движении становится очевидной, когда мы применяем различные векторные операции. Хотя большинство этих операций зарезервировано для будущих уроков мы можем рассмотреть геометрическое приложение, включающее сложение векторов. Напомним, что сложение двух векторов ⃑𝑣 и ⃑𝑤 можно представить на декартовой сетке, соединив два вектора так что начальный конец одного вектора лежит на конце стрелки другого вектора.
 Затем полученный вектор можно нарисовать, соединив
два конечных пункта. Это показано на диаграмме ниже.
Затем полученный вектор можно нарисовать, соединив
два конечных пункта. Это показано на диаграмме ниже.Это геометрическое свойство сложения векторов полезно при моделировании реального движения. В нашем последнем примере мы будем использовать сложение векторов, чтобы найти расстояние между двумя точками при заданных перемещениях по трем точкам.
Пример 5. Расчет величины смещения с использованием векторов
Частица движется из точки 𝐴 в точку 𝐵 и затем в точку 𝐶. Водоизмещение из точки 𝐴 в точку 𝐵 есть 3⃑𝑖+5⃑𝑗 см, а перемещение из точки 𝐵 в точку 𝐶 равно ⃑𝑖−7⃑𝑗 см. Найдите расстояние между точкой 𝐴 и точка 𝐶 округляется до ближайшей одной сотой сантиметр.
Ответ
Напомним, что смещение — это векторная величина, которая указывает и направление, и величину, а расстояние — это скалярная величина, представляющая только величина. Расстояние, которое мы ищем, находится между точкой 𝐴 и точкой 𝐶, что является величиной смещение от 𝐴 к 𝐶.
 Сначала найдем это смещение.
Сначала найдем это смещение.Напомним, что сложение двух векторов можно представить на декартовой сетке, соединив два вектора так, чтобы начальный конец одного вектор лежит на конце стрелки другого вектора. Чтобы визуализировать этот процесс, давайте нарисуем диаграмму, содержащую три точки вместе с два заданных перемещения.
Нижний вектор представляет собой смещение от 𝐴 до 𝐶, которое мы ищем. Использование геометрического свойство сложения векторов, мы можем видеть, что путешествие из 𝐴 в 𝐵 затем из 𝐵 в 𝐶 эквивалентно перемещению из 𝐴 в 𝐶. Другими словами, 𝐴𝐵+𝐵𝐶=𝐴𝐶.
Вычислим это сложение векторов: 3⃑𝑖+5⃑𝑗+⃑𝑖−7⃑𝑗=(3+1)⃑𝑖+(5+(−7))⃑𝑗=4⃑𝑖−2⃑𝑗.
Это говорит нам о том, что смещение от точки 𝐴 к точке 𝐶 равно 4⃑𝑖−2⃑𝑗 см. С расстояния является величиной смещения, мы можем найти расстояние между этими двумя точками, вычислив величину этого вектора. Напомним, что величина вектора 𝑎⃑𝑖+𝑏⃑𝑗 определяется выражением ‖‖𝑎⃑𝑖+𝑏⃑𝑗‖‖=√𝑎+𝑏.

Следовательно, величину 4⃑𝑖−2⃑𝑗 можно найти, подставив 𝑎=4 и 𝑏=−2 в приведенную выше формулу: 4+(−2)=√20=4,4721….
Округлив до ближайшей одной сотой сантиметра, расстояние между точкой 𝐴 и точкой 𝐶 равно 4,47 см.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые точки
- Векторные величины указывают как направление, так и величину, тогда как скалярные величины указывают только величину. Векторная величина несет в себе той же единице, что и его скалярный аналог.
- Примеры векторных величин и их скалярных аналогов приведены в следующей таблице.
Vector Scalar Блок Дистанция VELOCITE 2 Сила Величина силы N - Чтобы задать направление движения объекта по прямой,
- определить положительное направление,
- сравнить заданное направление с положительным направлением:
- если направление совпадает с положительным направлением , знак плюс ставится (часто опускается) перед скалярным аналогом;
- если направление не совпадает с положительным направлением, перед скалярным аналогом ставится знак минус.

- Направления скорости и ускорения движущегося объекта связаны следующим образом:
- Если скорость и ускорение имеют один и тот же знак, то скорость объекта увеличивается.
- Если скорость и ускорение имеют разные знаки, то скорость объекта уменьшается.
- При плоском движении векторные величины представляются с помощью векторов.
- Операции с векторами, такие как сложение векторов, могут быть полезны при моделировании реальных ситуаций.
Скаляр и вектор: определение, количество, примеры
В повседневной жизни мы взаимозаменяемо используем расстояние, перемещение, скорость, скорость, ускорение и т. д. Для физиков все величины, будь то статические или движущиеся, могут быть дифференцированы путем классификации их как либо скаляры, либо векторы.
Величина с величиной (размером) только называется скалярной величиной . Масса, энергия, мощность, расстояние и время — вот некоторые примеры скалярных величин, потому что с ними не связано направление.

Величина, имеющая величину и связанное с ней направление , является векторной величиной . Ускорение, сила, сила тяжести и вес являются некоторыми векторными величинами. Все векторные величины связаны с определенным направлением.
Скаляры и векторы: значение и примеры
Как мы уже говорили, величина, имеющая модуль и направление, называется векторной величиной.
Вес является примером векторной величины, поскольку он является произведением массы и ускорения свободного падения. ускорение силы тяжести направлено вертикально вниз , что делает вес векторной величиной.
Давайте рассмотрим несколько примеров скаляров и векторов.
Предположим, у вас есть ящик, и вы перемещаете его на расстояние 5 метров.
Рис. 1. Движение объекта из точки A в точку B в заданном направлении представляет собой вектор. Oğulcan Tezcan – StudySmarter Originals
Если вы скажете кому-нибудь, что расстояние между точками A и B составляет 5 метров, вы говорите о скалярная величина потому что вы не указываете направление .
 Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.
Пять метров — это всего лишь величина (расстояние), а направление может быть любым. Таким образом, расстояние является скалярной величиной.Однако, если вы скажете кому-нибудь , что переместили ящик на 5 метров вправо (на восток) , как показано на рисунке 1, вы теперь говорите о векторной величине . Почему? Поскольку у вас есть , теперь указано направление, связанное с движением . А в физике это называется смещение . Следовательно, перемещение является векторной величиной.
Теперь предположим, что вам потребовалось 2 секунды, чтобы передвинуть коробку вправо.
Рис. 2. Диаграмма, показывающая вектор смещения относительно времени. Oğulcan Tezcan – StudySmarter Originals
Если бы вам нужно было вычислить, как быстро вы переместили коробку, вы вычислили бы скорость движения . В приведенном выше примере скорость равна:
Скорость является скалярной величиной , поскольку она не имеет направления.

Однако, если вы скажете, что ящик двигался со скоростью 2,5 м/с вправо , это становится векторной величиной . Скорость с направлением — это скорость, , а изменение скорости, в свою очередь, известно как ускорение (м/с 2 ), которое также является векторной величиной.
Скаляр Вектор Расстояние Перемещение Скорость Скорость и ускорение Масса и вес: что из них скалярная, а какая векторная?
Масса и вес тела могут казаться одинаковыми, но это не так.
Масса: количественная мера инерции тела , которая представляет собой тенденцию тела сопротивляться силе, которая может вызвать изменение его скорости или положения. Масса имеет единицу СИ килограмм.
Вес: Гравитационное притяжение , действующее на массу. Единицей измерения СИ являются ньютоны.

Скаляр
Масса не имеет никакого направления, и она будет одинаковой, где бы вы ни находились во Вселенной! Таким образом, мы можем классифицировать массу как скалярную величину .
Вектор
Вес, с другой стороны, это сила, действующая на объект, и поскольку сила имеет направление, вес является векторной величиной .
Другой способ посмотреть на это, если вы поместите один объект на Землю, а другой объект с той же массой на Луну. Оба объекта будут иметь одинаковую массу, но разный вес из-за гравитационного притяжения Луны (1,62 м/с 2 ), что меньше по сравнению с Землей.
Как мы можем представить векторы?
Мы можем представить векторы стрелкой, как показано ниже.
Рис. 3. Представление вектора. Wikimedia Commons
Длина отображает величину, хвост — начальную точку вектора, смысл вектора определяется порядком двух точек на линии, параллельной вектору, а ориентация говорит вам, под каким углом вектор указывает.
 Комбинация ориентации и смысла определяет направление вектора.
Комбинация ориентации и смысла определяет направление вектора.Примеры векторов: как выполнить сложение векторов?
Давайте рассмотрим несколько примеров выполнения сложения векторов.
Допустим, у вас есть два вектора 10 северной широты и 15 северной широты, и оба они указывают на восток. Сумма этих векторов становится 25N на восток.
Рисунок 4. Добавление векторов в одном направлении. Усама Адил — StudySmarter Originals.
Теперь, если мы изменим направление 15 северной широты на запад (-15 северной широты), результирующий вектор становится -5 N (указывая на запад). Векторная величина может иметь положительные и отрицательные знаки . Знак вектора показывает, что направление вектора противоположно опорному направлению (которое произвольно).
Рис. 5. Вычитаются векторы в противоположном направлении. Usama Adeel — StudySmarter Originals
Теперь, конечно, все сложения векторов не так просты, как показано выше.
 Что бы вы сделали, если бы два вектора были перпендикулярны друг другу? Здесь нам нужно немного импровизировать.
Что бы вы сделали, если бы два вектора были перпендикулярны друг другу? Здесь нам нужно немного импровизировать.Правило «голова к хвосту»
С помощью этого правила мы можем вычислить результирующий вектор, соединив конец первого вектора с началом второго вектора . Взгляните на рисунки ниже.
Рис. 6. Перпендикулярные векторы соединяются по правилу «голова к хвосту». Usama Adeel – StudySmarter Originals
Векторная сила 30 Н действует в восточном направлении, а векторная сила 40 Н действует в северном направлении. Мы можем вычислить результирующий вектор, соединив хвост вектора 30N с головой вектора 40N. Вектора перпендикулярны, поэтому мы можем используйте теорему Пифагора для решения результирующего вектора, как показано на рисунке 7.
Рисунок 7. Перпендикулярное сложение вектора. Usama Adeel – StudySmarter Originals
Немного тригонометрии и применения теоремы Пифагора результирующий вектор становится равным 50N.
 Теперь, как мы обсуждали, векторная величина имеет не только направление, но и величину, поэтому мы можем вычислить угол вектора 50N, используя арктангенс 40/30 (перпендикуляр/основание). Тогда угол составляет 53,1 ° от горизонтали для приведенного выше примера.
Теперь, как мы обсуждали, векторная величина имеет не только направление, но и величину, поэтому мы можем вычислить угол вектора 50N, используя арктангенс 40/30 (перпендикуляр/основание). Тогда угол составляет 53,1 ° от горизонтали для приведенного выше примера.Разложение вектора на его компоненты
Используя тот же пример выше, что, если бы у нас была только векторная сила 50 Н с углом от горизонтали, и нас попросили найти ее горизонтальную и вертикальную составляющие?
Разделение одного вектора на два или более векторов, производящих эффект, аналогичный исходному вектору, называется разрешением векторов .
Давайте рассмотрим пример, объясняющий эту концепцию.
Предположим, что вектор силы F в 150 Н приложен под углом 30 градусов к поверхности.
Рис. 8. Вектор под углом. Usama Adeel – StudySmarter Originals
Мы можем разделить вектор F на горизонтальную составляющую (Fx) и вертикальную (Fy) составляющую, как показано ниже:
Рисунок 9.
 Разрешение векторов. Usama Adeel — StudySmarter Originals
Разрешение векторов. Usama Adeel — StudySmarter OriginalsВычисление Fx и Fy с помощью тригонометрии дает нам:
Разложение компонентов силы на наклонной плоскости
Как вы, возможно, уже поняли, расчеты в физике никогда не бывают такими простыми ! Не каждая поверхность горизонтальна — иногда поверхности могут быть наклонными, и вам придется рассчитывать и разрешать компоненты вдоль наклонной плоскости.
Рисунок 10. Направление веса на наклонной плоскости. Usama Adeel – StudySmarter Originals
На рис. 10 показана коробка на поверхности под углом θ к горизонтали. Вес коробки, mg, действует вниз с массой m и гравитационным притяжением g.
Если мы разделим вектор mg на горизонтальную и вертикальную составляющие,
- вертикальная составляющая будет перпендикулярна наклонной поверхности, а
- горизонтальная составляющая mg будет параллельна к наклонной поверхности.
Рис.
 11. Разрешение вектора мг на наклонной поверхности. Usama Adeel – StudySmarter Originals
11. Разрешение вектора мг на наклонной поверхности. Usama Adeel – StudySmarter OriginalsУгол θ между mg и mgcosθ будет таким же, как угол наклонной поверхности от горизонтали. Сила, которая разгонит ящик вниз по склону, составит mgsin θ (Fg) , а сила реакции Fn (из третьего закона Ньютона) будет равна mgcos θ . Отсюда
Рис. 12. Разрешение векторов и направление движения на наклонной плоскости. Usama Adeel – StudySmarter Originals
Равновесие компланарных силовых систем
Если силы действуют на тело, и тело неподвижно или движется с постоянной скоростью (без ускорения), такой случай называется равновесием . Силовые линии должны проходить через одну и ту же точку, чтобы тело находилось в равновесии.
На приведенном ниже рисунке однородная лестница прислонена к гладкой стене (трение отсутствует).
 Вес лестницы действует вниз, а нормальная сила реакции действует под углом 90° к стене.
Вес лестницы действует вниз, а нормальная сила реакции действует под углом 90° к стене.Рис. 13. Лестница, прислоненная к стене, является примером тела, находящегося в равновесии. Usama Adeel — StudySmarter Originals
Если вы расширите эти силы, вы увидите, что они пересекаются в определенной точке. Поскольку объект находится в равновесии, сила от земли также должна проходить через ту же точку, что и другие силы.
Рис. 14. Силовые линии пересекаются в одной точке, если тело находится в равновесии. Usama Adeel – StudySmarter Originals
При разделении силы от земли на ее вертикальную и горизонтальную составляющие, нормальная сила реакции от земли действует вверх, а сила трения от земли действует вдоль поверхности.
Рис. 15. Результирующая векторов трения и грунта. Usama Adeel – StudySmarter Originals
В сущности, происходит то, что все силы компенсируют друг друга.
- Нормальная сила от стены (правая сила) = сила трения, действующая на землю (левая сила).

- Вес от лестницы (сила, направленная вниз) = сила реакции от земли (сила, направленная вверх).
Скаляр и вектор – ключевые выводы
- Скалярная величина имеет только величину, тогда как векторная величина имеет величину и направление.
- Вектор может быть представлен стрелкой.
- Чтобы найти результирующий вектор, векторы в одном направлении складываются, а векторы в противоположном направлении вычитаются.
- Результирующий вектор двух векторов можно вычислить по правилу «голова к хвосту», а результирующий вектор перпендикулярных векторов можно рассчитать по теореме Пифагора.
- Если вектор расположен под углом к горизонтали (или вертикали), его можно разложить на компоненты x и y.
- Силовые линии должны пересекаться в одной точке и уравновешивать друг друга, чтобы объект находился в равновесии.
В чем разница между векторами и скалярами?
Скаляр — это величина, которая полностью определяется своей величиной и не имеет направления.
 Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время.
Скаляр может быть описан либо безразмерно, либо в терминах некоторой физической величины. Примеры скаляров: масса, объем, расстояние, энергия и время.Скалярными величинами можно управлять с помощью законов арифметики, применимых к натуральным числам. Например, если я добавляю 20 граммов сахара в рецепт, а затем добавляю еще 20 граммов, в результате получается 40 граммов сахара в рецепте. Если я куплю литровую (1000 мл) бутылку воды и выпью 250 мл, останется 750 мл.
Вектор – это величина, которая определяет как величину, так и направление. Такая величина может быть представлена геометрически стрелкой длины, пропорциональной ее величине, указывающей в заданном направлении. Примеры векторов: перемещение, скорость, ускорение, сила и электрическое поле. Векторы можно складывать простыми способами, как и скаляры. Например: Самолет летит на юг со скоростью 500 миль/час. Ветер дует с востока со скоростью 100 миль в час. Результирующая скорость не 600 миль в час и не 400 миль в час.
 92)
92)R = 509,9 миль/ч.
Направление плоскости можно вычислить с помощью функции косинуса.
тангенс = 100/500 = 11,31 градуса
(Примечание: схема выполнена не в масштабе)
1. ___ _ пример скалярной величины
а) скорость
б) сила
в) том
г) ускорение2. ___ является примером векторной величины
а) масса
б) сила
в) том
г) плотность3. Скалярная величина:
а) всегда имеет массу
б) есть величина, полностью определяемая своей величиной
в) показывает направление
г) не имеет единиц4. Векторная величина
а) может быть безразмерной величиной
б) указывает только величину
в) указывает только направление
г) определяет как величину, так и направление5.
 Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
Мальчик давит на стену с силой 50 фунтов. Стена не двигается. Результирующая сила:
а) -50 фунтов
б) 100 фунтов
в) 0 фунтов
г) -75 фунтов6. Человек прошел 3 мили на север, затем повернул направо и прошел 4 мили на восток. Результирующее смещение:
а) 1 миля ЮЗ
б) 7 миль NE
в) 5 миль NE
d) 5 миль E7. Самолет, летящий со скоростью 500 миль/час строго на север, имеет попутный ветер 45 миль/час, результирующая скорость:
а) 545 миль/час на юг.
б) 455 миль/час на север.
c) 545 миль/ч строго на север.
г) 455 миль/час строго на юг8. Разница между скоростью и скоростью:
а) скорость не имеет единиц
б) скорость показывает только величину, а скорость представляет и величину (силу), и направление
в) они используют разные единицы для представления своей величины
г) скорость имеет большую величину9.
 Результирующая величина двух векторов
Результирующая величина двух векторов а) всегда положительный
б) никогда не может быть нулевым
в) Никогда не может быть отрицательным
г) Обычно равен нулю10. Что из следующего неверно.
а) скорость может быть отрицательной
б) скорость есть вектор
б) скорость является скаляром
г) скорость может быть отрицательнойСила, работа и энергия
Скорость, скорость и ускорение: В чем разница между скоростью и скоростью? Что такое ускорение? График скорости и ускорения. Проверка вашего понимания.
Сила: Что такое сила? Измерение сил. Описание Сил. Что делает сила? Что такое трение? Оценочные вопросы.
Векторы и скаляры: Что такое векторная величина? Примеры векторов. Что такое скалярная величина? Примеры скаляров.
 Проверьте свое понимание векторов и скаляров.
Проверьте свое понимание векторов и скаляров.Три закона движения Ньютона: См. «Три закона Ньютона» на латыни и английский перевод. Приведены примеры для каждого закона..
Работа, энергия и мощность: определения работы, энергии и мощности. Виды энергии, расчет работы и мощности.
Разница между массой и весом: Отличная страница для одаренных и талантливых учащихся! Несколько отличных сложных задач.
Гравитация, масса и вес: Гравитация, масса и вес по отношению к Солнечной системе
Основные и производные единицы: Основные и производные единицы, включая физические величины, символы единиц измерения.
Математические отношения в науке: см. лабораторную работу 5, Ускорение.
Связанные виды деятельности
Понимание скалярных и векторных величин
Все ресурсы по физике для старших классов
6 Диагностические тесты 233 практических теста Вопрос дня Карточки Учитесь по концепции
← Предыдущая 1 2 3 4 Следующая →
Школа физики Помощь » Вводные принципы » Понимание скалярных и векторных величин
Что из следующего может быть результатом произведения векторной величины на скалярную величину?
Возможные ответы:
Напряжение
Работа
Вес
Скорость
Все это результат произведения вектора и скаляра
900
Вес
Объяснение:
Скалярные величины определяются величиной без применимого направления.
 Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.Произведение векторной величины на скалярную величину всегда будет векторной величиной. Сила является результатом произведения массы (скаляр) и ускорения (вектор). Вес — это тип силы, создаваемой ускорением свободного падения.
Напряжение является скалярной величиной и может быть рассчитано как произведение тока (скалярное) на сопротивление (скалярное).
Работа является векторной величиной и может быть рассчитана как произведение силы (вектор) и смещения (вектор).
Скорость является вектором и может быть рассчитана как частное смещения (вектор) в единицу времени (скаляр).
Сообщить об ошибке
Скорость является скалярной величиной. Какая векторная величина представляет скорость в приложенном направлении?
Возможные ответы:
Расстояние
Перемещение
Скорость
Вес
Ускорение
Правильный ответ:
Скорость
Объяснение:
Скалярные величины определяются величиной без применимого направления.
 Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.Скорость определяется изменением расстояния в единицу времени. Поскольку расстояние и время являются скалярными величинами, результирующая скорость также является скалярной. Напротив, скорость определяется изменением смещения в единицу времени. Поскольку смещение является вектором, результирующая скорость также является вектором. Величина заданной скорости и заданной скорости могут быть равны, но член скорости будет представлять скорость, приложенную в определенном направлении.
Ускорение — векторная величина, определяемая изменением скорости в единицу времени. Вес создается силой тяжести на объекте; все силы являются векторами.
Сообщить об ошибке
Что из следующего является скалярной величиной?
Возможные ответы:
Ускорение
Сила
Расстояние
Смещение
Velocity
Правильный ответ:
Расстояние
Объяснение:
Скалярные величины определяются величиной без применимого направления.
 Напротив, векторные величины должны иметь как величину, так и направление действия.
Напротив, векторные величины должны иметь как величину, так и направление действия.Некоторыми распространенными скалярными величинами являются расстояние, скорость, масса и время. Некоторыми распространенными векторными величинами являются сила, скорость, смещение и ускорение.
Сообщить об ошибке
Что из этого является вектором?
Возможные ответы:
Емкость
Время
Скорость
Сила
Расстояние
Правильный ответ:
Сила
Объяснение:
Вектор имеет как величину, так и направление, тогда как скаляр имеет только величину. Спрашивая, является ли что-то вектором или скаляром, спросите, имеет ли смысл направление — в этом случае единственным вектором является сила. Хотя направление помогло бы со скоростью и расстоянием, они оба являются скалярами; векторная версия скорости — это скорость, а векторная версия расстояния — это перемещение.

Сообщить об ошибке
Какая из этих величин является скалярной?
Возможные ответы:
Velocity
Force
Momentum
Смещение
MASS
Правильный ответ:
MASS
Объяснение:
Скалярная величина может быть определена только величиной, тогда как векторная величина должна определяться как величиной, так и направлением действия.
Из предложенных вариантов ответа масса является единственной скалярной величиной. Масса имеет величину, как правило, в килограммах, но не может действовать в направлении. «7kg west», например, бессмысленно.
Напротив, перемещение, скорость, сила и импульс должны быть приложены в заданном направлении. Перемещение — это векторный эквивалент скалярной величины расстояния, а скорость — векторный эквивалент скалярной величины скорости.
 Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.
Силы должны всегда действовать в заданном направлении и не иметь скалярного эквивалента. Точно так же импульс всегда должен быть направленным.Сообщить об ошибке
Ребенок катится по краю катка и финиширует там же, где и начал. Если каток имеет радиус , каково полное перемещение фигуриста?
Возможные ответы:
Правильный ответ:
Объяснение:
Между измерением смещения и измерением расстояния есть четкое и важное различие. Расстояние является скалярной величиной, что означает, что оно зависит от пройденного пути и не зависит от пройденного направления. Расстояние измеряет общую пройденную длину без какой-либо привязки к начальной точке.
Смещение, напротив, является векторной величиной. Это означает, что при расчете необходимо учитывать как величину длины, так и ее направление. Смещение — это, по сути, чистое расстояние, пройденное относительно начальной точки, независимо от пройденного пути.

В этом вопросе фигуристка финиширует точно в том же месте, где и начала. Без какой-либо другой информации мы можем сделать вывод, что ее водоизмещение равно нулю. Неважно, какой путь она выбрала, чтобы вернуться к исходной точке; она могла сделать шаг вперед и шаг назад, проехать весь каток семнадцать раз или просто прыгнуть и приземлиться. Все эти возможности привели бы к нулевому смещению.
Сообщить об ошибке
Какая из следующих величин не является векторной?
Возможные ответы:
Смещение
Ускорение
Вязкость
Velocity
Force
Правильный ответ:
Взысканность
44. Пояснение:
Вязкость – это измерение «густоты» жидкости. Патока, например, является более вязкой жидкостью, чем вода.
Векторные измерения определяются величиной и направлением.
 Для жидкости иметь измеримую «толщину» логично, но жидкость не может иметь вязкость в направлении. Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.
Для жидкости иметь измеримую «толщину» логично, но жидкость не может иметь вязкость в направлении. Говорить о том, что жидкость имеет вязкость Восточная, не имеет смысла. Вязкость является скалярной величиной.Перемещение, сила, скорость и ускорение имеют связанные направления и классифицируются как векторные величины.
Сообщить об ошибке
Какая из следующих величин является векторной?
Возможные ответы:
Расстояние
Масса
Яркость
Время
Сила
Правильный ответ:
2 Сила Объяснение:
Векторные величины определяются как величиной параметра, так и направлением действия. В контракте скалярные величины не зависят от направления и зависят только от величины параметра.
Масса, расстояние, время и яркость — все это скалярные величины. Это означает, что ни один из этих терминов не может быть применен в данном направлении.
 Было бы нелогично иметь «три грамма на запад» или «восемнадцать секунд налево». Расстояние является скалярным эквивалентом вектора смещения.
Было бы нелогично иметь «три грамма на запад» или «восемнадцать секунд налево». Расстояние является скалярным эквивалентом вектора смещения.Сила всегда векторная величина, так как направление силы имеет значение при определении параметра. «Четыре ньютона вправо» количественно отличается от «четыре ньютона вниз» или «четыре ньютона влево».
Сообщить об ошибке
Каковы модуль и угол для следующего вектора, измеренного против часовой стрелки от оси x?
Возможные ответы:
Правильный ответ:
Объяснение:
Величина вектора находится по формуле расстояния:
Чтобы вычислить угол, мы должны сначала найти арктангенс:
Это значение угла является главным арктангеном, но оно находится в четвертом квадранте, а наш вектор — во втором.


 СТО
СТО 2/2 выразить начальную скорость, ускорение.
2/2 выразить начальную скорость, ускорение.  Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами.
Они имеют единицы измерения и зависят от физических законов и аксиом. Выделяют скалярные и векторные величины, обладающие различными характеристиками и параметрами. Измеряется в килограммах и обозначается буквой латинского алфавита m.
Измеряется в килограммах и обозначается буквой латинского алфавита m. Измеряется в м3.
Измеряется в м3. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта. Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.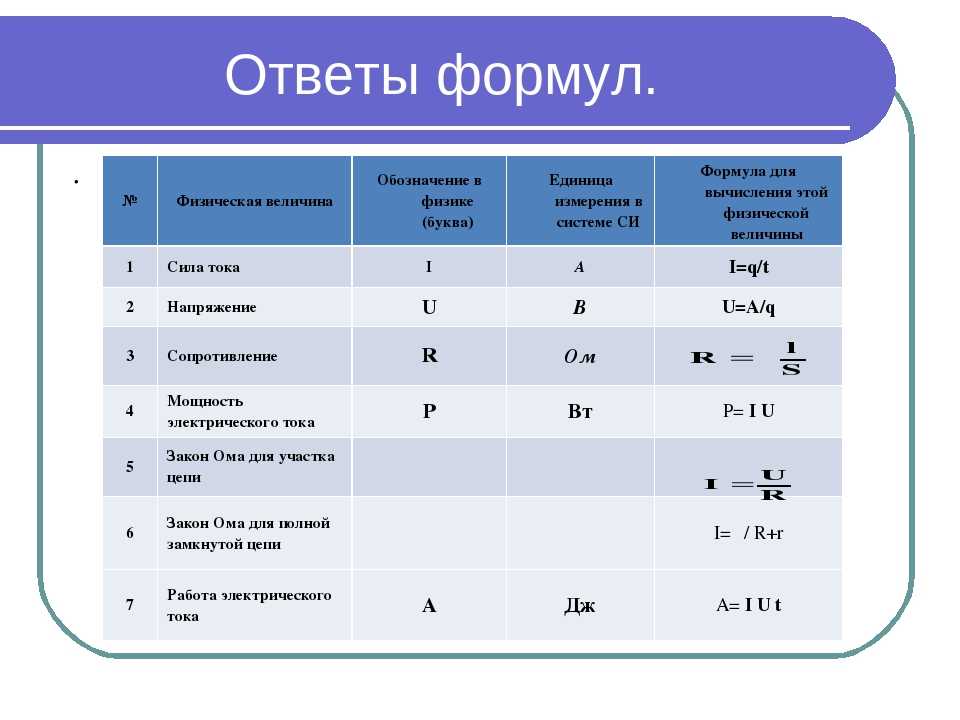 Оно направлено к ядру Земли и равняется 9,8 м/с2
Оно направлено к ядру Земли и равняется 9,8 м/с2  Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции: Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.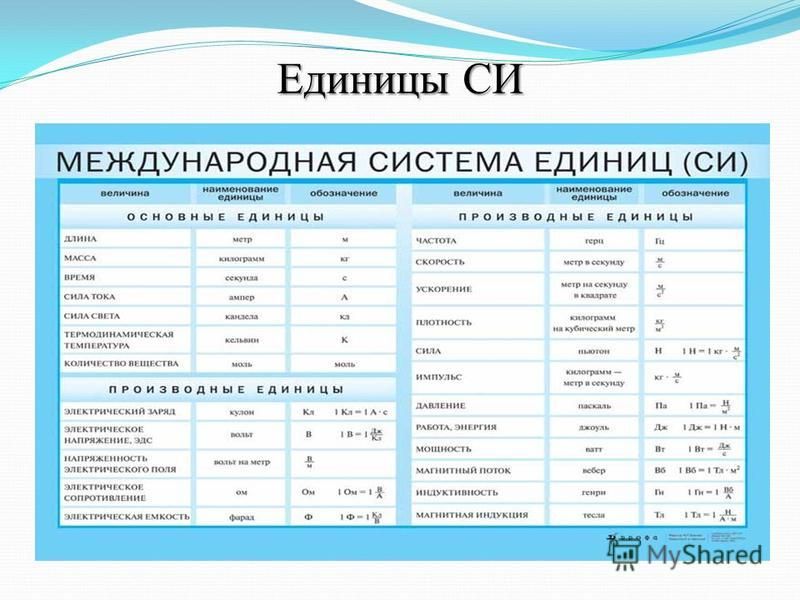
 Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления.
Рассмотрим простую
задачу. Пусть идет пешеход с постоянной
скоростью 5 км/ч. Известно, что в 12 часов
дня он находился в пункте А. Требуется
определить, где будет находиться пешеход
в 14 часов. Зная только величину скорости
пешехода, мы можем только сказать, что
в 14 часов он будет находиться на расстоянии
10 км от пункта А. Но все возможные точки
нахождения пешехода будут находиться
на окружности радиусом 10 км с центром
в точке А. Для определения точного
положения пешехода нам нужно еще знать
в какую сторону он идет. Значит, для
практических целей нам недостаточно
знать величину скорости тела. Требуется
еще знать, куда эта скорость направлена.
Имеется еще очень много физических
величин, для характеристики которых
требуется знание, как размера этой
величины так и ее направления.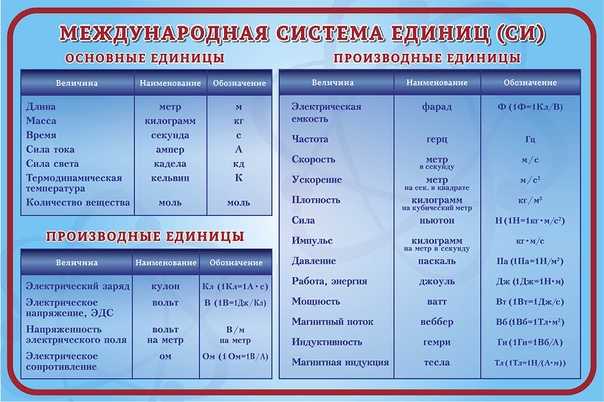 Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов.
Значение скалярной величины иногда
может иметь знак. При этом говорят, что
скалярная величина характеризуется
своим значением (которое тоже часто
называется модулем) и знаком. При этом
имеются скалярные величины, которые по
своему физическому смыслу не могут
принимать отрицательные значения
(например, масса или пройденный путь).
А некоторые скалярные величины могут
быть как положительными, так и
отрицательными. Заметим, что векторные
величины знаком не характеризуются, то
есть не бывает отрицательных векторов.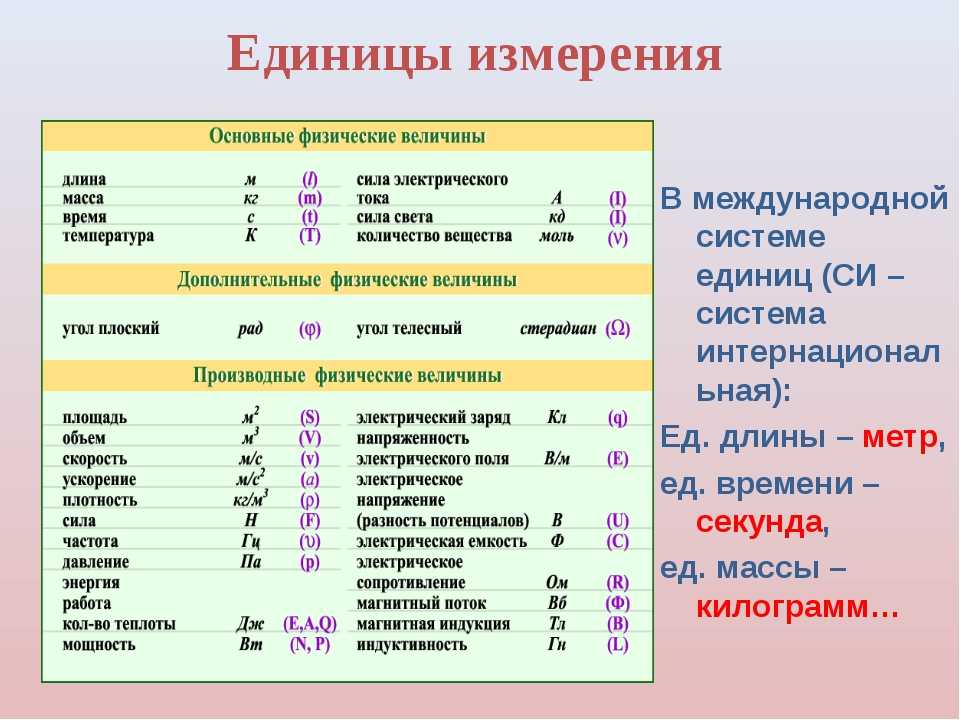 Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля.
Расстоянием между двумя точками
называется длина отрезка прямой,
соединяющего эти точки. Определяемое
таким образом пройденное расстояние
называется перемещением. Причем,
перемещение – векторная величина.
Перемещением — Δr — называется вектор, начало которого
совпадает с начальным положением тела
(точка А), а конец — с конечным положением
(точка В). Однако, тело из начальной точки
в конечную перемещалось не обязательно
по прямолинейной траектории. Поэтому
существует еще одна величина,
характеризующая величину изменения
положения тела – путь. Пройденным
путем — S — называется длина
траектории перемещения тела. Путь –
скалярная и всегда положительная
величина. Причем путь всегда больше или
равен модуля вектора перемещения. Так
если в результате движения тело вернулось
в исходное положение, то есть точки А и
В совпадают, то перемещение тела равно
нулю, а путь больше нуля. Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника.
Суммарное перемещение ΔrAC равно сумме перемещений ΔrAВ и ΔrВC.
На рисунке суммарный вектор ΔrAC является третьей стороной в треугольнике,
образованном векторами ΔrAВ и ΔrВC.
Аналогичным образом складываются все
векторные величины. Для того, чтобы
сложить два вектора а и b,
необходимо нарисовать их друг за другом
так, чтобы начало вектора b совпадало с концом вектора а.
Вектор с, начало которого
совпадает с началом вектора а,
а конец – с концом вектора b и является суммой векторов а и b. (c = a + b).
Этот способ сложения векторов называется
правилом треугольника. Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a.
Можно складывать
вектора по правилу параллелограмма.
Для этого складываемые вектора надо
нарисовать из одной точки, дорисовать
получившуюся фигуру до параллелограмма
и провести в нем из той же точки диагональ.
Она и будет суммой векторов. Для того,
чтобы сложить более чем два вектора,
можно сложить сначала два из них, затем
к их сумме прибавить третий и так далее.
Естественно, для суммы векторов
справедливо правило: a + b = b + a. Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.
Кстати, введенный
выше вектор перемещения равен разности
конечного и начального радиус – векторов,
определяющих положения тела: Δr = r2 – r1.
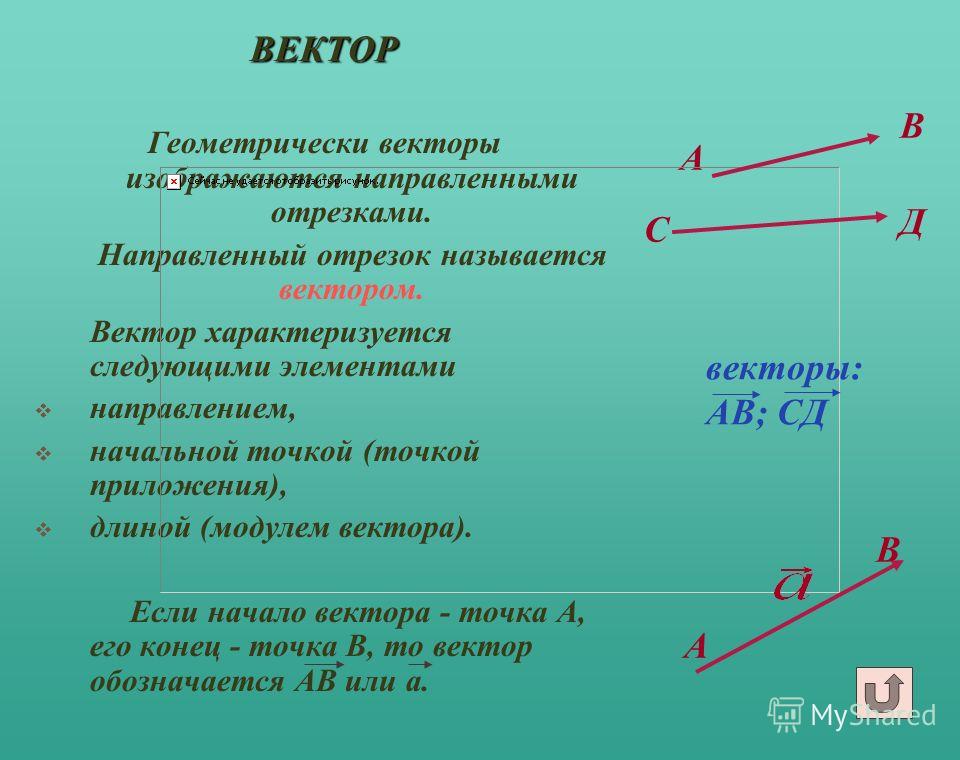 При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
.
При этом проекция вектора а на ось Х равна
,
а на ось Y -.
Если известны проекции вектора на оси
прямоугольной декартовой системы
координат, то модуль вектора можно
выразить как
. Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных:
Большинство людей знакомятся с переносчиками в старшей школе или колледже.
но для учеников начальной и средней школы или математически сложных:  Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной .
Например,
объем
объекта, трехмерное пространство, которое занимает объект,
не зависит от направления.
Если у нас есть блок железа объемом 5 кубических футов, и мы перемещаем его вверх и вниз и
затем влево и вправо, у нас все еще есть 5-кубовый блок железа.
С другой стороны,
расположение,
объекта зависит от направления.
Если мы переместим блок объемом 5 кубических футов на 5 миль в
север, результирующее местоположение сильно отличается от
если мы переместим его на 5 миль на восток.
Математики и ученые называют количество
который зависит от направления a количество векторов . Количество
которая не зависит от направления, называется скалярной величиной . .) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры.
.) вы должны
рассмотреть возможность
как по величине, так и по направлению. Это делает работу с вектором
величины немного сложнее, чем скаляры. Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество».
Тот факт, что величина встречается как для скаляров, так и для векторов, может
привести к некоторой путанице.
Есть некоторые величины, такие как скорость , которые имеют
очень специальные определения для ученых. По определению,
скорость является скалярной величиной вектора скорости . Автомобиль
едет по дороге со скоростью 50 миль в час. Его скорость
составляет 50 миль в час в северо-восточном направлении. Это может стать очень
сбивает с толку, когда термины используются взаимозаменяемо! Другой пример масса и масса . Вес — это сила, которая является вектором
и имеет величину и направление. Масса является скаляром.
Вес и масса
связаны друг с другом, но это не одно и то же количество». Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.
Масса и энергия
— скалярные величины, а импульс — вектор
количество. В результате получается связанный набор уравнений,
называется
уравнения Навье-Стокса,
которые описывают поведение жидкости под действием внешних сил.
Эти уравнения являются жидким эквивалентом законов движения Ньютона.
и очень трудно решить и понять.
Упрощенная версия уравнений, называемая
уравнения Эйлера
может быть решена для некоторых проблем с жидкостями.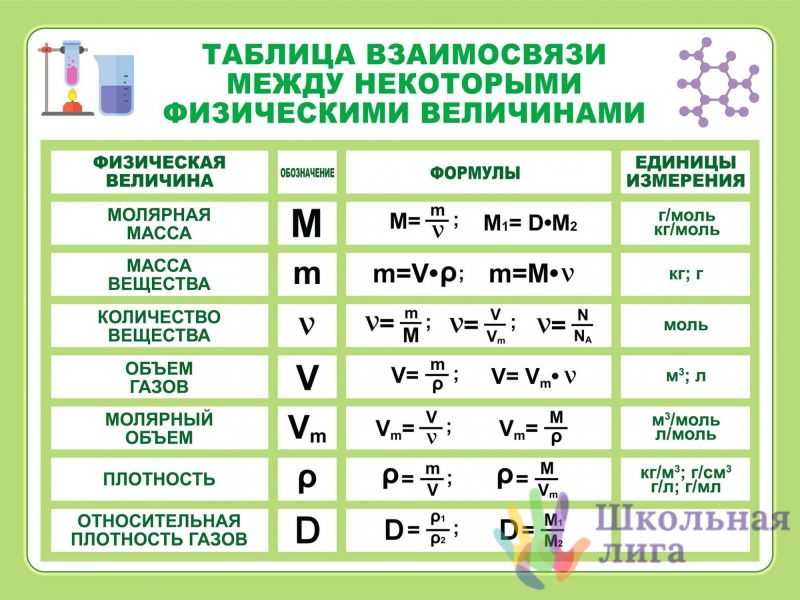
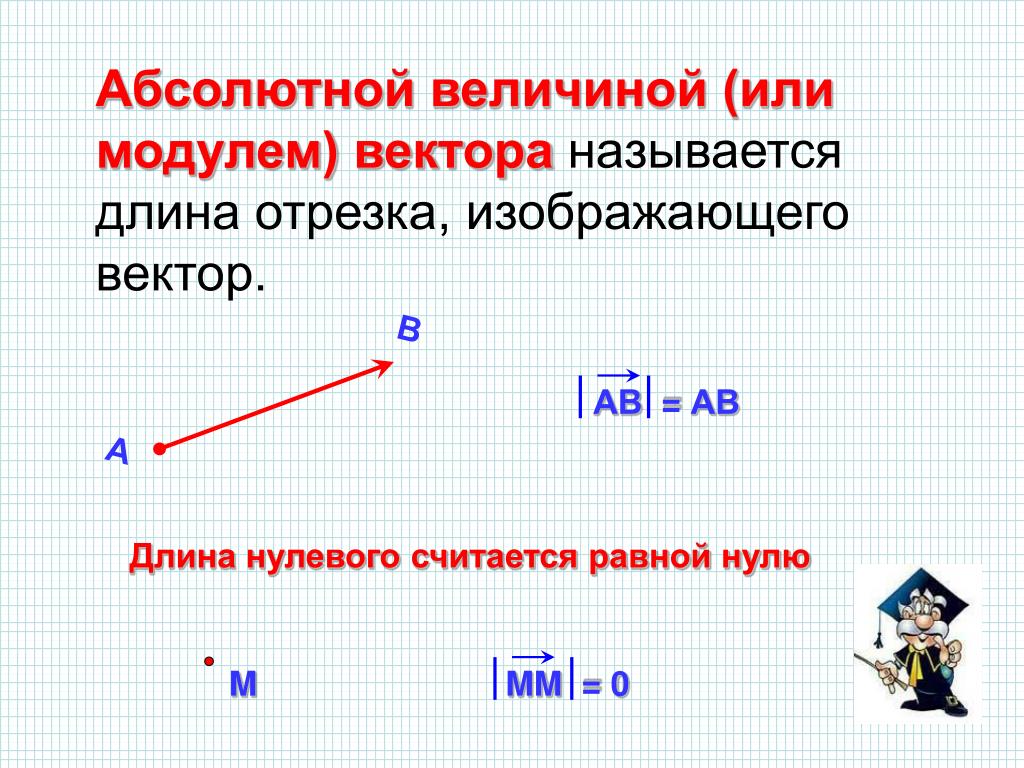 Исследуйте 10 примеров скалярных величин.
Исследуйте 10 примеров скалярных величин.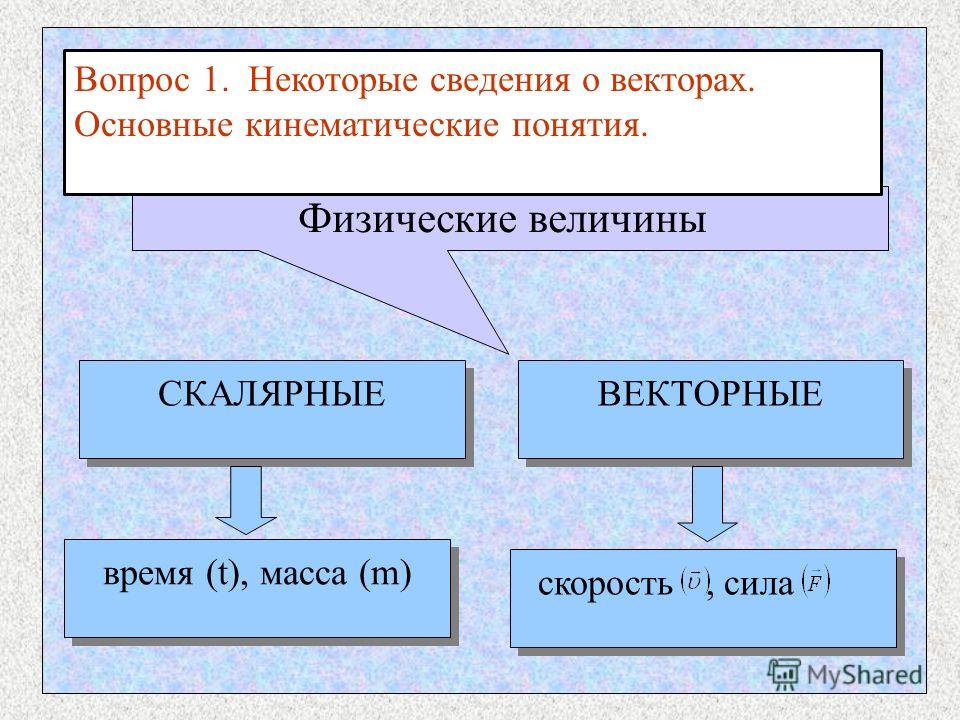

 Он учитывает период времени, а также направление, что делает его векторной величиной.
Он учитывает период времени, а также направление, что делает его векторной величиной. 
 Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями.
Чтобы измерить векторную величину среды, необходимо применить направленное измерение к скалярной величине. Другим элементом направления, который может быть применен к векторной величине, является разница между вертикальным и горизонтальным перемещениями. Вы также можете больше углубиться в законы физики с повседневными примерами инерции.
Вы также можете больше углубиться в законы физики с повседневными примерами инерции.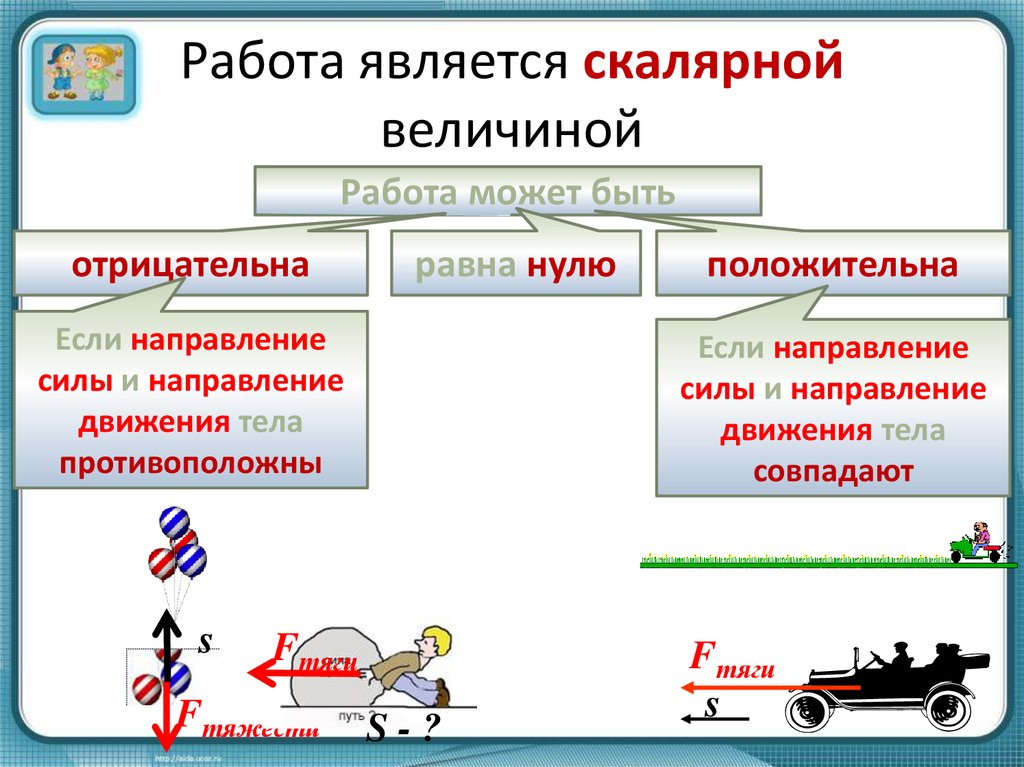
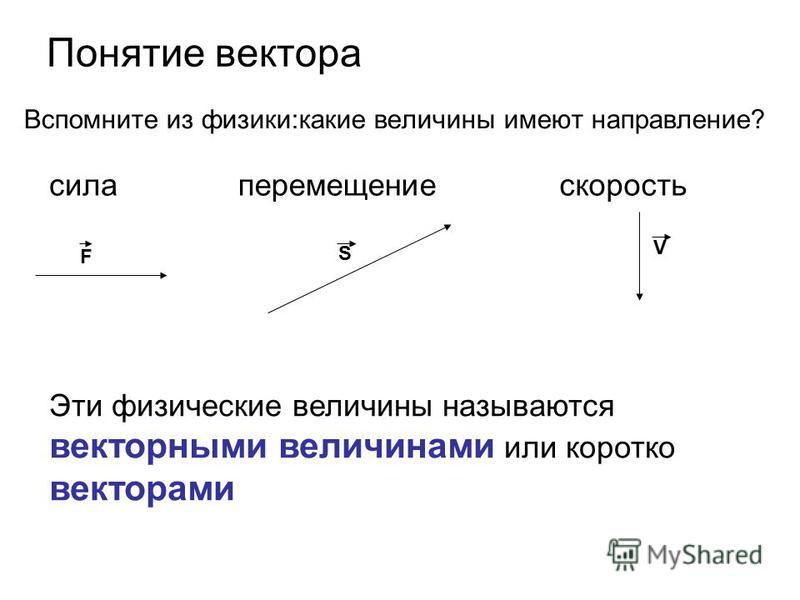 скалярный аналог;
скалярный аналог; Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую.
Даже когда эти две величины принимают одинаковую форму, они имеют разные значения. Следовательно, скалярные и векторные величины не сравнимы напрямую. Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.
Векторные величины представляют
направление и величина, в то время как скалярные величины указывают только величину. Напомним, что при прямолинейном движении направление векторной величины
можно определить только в терминах положительного или отрицательного знака. Данная цифра указывает на то, что положительное направление направлено вправо,
что означает, что положительный знак означает правое направление, а отрицательный знак означает левое направление.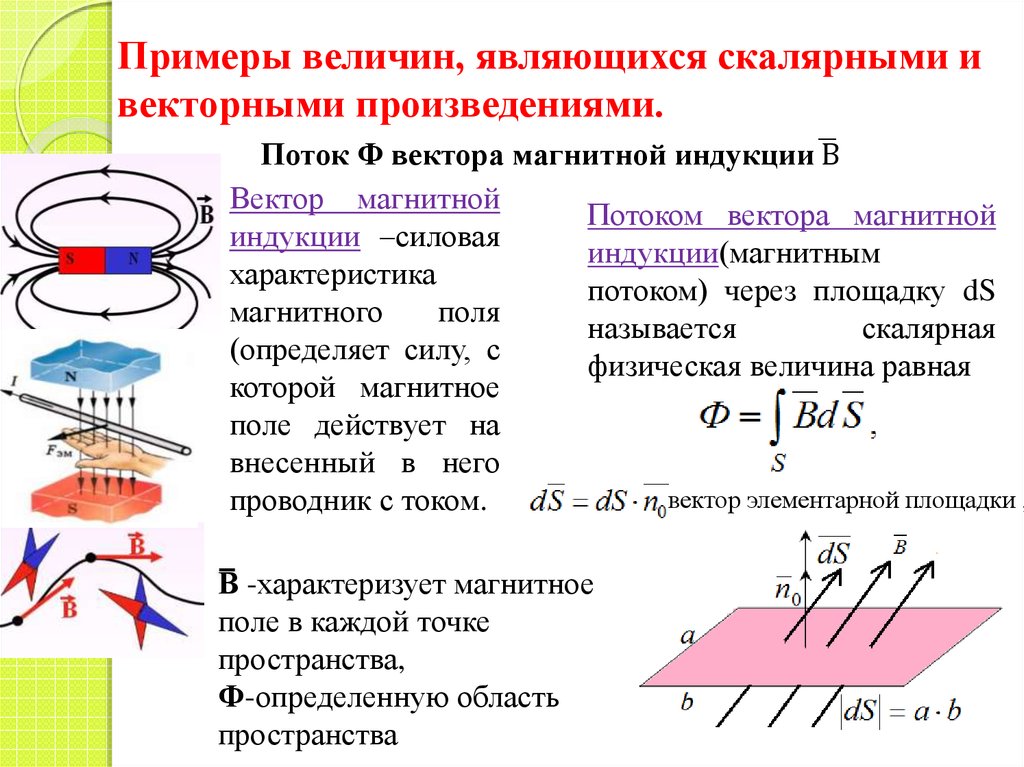 Это дает нам
−30 км.
Это дает нам
−30 км. И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже.
И векторные, и скалярные аналоги
делят одни и те же единицы. Например, ускорение, как и величина ускорения, может иметь единицу
метры в секунду в квадрате
(м/с 2 ), а условной единицей силы и ее величины является
ньютоны (Н). Мы резюмируем
векторные и скалярные аналоги в таблице ниже.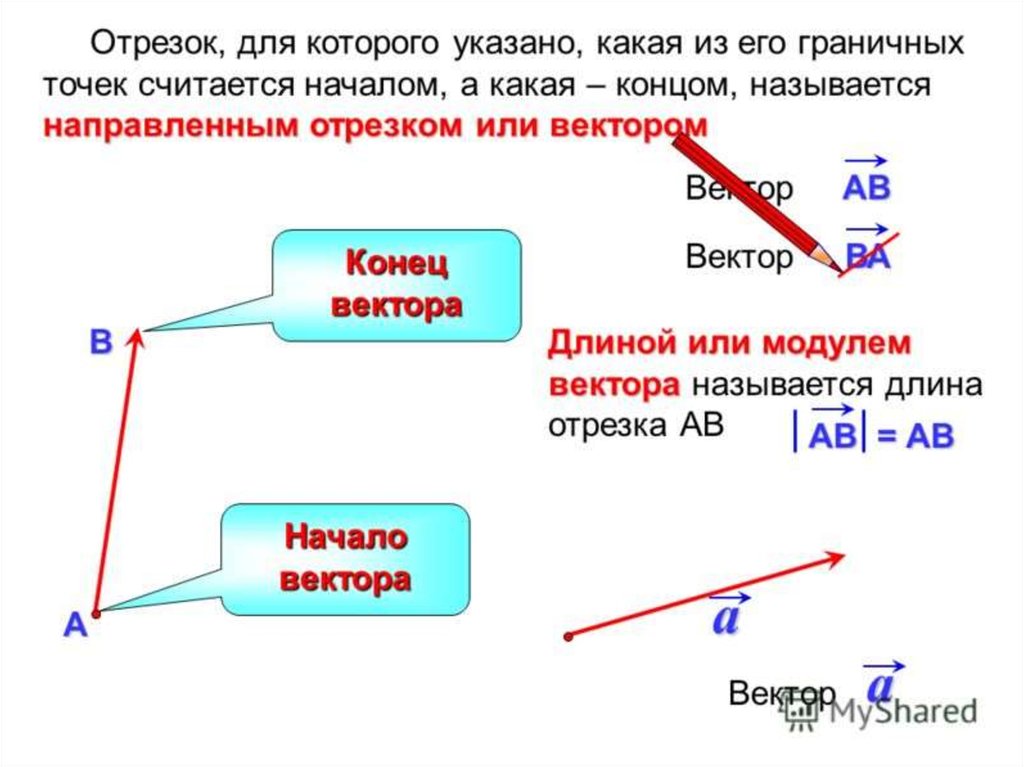

 Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево.
Направление движения объекта указывается его скоростью, поэтому мы можем видеть, что частица движется влево. е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.
е. двумерное или плоское движение, мы видим, что существует более двух
возможные направления. Например, автомобиль может двигаться на север, юг, восток или запад, что дает нам четыре направления. Но это не
единственные возможности направления в плоскостном движении. Автомобиль мог двигаться на северо-запад, северо-северо-запад или вообще в любом направлении, заданном
угол, начинающийся с северного направления. Это приводит к бесконечному числу возможных направлений плоскостного движения. Следовательно, мы не можем
надеемся уловить направление в двух измерениях так же, как мы это сделали для одномерного движения.