Математика 5 класс. Задачи на движение | План-конспект урока по математике (5 класс):
Слайд 1
целеполагание Задачное множество Если хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их. Дж . Пойа
Слайд 2
Проверяем порядок действий Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Выполните действия: Повторение №1 7470 : 18 = 415 1 а) (7470 : 18 – 319 ) – (103 ∙ 20 – 24 ∙ 45) : 28 415 – 319 = 96 2 103 ∙ 20 = 2060 3 24 ∙ 45 = 1080 4 2060 – 1080 = 980 5 980 : 28 = 35 6 96 – 35 = 61 7
Слайд 3
Проверяем Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Запишите число, которое представлено в виде суммы разрядных слагаемых: Повторение №2 в) 2 ∙ 10 3 + 8 ∙ 10 2 + 7 ∙ 10 + 3 = 2873 ?
Слайд 4
Обсуждаем Вхождение в тему урока и создание условий для осознанного восприятия нового материала. От железнодорожной станции до поселка 72 км. От станции и из поселка одновременно и навстречу друг другу выехали два велосипедиста. Один из них едет со скоростью 13 км/ч, другой – 11 км/ч. Через сколько часов велосипедисты встретятся, если будут ехать без остановок? ЗАДАЧА №3 72 : (13 + 11) = 3 (ч) ? . . 13 км/ч 11 км/ч . 72 км с п
От станции и из поселка одновременно и навстречу друг другу выехали два велосипедиста. Один из них едет со скоростью 13 км/ч, другой – 11 км/ч. Через сколько часов велосипедисты встретятся, если будут ехать без остановок? ЗАДАЧА №3 72 : (13 + 11) = 3 (ч) ? . . 13 км/ч 11 км/ч . 72 км с п
Слайд 5
Обсуждаем Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Из двух сел, расстояние между которыми 28 км, одновременно навстречу друг другу вышли два пешехода. Один шел со скоростью 4 км/ч, другой – со скоростью 5 км/ч. Какое расстояние будет между ними через 3 ч? ЗАДАЧА №4 28 – (4 ∙ 3 + 5 ∙ 3 )= 1 (км) ? . . 4 км/ч 5 км/ч . 28 км с1 с2 . 3 ч 3 ч
Слайд 6
Расстояние между шариками Скорость черного Скорость белого Время 2 м/с 3 м/с 4с 30 м 4 м/с 2 м/с 27 м 4 м/с 3 с Математическая разминка Вхождение в тему урока и создание условий для осознанного восприятия нового материала. 1) Черный и белый шарики покатились одновременно в противоположных направлениях из одной точки. Какие величины должны стоять в пустых клетках таблицы? 20 м ? 5 с ? 5 м/с ?
Какие величины должны стоять в пустых клетках таблицы? 20 м ? 5 с ? 5 м/с ?
Слайд 7
Разбираем задачу Вхождение в тему урока и создание условий для осознанного восприятия нового материала. Два поезда движутся навстречу друг другу со скоростями 60 км/ч и 80 км/ч. На каком расстоянии друг от друга будут они за 1 ч до встречи? За 2 ч до встречи? Задача №5 (60 + 80) ∙ 1 = 140 км з а 1 ч до встречи . . 60 км/ч 80 км/ч . 1 ч п1 п2 . . (60 + 80) ∙ 2 = 280 км з а 2 ч до встречи
Слайд 8
Отправляемся в плавание по реке целеполагание Попробуйте сформулировать тему урока ЗАДАЧИ НА ДВИЖЕНИЕ
Слайд 9
Движение по реке Организация и самоорганизация учащихся. Организация обратной связи . В задачах на движение по реке приходится различать скорость движения по течению и скорость движения против течения.
Слайд 10
Движение по реке Организация и самоорганизация учащихся. Организация обратной связи . Пусть собственная скорость лодки (скорость в стоячей воде) равна 7 км/ч, а скорость течения реки – 2 км/ч. Тогда скорость лодки по течению, складывается из ее собственной скорости и скорости течения : 7 + 2 = 9 (км/ч) А скорость лодки против течения реки получается вычитанием из собственной скорости лодки скорости течения реки: 7 – 2 = 5 км/ч.
Тогда скорость лодки по течению, складывается из ее собственной скорости и скорости течения : 7 + 2 = 9 (км/ч) А скорость лодки против течения реки получается вычитанием из собственной скорости лодки скорости течения реки: 7 – 2 = 5 км/ч.
Слайд 11
Скорость катера по течению реки равна 15 + 3 = (18 км/ч) За 2 часа он проплыл по течению 18 ∙ 2 = 36 (км) Скорость катера против течения реки равна 15 – 3 = ( 12 км/ч ) поэтому время, которое катер затратил на обратный путь, равно 36 : 12 = 3 (ч) Решим задачу Организация и самоорганизация учащихся. Организация обратной связи . Катер плывет от одной пристани до другой вниз по течению реки 2 ч. Какое расстояние проплыл катер, если его собственная скорость равна 15 км/ч, а скорость течения реки 3 км/ч? За какое время катер проплыл обратный путь, плывя против течения?
Слайд 12
Движение по реке практикум б) На путь из пункта А в пункт В теплоход затратил 1 ч 40 мин, а на обратный путь – 2 ч. В каком направлении течет река? УЧЕБНИК У: № 291 Река течет в направлении от А к В, т. к. время движения от А к В меньше чем от В к А. ответ в) Скорость течения реки 2 км/ч. На сколько километров река отнесет плот за 1 ч? За 5 ч? За 1 ч на 2км, за 5ч – на 10 км. ответ
к. время движения от А к В меньше чем от В к А. ответ в) Скорость течения реки 2 км/ч. На сколько километров река отнесет плот за 1 ч? За 5 ч? За 1 ч на 2км, за 5ч – на 10 км. ответ
Слайд 13
Работаем устно практикум Скорость катера в стоячей воде равна 18 км/ч. Скорость течения реки равна 2 км/ч. Задача №6 По течению – 20 км/ч. Против течения – 16 км/ч. ответ 1) С какой скоростью будет двигаться катер по течению реки? Против течения реки? По течению – 40 км. Против течения – 48 км. ответ 2) Какой путь пройдет катер по течению реки за 2 ч? Против течения реки за 3 ч?
Слайд 14
Работаем устно практикум Скорость катера в стоячей воде равна 18 км/ч. Скорость течения реки равна 2 км/ч. Задача №7 По течению – 4 ч. Против течения – 5 ч. ответ 3) Сколько времени затратит катер, чтобы пройти 80 км по течению реки? Против течения реки?
Слайд 15
Решаем задачу практикум Катер, имеющий собственную скорость 15 км/ч, проплыл 2 ч по течению реки и 3 ч против течения реки. Какое расстояние проплыл катер за это время, если скорость течения реки 2 км/ч ? УЧЕБНИК № 294 (15 + 2) ∙ 2 + (15 – 2 ) ∙ 3 = 73 (км) решение
Какое расстояние проплыл катер за это время, если скорость течения реки 2 км/ч ? УЧЕБНИК № 294 (15 + 2) ∙ 2 + (15 – 2 ) ∙ 3 = 73 (км) решение
Слайд 16
Движение по реке Проверка полученных результатов. Коррекция. . Расстояние между причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч? УЧЕБНИК №297 24 : (10 + 2) + 24 : (10 – 2 ) = 5 (ч) решение
Слайд 17
Движение по реке (для продвинутых) Проверка полученных результатов. Коррекция. . Лодка плывет по течению реки. Скорость течения реки 2 км/ч. В некоторый момент гребец уронил в воду шляпу и, не заметив этого, продолжал плыть дальше. Какое расстояние будет между лодкой и шляпой через 15 мин, если собственная скорость лодки 9 км/ч? Изменится ли ответ, если скорость течения будет другой? Подумай! №8 Шляпа будет плыть по реке со скоростью течения реки. Скорость лодки в стоячей воде равна 9 ∙ 1000/60 = 150 (м/мин). Значит через 15 мин после падения шляпы расстояние между лодкой и шляпой будет равно 150 ∙ 15 = 2250 (м). При изменении скорости реки ответ не изменится. решение
Значит через 15 мин после падения шляпы расстояние между лодкой и шляпой будет равно 150 ∙ 15 = 2250 (м). При изменении скорости реки ответ не изменится. решение
Слайд 18
Подведение итогов, рефлексия, домашнее задание. Подведем итоги — По каким вопросам ваше мнение не изменилось? — Объясните, почему вы так решили. — По каким вопросам ваше мнение изменилось и почему? Домашнее задание п.3.5, №292, №295
Слайд 19
Проверочная работа Проверка полученных результатов. Коррекция. . 1) Реши задачу: Собственная скорость теплохода равна 20 км/ч, скорость течения реки – 2 км/ч. С какой скоростью теплоход идет по течению реки и с какой – против течения? : 2) Выполни действия : (7470 : 18 – 319 ) – (103 ∙ 20 – 24 ∙ 45) : 28
Тесты по математике для 5 класса онлайн
Проценты НОД НОК Натуральные числа Дроби
-
ВПР 5 класс математика (1 вариант)
04.
 05.2017
66541
05.2017
66541
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
ВПР 5 класс математика (5 вариант)
05.05.2017 92403
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
Таблица умножения
08.07.2017 294387
Тест предназначен для закрепления изученного материала и его повторения.
 Удачи в прохождении!
Удачи в прохождении! -
Натуральные числа на координатной прямой
07.08.2022 461 0
Тест по математике для учащихся 5 класса. Тема: «Натуральные числа на координатной прямой». Для любого УМК из действующего ФПУ.
-
Прямая. Луч. Отрезок.
08.11.2020 5212
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
ВПР 5 класс математика (2 вариант)
 05.2017
16628
05.2017
16628
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
Математика решение задач
30.01.2021 57446
тест для учащихся 3-4 классов по математике задания не простые. Пожелаем удачи.
-
таблица умножения от 2 до 15
04.10.2020 22795
13 заданий. Критерии: «5» — 13 баллов, «4» — 11-12 баллов, «3» — 9-10 баллов.
-
Тест по математике «Натуральные числа»
16.
 02.2021
1133
02.2021
1133
Данный тест предназначен для повторения материала по теме «Натуральные числа»
-
ВПР 5 класс математика (3 вариант)
05.05.2017 7652
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
Десятичные дроби
06.03.2014 66739
Простой тест по математике для учащихся 5 класса из 10 вопросов. Данный тест поможет проверить свои навыки и умения выполнять тестовые задания, проверить знания учащихся по темам «Десятичная запись дробных чисел», «Сравнение десятичных дробей», «Сложение и вычитание десятичных дробей».

-
Викторина о римских цифрах
02.03.2022 498
Викторина о цифрах, которые мы встречаем на циферблатах часов и в исторических датах.
-
5 класс математика домашняя работа «Задачи на совместную работу»
27.04.2020 3945
Домашняя работу на тему Задаси на совместную работу». Состоит из пяти задач.
-
Тест по математике. 5 класс
01.05.2017 62699
В этом тесте вам предлагается вспомнить краткий материал по математике из курса 5 класса.

-
Округление десятичных дробей
10.04.2015 28959
Тест для учащихся 5 классов состоит из 7 вопросов по теме «Округление десятичных дробей». Выполняется для закрепления изученного материала.
-
Олимпиада по математике 5 класс
27.01.2014 44400
Данный тест можно использовать как дистанционную олимпиаду.
-
Сложение и вычитание десятичных дробей
21.05.2015 11625
Тест для учащихся 5 классов из 10 вопросов по теме курса «Сложение и вычитание десятичных дробей», выполняется при подготовке к контрольной работе.

-
ВПР 5 класс математика (4 вариант)
05.05.2017 4216
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
Текстовые задачи на проценты (с десятичными дробями)
19.09.2020 1402 0
Задачи для закрепления материала по теме «Проценты». В тест случайным образом выбираются 5 задач из общей базы задач по теме. За каждое верно выполненное задание начисляется 1 балл. По окончании теста сразу видны результат и оценка. Критерии: «3» — 3 балла, «4» — 4 балла, «5» — 5 баллов.

-
Тест Обыкновенные дроби 5 класс
29.03.2020 32898
Тест по математике на тему: Обыкновенные дроби (5 класс) включает в себя 10 заданий
-
ВПР 5 класс математика (6 вариант)
06.05.2017 3547
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
Десятичные дроби и проценты
14.
 01.2016
17943
01.2016
17943
Тест для учащихся 5-6 классов по теме «Десятичные дроби и проценты» предназначен для отработки практических навыков учащихся по данной теме
-
МАТЕМАТИКА 5 СИНФ
12.05.2020 3868
Тестҳои мазкур барои хонандагони синфи 5-уми мактабҳои тоҷикӣ ва ӯзбекӣ тайёр карда шудааст
-
Тест по теме проценты для 5 класса по математике
01.02.2014 47119
Тест по математике с одним правильным вариантом ответа для 5 класса по теме проценты.
-
Делимость чисел
20.
 09.2018
4258
09.2018
4258
Тест среднего уровня сложности. Проверяет базовые владения признаками делимости, а также их комбинациями. Подходит для программы 5 и 6 классов.
-
Самостоятельная работа №11. Нахождение части целого и целого по его части. 5 класс
11.04.2021 2278 0
Тест содержит 8 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 4-5 баллов, «4» 6-7 баллов, «5» 8 баллов. Оценка выставляется сразу после прохождения теста.
-
Взаимно обратные числа. Деление
21.11.2020 810 0
В тест включены вопросы по темам «Взаимно обратные числа», «Деление обыкновенных дробей».
 Задания составлены с учетом типичных ошибок, которые допускают учащиеся.
Задания составлены с учетом типичных ошибок, которые допускают учащиеся. -
Готовимся к ВПР. Задание № 2 «Арифметические действия с числами»
29.07.2022 492
Готовимся к ВПР: задание № 2. Тест по теме: «Арифметические действия с числами». Предназначен для проверки знаний обучающихся о порядке действий в выражениях со скобками и без на основе четырех арифметических действий.
-
ВПР 5 класс математика (7 вариант)
06.05.2017 2364
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.

-
Уравнения. Математика 5 класс.
27.11.2019 16464
тест предназначен для контроля знаний по теме «Решение уравнений» в 5 классе
-
Проценты. Решение задач
21.04.2020 2774 0
Тест по теме «Проценты. Решение задач» предназначен для обучающихся 5-6 классов, содержит текстовые задачи по теме «Процентные вычисления»
-
5 класс математика домашняя работа «Задачи на движение»
27.
 04.2020
1199
0
04.2020
1199
0
Домашняя работа «Задачи на движение». Состоит из четырех задач.
-
Домашняя самостоятельная работа по теме Луч, прямая и плоскость. 5 класс
17.09.2019 1619
Данный тест предназначен для домашней работы в качестве закрепления знаний по темам в 5 классе по учебнику Виленкин Луч и плоскость.
-
Математика, 5 класс. Тест по теме «Натуральные числа и шкалы»
27.02.2018 2356
Данный тест создан на основе первых четырёх тестов по теме «Натуральные числа и шкалы» из учебно-методического пособия Л.
 П. Поповой «Контрольно-измерительные материалы. Математика. 5 класс». Тест содержит 18 вопросов, которые случайным образом выбираются из 56 сгруппированных по подтемам вопросов. Содержание некоторых вопросов было изменено. Также изменён тип некоторых вопросов (например, вместо выбора ответа из предложенных вариантов — ввод ответа с клавиатуры). К большинству вопросов имеются комментарии (просмотр доступен после ввода ответа), в которых даны ссылки на соответствующие тематике вопросов материалы, к некоторым вопросам в комментариях даны решения. Время выполнения теста не ограничено, однако рекомендуется выделить не более 45 минут.
П. Поповой «Контрольно-измерительные материалы. Математика. 5 класс». Тест содержит 18 вопросов, которые случайным образом выбираются из 56 сгруппированных по подтемам вопросов. Содержание некоторых вопросов было изменено. Также изменён тип некоторых вопросов (например, вместо выбора ответа из предложенных вариантов — ввод ответа с клавиатуры). К большинству вопросов имеются комментарии (просмотр доступен после ввода ответа), в которых даны ссылки на соответствующие тематике вопросов материалы, к некоторым вопросам в комментариях даны решения. Время выполнения теста не ограничено, однако рекомендуется выделить не более 45 минут. -
5 класс. Математика. Чтение и запись натуральных чисел №2
21.07.2018 929 0
Тест предназначен для учащихся 5 классов при отработке навыка чтения и записи натуральных чисел.

-
Задачи на дроби
30.06.2020 2879
Проверь, умеешь ли ты решать простейшие задачи на дроби. Тест содержит всего 6 задачек для решения которых нужно уметь находить часть от величины, величину по её части, какую часть составляет одна величина от другой. На этих задачах удобно «отрабатывать» применение моделей для решения задач где встречаются величины одного рода. Желаем удачи!
-
Математика 5 класс ВПР 2020
29.03.2020 9809
Проверочная работа по математике Демоверсии ВПР 2020 года для 5 класса Образец
-
Сложение и вычитание натуральных чисел
15.
 11.2013
11047
11.2013
11047
Тест состоит из 11 вопросов. Каждый вопрос имеет 4 варианта ответов. За верный ответ на 1 — 7,9 вопросы Вы получаете по 1 баллу, за верный ответ на 8 вопрос-2балла,за верный ответ на 10и11 вопросы-по 3 балла. Максимальное количество баллов -13. После окончания тестирования будет выведен итог.
-
Обыкновенные дроби. Тест по математике 5 класс
14.03.2021 3143
Предлагаем вам пройти наш новый тест по математике для 5 классов.
-
Итоговый тест в 5 классе
28.01.2013 73946
Тест для учащихся 5 классов из 10 вопросов по всем темам курса, выполняется при подготовке к итоговой контрольной работе.

-
Сравнение обыкновенных дробей
04.03.2014 16279
Тест для учащихся 5 классов из 7 вопросов по теме «Сравнение дробей», выполняется при закреплении изученной темы.
-
Тест по теме «Окружность» 5 класс
10.01.2015 7819
Тест проверяет усвоение понятий окружность, радиус окружности, диаметр окружности.
-
Диагностический тест по математике 5 класс
04.09.2016 2762
С помощью данного теста можно повторить материал по математике за 4 класс и подготовиться к диагностической контрольной работе в 5 классе
-
Таблица умножения 4
05.
 02.2021
799
02.2021
799
Это таблица умножения 4, от 1 до 100. Самая усложнённая венрсия на данный момент.
-
Готовимся к ВПР. Задание № 3 «Арифметический метод».
31.07.2022 524
Готовимся к ВПР: задание № 3. Тест по теме: «Арифметический метод». Предназначен для проверки умения решать практико-ориентированные задачи.
-
Тест по теме «Натуральные числа и шкалы» (вариант 1)
20.02.2014 5802
Тест по математике для 5 класса к учебнику Виленкина В.Я. по теме «Натуральные числа и шкалы».

-
Умножение и деление десятичных дробей
29.03.2020 9400
Тестовые задания для проверки знаний учащихся для 5 класса. В тесте проверяются темы: умножение и деление на десятичную дробь, на разрядную единицу, решение текстовых задач
-
Вычисление процентов от числа (50, 100, 150, 200, 300)
19.09.2020 1404 0
Тренировка на вычисление процентов от заданного числа (50, 100, 150, 200 и 300). В тесте 11 заданий, которые выбираются случайным образом из общей базы — 100 заданий. Оценка «5» — за 91-100%, «4» — за 70-90%, «3» — за 50-69% верных ответов.

-
8 задание ВПР 5 кл. Действия с процентами (10 вопросов)
08.05.2017 934
Восьмое задание ВПР по математике для 5 класса, действия с процентами. Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
5 класс. Математика. Чтение и запись натуральных чисел №1
21.07.2018 438
Тест предназначен для учащихся 5 классов при отработке навыка чтения и записи натуральных чисел.
-
Округление десятичных дробей
03.
 12.2020
4090
0
12.2020
4090
0
В тест включены задания на округление десятичных дробей до тысяч, до сотен, до десятков, до единиц, до десятых, до сотых. В тест случайным образом выбираются 10 заданий из общей базы упражнений. Оценка «5» — за 91-100%, «4» — за 70-90%, «3» — за 50-69% верных ответов.
-
Таблица умножения 2
02.02.2021 3720
Это тест по таблице умножения 2. Тут более все усложненноё и для 3 класса и выше. Удачи в прохождении и надеемся что наш тест вам понравится.
-
Итоговый тест по математике за 5 класс
02.12.2021 2451
Назначение работы – определение соответствия содержания и качества подготовки обучающихся 5 класса федеральному государственному образовательному стандарту по математике для основной общей школы.

-
математика 5 класс. (контрольная работа)
26.03.2020 2500
Это наш новый тест по математике для 5 класса.Темы,контрольная работа,тест.Решать только без калькулятора. Математика ,тест ,контроль знаний.
-
Математика 5 класс. Тема «Умножение натуральных чисел и его свойства»
31.10.2015 10021
тест по математике с вариантами ответов проверяет знания учащихся по теме: «умножение натуральных чисел и его свойства»
-
СРАВНЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ
17.
 04.2020
3960
04.2020
3960
Тест для обучающихся в 5 классе по темам «Запись десятичных дробей. Спавнение десятичных дробей»
-
Тест по теме «Формулы» в формате PISA 5 классс
06.11.2020 684
Задания даны в формате PISA, требующие применение знаний обучающихся в нестандартных ситуациях.
-
Деление с остатком
26.11.2012 7300
Умение решать текстовые задачи — показатель математической грамотности. Текстовые задачи позволяют ученику освоить способы выполнения различных операций, подготовиться к овладению алгеброй, к решению задач по геометрии, физике, химии.

-
Тест по теме «Проценты»
31.03.2020 3972
Тест создан для обобщения и систематизации знаний по теме «Проценты».
-
устный счёт «Сложение и вычитание в пределах 100″
20.09.2020 1279 0
Задания для устного счета на сложение и вычитание натуральных чисел с переходом через десяток. В тесте 20 заданий, которые выбираются случайным образом из базы заданий. Оценка «5» — за 91-100%, «4» — за 70-90%, «3» — за 50-69% верных ответов.
-
Числа и точки на прямой
21.
 09.2020
900
0
09.2020
900
0
5 заданий на определение координат точки и 6 заданий на сравнение чисел с помощью координатной прямой. Оценка «5» — за 91-100%, «4» — за 70-90%, «3» — за 50-69% верных ответов.
-
Десятичные дроби. Разряды. Запись обыкновенной дроби в виде десятичной.
18.10.2020 2565 0
Задания для устного счета на десятичные дроби. В тесте три группы заданий: (1)Разрядность десятичных дробей, (2)Перевод обыкновенной дроби со знаменателем 10,100,1000 в десятичную, и (3)перевод обыкновенной дроби со знаменателем 2 и 4 в десятичную. В тест выбираются по 2 задания из каждой группы случайным образом. Критерии: «3» от 50 до 69%, «4» от 70 до 90%, «5» от 91 до 100%.
-
Представление натуральных чисел на координатном луче.

22.11.2020 779
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
Тестовое задание на тему: «Действия с натуральными числами» для 5 класса.
25.03.2021 53 0
Тестовое задание на тему: «Действия с натуральными числами» для 5 класса. Учебник: А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. Издательство: Вентана-граф, 2016 г.
-
4 задание ВПР 5 кл. Нахождение части числа и числа по его части (15 вопросов)
08.
 05.2017
3809
05.2017
3809
Четвертое задание ВПР по математике для 5 класса, нахождение части числа. Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
11 задание ВПР 5 кл. Работа с таблицами, диаграммами (10 вопросов)
10.05.2017 2754
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
Среднее арифметическое
21.04.2020 9991
Тест «Среднее арифметическое чисел» 5 класс.
 Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического.
Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического. -
Итоговая контрольная работа (Петерсон, 5 класс)
08.05.2020 707
Тест содержит 8 заданий. Максимальное количество баллов — 12.Система оценивания: более 83% выполнено верно — «5» от 71% до 82% выполнено верно — «4» от 50% до 70% выполнено верно — «3» менее 50% выполнено верно — «2» Оценка выставляется автоматически.
-
Повторение материала 5 класса (Виленкин)
04.
 05.2021
436
0
05.2021
436
0
Тест №1 «Повторение материала 5 класса», автор Н.Я. Виленкин. Предназначен для учеников 5 класса, завершающих изучение материала.
-
Проценты, вычисление процентов
09.06.2021 199 0
Тест на усвоение начального понятия по теме «Процеты», на решение простейших задач на перевод числа в проценты и процента в дробь, решение простейших задач на вычисление процентов
-
Обозначение натуральных чисел
07.08.2013 1901
Самостоятельная работа в 5 классе по математике к учебнику Н.
 Я. Виленкина и др. «Математика. 5 класс»
Я. Виленкина и др. «Математика. 5 класс» -
Площадь квадрата и прямоугольника
11.12.2013 19111
Тест содержит 8 вопросов на знание формул площади квадрата и прямоугольника и умение применять их к решению задач. К каждому вопросу предлагается 4 варианта ответов.
-
Сложение десятичных дробей
19.02.2015 2552
Тест «Сложение десятичных дробей» проверяет вычислительные навыки устного счета
-
ВПР 5 класс. Математика 2017 год
25.
 04.2017
9482
04.2017
9482
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. При необходимости можно пользоваться черновиком.
-
2 задание ВПР 5 кл. Обыкновенная дробь (15 вопросов)
07.05.2017 3818
Второе задание ВПР по математике для 5 класса, обыкновенные дроби. Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
Сравнение обыкновенных дробей
15.02.2018 635
Тест предназначен для учащихся 5 класса при изучении темы «Сравнение обыкновенных дробей».
 Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей.
Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей. -
Основное свойство дроби 5 класс
28.04.2020 434
Тест предназаначен для закрепления темы «Основное свойство дроби» курса математики 5 класса.
-
Понятие дроби.
08.02.2021 576 0
Данный тест будет полезным учителю для осуществления быстрого контроля на уроке, а также ребятам, которые желают проверить свои знания по данной теме.
-
ВПР по Математике 5 класс
28.
 03.2021
336
03.2021
336
Каждый месяц мы составляем варианты для самопроверки. Варианты составляются компьютером из новых заданий и заданий, оказавшихся самыми сложными по результатам предудущего месяца. По окончании работы система проверит ваши ответы, покажет правильные решения и выставит оценку.Чтобы целенаправленно тренироваться по определённым темам, вы можете составить вариант из необходимого количества заданий по конкретным разделам задачного каталога. Для быстрого составления типового варианта используйте кнопки справа.
-
Контрольная работа №1 «Сложение и вычитание натуральных чисел»
03.10.2021 401 0
Тест предназначен для проверить знаний учащихся 5 класса по теме «Сложение и вычитание» .
-
Тест по математике для 5 класса по теме «Вычитание десятичных дробей»
26.
 08.2015
2379
08.2015
2379
Данный тест предназначен для учеников 5-х классов. Тема: «Вычитание десятичных дробей».
-
Деление с остатком. 5 класс
18.11.2015 5132
Тип теста — контрольный. Проверяется умение находить компоненты при делении с остатком натуральных чисел: делимое, делитель, неполное частное, остаток.
-
Контрольный устный счет «Действия с десятичными дробями»
08.12.2015 2104
Тест содержит 12 заданий на все действия с десятичными дробями. Тест можно использовать для проверки навыков устного счета учащихся 5-6 классов.
 Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста.
Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста. -
5 класс. Обыкновенные дроби. Правильные и неправильные дроби.
16.01.2016 7436
Тест предназначен для учащихся 5, 6 классов при отработке навыков устного счёта по теме «Обыкновенные дроби. Правильные и неправильные дроби».
-
5 класс. Математика. Действия с натуральными числами №2
02.07.2016 2298
Тест предназначен для учащихся 4, 5 классов при отработке устного счёта на все действия с натуральными числами
-
7 задание ВПР 5 кл.
 Сюжетные задачи на все арифметические действия (10 вопросов)
Сюжетные задачи на все арифметические действия (10 вопросов)
08.05.2017 868 0
Седьмое задание ВПР по математике для 5 класса, сюжетные задачи. Обязательно решение всех задач теста. Вновь открытый тест содержит другие задачи из банка вопросов.
-
10 задание ВПР 5 кл. Задачи на покупки, логические задачи (8 вопросов)
10.05.2017 895
При выполнении работы нельзя пользоваться учебниками, рабочими тетрадями, справочниками, калькулятором. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
Нахождение числа по проценту 5 класс
14.
 04.2020
8107
0
04.2020
8107
0
Данный тест предназначен для закрепления материала по теме «Проценты». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
Круговые диаграммы 5 класс
25.04.2020 4904
Данный тест предназначен для закрепления материала по теме «Круговые диаграммы». Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
Действия с десятичными дробями 5 класс
06.05.2020 1649 0
Данный тест предназначен для закрепления материала по теме «Действия с десятичными дробями».
 Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!! -
Объем прямоугольного параллелепипеда. 5 класс
10.05.2020 1598
Данный тест предназначен для закрепления материала по теме «Объем прямоугольного параллелепипеда» 5 класс. Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
-
Итоговый тест по математике 5 класс (Мерзляк А.Г.)
07.06.2020 2323 0
Данный тест является итоговым за курс математики 5 класса ( УМК Мерзляк А.Г., Полонский В.Б., Якир М.С.).
-
«Площадь прямоугольного треугольника и некоторых видов многоугольников», 5 кл
17.
 04.2022
117
0
04.2022
117
0
Тест предназначен для учащихся 5 классов. Тест состоит из пяти вопросов.
-
Тест по наглядной геометрии
16.05.2013 3337 0
Итоговый тест по курсу «Наглядная геометрия» за 5 класс. Содержит как теоретические, так и практические вопросы
-
Тест по теме «Натуральные числа и шкалы» (вариант 2)
21.02.2014 3641
Тест по математике для 5 класса к учебнику Виленкина В.Я. по теме «Натуральные числа и шкалы».
-
Тест на тему «Делимость чисел»
06.
 12.2015
2389
12.2015
2389
Образовательный тест по математике на тему «Делимость чисел». В данном тесте сосредоточены вопросы по основным свойствам делимости натуральных чисел. Тест подходит для учеников 5-6 классов.
-
Понятие дроби
15.01.2016 5818
Тест для учащихся 5 класса по теме «Понятие дроби» предназначен для проверки знаний учащихся по данной теме.
-
1 задание ВПР 5 кл. Натуральное число (15 вопросов)
07.05.2017 1226 0
Первое задание ВПР по математике для 5 класса, натуральное число.
 Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов. -
3 задание ВПР 5 кл. Десятичная дробь (15 вопросов)
08.05.2017 1116
Третье задание ВПР по математике для 5 класса, десятичные дроби. Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
-
5 задание ВПР 5 кл. Действия с рациональными числами (15 вопросов)
08.05.2017 499 0
Пятое задание ВПР по математике для 5 класса, действия с рациональными числами. Обязательные ответы на все вопросы теста.
 Вновь открытый тест содержит другие вопросы из банка вопросов.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Урок математики в 5-м классе по теме «Задачи на движение по реке»
- Зеленская Татьяна Александровна
Разделы: Математика
Тема: Задачи на движение по реке.
Цели:
- обобщить и систематизировать знания по теме «Задачи на движение по реке»;
- проверить знание теоретического материала, умение решать задачи арифметическим способом;
- развивать кругозор, мышление, внимание, культуру математической речи;
- прививать интерес к математике.
Методы обучения: частично-поисковый
(эвристический), системные обобщения,
самопроверка, взаимопроверка.
Формы организации урока: фронтальная, индивидуальная.
Оборудование: презентация к уроку, листы учета знаний.
ХОД УРОКА
I. Организационный момент
Сообщить учащимся цели урока. Настроить ребят на активную работу.
II. Проверка домашнего задания
№ 391(а).
Собственная скорость теплохода 27км/ч, скорость течения реки 3 км/ч. Сколько времени затратит теплоход на путь по течению реки между двумя причалами, если расстояние между ними 120 км?
Решение:
1) Vпо теч.= Vсоб.+ Vтеч. = 27 + 3 = 30 (км/ч).
2) tпо теч.= S : Vпо теч.= 120 : 30 = 4 (ч.)
Ответ: 4 часа.
№ 392.
Катер, имеющий собственную скорость 15 км/ч, проплыл 2 часа по течению реки и 3часа против течения. Какое расстояние проплыл катер за все время, если скорость течения реки 2 км/ч?
Решение:
1) Vпо теч. = Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
= Vсоб. + Vтеч.= 15 + 2 = 17 (км/ч.)
2) Vпр. теч.= Vсоб. – Vтеч.= 15 – 2 = 13 (км/ч.)
3) Sпо теч.= Vпо теч. · tпо теч. = 17 · 2 = 34 (км)
4) Sпр теч.= Vпр. теч.· t пр. теч.=13 · 3 = 39 (км)
5) S=Sпо теч.+ Sпр. теч. = 34 + 39 = 73 (км)
Ответ: 73 км
III. Актуализация знаний
(Фронтальная работа)
Вопросы: (устно или с использованием проектора.)
1. Что такое собственная скорость катера? Ответ:
скорость катера в стоячей воде (озере, пруду).
2. Что такое скорость течения? Ответ: на какое
расстояние относит река предмет за единицу
времени.
3. Как определяется скорость катера по течению
реки? Ответ: как сумма скорости собственной и
течения.
4. Как определяется скорость катера против
течения? Ответ: как разность скорости
собственной и течения.
5. Как определяется скорость движения плота по
реке? Ответ: как скорость течения реки.
Подведем итог:
Vпо течению – сумма V течения и V
собственной.
V против течения – разность Vсобственной и
Vтечения.
Значит, зная Vпо течению и Vпротив течения, можно
найти Vтечения и Vсобственной.
Вспомним задачу на нахождение двух чисел по их сумме и разности.
1) (V по теч. – V пр. теч.) : 2 = Vтеч.
2) Vпо теч. – Vтеч. = Vсоб.
IV. Решение задач
№ 1.
Из четырех скоростей (Vсоб.,Vпо теч.,Vпр. теч.,Vтеч. ) две заданы и изображены отрезком. Вычислите две другие скорости и изобразите их отрезками:
№ 2. Заполним таблицу.
Vсоб, км/ч |
V теч, км/ч |
Vпо теч, км/ч |
Vпр. |
15 |
3 |
? |
? |
16 |
? |
18 |
? |
13 |
? |
? |
10 |
? |
2 |
11 |
? |
? |
3 |
? |
15 |
? |
? |
28 |
24 |
№ 3
Решим задачу № 393 (а).
Расстояние между двумя причалами 24 км. Сколько времени потратит моторная лодка на путь от одного причала до другого и обратно, если собственная скорость моторной лодки 10 км/ч, а скорость течения 2 км/ч?
Решение:
1) Vпо теч.= Vтеч.+ Vсоб.= 2 + 10 = 12 (км/ч)
2) Vпр. теч. = Vсоб. – Vтеч.= 10 – 2 = 8 (км/ч)
3) tпо теч.= S : Vпо теч.= 24 : 12 = 2 (ч)
4) tпр. теч.= S : Vпр. теч.= 24 : 8 = 3 (ч)
5) t = tпо теч. + tпр. теч.= 2 + 3 = 5 (ч)
Ответ: 5 часов.
V. Самостоятельная работа
I вариант |
II вариант |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1) Скорость моторной лодки в стоячей
воде 15км/ч, а скорость течения реки 3 км/ч. Сколько времени потратит моторная лодка на путь от одной пристани до другой и обратно, если расстояние между пристанями 36 км? 2)
|
1) Скорость моторной лодки в стоячей
воде 10 км/ч, а скорость течения реки 2 км/ч. Сколько времени потратит моторная лодка на движение от одной пристани до другой и обратно, если расстояние между пристанями 24 км? 2)
|
VI. Подведение итогов урока
Заполнить карточку самоанализа.
Объявление оценок за урок.
VII. Определение домашнего задания
№ 393 (б), 394 С.М.Никольский, М.К.Потапов, Н.Н.Решетников, А.В.Шевкин. Математика: учебник для 6 кл. общеобразовательных учреждений.– М.: Просвещение, 2008 г.
Презентация
Список литературы:
1. С.М.Никольский, М.К.Потапов, Н.Н.Решетников,
А.В.Шевкин. Математика: учебник для 6 кл.
общеобразовательных учреждений. – М.:
Просвещение, 2008 г.
2. А.В.Шевкин. Обучение решению текстовых
задач в 5-6 классах. – М.: «Русское слово», 2001г.
Текстовые задачи на движение – легко! Алгоритм решения и успех на ЕГЭ
Смотри видео «Текстовые задачи на ЕГЭ по математике».
Почему текстовые задачи относятся к простым?
Во-первых, все такие задачи решаются по единому алгоритму, о котором мы вам расскажем. Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Во-вторых, многие из них однотипны — это задачи на движение или на работу. Главное — знать к ним подход.
Внимание! Чтобы научиться решать текстовые задачи, вам понадобится всего три-четыре часа самостоятельной работы, то есть два-три занятия. Всё, что нужно, — это здравый смысл плюс умение решать квадратное уравнение. И даже формулу для дискриминанта мы вам напомним, если вдруг забыли.
Прежде чем перейти к самим задачам — проверьте себя.
Запишите в виде математического выражения:
- на больше
- в пять раз больше
- на меньше, чем
- меньше в раза
- на меньше, чем
- частное от деления на в полтора раза больше
- квадрат суммы и равен
- составляет процентов от
- больше на процентов
Пока не напишете — в ответы не подглядывайте! 🙂
Казалось бы, на первые три вопроса ответит и второклассник. Но почему-то у половины выпускников они вызывают затруднения, не говоря уже о вопросах и . Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Из года в год мы, репетиторы, наблюдаем парадоксальную картину: ученики одиннадцатого класса долго думают, как записать, что « на больше ». А в школе в этот момент они «проходят» первообразные и интегралы 🙂
Итак, правильные ответы:
больше, чем . Разница между ними равна пяти. Значит, чтобы получить большую величину, надо к меньшей прибавить разницу.
больше, чем , в пять раз. Значит, если умножить на , получим .
меньше, чем . Разница между ними равна . Чтобы получить меньшую величину, надо из большей вычесть разницу.
меньше, чем . Значит, если из большей величины вычтем разницу, получим меньшую.
На всякий случай повторим терминологию:
Сумма — результат сложения двух или нескольких слагаемых.
Разность — результат вычитания.
Произведение — результат умножения двух или нескольких множителей.
Частное — результат деления чисел.
Мы помним, что .
Если принять за , то на процентов больше, то есть .
Начнем мы с задач на движение. Они часто встречаются в вариантах ЕГЭ. Здесь всего два правила:
- Все эти задачи решаются по одной-единственной формуле: , то есть расстояние скорость время. Из этой формулы можно выразить скорость или время .
- В качестве переменной удобнее всего выбирать скорость. Тогда задача точно решится!
Для начала очень внимательно читаем условие. В нем все уже есть. Помним, что текстовые задачи на самом деле очень просты.
. Из пункта в пункт , расстояние между которыми км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт на часа позже автомобилиста. Ответ дайте в км/ч.
Что здесь лучше всего обозначить за ? Скорость велосипедиста. Тем более, что ее и надо найти в этой задаче. Автомобилист проезжает на километров больше, значит, его скорость равна .
Нарисуем таблицу. В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
В нее сразу можно внести расстояние — и велосипедист, и автомобилист проехали по км. Можно внести скорость — она равна и для велосипедиста и автомобилиста соответственно. Осталось заполнить графу «время».
Его мы найдем по формуле: . Для велосипедиста получим , для автомобилиста .
Эти данные тоже запишем в таблицу.
Вот что получится:
| велосипедист | |||
| автомобилист |
Остается записать, что велосипедист прибыл в конечный пункт на часа позже автомобилиста. Позже — значит, времени он затратил больше. Это значит, что на четыре больше, чем , то есть
Решаем уравнение.
Приведем дроби в левой части к одному знаменателю.
Первую дробь домножим на , вторую — на .
Если вы не знаете, как приводить дроби к общему знаменателю (или — как раскрывать скобки, как решать уравнение. ..), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
..), подойдите с этим конкретным вопросом к вашему учителю математики и попросите объяснить. Бесполезно говорить учительнице: «Я не понимаю математику» — это слишком абстрактно и не располагает к ответу. Учительница может ответить, например, что она вам сочувствует. Или, наоборот, даст какую-либо характеристику вашей личности. И то и другое неконструктивно.
А вот если вы зададите конкретный вопрос: «Как приводить дроби к одному знаменателю» или «Как раскрывать скобки» — вы получите нужный вам конкретный ответ. Вам ведь необходимо в этом разобраться! Если педагог занят, договоритесь о времени, когда вы можете с ним (или с ней) встретиться, чтобы получить консультацию. Используйте ресурсы, которые у вас под рукой!
Получим:
Разделим обе части нашего уравнения на . В результате уравнение станет проще. Но почему-то многие учащиеся забывают это делать, и в результате получают сложные уравнения и шестизначные числа в качестве дискриминанта.
Умножим обе части уравнения на . Получим:
Получим:
Раскроем скобки и перенесем всё в левую часть уравнения:
Мы получили квадратное уравнение. Напомним, что квадратным называется уравнение вида . Решается оно стандартно — сначала находим дискриминант по формуле , затем корни по формуле .
В нашем уравнении , , .
Найдем дискриминант и корни:
, .
Ясно, что не подходит по смыслу задачи — скорость велосипедиста не должна быть отрицательной.
Ответ: .
Следующая задача — тоже про велосипедиста.
2. Велосипедист выехал с постоянной скоростью из города в город , расстояние между которыми равно км. На следующий день он отправился обратно со скоростью на км/ч больше прежней. По дороге он сделал остановку на часа. В результате он затратил на обратный путь столько же времени, сколько на путь из в . Найдите скорость велосипедиста на пути из в . Ответ дайте в км/ч.
Пусть скорость велосипедиста на пути из в равна . Тогда его скорость на обратном пути равна . Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
Расстояние в обеих строчках таблицы пишем одинаковое — километров. Осталось записать время. Поскольку , на путь из в велосипедист затратит время , а на обратный путь время .
| туда | |||
| обратно |
На обратном пути велосипедист сделал остановку на часа и в результате затратил столько же времени, сколько на пути из в . Это значит, что на обратном пути он крутил педали на часа меньше.
Значит, на три меньше, чем . Получается уравнение:
Как и в предыдущей задаче, сгруппируем слагаемые:
Точно так же приводим дроби к одному знаменателю:
Разделим обе части уравнения на .
Напомним — если вам непонятны какие-либо действия при решении уравнений, обращайтесь к учительнице! Показывайте конкретную строчку в решении задачи и говорите: «Пожалуйста, объясните, как это делать». Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Для нее такое объяснение — дело пятнадцати минут, а вы наконец научитесь решать уравнения, что очень важно для сдачи ЕГЭ по математике.
Умножим обе части уравнения на , раскроем скобки и соберем все в левой части.
Находим дискриминант. Он равен .
Найдем корни уравнения:
. Это вполне правдоподобная скорость велосипедиста. А ответ не подходит, так как скорость велосипедиста должна быть положительна.
Ответ: .
Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход, катер или моторная лодка. Обычно в условии говорится о собственной скорости плавучей посудины и скорости течения. Собственной скоростью называется скорость в неподвижной воде.
При движении по течению эти скорости складываются. Течение помогает, по течению плыть — быстрее.
Скорость при движении по течению равна сумме собственной скорости судна и скорости течения.
А если двигаться против течения? Течение будет мешать, относить назад. Теперь скорость течения будет вычитаться из собственной скорости судна.
Теперь скорость течения будет вычитаться из собственной скорости судна.
3. Моторная лодка прошла против течения реки км и вернулась в пункт отправления, затратив на обратный путь на часа меньше. Найдите скорость лодки в неподвижной воде, если скорость течения равна км/ч. Ответ дайте в км/ч.
Пусть скорость лодки в неподвижной воде равна .
Тогда скорость движения моторки по течению равна , а скорость, с которой она движется против течения .
Расстояние и в ту, и в другую сторону одинаково и равно км.
Занесем скорость и расстояние в таблицу.
Заполняем графу «время». Мы уже знаем, как это делать. При движении по течению , при движении против течения , причем на два часа больше, чем .
| по течению | |||
| против течения |
Условие « на два часа больше, чем » можно записать в виде:
Составляем уравнение:
и решаем его.
Приводим дроби в левой части к одному знаменателю
Раскрываем скобки
Делим обе части на , чтобы упростить уравнение
Умножаем обе части уравнения на
Вообще-то это уравнение имеет два корня: и (оба этих числа при возведении в квадрат дают ). Но конечно же, отрицательный ответ не подходит — скорость лодки должна быть положительной.
Ответ: .
4. Теплоход проходит по течению реки до пункта назначения км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна км/ч, стоянка длится часов, а в пункт отправления теплоход возвращается через часов после отплытия из него. Ответ дайте в км/ч.
Снова обозначим за скорость течения. Тогда скорость движения теплохода по течению равна , скорость его движения против течения равна . Расстояния — и туда, и обратно — равны км.
Теперь графа «время».
Поскольку , время движения теплохода по течению равно , которое теплоход затратил на движение против течения, равно .
| по течению | |||
| против течения |
В пункт отправления теплоход вернулся через часов после отплытия из него. Стоянка длилась часов, следовательно, часов теплоход плыл — сначала по течению, затем против.
Значит,
Прежде всего разделим обе части уравнения на . Оно станет проще!
Мы не будем подробно останавливаться на технике решения уравнения. Всё уже понятно — приводим дроби в левой части к одному знаменателю, умножаем обе части уравнения на , получаем квадратное уравнение . Поскольку скорость течения положительна, получаем: .
Ответ: .
Наверное, вы уже заметили, насколько похожи все эти задачи. Текстовые задачи хороши еще и тем, что ответ легко проверить с точки зрения здравого смысла. Ясно, что если вы получили скорость течения, равную километров в час — задача решена неверно.
5. Баржа в вышла из пункта в пункт , расположенный в км от . Пробыв в пункте — час минут, баржа отправилась назад и вернулась в пункт в . Определите (в км/час) скорость течения реки, если известно, что собственная скорость баржи равна км/ч.
Пусть скорость течения равна . Тогда по течению баржа плывет со скоростью , а против течения со скоростью .
Сколько времени баржа плыла? Ясно, что надо из вычесть , а затем вычесть время стоянки. Обратите внимание, что час минут придется перевести в часы: час минут часа. Получаем, что суммарное время движения баржи (по течению и против) равно часа.
| по течению | |||
| против течения |
Возникает вопрос — какой из пунктов, или , расположен выше по течению? А этого мы никогда не узнаем! 🙂 Да и какая разница — ведь в уравнение входит сумма , равная .
Итак,
Решим это уравнение. Число в правой части представим в виде неправильной дроби: .
Приведем дроби в левой части к общему знаменателю, раскроем скобки и упростим уравнение. Получим:
Работать с дробными коэффициентами неудобно! Если мы разделим обе части уравнения на и умножим на , оно станет значительно проще:
Поскольку скорость течения положительна, .
Ответ: 2.
Еще один тип текстовых задач в вариантах ЕГЭ по математике — это задачи на работу.
Текстовые задачи. Задачи на движение с решениями
Математика
Задачи на движение с решениями
перейти к содержанию курса текстовых задач
- Первый турист проехал 2 ч на велосипеде со скоростью 16 км/ч. Отдохнув 2 ч, он отравился дальше с прежней скоростью. Спустя 4 ч после старта велосипедиста ему вдогонку выехал второй турист на мотоцикле со скоростью 56 км/ч.
 На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение
На каком расстоянии от места старта мотоциклист догонит велосипедиста? Решение - Из пункта A в пункт B отправились три машины друг за другом с интервалом в 1 ч. Скорость первой машины равна 50 км/ч, а второй — 60 км/ч. Найти скорость третьей машины, если известно, что она догнала первые две машины одновременно. Решение
- Поезд был задержан в пути на 12 мин, а затем на расстоянии 60 км наверстал потерянное время, увеличив скорость на 15 км/ч. Найти первоначальную скорость поезда. Решение
- Расстояние между станциями A и B равно 103 км. Из A в B вышел поезд и, пройдя некоторое расстояние, был задержан, а потому оставшийся до B путь проходил со скоростью, на 4 км/ч большей, чем прежняя. Найти первоначальную скорость поезда, если известно, что оставшийся до B путь был на 23 км длиннее пути, пройденного до задержки, и что на прохождение пути после задержки было затрачено на 15 мин больше, чем на прохождение пути до нее. Решение
- Скорость автомобиля по ровному участку на 5 км/ч меньше, чем скорость под гору, и на 15 км/ч больше, чем скорость в гору.
 Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение
Дорога из A в B идет в гору и равна 100 км. Определить скорость автомобиля по ровному участку, если расстояние от A до B и обратно он проехал за 1 ч 50 мин. Решение - Автобус проходит расстояние между пунктами A и B по расписанию за 5 ч. Однажды, выйдя из A, автобус был задержан на 10 мин в 56 км от A и, чтобы прибыть в B по расписанию, он должен был оставшуюся большую часть пути двигаться со скоростью, превышающей первоначальную на 2 км/ч. Найти скорость движения автобуса по расписанию и расстояние между пунктами A и B, если известно, что это расстояние превышает 100 км. Решение
- Поезд проходит мимо платформы за 32 с. За сколько секунд поезд проедет мимо неподвижного наблюдателя, если длина поезда равна длине платформы? Решение
- Два поезда отправляются навстречу друг другу с постоянными скоростями, один из А в В, другой из В в А. Они могут встретиться на середине пути, если поезд из А отправится на 1,5 ч раньше. Если бы оба поезда вышли одновременно, то через 6 ч расстояние между ними составило бы десятую часть первоначального.
 Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение
Сколько часов каждый поезд тратит на прохождение пути между А и В? Решение - От пристани А одновременно отправились вниз по течению катер и плот. Катер спустился вниз на 96 км, потом повернул обратно и вернулся в А через 14 ч. Найти скорость катера в стоячей воде и скорость течения, если известно, что катер встретил плот на обратном пути расстоянии 24 км от А. Решение
- Пункт В находится по реке ниже пункта А. В одно и то же время из пункта А отплыли плот и первая моторная лодка, а из пункта В — вторая моторная лодка. Через некоторое время лодки встретились в пункте С, а плот за это время проплыл третью часть пути от А до С. Если бы первая лодка без остановки доплыла до пункта В, то плот за это время прибыл бы в пункт С. Если бы из пункта А в пункт В отплыла вторая лодка, а из пункта В в пункт А — первая лодка, то они встретились бы в 40 км от пункта А. Какова скорость обеих лодок в стоячей воде, а также расстояние между пунктами А и В, если скорость течения реки равна 3 км/ч? Решение
- Два тела, двигаясь по окружности в одном направлении, встречаются через каждые 112 мин, а двигаясь в противоположных направлениях — через каждые 16 мин.
 Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение
Во втором случае расстояние между телами уменьшилось с 40 м до 26 м за 12 с. Сколько метров в минуту проходит каждое тело и какова длина окружности? Решение - Две точки, двигаясь по окружности в одном направлении, встречаются каждые 12 мин, причем первая обходит окружность на 10 с быстрее, чем вторая. Какую часть окружности проходит за 1 с каждая точка? Решение
- Два тела движутся навстречу друг другу из двух точек, расстояние между которыми 390 м. Первое тело прошло в первую секунду 6 м, а в каждую последующую секунду проходило на 6 м больше, чем в предыдущую. Второе тело двигалось равномерно со скоростью 12 м/c и начало движение спустя 5 с после первого. Через сколько секунд после того, как начало двигаться первое тело, они встретятся? Решение
Задачи для самостоятельного решения
- Дорога от A до D длиной в 23 км идет сначала в гору, затем — по ровному участку, а потом — под гору. Пешеход, двигаясь из A в D, прошел весь путь за 5 ч 48 мин, а обратно, из D в A, — за 6 ч 12 мин.
 Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ: 8 км
Скорость его движения в гору равна 3 км/ч, по ровному участку — 4 км/ч, а под гору — 5 км/ч. Определить длину дороги по ровному участку. Ответ: 8 км - В 5 ч утра со станции A вышел почтовый поезд по направлению к станции B, отстоящей от A на 1080 км. В 8 ч утра со станции B по направлению к A вышел пассажирский поезд, который проходил в час на 15 км больше, чем почтовый. Когда встретились поезда, если их встреча произошла в середине пути AB? Ответ: в 5 ч дня
- Из пункта A впунктB отправились три велосипедиста. Первый из них ехал со скоростью 12 км/ч. Второй отправился на 0,5 ч позже первого и ехал со скоростью 10 км/ч. Какова скорость третьего велосипедиста, который отправился на 0,5 ч позже второго, если известно, что он догнал первого через 3 ч после того как догнал второго? Ответ: 15 км/ч
- Два поезда — товарный длиной в 490 м и пассажирский длиной в 210 м — двигались навстречу друг другу по двум параллельным путям. Машинист пассажирского поезда заметил товарный поезд, когда он находился от него на расстоянии 700 м; через 28 с после этого поезда встретились.
 Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ: 36 км/ч; 54 км/ч
Определить скорость каждого поезда, если известно, что товарный поезд проходит мимо светофора на 35 с медленнее пассажирского. Ответ: 36 км/ч; 54 км/ч - Турист A и турист B должны были выйти одновременно навстречу друг другу из поселка M ипоселкаN соответственно. Однако турист A задержался и вышел позже на 6 ч. При встрече выяснилось, что A прошел на 12 км меньше, чем B. Отдохнув, туристы одновременно покинули место встречи и продолжили путь с прежней скоростью. В результате A пришел в поселок N через 8 ч, а B пришел в поселок M через 9 ч после встречи. Определить расстояние MN и скорости туристов. Ответ: 84 км; 6 км/ч; 4 км/ч.
- Пешеход, велосипедист и мотоциклист движутся по шоссе в одну сторону с постоянными скоростями. В тот момент, когда пешеход и велосипедист находились в одной точке, мотоциклист был на расстоянии 6 км позади них, а тот момент, когда мотоциклист догнал велосипедиста, пешеход отстал от них на 3 км. На сколько километров велосипедист обогнал пешехода в тот момент, когда пешехода настиг мотоциклист? Ответ: 2 км
- Два туриста вышли одновременно из пункта A в пункт B.
 Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
Первый турист проходил каждый километр на 5 мин быстрее второго. Пройдя 20% расстояния от A до B, первый турист повернул обратно, пришел в A, пробыл там 10 мин, снова пошел в B и оказался там одновремен-
но со вторым туристом. Определить расстояние от A до B, если второй турист прошел его за 2,5 ч. Ответ: 10 км - Рыбак проплыл на лодке от пристани против течения 5 км и возвратился обратно на пристань. Скорость течения реки равна 2,4 км/ч. Если бы рыбак греб с той же силой в неподвижной воде озера на лодке с парусом, увеличивающим скорость на 3 км/ч, то он за то же время проплыл бы 14 км. Найти скорость лодки в неподвижной воде. Ответ: 9,6 км/ч
- Моторная лодка проплыла по озеру, а потом спустилась вниз по реке, вытекающей из озера. Расстояние, пройденное лодкой по озеру, на 15% меньше расстояния, пройденного по реке. Время движения лодки по озеру на 2% больше, чем по реке. На сколько процентов скорость движения лодки вниз по реке больше скорости движения по озеру? Ответ: на 20%
- Турист проплыл в лодке по реке из города A в город B и обратно, затратив на это 10 ч.
 Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч
Расстояние между городами равно 20 км. Найти скорость течения реки, зная, что турист проплывал 2 км против течения реки за такое же время, как 3 км по течению. Ответ: 5/6 км/ч - По окружности длиной 60 м равномерно в одном направлении движутся две точки. Одна из них совершает полный оборот на 5 с быстрее другой. При этом совпадение точек происходит каждый раз через 1 мин. Определить скорости точек. Ответ: 4 м/с; 3 м/с.
- Из точек A и B одновременно начали двигаться два тела навстречу друг другу. Первое в первую минуту прошло 1 м, а в каждую последующую проходило на 0,5 м больше, чем в предыдущую. Второе тело проходило каждую минуту по 6 м. Через сколько минут оба тела встретились, если расстояние между A и B равно 117 м? Ответ: через 12 мин.
- Два приятеля в одной лодке прокатились по реке вдоль берега и вернулись по одной и той же речной трассе через 5 ч с момента отплытия. Протяженность всего рейса составила 10 км. По их подсчетам получилось, что на каждые 2 км против течения в среднем потребовалось столько же времени, сколько на каждые 3 км по течению.
 Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ: 5/12 км/ч; 2 ч и 3 ч.
Найти скорость течения реки, а также время проезда туда и время проезда обратно. Ответ: 5/12 км/ч; 2 ч и 3 ч.
Метки движение, текстовые задачи. Смотреть запись.
Занимательные задачи по математике (5 класс)
Похожие презентации:
Задачи на дроби. Урок математики 5 класс
Урок математики. Занимательные задачи
Эти увлекательные и занимательные задачи. 5 класс
ЕГЭ по математике. Задачи
Математика и космос. Задачи
Готовимся к ОГЭ. Текстовые задачи по математике
Задачи на движение. 5 класс
Математика и спорт. Задачи
ЕГЭ по математике. Решение заданий В13 (задачи на прогрессии
ЕГЭ — 2017 по математике. Базовый уровень. Задачи на логику и смекалку
Загадка:
У нее нет ничего:
Нет ни глаз, ни рук, ни носа,
Состоит она всего
Из условия с вопросом.
Занимательные
задачи
Материал подготовила:
учитель математики
МКОУ «Хохольский лицей»
Соболева Инна Ивановна.
р/п Хохольский
Хохольский район
Воронежская область
1. Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?…
РЕШИ устно
3. К трем лягушкам у болота
Прибежали два енота,
Прискакала тетя жаба
И пришла наседка Ряба.
Сколько в камышах болотных
Оказалось земноводных?…
2. Столько книжек у ребяток,
Сколько у Алеши пяток.
Принесла ребяткам Галя
Мячик, книжку, мишек.
Вы, ребята, посчитали,
Сколько стало книжек?…
2
3. Задачи об многоэтажном доме
ЗАДАЧИ ОБ МНОГОЭТАЖНОМ ДОМЕ4. Лена живет на четвертом этаже, при
этом, поднимаясь к себе домой, она
проходит по лестнице 60 ступенек. Юля
живет в этом же подъезде на втором
этаже. Сколько ступенек проходит Юля,
поднимаясь к себе домой
на второй этаж?
5. Карл и Клара живут в многоэтажном
доме . Клара живет на 12 этажей выше ,
чем Карл. Однажды Карл пошел в гости к
Кларе.
 Пройдя половину пути , он оказался
Пройдя половину пути , он оказалсяна 8 этаже. На каком этаже живет Клара ?
3
Задача о животных.
Знаешь ли ты, что среди всех пород кошачьих только гепарды не
втягивают когти. Когти у них всегда снаружи, как у собак.
6. Среди обитателей площадки в зоопарке молодняка 18 – котята и
щенята разных пород. Из них 9 – щенята, а 13 не втягивают
когти. Сколько обитателей – гепарды и сколько котят других
пород?
4
5. Задача на движение.
ЗАДАЧА НА ДВИЖЕНИЕ.7. Могут ли три человека преодолеть расстояние 60 км
за 3 часа, если в из распоряжении имеется двухместный
мотоцикл? Скорость мотоцикла 50 км/ч, скорость
пешехода 5 км/ч.
5
Решение:
1 час : Два человека (1 и 2) едут на мотоцикле и
проезжают 50 км., а третий человек (3) идёт пешком и
проходит 5 км.
2 час: Человек (2) сходит с мотоцикла и идёт
пешком. Он проходит 5 км. Человек (3) идёт пешком
и проходит ещё 5 км. Человек (1) возвращается на 40
км и ждёт человека (3) там.

3 час: Два человека (1 и 3) на мотоцикле
добираются до пункта назначения. Человек (2)
проходит ещё 5 км и оказывается в пункте
назначения.
6
7. Задачи о профессиях
ЗАДАЧИ О ПРОФЕССИЯХ8. Один кирпич весит 1 килограмм
и еще полкирпича.
Сколько весит один кирпич?
9. Врач прописал больному 3 укола через
каждые полчаса. Первый укол сделали в 8
часов. В какое время сделают последний
укол?
7
8. Геометрическая задача (задача 10)
ГЕОМЕТРИЧЕСКАЯ ЗАДАЧА (ЗАДАЧА 10)Сколько на этом рисунке треугольников?
А четырёхугольников?
Треугольников – 8, Четырёхугольников — 11
8
9. История одной геометрической игры
ИСТОРИЯ ОДНОЙ ГЕОМЕТРИЧЕСКОЙ ИГРЫДревние
греки любили геометрические игры.
Одна из них называлась «СТОМАХИОН». В этой
игре надо было из 14 частей квадрата
складывать различные фигуры. Этой игрой
увлекались настолько, что сам великий ученый
АРХИМЕД написал о ней сочинение.

Похожей игрой развлекались и древние
китайцы. Только они делили квадрат не на 14, а
на 7 частей и называли свою игру «ЧИ-ЧАО-ТЮ»
(что означает «ХИТРОУМНЫЙ УЗОР ИЗ СЕМИ
ЧАСТЕЙ»). Эту игру называют также «ТАНГРАМ».
9
10
11. Правила игры
ПРАВИЛА ИГРЫСуть игры заключается в конструировании на
плоскости разнообразных предметных силуэтов.
Необходимо, чтобы
В
каждую собираемую фигуру вошли
непременно все семь элементов.
При составлении фигуры элементы не налегали
друг на друга, т.е. располагались только в одной
плоскости.
Элементы фигур примыкали один к другому.
11
12
13
Игрой внешне близкой к «Танграм»
являются
пазлы.
14
15. И ещё задания…
И ЕЩЁ ЗАДАНИЯ…Можно ли, не отрывая от
бумаги и не проводя по
линии дважды, нарисовать
распечатанный конверт
одним росчерком?
А эту фигуру?
15
ДОМАШНЕЕ ЗАДАНИЕ:
Вася записал на листе бумаги несколько
нечётных чисел.
 Петя их не видел, но утверждает,
Петя их не видел, но утверждает,что по количеству записанных чисел легко
определит, чётная или нечётная у них сумма.
Прав ли Петя?
17
17. Домашнее задание:
Если все наши заданияТы освоил(а) без труда,
Если было интересно,
А не скука-маята,
Назовись на этой строчке
Я
________имя твоё_________
МОЛОДЕЦ!
И бегите гулять скорее,
На сегодня всё, конец!
English Русский Правила
Ознакомьтесь с этими 50 задачами дня по математике для пятого класса
Начните свой ежедневный урок математики со словесной задачи дня по математике для пятого класса — это отличный способ подготовить почву для обучения! Включите их в начале своего математического блока, чтобы укрепить уверенность, навыки критического мышления и обучающееся сообщество. Студенты привыкнут читать по смыслу, а также определять ключевую информацию. Предложите учащимся записывать уравнения и рисовать картинки, чтобы объяснить свое мышление, так как это помогает им увидеть свет, когда они застряли!
Темы в этих математических задачах пятого класса охватывают закономерности и разрядность, сложение/вычитание, умножение, деление, дроби, десятичные дроби, измерения и сравнения. Если вы хотите еще математических задач из слов, мы ежедневно публикуем их на нашем сайте для детей: Daily Classroom Hub. Обязательно добавьте ссылку в закладки!
Если вы хотите еще математических задач из слов, мы ежедневно публикуем их на нашем сайте для детей: Daily Classroom Hub. Обязательно добавьте ссылку в закладки!
Хотите весь этот набор текстовых задач в одном простом документе? Получите бесплатный пакет PowerPoint, отправив сообщение электронной почты здесь. Все, что вам нужно сделать, это опубликовать одну из задач на доске или экране проектора. Тогда пусть дети взять его оттуда.
1. Три поезда подошли к станции в 15:00. В поезде Menton было 2589 пассажиров. В Рестонском поезде был 671 пассажир. В поезде Пирсон-Сити было 1024 пассажира. Сколько пассажиров было вместе?
2. В магазин Grow Up Farmer’s Market было доставлено 4 ящика лимонов. В одном ящике было 2100 лимонов. В двух других ящиках было 2010 лимонов. В последнем ящике было 1999 лимонов. Сколько лимонов было доставлено всего?
3. Ruffle Truffle Candy Компания получила заказ на 850 шоколадных трюфелей от кондитерской.
 Они также получили заказ на 7 309трюфели из продуктового магазина. Затем поступил еще один заказ на 3125 трюфелей из ресторана. Сколько трюфелей должна произвести фабрика, чтобы выполнить эти заказы?
Они также получили заказ на 7 309трюфели из продуктового магазина. Затем поступил еще один заказ на 3125 трюфелей из ресторана. Сколько трюфелей должна произвести фабрика, чтобы выполнить эти заказы?4. На полуострове Три-Сити есть 3 города. В Сансет-Сити проживает 405 245 человек. В Санрайз-Сити проживает 695 212 человек. В городе Сунуп проживает 415 937 человек. Сколько людей вместе проживает на полуострове Три-Сити?
5. Магазин поздравительных открыток Smiley’s в прошлом году заказал 25 294 поздравительных открытки и 15 280 открыток ко Дню матери. Они продали 11 065 открыток ко Дню матери и 24 229поздравительные открытки. Сколько поздравительных открыток у них осталось?
6. Авиакомпания Flyaway Airlines выполняет 3 рейса в Нью-Парк-Сити каждый день из Сан-Сандоса. Каждый самолет рассчитан на 400 пассажиров. В понедельник на первом рейсе было 325 пассажиров. На втором рейсе было 387 пассажиров. На третьем рейсе был 221 пассажир.
 Сколько свободных мест было всего вместе?
Сколько свободных мест было всего вместе?7. В 1999 году в Западной Дескатерии проживало миллион человек. 350 268 человек являются уроженцами этой страны. Остальные переехали туда из другой страны. Сколько людей переехало туда откуда-то еще?
8. Свечи ко дню рождения от The Happy Hippy Candle Company продаются упаковками по 8 штук. На прошлой неделе они произвели 6000 коробок и продали 8000 свечей. Сколько коробок свечей они продали на прошлой неделе?
9. Некоторые из новых книг в библиотеке Южного города были научно-популярными. Было выпущено 25 025 новых книг в твердом переплете и 7 333 новых книги в мягкой обложке. 15 000 экземпляров в твердом переплете были фикцией. Сколько книг в твердом переплете были научно-популярными?
10. Giganto Mall имеет 6 этажей. Каждый из 5 верхних уровней имеет по 2,950 рабочих. В торговом центре работает 15 000 человек. Сколько рабочих работает на нижнем уровне?
11.
 В морозильнике Frosty Food Mart находится 96 замороженных индеек и 65 ветчин. Каждая индейка весит 19 фунтов. Каждая ветчина весит 10 фунтов. Сколько весят индюки все вместе?
В морозильнике Frosty Food Mart находится 96 замороженных индеек и 65 ветчин. Каждая индейка весит 19 фунтов. Каждая ветчина весит 10 фунтов. Сколько весят индюки все вместе?12. Каждый новый словарь, приобретенный для школы, содержит 355 страниц. Для каждого класса подготовлено 35 словарей. Они весят почти 300 фунтов. Сколько это всего страниц?
13. На каждом фруктовом дереве пингвинов 10 251 лист. В саду дяди Арча было 96 фруктовых деревьев. Половина из них были фруктовыми деревьями пингвинов. Сколько всего листьев было на фруктовых деревьях пингвинов?
14. Магазин Benny’s Bait Shop продает червей по 12 упаковок. В брутто двенадцать пачек. На этой неделе продали 12 брутто червей. Сколько червей они продали на этой неделе?
15. Компания по прокату автомобилей Kwik Kar имеет 27 офисов в 12 штатах. У них есть 1350 автомобилей, которые можно сдать в аренду. Если они равномерно распределит все автомобили по своим точкам, сколько машин получит каждая точка?
16.
 На футбольном матче был аншлаг. На мероприятии присутствовало 42 500 болельщиков. Каждое место было занято. Вокруг стадиона расположены 85 рядов сидений. В каждом ряду одинаковое количество мест. Сколько болельщиков сидело в каждом ряду?
На футбольном матче был аншлаг. На мероприятии присутствовало 42 500 болельщиков. Каждое место было занято. Вокруг стадиона расположены 85 рядов сидений. В каждом ряду одинаковое количество мест. Сколько болельщиков сидело в каждом ряду?17. У мистера Скетча в ящике для рисования в классе было 180 цветных карандашей. Он купил новые коробки цветных карандашей, по 10 штук в коробке. Теперь у него 400 цветных карандашей. Сколько новых коробок он купил?
18. На стадион на рок-концерт на автобусах прибыло 4500 человек. Еще 4500 человек прибыли поездом. Остальные приехали на машинах. Каждый автобус мог вместить 225 человек, и все автобусы были заполнены. Сколько автобусов было?
19. Super Duper Corporation каждый месяц платит арендную плату за свое большое здание штаб-квартиры. В прошлом году они заплатили 60 756 долларов за аренду и примерно столько же за отопление. Каждый месяц они платят одну и ту же сумму за аренду. Сколько стоит аренда в месяц?
20.
 В прошлом месяце компания Straight Arrow Dress Shirts продала много классических рубашек. Каждая рубашка имеет 7 пуговиц спереди и по 1 пуговице на каждом рукаве. Они использовали 72 000 пуговиц на рубашках, проданных в прошлом месяце. Сколько рубашек они продали?
В прошлом месяце компания Straight Arrow Dress Shirts продала много классических рубашек. Каждая рубашка имеет 7 пуговиц спереди и по 1 пуговице на каждом рукаве. Они использовали 72 000 пуговиц на рубашках, проданных в прошлом месяце. Сколько рубашек они продали?21. На озере Луи есть лодки, которые отправляют туристов в круизы по озеру. В субботу 8 112 туристов захотели прокатиться по озеру. В смену курсируют 3 катера. Каждая лодка вмещает 500 человек. Круиз длится 30 минут. Сколько смен им нужно было отработать, чтобы каждый турист мог путешествовать?
22. Суперзвезда Сэм — профессиональный игрок в бейсбол и каждый день занимается подачей мяча. В июле он провел 12 000 минут, тренируясь. Он тренируется бить ватин 1 час каждую неделю. Сколько часов он тренировал свою подачу в июле?
23. Новый тротуар, ведущий к парадной двери начальной школы Elemental, имел длину 55 футов и ширину 36 дюймов. 25 футов из него были выкрашены в золото, а остальные — в серебро.
 Сколько дюймов в длину было серебряное сечение?
Сколько дюймов в длину было серебряное сечение?24. Горнодобывающая компания Dig-It выкапывала 12 000 фунтов редкого минерала, бободиума, каждый день в течение недели. Они продают его в коробках по 8 унций. Сколько коробок им понадобится, чтобы упаковать Бободиум на этой неделе?
25. Рита Райталот, известная писательница, посещает коллегиальный колледж и дарит всем, кто посетит одну из двух ее лекций, две свои книги. На ее первую лекцию пришло 600 человек. На вторую лекцию также пришла хорошая явка. Всего она раздала 2468 книг. Сколько человек пришло на ее вторую лекцию?
26. Мистер Удивительный готовит свое магическое действие. У него есть 12 366 золотых монет, которые он использует в одном из своих действий. Он использует некоторые из них в каждом запланированном появлении. Он откладывал по 229 золотых монет за каждое появление. Сколько выступлений он планирует?
27. У Рика 4/5 шоколадки. У Сида 6/7 шоколадки.
 У Ника 6/8 шоколадки. У кого самый большой кусок шоколадного батончика?
У Ника 6/8 шоколадки. У кого самый большой кусок шоколадного батончика?28. У Джинни 6/4 арбузов. У Уильяма есть 3/9 другого арбуза. У Стива есть ½ другого арбуза. У кого меньше всего арбузов?
29. Луз собирается приготовить сырный соус. Она купила ½ фунта американского сыра. Она также купила ¾ фунта швейцарского сыра и ¼ фунта сыра Чеддер. Сколько сыра она купила?
30. Мерси должна была выбрать, сколько пиццы пепперони она хочет. У нее могло быть 7/8, 8/16 или 8/10. Если она хочет больше всего пиццы, какую сумму ей выбрать?
31. Исследователь Elmo Adventure нашел древнее место с золотыми слитками. Он нашел три. Первый был 5/12 фунта. Второй слиток весил 7/12 фунта, а третий — 3/6 фунта. Сколько весили бруски все вместе?
32. Сэнди съела 3/4 буханки свежеиспеченного хлеба, приготовленного ее мамой. Половину она отдала своей кузине Стелле. Сколько хлеба осталось у Сэнди?
33.
 Учительница пятого класса, мисс Марвелус, съела 9/10 яблочного пирога. Она дала 3/10 своему директору, мистеру Палу, и 3/10 своему коллеге, миссис Мерри. Сколько пирога осталось у мисс Марвелус?
Учительница пятого класса, мисс Марвелус, съела 9/10 яблочного пирога. Она дала 3/10 своему директору, мистеру Палу, и 3/10 своему коллеге, миссис Мерри. Сколько пирога осталось у мисс Марвелус?34. Грейс укладывала ленточки, которые у нее были, встык. Синий кусок был 3/12 фута. Красный кусок был ½ фута, а белый кусок был 8/12 фута в длину. Сколько времени было в общей сложности?
35. Роб читал книгу, в которой было 400 страниц. Он прочитал 1/3 его в понедельник и еще 1/4 во вторник. Какую часть книги ему осталось прочитать?
36. У Тая осталась половина торта на день рождения. Он отдал своей сестре Джанель четверть этой суммы. Сколько всего торта досталось Джанель?
37. Футбольная команда старшей школы впервые собиралась на тренировку. Было 64 игрока. ¾ из них были пенсионеры. Остальные были младшеклассниками. Сколько игроков было младшеклассниками?
38. Охотники за сокровищами выкопали обувную коробку с 1500 долларами.
 В команде охотников за сокровищами было пять человек, поэтому каждый должен был оставить себе 1/5 денег. Сколько денег осталось у каждого?
В команде охотников за сокровищами было пять человек, поэтому каждый должен был оставить себе 1/5 денег. Сколько денег осталось у каждого?39. Тристану осталось покрасить только 1/8 колоды. Вся палуба имеет общую площадь 100 квадратных футов. Он рассчитывал, что сможет сделать половину того, что осталось, в пятницу, а остальное — в субботу. Какую часть общей колоды он планирует раскрасить в субботу?
40. Трое друзей следили за своим бегом. Таковы результаты их пробежек в субботу. Пейдж пробежала 0,75 мили. Таннер пробежал 0,09 мили. Лиза пробежала 0,706 мили. Кто пробежал дальше всех?
41. Профессиональные кикбольные карточки Гэри разделены между 3 командами. ¼ его карточек — игроки «Сан-Франциско Силз». 0,25 — игроки «Нью-Йорк Якс». Остальные играют за лосося Новой Шотландии. Какая десятичная дробь лучше всего описывает, сколько в его коллекции игроков из Лосося?
42. Шахтер Молли взвешивала небольшое количество золотой пыли.
 У нее было 3 пакета золотой пыли. Они весили 0,29 унции, 1,07 унции и 0,92 унции. Она должна получить 3 унции золотого песка, прежде чем продать его. Сколько еще золотой пыли ей нужно, чтобы совершить продажу?
У нее было 3 пакета золотой пыли. Они весили 0,29 унции, 1,07 унции и 0,92 унции. Она должна получить 3 унции золотого песка, прежде чем продать его. Сколько еще золотой пыли ей нужно, чтобы совершить продажу?43. У Хизер 4 банковских счета. В первом есть 25,09 долларов. У второго по 106,75 долларов, а у третьего и четвертого по 108,08 долларов. Какова общая сумма денег у Хизер на этих счетах?
44. Каждый член семьи Кирка получил выплату в размере 1070,09 долларов США от своего семейного бизнеса. В семье Кирка 12 человек, включая его самого. Их возраст варьируется от 12 до 99 лет. Сколько всего семья получила?
45. Количество футболок, которые Олли продает на блошином рынке, имеет предсказуемый характер. Он продал 120 рубашек в январе, 60 рубашек в феврале, 240 рубашек в марте, 120 рубашек в апреле, 480 рубашек в мае и 240 рубашек в июне. Если схема продаж сохранится, сколько рубашек он продаст в августе?
46.
 Для разблокировки специального хранилища используется числовой код. Необходимо ввести три цифры в правильном порядке на клавиатуре с цифрами от 0 до 100. Первое — нечетное число меньше 20, состоящее из 2 одинаковых цифр. Второе число четное и составляет ½ от числа, которое составляет ¼ от 16. Третье число является произведением первых двух чисел, а затем удвоено. Что такое код?
Для разблокировки специального хранилища используется числовой код. Необходимо ввести три цифры в правильном порядке на клавиатуре с цифрами от 0 до 100. Первое — нечетное число меньше 20, состоящее из 2 одинаковых цифр. Второе число четное и составляет ½ от числа, которое составляет ¼ от 16. Третье число является произведением первых двух чисел, а затем удвоено. Что такое код?47. Ким заметила этот узор на старом листе пергамента. 2, 5, 11, 23, 47, 95. Ким вычислила следующие два числа. Кто они такие?
48. Эл на 5 лет старше Теда. Тед на 2 года старше Алисы. Алиса на год моложе Фрэн. Фрэн 8 лет. Сколько лет Алу?
49. Лиам наконец добрался до паромного причала в 4 часа дня. Он сел на поезд до парома со станции Чайртаун. Этому поезду потребовалось полчаса, чтобы добраться до парома. Чтобы добраться до станции, он ехал 4 с половиной часа из аэропорта Десквилл. Тем утром он прилетел в Десквилл из аэропорта Тейблтауна. Полет был 2 с половиной часа.
 Во сколько он вылетел из аэропорта Тейблтауна?
Во сколько он вылетел из аэропорта Тейблтауна?50. В субботу Крис работал на трех работах. Она косила газон и закончила это в 6 часов вечера. Она мыла окна 3 часа. Она также помыла, натерла воском и пропылесосила 3 машины. На каждую машину уходило полтора часа. Крис начала свой рабочий день в 9 утра. Сколько минут ей потребовалось, чтобы подстричь газон?
Наслаждаетесь задачками по математике в пятом классе? Посетите наш центр пятого класса, чтобы получить еще больше ресурсов.
Получите версию этих текстовых задач в формате PPT.
55 Сложные задачи со словами для 5-х классов
Почему бы не добавить несколько красочных манипуляторов, чтобы сделать обучение в 5-м классе более конкретным, проверить основные навыки счета с помощью рабочих листов или включить их в ежедневный урок математики, чтобы развить беглость решения задач?
Эти многошаговые словесные задачи включают сложение, вычитание, умножение и деление, а также время, деньги, разрядность и дроби. Поскольку они включают более одного шага, учащимся следует предлагать выражать свои мысли с помощью картинок и слов, чтобы помочь спланировать, решить и проверить каждую задачу.
Поскольку они включают более одного шага, учащимся следует предлагать выражать свои мысли с помощью картинок и слов, чтобы помочь спланировать, решить и проверить каждую задачу.
 Сколько бы каждый из них заработал, если бы они разделили свой заработок поровну? 6. Стив и Пол играли в футбол. Стив набрал 82 ярда, а Пол набрал 35 ярдов. Какое общее количество ярдов набрали оба мальчика во время игры? 7. Патрик купил обед на школьной ярмарке. Он купил 3 хот-дога по 4,50 доллара каждый и 2 гамбургера по 5,60 доллара каждый. Он также использовал купон на 2 доллара от цены обеда. Сколько всего денег он потратил на обед? 8. Школьный автобус рассчитан на 85 мест. На первой остановке из автобуса вышли 16 студентов. На второй остановке из автобуса вышли еще 18 студентов. Сколько учеников осталось в автобусе? 9. Сандра потратила 135 долларов на новую одежду. Она купила блузку за 48 долларов и две футболки по 23 доллара каждая. Сколько денег у нее осталось? 10. Четыре учителя раздали карандаши своим ученикам.
Сколько бы каждый из них заработал, если бы они разделили свой заработок поровну? 6. Стив и Пол играли в футбол. Стив набрал 82 ярда, а Пол набрал 35 ярдов. Какое общее количество ярдов набрали оба мальчика во время игры? 7. Патрик купил обед на школьной ярмарке. Он купил 3 хот-дога по 4,50 доллара каждый и 2 гамбургера по 5,60 доллара каждый. Он также использовал купон на 2 доллара от цены обеда. Сколько всего денег он потратил на обед? 8. Школьный автобус рассчитан на 85 мест. На первой остановке из автобуса вышли 16 студентов. На второй остановке из автобуса вышли еще 18 студентов. Сколько учеников осталось в автобусе? 9. Сандра потратила 135 долларов на новую одежду. Она купила блузку за 48 долларов и две футболки по 23 доллара каждая. Сколько денег у нее осталось? 10. Четыре учителя раздали карандаши своим ученикам. В двух классах было по 24 ученика, в третьем классе было 29 учеников, а в четвертом — 27 учеников. Сколько всего карандашей было роздано? 11. Эндрю наблюдал за шимпанзе в зоопарке. 45 из них ели жуков, 36 играли с палками, а остальные дремали. Если всего было 122 шимпанзе, сколько дремало? 12. Уильям кормит своих рыбок 8 контейнерами корма для рыб каждый день. Каждый контейнер стоит 3,25 доллара. Сколько денег Уильям тратит на корм для рыб за неделю? 13. Элизабет делает ожерелья из ракушек для своих 7 друзей. Ей нужно 23 ракушки, чтобы сделать каждое ожерелье. На данный момент она собрала 89 ракушек. Сколько еще ракушек ей нужно, чтобы сделать все 7 ожерелий? 14. Эдвард и Карл играли в видеоигру. Эдвард набрал 835 очков, а Карл — 345 очков. На сколько больше очков набрал Эдвард, чем Карл? 15.
В двух классах было по 24 ученика, в третьем классе было 29 учеников, а в четвертом — 27 учеников. Сколько всего карандашей было роздано? 11. Эндрю наблюдал за шимпанзе в зоопарке. 45 из них ели жуков, 36 играли с палками, а остальные дремали. Если всего было 122 шимпанзе, сколько дремало? 12. Уильям кормит своих рыбок 8 контейнерами корма для рыб каждый день. Каждый контейнер стоит 3,25 доллара. Сколько денег Уильям тратит на корм для рыб за неделю? 13. Элизабет делает ожерелья из ракушек для своих 7 друзей. Ей нужно 23 ракушки, чтобы сделать каждое ожерелье. На данный момент она собрала 89 ракушек. Сколько еще ракушек ей нужно, чтобы сделать все 7 ожерелий? 14. Эдвард и Карл играли в видеоигру. Эдвард набрал 835 очков, а Карл — 345 очков. На сколько больше очков набрал Эдвард, чем Карл? 15. Ава купила 8 печений по 2,25 доллара каждое, 5 плиток шоколада по 1,50 доллара каждое и 6 кексов по 1,25 доллара каждое. Сколько сдачи она должна получить, если расплачивается 50-долларовой купюрой? 16. В субботу парк аттракционов посетили 320 человек. В четыре раза больше посетителей в воскресенье. Сколько человек посетило парк развлечений в выходные? 17. Стефани купила 45 простых печенек по 2,20 доллара каждое. Она украсила их глазурью и продала по 3,75 доллара за штуку. Какую прибыль она получила, продавая свое украшенное печенье? 18. Майлз сделал 45 футболок для продажи в Интернете. Он продал каждую по 30 долларов, но ей пришлось заплатить налог в размере 8,50 долларов за каждую рубашку. Сколько денег он заработал всего? 19. Эми ходила в спортзал 15 лет. Каждый год она тренировалась три раза в неделю. Сколько раз она ходила в спортзал за 15 лет? 20.
Ава купила 8 печений по 2,25 доллара каждое, 5 плиток шоколада по 1,50 доллара каждое и 6 кексов по 1,25 доллара каждое. Сколько сдачи она должна получить, если расплачивается 50-долларовой купюрой? 16. В субботу парк аттракционов посетили 320 человек. В четыре раза больше посетителей в воскресенье. Сколько человек посетило парк развлечений в выходные? 17. Стефани купила 45 простых печенек по 2,20 доллара каждое. Она украсила их глазурью и продала по 3,75 доллара за штуку. Какую прибыль она получила, продавая свое украшенное печенье? 18. Майлз сделал 45 футболок для продажи в Интернете. Он продал каждую по 30 долларов, но ей пришлось заплатить налог в размере 8,50 долларов за каждую рубашку. Сколько денег он заработал всего? 19. Эми ходила в спортзал 15 лет. Каждый год она тренировалась три раза в неделю. Сколько раз она ходила в спортзал за 15 лет? 20. Лиза продавала свитера. Она продала 899 свитеров в первый год своего бизнеса, 1450 — во второй год и 2450 — в третий год. Сколько всего она заработала, если каждый свитер стоил 29 долларов?? 21. Тайлер ловил бабочек. За первый час он поймал 7 бабочек. За второй час он поймал 9 бабочек. За третий час он поймал 11 бабочек. Если бы эта закономерность продолжалась, сколько часов ему потребуется, чтобы поймать более 60 бабочек? 22. Каждую неделю Питер видит, как мимо его дома проезжает 144 машины. Сколько машин он увидит за 3 года? 23. Шеннон должна зарезервировать автобусы для экскурсии. У нее 271 ребенок, 12 учителей и 9родители. Каждый автобус рассчитан на 22 пассажира. Сколько автобусов ей понадобится и сколько свободных мест останется? 24. Джон хочет испечь 1400 кексов для школьной распродажи выпечки. Он может испечь 36 кексов в день.
Лиза продавала свитера. Она продала 899 свитеров в первый год своего бизнеса, 1450 — во второй год и 2450 — в третий год. Сколько всего она заработала, если каждый свитер стоил 29 долларов?? 21. Тайлер ловил бабочек. За первый час он поймал 7 бабочек. За второй час он поймал 9 бабочек. За третий час он поймал 11 бабочек. Если бы эта закономерность продолжалась, сколько часов ему потребуется, чтобы поймать более 60 бабочек? 22. Каждую неделю Питер видит, как мимо его дома проезжает 144 машины. Сколько машин он увидит за 3 года? 23. Шеннон должна зарезервировать автобусы для экскурсии. У нее 271 ребенок, 12 учителей и 9родители. Каждый автобус рассчитан на 22 пассажира. Сколько автобусов ей понадобится и сколько свободных мест останется? 24. Джон хочет испечь 1400 кексов для школьной распродажи выпечки. Он может испечь 36 кексов в день. Он уже испек 396. За сколько дней он испечет 1400 кексов? 25. Бен и его 4 друга прочитали 60 книг за год. В каждой книге в среднем 235 страниц. Сколько всего страниц они прочитали за год? 26. У Мэнди день рождения. Она пригласила 25 друзей и испекла 432 печенья. Она хочет поделиться печеньем на своей вечеринке, но также хочет сохранить 35 для своих братьев и сестер. Сколько печенья получит каждый на вечеринке? 27. Эдвард хотел раздать свои марки 12 друзьям. У него 624 марки. Сколько марок получит каждый друг и сколько останется? 28. Билеты в кино стоят 24 доллара США за взрослого и 1/4 этой цены за ребенка. Сколько всего заплатит семья из 2 взрослых и 5 детей? 29. Мелисса заработала 560 долларов в сентябре и только 2/5 этой суммы в октябре. Сколько денег она заработала в октябре? 30.
Он уже испек 396. За сколько дней он испечет 1400 кексов? 25. Бен и его 4 друга прочитали 60 книг за год. В каждой книге в среднем 235 страниц. Сколько всего страниц они прочитали за год? 26. У Мэнди день рождения. Она пригласила 25 друзей и испекла 432 печенья. Она хочет поделиться печеньем на своей вечеринке, но также хочет сохранить 35 для своих братьев и сестер. Сколько печенья получит каждый на вечеринке? 27. Эдвард хотел раздать свои марки 12 друзьям. У него 624 марки. Сколько марок получит каждый друг и сколько останется? 28. Билеты в кино стоят 24 доллара США за взрослого и 1/4 этой цены за ребенка. Сколько всего заплатит семья из 2 взрослых и 5 детей? 29. Мелисса заработала 560 долларов в сентябре и только 2/5 этой суммы в октябре. Сколько денег она заработала в октябре? 30. Пол съел 1¼ пиццы, а Сэм съел 3 ¾ пиццы. Сколько всего пицц они съели? 31. Джейми заработал 800 долларов за первый год работы в бизнесе. Если он поделится 3/4 своего заработка со своей семьей, сколько денег у него останется? 32. Саре нужно было распилить кусок дерева длиной 230 м на 5 частей. Какой длины будет каждая часть после разрезания? 33. Школа из 385 учеников и 12 учителей собиралась в поход и нуждалась в резервировании автобусов. Если один автобус может перевозить 70 человек, сколько автобусов им потребуется? 34. Джеймс продает свой дом. 70% прибыли он оставит себе, а 30% отдаст матери. Если дом будет продан за 300 000 долларов, сколько денег получит каждый из них? 35. Стивен заработал 200 долларов за 1 неделю работы. На следующей неделе он заработал на 30% больше. Сколько денег он заработал за 2 недели? 36.
Пол съел 1¼ пиццы, а Сэм съел 3 ¾ пиццы. Сколько всего пицц они съели? 31. Джейми заработал 800 долларов за первый год работы в бизнесе. Если он поделится 3/4 своего заработка со своей семьей, сколько денег у него останется? 32. Саре нужно было распилить кусок дерева длиной 230 м на 5 частей. Какой длины будет каждая часть после разрезания? 33. Школа из 385 учеников и 12 учителей собиралась в поход и нуждалась в резервировании автобусов. Если один автобус может перевозить 70 человек, сколько автобусов им потребуется? 34. Джеймс продает свой дом. 70% прибыли он оставит себе, а 30% отдаст матери. Если дом будет продан за 300 000 долларов, сколько денег получит каждый из них? 35. Стивен заработал 200 долларов за 1 неделю работы. На следующей неделе он заработал на 30% больше. Сколько денег он заработал за 2 недели? 36. Алекс заработал 540 долларов, продавая пуговицы на гаражной распродаже, а Энди заработал 2/5 суммы Алекса. Сколько денег заработал Энди? 37. У Дженнифер есть задний двор размером 13 на 9 метров. Она хочет добавить сад размером 7 на 4 метра. Сколько метров площади останется у нее на заднем дворе? 38. Сандра купила школьных принадлежностей на 250 долларов. В магазине была распродажа, поэтому она получила 30% скидку. Сколько она должна была заплатить? 39. Дэнни строил большой игровой домик для своей дочери. Периметр кукольного домика представлял собой квадрат. Если бы длина одной стороны была 21 м, какой длины был бы весь периметр? 40. Кимберли нарисовала новую картину. Она потратила 530 долларов на краски, 223 доллара на мольберт, 55 долларов на раму и 421 доллар на холст. Она продала свою картину за 3264 доллара. Какую прибыль она получила? 41.
Алекс заработал 540 долларов, продавая пуговицы на гаражной распродаже, а Энди заработал 2/5 суммы Алекса. Сколько денег заработал Энди? 37. У Дженнифер есть задний двор размером 13 на 9 метров. Она хочет добавить сад размером 7 на 4 метра. Сколько метров площади останется у нее на заднем дворе? 38. Сандра купила школьных принадлежностей на 250 долларов. В магазине была распродажа, поэтому она получила 30% скидку. Сколько она должна была заплатить? 39. Дэнни строил большой игровой домик для своей дочери. Периметр кукольного домика представлял собой квадрат. Если бы длина одной стороны была 21 м, какой длины был бы весь периметр? 40. Кимберли нарисовала новую картину. Она потратила 530 долларов на краски, 223 доллара на мольберт, 55 долларов на раму и 421 доллар на холст. Она продала свою картину за 3264 доллара. Какую прибыль она получила? 41. Кайл, Джек и Джейми пошли на вечеринку с пиццей, где каждый съел по 3¼ куска пиццы. Сколько кусков пиццы они съели всего? 42. В феврале Сэм заработал 500 долларов на продаже бейсбольных карточек. В марте он заработал на 40% больше. Сколько он заработал за эти месяцы? 43. Мэри хочет добавить ковер в свою гостиную. Площадь ее гостиной составляет 123 м2, а ковер стоит 8 долларов за квадратный метр. Сколько вообще будет стоить ковер? 44. Эми покупала закуски для вечеринки. Она купила 35 упаковок чипсов по 2,50 доллара каждая, 6 бутылок газировки по 4,50 доллара каждая и большой торт по 77 долларов. Сколько всего она потратила на вечеринку? 45. Саманта хотела покрасить стены новыми обоями. Каждая стена была 8 м на 13 м, и ей нужно было покрыть 7 стен. Какую площадь она должна была покрыть всего? 46.
Кайл, Джек и Джейми пошли на вечеринку с пиццей, где каждый съел по 3¼ куска пиццы. Сколько кусков пиццы они съели всего? 42. В феврале Сэм заработал 500 долларов на продаже бейсбольных карточек. В марте он заработал на 40% больше. Сколько он заработал за эти месяцы? 43. Мэри хочет добавить ковер в свою гостиную. Площадь ее гостиной составляет 123 м2, а ковер стоит 8 долларов за квадратный метр. Сколько вообще будет стоить ковер? 44. Эми покупала закуски для вечеринки. Она купила 35 упаковок чипсов по 2,50 доллара каждая, 6 бутылок газировки по 4,50 доллара каждая и большой торт по 77 долларов. Сколько всего она потратила на вечеринку? 45. Саманта хотела покрасить стены новыми обоями. Каждая стена была 8 м на 13 м, и ей нужно было покрыть 7 стен. Какую площадь она должна была покрыть всего? 46. Пэм купила новую стиральную машину за 1500 долларов и сушилку за 850 долларов. Она получила 20% от суммы. Сколько она должна была заплатить? 47. Тэмми купила пачку наклеек, внутри было 78 наклеек. Она решила оставить себе 2/3 из них и отдать 1/3 сестре. Сколько наклеек получила ее сестра? 48. Джеймс заработал 900 долларов в октябре на уборке газонов. Сэм заработал 8/9 этой суммы. Сколько денег заработал Сэм? 49. Патриция разрезала плитку шоколада на равные кусочки, чтобы разделить их с тремя друзьями. Если длина плитки шоколада 42,6 см, то какой длины каждая из трех частей? 50. Джеймс съел 4/5 торта, а Эми съела 2/3. Сколько всего они съели? 51. Родители Стэнли согласились позволить ему купить новую игровую приставку, если он заплатит за ее половину. Они дали ему 180 долларов за свою порцию.
Пэм купила новую стиральную машину за 1500 долларов и сушилку за 850 долларов. Она получила 20% от суммы. Сколько она должна была заплатить? 47. Тэмми купила пачку наклеек, внутри было 78 наклеек. Она решила оставить себе 2/3 из них и отдать 1/3 сестре. Сколько наклеек получила ее сестра? 48. Джеймс заработал 900 долларов в октябре на уборке газонов. Сэм заработал 8/9 этой суммы. Сколько денег заработал Сэм? 49. Патриция разрезала плитку шоколада на равные кусочки, чтобы разделить их с тремя друзьями. Если длина плитки шоколада 42,6 см, то какой длины каждая из трех частей? 50. Джеймс съел 4/5 торта, а Эми съела 2/3. Сколько всего они съели? 51. Родители Стэнли согласились позволить ему купить новую игровую приставку, если он заплатит за ее половину. Они дали ему 180 долларов за свою порцию. Если Стэнли уже сэкономил 108,70 долларов, сколько еще денег ему нужно, чтобы купить консоль? 52. Стефани приготовила пирожные для классной распродажи выпечки. На коробке написано, что из кастрюли получится 12 порций. Если каждая порция содержит 250 калорий, сколько калорий будет на всей сковороде? 53. Каждый месяц семья Смитов платит 45 долларов за базовый тарифный план мобильного телефона плюс 6,95 долларов за каждый из своих 4 телефонов. Они также платят 29,99 долларов за план передачи данных и текстовых сообщений и дополнительные 7,45 долларов в виде налогов. Сколько составляет их ежемесячный счет? 54. Длина жука составляет около 3/4 дюйма. Гремучая змея примерно в 30 раз длиннее. Какой длины гремучая змея? 55. Ясмин нужно было 45 фактов о жирафах для ее научного проекта. Она записала 2/5 необходимых ей фактов из первой книги, 12 фактов из второй книги и 1/9нужных ей фактов из третьей книги.
Если Стэнли уже сэкономил 108,70 долларов, сколько еще денег ему нужно, чтобы купить консоль? 52. Стефани приготовила пирожные для классной распродажи выпечки. На коробке написано, что из кастрюли получится 12 порций. Если каждая порция содержит 250 калорий, сколько калорий будет на всей сковороде? 53. Каждый месяц семья Смитов платит 45 долларов за базовый тарифный план мобильного телефона плюс 6,95 долларов за каждый из своих 4 телефонов. Они также платят 29,99 долларов за план передачи данных и текстовых сообщений и дополнительные 7,45 долларов в виде налогов. Сколько составляет их ежемесячный счет? 54. Длина жука составляет около 3/4 дюйма. Гремучая змея примерно в 30 раз длиннее. Какой длины гремучая змея? 55. Ясмин нужно было 45 фактов о жирафах для ее научного проекта. Она записала 2/5 необходимых ей фактов из первой книги, 12 фактов из второй книги и 1/9нужных ей фактов из третьей книги. Сколько еще фактов ей нужно, чтобы завершить свой проект?
Сколько еще фактов ей нужно, чтобы завершить свой проект? Задачи со словами
Задачи со словами — это один из первых способов, с помощью которых мы знакомимся с прикладной математикой, а также одна из самых тревожных математических задач, с которыми сталкиваются многие школьники. На этой странице собрана большая коллекция текстовых задач, которые обеспечивают легкое введение в текстовые задачи для всех четырех основных математических операций. Вы найдете задачи на сложение слов, задачи на вычитание, задачи на умножение и деление слов, все они начинаются с простых простых вопросов, которые переходят в более сложные навыки, необходимые для многих стандартизированных тестов. По мере их продвижения вы также найдете набор операций, которые требуют от учащихся выяснить, какой тип сюжетной задачи им нужно решить. А если вам нужна помощь, ознакомьтесь с советами по решению задач со словами внизу этой страницы!
Сложные задачи на сложение
20 рабочих листов с задачами на сложение
Эти вводные задачи на сложение идеально подходят для первого или второго класса прикладной математики.
Задачи на сложение
Задачи на вычитание
Рабочие листы с задачами на 20 слов
Эти рабочие листы включают простые задачи на вычитание с меньшими количествами. Следите за такими словами, как разница и оставшийся.
Словесные задачи на вычитание
Смешанные словесные задачи на сложение и вычитание
8 Рабочие листы со словесными задачами
Этот набор рабочих листов включает в себя смешанные словесные задачи на сложение и вычитание. Учащиеся должны выяснить, какую операцию применить в контексте проблемы.
Смешанные словесные задачи на сложение и вычитание
Словесные задачи на умножение
20 словесных задач
Это первый набор рабочих листов с текстовыми задачами, в которых представлено умножение. Эти рабочие листы включают только задачи на умножение; см. рабочие листы в следующих разделах для смешанных операций.
рабочие листы в следующих разделах для смешанных операций.
Задачи на умножение
Задачи на деление
Рабочие листы задач на 20 слов
Эти задачки на деление имеют дело только с целыми делениями (частное без остатка). Это отличный первый шаг к распознаванию ключевых слов, которые сигнализируют о том, что вы решение задачи на деление слов.
Дивизион Word Problems
Girl Scout Cookie Division
20 Рабочих листов Word Tasks
Если вы когда-нибудь работали Печенькой, Мама (или Папа!), вы знаете, какую математику мы практикуем … Эти рабочие листы в основном представляют собой задачи на деление слов, которые вводят остатки. Достаньте из коробки свои тагалонги или тонкие мятные леденцы и узнайте, сколько остатков вам будет разрешено съесть!
Отдел печенья девочек-скаутов
Задачи на деление с остатком
24 Рабочие листы со словесными задачами
Рабочие листы в этом разделе состоят из задачников на деление и на остаток. Они похожи на задачи девочек-скаутов из предыдущего раздела, но с другими единицами измерения.
Они похожи на задачи девочек-скаутов из предыдущего раздела, но с другими единицами измерения.
Задачи на деление с остатком
Смешанные задачи на умножение и деление
Рабочие листы с задачами на 8 слов
Эти рабочие листы сочетают в себе базовые задачи на умножение и деление. В задачах на деление не учитываются остатки. Эти рабочие листы требуют, чтобы учащиеся различали формулировку сюжетной задачи, требующей умножения, от задачи, требующей деления для получения ответа.
Смешанные задачи на умножение и деление
Смешанные задачи на операции
8 задач со словами
Целая энчилда! Эти задания сочетают в себе задачи на сложение, вычитание, умножение и деление. Эти рабочие листы проверят способность учащихся выбирать правильную операцию на основе текста задачки.
Словесные задачи со смешанными операциями
Дополнительные факты Словесные задачи сложения
20 Рабочие листы текстовых задач
Один из способов немного усложнить текстовую задачу — включить в текст задачи дополнительную (но неиспользованную) информацию. В этих рабочих листах есть задачи на добавление слов с дополнительными неиспользованными фактами в задаче.
В этих рабочих листах есть задачи на добавление слов с дополнительными неиспользованными фактами в задаче.
Дополнительные факты Словесные задачи на сложение
Дополнительные факты Словесные задачи на вычитание
20 словесных задач Рабочие листы
Словесные задачи на вычитание с дополнительными неиспользованными фактами в каждой задаче. Рабочие листы начинаются с задач на вычитание с меньшими значениями и переходят к более сложным задачам.
Дополнительные факты Словесные задачи на вычитание
Дополнительные факты Словесные задачи на сложение и вычитание
8 Рабочие листы со словесными задачами
Рабочие листы со смешанными операциями на сложение и вычитание с дополнительными неиспользованными фактами в задачах.
Дополнительные факты Словесные задачи на сложение и вычитание
Дополнительные факты Умножение словесных задач
20 словесных задач Рабочие листы
Словесные задачи на умножение с дополнительными неиспользованными фактами в задаче. Рабочие листы в этом наборе начинаются с задач на умножение с меньшими значениями и переходят к более сложным задачам.
Рабочие листы в этом наборе начинаются с задач на умножение с меньшими значениями и переходят к более сложным задачам.
Дополнительные факты Задачи на умножение
Дополнительные факты Задачи на деление
Рабочие листы задач на 20 слов
Рабочие листы в этом разделе включают математические задачи на деление с дополнительными неиспользованными фактами в задаче. Частные в этих задачах на деление не включают остатки.
Дополнительные факты Словесные задачи на деление
Дополнительные факты Умножение и деление словесные задачи
16 Словесные задачи
Это набор рабочих листов со смешанными задачами на умножение и деление и дополнительными неиспользованными фактами в задаче. Частные в этих задачах на деление не включают остатки.
Дополнительные факты Словесные задачи на умножение и деление
Словесные задачи на время в пути (обычные)
Рабочие листы на 28 словесных задач
Эти сюжетные задачи касаются времени в пути, включая определение расстояния в пути, времени в пути и скорости с использованием миль ( обычные единицы). Это очень распространенный класс текстовых задач, и специальная практика с этими рабочими листами подготовит учащихся, когда они столкнутся с похожими задачами на стандартизированных тестах.
Это очень распространенный класс текстовых задач, и специальная практика с этими рабочими листами подготовит учащихся, когда они столкнутся с похожими задачами на стандартизированных тестах.
Задания на время в пути (обычные)
Задания на время в пути (метрические)
28 Рабочие листы с заданиями на время в пути
Хотите знать, когда прибывает поезд? Эти сюжетные задачи касаются времени в пути, включая определение расстояния в пути, времени в пути и скорости с использованием километров (метрических единиц).
Словесные задачи на время в пути (метрические)
Приемы решения текстовых задач
Рабочие листы по математике в этом разделе сайта посвящены простым текстовым задачам, подходящим для начальных классов. Задачи на простое сложение можно вводить очень рано, в первом или втором классе, в зависимости от способностей ученика. Следуйте этим рабочим листам со словесными задачами на вычитание после того, как будет рассмотрена концепция вычитания, а затем приступайте к умножению и делению словесных задач таким же образом.
Проблемы со словами часто являются источником беспокойства для учащихся, потому что мы склонны вводить математические операции в абстракцию. Учащиеся с трудом применяют даже элементарные операции к текстовым задачам, если их не учили постоянно думать о математических операциях в повседневной жизни. Регулярные разговоры с детьми о том, «сколько еще вам нужно» или «сколько у вас осталось», или другие, казалось бы, простые вопросы, если их задавать регулярно, могут развить это базовое чувство числа, которое чрезвычайно помогает, когда начинают проявляться проблемы со словами и прикладная математика. .
Существует множество приемов решения текстовых задач, которые могут заполнить пробел, и они могут быть полезными инструментами, если учащиеся либо не могут решить, с чего начать решение задачи, либо просто нуждаются в способе проверить свое мышление по конкретной проблеме.
Убедитесь, что ваш ученик сначала прочитал задачу целиком. Очень легко начать читать словесную задачу и подумать после первого-двух предложений: «Я знаю, о чем они просят…», а затем заставить проблему принять совершенно другой оборот. Преодоление этой склонности к раннему решению может быть трудным, и гораздо лучше выработать привычку полностью обойти проблему, прежде чем выбрать путь к решению.
Преодоление этой склонности к раннему решению может быть трудным, и гораздо лучше выработать привычку полностью обойти проблему, прежде чем выбрать путь к решению.
Есть определенные слова, которые появляются в задачах со словами для различных операций, которые могут подсказать вам, какая операция может быть правильной для применения. Эти ключевые слова не являются безошибочным способом узнать, что делать с проблемой, но они могут стать полезной отправной точкой.
Например, такие фразы, как «вместе», «всего», «вместе» или «сумма», очень часто сигнализируют о том, что задача будет включать сложение.
В задачах на вычитание очень часто в формулировках используются такие слова, как «разница», «меньше» или «уменьшение». В задачах со словами для младших детей также используются такие глаголы, как «дали» или «поделились» в качестве замены для вычитания.
Ключевые фразы, на которые следует обращать внимание при решении задач на умножение слов, включают очевидные фразы, такие как «times» и «product», но также обращайте внимание на «for each» и «every». задачки со словами могут быть сложными, особенно для детей младшего возраста, которые еще не полностью развили представление о том, для чего можно использовать деление… Но именно поэтому задачи со словами на деление могут быть такими полезными! Если вы видите такие слова, как «за» или «среди» в тексте словесной задачи, ваш радар дивизии должен звучать негромко и четко. Обратите внимание на «общий доступ» и убедитесь, что учащиеся не путают эту формулировку с задачей на вычитание. Это яркий пример того, когда внимание к языку очень важно.
задачки со словами могут быть сложными, особенно для детей младшего возраста, которые еще не полностью развили представление о том, для чего можно использовать деление… Но именно поэтому задачи со словами на деление могут быть такими полезными! Если вы видите такие слова, как «за» или «среди» в тексте словесной задачи, ваш радар дивизии должен звучать негромко и четко. Обратите внимание на «общий доступ» и убедитесь, что учащиеся не путают эту формулировку с задачей на вычитание. Это яркий пример того, когда внимание к языку очень важно.
Нарисуй картинку!
Один из ключевых советов, особенно для простых задач со словами, состоит в том, чтобы поощрять учащихся рисовать картинки. Большинство задач со словами в начальной школе представляют собой базовые упражнения на счет, когда вы имеете дело с количествами или наборами, которые довольно малы. Если учащиеся могут нарисовать проблему (даже используя простые представления, такие как квадраты или круги для единиц, обсуждаемых в задаче), это может помочь им точно визуализировать то, что происходит.
Другой полезной стратегией визуализации является использование манипуляций. Вместо предмета задачи могут стоять скрепки, шашки или другие подручные предметы, что дает возможность проработать другие простые примеры с другими номерами.
| Вы здесь: Главная → Рабочие листы → 5 класс Это обширная коллекция бесплатных печатных листов по математике для 5 класса, организованных по таким темам, как сложение, вычитание, алгебраическое мышление, разрядность, умножение, деление, разложение на простые множители, десятичные числа, дроби, измерения, координатная сетка и геометрия. Они генерируются случайным образом, могут быть распечатаны из вашего браузера и содержат ключ ответа. Рабочие листы поддерживают любую математическую программу для пятого класса, но особенно хорошо подходят для математической программы IXL для 5-го класса и их новых уроков в нижней части страницы. Jump to: Рабочие листы генерируются случайным образом каждый раз, когда вы нажимаете на приведенные ниже ссылки. Вы также можете получить новый, другой, просто обновив страницу в браузере (нажмите F5). Вы можете распечатать их прямо из окна браузера, но сначала проверьте, как это выглядит в «Предварительном просмотре». Если рабочий лист не помещается на странице, отрегулируйте поля, верхний и нижний колонтитулы в настройках страницы вашего браузера. Все рабочие листы поставляются с ключом ответа, размещенным на 2-й странице файла. Алгебра
Задача по математике для начальных классов Эдвард Заккаро Хорошая книга по решению проблем с очень разнообразными текстовыми задачами и стратегиями решения проблем. Сложение и вычитание в столбцах (числа друг под другом)
Разрядное значение и округление
Пропуск счета
Округление
УмножениеУмножение в уме
Длинное умножение (в столбцах)
ОтделМентальное отделение
Длинное деление
Следующие четыре типа рабочих листов не
Стандарты Common Core для пятого класса.
Факторинг
Сложение и вычитание дробейПодобные дроби/дробные части
В отличие от дробей/дробных частей
Умножение дробей
Дробное деление
Следующие типы рабочих листов не соответствуют стандартам Common Core.
Преобразование дробей в смешанные числа и наоборот
Эквивалентные дроби и упрощение дробей
Запись дробей в виде десятичных и наоборот В таблицах ниже ключ ответа не дает дроби в упрощенной форме.
Десятичное сложениеМатематика в уме Десятичные цифры от 0 до 1
от 0 до 2 десятичных цифр
Дополнение к колонке
Десятичное вычитаниеМатематика в уме Десятичные цифры от 0 до 1
от 0 до 2 десятичных цифр
Задачи: арифметика в уме
Вычитание столбцов
Проблемы: алгебраическое мышление
Десятичное умножениеМатематика в уме
Умножение столбцами
Десятичное делениеМатематика в уме
Длинная часть
Измерительные блокиТрадиционная система
Метрическая система
Координатная сетка
Геометрия
Если вы хотите лучше контролировать такие параметры, как количество задач, размер шрифта, расстояние между задачами или диапазон чисел, просто щелкните по этим ссылкам, чтобы самостоятельно использовать генераторы рабочих листов: Меню математики 1 -й класс римские цифры Классификация треугольников Канадские деньги Рабочие листы дробей 1 Десятичные рабочие листы процент. Калькулятор уравнений |
Математические задачи KidZone
[1 класс] [Оценка 2] [3-й степени] [Оценка 4] [5 класс]
Введение:
Задачи Word перечислены по классам и внутри каждого класса по тема. Я всегда нахожу, что предоставление сезонной рабочей таблицы помогает сохранить мою дочь с удовольствием выполняет свою работу.
Уровни обучения являются ориентировочными.
суждение, основанное на способностях и стремлении вашего ребенка (моя старшая дочь
всегда использовал класс ниже, тогда как моя младшая дочь, кажется, класс
или два выше — пойди разберись). Имейте в виду, что задачи по математике
требует навыков чтения, понимания и математики, поэтому ребенок, хорошо разбирающийся в
основные математические уравнения могут столкнуться с большими трудностями, чем вы ожидаете. с задачами по математике.
с задачами по математике.
Все текстовые задачи динамические (другими словами, они создают новую проблему каждый раз, когда вы их открываете). или нажмите «Обновить» в браузере). Слова в частности проблема не изменится, но цифры изменятся. Дети, которые борются преобразование текстовой задачи в математическое уравнение покажется обнадеживающим (построение уверенности) повторно обращаться к одним и тем же словесным подсказкам с разными чисел, поэтому рассмотрите возможность печати пары регенераций каждой задачи. В классе вы можете предложить проблему партнерам или группе учащиеся решают вместе, а затем обеспечивают регенерацию одного и того же проблема для детей, чтобы сделать соло.
Со старшей дочерью, однажды я понял, насколько она
боролся с математикой, когда она не была записана в красивом аккуратном уравнении, я
часто решали с ней математическую задачу (выполняя большую часть работы
себя), а затем предоставил ей несколько регенераций той же проблемы с
разные номера для нее, чтобы сделать соло. Через несколько недель после этого она
смог сделать их без прохождения от мамы. Она одна из
те дети, которые говорят: «Это слишком сложно!» довольно быстро так
укрепление доверия важно — если она думает, что не может что-то сделать
она не может — если она думает, что может сделать что-то, она может. Теперь, как сделать
Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? *смех*
Через несколько недель после этого она
смог сделать их без прохождения от мамы. Она одна из
те дети, которые говорят: «Это слишком сложно!» довольно быстро так
укрепление доверия важно — если она думает, что не может что-то сделать
она не может — если она думает, что может сделать что-то, она может. Теперь, как сделать
Я убеждаю ее, что она МОЖЕТ содержать свою комнату в чистоте? *смех*
- Общие задачи со словами для 1 класса
— Мешки с фасолью
— Ковши
— Собачьи кости
— Время в школу (картинка предложений)
Тематические задачи для 1 класса
Примечание: проблема генерируется с новыми номерами каждый раз, когда вы нажимаетеОсень Рождество Пружина День Земли ул. Патрика День Лето Пасха День Благодарения Зимний Хэллоуин День святого Валентина День
Словесные задачи для 2 класса
Тематические задачи со словами для 2 класса
Примечание: проблема генерируется с новыми номерами каждый раз, когда вы нажимаетеОсень Рождество Пружина День Земли ул.  Патрика
День
Патрика
ДеньЛето Пасха День Благодарения Зимний Хэллоуин День святого Валентина День
Словесные задачи для 3 класса
Тематические словесные задачи для 3 класса
Примечание: проблема генерируется с новыми номерами каждый раз, когда вы нажимаетеОсень Рождество Пружина День Земли ул. Патрика День Лето Пасха День Благодарения Зимний Хэллоуин День святого Валентина День
Словесные задачи для 4 класса
Тематические задачи для 4 класса
Примечание: проблема генерируется с новыми номерами каждый раз, когда вы нажимаетеОсень Рождество Весна День Земли ул.  Патрика
День
Патрика
ДеньЛето Пасха День Благодарения Зимний Хэллоуин День святого Валентина День
Словесные задачи для 5 класса
Тематические задачи для 5 класса
Примечание: проблема генерируется с новыми номерами каждый раз, когда вы нажимаетеОсень Рождество Пружина День Земли ул. Патрика День Лето Пасха День Благодарения Зимний Хэллоуин День святого Валентина День
3 совета по составлению математических задач, которые развивают критическое мышление учащихся начальной школы
Образовательный фонд Джорджа Лукаса
EdutopiaEdutopia
Поиск
Критическое мышление
Хорошо продуманные текстовые задачи дают учащимся начальной школы реальный контекст для понимания математических концепций.
Брэкстон Холл
12 февраля 2021 г.
ZUMA Press Inc / Alamy
«У Дэнни 564 помидора. Затем он покупает 623 моркови. Сколько времени ему понадобится, чтобы вернуться домой?» Этот сценарий представляет собой то, что многие люди представляют, когда мы упоминаем проблемы со словами. Многие педагоги считают, что это табу. Некоторые утверждают, что многие учащиеся не могут получить доступ к контенту из-за чтения, а сами проблемы могут быть неуместными с культурной точки зрения. Все эти идеи можно считать верными, если словесная задача создана или выполнена неправильно.
Как специальный педагог, который работал в городских и сельских школах, у меня всегда было отношение любви-ненависти к текстовым задачам. Раньше я был одним из учителей, которые заявляли: «Я пытаюсь оценить их математические рассуждения, а не навыки чтения». Мне было трудно понять, что задачи на истории могут дать нашим ученикам ощутимый контекст, с которым они могут связаться, чтобы понять концепцию, которую мы преподаем. Этот контекст важен при первом знакомстве наших студентов с более абстрактным содержанием.
Этот контекст важен при первом знакомстве наших студентов с более абстрактным содержанием.
Я помню, как в начале учебного года работал с группой третьеклассников, обсуждая простую арифметическую задачу 25 + __ = 50. Этим ученикам показали, что 25 + 25 = 50, но они не понимали, почему пробел был в середине проблемы. Как только я придумала задачу-рассказ о размещении пакетов с горячим шоколадом в контейнерах для классной вечеринки, у учеников сразу же вспыхнули лампочки над головами. Затем они нарисовали представление задачи и решили, что им нужно продолжать прибавлять к 25, пока не получится 50. Я понял, что мы даем в основном числовые задачи, а не концептуальные словесные задачи. Это похоже на то, как мы предлагаем учащимся указания, как добраться до магазина, не показывая им ориентиры, которые им нужны, чтобы добраться до места назначения. Неудивительно, что они теряются в шагах, и наша инструкция становится скорее контрольным списком, а не отработкой навыков критического мышления и решения проблем.
Создание задачи на правильное слово — это своего рода искусство. К счастью, как и в случае с художественным проектом, текстовые задачи не обязательно должны быть идеальными.
3 ключа к созданию сложных словесных задач
1. Они должны быть понятны учащимся. Это может показаться пустяком, но я вижу так много словесных задач, которые с самого начала похожи на мой пример. Слишком часто они говорят о чрезмерном количестве вещей или о теме, которую ученики не могут понять. При разработке текстовой задачи нам нужно убедиться, что учащиеся могут подключиться или представить себе, что происходит. Это происходит от знания ваших студентов и их интересов. В моем классе карточки с покемонами и мешочки со слизью — самые популярные вещи. Поэтому, когда мы создаем текстовые задачи и используем эти темы, учащиеся проявляют интерес к истории и могут визуализировать происходящее. Им особенно нравится, когда вы используете их имена, чтобы сделать их звездой словесной проблемы.
Поскольку мы работаем над очень абстрактными темами рассуждений, учащимся нужно иметь что-то реальное, за что можно уцепиться, помогая им приземлиться к реальности во время выполнения задания. Не имея возможности понять проблему, мы, скорее всего, потеряем их, и они просто выберут операцию наугад и попытаются решить ее таким образом.
2. Словесные задачи должны быть разрешимы. Задачи не должны быть слишком сложными; простая задача, требующая критического мышления, поможет. Многие стандартизированные тесты создают каверзные формулировки при задании словесных задач и утверждают, что это усложняет решение задачи. На самом деле, если мы просто усложним формулировку, а не заставим ситуацию задуматься, все, что мы делаем, — это разочаровываем наших учеников, а не побуждаем их думать.
3. Словесные задачи должны быть открытыми. Последнее, что нужно задаче с функциональными словами, это быть открытым. «У Джона есть четыре игрушечных машинки, а затем он получает еще четыре. Сколько у него сейчас? скучно и довольно просто. Хотя это вызовет трудности у некоторых студентов на короткое время, это не заставит ни одного студента критически мыслить, и наши студенты могут решить ограниченное количество точек входа.
Сколько у него сейчас? скучно и довольно просто. Хотя это вызовет трудности у некоторых студентов на короткое время, это не заставит ни одного студента критически мыслить, и наши студенты могут решить ограниченное количество точек входа.
Просто перефразировав вопрос, мы обеспечиваем задание, которое заставляет наших учащихся критически осмыслить происходящее в этой истории. «У Джона четыре машины. Его брат дал ему еще немного, и теперь у него их восемь. Сколько дал ему его брат?» Эта проблема позволяет использовать множество точек входа и возможностей попробовать различные стратегии, одновременно побуждая учащихся мыслить абстрактно с помощью математических рассуждений и чувства чисел.
Как педагоги мы должны быть бдительны в отношении задач и текстовых задач, которые мы создаем. Рассматривая возможные текстовые задачи, мы должны спросить себя: «Интересна ли эта текстовая задача? Это разрешимо? Он открытый?» Если ответ на любой из этих вопросов отрицательный, подумайте о том, чтобы переоценить проблемы через призму критического мышления, чтобы сделать их более эффективными и полезными для ваших учеников.

 05.2017
66541
05.2017
66541
 Удачи в прохождении!
Удачи в прохождении! 05.2017
16628
05.2017
16628
 02.2021
1133
02.2021
1133



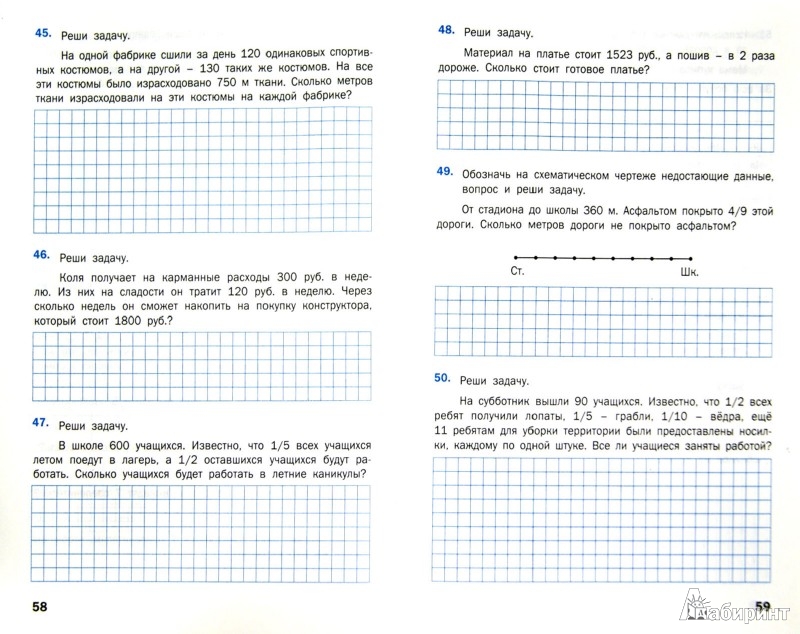
 01.2016
17943
01.2016
17943
 09.2018
4258
09.2018
4258
 Задания составлены с учетом типичных ошибок, которые допускают учащиеся.
Задания составлены с учетом типичных ошибок, которые допускают учащиеся.
 04.2020
1199
0
04.2020
1199
0
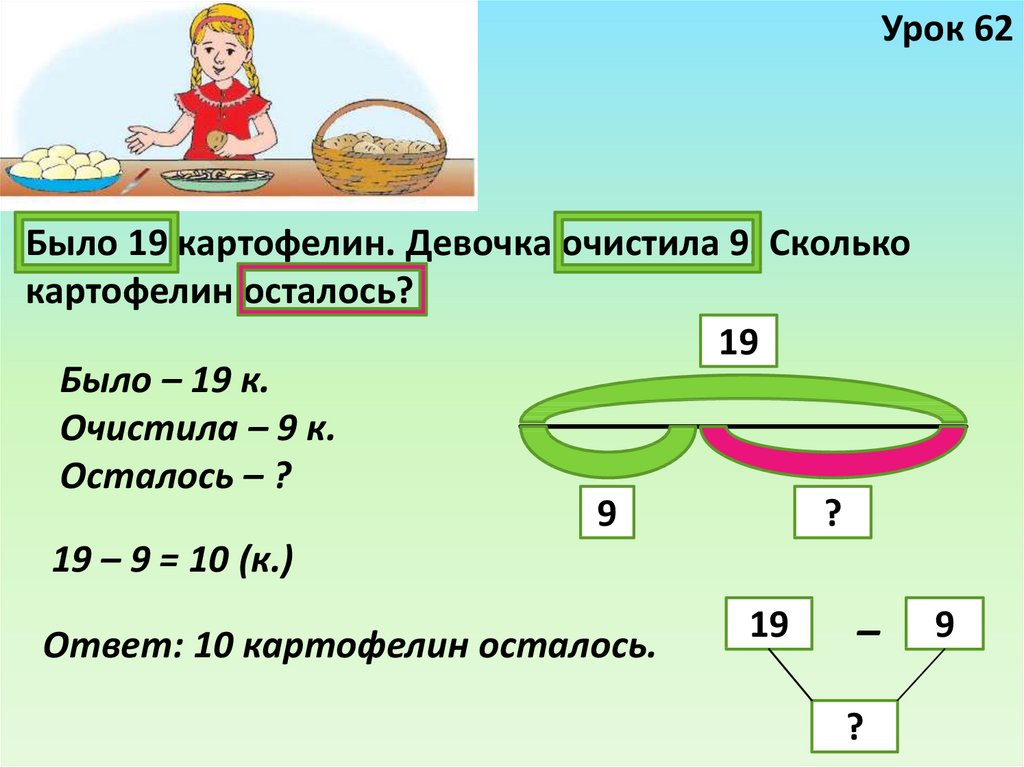 П. Поповой «Контрольно-измерительные материалы. Математика. 5 класс». Тест содержит 18 вопросов, которые случайным образом выбираются из 56 сгруппированных по подтемам вопросов. Содержание некоторых вопросов было изменено. Также изменён тип некоторых вопросов (например, вместо выбора ответа из предложенных вариантов — ввод ответа с клавиатуры). К большинству вопросов имеются комментарии (просмотр доступен после ввода ответа), в которых даны ссылки на соответствующие тематике вопросов материалы, к некоторым вопросам в комментариях даны решения. Время выполнения теста не ограничено, однако рекомендуется выделить не более 45 минут.
П. Поповой «Контрольно-измерительные материалы. Математика. 5 класс». Тест содержит 18 вопросов, которые случайным образом выбираются из 56 сгруппированных по подтемам вопросов. Содержание некоторых вопросов было изменено. Также изменён тип некоторых вопросов (например, вместо выбора ответа из предложенных вариантов — ввод ответа с клавиатуры). К большинству вопросов имеются комментарии (просмотр доступен после ввода ответа), в которых даны ссылки на соответствующие тематике вопросов материалы, к некоторым вопросам в комментариях даны решения. Время выполнения теста не ограничено, однако рекомендуется выделить не более 45 минут.
 11.2013
11047
11.2013
11047
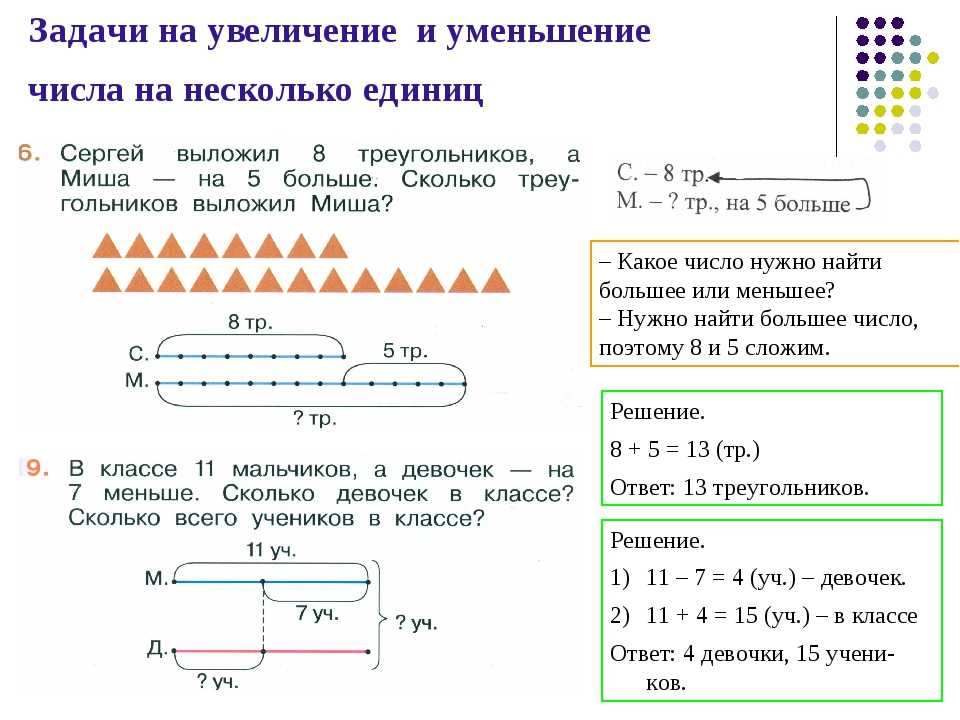
 02.2021
799
02.2021
799


 12.2020
4090
0
12.2020
4090
0

 04.2020
3960
04.2020
3960

 09.2020
900
0
09.2020
900
0

 05.2017
3809
05.2017
3809
 Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического.
Данная разработка представляет собой работу по математике в 5 классе на тему: » Среднее арифметическое». Эта тема кажется ребятам достаточно простой, но на самом деле является очень важной и требует тщательной отработки. Необходимо научиться выражать любой элемент из определения среднего арифметического. 05.2021
436
0
05.2021
436
0
 Я. Виленкина и др. «Математика. 5 класс»
Я. Виленкина и др. «Математика. 5 класс» 04.2017
9482
04.2017
9482
 Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей.
Тест проверяет умение применять изученные правила при сравнении обыкновенных дробей. 03.2021
336
03.2021
336
 08.2015
2379
08.2015
2379
 Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста.
Для того, чтобы выполнить задание, нужно использовать ответ предыдущего задания. Об этом нужно сообщить учащимся до выполнения теста.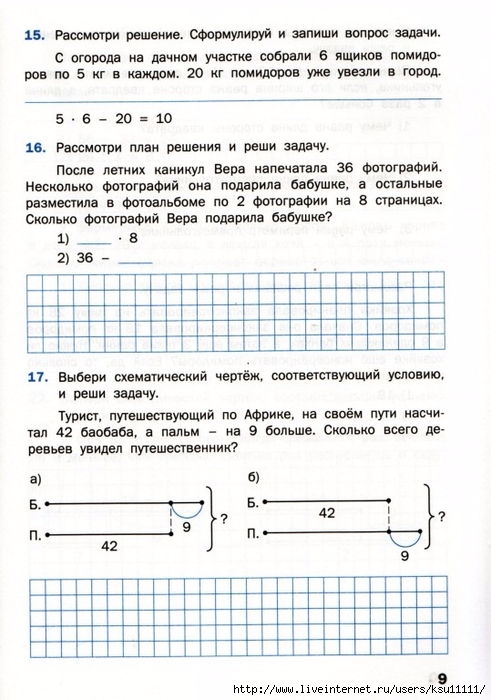 Сюжетные задачи на все арифметические действия (10 вопросов)
Сюжетные задачи на все арифметические действия (10 вопросов)
 04.2020
8107
0
04.2020
8107
0
 Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!
Очень внимательно читайте задание и инструкцию к работе. Желаю удачи!!!  04.2022
117
0
04.2022
117
0
 12.2015
2389
12.2015
2389
 Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов.
Обязательные ответы на все вопросы теста. Вновь открытый тест содержит другие вопросы из банка вопросов. Вновь открытый тест содержит другие вопросы из банка вопросов.
Вновь открытый тест содержит другие вопросы из банка вопросов. теч, км/ч
теч, км/ч теч, км/ч
теч, км/ч теч, км/ч
теч, км/ч