Стороны оснований правильной усеченной треугольной пирамиды 4 и 12 дм. боковая грань образует с большим основанием угол 60 градусов. Найдите высоту.
Стороны оснований правильной усеченной треугольной пирамиды 4 и 12 дм. боковая грань образует с большим основанием угол 60 градусов. Найдите высоту.
|
Читайте также:
|
В пирамиде ABCS построим еще пирамиду A1B1C1S
Так как пирамида правильная следует полагать что плоскости построенные на треугольниках ABC и A1B1C1 параллельны. А значит что пирамида ABCS подобна A1B1C1S.
Тут идея простая если ∠BAC=∠ABS=60 градусов, то тогда получается что боковые грани AS,BS,CS пирамиды ABCS равны AB,BC,CA=12 дм.
То же самое могу сказать про пирамиду A1B1C1S. Нам точно известно что A1B1,B1C1,C1A1=4 дм. (но это не понадобится)
Итак для того чтобы найти высоту пирамиды ABCS — SO2 нужно обратить внимание на прямоугольный треугольник AO2S.
∠SAO2=60, а значит что угол ASO2=30. А напротив угла 30 градусов лежит сторона равная половине гипотенузы.
AO2=12/2=6
Значит высота AO2 пирамиды ABCS = √(144-36)=√9*4*3=6√3
Теперь на чем основывается принцип подобия фигур?
Если у нас пирамида ABCS подобная A1B1C1S имеет высоту равную 6√3, то другая будет иметь высоту во столько раз меньше, во сколько относятся стороны этих пирамид.
Иначе говоря найдем коэффициент подобия фигур
k=12/4=3
Значит что высота O1S=(6√3)/3=2√3
Получается что O1O2=6√3-2√3=4
Основанием пирамиды SABC служит треугольник, у которого АВ=ВС=20 с, АС=32 см; углы между плоскостью основания и каждой из боковых граней равны 45 (градусов).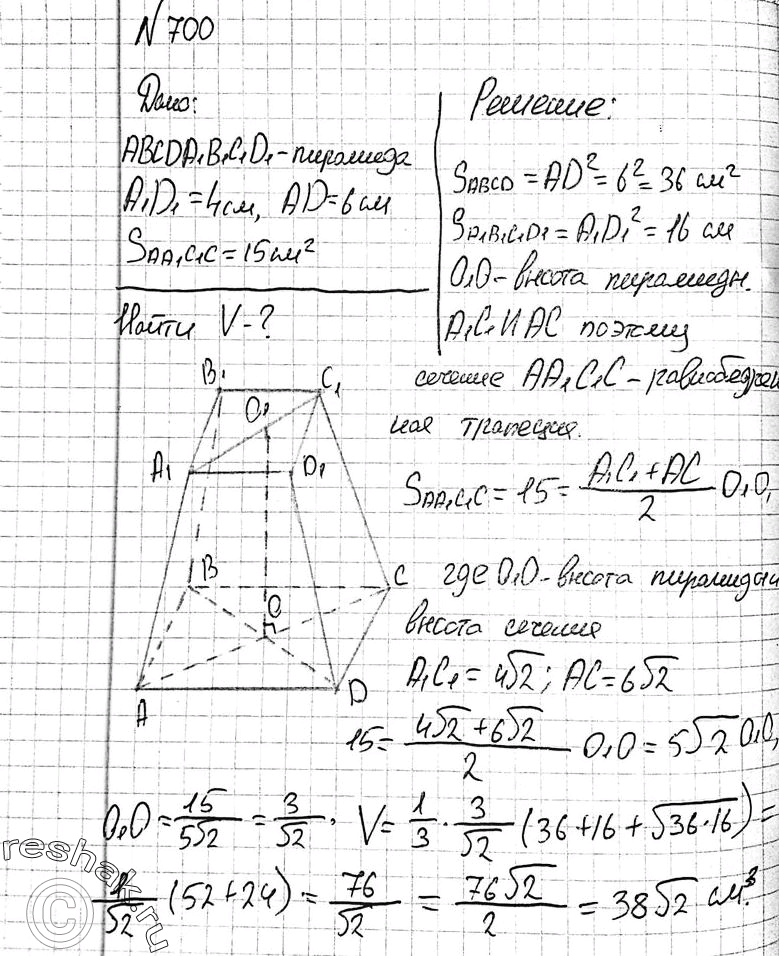 Найдите объем пирамиды
Найдите объем пирамиды
Пусть дана пирамида ABCD. В основание впишем окружность и найдем OE. ∠EOD=90, ∠OED=∠EDO=45 отсюда следует найдем EO найдем и высоту пирамиды.
EO=Rвпис.окр=Sосн/p, где p — полупериметр. p=(40+32)/2=36
DO=Sосн/36
Потом по формуле V=(Sосн)2/3
Найдем площадь основания по формуле Sосн=a*h, где a-AC, h=12 (Правило идеальных треугольников в принципе если непонятно просто проведи высоту к стороне AC, затем найди эту высоту по формуле Пифагора, просто облегчают такие цифры решение как 20-16-12, 10-8-6, 5-4-3 это все треугольники прямоугольные с такими сторонами запутал наверное).
Sосн=32*12=384
V=384*384/3=49152
Стороны прямоугольника относятся как 2:3.найдите отношение площадей основания тех цилиндров, боковая поверхность которых развертывается в такой прямоугольник.
Довольно простая задача. Просто одна сторона у прямоугольника например 4π, а вторая значит будет равна 6π.
Просто одна сторона у прямоугольника например 4π, а вторая значит будет равна 6π.
При развертке цилиндра сторона которая будет равна длине окружности цилиндра.
Т.е. 2πR=4π, отсюда R=2 S=4π
теперь развернем по другому и получим 2πR=6π
R=3, S=9π
Получается что отношение площадей 9/4
Плоскость, паралл-ая оси цилиндра, пересекает основание цилиндра по хорде, составляющей с диагональю данного сечения угол бетта. Радиус осн.цилиндра, проведенный в один из концов хорды, образует с плоскостью сечения угол альфа. Высота цил.равна Н. Найти площ.осевого сечения.
Сечение ABCD
∠DBA=β
OA=OB=SC=SD=Rокр
∠SCB=α
CD,BA – хорды
Две параллельные плоскости α β пересекают сторону АВ треугольника АВС в точках D и D1,а сторону ВС-соответственно в точках Е и Е1. Найдите длину отрезка DЕ, если BD=12см,BD1=18, D1E1=54.
Никогда не забывайте. Что в результате пересечения двух параллельных плоскостей плоскостей, как показано на рисунке получаются два подобных треугольника BDE и BD1E1.
А мы знаем уже что такое коэффициент подобия и поэтому легко найдем DЕ.
k=18/12
k=D1E1/DE
18/12=54/DE
DE=54*12/18=36
В основании наклонной призмы ромб с диагональю равной 24 см и стороной равной 37 см. Определите объём призмы, если перпендикулярное сечение, проходящее через большую диагональ ромба, имеет площадь равную 1400 см2.отв: 16800 см3
Большая диагональ равна 2* √(37*37-12*12)=2*35=70
H=1400/70=20
V=Sосн*H=(24*70/2)*20=16800 см3ъ
Дата добавления: 2015-10-30; просмотров: 905 | Нарушение авторских прав
 Найти радиус описанного около пирамиды шара. | В основании пирамиды треугольник со сторонами 13см, 14 см, 15 см. Найти высоту пирамиды, если все высоты боковых граней 14 см. | Найдите площади боковой и полной поверхностей правильной треугольной усеченной пирамиды со сторонами основании 10 и 4см и боковым ребром 5см | Объем прямоугольного параллелепипеда равен 2520 см(в кубе),а площадь основания 168 см(в квадрате),и длина на 2 см больше ширины. Найдите сумму длин всех ребер параллелепипеда. | Цилиндр катится по некоторой плоскости .Какую фигуру образует при этом ось цилиндра? | Найдите периметр ромба с наибольшей площадью если сумма длин его диагоналей равна 10. | Периметры двух подобных четырехугольников относятся как 2:3.Найдите отношение их площадей | В шар вписана правильная четырёхугольная пирамида, все рёбра которой равны 12см. Вычислите радиус шара. |
Найти радиус описанного около пирамиды шара. | В основании пирамиды треугольник со сторонами 13см, 14 см, 15 см. Найти высоту пирамиды, если все высоты боковых граней 14 см. | Найдите площади боковой и полной поверхностей правильной треугольной усеченной пирамиды со сторонами основании 10 и 4см и боковым ребром 5см | Объем прямоугольного параллелепипеда равен 2520 см(в кубе),а площадь основания 168 см(в квадрате),и длина на 2 см больше ширины. Найдите сумму длин всех ребер параллелепипеда. | Цилиндр катится по некоторой плоскости .Какую фигуру образует при этом ось цилиндра? | Найдите периметр ромба с наибольшей площадью если сумма длин его диагоналей равна 10. | Периметры двух подобных четырехугольников относятся как 2:3.Найдите отношение их площадей | В шар вписана правильная четырёхугольная пирамида, все рёбра которой равны 12см. Вычислите радиус шара. || | | следующая страница ==> | |
Площадь равнобедренного прямоугольного треугольника равна 36.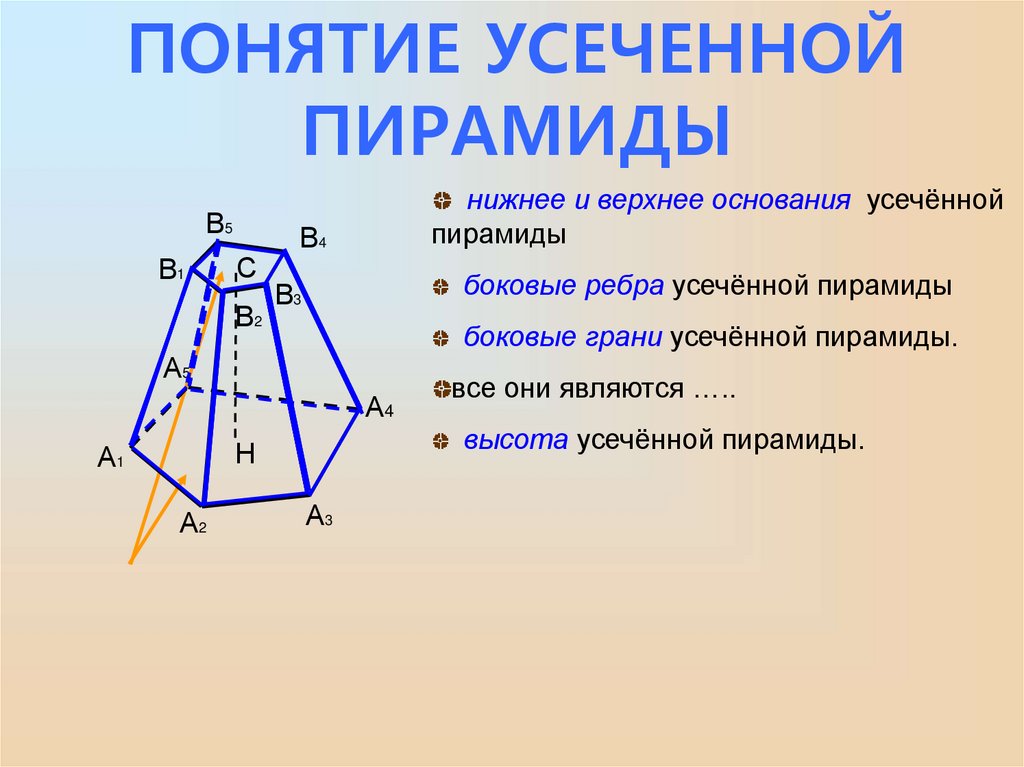 Найти длину гипотенузы Найти длину гипотенузы | | | Полукруг свернут в коническую поверхность. сколько градусов содержит угол между образующей и высотой конуса. |
Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука > Математика
| Похожие вопросы |
Задача. Полина старше Аллы на 9 лет вместе им 15. сколько бедет лет Алле через два года?
Полина старше Аллы на 9 лет вместе им 15. сколько бедет лет Алле через два года?
Решено
Синус двугранного угла при боковом ребре правильной четырёхугольной пирамиды равен 4√2/ 9. Найдите площадь боковой поверхности пирамиды, если
Решено
Какую часть площади квадрата занимает вписанный в него круг? Ответ дайте в процентах, округлив его до целых.
Полина старше Аллы на 9 лет. Вместе им 15 лет. Сколько лет будет Алле через 2 года
Коля, Дима и Саша собрали…
Пользуйтесь нашим приложением
ПОВЕРХНОСТЬ ПИРАМИДЫ И УСЕЧЕННОЙ ПИРАМИДЫ
Определение: Площадью полной поверхности пирамиды (усечённой пирамиды) называется сумма площадей всех её граней.
Определение: Площадью боковой поверхности пирамиды (усечённой пирамиды) называется сумма площадей её боковых граней.
Теорема: Площадь боковой поверхности правильной пирамиды равна половине произведения периметра её основания на апофему.
Дано:
SABC – правильная пирамида; ;
; – апофема;
.
Доказать: .
Теорема: Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров её оснований на апофему.
Дано:
– правильная усечённая пирамида;
; ;
; ;
– апофема;
Доказать:
.
Пример: В основании пирамиды лежит равнобедренный прямоугольный треугольник, катеты которого равны а.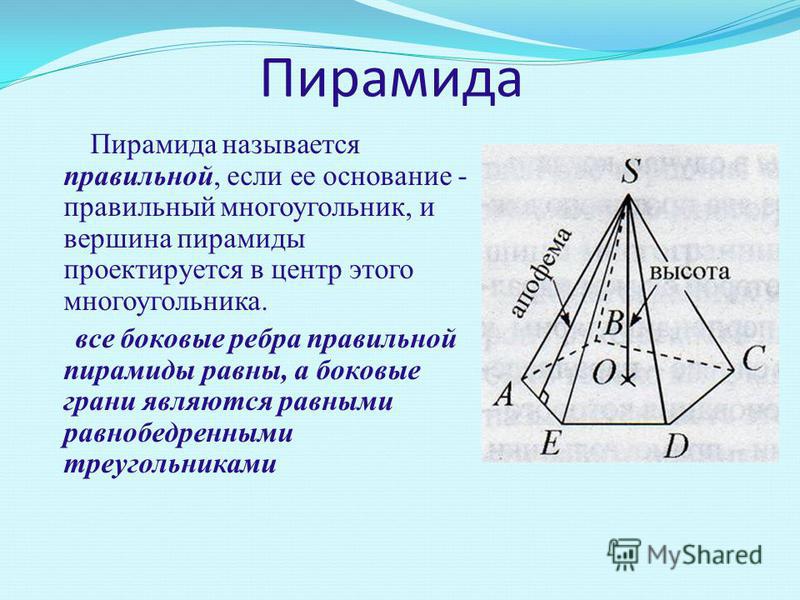 Боковые рёбра пирамиды наклонены к основанию под углом 60°. Найти площадь полной поверхности пирамиды.
Боковые рёбра пирамиды наклонены к основанию под углом 60°. Найти площадь полной поверхности пирамиды.
Дано:
— пирамида;
; ; ;
;
Определить:
Решение:
; ; ; ;
; ; .
по стороне и прилежащим к ней углам:
1) SO — общая сторона;
2) , так как , , ;
3) .
Из равенства треугольников следует, что и .
Точка О одинаково удалена от вершин треугольника АВС, следовательно, она является центром окружности, описанной около этого треугольника. Центр окружности, описанной около прямоугольного треугольника, есть середина гипотенузы. Точка О — середина гипотенузы.
.
; .
; ; ; ; .
; , следовательно, .
— равносторонний треугольник, значит, .
; .
по трём сторонам, следовательно, .
;
; ;
;
.
.
Ответ: .
Замечание: Площадь боковой поверхности неправильнойусечённой пирамиды вычисляется по определению, каксумма площадей её боковых граней.
Упражнения:
- Найти площадь полной поверхности пирамиды, основанием которой служит ромб с диагоналями 12 см и 16 см, а высота проходит через точку пересечения диагоналей ромба и равна 6,4 см.

- Основанием пирамиды SABC является прямоугольный треугольник АВС с гипотенузой АВ = 25 см и катетом ВC = 7 см. Ребро SA перпендикулярно основанию и равно 18 см. Найти площадь полной поверхности пирамиды.
- Найти площадь боковой поверхности правильной шестиугольной пирамиды, высота которой равна 4 дм, а боковое ребро равно 16 дм.
- Найти площадь полной поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 18 см и 8 см, а высота равна 12 см.
- Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды вдвое меньше площади её полной поверхности. Стороны её оснований равны 12 дм и 6 дм. Найти высоту усечённой пирамиды.
- Сторона нижнего основания правильной треугольной усечённой пирамиды равна 4 дм. Боковое ребро наклонено к плоскости основания под углом 60°. Найти площадь боковой поверхности усечённой пирамиды, если её высота равна 1 дм.
 АВС; SО = h.
АВС; SО = h.
Доказать:
9. ОБЪЁМ УСЕЧЕННОЙ ПИРАМИДЫ
Дано:
ABCDA1B1C1D1 — усечённая пирамида;
S(ABCD) = Sн.о.; S (A1B1C1D1) = Sв.о.
h — высота усечённой пирамиды;
Определить: Vус.пир.— ?
.
Упражнения:
- Диагональ квадратного основания правильной пирамиды равна 6 см, высота пирамиды равна 15 см. Найти её объём.
- Боковое ребро правильной шестиугольной пирамиды равно 14 дм, сторона её основания равна 2 дм. Найти объём пирамиды.

- Основанием пирамиды является ромб со стороной 15 см. Боковые грани пирамиды наклонены к плоскости основания под углом 45°. Большая диагональ основания равна 24 см. Найти объём пирамиды.
- Найти объём усечённой пирамиды, если площади её оснований равны 98 см2 и 32 см2, а высота соответствующей полной пирамиды равна 14 см.
- В пирамиде через середину высоты проведена плоскость, параллельная её основанию. Определить объём образовавшейся усечённой пирамиды, если высота данной пирамиды равна 18 см, а площадь её основания равна 400 см2.
- Найти объём треугольной пирамиды, боковые рёбра которой попарно перпендикулярны и равны 10 см, 15 см, 9 см.
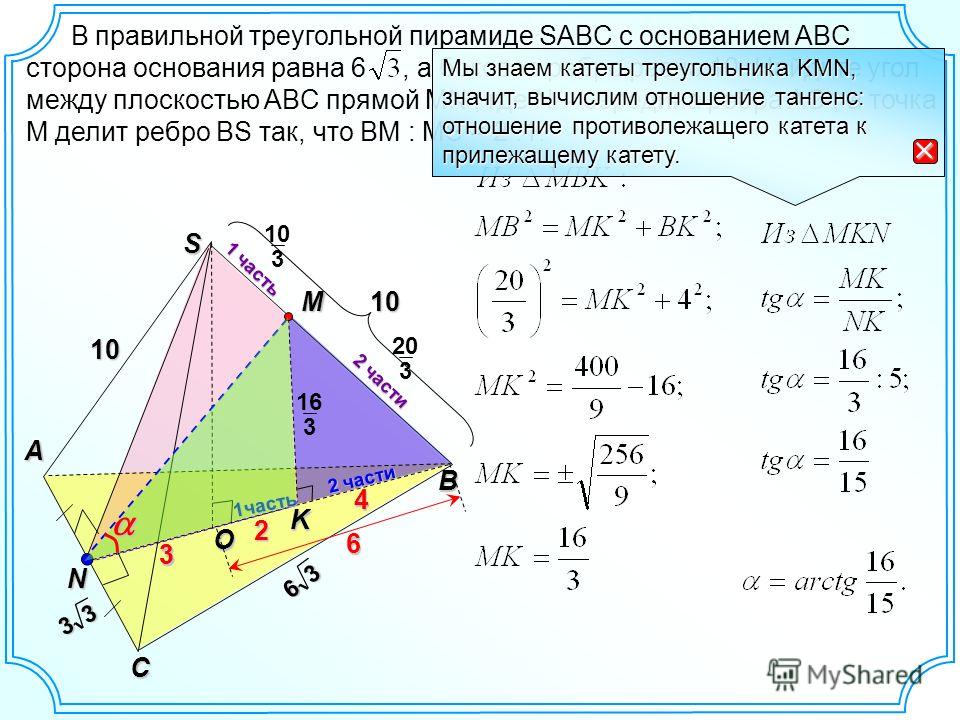
- В треугольной усечённой пирамиде высота равна 10 см, стороны нижнего основания равны 27 м, 29 м, 52 м, а периметр верхнего основания равен 72 м. Найти объём усечённой пирамиды.

- Стороны оснований правильной четырёхугольной усечённой пирамиды равны 40 см и 10 см. Площадь её полной поверхности равна 3400 см2. Найти объём усечённой пирамиды.
ЦИЛИНДР. ПОВЕРХНОСТЬ И ОБЪЕМ ЦИЛИНДРА.
Определение: Геометрическое тело, полученное при вращении прямоугольника вокруг одной из его сторон, называется прямым круговым цилиндром.
Определение: Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.
AB – ось симметрии, высота цилиндра;AB = H;
AD– радиус основания цилиндра;AD = R.
Определение: Расстояние между плоскостями оснований является высотой прямого кругового цилиндра.
Радиусом цилиндра называется радиус его основания.
 Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.Два круга являются основаниями прямого кругового цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный плоскостям оснований, называется образующей прямого кругового цилиндра.
Определение: Прямоугольник, одна сторона которого равна длине окружности основания цилиндра, а другая – его высоте, называется разверткой боковой поверхности цилиндра.
Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.
В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.
Определение: Цилиндр называется равносторонним, если его высота равна диаметру основания.
Сечения цилиндра.
Сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник.
 Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.В частности, прямоугольником является осевое сечение. Осевое сечение — сечение цилиндра плоскостью, проходящей через его ось.
Сечение цилиндра плоскостью, параллельной основанию − круг.
Сечение цилиндра плоскостью не параллельной основанию и его оси – овал.
Теорема: Площадь боковой поверхности цилиндра равна произведению длины окружности его основания на высоту (Sбок. = 2πRH, где R − радиус основания цилиндра, Н − высота цилиндра).
Определение: Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований.
Sосн. = πR2 Sбок. = 2πRH Sполн.= 2πRH + 2πR2.
Рассмотрим п-угольную прямую призму.
 При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.
При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.Определение: Призма называется вписанной в цилиндр, если её основания вписаны в основания цилиндра.
Определение: Цилиндр называется вписанным в призму, если его основания вписаны в основания призмы.
Упражнения:
1. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найти: высоту, радиус основания, площадь основания цилиндра.
2. Площадь осевого сечения цилиндра равна 10 см2, а площадь основания — 5 см2.
 Найти высоту цилиндра.
Найти высоту цилиндра.3. Радиус основания цилиндра равен 4 см, а площадь его осевого сечения равна 72 см2. Найти объём цилиндра.
Что делать, если нет взаимности? А теперь спустимся с небес на землю. Приземлились? Продолжаем разговор…
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования…
ЧТО ТАКОЕ УВЕРЕННОЕ ПОВЕДЕНИЕ В МЕЖЛИЧНОСТНЫХ ОТНОШЕНИЯХ? Исторически существует три основных модели различий, существующих между…
Что будет с Землей, если ось ее сместится на 6666 км? Что будет с Землей? — задался я вопросом…
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Геометрия Усеченная пирамида
Материалы к уроку
Конспект урока
Многогранники.
 Усечённая пирамида.
Усечённая пирамида.Мы продолжаем знакомство с многогранниками.
На прошлом занятии вы познакомились с частным видом пирамиды –правильной пирамидой.
Напомню, что пирамида называется правильной, если в её основании лежит правильный многоугольник. Высотой такой пирамиды называется отрезок, проведённый из вершины в центр основания.
Если ABCDE –правильный пятиугольник, то SABCDE-правильная пирамида.
SO-высота.
SO┴( ABCDE)
1.Изобразим произвольную пирамиду SA1 A2… An.
2. Проведём секущую плоскость параллельно основанию, пересекающую боковые рёбра пирамиды в точках В1 В2… Вn.
3.Секущая плоскость разбила пирамиду на два многогранника, один из которых так же является пирамидой.
 , а другой называется усечённой пирамидой.
, а другой называется усечённой пирамидой.Итак, усечённой пирамидой называется многогранник, гранями которого являются многоугольники А1 А2… Аn и В1 В2… Вn(верхнее и нижнее основания), расположенных на параллельных плоскостях и четырёхугольников А1 А2 В1 В2, А2 А3 В2 В3,…Аn-1 Аn Вn-1 Вn(боковые грани).
Отрезки, соединяющие вершины оснований называются боковыми рёбрами усечённой пирамиды.
На чертеже изображена усечённая пирамида ABCDA1 B1 C1 D1.
Высотой пирамиды называется перпендикуляр, проведённый из любой точки основания к плоскости другого.

ABCDA1 B1 C1 D1-усечённая пирамида.
ABCD и A1 B1 C1 D1 –основания
А А1В1 В-боковая грань
А А1-боковое ребро
ОО1-высота
Рассмотрим боковую грань А1 А2 В1 В2 усечённой пирамиды .
Стороны А1 А2 и В1 В2 параллельны, так как принадлежат параллельным прямым по которым плоскость S А1 А2 пересекается с параллельными плоскостями альфа и бета.
Стороны А1 В1 и А2 В2 не параллельны, так как их продолжения пересекаются в точке S.

Таким образом мы доказали, что боковая грань правильной усечённой пирамиды
А1 А2 В1 В2 -является трапецией.
Очевидно, что все боковые грани усечённой пирамиды являются трапециями.
(желательно сопоставлять объекты чертежа со словами, можно анимацией либо просто выделять)
Если усечённая пирамида получена путём сечения параллельно основанию правильной пирамиды , то усеченная пирамида будет так же правильной.
Основания правильной усечённой пирамиды –это правильные многоугольники, а боковые грани- равнобедренные трапеции.
Высота боковой грани называется апофемой.

А А1В1 В- равнобедренная трапеция.
В1Е-апофема.
Сумма площадей боковых граней называется площадью боковой поверхности усечённой пирамиды. Эта площадь равна произведению апофемы на полусумму периметров.
Доказательство следует из того, что боковые грани усечённой пирамиды- это равные равнобедренные трапеции, площади которых равны произведению полусуммы оснований на высоту- апофему. Вынося за скобку общий множитель –апофему и1/2, в скобках получим сумму оснований. А это в свою очередь есть периметр оснований- правильных многоугольников.
Применим свои знания при решении задач:
Задача 1.

Стороны оснований правильной треугольной усечённой пирамиды равны 4 дм и 2 дм. Точки О и О1-центры оснований пирамиды. Найти высоту и апофему пирамиды, если боковое ребро равно 2 дм.
Для начала проведём краткий анализ задачи: так как усечённая пирамида правильная, то боковые рёбра-равные равнобедренные трапеции. В основании лежат правильные треугольники, значит все углы этих треугольников будут по 60 градусов.
Решение:
1. Дополнительное построение: построим СМ перпендикулярно АВ, С1М1 перпендикулярно А1В1 и соединим точки М1 и М.
По теореме о трёх перпендикулярах М1М перпендикулярен АВ(одновременно М1М перпендикулярна А1В1), значит М1М-апофема.
Дано:АВСА1 В1 С1-усечённая пирамида, АВ=ВС=АС=4 дм, А1В1=В1С1=А1С1=2 дм, АА1=2 дм
Найти: высоту, апофему
Решение:
1.
 Д.п. СМ┴АВ, С1М1┴ А1В1→ М1М┴ АВ и
Д.п. СМ┴АВ, С1М1┴ А1В1→ М1М┴ АВ иМ1М┴ А1В1( по т.т.п.)
М1М-апофема.
2. ОО1-высота h.
Д.п. С1L┴ СМ, М1 N┴ СМ.
С1L= ОО1= М1 N=h(как расстояния между параллельными прямыми).
Ответ: M1М=√3 дм, О1О=2√6 дм
Сегодня мы расширили свои знания по теме многогранник, познакомились с новой фигурой-пирамидой и её элементами, научились решать задачи применяя новые полученные знания.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
Урок геометрии в 11-м классе: «Объём пирамиды»
Цели и задачи урока:
- вывести формулы: объема пирамиды с использованием основной формулы объема тел и объема усеченной пирамиды.

- систематизировать теоретические знания по теме нахождения объема пирамиды.
- сформировать навык нахождения объема пирамиды, у которой вершина проецируется в центр вписанной или описанной около основания окружности.
- выработать навыки решения типовых задач на применение формул объемов пирамиды и усеченной пирамиды.
Ход урока
I. Объяснение нового материала.
Доказательство теоремы выполняется с помощью мультимедийного проектора
Докажем теорему: объем пирамиды равен одной трети, произведения площади основания на высоту.
Рис. 1
Доказательство:
Сначала докажем теорему для треугольной пирамиды, затем для произвольной.
1. Рассмотрим треугольную пирамиду ОАВС с объемом V, площадью основания S и высотой h .
 Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, что
Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, чтоВ самом деле , следовательно, .
Прямоугольные треугольники , тоже подобны (они имеют общий острый угол с вершиной О).
Применим теперь основную формулу для вычисления объемов тел при a = 0, b = h получаем
Pис. 2
2. Докажем теперь теорему для произвольной пирамиды с высотой h и площадью основания S . Такую пирамиду можно разбить на треугольные пирамиды с общей высотой h.
 Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид, т.е. площадь S оснований исходной пирамиды.
Выразим объем каждой треугольной пирамиды по доказанной нами формуле и сложим эти объемы. Вынося за скобки общий множитель , получим в скобках сумму оснований треугольных пирамид, т.е. площадь S оснований исходной пирамиды.Таким образом, объем исходной пирамиды равен . Теорема доказана.
II. решить задачи по готовым чертежам .
Задача 1. (рис. 3)
Дано: АВСD – правильная пирамида, АВ =3; AD= . Найти: а)Sосн; б) АО; в) DO г) V.
Задача 2. (рис. 4)
Дано: АВСDF – правильная пирамида, .
Задача 3. (рис. 5)
Дано : АВСDEKF – правильная пирамида,
Найти: а) Sосн; б) V.

Задача 4. (рис. 6)
Найти: V.
Проверка задач выполняется с помощью мультимедийного проектора с подробным анализом поэтапного решения.
Задача 1. (рис. 3)
Решение:
а) (используется формула для вычисления площади правильного треугольника)
АВ = = 3, имеемб) (формула радиуса описанной окружности через сторону правильного треугольника) .
Задача 2. (рис. 4)
Решение:
1) Рассмотрим следовательно,
– равнобедренный, ОС = FО = 2.Задача 3. (рис. 5)
Решение:
Задача 4. (рис. 6)
Решение:
III. Проверка вывода формулы для вычисления объема усеченной пирамиды (сообщение ученика у доски выполняется с помощью мультимедийного проектора)
Ответ ученика:
Объем усеченной пирамиды рассматриваем как разность объемов полной пирамиды и той, что отсечена от нее плоскостью, параллельной основанию (рис.
 1).
1).Подставим это выражение для х в первую формулу,
Pабота в форме теста, с проверкой через мультимедийный проектор.
1.В наклонной призме боковое ребро равно 7 см, перпендикулярное сечение — прямоугольный треугольник с катетами: 4 см и 3 см. найдите объем призмы.
а) 10 см3, б) 42 см3, в) 60 см3, г) 30 см3.
2. В правильной шестиугольной пирамиде сторона ее основания 2 см. Объем пирамиды равен 6 см3. Чему равна высота?
3. Объем пирамиды равен 56 см3, площадь основания 14 см2. Чему равна высота?
а) 14 см, б) 12 см, в) 16 см.
4. В правильной треугольной пирамиде высота равна 5 см, стороны основания 3 см. Чему равен объем пирамиды?
5. В правильной четырехугольной пирамиде высота равна 9 см. Сторона основания 4 см. найдите объем пирамиды.

а) 50 см3, б) 48 см3, в) 16 см3.
6. Объем правильной четырехугольной пирамиды равен 27 см3, высота 9 см. найти сторону основания.
а)12 см, б) 9 см, в) 3 см.
7. Объем усеченной пирамиды равен 210 см3, площадь нижнего основания 36 см2, верхнего 9 см2. Найдите высоту пирамиды.
а) 1см, б) 15 см, в) 10см.
8. Равновеликие призма и правильная четырехугольная пирамида имеют равные высоты. Чему равна сторона основания пирамиды, если площадь основания призмы равна S?
Таблица ответов.
Задача 1 2 3 4 5 6 7 8 Ответ б а б а б в в в Домашняя работа: 1.
 Решить задачи №695в, №697, №690
Решить задачи №695в, №697, №6902. Рассмотреть базовые задачи
Задача 1.
Докажите, что если боковые ребра пирамиды равны (или составляют равные углы с плоскостью основания), то вершина пирамиды проецируется в центр окружности, описанной около основания.
Pис. 2
Задача 2.
Докажите, что если двугранные углы при основании пирамиды равны (или равны высоты боковых граней, проведенные из вершины пирамиды), то вершина пирамиды проецируется в центр окружности, вписанной в основание пирамиды.
Pис. 3
Пирамида. Усеченная пирамида
Пирамидой называется многогранник, одна из граней которого многоугольник (основание), а все остальные грани – треугольники с общей вершиной (боковые грани) (рис. 15). Пирамида называется правильной, если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис.
 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.
16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром.Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется апофемой. Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.
Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.
1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.

2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.
3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.
Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.
Основания усеченной пирамиды – подобные многоугольники. Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º. Найти тангенс угла наклона бокового ребра к плоскости основания.
Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС). Угол наклона бокового ребра (например SB) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD. Чтобы найти тангенс необходимо знать катеты SO и OB. Пусть длина отрезка BD равна 3а. Точкой О отрезок BD делится на части: и Из находим SO: Из находим:
Пример 2.
 Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.
Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:
Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.
Решение. Сделаем рисунок (рис. 19).
Рис. 19
Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота.
 Ее найдем из где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:
Ее найдем из где А1Е перпендикуляр из точки А1 на плоскость нижнего основания, A1D – перпендикуляр из А1 на АС. А1Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:MK = DE.
По теореме Пифагора из
Площадь боковой грани:
Рис. 20
Ответ:
Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j.
 Найти площадь полной поверхности пирамиды.
Найти площадь полной поверхности пирамиды.Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD.
Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:
Рис. 21
Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD. Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.
Рис.
 22
22Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем
Тогда
Площадь трапеции:
Значит,
Ответ:
Пример 5.Основание пирамиды – равносторонний треугольник со стороной а. Одна из боковых граней – равнобедренный прямоугольный треугольник, плоскость которого перпендикулярна плоскости основания. Найти площадь боковой поверхности пирамиды.
Решение. Сделаем рисунок (рис. 23).
Рис. 23
Площадь боковой поверхности данной пирамиды SABC состоит из суммы площадей ее боковых граней. Боковые грани – треугольники, один из которых прямоугольный и равнобедренный ( ), два других – равные треугольники Рассмотрим – по условию. Вычислим его площадь: Так как равнобедренный, то а так как то и следовательно в
Тогда
Рассмотрим SE найдем из По теореме Пифагора имеем Найдем DE.
 Для этого рассмотрим равносторонний треугольник основания (рис. 24). В отрезок DE является средней линией, значит, Находим SE:
Для этого рассмотрим равносторонний треугольник основания (рис. 24). В отрезок DE является средней линией, значит, Находим SE:Рис. 24
Теперь
Площадь боковой поверхности пирамиды равна:
Ответ:
Задания для самостоятельного решения
I уровень
1.1. Боковое ребро правильной четырехугольной пирамиды равно диагонали основания, длина которой см. Найдите высоту пирамиды и сторону ее основания.
1.2. Основанием пирамиды является треугольник со сторонами 6 см, 8 см и 10 см. Боковые грани наклонены к плоскости основания под углом 60º. Найдите высоту пирамиды.
1.3. Найдите площадь полной поверхности правильной шестиугольной пирамиды, зная, что апофема равна 10 см, а радиус окружности, описанной около основания, равен 6см.
1.
 4. Найдите высоту правильной четырехугольной пирамиды, сторона которой 6 см, если ее объем равен объему куба со стороной 4 см.
4. Найдите высоту правильной четырехугольной пирамиды, сторона которой 6 см, если ее объем равен объему куба со стороной 4 см.1.5. Боковые ребра треугольной пирамиды взаимно перпендикулярны и равны b. Найдите объем пирамиды.
1.6. Стороны оснований правильной усеченной четырехугольной пирамиды 8 см и 4 см. Боковое ребро см. Найдите высоту пирамиды.
1.7. Боковые ребра правильной усеченной шестиугольной пирамиды наклонены к плоскости нижнего основания под углом 45º. Стороны оснований равны 10 см и 5 см. Найдите длину бокового ребра и высоту пирамиды.
1.8. Боковая грань правильной семиугольной усеченной пирамиды – равнобедренная трапеция, средняя линия которой 13 см, а высота 8 см. Вычислите площадь боковой поверхности пирамиды.
1.9. Площадь полной поверхности правильной треугольной усеченной пирамиды равна см2. Стороны оснований 10 см и 6 см. Найдите тангенс угла между боковым ребром и стороной нижнего основания.

1.10. В правильной усеченной четырехугольной пирамиде стороны оснований равны 5 см и 17 см, боковые грани наклонены к плоскости основания под углом 45º. Вычислите объем пирамиды.
II уровень
2.1. По стороне основания, равной 5 см, и высоте, равной 12 см, Найдите апофему и боковое ребро правильной шестиугольной пирамиды.
2.2. Найдите расстояние между центрами окружностей вписанных в смежные боковые грани тетраэдра. Радиус окружности равен дм.
2.3. Основание пирамиды – ромб со стороной 6см и углом 45º, все двугранные углы при сторонах основания пирамиды равны 30º. Вычислите площадь полной поверхности пирамиды.
2.4. В правильной треугольной пирамиде боковое ребро равно 8 см, а плоский угол при вершине – 30º. Найдите площадь полной поверхности пирамиды.
2.5. Одно из самых грандиозных сооружений древности – пирамида Хеопса – имеет форму правильной четырехугольной пирамиды с высотой » 150 м и боковым ребром » 220 м.
 Найдите объем этой пирамиды.
Найдите объем этой пирамиды.2.6. Определите объем правильной треугольной пирамиды, если боковая грань наклонена к плоскости основания под углом 60º и удалена от противоположной вершины на расстояние, равное 3 см.
2.7. В правильной четырехугольной усеченной пирамиде стороны оснований равны 15 дм и 5 дм. Площадь диагонального сечения равна дм2. Найдите площадь полной поверхности пирамиды.
2.8. Основания усеченной пирамиды – равнобедренные треугольники, их равные стороны – 8 см и 4 см, углы при вершинах треугольников равны по 120º. Ребро, проходящее через вершины данных углов, перпендикулярно плоскости оснований и равно 3 см. Вычислите площадь боковой поверхности пирамиды.
2.9. Правильная четырехугольная пирамида, сторона основания которой 1500 см и высота 2000 см, пересечена плоскостью параллельной основанию. Найдите объем усеченной пирамиды, если ее высота 1400 см.
2.10. В правильной усеченной треугольной пирамиде стороны оснований равны 7 см и 3 см, а апофема – 5 см.
 Найдите объем пирамиды.
Найдите объем пирамиды.III уровень
3.1. Основанием пирамиды является равносторонний треугольник. Одна из боковых граней пирамиды перпендикулярна плоскости основания, две другие образуют с плоскостью основания угол a. Найдите косинус угла между этими гранями.
3.2. Все диагональные сечения правильной шестиугольной пирамиды SABCDEF равновелики. Найдите угол между плоскостью основания и плоскостью сечения SAC.
3.3. Точка М – середина ребра SB пирамиды SABC, основанием которой является правильный треугольник ABC, а боковое ребро SC перпендикулярно плоскости ABC и SC = 2AB. Найдите расстояние от точки М до прямой AC, если АВ = а.
3.4. Основанием пирамиды служит ромб со стороной а и острым углом a. Две боковые грани перпендикулярны основанию, а две другие наклонены к нему под углом j.
 Найдите площадь боковой поверхности пирамиды.
Найдите площадь боковой поверхности пирамиды.3.5. Основанием пирамиды является равнобокая трапеция, острый угол которой a, а площадь Q. Каждая боковая грань образует с основанием угол b. Найдите объем пирамиды.
3.16. Основание усеченной пирамиды – прямоугольник со сторонами 6 см и 8 см. Одно из боковых ребер перпендикулярно плоскости основания и равно 7 см. Вершина верхнего основания проектируется в точку пересечения диагоналей нижнего основания. Найдите длины остальных боковых ребер и угол наклона большего бокового ребра к плоскости основания.
3.7. Основания усеченной пирамиды – квадраты со сторонами 8 см и 4 см. Одна из боковых граней перпендикулярна плоскости основания и является равнобедренной трапецией. Противолежащая ей грань образует с плоскостью основания угол 60º. Найдите площади боковых граней пирамиды.
3.8. Стороны оснований и высота правильной четырехугольной усеченной пирамиды относятся, как 7 : 4 : 2, площадь боковой поверхности равна 110 дм2.
 Вычислите площадь полной поверхности пирамиды.
Вычислите площадь полной поверхности пирамиды.3.9. Найдите объем правильной треугольной усеченной пирамиды, у которой стороны оснований равны 3 м и 2 м, а площадь боковой поверхности равна сумме площадей оснований.
3.10. Стороны оснований правильной четырехугольной усеченной пирамиды равны 2 см и 1 см, высота – 3 см. Через точку пересечения диагоналей пирамиды, параллельно основаниям пирамиды, приведена плоскость, делящая пирамиду на две части. Найдите объем каждой из полученных частей.
Цилиндр
Цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой параллельно данной прямой (рис. 25).
Данная кривая называется направляющей, а прямые – образующими цилиндрической поверхности.
Прямой круговой цилиндрической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности перпендикулярно плоскости этой окружности.
 В дальнейшем эту поверхность будем кратко называть цилиндрической (рис. 26).
В дальнейшем эту поверхность будем кратко называть цилиндрической (рис. 26).Цилиндром (прямым круговым цилиндром) называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим поверхности (рис. 27).
Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг оси, содержащей одну из сторон прямоугольника.
Два круга, ограничивающие цилиндр, называются его основаниями. Прямая, проходящая через центры данных кругов, называется осью цилиндра. Отрезки, образующие цилиндрическую поверхность, называются образующими цилиндра. Высотой цилиндра называется расстояние между его основаниями. Осевым сечением называется сечение, проходящее через ось цилиндра. Разверткой боковой поверхности цилиндра называется прямоугольник со сторонами равными длине окружности основания и длине образующей цилиндра.

Рис. 25 Рис. 26 Рис. 27
Для цилиндра верны формулы:
(5)
(6)
где R – радиус основания;
H – высота;
Sосн – площадь основания;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем цилиндра.
Пример 1. Найти радиус основания цилиндра, если его высота равна 8 см, а диагональ осевого сечения составляет угол в 45º с плоскостью основания.
Решение. Сделаем рисунок (рис. 28).
Рис. 28
Осевое сечение цилиндра – это прямоугольник, одна сторона которого образующая (высота) цилиндра, вторая сторона – диаметр основания цилиндра.
 Рассмотрим треугольник АВС, у которого катетами являются диаметр основания АС и высота ВС, а гипотенузой – диагональ сечения АВ. Так как то – равнобедренный и АС = ВС = 8 см. АС – диаметр, значит, радиус
Рассмотрим треугольник АВС, у которого катетами являются диаметр основания АС и высота ВС, а гипотенузой – диагональ сечения АВ. Так как то – равнобедренный и АС = ВС = 8 см. АС – диаметр, значит, радиусОтвет: 4 см.
Пример 2. Цилиндр пересечен плоскостью параллельной оси. Найти площадь сечения, если радиус основания и высота цилиндра соответственно 5 см и 10 см, а расстояние от оси цилиндра до плоскости сечения 3 см.
Решение. Сделаем рисунок (рис. 29).
Рис. 29
Сечением цилиндра является прямоугольник, одна из сторон которого – хорда окружности основания (ВС), вторая – образующая цилиндра (ВА). Образующая равна высоте, значит ВА = 10 см. Необходимо найти хорду ВС. Расстояние от оси ОО1 до плоскости сечения – это перпендикуляр опущенный из точки О1 на хорду ВС.
 Проведя радиусы О1С и О1В, получим равнобедренный треугольник Высота O1D является его медианой, значит BD = DC. Из найдем BD:
Проведя радиусы О1С и О1В, получим равнобедренный треугольник Высота O1D является его медианой, значит BD = DC. Из найдем BD:Тогда BC = 2BD = 8 см. Площадь сечения:
Ответ: 80 см2.
Пример 3. Диагональ сечения цилиндра, параллельного его оси, равна d и образует угол a с образующей цилиндра. Найти площадь полной поверхности цилиндра, если секущая плоскость отсекает от окружности основания часть ее.
Решение. Сделаем рисунок (рис. 30).
Рис. 30
Площадь полной поверхности цилиндра вычисляется по формуле (5).
Чтобы найти высоту Н (образующую), рассмотрим .
 В нем Тогда
В нем ТогдаДля нахождения радиуса рассмотрим равнобедренный в котором OA = OD = R. Так как по условию сечение отсекает от окружности основания часть, значит По теореме косинусов найдем радиус:
т.е. .
Тогда , откуда получаем
Вычисляем
Ответ:
Пример 4.Диагонали развертки боковой поверхности цилиндра образуют острый угол равный a. Высота цилиндра равна h. Найти объем цилиндра.
Решение. Сделаем рисунок (рис. 31).
Рис. 31
Чтобы найти объем, необходимо знать радиус основания цилиндра. Рассмотрим развертку боковой поверхности цилиндра – прямоугольник ABCD: AD = h, BC = 2pR,где R – неизвестный радиус основания. Точка О – середина диагоналей.
 Из точки О опустим перпендикуляр OD,
Из точки О опустим перпендикуляр OD,с другой стороны
Приравнивая выражения для нахождения OD, находим R:
, т.е. .
Вычисляем объем цилиндра по формуле (6):
Ответ:
Задания для самостоятельного решения
I уровень
1.1. Найдите диагональ осевого сечения цилиндра, высота которого равна 8 см, а радиус основания – 3 см.
1.2. Осевое сечение цилиндра – квадрат, площадь которого 64 см2. Найдите площадь основания цилиндра.
1.3. Площадь осевого сечения цилиндра равна S, Найдите площадь его боковой поверхности.
1.4. Высота цилиндра равна 12 см, диагональ осевого сечения – 13 см. Найдите площадь боковой поверхности цилиндра.
1.5. Диагональ осевого сечения цилиндра равна см и составляет угол 45º с плоскостью основания.
 Найдите площадь боковой поверхности цилиндра.
Найдите площадь боковой поверхности цилиндра.1.6. Цилиндр образован вращением прямоугольника вокруг меньшей из сторон. Найдите площадь полной поверхности цилиндра, если диагональ прямоугольника равна 6 см и наклонена к большей стороне под углом 30º.
1.7. Определите давление кирпичной цилиндрической колонны на фундамент, если высота колонны 2 м, диаметр основания равен 0,75 м. Вес одного кубического метра кирпича необходимо принять равным 1,8 т.
1.8. Развертка боковой поверхности цилиндра – квадрат со стороной 18 см. Найдите объем цилиндра.
1.9. Как изменится объем цилиндра, если радиус основания увеличить в три раза, а высоту уменьшить в четыре раза?
1.10. Два различных цилиндра имеют равные площади боковых поверхностей. Найдите отношение радиусов оснований, если их высоты относятся как 3 : 1.
II уровень
2.1. Цилиндр, радиус основания которого равен 13 см, а высота – 10 см, пересечен плоскостью так, что в сечении получился квадрат.
 Определите, на каком расстоянии от оси цилиндра проведено сечение.
Определите, на каком расстоянии от оси цилиндра проведено сечение.2.2. Через образующую цилиндра проведены две взаимно перпендикулярные плоскости. Площадь каждого из полученных сечений равна 71 дм2. Найдите площадь осевого сечения цилиндра.
2.3. Радиус основания цилиндра в три раза меньше его высоты. Найдите угол между диагоналями осевого сечения цилиндра.
2.4. Цилиндрическая дымовая труба диаметром 60 см имеет высоту 20 м. Определите, сколько квадратных метров листового железа потребуется на ее изготовление, если на заклепки уходит 10 % всего необходимого количества железа.
2.5. Развертка боковой поверхности цилиндра – квадрат. Найдите объем цилиндра, если радиус его основания на 3 см меньше высоты.
2.6. Площадь основания цилиндра равновелика площади развертки его боковой поверхности. Найдите тангенс угла наклона диагонали осевого сечения к плоскости основания цилиндра.
2.7. Прямоугольник со сторонами m и b является разверткой боковых поверхностей двух различных цилиндров.
 Найдите отношение объемов этих цилиндров.
Найдите отношение объемов этих цилиндров.2.8. Кусок льда, имеющий форму прямоугольного параллелепипеда, размером 0,6 м ´ 0,4 м ´ 0,5 м, помещен в цилиндрический сосуд диаметра 0,9м. Определите, какова будет высота слоя воды после того, как лед растает. Удельный вес льда необходимо считать равным 0,92 г/см3.
III уровень
3.1. Точка окружности верхнего основания цилиндра соединена с точкой окружности нижнего основания. Угол между радиусами, проведенными в эти точки, равен a. Найдите угол между осью цилиндра и отрезком, соединяющим данные точки, если высота цилиндра равна его диаметру.
3.2. К цилиндру проведена касательная прямая под углом a к плоскости основания. Определите расстояние от центра нижнего основания до прямой, если расстояние от центра до точки касания равно d,а радиус основания равен R.
3.3. Высота цилиндра равна радиусу его основания и имеет длину а.
 Через ось цилиндра проведена вторая цилиндрическая поверхность, которая делит окружность основания на две дуги, длины которых относятся как 2 : 1. Найдите объем большей части цилиндра, на которые цилиндрическая поверхность делит цилиндр.
Через ось цилиндра проведена вторая цилиндрическая поверхность, которая делит окружность основания на две дуги, длины которых относятся как 2 : 1. Найдите объем большей части цилиндра, на которые цилиндрическая поверхность делит цилиндр.3.4. Два равных цилиндра, высоты которых больше их диаметров, расположены так, что их оси пересекаются под прямым углом и точка пересечения осей равноудалена от оснований цилиндров. Найдите объем общей части этих цилиндров, если радиус каждого из них равен 1 см.
Конус. Усеченный конус
Конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной кривой и точку вне кривой (рис.32).
Данная кривая называется направляющей, прямые – образующими, точка – вершиной конической поверхности.
Прямой круговой конической поверхностью называется поверхность, образованная всеми прямыми, проходящими через каждую точку данной окружности и точку на прямой, которая перпендикулярна плоскости окружности и проходит через ее центр.
 В дальнейшем эту поверхность будем кратко называть конической поверхностью (рис.33).
В дальнейшем эту поверхность будем кратко называть конической поверхностью (рис.33).Конусом (прямым круговым конусом) называется геометрическое тело, ограниченное конической поверхностью и плоскостью, которая параллельна плоскости направляющей окружности (рис.34).
Рис. 32 Рис. 33 Рис. 34
Конус можно рассматривать как тело, полученное при вращении прямоугольного треугольника вокруг оси, содержащей один из катетов треугольника.
Круг, ограничивающий конус, называется его основанием. Вершина конической поверхности называется вершиной конуса. Отрезок, соединяющий вершину конуса с центром его основания, называется высотой конуса.
 Отрезки, образующие коническую поверхность, называются образующими конуса. Осью конуса называется прямая, проходящая через вершину конуса и центр его основания. Осевым сечением называется сечение, проходящее через ось конуса. Разверткой боковой поверхности конуса называется сектор, радиус которого равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
Отрезки, образующие коническую поверхность, называются образующими конуса. Осью конуса называется прямая, проходящая через вершину конуса и центр его основания. Осевым сечением называется сечение, проходящее через ось конуса. Разверткой боковой поверхности конуса называется сектор, радиус которого равен длине образующей конуса, а длина дуги сектора равна длине окружности основания конуса.Для конуса верны формулы:
(7)
где R – радиус основания;
H – высота;
l – длина образующей;
Sосн – площадь основания;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем конуса.
Усеченным конусом называется часть конуса, заключенная между основанием и секущей плоскостью, параллельной основанию конуса (рис.
 35).
35).Рис. 35
Усеченный конус можно рассматривать как тело, полученное при вращении прямоугольной трапеции вокруг оси, содержащей боковую сторону трапеции, перпендикулярную основаниям.
Два круга, ограничивающие конус, называются его основаниями. Высотой усеченного конуса называется расстояние между его основаниями. Отрезки, образующие коническую поверхность усеченного конуса называются образующими. Прямая, проходящая через центры оснований, называется осью усеченного конуса. Осевым сечением называется сечение, проходящее через ось усеченного конуса.
Для усеченного конуса верны формулы:
(8)
где R – радиус нижнего основания;
r – радиус верхнего основания;
H – высота, l – длина образующей;
Sбок – площадь боковой поверхности;
Sполн – площадь полной поверхности;
V – объем усеченного конуса.

Пример 1.Сечение конуса параллельное основанию делит высоту в отношении 1:3, считая от вершины. Найти площадь боковой поверхности усеченного конуса, если радиус основания и высота конуса равны 9 см и 12 см.
Решение. Сделаем рисунок (рис. 36).
Для вычисления площади боковой поверхности усеченного конуса используем формулу (8). Найдем радиусы оснований О1А и О1В и образующую АВ.
Рассмотрим подобные треугольники SO2B и SO1A, коэффициент подобия , тогда
Отсюда
Из SO1A
Так как то
Площадь боковой поверхности усеченного конуса равна:
Ответ: .
⇐ Предыдущая12345Следующая ⇒
Калькулятор объема треугольной пирамиды
Автор Анна Щепанек, доктор философии
Рецензию сделали Богна Шик и Джек Боуотер
Последнее обновление: 11 марта 2022 г.
Содержание:
- Как пользоваться нашим калькулятором объема треугольной пирамиды?
- Формула объема треугольной пирамиды
- Как вручную найти объем треугольной пирамиды?
- Объем тетраэдра
- Объем прямоугольной пирамиды
Наш калькулятор объема треугольной пирамиды позволяет найти объем любой пирамиды с треугольным основанием, независимо от того, знаете ли вы площадь ее основания. Если вы хотите определить объем прямоугольной пирамиды или правильного тетраэдра, вы попали по адресу.
Вам нужно научиться находить объем треугольной пирамиды вручную? Продолжайте читать, поскольку мы даем как формулу, так и примеры того, как ее использовать.Как пользоваться нашим калькулятором объема треугольной пирамиды?
Треугольная пирамида представляет собой твердый объект, образованный соединением треугольного основания с точкой, называемой вершиной . Это создает четыре грани , каждая из которых представляет собой треугольник.
 Если вы можете вращать пирамиду, каждая грань может играть роль основания пирамиды. Отрезок, перпендикулярный основанию и проходящий через вершину, называется 9.0026 высота пирамиды.
Если вы можете вращать пирамиду, каждая грань может играть роль основания пирамиды. Отрезок, перпендикулярный основанию и проходящий через вершину, называется 9.0026 высота пирамиды.Здесь темно-синий треугольник — основание пирамиды, а черный пунктирный сегмент — высота:
Чтобы использовать наш калькулятор объема треугольной пирамиды, выполните следующие действия:
- Знаете ли вы площадь основания пирамиды?
- Если да, введите его в калькулятор.
- Если нет, проверьте, какие данные о базе вам известны: выберите подходящий вариант в нашем калькуляторе и введите свои данные. Базовая площадь будет рассчитана для вас.
Введите высоту пирамиды.
Калькулятор объема треугольной пирамиды вернет объем вашей пирамиды 🙂
Формула объема треугольной пирамиды
Формула объема треугольной пирамиды напоминает формулу объема любой другой пирамиды или конуса:
V = A * H / 3где:
-
A 9007 основание пирамиды -
Нвысота от основания до вершины
Прописью: объем треугольной пирамиды равен одной трети произведения площади основания и высоты пирамиды.

Как вручную найти объем треугольной пирамиды?
В этой части текста мы покажем вам, как применять формулу объема треугольной пирамиды. В качестве примера рассмотрим треугольную пирамиду высотой 10 см и основанием со сторонами 3 см, 4 см и 5 см в длину (что делает ее египетским прямоугольным треугольником):
- Определить площадь основания : площадь египетского треугольника можно вычислить как
3 * 4 / 2 = 6 - Найдите высоту пирамиды : в нашем случае она равна
10 - Применить формулу объема треугольной пирамиды :
6 * 10/3 = 20
Самым сложным шагом обычно является вычисление площади основания. Чтобы узнать больше об этом, вы можете проверить наш общий калькулятор площади треугольника или один из калькуляторов, предназначенных для каждого особого типа треугольника, будь то
равносторонний,
равнобедренный или
прямоугольный (или один из частных случаев прямоугольного треугольника,
треугольник 45 45 90 или треугольник
30 60 90).
Если вам нужно знать, как найти объем треугольной пирамиды, которая является правильным тетраэдром или прямоугольной треугольной пирамидой, то ознакомьтесь с двумя оставшимися разделами, где мы приводим соответствующие формулы.
Объем тетраэдра
Треугольная пирамида, гранями которой являются равносторонние треугольники, называется 9-гранной.0026 правильный тетраэдр .
Объем тетраэдра со стороной длиной a можно выразить как:
V = a³ * √2 / 12,что примерно равно
V = 0,12 * a³.Например, объем тетраэдра со стороной 10 см равен
V = 6³ * √2 / 12 = 18 √2,, что можно приблизительно представить как
0,12 * 6³ = 20,67 90.Объем прямоугольной пирамиды
Прямоугольная треугольная пирамида представляет собой треугольную пирамиду с равносторонним основанием, вершина которой находится непосредственно над центром тяжести основания (его центром масс), который в данном случае совпадает с ортоцентром (точкой пересечения всех трех высот).
 ).
).- Объем прямоугольной пирамиды со стороной длиной a и высотой H определяется по формуле:
В = a 2 * Н * √3 / 12- С помощью теоремы Пифагора мы можем найти объем прямоугольной пирамиды с длиной стороны основания a , а ребра между основанием и вершиной имеют длину b . Формула гласит:
V = √ (B 2 - A 2 /3) * A 2 * √3 / 12Anna Szczepanek, PhD
Triangle Type
(B) Base Base B. B. B. B. B. B. B. B. B. B. B.)
. (h)Основание пирамиды
Высота пирамиды (H)
Объем
Посмотреть 20 похожих калькуляторов трехмерной геометрии 📦
Площадь полушарияCubeCube Calc: найти v, a, d… еще 17
Калькулятор объема пирамиды и Стивен Вудинг
Отзыв от Bogna Szyk, Jack Bowater и Adena Benn
Последнее обновление: 10 сентября 2022 г.
Содержание:
- Формула объема пирамиды
- Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды
- Названия объемов пирамид
- Расчет объема тетраэдра
- Что дальше?
- Часто задаваемые вопросы
Определите объем любой твердой пирамиды с помощью нашего калькулятора объема пирамиды. Выберите один из двух вариантов: рассчитать объем пирамиды с правильным основанием, поэтому вам нужно указать только сторону, форму и высоту, или напрямую ввести площадь основания и высоту пирамиды. У калькулятора нет проблем с определением объема тетраэдра или объема квадратной пирамиды. Если вы все еще не знаете, как использовать инструмент и как рассчитать объем пирамиды - продолжайте читать!
Формула объема пирамиды
Пирамида – это многогранник, образованный соединением многоугольного основания и вершины. Основная формула для объема пирамиды такая же, как и для конуса:
-
объем = (1/3) * площадь основания * высота, гдевысота— высота от основания до вершины.
Эта формула работает для любого типа базового многоугольника, наклонных и прямых пирамид. Все, что вам нужно знать, это эти два значения — площадь основания и высота.
Однако есть и другие полезные формулы на случай, если вы не знаете базовую площадь. Для любой пирамиды с правильным основанием можно использовать уравнение:-
объем = (n/12) * высота * длина_стороны² * раскладушка (π/n), гдеn— количество сторон основания правильного многоугольника
Как рассчитать объем пирамиды? Пример расчета объема квадратной пирамиды
Формулу мы знаем, а что дальше? Как использовать этот калькулятор объема пирамиды? Лучший способ продемонстрировать, как это работает, — самая известная в мире пирамида — пирамида Хеопса:
- Выберите форму основания . Пирамида Хеопса, также называемая пирамидой Хуфу, представляет собой квадрат. Конечно, это не идеальный квадрат, но можно предположить, что это так - разница между длинами ребер меньше 1‰.

- Введите высоту пирамиды . Высота пирамиды Хуфу равна 146 м (вы можете изменить единицы измерения на метры простым нажатием на единицу измерения. Также вы можете проверить наш конвертер объемов).
- Определить длину стороны . Длина ребра пирамиды Хеопса составляет в среднем 230,36 м.
- Приблизительный объем квадратной пирамиды равен 2 582 532 м³.
Имена томов пирамиды
Пирамида с n-сторонним основанием имеет:
- n+1 граней (n-треугольников + 1 n-угольник)
- 2 кромки
- n+1 вершин
Название пирамиды происходит от формы ее основания:
Грани
Края
Вершины
Форма основания
Название пирамиды
4
6
4
треугольник
тетраэдр/треугольная пирамида
5
8
5
квадратный
квадратная пирамида
6
10
6
пятиугольник
пятиугольная пирамида
7
12
7
шестигранник
шестигранная пирамида
8
14
8
семиугольник
семиугольная пирамида
9
16
9
восьмиугольник
восьмиугольная пирамида
Расчет объема тетраэдра
В качестве примера возьмем пирамиду из листового чая:
- Выберите форму основания .
 В нашем случае это правильный треугольник.
В нашем случае это правильный треугольник. - Введите высоту пирамиды . Предположим, что для чайной пирамиды она равна 1,2 дюйма 9.0010
- Введите длину стороны . Например, 1,5 дюйма
- Объем тетраэдра появляется ниже . Для нашей чайной пирамидки он равен 0,39 у.е.
Если вы хотите рассчитать объем правильного тетраэдра - того, у которого все четыре грани являются равносторонними треугольниками, а не только основание - вы можете воспользоваться формулой:
объем = a³/6√2, гдеa— край твердого телаВысота в этом случае может быть рассчитана как:
высота = a√3 / 6 ~ 0,2887 * a, поэтому, если вы хотите рассчитать, например, объем правильного многогранника с ребром = 3, введите 3 * 0,2887 в поле «Высота» калькулятора объема пирамиды.Что дальше?
Теперь вы эксперт и точно знаете, как рассчитать объем пирамиды! Почему бы не проверить наши другие калькуляторы объемов?
- объем конуса
- объем цилиндра
- объем сферы
Часто задаваемые вопросы
Как найти объем пирамиды?
Чтобы оценить объем любой пирамиды:
- Оцените площадь основания пирамиды .

- Умножьте площадь основания на высоту .
- Разделить все на 3 .
- Хорошо, что этот алгоритм отлично работает для всех типов пирамид, как для правильных, так и для наклонных .
Как найти объем шестиугольной пирамиды?
Чтобы получить объем правильная шестиугольная пирамида с длиной стороны
aи высотойh:- Возведите длину стороны в квадрат, чтобы получить
a². - Умножить a² на высоту,
h. - Умножьте этого произведения на квадратный корень из трех,
√3. - Разделить все на
2. - Результат - желаемый объем! Кроме того, вы можете записать это в виде одной формулы:
В = √3 / 2 × a² × h.
Каков объем Великой пирамиды Гизы?
Объем Великой пирамиды в Гизе составляет примерно
92 миллиона футов³или2,6 миллиона м³. Мы можем получить это значение, предположив, что пирамида Хуфу является прямоугольной пирамидой. Он имеет длину756,4 футов (230,6 м)и высоту481,4 футов (146,7 м).Как найти объем пятиугольной пирамиды?
Чтобы получить объем правильная пятиугольная пирамида с длиной стороны
aи высотойh:- Возведите длину стороны в квадрат, чтобы получить
a². - Умножить a² на высоту,
h. - Умножьте этого произведения на
√(25 + 10√5). - Разделить все на
12. - Вы также можете записать полученную формулу в виде:
В = √(25 + 10√5) / 12 × a² × h.
Как найти объем восьмиугольной пирамиды?
Чтобы получить объем правильной восьмиугольной пирамиды с длиной стороны
aи высотойh:- Возведите длину стороны в квадрат, чтобы получить
a². - Умножить a² на высоту,
h. - Умножить этого произведения на
2×(1 + √2). - Разделить все на
3. - Вот и все! Общая формула правильной восьмиугольной пирамиды гласит:
V = 2 × (1 + √2) / 3 × a² × h.
Ханна Памула, кандидат наук и Стивен Вудинг
Базовый тип
Формула объема работает как для прямых, так и для наклонных пирамид.
Форма основания
Высота (h)
Длина стороны (a)
Объем
Используйте Расширенный режим , чтобы показать наклонную высоту, длину бокового края и площадь поверхности для прямоугольных пирамид.

Посмотреть 20 похожих калькуляторов 3d геометрии 📦
Площадь полушарияКубКуб Рассчитать: найти v, a, d… еще 17
Объем усеченной пирамиды
Объем усеченной пирамиды равен емкости усеченной пирамиды. Пирамида — это многогранник, представляющий собой объемную трехмерную фигуру с многоугольным основанием и вершиной, называемой вершиной. Когда пирамиду разрезают вдоль ее поперечного сечения, получают меньшую пирамиду и усеченную пирамиду. В этом разделе мы узнаем об объеме усеченной пирамиды. Оставайтесь с нами, чтобы узнать больше!!!
1. Каков объем усеченной пирамиды? 2. Формула объема усеченной пирамиды 3. Вывод объема усеченной пирамиды 4. Как найти объем усеченной пирамиды? 5. FAQ по объему усеченной пирамиды Каков объем усеченной пирамиды?
Объем усеченной пирамиды — это количество кубических единиц, которые может вместить усеченная пирамида.
 Пирамида имеет вершину и только одну грань основания, тогда как усеченная пирамида не имеет вершины и имеет две грани основания, одну вверху и одну внизу. Только основание пирамиды — многоугольник, остальные грани — треугольники. Пирамида может быть «правой», в которой ее вершина находится прямо над центром тяжести над ее основанием, или же пирамида может быть «наклонной», что в основном является неправильным. Пирамиды называются по их основаниям, например, пирамида с треугольным основанием называется треугольным основанием, пирамида с квадратным основанием называется квадратной пирамидой, пирамида с восьмиугольным основанием называется восьмиугольной пирамидой и так далее. Пирамида с n-сторонним основанием имеет n+1 вершин, n+1 граней и 2n ребер. В случае усеченной пирамиды обе грани основания должны иметь равные стороны, поэтому усеченная пирамида с n-сторонними гранями основания имеет «2n» вершин, «n+2» граней и «3n» ребер. Например, это может быть выражено как m 3 , см 3 , в 3 и т.
Пирамида имеет вершину и только одну грань основания, тогда как усеченная пирамида не имеет вершины и имеет две грани основания, одну вверху и одну внизу. Только основание пирамиды — многоугольник, остальные грани — треугольники. Пирамида может быть «правой», в которой ее вершина находится прямо над центром тяжести над ее основанием, или же пирамида может быть «наклонной», что в основном является неправильным. Пирамиды называются по их основаниям, например, пирамида с треугольным основанием называется треугольным основанием, пирамида с квадратным основанием называется квадратной пирамидой, пирамида с восьмиугольным основанием называется восьмиугольной пирамидой и так далее. Пирамида с n-сторонним основанием имеет n+1 вершин, n+1 граней и 2n ребер. В случае усеченной пирамиды обе грани основания должны иметь равные стороны, поэтому усеченная пирамида с n-сторонними гранями основания имеет «2n» вершин, «n+2» граней и «3n» ребер. Например, это может быть выражено как m 3 , см 3 , в 3 и т. д. в зависимости от заданных единиц.
д. в зависимости от заданных единиц.Формула объема усеченной пирамиды
Поскольку мы знаем, что усеченная пирамида образуется путем разрезания пирамиды вдоль ее поперечного сечения, это понятие поможет нам понять формулу объема усеченной пирамиды.
Следовательно, объем усеченной пирамиды = объем всей пирамиды - объем малой пирамиды.
Таким образом, формула объема усеченной пирамиды V = 1/3 × h × (a 2 + b 2 + ab), где «V», «h», «a» и « b" - объем усеченной пирамиды, высота усеченной пирамиды, длина стороны основания всей пирамиды и длина стороны основания меньшей пирамиды.
Определение объема усеченной пирамиды
Теперь найдем формулу объема усеченной пирамиды.
Предположим, что основанием всей пирамиды является квадрат со стороной "a" единиц, а основанием маленькой пирамиды на вершине является квадрат со стороной "b" единиц. Также примем высоту всей пирамиды за «H» единиц, высоту усеченной пирамиды за «h» единиц, следовательно, высоту малой пирамиды за «H-h» единиц.

Объем усеченной пирамиды, V = Объем всей пирамиды - Объем малой пирамиды.
⇒ V = (1/3 × площадь основания всей пирамиды × высота всей пирамиды) — (1/3 × площадь основания малой пирамиды × высота малой пирамиды)
⇒ V = (1/3 × a 2 × H) — (1/3 × b 2 × (H — h)
⇒ V = 1/3 × (а 2 H - b 2 (H - h))
⇒ V = 1/3 × (a 2 H - b 2 H + b 2 h)
⇒ V = 1/3 × ((a 2 - b 2 )H + b 2 h) ...(1)Теперь соотношение между высотами всей пирамиды и малой пирамиды , Н:(Н - h) = а:b. Следовательно, соотношение между целой пирамидой и усеченной пирамидой будет H:h = a:(a - b)
⇒ Н/ч = а/(а - б)
⇒ H = (a/(a - b)) × h ...(2)Подставляя значение «H» из уравнения (2) в уравнение (1), получаем:
⇒ V = 1 /3 × ((a 2 - b 2 )(a/(a - b)) × h) + b 2 h))
⇒ V = 1/3 × (((a + b)(a - b) × a)/(a - b)) × h + b 2 ч
⇒ V = 1/3 × (a + b) × a × h + b 2 ч
⇒ V = 1/3 × h × (a 2 + b 2 + ab)Таким образом, объем усеченной пирамиды определяется как V = 1/3 × h × (a 2 + б 2 + аб).

Как найти объем усеченной пирамиды?
Мы можем найти объем усеченной пирамиды, используя следующие шаги:
- Шаг 1: Определите заданные размеры как высоту усеченной пирамиды, длину стороны основания всей пирамиды и сторону длина меньшей пирамиды.
- Шаг 2: Подставьте значения в формулу V = 1/3 × h × (a 2 + б 2 + аб) для определения величины объема усеченной пирамиды.
- Шаг 3: Запишите полученный ответ в кубических единицах.
Пример: Найдите объем усеченной пирамиды, высота которой равна 9 единицам, если длина стороны основания всей пирамиды равна 5 единицам, а длина стороны основания меньшей пирамиды равна 3 единицам.
Решение: Учитывая h = 9 единиц, a = 5 единиц и b = 3 единиц.
Объем усеченной пирамиды, V = 1/3 × h × (a 2 + b 2 + ab)
⇒ V = 1/3 × 9 × (5 2 + 3 2 + 15)
⇒ V = 3 × 49 = 147 кубических единицТаким образом, объем усеченной пирамиды равен 147 кубических единиц.

Часто задаваемые вопросы об объеме усеченной пирамиды
Каков объем усеченной пирамиды?
Объем усеченной пирамиды определяется как емкость усеченной пирамиды. Усеченная пирамида получается, когда мы разрезаем пирамиду вдоль ее поперечного сечения. Таким образом, объем усеченной пирамиды получается, если из объема всей пирамиды вычесть объем меньшей пирамиды.
Какова формула объема усеченной пирамиды?
Объем усеченной пирамиды определяется по формуле V = 1/3 × h × (a 2 + b 2 + ab), где «V», «h», «a» и «b - объем усеченной пирамиды, высота усеченной пирамиды, длина стороны основания всей пирамиды и длина стороны основания меньшей пирамиды.
Какие единицы измерения используются при нахождении объема усеченной пирамиды?
Единицей объема усеченной пирамиды являются «кубические единицы». Например, это может быть выражено как m 3 , см 3 , в 3 и т. д. в зависимости от заданных единиц.

Как найти объем усеченной пирамиды?
Мы можем найти объем усеченной пирамиды, используя следующие шаги:
- Шаг 1: Обозначьте заданные размеры как "h", "a" и "b".
- Шаг 2: Теперь определим значение объема усеченной пирамиды, подставив значения в формулу V = 1/3 × h × (a 2 + б 2 + аб).
- Шаг 3: Полученный ответ представить в кубических единицах.
Как найти объем усеченной пирамиды, если известны объемы всей пирамиды и меньшей пирамиды?
Мы можем найти объем усеченной пирамиды, если даны объемы всей пирамиды и меньшей пирамиды, используя следующие шаги:
- Шаг 1: Определите данные размеры как объемы всей пирамиды и меньшей пирамида.
- Шаг 2: Теперь определим значение объема усеченной пирамиды, подставив значения в формулу V = Объем всей пирамиды - Объем малой пирамиды.
- Шаг 3: Полученный ответ представить в кубических единицах.

Что произойдет с объемом усеченной пирамиды, если высоту пирамиды увеличить вдвое?
Объем усеченной пирамиды удваивается, если высота пирамиды удваивается, поскольку «h» заменяется на «2h», что дает формулу V = 1/3 × h × (a 2 + b 2 + ab) = 1/3 × (2h) × (a 2 + b 2 + ab) = 2(1/3 × h × (a 2 + b ) 2 + ab)) что дает удвоенное исходное значение объема.
Что произойдет с объемом усеченной пирамиды, если высоту пирамиды уменьшить вдвое?
Объем усеченной пирамиды уменьшится вдвое, если высота пирамиды уменьшится вдвое, поскольку «h» заменяется на «h/2», что дает формулу V = 1/3 × h × (a 2 + b 2 + ab) = 1/3 × (h/2) × (a 2 + b 2 + ab) = (1/2) × (1/3 × h × (a 2 + b ) 2 + ab)) что дает половину первоначального значения объема.
Вычислить объем усеченной пирамиды
и площадь поверхности, отношение площади поверхности к объему, длину наклона и длину ребра для прямоугольных усеченных пирамид вершина отсекается плоскостью, параллельной основанию.
 Расстояние между нижним и верхним основаниями равно высоте усеченной пирамиды ч . На этой странице вычисляется объем любой усеченной пирамиды, нижнее и верхнее основания которой представляют собой прямоугольники со сторонами a , b и c , d соответственно. Эта усеченная пирамида имеет 6 граней: основание, вершину и 4 боковые грани.
Расстояние между нижним и верхним основаниями равно высоте усеченной пирамиды ч . На этой странице вычисляется объем любой усеченной пирамиды, нижнее и верхнее основания которой представляют собой прямоугольники со сторонами a , b и c , d соответственно. Эта усеченная пирамида имеет 6 граней: основание, вершину и 4 боковые грани.База a:База b:
Верх c:Верх d:Высота h:дюйм:дюймфутсантиметрметрсм. другие единицы
точность:0123456789Отношение поверхности к объему | Преобразуйте 196 дюйм³ в вес для: составов | еда | гравийпоказать все единицы
The volume of the
truncated pyramid
= 196centimeter³ 3 211.86 inch³ 196 foot³ 0.11 meter³ 0 показать все единицы измерения
Длина ребра
усеченной пирамиды
= 328828005938"> 12,33сантиметр 31,32 77 0091 inch 12.33 foot 1.03 meter 0.31 The surface to volume ratio of this truncated pyramid
= 1.19 Surface area to volume Отношение также известно как отношение поверхности к объему и обозначается как sa÷vol, где sa — площадь поверхности, а vol — объем.Блок
всеThe area of the base
of the
truncated
pyramid
= 35top
of the
truncated
pyramid
= 3centimeter² 225.81 19.35 foot² 0.  24
240.02 inch² 35 3 meter² 0.02 0 Unit
allThe area of the plane ac of the
truncated
pyramid
= 36.5bd of the
truncated
pyramid
= 60.83centimeter² 235.46 392.44 foot² 0.25 0.42 inch² 36.5 60.83 meter² 0.02 0.04 Unit
allThe lateral
surface
area
of the
truncated
пирамида
= 64840096954"> 194,65Общая
поверхность
площадь
усеченной
пирамиды
= 232,651centimeter² 1 255.79 1 500.95 foot² 1.35 1.62 inch² 194.65 232.65 meter² 0.13 0,15 Блок
всеДлина основание
сторона
a
= 5 53base
side
b
= 7top
side
c
= 1top
side
d
= 3centimeter 12.7 17.78 2.54 7.  62
62foot 0.42 0.58 0.08 0.25 inch 5 7 1 3 meter 0.13 0.18 0.03 0.08 Unit
allThe perimeter of the base
of the
Усеченная
Pyramid
= 24Верх
из
Truncated
Pyramid
= 8SENTIMET0317 foot 2 0.67 inch 24 8 meter 0.61 0.2 Unit
allДлина высота h
усеченная
пирамида
= 12наклон a
9021 усеченная пирамида0021 = 165525060596"> 12.17slant b
of the
truncated
pyramid
= 12.17centimeter 30.48 30.9 30.9 foot 1 1.01 1.01 inch 12 12.17 12.17 МЕТР 0,3 0,31 0,31 - Об этой странице: усопшированный пирамидный калькулятор
- , как нахожу на поисках VOMUTADATED TRA -TRA -TRA -TRA -TRA -TRA -TRA -TRA?
V = 1⁄6×h×(A основание +(a+c)×(b+d)+A верх ) = 1/6×h×(a×b+(a+c)× (b+d)+c×d) - Как найти площадь основания усеченной пирамиды?
A основание = a×b - Как найти площадь вершины усеченной пирамиды?
A top = c×d - Как найти площадь плоскости ac усеченной пирамиды? *
A ac = ½×(a+c)×slant a = ½×(a+c)×√¼×(b−d)²+h² - Как найти площадь плоскости бд усеченной пирамиды? *
A bd = ½×(b+d)×slant b = ½×(b+d)×√¼×(a−c)²+h² - Как найти боковую площадь поверхности усеченной пирамиды? *
A боковой = 2×A ac +2×A bd = (a+c)×наклон a +(b d)×наклон )×√¼×(b−d)²+h²+(b+d)×√¼×(a−c)²+h² - Как найти полную площадь поверхности усеченной пирамиды? *
A Всего = A BASE +A TOP +A Lateal = A × B +C × D +2 × A AC +2 × A BD = 2 × A BD AC +2 × A BD AC +2 × A BD AC +2 × A BD AC +2 × A BD AC +2 × A BD AC +2 × A BD AC +2 × A +c×d+(a+c)×наклон a +(b+d)×наклон b = a×b+c×d+(a+c)×√¼×(b−d)²+h² +(b+d)×√¼×(a−c)²+h² - Как найти периметр основания усеченной пирамиды?
p основание = 2×(a+b) - Как найти периметр вершины усеченной пирамиды?
p вершина = 2×(c+d) - Как найти длину наклона a усеченной пирамиды? +h²
- Как найти длину наклона b усеченной пирамиды?*
наклон b = √¼×(a−c)²+h² - Как найти длину ребра усеченной пирамиды?*
e = √¼×(a−c)²+slant(a) ² = √¼×((a−c)²+(b−d)²)+h² - где:
наклон a — расстояние между сторонами пирамиды a и c;
наклон b — расстояние между сторонами пирамиды b и d.
- [ * ] обозначает расчеты, действительные только для прямоугольных усеченных пирамид.
- , как нахожу на поисках VOMUTADATED TRA -TRA -TRA -TRA -TRA -TRA -TRA -TRA?
- Ссылка (ID: N/A)
- 1. И.Н. Бронштейн, К.А. Семендяев, Герхард Мусиол, Хайнер Мюлиг. Справочник по математике 6-е изд. Спрингер. Берлин, Гейдельберг, Нью-Йорк. 2015. Последний доступ: 29 августа 2020 г. (платная ссылка amazon.com).
Пищевые продукты, питательные вещества и калории
ЯДРА ПОПКОРНА, UPC: 051933345089 весят 203 грамма на метрическую чашку или 6,8 унций на чашку в США и содержат 361 калорию на 100 граммов (≈3,53 унции) вес к объему | объем к весу | цена | плотность ]
10787 продукты, содержащие витамин D . Список этих продуктов, начиная с самого высокого содержания витамина D и с самым низким содержанием витамина D, и рекомендуемых пищевых норм (RDA) для витамина D
Гравий, вещества и масла
CaribSea, Freshwater, Super Naturals, Zen Garden весит 1 473,7 кг/м³ (92,00009 фунтов/фут³) с удельным весом 1,4737 относительно чистой воды.
 Подсчитайте, сколько этого гравия требуется для достижения определенной глубины в цилиндрическом, четвертьцилиндрическом или прямоугольном аквариуме или пруду [вес к объему | объем к весу | цена ]
Подсчитайте, сколько этого гравия требуется для достижения определенной глубины в цилиндрическом, четвертьцилиндрическом или прямоугольном аквариуме или пруду [вес к объему | объем к весу | цена ]Динитрат никеля гексагидрат [Ni(NO 3 ) 2 ⋅ 6H 2 O] весит 2 050 кг/м³ (127,97732 фунта/фут³) [ вес к объему | объем к весу | цена | моль к объему и весу | масса и молярная концентрация | плотность ]
Преобразование объема в вес, веса в объем и стоимости для Масло Lesquerella с температурой в диапазоне от 23,9°C (75,02°F) до 110°C (230°F)
Веса и измерения
A световой год на час в квадрате — это единица измерения ускорения
Сила света – это световой поток, излучаемый источником света в определенном направлении в пределах телесного угла.
Таблица преобразования дедвейта/мл в т/л, конвертер единиц дедвейта/мл в т/л или конвертация между всеми единицами измерения плотности.
Калькуляторы
Калькулятор стоимости электроэнергии в часах, днях, неделях, месяцах и годах
Площадь поверхности пирамиды – объяснение и примеры
Прежде чем мы начнем, давайте рассмотрим, что такое пирамида.
 В геометрии пирамида — это трехмерное тело, основанием которого является любой многоугольник, а боковыми гранями — треугольники.
В геометрии пирамида — это трехмерное тело, основанием которого является любой многоугольник, а боковыми гранями — треугольники.В пирамиде боковые грани (треугольники) сходятся в одной точке, называемой вершиной. Название пирамиды происходит от названия многоугольника, образующего ее основание. Например, квадратная пирамида, прямоугольная пирамида, треугольная пирамида, пятиугольная пирамида и т. д.
Площадь поверхности пирамиды равна сумме площадей боковых граней.
В этой статье мы обсудим как найти общую площадь поверхности и площадь боковой поверхности пирамиды .
Как найти площадь поверхности пирамиды?
Чтобы найти площадь поверхности пирамиды, вы должны получить площадь основания, а затем добавить площадь боковых сторон, которая равна одной грани, умноженной на количество сторон.
Формула поверхности пирамиды
Общая формула площади поверхности любой пирамиды (правильной или неправильной) задается следующим образом:
Площадь поверхности = Площадь основания + Площадь боковой стороны
Площадь поверхности = B + LSA
Где TSA = общая площадь поверхности
B = площадь основания
LSA = площадь боковой поверхности.

Для правильной пирамиды формула задается следующим образом:
Общая площадь поверхности правильной пирамиды = B + 1/2 ps
, где p = периметр основания, а s = высота наклона.
Примечание. Никогда не путайте наклонную высоту (s) и высоту (h) пирамиды. Перпендикулярное расстояние от вершины до основания пирамиды известно как высота (h), а расстояние по диагонали от вершины пирамиды до края основания известно как наклонная высота (s).
Площадь поверхности квадратной пирамиды
Для квадратной пирамиды общая площадь поверхности = b (b + 2s)
Где b = длина основания, а s = высота наклона
Площадь поверхности треугольной пирамиды
Площадь поверхности треугольной пирамиды = ½ b (a + 3s)
Где, a = длина апофемы пирамиды
b = длина основания
s = высота наклона
Площадь поверхности пятиугольной пирамиды
Полная площадь поверхности правильной пятиугольной пирамиды равна;
Площадь поверхности пятиугольной пирамиды = 5/2 b (a + s)
Где, a = длина апофемы основания
и b = длина стороны основания, s = высота наклона пирамиды
Площадь поверхности шестиугольной пирамиды
Шестиугольная пирамида — это пирамида с шестиугольником в основании.

Общая площадь поверхности шестиугольной пирамиды = 3b (a + s)
Площадь боковой поверхности пирамиды
Как было сказано ранее, площадь боковой поверхности пирамиды – это площадь боковых граней пирамиды. Так как все боковые грани пирамиды треугольники, то площадь боковой поверхности пирамиды равна половине произведения периметра основания пирамиды на высоту наклона.
Площадь боковой поверхности (LSA = 1/2 ps)
Где p = периметр основания, а s = наклонная высота.
Давайте получим представление о площади поверхности формулы пирамиды, решив несколько примеров задач.
Пример 1
Какова площадь поверхности квадратной пирамиды, длина основания которой 4 см, а высота наклона 5 см?
Раствор
Дано:
Длина основания, b = 4 см
Наклонная высота, s =5 см
По формуле,
Общая площадь поверхности квадратной пирамиды = b (b + 2s)
TSA = 4(4 + 2 x 5)
= 4(4 + Пример 2
Решение
Дано;
Перпендикулярная высота, h = 8 м
Длина основания, b =12
Чтобы получить наклонную высоту s, применим теорему Пифагора.

S = √ [8 2 + (12/2) 2 ]
S = √ [8 2 + 6 2 ]
S = √ (64 + 36)
S =
S = √ (64 + 36)
S =
S = √ (64 + 36) √100
= 10
Следовательно, наклонная высота пирамиды равна 10 м
Теперь вычислите площадь поверхности пирамиды.
SA = b (b + 2s)
= 12 (12 + 2 x 10)
= 12 (12 + 20)
= 12 х 32
= 384 м 2 .
Пример 3
Вычислите площадь поверхности пирамиды, высота наклона которой равна 10 футов, а основание представляет собой равносторонний треугольник со стороной 8 футов. = 8 футов
Наклонная высота = 10 футов
Примените теорему Пифагора, чтобы получить длину апофемы пирамиды.
а = √ [8 2 – (8/2) 2 ]
= √ (64 – 16)
= √48
a = 6,93 фута
Таким образом, длина апофемы пирамиды равна 6,93 фута.
= площадь поверхности треугольника ½ B (A + 3S)
TSA = ½ x 8 (6,93 + 3 x 10)
= 4 (6,93 + 30)
= 4 x 36,93
= 147,72 FT 2
Пример 4.

Найдите площадь поверхности пятиугольной пирамиды, у которой длина апофемы 8 м, длина основания 6 м, а высота наклона 20 м.
Решение
Дано;
Длина апофемы, a = 8 м
Длина основания, b = 6 м
Наклонная высота, s = 20 м
Площадь поверхности пятиугольной пирамиды = 5/2 b (a + s)
TSA = 5 /2 x 6(8 + 20)
= 15 x 28
= 420 м 2 .
Пример 5
Рассчитайте общую площадь поверхности и площадь боковой поверхности шестиугольной пирамиды с апофемой 20 м, длиной основания 18 м и наклонной высотой 35 м.
Решение
Дано;
Апофема, a = 20 м
Длина основания, b = 18 м
Наклонная высота, s = 35 м
Площадь поверхности шестиугольной пирамиды = 3b (a + s)
= 3 x 1108 20 + 35)
= 54 х 55
= 2970 м 2 .
Площадь боковой поверхности пирамиды =1/2 ps
Периметр, p = 6 x 18
= 108 м
LSA = ½ x 108 x 35
= 1890 м 2
youtube.com/embed/vCf2yK4tzkk?rel=0;controls=0;showinfo=0;theme=light" frameborder="0" allowfullscreen="allowfullscreen">Правильная треугольная пирамида - Калькулятор геометрии
Геометрия | Формы | Контакты и конфиденциальность Геометрические калькуляторы Немецкий: Geometriechner, Formen 1DЛиния, дуга окружности, парабола, спираль, кривая Коха 2D Правильные многоугольники:
Равносторонний треугольник, квадрат, пятиугольник, шестиугольник, семиугольник, восьмиугольник, многоугольник, десятиугольник, десятиугольник, додекагон, шестиугольник, N-угольник, кольцо многоугольникаДругие многоугольники:
Треугольник, прямоугольный треугольник, равнобедренный треугольник, ИК-треугольник, четырехугольник, прямоугольник, золотой прямоугольник, ромб, параллелограмм, полуквадрат, прямой змей, воздушный змей, правильная трапеция, равнобедренная трапеция, трехравносторонняя трапеция, трапеция , Тупоугольная трапеция, Циклический четырехугольник, Касательный четырехугольник, Острие стрелки, Вогнутый четырехугольник, Перекрещенный прямоугольник, Антипараллелограмм, Форма дома, Симметричный пятиугольник, Восьмиугольник, разделенный пополам по диагонали, Вырезанный прямоугольник, Вогнутый пятиугольник, Вогнутый правильный пятиугольник, Вытянутый пятиугольник, Прямой восьмиугольник, разделенный пополам, Вытянутый шестиугольник , симметричный шестиугольник, параллелогон, вогнутый шестиугольник, шестиугольник со стрелкой, прямоугольный шестиугольник, L-образная форма, острый излом, Т-образная форма, усеченный квадрат, вытянутый восьмиугольник, рамка, открытая рамка, сетка, крест, X-образная форма, H-образная форма, Threestar, Fourstar, Pentagram, Hexagram, Unicursal Hexagram, Oktagram, Star of Lakshmi, Double Star Polygon, Polygram, PolygonКруглые формы:
3Д Platonic Solids:
Круг, Полукруг, Круглый сектор, Круглый сегмент, Круглый слой, Круглый центральный сегмент, Круглый угол, Круглый угол, Круговая касательная стрелка, Форма капли, Полумесяц, Заостренный овал, Два круга, Стрельчатая арка, Холм , Кольцо, Сектор кольца, Изогнутый прямоугольник, Скругленный многоугольник, Скругленный прямоугольник, Эллипс, Полуэллипс, Эллиптический сегмент, Эллиптический сектор, Эллиптическое кольцо, Стадион, Спираль, Бревно. Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Спираль, треугольник Рело, циклоида, двойная циклоида, астроида, гипоциклоида, кардиоида, эпициклоида, параболический сегмент, сердце, треугольник, междуговой треугольник, круговой треугольник, междуговой четырехугольник, межокружной четырехугольник, круговой четырехугольник, дуговой многоугольник, коготь, полуинь -Ян, Арбелос, Салинон, Выпуклость, Луна, Три круга, Многоугольник, Круглый многоугольник, Роза, Шестерня, Овал, Яйцо-профиль, Лемниската, Сквиркл, Круглый квадрат, Дигон, Сферический треугольник
Tetrahedron, Cube, Octahedron, Dodecahedron, IcosahedronArchimedean Solids:
Truncated Tetrahedron, Cuboctahedron, Truncated Cube, Truncated Octahedron, Rhombicuboctahedron, Truncated Cuboctahedron, Icosidodecahedron, Truncated Dodecahedron, Truncated Icosahedron, Snub Cube, Rhombicosidodecahedron , Truncated Icosidodecahedron, Snub DodecahedronCatalan Solids:
Triakis Tetrahedron, Rhombic Dodecahedron, Triakis Octahedron, Tetrakis Hexahedron, Deltoidal Icositetrahedron, Hexakis Octahedron, Rhombic Triacontahedron, Triakis Icosahedron, Pentakis Dodecahedron, Pentagonal Icositetrahedron, Deltoidal Hexecontahedron, Hexakis Icosahedron, Пятиугольный шестигранникJohnson Solid:
пирамиды, Cupolae, ротонда, удлиненные пирамиды, гиросельные пирамиды, бипирамиды, удлиненные бипирамиды, дипирамиды 96060, дискоировая дипирамида, ах -дипирамиды, громфен -дипирамид, гиробифастиджий, дискенфен -дипирамид. Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдр
Столб, Треугольная Пирамида, Квадратная Пирамида, Правильная Пирамида, Пирамида, Квадратная Усеченная, Правильная Усеченная, Усеченная, Изогнутая Пирамида, Правильная Бипирамида, Бипирамида, Двуусеченная, Усеченная-Пирамида, Пандус, Прямой Клин, Клин, Половина Тетраэдра, Ромбоэдр, Параллелепипед, Правильный Призма, призма, косая призма, антикуб, антипризма, призматоид, трапецоэдр, дисфеноид, угол, общий тетраэдр, клиновидный куб, полукубовид, косой кубоид, слиток, наклонная трехгранная призма, кубовид с вырезом, усеченный кубоид, кубовид с тупыми краями, Удлиненный додекаэдр, усеченный ромбоэдр, обелиск, изогнутый куб, полый куб, полая пирамида, полая усеченная пирамида, звездчатая пирамида, звездчатый октаэдр, Sma ll Звёздчатый додекаэдр, Большой звёздчатый додекаэдр, Большой додекаэдр, Большой икосаэдрКруглые формы:
4Д Тессеракт, Гиперсфера
Сфера, полусфера, сферический угол, цилиндр, срезанный цилиндр, косой цилиндр, изогнутый цилиндр, эллиптический цилиндр, обобщенный цилиндр, конус, усеченный конус, наклонный круговой конус, эллиптический конус, усеченный эллиптический конус, общий конус , Общий усеченный конус, двояконус, усеченный двояконус, заостренный столб, закругленный конус, капля, сфероид, эллипсоид, полуэллипсоид, сферический сектор, сферическая крышка, сферический сегмент, сферический центральный сегмент, двойной калот, сферический клин, полуцилиндр, диагонально разделенный пополам Цилиндр, Цилиндрический клин, Цилиндрический сектор, Цилиндрический сегмент, Цилиндр с плоским концом, Полуконус, Конический сектор, Конический клин, Сферическая оболочка, Полусферическая оболочка, Цилиндрическая оболочка, Вырезанная цилиндрическая оболочка, Наклонная цилиндрическая оболочка, Полый конус, Усеченный полый конус, Сферический Кольцо, тор, тор веретена, тороид, сектор тора, сектор тора, арка, тетраэдр Рело, капсула, сегмент капсулы, двойная точка, антиконус, усеченный антиконус, Sphe повторный цилиндр, линза, вогнутая линза, бочонок, форма яйца, параболоид, гиперболоид, олоид, тела Штейнмеца, тело вращенияAnzeige
Вычисления на правильной треугольной пирамиде.


 Найдите соответствие между словосочетаниями в колонках А
Найдите соответствие между словосочетаниями в колонках А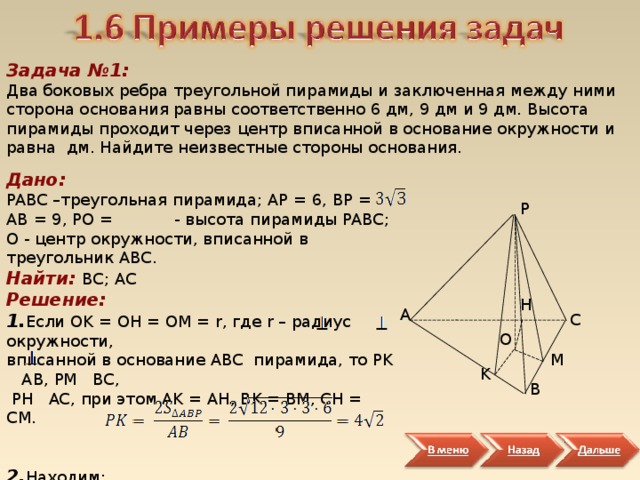 12.17
12.17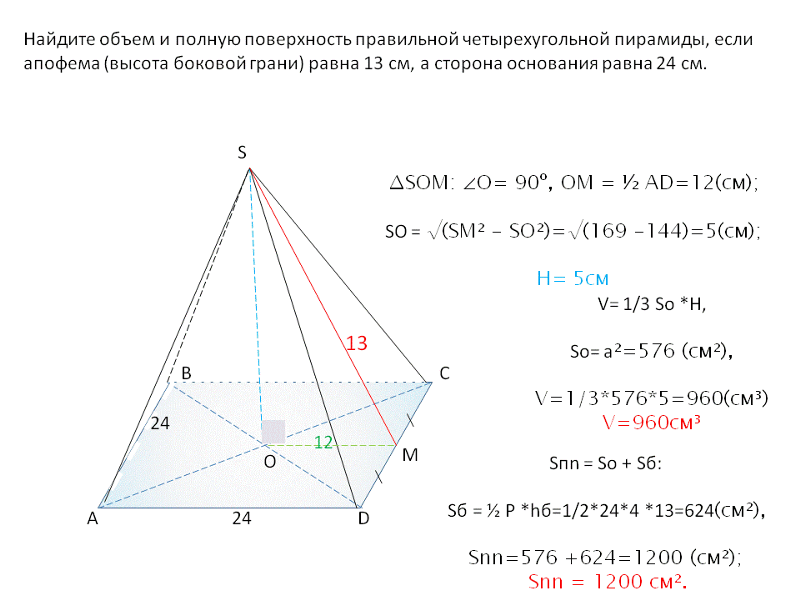
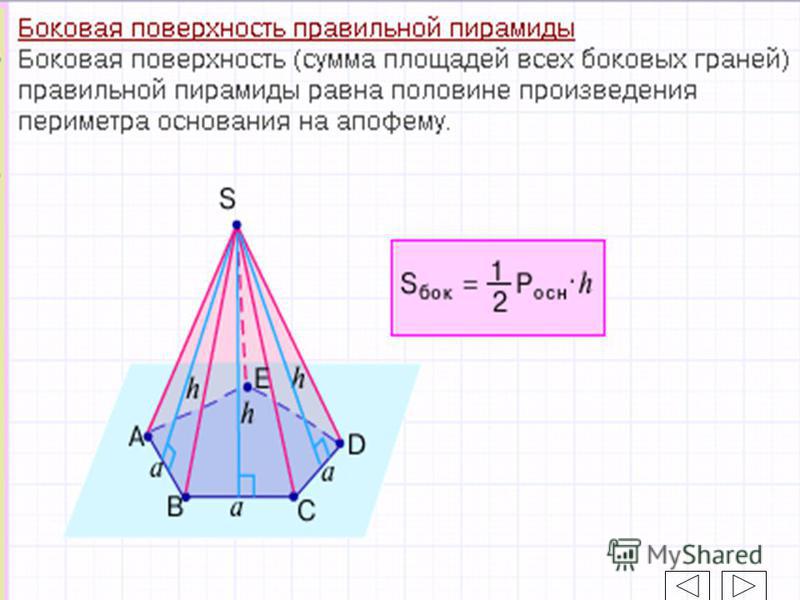 АВС; SО = h.
АВС; SО = h.
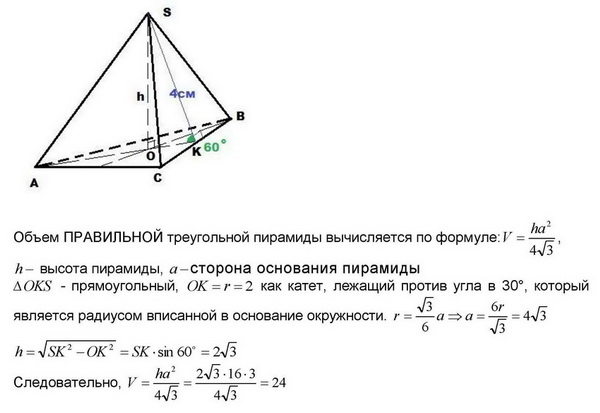
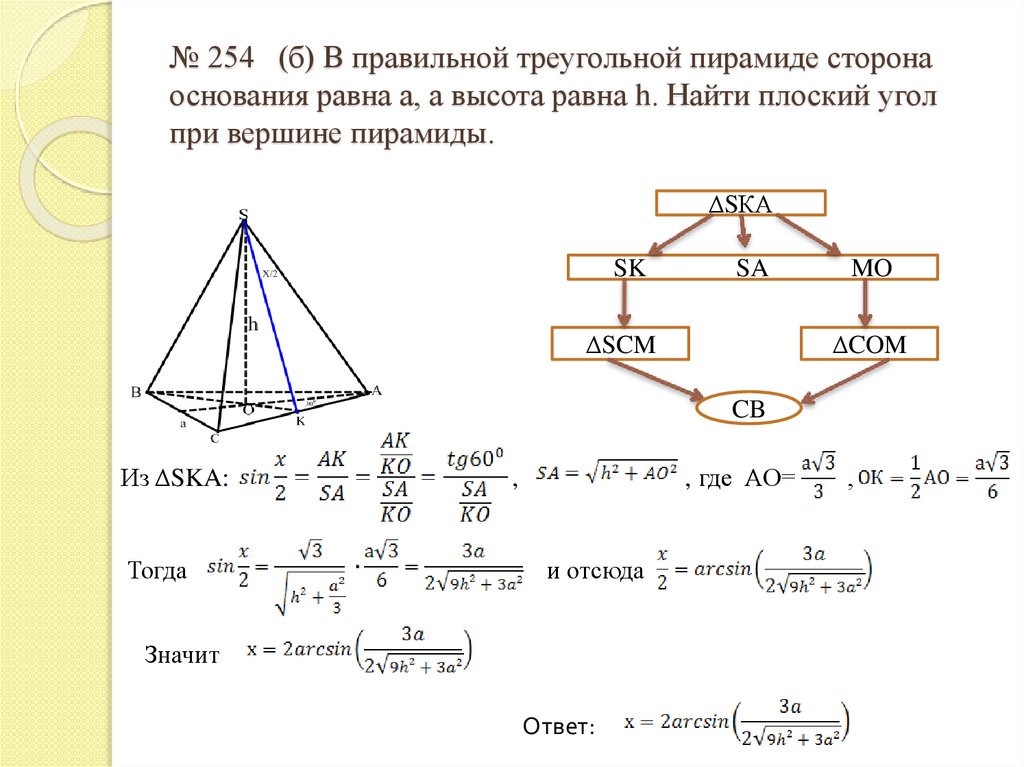
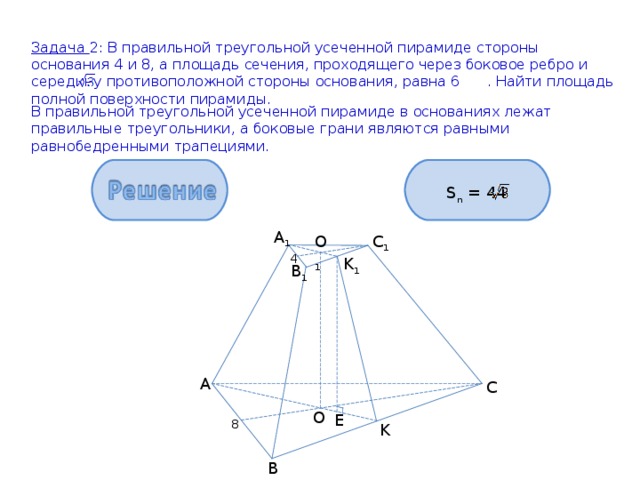 Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.
Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим. Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований.
Две его стороны − образующие цилиндра, а две другие − параллельные хорды оснований. При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра.
При п→∞ периметр многоугольника, лежащего в основании призмы, будет стремиться к длине окружности основания цилиндра, площадь многоугольника, лежащего в основании призмы, будет стремиться к площади круга, являющегося основанием цилиндра. Объём п-угольной прямой призмы будет стремиться к объёму прямого кругового цилиндра. Найти высоту цилиндра.
Найти высоту цилиндра. Усечённая пирамида.
Усечённая пирамида.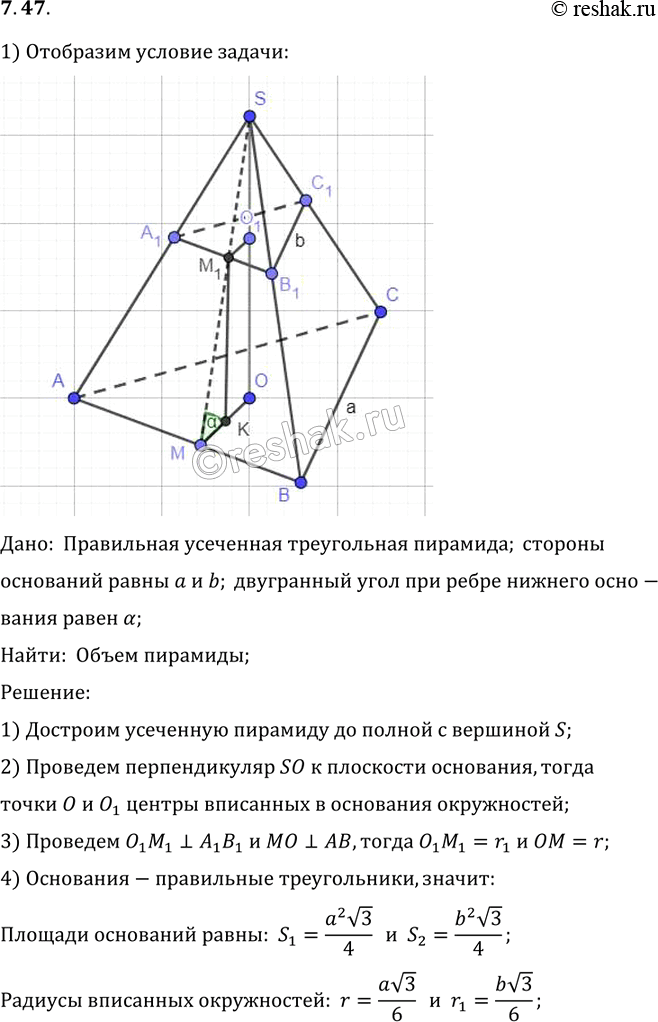 , а другой называется усечённой пирамидой.
, а другой называется усечённой пирамидой.



 Д.п. СМ┴АВ, С1М1┴ А1В1→ М1М┴ АВ и
Д.п. СМ┴АВ, С1М1┴ А1В1→ М1М┴ АВ и
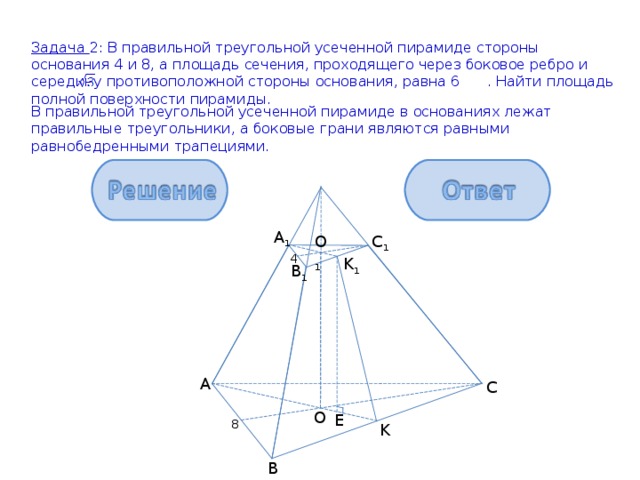 Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, что
Проведем ось ох (ОМ2— высота), рассмотрим сечение А1В1С1пирамиды плоскостью, перпендикулярной к оси ох и, значит, параллельной плоскости основания. Обозначим через х абсциссу точки М1пересечения этой плоскости с осью ох, а через S{x) — площадь сечения. Выразим S(x) через S, h и х . Заметим, что