Задача Коши. Общее и частное решения
При
решении многих задач требуется найти
не все решения уравнения (1.3), а только
такое, которое принимает заданное
значение при заданном значении независимой
переменной, а именно, требуется найти
решение 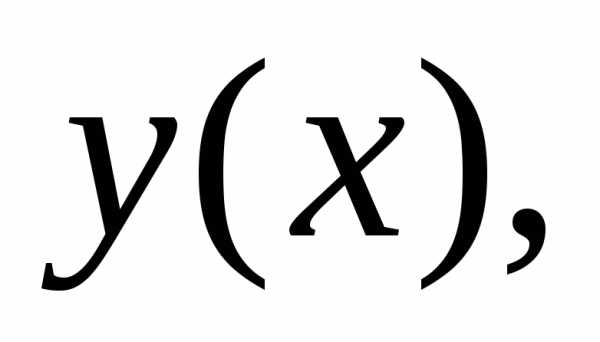 удовлетворяющее условию
удовлетворяющее условию
(1.4)
где 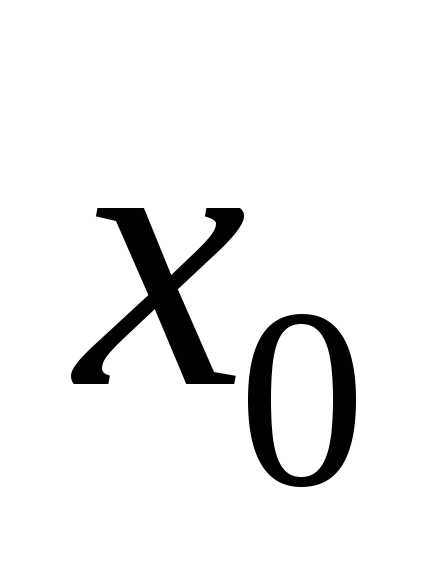 и
и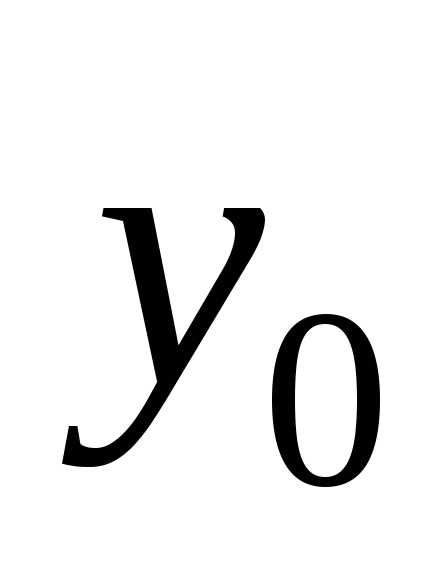 любые числа, для которых определена
функция
любые числа, для которых определена
функция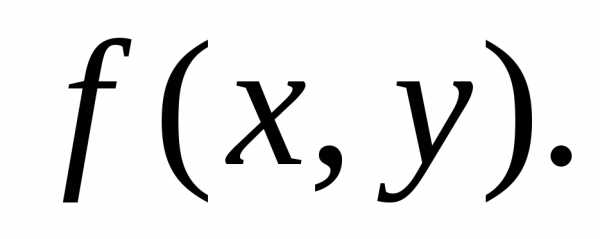 Условие (1.4) называютначальным
условием,
числа
Условие (1.4) называютначальным
условием,
числа 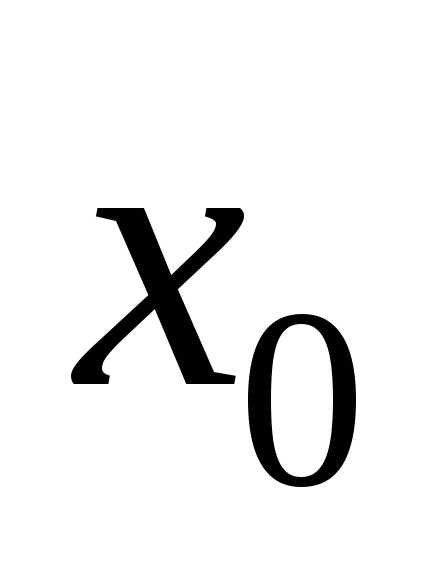 и
и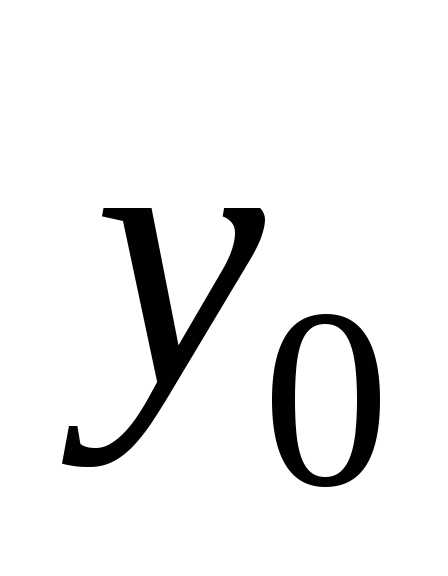 —начальными
значениями решения уравнения (1.3), а саму задачу — задачей Коши
—начальными
значениями решения уравнения (1.3), а саму задачу — задачей Коши
На вопрос о существовании и единственности решения задачи Коши отвечает следующая теорема, которую мы приводим без доказательства и в упрощенной формулировке.
Теорема
1.1. Если в
уравнении
функция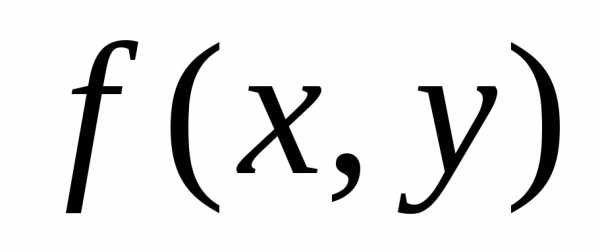 и ее частная производная
и ее частная производная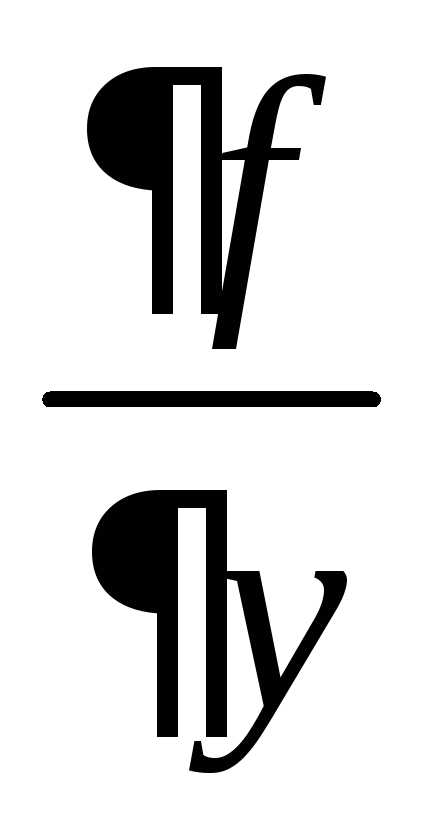 непрерывны в некоторой области
непрерывны в некоторой области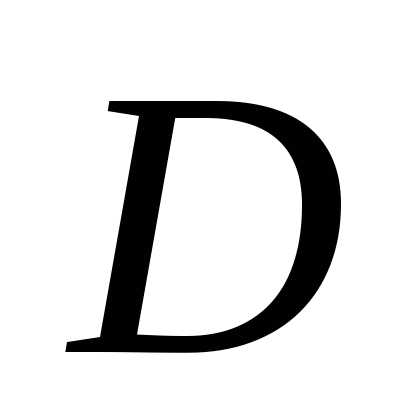 на плоскости
на плоскости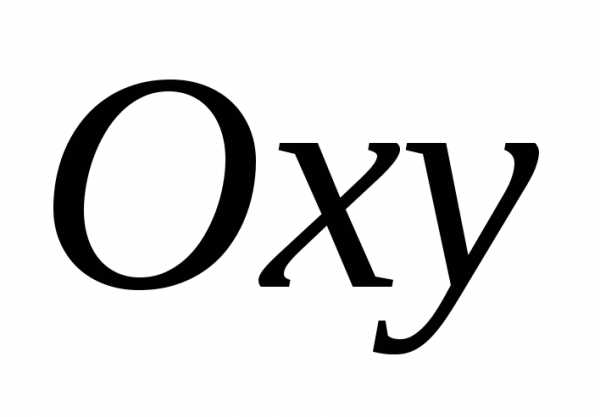 ,
то какова бы ни была точка
,
то какова бы ни была точка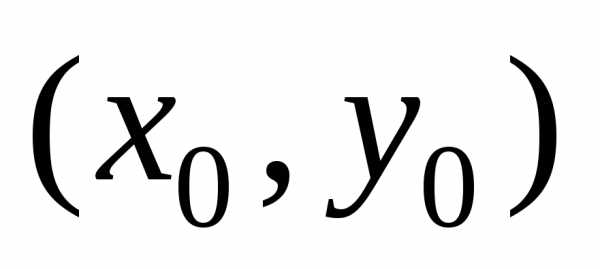 области
области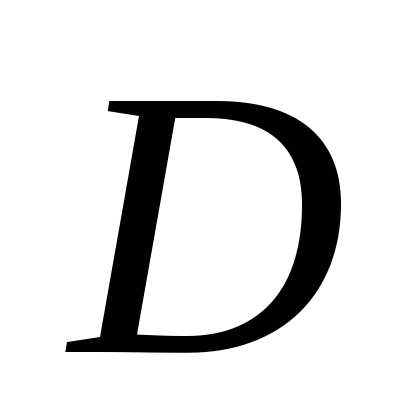 ,
существует единственное решение
,
существует единственное решение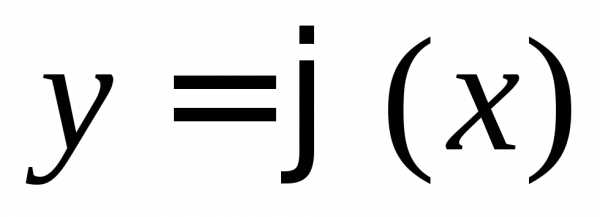 уравнения (1.3), определенное в некотором
интервале, содержащем точку
уравнения (1.3), определенное в некотором
интервале, содержащем точку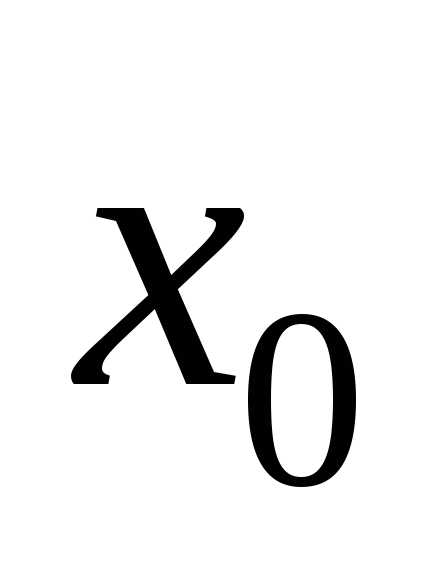
В
частности, если два решения 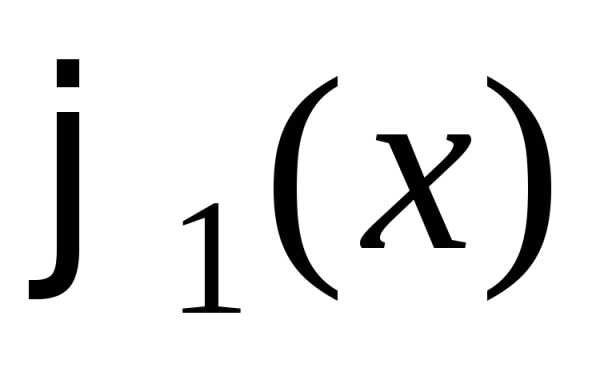 и
и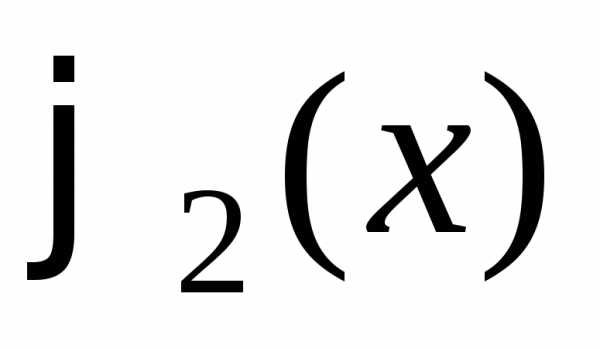 уравнения (1.3) совпадают хотя бы для
одного значения
уравнения (1.3) совпадают хотя бы для
одного значения ,
то эти решения тождественно равны для
всех тех значений
,
то эти решения тождественно равны для
всех тех значений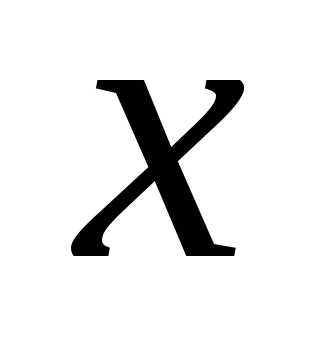 ,
для которых они оба определены.
,
для которых они оба определены.
Геометрический
смысл этой теоремы состоит в том, что
через каждую точку 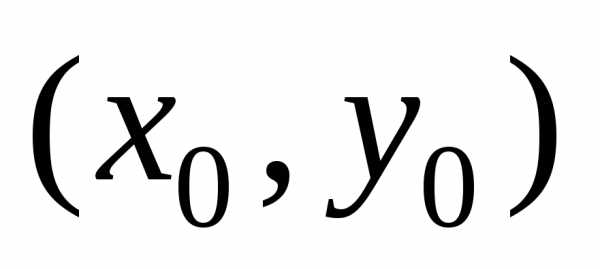 области
области проходит одна и только одна интегральная
кривая уравнения (1.3) или, другими словами,
вся область
проходит одна и только одна интегральная
кривая уравнения (1.3) или, другими словами,
вся область покрыта интегральными кривыми уравнения
(1.3), которые нигде не пересекаются между
собой.
покрыта интегральными кривыми уравнения
(1.3), которые нигде не пересекаются между
собой.
Общее,
частное и особое решения.
Если закрепить начальное значение
абсциссы 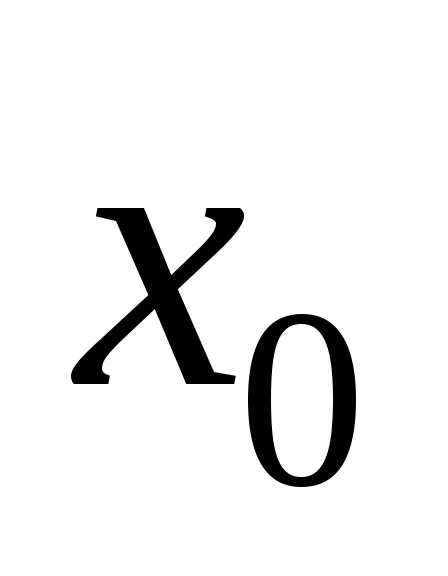 ,
а начальному значению
,
а начальному значению придавать различные допустимые значениято каждому такому значению будет
соответствовать единственная интегральная
кривая (рис. 1.1) и, следовательно, в области
придавать различные допустимые значениято каждому такому значению будет
соответствовать единственная интегральная
кривая (рис. 1.1) и, следовательно, в области множество всех интегральных кривых
образует семейство кривых, зависящих
от одного параметра, который может
изменяться в определенных пределах и
который принято обозначать через
множество всех интегральных кривых
образует семейство кривых, зависящих
от одного параметра, который может
изменяться в определенных пределах и
который принято обозначать через ,
так что все семейство интегральных
кривых может быть описано уравнением
,
так что все семейство интегральных
кривых может быть описано уравнением
Определение. Функция
(1.5)
непрерывно
дифференцируемая по 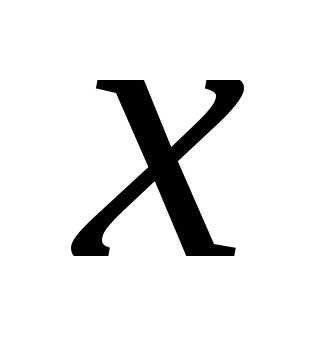
 ,
если она удовлетворяет следующим двум
условиям:
,
если она удовлетворяет следующим двум
условиям: 1)
равенство (1.5) разрешимо в области  относительно произвольной постоянной
относительно произвольной постоянной
(1.6)
2)
функция 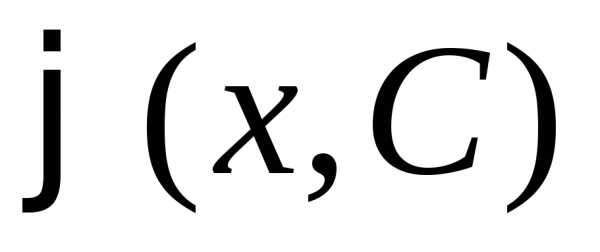 является решением уравнения (1.3) для
всякого значения постоянной
является решением уравнения (1.3) для
всякого значения постоянной ,
полученной из формулы (1.6), в которой
точка
,
полученной из формулы (1.6), в которой
точка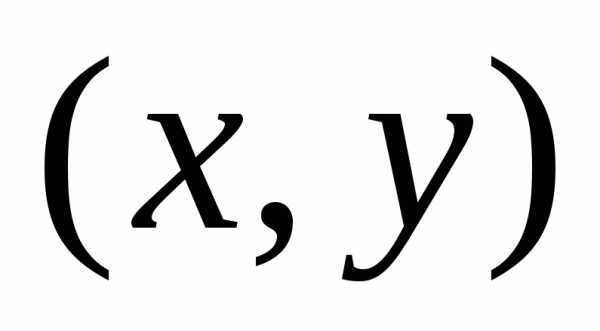 — любая точка из области
— любая точка из области .
.
Естественно,
что знание общего решения (1.5) дает
возможность решить задачу Коши для
любых начальных значений 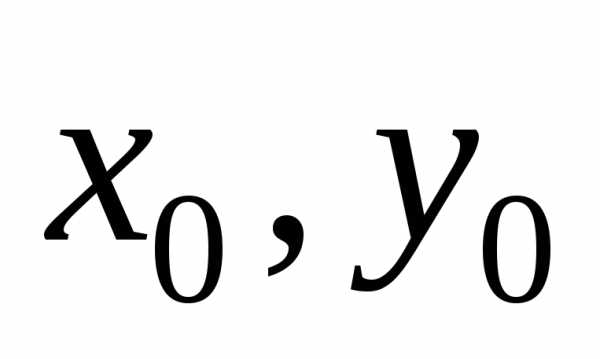
 .
Для этого достаточно заменить в формуле
(1.5) переменные
.
Для этого достаточно заменить в формуле
(1.5) переменные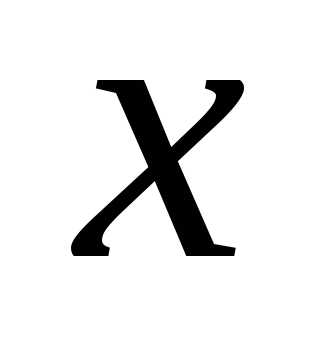 и
и числами
числами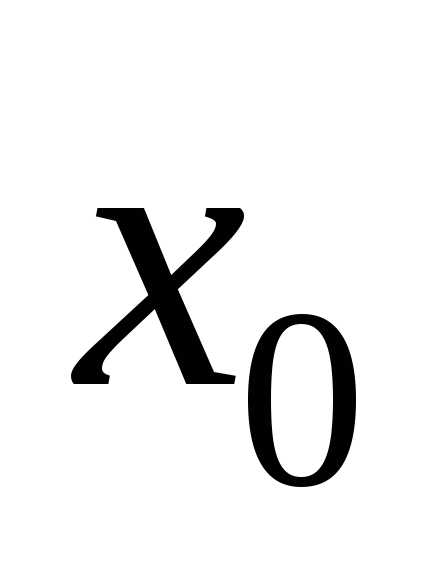 и
и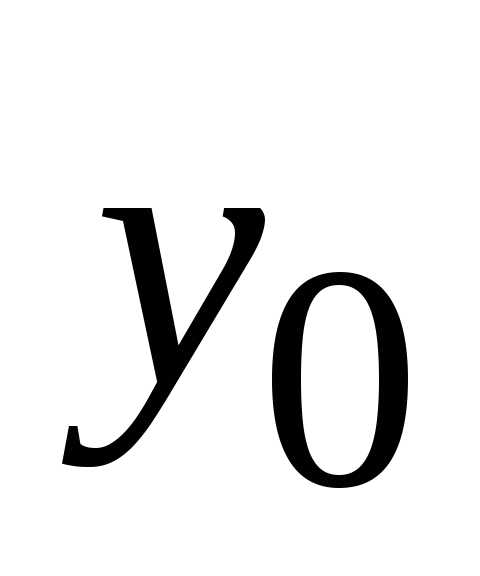 ,
решить полученное уравнениеотносительно
,
решить полученное уравнениеотносительно ,
т.е. получить соотношениеи подставить найденное значение в общее
решение (1.5). Полученная функцияи есть искомое решение. Общее решение
уравнения (1.3), записанное в виде, не
разрешенном относительно искомой
функции, т.е. в виде
,
т.е. получить соотношениеи подставить найденное значение в общее
решение (1.5). Полученная функцияи есть искомое решение. Общее решение
уравнения (1.3), записанное в виде, не
разрешенном относительно искомой
функции, т.е. в видеили ,
называют общим интегралом этого уравнения.
Решение,
которое получается из общего решения
если в последнем произвольной постоянной
Решение, которое не может быть получено из общего решения (общего интеграла) ни при каком конкретном значении произвольной постоянной, называется особым решением. Геометрически особому решению соответствует интегральная кривая, не содержащаяся в семействе интегральных кривых, составляющих общее решение (общий интеграл). Особое решение примечательно тем, что через каждую точку изображающей его интегральной кривой проходит, по крайней мере, еще одна интегральная кривая того же уравнения, имеющая в этой точке ту же касательную.
Если
правая часть уравнения (1.3) удовлетворяет
в области  условиям теоремы 1.1, то это уравнение
не имеет в области
условиям теоремы 1.1, то это уравнение
не имеет в области
Пример 1.1. Рассмотрим уравнение
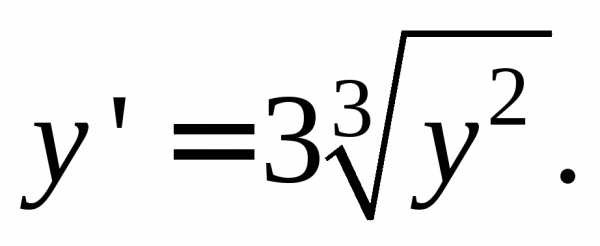 (1.7)
(1.7)
Так
как правая часть уравнения (1.7) и ее
частная производная
удовлетворяют условиям теоремы 1.1 во
всех точках плоскости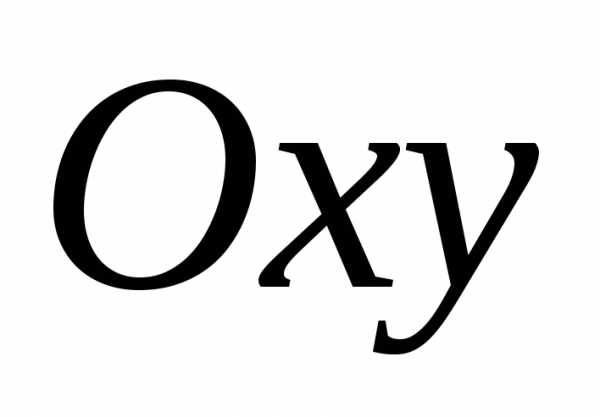 за исключением точек оси
за исключением точек оси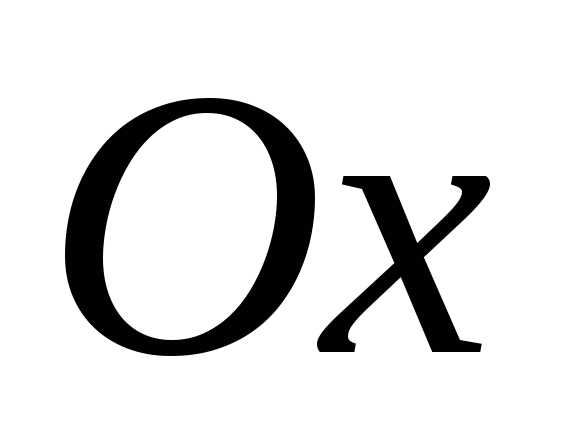 ,
то через любую точку
,
то через любую точку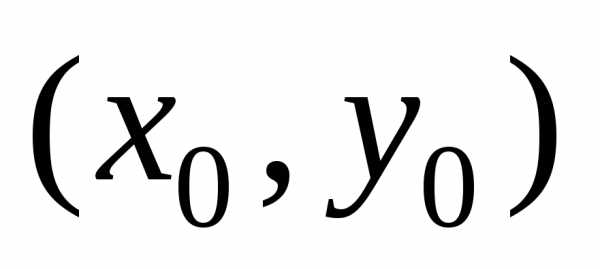 при
при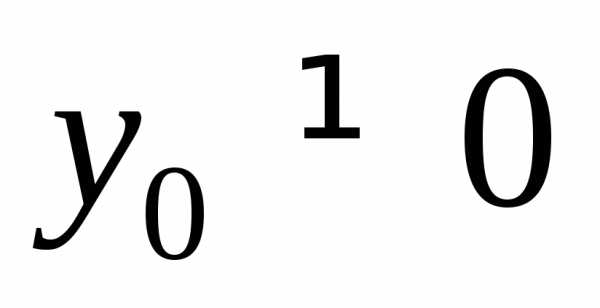 проходит единственная интегральная
кривая уравнения (1.7). Для отыскания
общего решения запишем уравнение (1.7) в
виде
проходит единственная интегральная
кривая уравнения (1.7). Для отыскания
общего решения запишем уравнение (1.7) в
виде
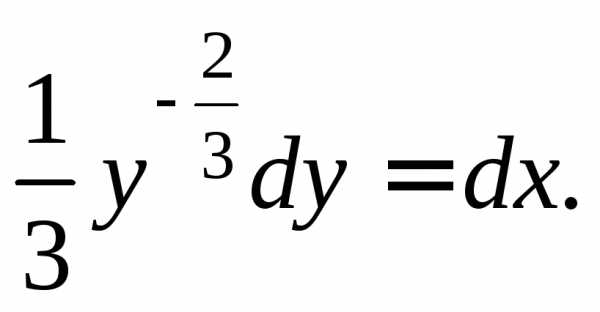
В
левой части равенства стоит дифференциал
функции 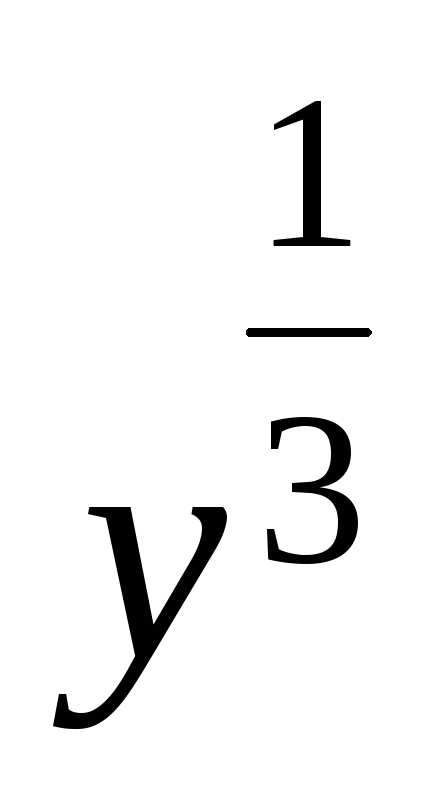 ,
а в правой — дифференциал функции
,
а в правой — дифференциал функции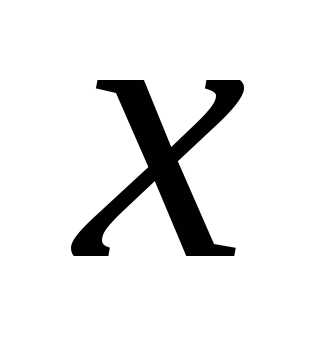
 ,
так что можем написать
,
так что можем написать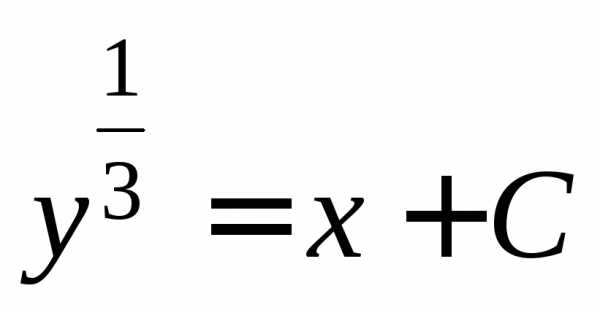 или в таком виде
или в таком виде(1.8)
Функция
(1.8) является общим решением уравнения
(1.7) всюду на плоскости 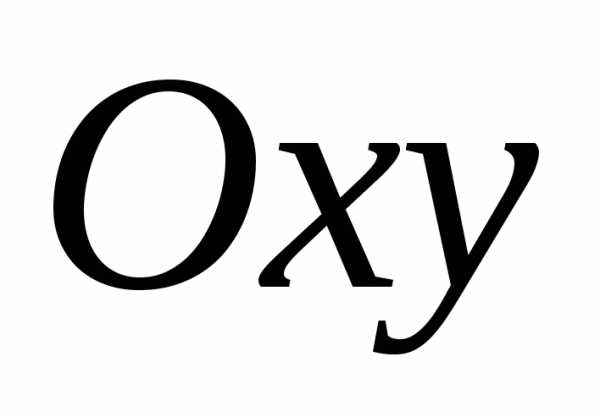 за исключением оси
за исключением оси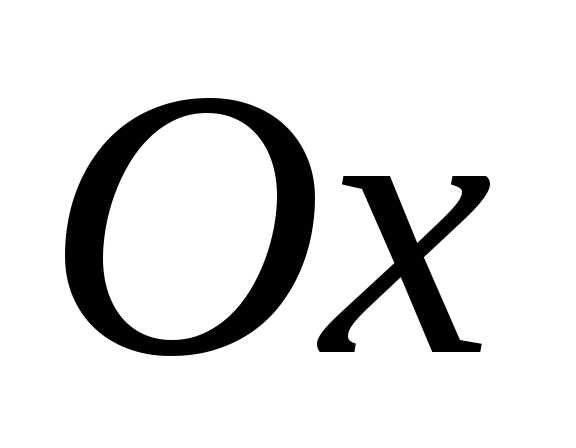 .
.
Непосредственно
видно, что, подставив функцию 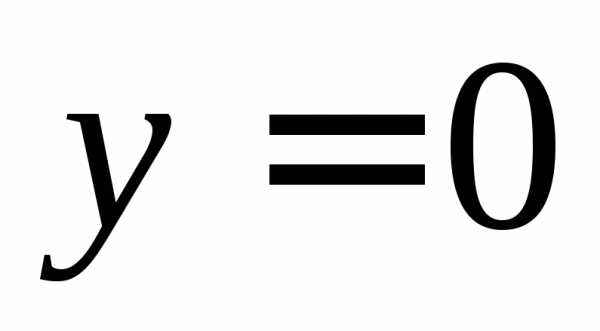 в уравнение (1.7), получим тождество, т.е.
в уравнение (1.7), получим тождество, т.е.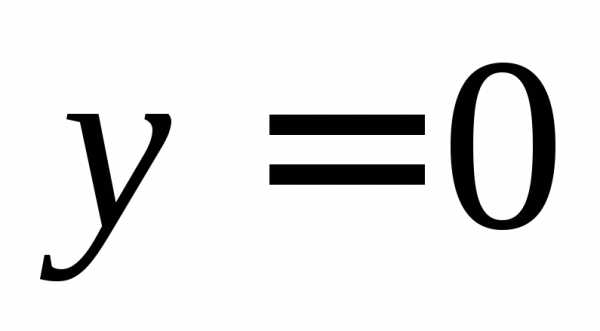 является решением данного уравнения,
притом особым решением, так как оно не
может быть получено из общего решенияни при каком значении постоянной
является решением данного уравнения,
притом особым решением, так как оно не
может быть получено из общего решенияни при каком значении постоянной
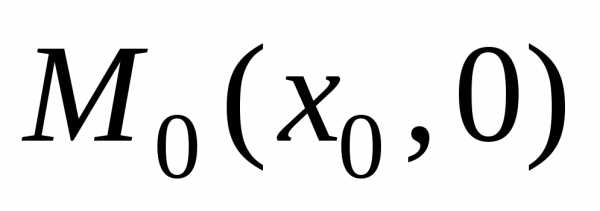 оси
оси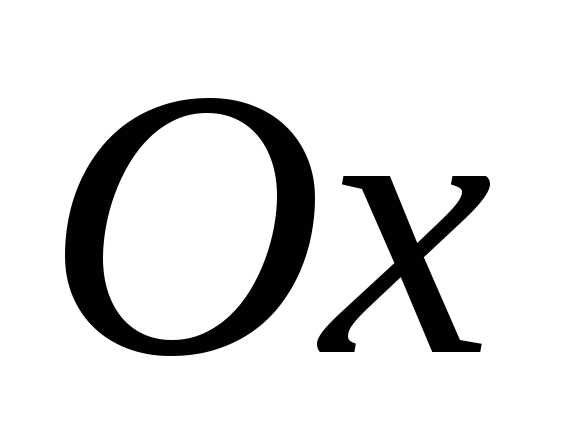 проходит криваясовпадающая при
проходит криваясовпадающая при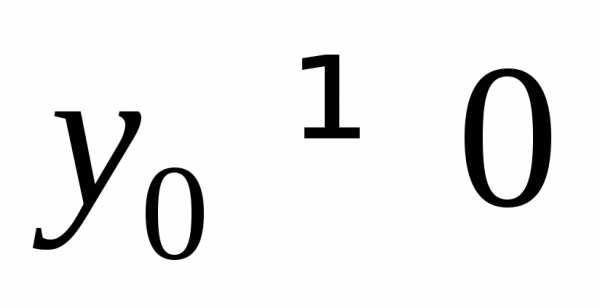 с общим решением (1.8) и касательной к
которой в этой точке является сама ось
с общим решением (1.8) и касательной к
которой в этой точке является сама ось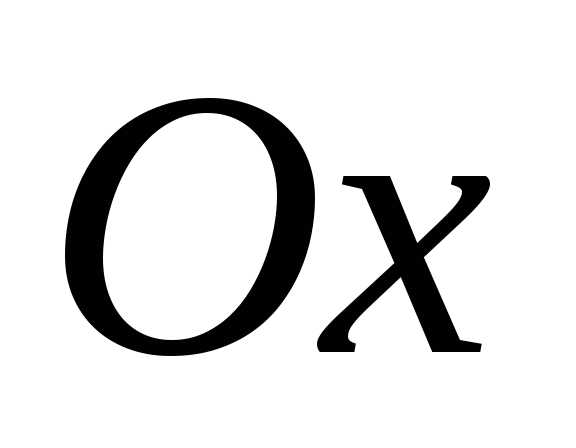 (рис. 1.2).
(рис. 1.2).В дальнейшем слова решить (проинтегрировать) дифференциальное уравнение будут означать одно из двух:
а) найти его общее решение (общий интеграл), если начальные условия не заданы;
б) найти частное решение (частный интеграл), удовлетворяющее заданным начальным условиям.
Далее будут рассмотрены типы дифференциальных уравнений первого порядка, интегрируемых в квадратурах, и указаны пути получения общего решения (общего интеграла).
studfiles.net
Задача Коши — Викиверситет
Определения[править]
Задача Коши, x0{\displaystyle x_{0}}, y0{\displaystyle y_{0}} — начальные данные:
- {dydx=f(x,y),(1)y(x0)=y0;(2) начальное условие{\displaystyle {\begin{cases}{\frac {dy}{dx}}=f(x,y),&{\text{(1)}}\\y(x_{0})=y_{0};&{\text{(2) начальное условие}}\end{cases}}}
Решением задачи Коши является функция, определённая на интервале <a,b>, включающем x0{\displaystyle x_{0}}, являющаяся решением уравнения (1) и удовлетворяющая начальному условию (2).
Определение. Решением интегрального уравнения:- y(x)=y0+∫x0xf(s,y(s))ds,(3){\displaystyle y(x)=y_{0}+\int _{x_{0}}^{x}f(s,y(s))ds,{\text{(3)}}}
является функция y=ϕ(x){\displaystyle y=\phi (x)}, которая определена на <a,b>∋x0{\displaystyle \ni x_{0}} и
- ϕ∈C<a,b>{\displaystyle \phi \in C<a,b>} (непрерывна)
ru.wikiversity.org
Лекция_11_ИЭТ 2011 Задача Коши
Методы вычислений. ИЭТ. 4-й семестр. Лекция 11. Стр. 7
МЕТОДЫ ВЫЧИСЛЕНИЙ
ИЭТ, 4-й семестр, 22
Лекция 11
Численные методы решения задачи Коши
для систем обыкновенных дифференциальных уравнений
Метод Эйлера, методы Рунге-Кутты. Многошаговые методы Адамса
Основные понятия
и обозначения. Обыкновенным
дифференциальным уравнением первого
порядка называется уравнение вида
,
где  — известная функция трех переменных,
определенная в области
— известная функция трех переменных,
определенная в области 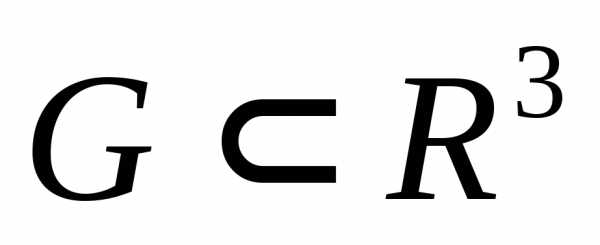 , x — независимая переменная,
, x — независимая переменная, 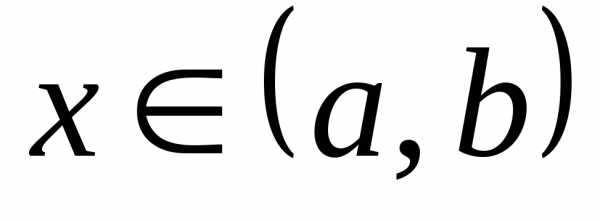 ,
, 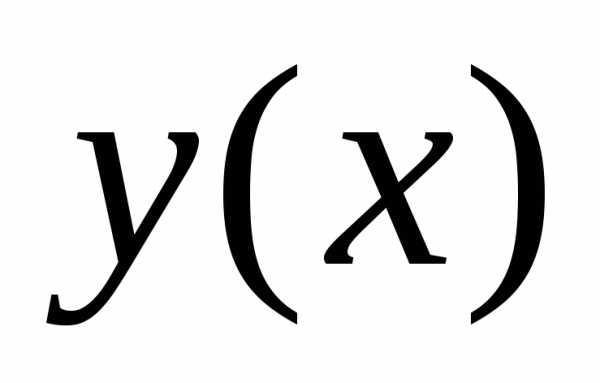 —
неизвестная функция,
—
неизвестная функция,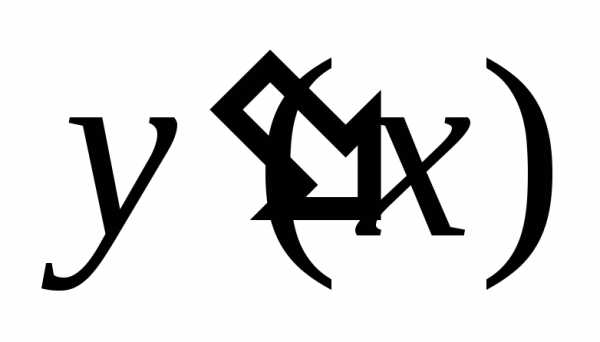 — ее производная. Функция
— ее производная. Функция 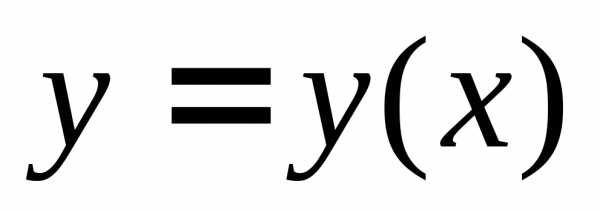 называется решением
дифференциального уравнения, если
она непрерывно дифференцируема на
называется решением
дифференциального уравнения, если
она непрерывно дифференцируема на 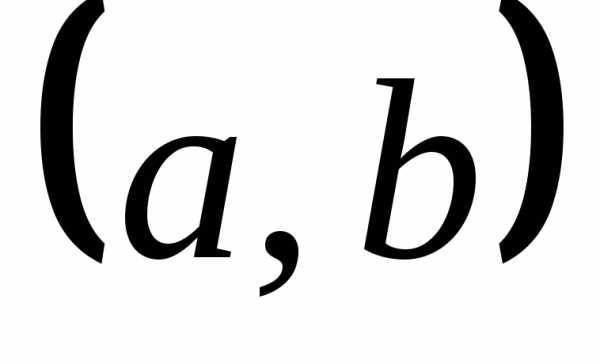 и при всех
и при всех 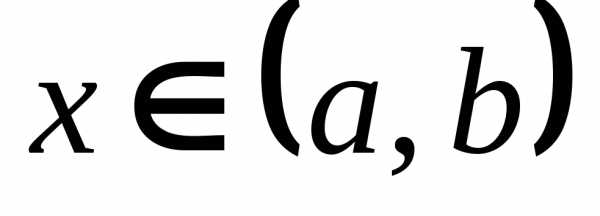 . График
решения дифференциального уравнения
называют интегральной
кривой дифференциального уравнения. В дальнейшем
будем рассматривать обыкновенные
дифференциальные уравнения в нормальной
форме, т.е.
уравнения, разрешенные относительно
производной.:.(1)
. График
решения дифференциального уравнения
называют интегральной
кривой дифференциального уравнения. В дальнейшем
будем рассматривать обыкновенные
дифференциальные уравнения в нормальной
форме, т.е.
уравнения, разрешенные относительно
производной.:.(1)
Если дифференциальное
уравнение первого порядка
, 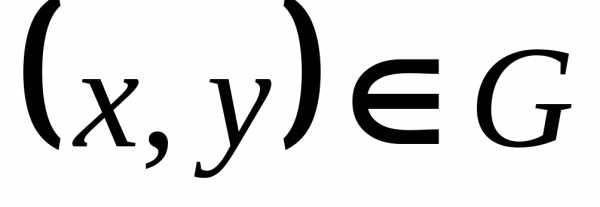 имеет в области
имеет в области  решение, то, вообще говоря, таких решений
бесконечно много, они могут быть заданы
в виде
,
где
решение, то, вообще говоря, таких решений
бесконечно много, они могут быть заданы
в виде
,
где  —
произвольная константа; и
.
Однако, если требуется найти решение,
удовлетворяющее начальному
условию ,
то при определенных условиях такая
задача имеет единственное решение.
Задача об отыскании решения дифференциального
уравнения, удовлетворяющего заданному
начальному условию, называется задачей
Коши. Начальные
условия для обыкновенных дифференциальных
уравнений называют условиями
Коши
—
произвольная константа; и
.
Однако, если требуется найти решение,
удовлетворяющее начальному
условию ,
то при определенных условиях такая
задача имеет единственное решение.
Задача об отыскании решения дифференциального
уравнения, удовлетворяющего заданному
начальному условию, называется задачей
Коши. Начальные
условия для обыкновенных дифференциальных
уравнений называют условиями
Коши
Справедлива следующая теорема существования и единственности
Теорема. Если
функция 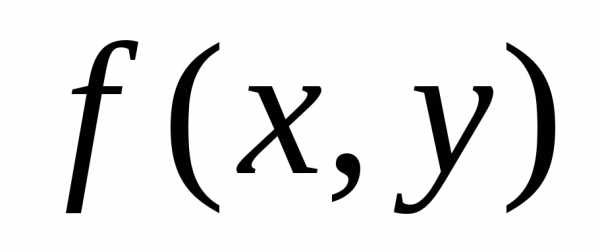 и ее частная производная
и ее частная производная 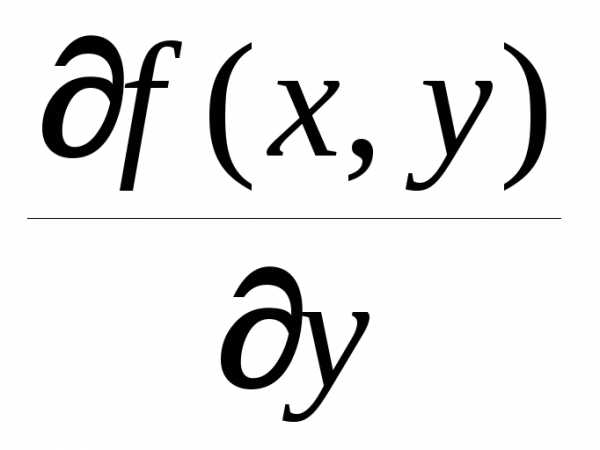 непрерывны в области
непрерывны в области  ,
,
то на некотором интервале существует единственное решение
уравнения
,
удовлетворяющее начальному условию
.
,
,
то на некотором интервале существует единственное решение
уравнения
,
удовлетворяющее начальному условию
.
Для дифференциального уравнения теорема существования и единственности имеет простую геометрическую интерпретацию: через каждую точку проходит только одна интегральная кривая семейства такая, что .
Обыкновенным
дифференциальным уравнением 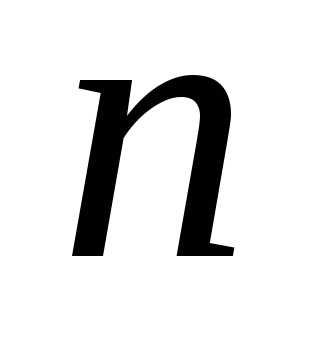 -го
порядка называется
уравнение вида
-го
порядка называется
уравнение вида
,
где 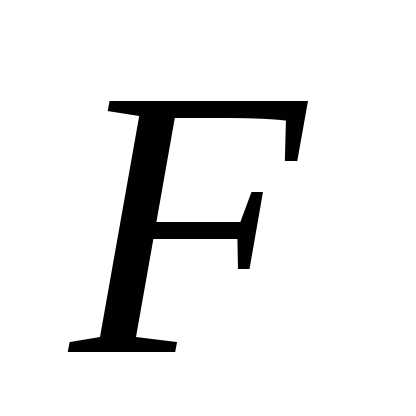 — известная функция
— известная функция 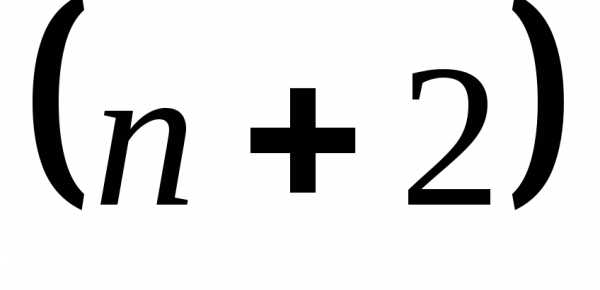 переменных, определенная в области
,
переменных, определенная в области
, 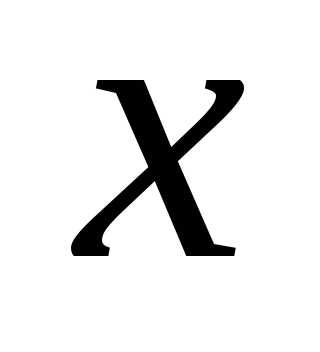 — независимая переменная
— независимая переменная 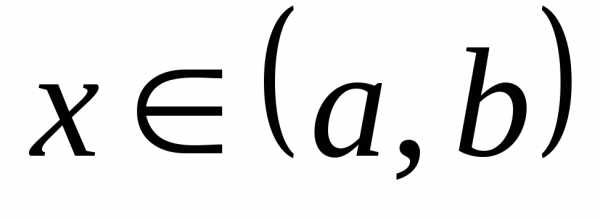 ,
, 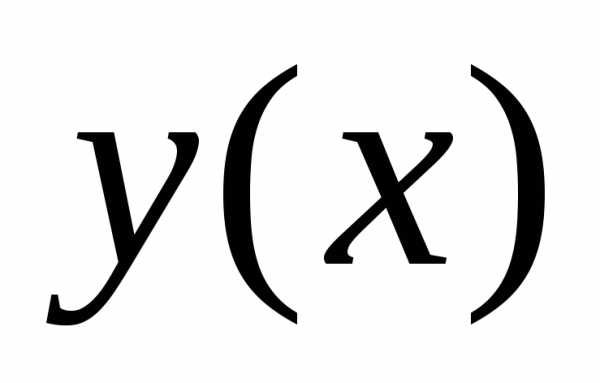 —
неизвестная функция,
—
неизвестная функция, 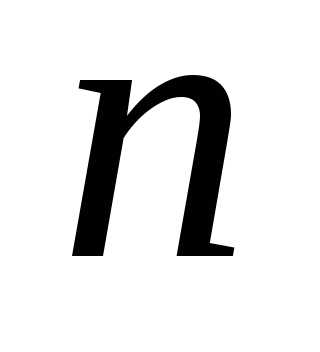 — порядок уравнения. Функция
— порядок уравнения. Функция 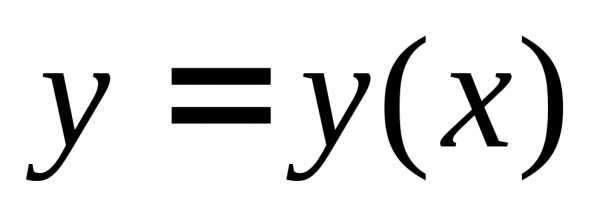 называется решением дифференциального
уравнения, если она
называется решением дифференциального
уравнения, если она 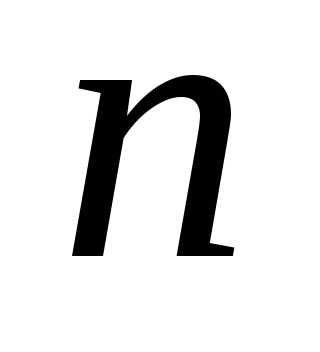 раз непрерывно
дифференцируема на
раз непрерывно
дифференцируема на 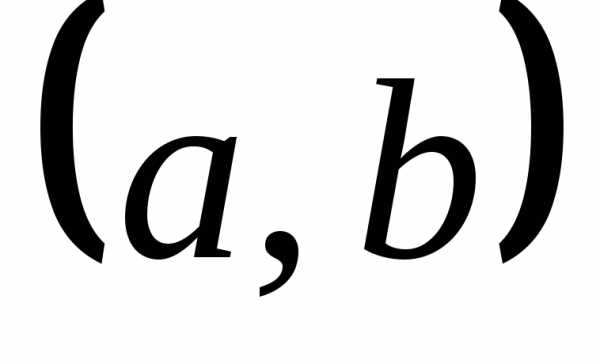 и для всех
и для всех 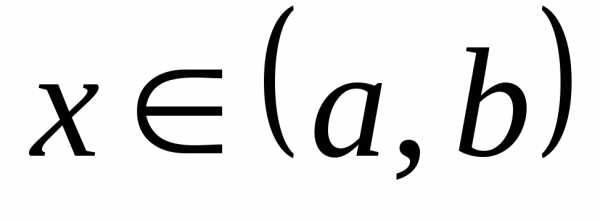 . В дальнейшем
будем рассматривать обыкновенные
дифференциальные уравнения в нормальной
форме:.
. В дальнейшем
будем рассматривать обыкновенные
дифференциальные уравнения в нормальной
форме:.
Дифференциальное
уравнение 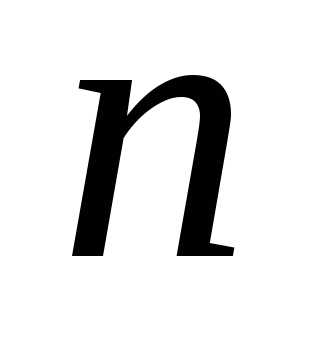 -го
порядка имеет, вообще говоря, бесконечное
множество решений. Однако задача об
отыскании решения, удовлетворяющего начальному
условию
-го
порядка имеет, вообще говоря, бесконечное
множество решений. Однако задача об
отыскании решения, удовлетворяющего начальному
условию
, , …, , при определенных ограничениях на правую часть уравнения имеет единственное решение. Справедлива следующая теорема.
Теорема. Если функция 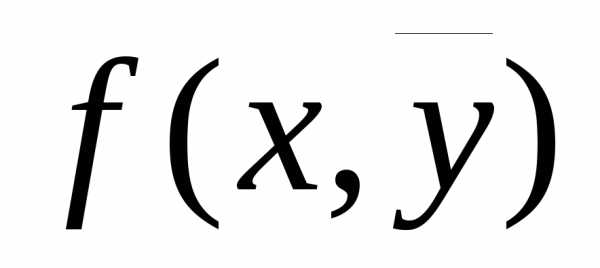 ,,
и ее частные производные
,,
и ее частные производные 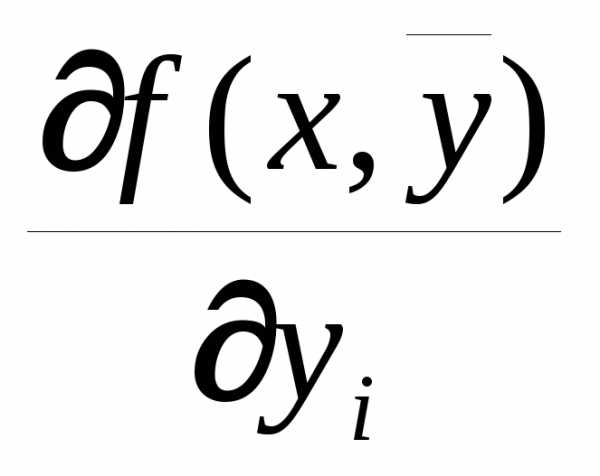 ,
непрерывны в области
,
непрерывны в области  ,
,
то на некотором интервале существует единственное решение
уравнения
,
удовлетворяющее начальным условиям:
,
,
то на некотором интервале существует единственное решение
уравнения
,
удовлетворяющее начальным условиям:
, , …, , .
Задача Коши для
дифференциального уравнения 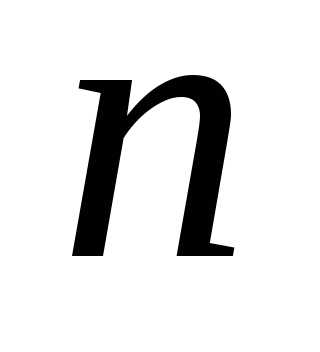 -го
порядка
-го
порядка
, , , …,
может быть сведена
к задаче Коши для системы 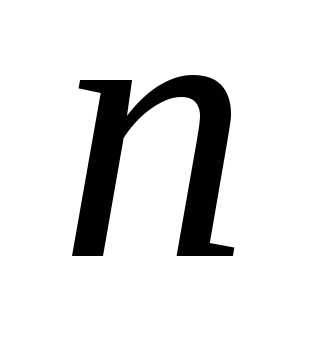 —го
порядка ( системы n дифференциальных уравнений 1-го порядка),
которая в векторной форме имеет вид
,
,
где
,
.
—го
порядка ( системы n дифференциальных уравнений 1-го порядка),
которая в векторной форме имеет вид
,
,
где
,
.
Обусловленность задачи Коши. В силу приведенных выше теорем существования и единственности решения задачи Коши и известной из курса дифференциальных уравнений непрерывной зависимости решения задачи Коши от начальных данных, эта задача корректна. Однако применять численные методы решения задачи имеет смысл только к хорошо обусловленным задачам. В инженерных и научных расчетах достаточно часто возникают плохо обусловленные задачи.
Пример плохо
обусловленной задачи Коши. Рассмотрим
задачу Коши
, 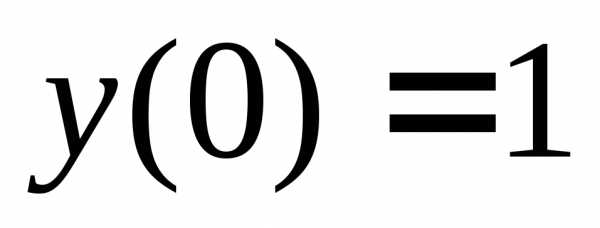 ,
.
Легко видеть, что общее решение задачи
,
а решение задачи Коши и
.
Однако, если начальные данные содержат
малую погрешность,
,
то и
.
Здесь важно понимать, что плохая
обусловленность задачи проявляется на
относительно длинном промежутке
интегрирования уравнения.
,
.
Легко видеть, что общее решение задачи
,
а решение задачи Коши и
.
Однако, если начальные данные содержат
малую погрешность,
,
то и
.
Здесь важно понимать, что плохая
обусловленность задачи проявляется на
относительно длинном промежутке
интегрирования уравнения.
Модельная задача. Полезно рассмотреть модельную
задачу ,
решение которой 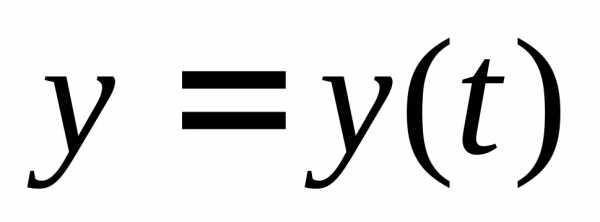 имеет вид
.
Погрешность , вызванная возмущением
начальных условий
имеет вид
.
Погрешность , вызванная возмущением
начальных условий 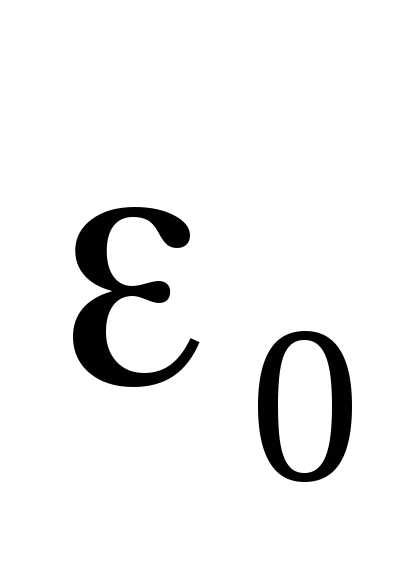 ,
определяется формулой
,
определяется формулой 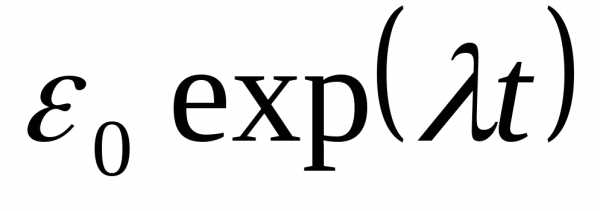 .
Очевидно, что задача хорошо
обусловлена при и плохо
обусловлена при
.
В этой задаче видно как распространяется
возмущение начальных данных.
.
Очевидно, что задача хорошо
обусловлена при и плохо
обусловлена при
.
В этой задаче видно как распространяется
возмущение начальных данных.
Задача Коши на
конечном отрезке. Рассмотрим процесс распространения
погрешностей ,внесенных в начальные
значения. Пусть 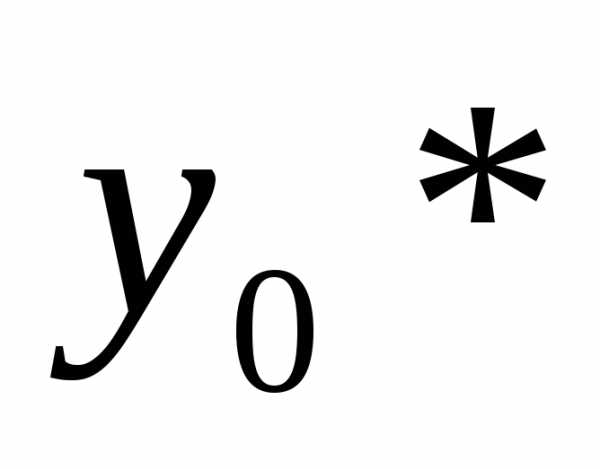 — возмущенное начальное значение, — его погрешность, а
— возмущенное начальное значение, — его погрешность, а 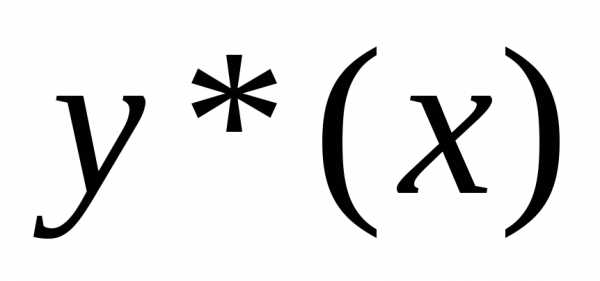 — решение соответствующей задачи Коши
— решение соответствующей задачи Коши
Вычтем из уравнения (1) уравнение (2) и воспользуемся формулой конечных приращений Лагранжа:
где 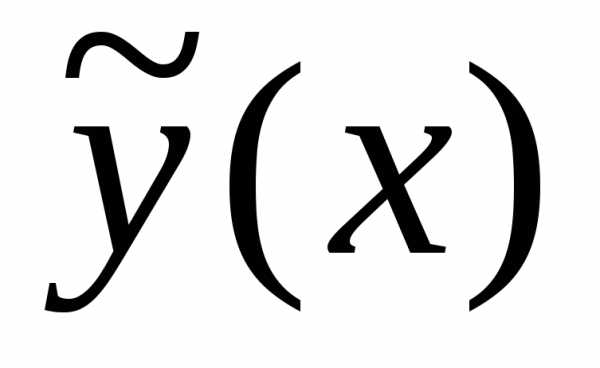 некоторое промежуточное значение. В
результате получим, что погрешность удовлетворяет дифференциальному
уравнению:
некоторое промежуточное значение. В
результате получим, что погрешность удовлетворяет дифференциальному
уравнению:
и начальному
условию 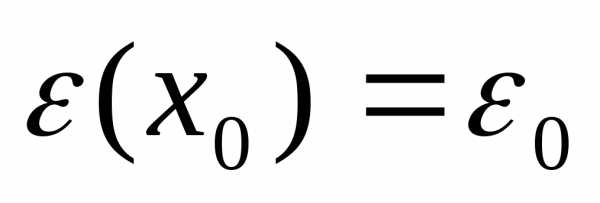 .
Решение этой задачи Коши выражается
формулой
.
Решение этой задачи Коши выражается
формулой
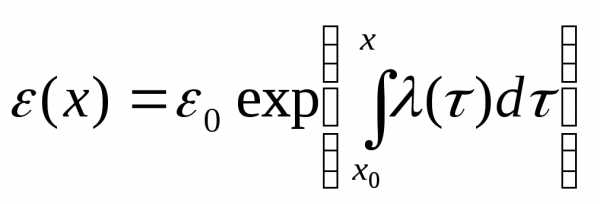
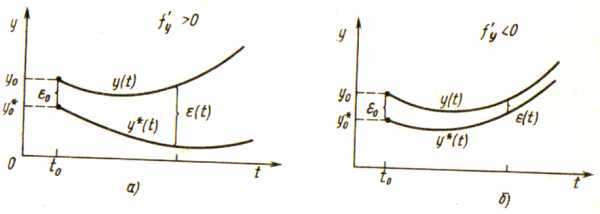 .Таким
образом, величина
играет в задаче Коши роль коэффициента
роста ошибки. Заметим, что знак производной
.Таким
образом, величина
играет в задаче Коши роль коэффициента
роста ошибки. Заметим, что знак производной 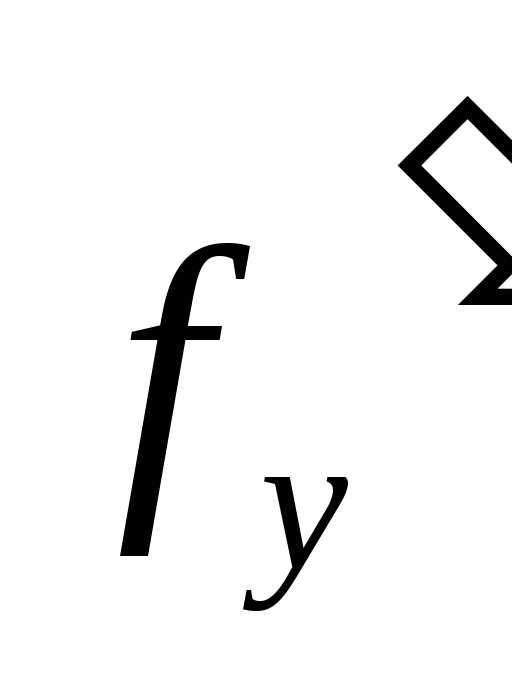 оказывает существенное влияние на
поведение погрешности
оказывает существенное влияние на
поведение погрешности 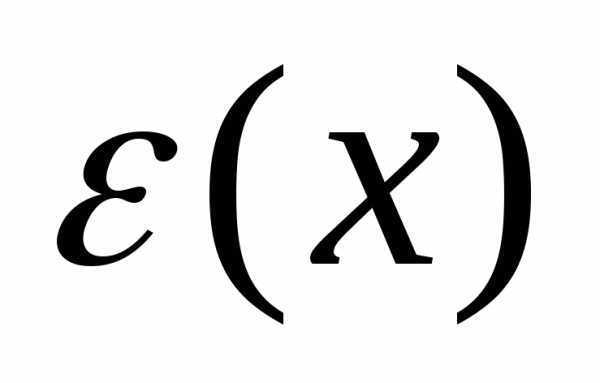 .
Если
.
Если 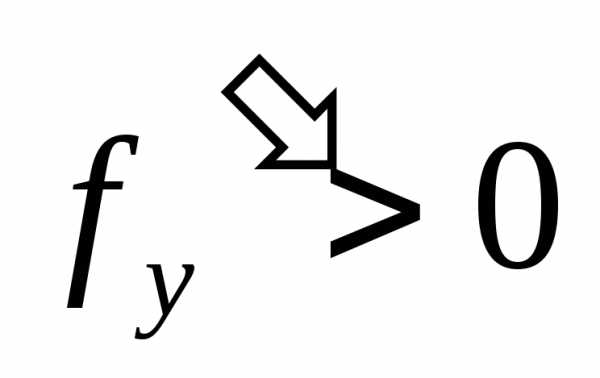 ,
то величина
,
то величина 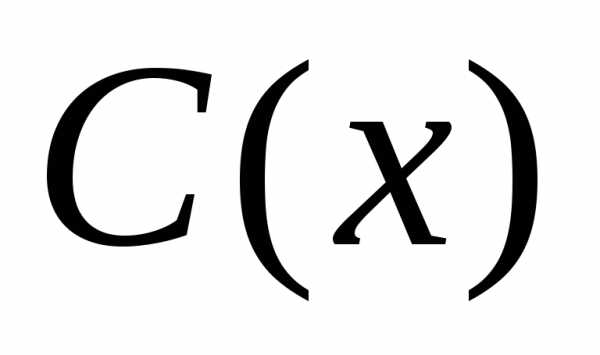 ,
а вместе с ней и модуль погрешности
монотонно возрастают. При этом
соответствующие интегральные кривые
расходятся. ( см. рис.) Иначе ведет себя
погрешность в случае
,
а вместе с ней и модуль погрешности
монотонно возрастают. При этом
соответствующие интегральные кривые
расходятся. ( см. рис.) Иначе ведет себя
погрешность в случае 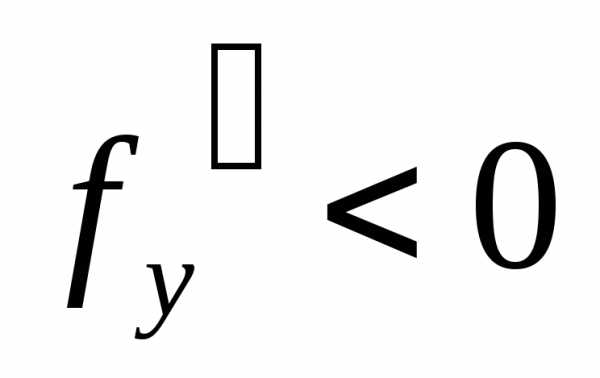 .
Здесь
.
Здесь 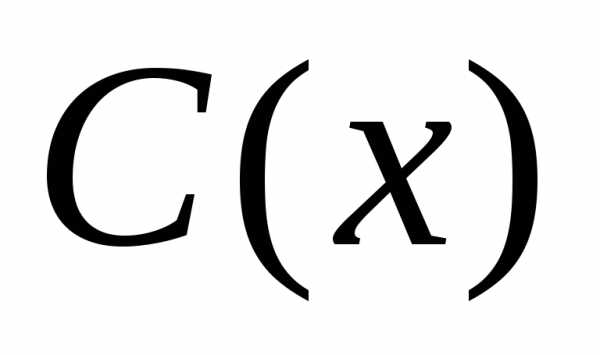 и
и 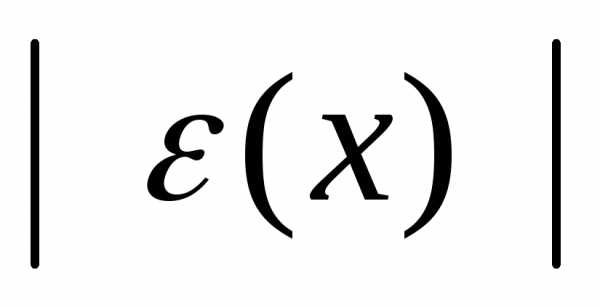 с ростом
с ростом 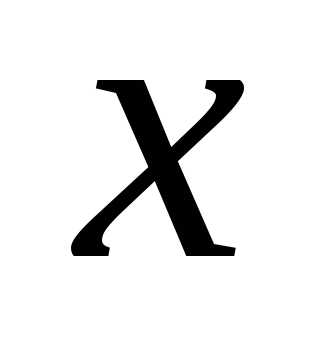 монотонно убывают, а соответствующие
интегральные кривые сближаются. Ошибка,
внесенная в начальное значение, имеет
тенденцию к затуханию. В случае, когда
производная
монотонно убывают, а соответствующие
интегральные кривые сближаются. Ошибка,
внесенная в начальное значение, имеет
тенденцию к затуханию. В случае, когда
производная 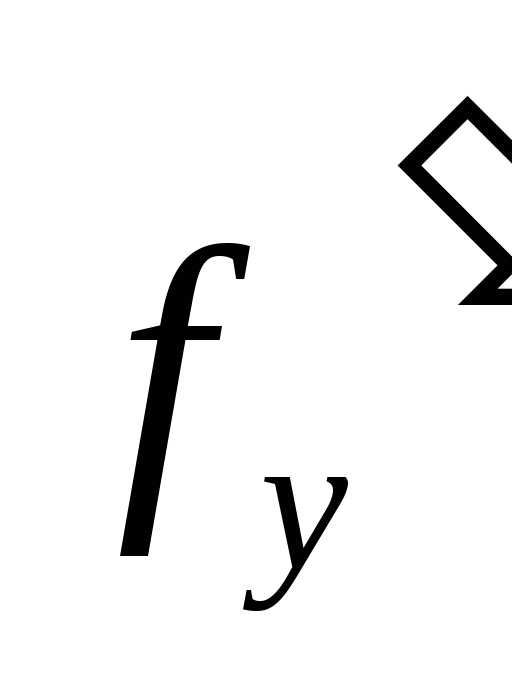 незнакопостоянна, поведение погрешности
может быть более сложным.
незнакопостоянна, поведение погрешности
может быть более сложным.
Постановка задачи численного решения задачи Коши. Аналитическое выражение для решений дифференциальных уравнений, за исключением линейных дифференциальных уравнений с постоянными коэффициентами, удается получить достаточно редко.
Численное решение задачи Коши состоит в построении таблицы
приближенных значений решения 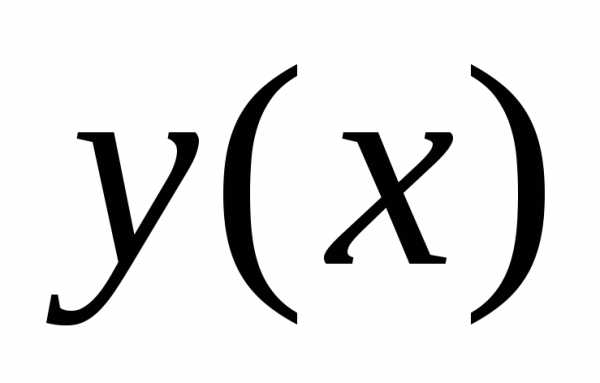 в узлах сетки
,
.
Если
,
,
то сетка называется равномерной,
в узлах сетки
,
.
Если
,
,
то сетка называется равномерной, 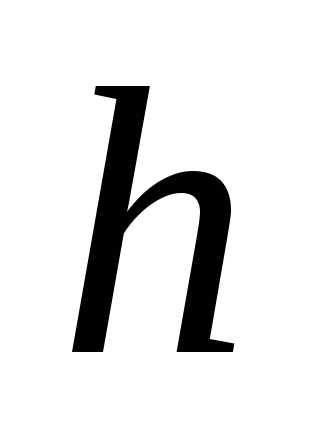 — шаг сетки.
— шаг сетки.
Как уже говорилось,
задача Коши для любого дифференциального
уравнения 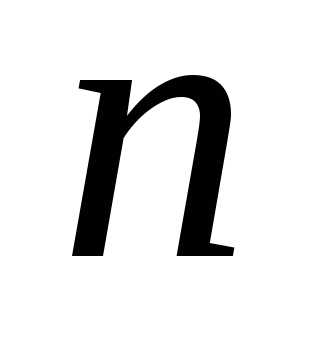 -го
порядка
-го
порядка
сводится к задаче
Коши для системы 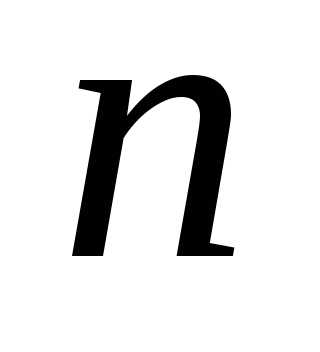 дифференциальных уравнений 1-го порядка. Численное
решение задачи Коши для системы дифференциальных уравнений состоит в
построении таблицы приближенных значений компонент
дифференциальных уравнений 1-го порядка. Численное
решение задачи Коши для системы дифференциальных уравнений состоит в
построении таблицы приближенных значений компонент 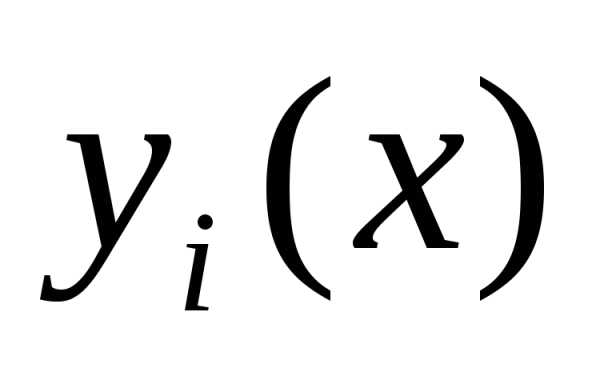 вектора решения
вектора решения 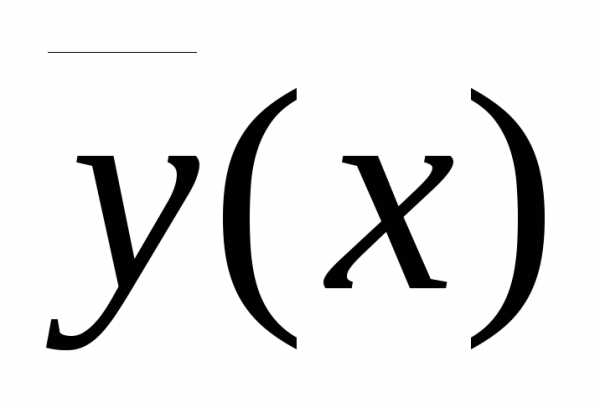 в точках
.
в точках
.
В дальнейшем будем заниматься численным решением задачи Коши для дифференциального уравнения первого порядка, записанного в нормальной форме. Используемые при этом подходы без труда переносятся на системы дифференциальных уравнений.
Классификация
методов численного решения задачи Коши. Численный
метод решения задачи Коши называется одношаговым,
если для вычисления решения в точке 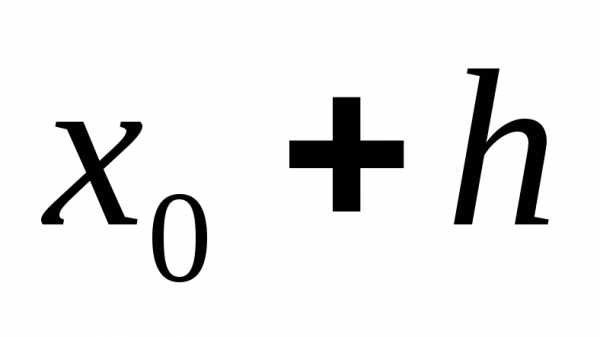 используется информация о решении
только в точке
используется информация о решении
только в точке 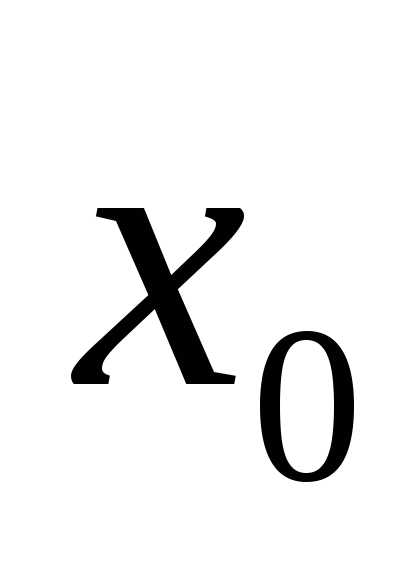 .
В противном случае метод называется многошаговым.
.
В противном случае метод называется многошаговым.
Если при этом
,
т.е. решение в точке 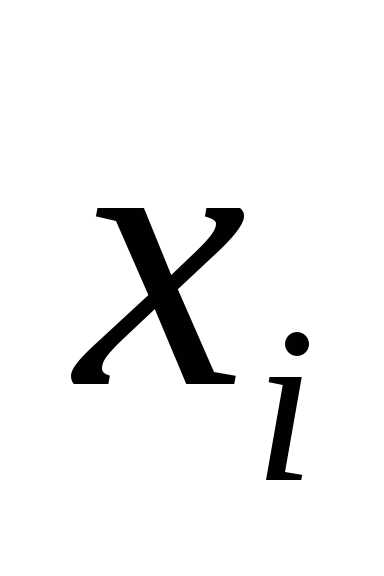 явно выражается через значения в
«предыдущих» точках,
то
метод относится к явным методам.
Если же
,
то метод неявный.
явно выражается через значения в
«предыдущих» точках,
то
метод относится к явным методам.
Если же
,
то метод неявный.
Для оценки
погрешности метода на одном шаге сетки
обычно точное решение раскладывают по
формуле Тейлора в окрестности узла 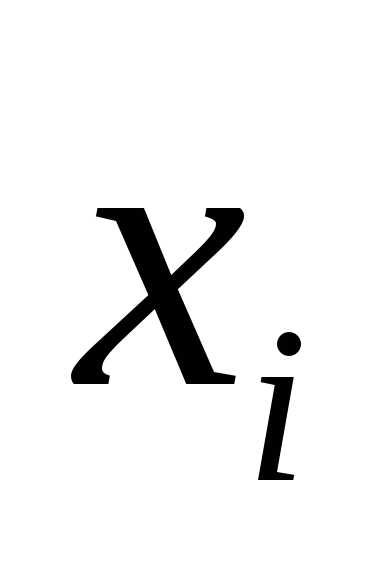 :
:
.
Если значение  в точке
в точке 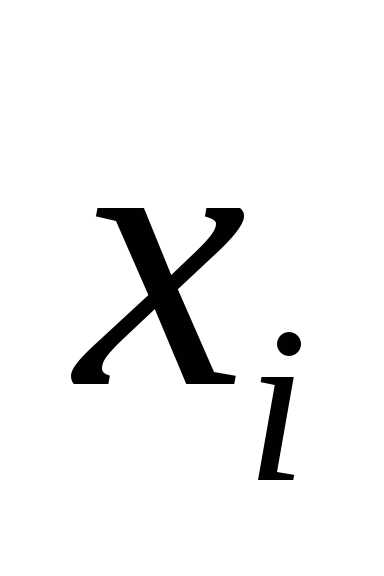 известно, то в силу равенства значение производной
известно, то в силу равенства значение производной  также можно считать известным. Для того
чтобы вычислить производные
более высокого порядка, входящие в
формулу, продифференцируем равенство по t
, используя правило дифференцирования
сложной функции. Получим
также можно считать известным. Для того
чтобы вычислить производные
более высокого порядка, входящие в
формулу, продифференцируем равенство по t
, используя правило дифференцирования
сложной функции. Получим
и т.д.
Если расчетные
формулы численного метода согласуются
с разложением по формуле Тейлора до
членов порядка 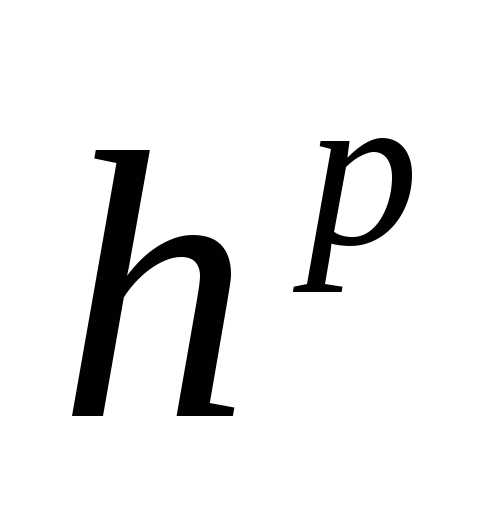 ,
то число
,
то число 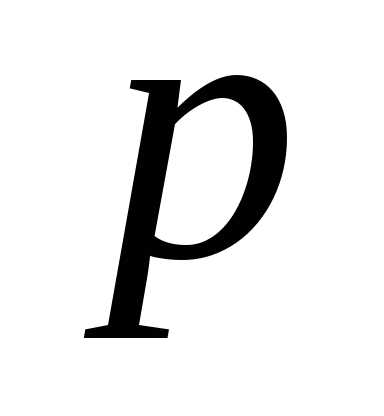 называется порядком
метода.
называется порядком
метода.
Построение численных методов решения задачи Коши. Основной этап численного решения задачи Коши состоит в построении дискретной задачи Коши.
Прежде чем описывать общий подход, построим простейшую дискретную задачу.
Пусть
.
Обозначим 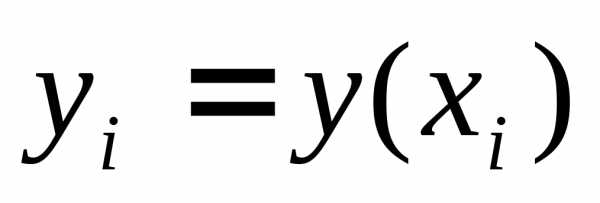 и запишем уравнение во всех узлах сетки
и запишем уравнение во всех узлах сетки 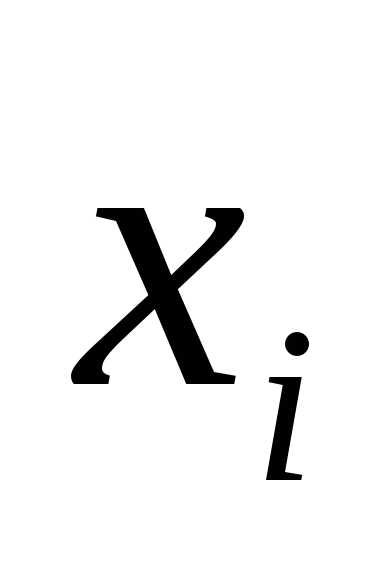 ,
заменяя точное значение производной
,
заменяя точное значение производной 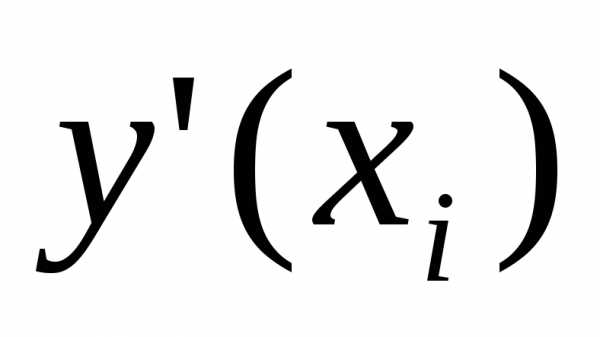 значением
разностной производной
значением
разностной производной 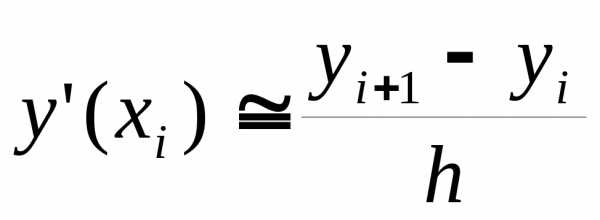 .
Подставив разностную производную в
уравнение, получим систему N линейных
уравнений
, относительно N неизвестных
(значение
.
Подставив разностную производную в
уравнение, получим систему N линейных
уравнений
, относительно N неизвестных
(значение 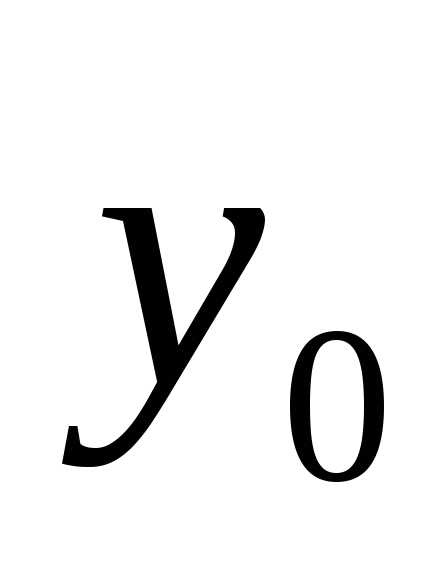 известно из начальных условий). Эта
система уравнений и представляет собой
один из вариантов дискретной
задачи Коши. Положив
известно из начальных условий). Эта
система уравнений и представляет собой
один из вариантов дискретной
задачи Коши. Положив  ,
,
получим формулу
Эйлера численного
решения задачи Коши
приближенное решение
,
вычисленное методом
Эйлера.
,
,
получим формулу
Эйлера численного
решения задачи Коши
приближенное решение
,
вычисленное методом
Эйлера.
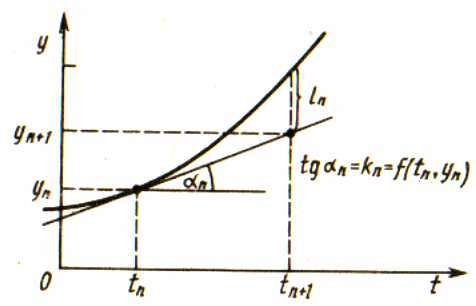
Итак, формулы — расчетные формулы метода Эйлера приближенного решения задачи Коши .
Метод
Эйлера допускает простую геометрическую
интерпретацию. Пусть известна точка 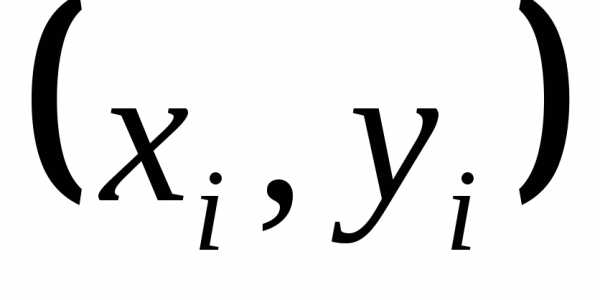 интегральной кривой уравнения
.
Касательная
к интегральной кривой уравнения,
проходящая через эту точку определяется
уравнением . Следовательно, вычисленная методом
Эйлера точка
интегральной кривой уравнения
.
Касательная
к интегральной кривой уравнения,
проходящая через эту точку определяется
уравнением . Следовательно, вычисленная методом
Эйлера точка 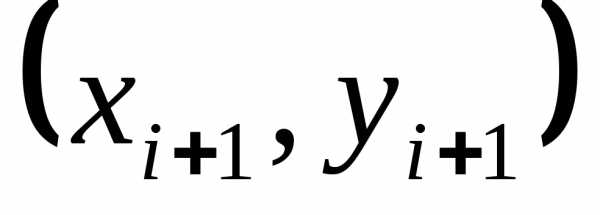 ,
,
,
лежит на этой касательной. Таким образом,
после выполнения N
шагов неизвестная интегральная кривая
заменяется ломаной линией( ломаной
Эйлера), для которой угловой коэффициент звена равен значению
,
,
,
лежит на этой касательной. Таким образом,
после выполнения N
шагов неизвестная интегральная кривая
заменяется ломаной линией( ломаной
Эйлера), для которой угловой коэффициент звена равен значению 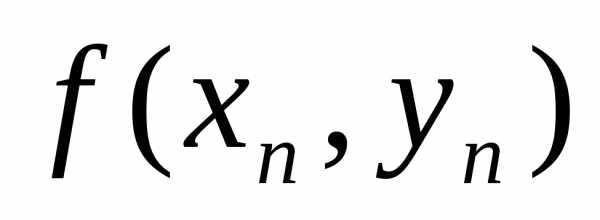 .
.
Метод
Эйлера представляет явный одношаговый
метод. Для него погрешность аппроксимации
имеет вид 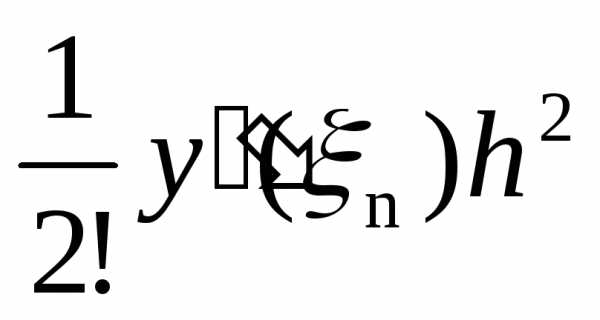 .
.
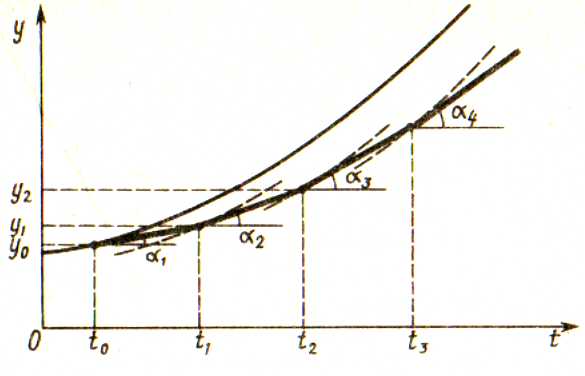
Оценка погрешности. Для метода Эйлера справедлива такая оценка глобальной погрешности:.
Влияние
вычислительной погрешности. Оценивая
метод Эйлера необходимо учитывать, что
при его реализации на ЭВМ неизбежно
возникнут ошибки округления. В результате
фактически вычисляемые значения 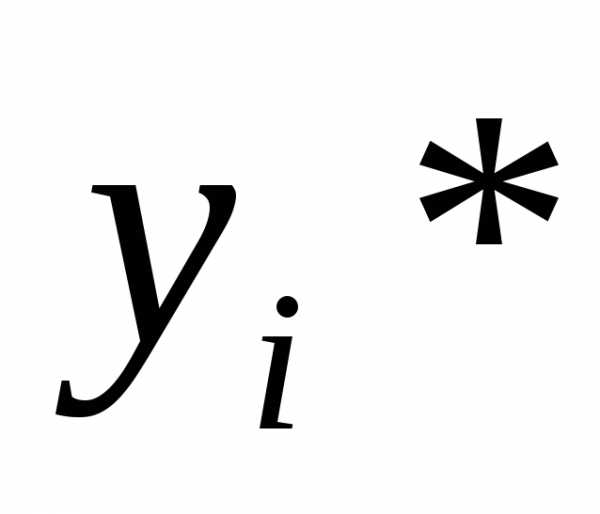 будут удовлетворять соотношению
.
Величины
будут удовлетворять соотношению
.
Величины  учитывают вклад погрешностей округления.
Оценка погрешности фактически вычисляемых
значений
учитывают вклад погрешностей округления.
Оценка погрешности фактически вычисляемых
значений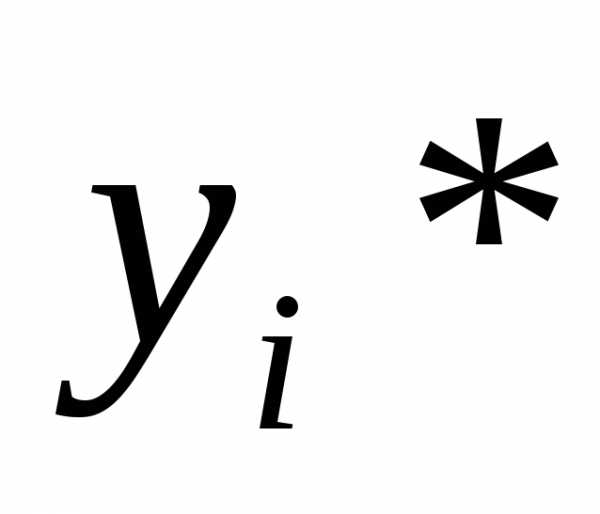 :
.
Оказывается, что полная погрешность
убывает только лишь при уменьшении шага
:
.
Оказывается, что полная погрешность
убывает только лишь при уменьшении шага 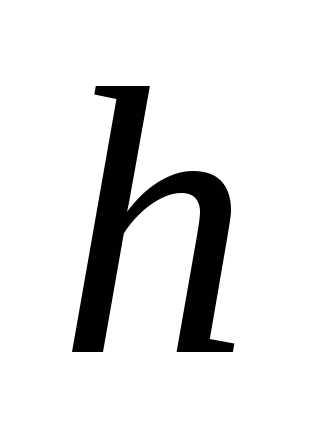 до некоторого значения
до некоторого значения 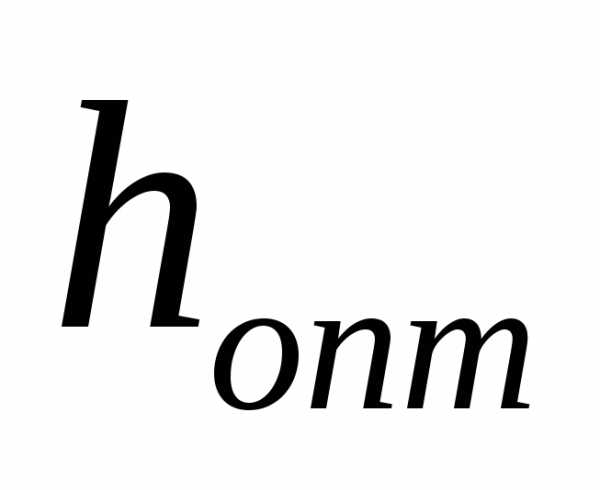 .
.
Вернемся к построению
дискретной задачи Коши. Построение
дискретной задачи заключается в
следующем. Сначала строим на 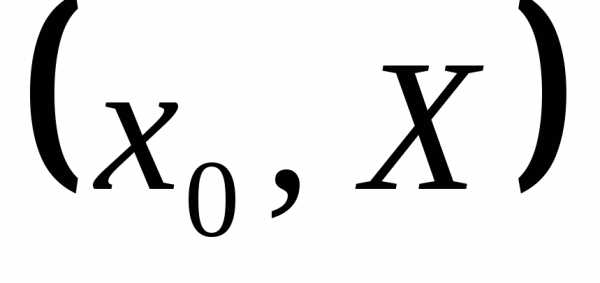 сетку
.
В каждом узле сетки запишем дискретный
аналог уравнения, заменяя производную
сетку
.
В каждом узле сетки запишем дискретный
аналог уравнения, заменяя производную 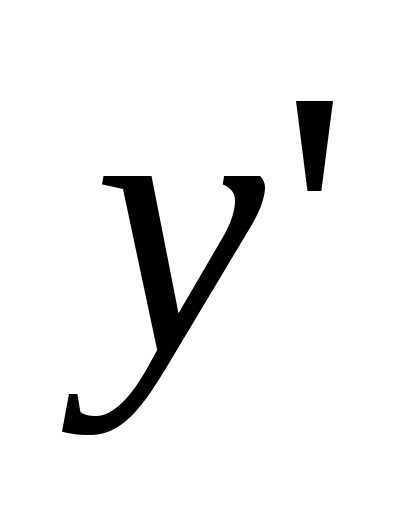 какой-либо разностной производной —
,
а правую часть заменяем какой-либо ее
аппроксимацией —
,
построенной на тех же узлах.
какой-либо разностной производной —
,
а правую часть заменяем какой-либо ее
аппроксимацией —
,
построенной на тех же узлах.
Полученная система N уравнений относительно N неизвестных значений и есть дискретная задача Коши.
В частности, дискретная задача Коши для явного одношагового метода имеет вид
, или, что то же самое .
Приближенное
решение задачи Коши в узлах сетки
полагаем равным вычисленным значениям  :
: 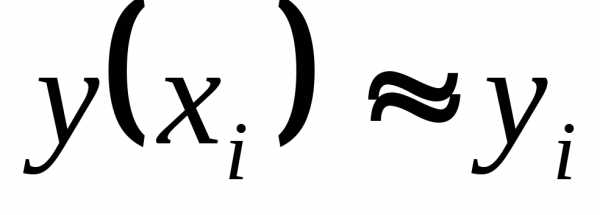 .
.
Основной характеристикой дискретной задачи Коши является степень аппроксимации.
Например, об одношаговой явной дискретной задаче Коши говорят, что дискретное уравнение аппроксимирует дифференциальное уравнение с порядком p, если , константа C не зависит от h.
Величина называется погрешностью аппроксимации.
Говорят, что
численный метод решения задачи Коши сходится с
порядком p,
если константа C не зависит
от h.
Величина 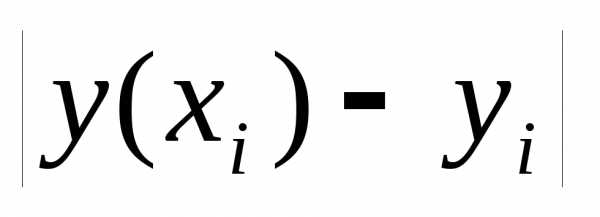 называется локальной
погрешностью метода.
называется локальной
погрешностью метода.
Численный метод
решения задачи Коши называется устойчивым, если для всех достаточно малых h справедливо
неравенство
.
Здесь константа 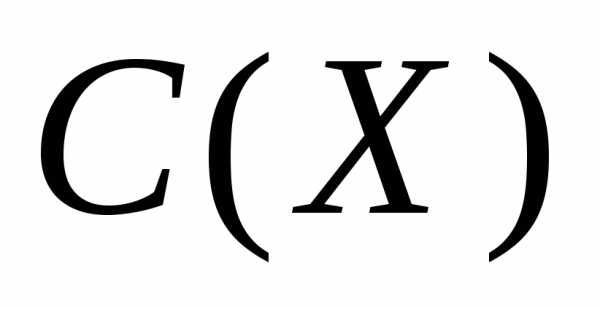 не зависит от h,
а звездочкой помечены приближенные
решения возмущенной задачи дискретной
задачи Коши.
не зависит от h,
а звездочкой помечены приближенные
решения возмущенной задачи дискретной
задачи Коши.
Доказано, что для устойчивой дискретной задачи Коши порядок аппроксимации и порядок сходимости совпадают. Этот порядок называется порядком метода.
Легко видеть, что
описанный выше метод Эйлера является
устойчивым методом первого порядка, а
локальная погрешность метода Эйлера —
величина 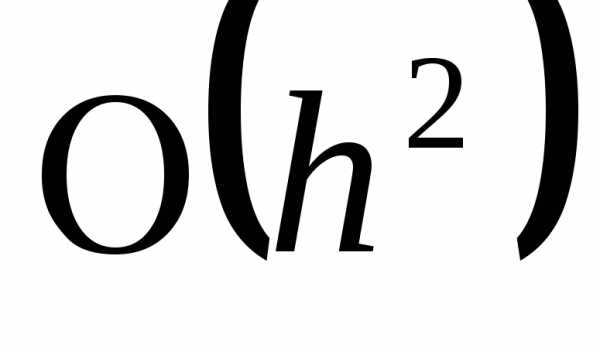 .
.
Численные методы решения задачи Коши различаются используемыми формулами численного дифференцирования и способами аппроксимации правой части уравнения.
Решение задачи Коши методом Рунге-Кутты
Методом Рунге—Кутты
обычно называют одношаговый метод
четвертого порядка, относящийся к
широкому классу методов Рунге—Кутты.
В этом методе величины 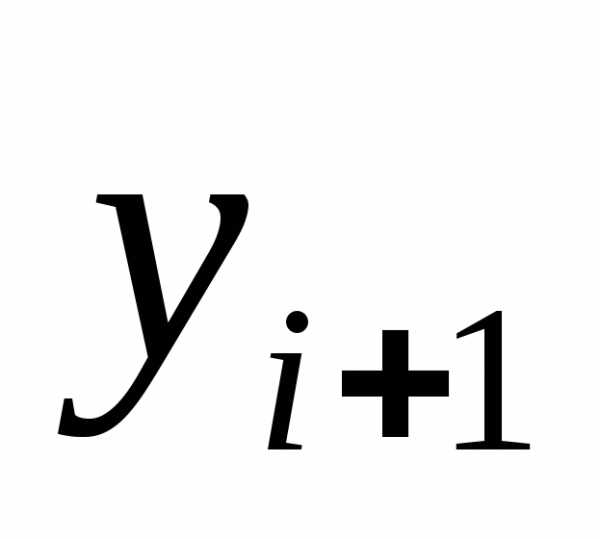 вычисляются по следующим формулам:
вычисляются по следующим формулам:
Построить расчетные формулы метода Рунге-Кутты можно различными способами. Например, можно использовать следующий прием. Положив , имеем . Затем, заменив интеграл в правой части специально построенной квадратурной формулой (вычислить интеграл иначе невозможно, поскольку он зависит от неизвестного искомого решения y(x)).
Если заменить интеграл формулой левых прямоугольников , получим метод Эйлера.
Если заменить
интеграл формулой трапеций
,
получим
.
Этот метод имеет второй порядок точности,
но является неявным. Заменим значение 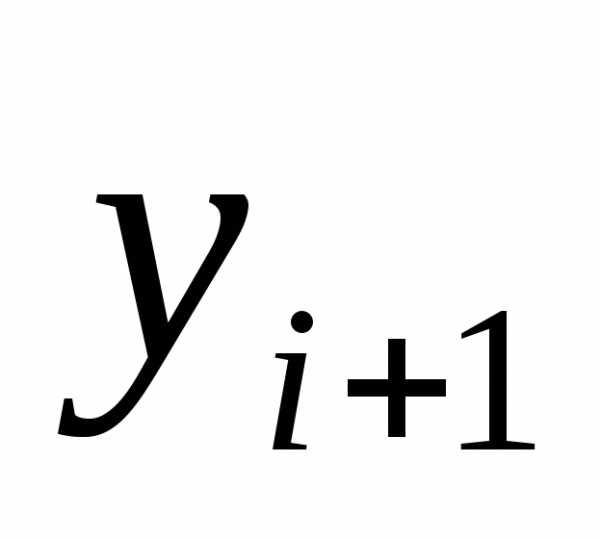 на «предсказываемое» методом Эйлера.
Получаем метод, который называют методом
Эйлера-Коши:
на «предсказываемое» методом Эйлера.
Получаем метод, который называют методом
Эйлера-Коши:
.
Метод Эйлера-Коши относятся к классу методов прогноза и коррекции.
Эта идея лежит в основе многих численных методов решения задачи Коши. Отличаются методы друг от друга используемыми квадратурными формулами. В качестве упражнения полезно попытаться получить таким способом расчетные формулы метода Эйлера. Используя более или менее точные квадратурные формулы можно получить расчетные формулы разных порядков точности. Однако в практических научных расчетах формулы Рунге-Кутты порядка выше четвертого используются крайне редко из-за громоздкости и высоких требований к гладкости правой части.
Метод Рунге-Кутты
устойчив. Локальная погрешность метода
равна 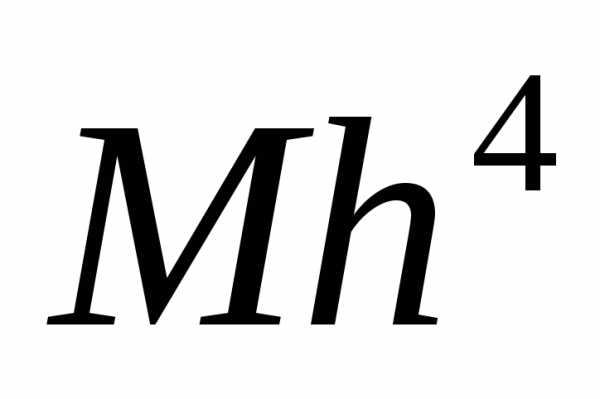 .
.
Практически оценить
величину 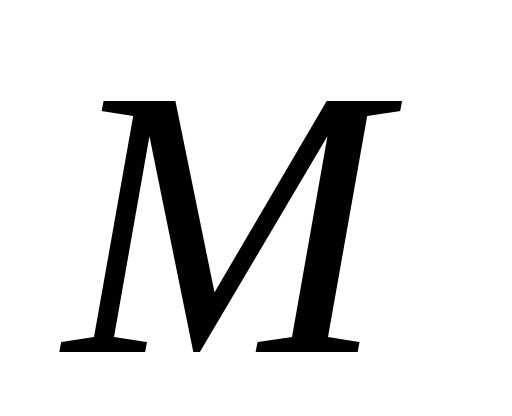 достаточно сложно. При оценке погрешности
обычно используют правило
Рунге. Для
этого сначала проводят вычисления с
шагом
достаточно сложно. При оценке погрешности
обычно используют правило
Рунге. Для
этого сначала проводят вычисления с
шагом 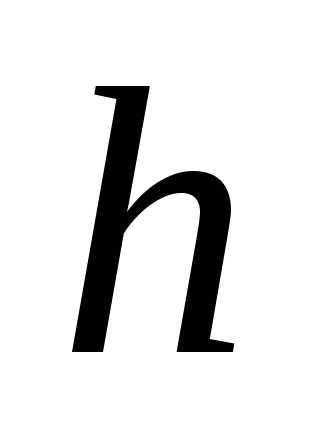 ,
а затем — с шагом
,
а затем — с шагом  .
Если
.
Если 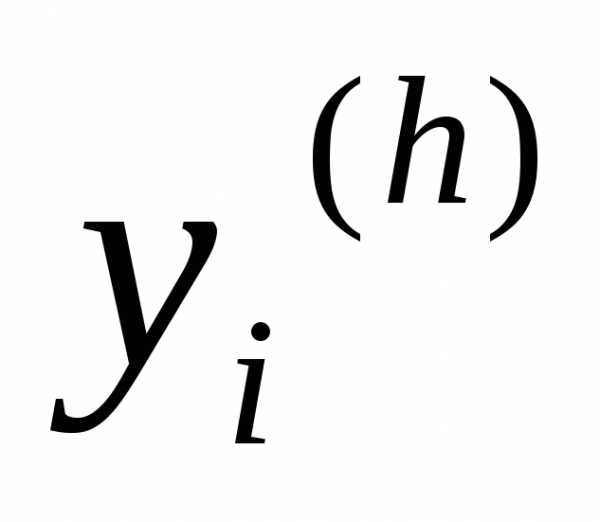 — приближение, вычисленное с шагом
— приближение, вычисленное с шагом 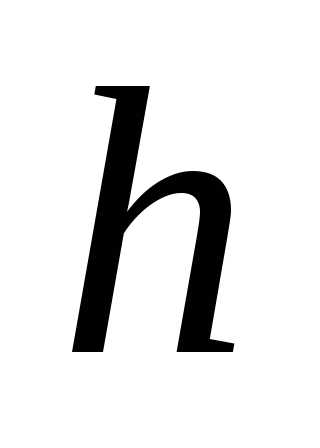 ,
а
,
а 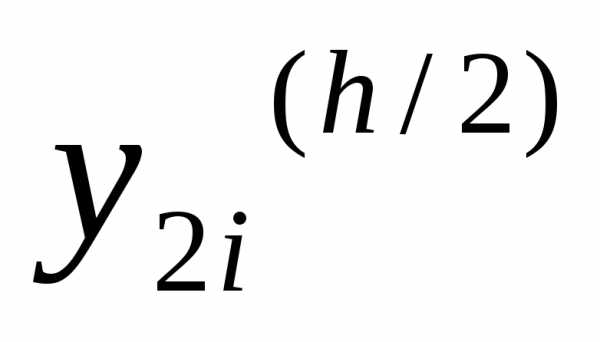 — с шагом
— с шагом  ,
то справедлива оценка
.
,
то справедлива оценка
.
studfiles.net
[Лекция 6]
2.2. О корректной постановке задачи Коши
Учитывая общую постановку задачи Коши в виде (2.5), (2.6), сформулируем задачу Коши для уравнения второго порядка с двумя независимыми переменными, то есть в пространстве :
в , (2.23)
, , (2.24)
где — плоская область в ;- линия внутри области ;заданные функции на линии(см. рис. 2.3).
Рис. 2.3
Для строгой математической постановки задачи (2.23), (2.24) необходимо ввести следующие пространства функций: — пространство начальных функций ;- пространство начальных функций ;- пространство функций , в котором отыскивается решение задачи (2.23), (2.24). Для классических решений.
Будем предполагать, что пространства являются метрическими пространствами, то есть наделены расстояниямимежду двумя функциями соответственно вВ случае нормированных линейных пространств,,, где- норма в нормированном пространстве
Определение 2.3. Рассмотрим две задачи Коши с различными начальными функциями:
,
,,.
Решение задачи Коши (2.23), (2.24) непрерывно зависит в пространстве от начальных функций,, если для любогонайдетсятакое, что из неравенств,следует неравенство.
Определение 2.4. Задача Коши (2.23), (2.24) поставлена корректно в пространствах , если выполнены три условия корректности:
для любых начальных функций ,существует решение задачи
для любых начальных функций ,решение единственно в пространстве
решение задачи непрерывно зависит от начальных функций,.
Если не выполнено хотя бы одно из условий корректности, то задача называется некорректно поставленной. Если же не выполнено третье условие корректности, то задача Коши называется неустойчивой по начальным данным.
2.3. Примеры некорректно поставленных задач Коши
Задача Коши для гиперболического уравнения с начальными условиями на характеристике. На плоскости рассмотрим простейшее гиперболическое уравнение (1.79), для которого два семейства координатных прямых линий,являются характеристиками. Выберем характеристическую линиюи поставим для нее задачу Коши в области:
в области , (2.25)
, ,, (2.26)
где ;.
Предположим, что задача (2.25), (2.26) имеет решение , обладающее непрерывной смешанной производнойв области. Так как линияпринадлежит области, то уравнение (2.25) должно выполняться и на линии, то есть
.
Учитывая второе начальное условие (2.26), получаем необходимое условие разрешимости задачи
. (2.27)
Если условие (2.27) не выполнено, то задача (2.25), (2.26) не имеет решений.
Построим решение задачи (2.25), (2.26), предполагая, что условие (2.27) выполнено. Воспользуемся общим решением (1.80) уравнения (2.25), где функции определим из начальных условий.
Удовлетворим первому начальному условию (2.26), тогда
.
Положим .
Удовлетворим второму начальному условию (2.26), тогда
.
Учитывая соотношение (2.27), получим соотношение . Таким образом, произвольная функцияудовлетворяет условиям,.
Общий вид такой функции
,
где произвольная функция ,
Таким образом, получено решение задачи (2.25), (2.26)
,
которое не единственно в силу произвольности функции .
Рассмотренный пример показывает, что задача Коши с начальными условиями на характеристике поставлена некорректно, так как не выполняется первое или второе условие корректности из определения 2.4.
Задача Коши для параболического уравнения с начальными условиями на характеристике. На плоскости с координатамирассмотрим параболическое уравнение (1.73) канонического видадля которого координатные линииявляются характеристиками. Выберем характеристическую линиюи поставим для нее задачу Коши в области:
в области , (2.28)
, ,(2.29)
Предположим, что классическое решение задачи (2.28), (2.29) существует для области . Так как линияпринадлежит области, то уравнение (2.28) должно выполняться и на линии, то есть
.
studfiles.net
Решить задачу Коши
Добрый вечер!
Я считаю, что лучше на примере показать как решить задачу Коши. Например, нам задано дифференциальное уравнение 1- порядка:
А также дано только одно начальное условие:
Исходя из того, что нам известно, мы сразу понимаем, что нам задана задача Коши.
Решить задачу Коши — это значит найти такое решение заданного условием дифференциального уравнения, которое сможет удовлетворить начальное условие, т.е. нам следует найти только частное решение данного дифференциального уравнения.
Первым делом мы находим общее решение, а также определяем тип дифференциального уравнения, которое нам задано.
Мы знаем, что
Выполняем замену:
Домножаем на :
У нас дифференциальное уравнение с разделяющимися переменными.
Теперь:
Из чего получаем:
Теперь у нас образовалось дифференциальное уравнение с разделёнными переменными. И мы можем проинтегрировать обе части:
Получаем общее решение заданного дифференциального уравнения:
Обращаемся к начальному условию:
Из чего получаем, что:
Подставим в общее решение:
Подставляем уже значение искомого в общее решение дифференциального уравнения, из чего и получим такое:
Это и будет наше с Вами решение
Ответ:
ru.solverbook.com
