Задачи на сопротивление цепи: Задачи на параллельное и последовательное соединение проводников с решением

Содержание

Задачи на параллельное и последовательное соединение проводников с решением

Что бы ни происходило в мире, учиться надо всегда. Кстати, для тех, кто не знает, как организовать учебу на удаленке, мы подготовили отдельную статью. А сегодня займемся решением задач на последовательное и параллельное соеднинение проводников. Решение задач – отличный способ, чтобы успокоить нервы и не поддаваться панике.

Присоединяйтесь к нам в телеграме: там вас ждут актуальные новости и приятные скидки.

Последовательное и параллельное соединение проводников: решение задач

Как решать задачи с параллельным и последовательным соединением проводников? Для начала повторите теорию, вспомните общую памятку по решению физических задач и на всякий случай держите под рукой формулы.

Задача №1 на последовательное соединение проводников

Условие

Проводники сопротивлением 20 Ом и 30 Ом соединены последовательно. Напряжение на концах первого проводника равно 12 В. Определите напряжение, сопротивление и силу тока в цепи на втором проводнике, а также полное напряжение.

Решение

По закону Ома:

Для последовательного соединения проводников:

Ответ: 50 Ом; 18 В; 0,6 А; 30 В.

Задача №2 на параллельное соединение проводников

Условие

Два проводника соединены параллельно. Сила тока в первом проводнике равна 0,5 А, во втором — 1 А. Сопротивление первого проводника составляет 18 Ом. Определите сопротивление второго проводника и силу тока на всем участке цепи.

Решение

Для параллельного соединения:

По закону Ома:

При решении задач не забывайте проверять размерности величин и при необходимости переводить их в систему СИ.

Ответ: 1,5 А; 9 Ом.

Задача №3 на последовательное и параллельное соединение проводников

Условие

Электрогрелка состоит из трех одинаковых секций.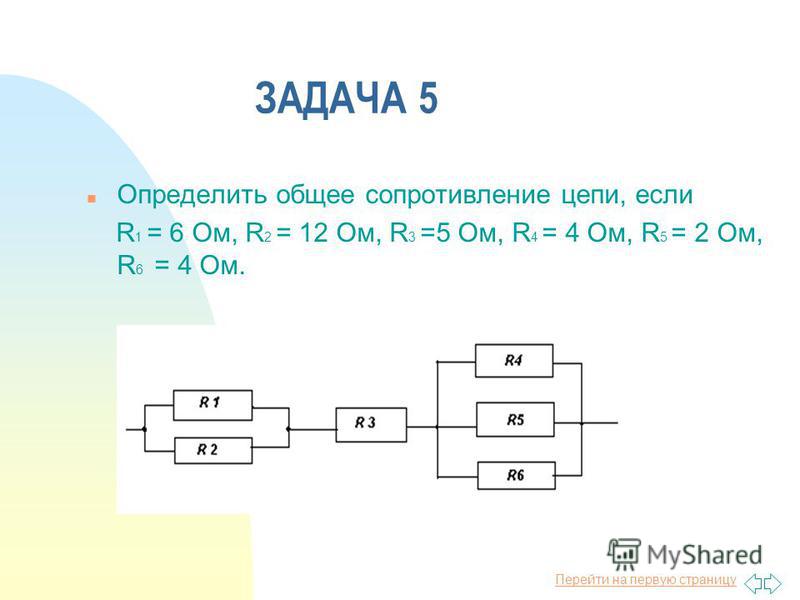 Во сколько раз быстрее грелка будет нагревать некоторое количество воды от 10 до 100 градусов Цельсия при параллельном включении всех секций, нежели при последовательном их включении?

Решение

Пусть сопротивление каждой секции равно R. Тогда при параллельном включении их в сеть напряжение на каждой секции равно напряжению в сети (U), и на трех секциях будет выделяться тепло:

При последовательном соединении суммарное сопротивление цепи равно 3R, а выделяющееся количество теплоты:

Как видим, выделяющееся тепло для первой схемы в 9 раз больше, так что и скорость нагрева воды будет в 9 раз выше.

Ответ: в 9 раз.

Задача №4 на смешанное соединение проводников

Условие

Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом. Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В.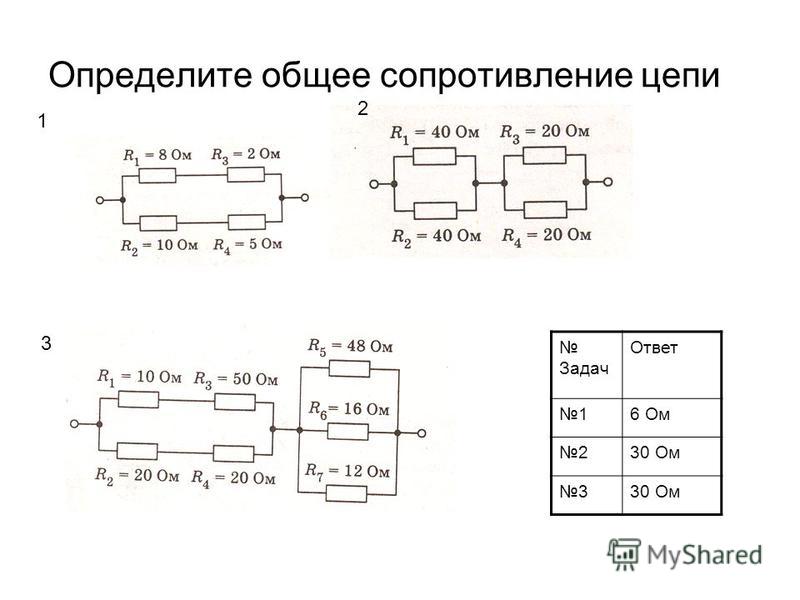 Определите силу тока во всей электрической цепи.

Решение

Согласно схеме, искомая сила тока – это сила тока, протекающая через амперметр.

Резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним.

Резисторы 1 и 2 можно заменить эквивалентным сопротивлением R со штрихом и перерисовать схему в упрощенном виде:

Сопротивления R3 и R со штрихом соединены параллельно, можно найти общее сопротивление электрической цепи по формуле для параллельного соединения:

Теперь цепь можно перерисовать в еще более упрощенном виде и рассчитать силу тока по закону Ома:

Ответ: 2.4 А.

Задача №5 на закон Кирхгофа

Правила Кирхгофа применяются для расчета сложных электрических цепей.

Условие

Три сопротивления R1 = 5 Ом, R2 = 1 Ом, R3 = 3 Ом и два источника тока соединены так, как показано на рисунке. Внутренними сопротивлениями источников тока можно пренебречь. ЭДС первого источника тока равна 1,4 В, и сила тока, текущего через сопротивление R3, равна I3= 1 А. Определите ЭДС второго источника тока.

Решение

Выберем направление обхода контуров по часовой стрелке и запишем закон Кирхгофа для точки A (расположим ее между двумя источниками и сопротивлением R2) и двух контуров:

Подставим числа, получим

Решая систему уравнений, получаем ответ: Е2=3.6 В.

Ответ: 3.6 В.

Вопросы на параллельное и последовательное соединение проводников

Вопрос 1. Схематически изобразите последовательное соединение проводников

Ответ. На рисунке ниже изображен участок цепи с последовательно соединенными проводниками:

Вопрос 2. Схематически изобразите параллельное соединение проводников

Ответ. На рисунке ниже изображено параллельное соединение проводников:

Вопрос 3. Приведите основные формулы и соотношения для последовательного соединения проводников.

Ответ. При последовательном соединении:

Сила тока во всех проводниках одинакова.
Общее напряжение равно сумме напряжений на каждом проводнике.
Полное сопротивление цепи равно сумме сопротивлений отдельных проводников.

Вопрос 4. Приведите основные формулы и соотношения для параллельного соединения проводников.

Ответ. Для параллельного соединения проводников:

Напряжение на всех проводниках одинаково.
Сила тока в неразветвленной цепи равна сумме токов в параллельно соединенных проводниках.
Величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.

Вопрос 5. Какие электрические цепи нельзя рассчитать с помощью формул для последовательного и параллельного соединения проводников?

Ответ. С помощью приведенных выше формул можно рассчитать лишь относительно простые электрические цепи. Для расчета сложных цепей, включающих в себя несколько источников тока и состоящих из многих резисторов, применяются правила Кирхгофа.

Нужна помощь в решении задач или любых других учебных заданий? Обращайтесь в профессиональный сервис для учащихся: мы найдем верное решение.

Решение задач по теме: «Смешанное соединение проводников» 8 класс онлайн-подготовка на Ростелеком Лицей

Необходимые для решения задач формулы и факты

Под соединением проводников подразумевается соединение резисторов – приборов, сделанных на основе сопротивления проводников. На предыдущих уроках были рассмотрены параллельное и последовательное соединения. На данном уроке будут рассмотрены задачи на смешанное соединение проводников, то есть когда в цепи присутствует и последовательное, и параллельное соединение.

Для решения задач сначала рассмотрим формулы для связи различных величин при параллельном и последовательном соединениях:

Если проводники соединены последовательно, то сила тока в них одинакова и равна силе тока в цепи. При этом общее напряжение в цепи будет состоять из суммы напряжений на каждом проводнике. А если говорить о сопротивлении этого участка цепи, в котором проводники соединены последовательно, то оно равно сумме сопротивлений проводников.

В параллельном соединении все по-другому. Сила тока в каждой ветке этой цепи будет различной, при этом общая сила тока в цепи будет вычисляться как сумма сил токов в проводниках. Напряжение на проводниках, соединенных последовательно, будет одинаковым. Общее сопротивление этого участка цепи, так называемое «эквивалентное сопротивление» R, будет вычисляться по следующей формуле: .

Также стоит отметить, что параллельное соединение обычно применяется при включении бытовых приборов, а последовательное – для того, чтобы создать длинную неразветвленную цепь.

Задача №1

Рассмотрим следующую задачу. Участок цепи состоит из двух последовательно соединенных сопротивлений, каждое из которых равно 1 Ом. К этим двум резисторам параллельно подключают еще одно сопротивление, значение которого составляет 2 Ом.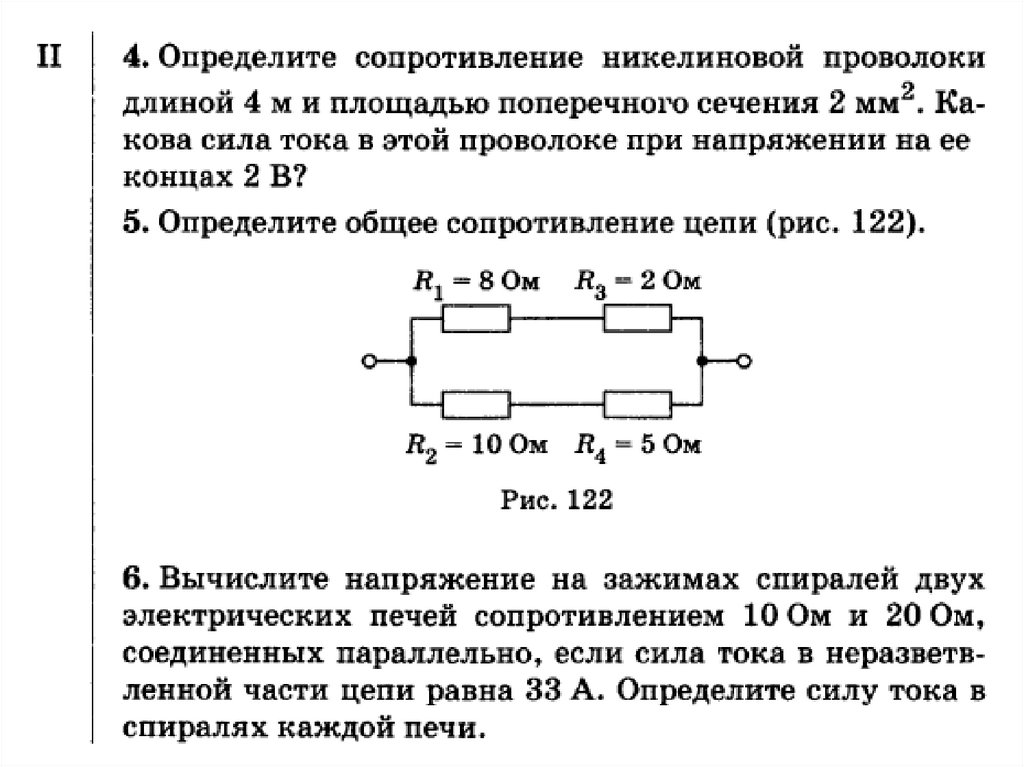 Всю эту цепь подключают к источнику тока, который создает на концах данного соединения напряжение 2,4 В. Необходимо определить силу тока во всей электрической цепи (рис. 1).

Рис. 1. Условия и рисунок задачи № 1

Как видим, резисторы R1 и R2 соединены последовательно, резистор R3 – параллельно к ним. Источник дает напряжение 2,4 В, соответственно, на участке АВ напряжение будет также 2,4 В. Сила тока, которую требуется найти, – это сила тока, протекающая через амперметр А.

Такое соединение проводников называется неразветвленным. В промышленности обычно изготавливается набор резисторов с четко определенными сопротивлениями, но для экспериментов могут понадобиться любые различные сопротивления. Тогда с помощью таких схем можно создавать нужное сопротивление для эксперимента или прибора.

Далее требуется определить эквивалентное сопротивление неразветвленной части. Сначала посмотрим, чему равно сопротивление R’ участка цепи АВ, который содержит только резисторы R1 и R2.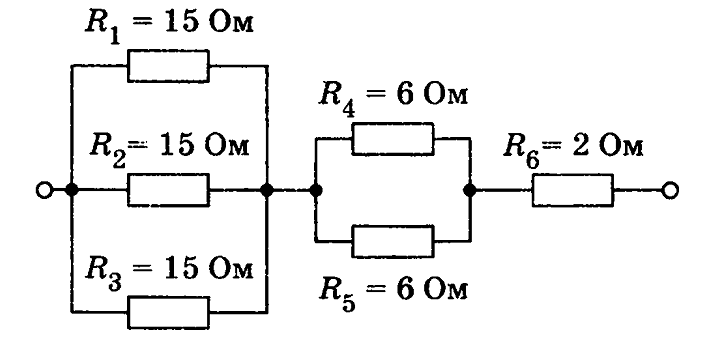 Они соединены последовательно, тогда R′=R1+R2=2 [Ом]. Теперь можно перерисовать электрическую цепь, заменив сопротивления R1 и R2 эквивалентным им сопротивлением R’ (рис. 2).

Рис. 2. Первая замена эквивалентным сопротивлением

Теперь можно сказать, что участок АВ включает в себя не три, а два сопротивления: R3 и R’. Эти два сопротивления соединены параллельно, соответственно, можно найти общее сопротивление электрической цепи по формуле . Выразив R и подставив значения , получаем:

Стоит отметить, что сопротивления были соединены, но общее сопротивление получилось все равно равным 1 Ом. Теперь электрическую цепь можно заменить следующей (рис. 3):

Рис. 3. Вторая замена эквивалентным сопротивлением

На рис. 3 сопротивление R=1 Ом называется эквивалентным сопротивлением, поскольку три сопротивления были заменены на одно. Чтобы рассчитать силу тока в цепи, надо использовать закон Ома для участка цепи: . Напряжение на сопротивлении R – это напряжение на участке АВ (Рис. 1), которое, в свою очередь, равно 2,4.Тогда . Это и будет значение силы тока в электрической цепи, которое покажет амперметр.

Задача №2

Теперь рассмотрим задачу, в которой также будет три сопротивления, но соединены они будут по-другому (рис. 4):

Рис. 4. Условие задачи № 2

Два сопротивления R1 и R2 соединены параллельно (R1=R2=2 Ом), к ним еще последовательно присоединено сопротивление R3=1 Ом. Амперметр показывает силу тока в цепи, равную I=0,5 А. Требуется определить напряжение на концах участка этой цепи, то есть на участке АВ.

Для начала определим сопротивление участка цепи, содержащего сопротивления R1 и R2. Эти два сопротивления соединены параллельно, значит, их эквивалентное сопротивление R’ можно найти из формулы . Подставляя значения, получаем:

Теперь можно сказать, что цепь включает в себя только два сопротивления: R’и R3, которые соединены последовательно.

Рис. 5. Замена параллельного соединения эквивалентным сопротивлением

В задаче требуется определить напряжение. Для этого используется прибор, который называется вольтметр. В цепь он включается параллельно. И рассмотрим участок цепи, в котором все три сопротивления уже заменены эквивалентным.

Рис. 6. Включение вольтметра в цепь

Вольтметр включен в месте, соответствующем участку АВ на рис. 4. Соответственно, он измеряет напряжение на это участке цепи. Чтобы найти значения этого напряжения, требуется сначала найти эквивалентное сопротивление. Сопротивления R’ и R3 соединены последовательно (рис. 5), значит, эквивалентное сопротивление определяется по формуле:

Теперь из закона Ома для участка цепи можно найти напряжение:

Значит, вольтметр должен будет показать значения напряжения в 1 В.

Расчет более сложных цепей

На уроке были рассмотрены соединения только трех сопротивлений, когда они были последовательные, к ним параллельно подключается третий, или когда два соединены параллельно, а к ним последовательно подключают третье сопротивление. Но реальные схемы значительно сложнее. Они содержат огромное количество различных элементов, сопротивлений, поэтому имеются достаточно сложные методы расчетов электрических цепей.

Впервые расчетами таких сложных электрических цепей озадачились ученые приблизительно в XIX веке, и появились новые правила, которые используются и по сей день. Немецкий ученый Кирхгоф разработал возможность расчета электрических сложных цепей, поэтому правила, которые используют для сложных цепей, называются «правилами Кирхгофа».

На следующих уроках будет рассмотрено понятие мощности и работы силы тока.

Список литературы

Генденштейн Л.Э, Кайдалов А.Б., Кожевников В.Б. / Под ред. Орлова В.А., Ройзена И.И. Физика 8. – М.: Мнемозина.
Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
Фадеева А.А., Засов А.В., Киселев Д.Ф. Физика 8. – М.: Просвещение.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

Festival. 1september.ru (Источник)
Electroandi.ru (Источник)
Bocharova.ucoz.ru (Источник)

Домашнее задание

Стр. 117: задачи № 4, 5. Перышкин А.В. Физика 8. – М.: Дрофа, 2010.
В каком случае эквивалентное сопротивление будет больше: если три проводника с сопротивлениями 1 Ом каждый соединить параллельно или последовательно?

Два сопротивления R1=1 Ом и R2= 2 Ом соединены последовательно, к ним параллельно присоединено сопротивление 3 Ом. Чему равно эквивалентное сопротивление?
Сколько различных цепей можно составить из трех резисторов с сопротивлениями 1 Ом каждый так, чтоб их эквивалентные сопротивления была различными?

«Задачи на параллельное соединение проводников».

Задача № 1. Конспект по теме «ЗАДАЧИ на Параллельное соединение проводников».

Название величины	Обозначение	Единица измерения	Формула
Сила тока	I	А	I = U / R
Напряжение	U	В	U = IR
Сопротивление	R	Ом	R = U / I
Сила тока на участке цепи	I	A	I = I₁ + I₂
Напряжение на концах участка	U	B	U = U₁ = U₂
Сопротивление участка цепи	R	Ом

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Два проводника сопротивлением 200 Ом и 300 Ом соединены параллельно. Определить полное сопротивление участка цепи.

Задача № 2. Два резистора соединены параллельно. Сила тока в первом резисторе 0,5 А, во втором — 1 А. Сопротивление первого резистора 18 Ом. Определите силу тока на всем участке цепи и сопротивление второго резистора.

Задача № 3. Две лампы соединены параллельно. Напряжение на первой лампе 220 В, сила тока в ней 0,5 А. Сила тока в цепи 2 А. Определите силу тока во второй лампе и сопротивление каждой лампы.

Задача № 4. Определите показания амперметра и вольтметра, если по проводнику с сопротивлением R₁ идёт ток силой 0,1 А. Сопротивлением амперметра и подводящих проводов пренебречь. Считать, что сопротивление вольтметра много больше сопротивлений рассматриваемых проводников.

Задача № 5. В цепи батареи параллельно включены три электрические лампы. Нарисуйте схему включения двух выключателей так, чтобы один управлял двумя лампами одновременно, а другой — одной третьей лампой.

Ответ:

Задача № 6. Лампы и амперметр включены так, как показано на рисунке. Во сколько раз отличаются показания амперметра при разомкнутом и замкнутом ключе? Сопротивления ламп одинаковы. Напряжение поддерживается постоянным.

Задача № 7. Напряжение в сети 120 В. Сопротивление каждой из двух электрических ламп, включенных в эту сеть, равно 240 Ом. Определите силу тока в каждой лампе при последовательном и параллельном их включении.

Задача № 8. Две электрические лампы включены параллельно под напряжение 220 В. Определите силу тока в каждой лампе и в подводящей цепи, если сопротивление одной лампы 1000 Ом, а другой 488 Ом.

Задача № 9. В цепь включены две одинаковые лампы. При положении ползунка реостата в точке В амперметр А1 показывает силу тока 0,4 А. Что показывают амперметры А и А2 ? Изменятся ли показания амперметров при передвижении ползунка к точке А?

Задача № 10.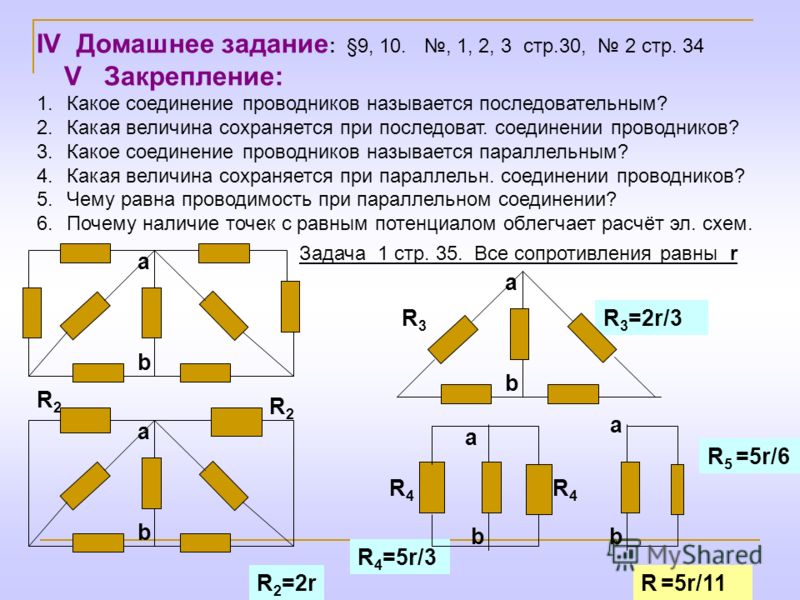 ОГЭ В сеть напряжением U = 24 В подключили два последовательно соединённых резистора. При этом сила тока составила I₁ = 0,6 А. Когда резисторы подключили параллельно, суммарная сила тока стала равной I₂ = 3,2 А. Определить сопротивления резисторов.

Задача № 11. ЕГЭ Миллиамперметр, рассчитанный на измерение тока до I_А = 25 мА, имеющий внутреннее сопротивление R_A = 10 Ом, необходимо использовать как амперметр для измерения токов до I = 5 А. Какое сопротивление должен иметь шунт?

Краткая теория для решения Задачи на Параллельное соединение проводников.

Это конспект по теме «ЗАДАЧИ на Параллельное соединение проводников». Выберите дальнейшие действия:

Урок физики в 8-м классе по теме

«Закон Джоуля–Ленца»

Цели урока:

объяснить явление нагревания проводников электрическим током;
установить зависимость выделяющейся при этом тепловой энергии от параметров электрической цепи;
сформулировать закон Джоуля – Ленца;
формировать умение применять этот закон для решения качественных и количественных задач.

Тип урока: комбинированный.

Задачи урока.

Образовательные:
- опираясь на знания, полученные ранее, аналитически установить связь выделяющейся тепловой энергии на проводнике с силой тока и сопротивлением проводника;
- анализируя опыты, установить эту же зависимость;
- опираясь на известные формулы, теоретически определить количество теплоты, выделяющейся на проводнике с током;
- подтвердить полученные выводы результатами экспериментов;
- сформулировать закон Джоуля – Ленца;
- формировать умение применять этот закон для решения задач.
Воспитательные:
- содействовать формированию мировоззренческой идеи познаваемости явлений и свойств окружающего мира;
- формировать умение работать в группах, уважительно относиться друг к другу, прислушиваться к мнению товарищей;
- побуждать использовать полученные на уроках знания в повседневной жизни.
Развивающие:

Оборудование: компьютер, презентация к уроку

Ход урока:

1.Организационный момент.

2.Актуализация знаний. Фронтально.

Вспомним некоторые вопросы, которые потребуются, чтобы изучить новую тему:

— Что называют электрическим током?
— Что представляет собой электрический ток в металлах?

— Какие действия может оказывать электрический ток?

— Какие три величины связывает закон Ома?

— Как формулируется закон Ома?

— Что такое работа тока?

-Как можно найти работу тока?

А теперь давайте поработаем в парах и разгадаем кроссворд.

Кроссворд.

Носитель свободного электрического заряда в металлах.
Вещество, непроводящее электрический ток.
Чертеж, на котором изображен способ соединения электрических приборов в цепь.
Явление упорядоченного движения заряженных частиц.
Единица измерения электрического напряжения.
Физическая величина, характеризующая проводник и измеряемая в Омах.
Часть электрической цепи, служащая для ее замыкания и размыкания.
Одно из мест на источнике тока, к которому присоединена клемма для включения его в электрическую цепь.
Единица измерения электрического заряда.
Единица измерения силы тока.

Давайте проверим ваши ответы.

Электрон.
Диэлектрик.
Схема.
Ток.
Вольт.
Сопротивление.
Полюс.
Кулон.
Ампер.

Новый материал.

Откройте, пожалуйста, тетради и запишите тему нашего урока «Закон Джоуля-Ленца».

На слайде изображены электроприборы(потребители электрического тока):

утюг, электроплитка, электрическая лампа, электрическая дрель, электрический чайник, паяльник
вопросы к учащимся:

-Назовите приборы изображенные на слайде.

-Какой прибор не вписывается в общий ряд? Уберите лишний.

-Чем вы руководствовались, делая выбор?

-Какое действие электрического тока проявляется в выбранных приборах?

Давайте с вами выясним, почему проводники нагреваются? Чаще всего мы сталкиваемся с электрическим током в металлах. Поэтому мы разберем нагрев именно металлического проводника.

-Что представляет собой кристаллическая решетка металлов?

Видеоролик.

-Как вы думаете от каких величин зависит нагревание проводника и то, какое количество теплоты отдаст проводник с током в окружающую среду?

Многочисленные опыты показывают, что чем больше сила тока в проводнике, тем и количество теплоты, выделившееся в проводнике будет больше. Значит, нагревание проводника зависит от силы тока (I). Был проведен эксперимент. Были взяты 3 проводника одинаковой длины и площади поперечного сечения, но из разного вещества. Все проводники соединены между собой последовательно. Следовательно, сила тока на всех участках цепи одинаковая. Но при включении в цепь все 3 проводника выделили разное количество теплоты.

-Итак , от чего зависит количество теплоты в проводнике с током?

Вывод: Количество теплоты, которое выделяется при протекании электрического тока по проводнику, зависит от силы тока в этом проводнике и от его электрического сопротивления.

Закон, определяющий тепловое действие тока – ЗАКОН ДЖОУЛЯ-ЛЕНЦА.

Работа с учебником.

-Как записывается закон Джоуля-Ленца?

Q=I²Rt

Q – количество теплоты — [Дж]

I – сила тока – [A]

R – сопротивление – [Ом]

t – время – [c]

-Как формулируется закон Джоуля- Ленца?

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени.

С точки зрения закона сохранения энергии работа, которую совершает электрическое поле, создавая электрический ток в проводнике, равна количеству теплоту, выделяемому проводником с током.

A=UIt из закона Ома I=U/R следует U=IR следовательно A=IRIt что соответствует закону Джоуля-Ленца Q=I²Rt.

Автобиографическая справка.

Рассказать о английском физике Джеймсе Прескотте Джоулье (1818-1889 гг)

Родился 24 декабря 1818 г. в городе Солфорд (графство Ланкашир). Получил домашнее образование. По профессии был пивоваром. Внёс значительный вклад в исследование электромагнетизма и тепловых явлений, в создание физики низких температур, в обоснование закона сохранения энергии. В 1850 г. Джоуль был избран членом Лондонского королевского общества. Он являлся непревзойдённым экспериментатором. Опыты были просты по идее, но в каждом из них обязательно содержалась некая изюминка — тонкость, которая позволяла получать очень точные результаты. Умер 11 октября 1889 г. в городе Сейл (графство Чешир).

Русском физике Ленце Эмилии Христиановиче (1804 – 1865)

Эмилий Ленц родился 24 февраля 1804 года в Дерпте (ныне Тарту). В 1820 году он окончил гимназию и поступил в университет. Самостоятельную научную деятельность Ленц начал в качестве физика в кругосветной экспедиции на шлюпке «Предприятие» (1823-1826). В очень короткий срок он создал уникальные приборы для глубоководных океанографических наблюдений. В июле 1829 года он участвовал в первом восхождении на Эльбрус. Замечательной чертой Ленца как ученого было глубокое понимание физических процессов и умение открывать их закономерности. В 1836 году Эмилий Ленц был приглашен в Петербургский университет и возглавил кафедру физики и физической географии, в 1863 году был избран ректором университета. В числе его учеников были Д.И. Менделеев, К.А. Тимирязев, П.П. Семенов-Тян-Шанский. Совместно с Борисом Семеновичем Якоби Ленц впервые разработал методы расчета электромагнитов в электрических машинах. Открыл обратимость электрических машин. Кроме того, он изучал зависимость сопротивления металлов от температуры. Эмилий Христианович Ленц умер 10 февраля 1865 года.

-С помощью каких формул ещё можно найти количество теплоты, выделяемое проводником с током?

Выясним, какую из этих формул удобнее применять для последовательного, а какую для параллельного соединения проводников. Для этого вспомним законы различных видов соединения.

(Два ученика на доске записывают законы последовательного и параллельного соединения проводников).

Последовательное соединение: I=I₁=I₂; U=U₁+U₂; R=R₁+R₂

Параллельное соединение:

U=U₁=U₂; I=I₁+I₂; 1/R=1/R₁+1/R₂.

Мы видим, что при последовательном соединении не изменяется сила тока (I) , то для этого вида соединения проводников удобнее использовать формулу: Q=I²Rt.

При параллельном соединении проводников не изменяется напряжение (U), тогда для этого вида соединения проводников удобнее использовать формулу: Q=U²t/R.

Физкультминутка.

Закрепление

1) В чем проявляется тепловое действие тока?

(В нагревании проводника)

2) Как можно объяснить нагревание проводника с током?

(Движущиеся электроны взаимодействуют с ионами кристаллической решетки и передают им свою энергию)

4) Как по закону Джоуля – Ленца рассчитать количество теплоты, выделяемое в проводнике?

(Q=I²Rt)

Решение задач

Давайте решим задачу на практике.

У вас на столе приборы. С их помощью мы рассчитаем количество теплоты, выделяемое проводником с током за 1 секунду. Но сначала вспомним правила техники безопасности.

1.Учащийся соблюдает дисциплину, сохраняет тишину; не делает резких движений, чтобы не зацепить оборудование руками. Учащийся без разрешения учителя не берёт приборы и другое оборудование для лабораторных работ.

2. Учащийся поддерживает порядок на своём рабочем месте в течение урока.

3. Учащиеся используют источники тока напряжением не выше 42В переменного и не выше 110В постоянного тока.

4. Производят сборку электрических цепей, переключение их, монтаж и ремонт электрических устройств только при отключенном источнике питания.

5. Следят, чтобы изоляция проводов была исправной, на концах проводов были наконечники.

6. При сборке электрических цепей, провода располагают аккуратно, наконечники проводов плотно зажимают клеммами.

7. По окончании работы необходимо отключить источник питания.

8. Обнаружив неисправность в электрических устройствах, находящихся под напряжением, немедленно отключите источники питания и сообщите об этом учителю.

9. По окончании лабораторной работы учащийся приводит в порядок рабочее место, аккуратно складывает приборы и оборудование в порядке, указанном учителем.

Определить количество теплоты, выделяемое проводником, сопротивление которого 35 Ом, в течении 5 минут. Сила тока в проводнике 5 А.

Дано:

R=35 Ом

t=5 мин

I=5 А

Q= ?

Си

—

300 с

—

Решение:

Q=I²Rt

Q= (5A)^{2 .}35 Ом ^.300 с = 262500Дж =

= 262,5 кДж

Ответ: Q=262,5 кДж

2. Проволочная спираль, сопротивление которой в нагретом состоянии 55 Ом, включена в сеть напряжением 127 В. Какое количество теплоты выделит спираль за 1 мин?

Мини тест.

Чье имя носит закон, выражающий зависимость количества теплоты, выделяемого проводником с током, от силы тока и сопротивления?

А) Ампера. Б)Ома. В) Джоуля-Ленца.

Какая формула выражает закон Джоуля-Ленца?

А) Q=I²Rt Б) Q=UIt В)Q=Pt

3. Как зависит количество теплоты, выделяемое проводником с током, от квадрата силы тока?

А) Прямо пропорционально. Б) Обратно пропорционально. В) Не зависит.

4. Как зависит количество теплоты, выделяемое проводником с током, от сопротивления проводника?

А) Обратно пропорционально. Б) Прямо пропорционально. В) Не зависит.

5. Как зависит количество теплоты, выделяемое проводником с током, от времени?

А)Не зависит. Б) Обратно пропорционально. В) Прямо пропорционально.

Поменяйтесь листочками и выполните взаимопроверку.

Ответы: 1.В 2.А 3.А 4. Б 5.В.

Решить задачу (устно)

Какую работу совершит ток силой 5 А за 2 с при напряжении в цепи 10 В?

(100 Дж)

Вспомним некоторые вопросы, которые потребуются, чтобы изучить новую тему:

1. Какие три величины связывают закон Ома?

(I, U, R; сила тока, напряжение, сопротивление.)

2. Как формулируется закон Ома?

(Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.)

3. Что представляет собой электрический ток в металлах?

(Эл-ий Ток в металлах представляет собой упорядоченное движение свободных электронов )

4. Какова зависимость силы тока от напряжения?

( Во сколько раз увеличивается напряжение в цепи, во столько же раз увеличивается и сила тока)

5. Как выразить работу тока за некоторое время?

( А=U*I*t )

6. Как рассчитать мощность электрического тока?

(P=U*I)

7. При каком соединении все потребители находятся при одной и той же силе тока?

(При последовательном соединении)

Новый материал.

На (слайде 4) изображены электроприборы(потребители электрического тока):

Назвать приборы изображенные на слайде.

Какой прибор не вписывается в общий ряд? Уберите лишний.

Чем вы руководствовались, делая выбор?

Какое действие электрического тока проявляется в выбранных приборах?

(тепловое)

Выяснить, почему проводники нагреваются? (слайд 5)

Электрический ток в металлическом проводнике – это упорядоченное движение

электронов. Провод — это кристалл из ионов, поэтому электронам приходится «течь»

между ионами, постоянно наталкиваясь на них. При этом часть кинетической энергии электроны передают ионам, заставляя их колебаться сильнее. Кинетическая энергия

ионов увеличивается, следовательно увеличивается внутренняя энергия проводника,

и следовательно его температура. А это и значит что, проводник нагревается

От каких величин зависит нагревание проводника? (слайд 6)

Многочисленные опыты показывают, что чем больше сила тока в проводнике тем и количество теплоты, выделившееся в проводнике будет больше. Значит, нагревание проводника зависит от силы тока (I).

(Чем больший электрический заряд пройдет через поперечное сечение проводника в единицу времени, тем большее количество теплоты он выделит)

Но не только сила тока отвечает за то, что выделяется большое количество теплоты.

Был проведен эксперимент.

(Были взяты 3 проводника одинаковой длины и площади поперечного сечения, но из разного вещества. Все проводники соединены между собой последовательно. Следовательно, сила тока на всех участках цепи одинаковая. Но при включении в цепь все 3 проводника выделили разное количество теплоты.

(Слайд 7)

Следовательно, количество теплоты зависит не только от силы тока, но и от того, из какого вещества изготовлен проводник. Точнее — от электрического сопротивления проводника (R)

(Сравнить удельное сопротивление проводников в таблице)

Вопр. Что нужно чтобы проводник нагревался сильнее?

Вывод: Чтобы проводник нагревался сильнее, он должен обладать большим удельным сопротивлением.

(Слайд 8)

От чего зависит количество теплоты в проводнике с током?

Вывод: Количество теплоты, которое выделяется при протекании электрического тока по проводнику, зависит от силы тока в этом проводнике и от его электрического сопротивления.

Закон, определяющий тепловое действие тока – ЗАКОН ДЖОУЛЯ-ЛЕНЦА

Автобиографическая справка

Рассказать о английском физике Джеймсе Прескотте Джоулье (1818-1889 гг. )

и русском физике Ленц Эмилий Христианович (1804 – 1865)

(Слайд 9)

Как записывается закон Джоуля-Ленца

Q=I²Rt

Количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени.

Q – количество теплоты — [Дж]

I – сила тока – [A]

R – сопротивление – [Ом]

t – время – [c]

Формулу, которую мы получили, в точности соответствует формуле, которую мы изучили ранее. Это формула работы электрического тока

A=UIt из закона Ома I=U/R следует U=IR следовательно A=IRIt что соответствует закону Джоуля-Ленца Q=I²Rt

Вывод: Количество теплоты электрического тока равно работе электрического тока.

Q=A

Закрепление (Систематизация знаний)

(Слайд 10)

1) В чем проявляется тепловое действие тока?

(В нагревании проводника)

2) Как можно объяснить нагревание проводника с током?

(Движущиеся электроны взаимодействуют с ионами кристаллической решетки и передают им свою энергию)

3) Какие превращения энергии происходят при протекании тока через проводник?

(Электрическая энергия превращается во внутреннюю)

4) Как по закону Джоуля – Ленца рассчитать количество теплоты, выделяемое в проводнике?

(Q=I²Rt)

Решение задач

(Слайд 11)

Определить количество теплоты, выделяемое проводником, сопротивление которого 35 Ом, в течении 5 минут. Сила тока в проводнике 5 А.

Решение типовых задач по содержательным линиям экзаменационных работ ОГЭ 2016 года

(Слайды 12 – 18)

Домашнее задание

(Слайд 19)

§53, вопросы на стр. 151, упр. 27(1-3).

Решение задач (последовательное и параллельное соединение проводников) – методическая разработка для учителей, Байбергенова Жанат Амангельдиновна

Цели обучения:	8.4.3.12 – рассчитывать электрические цепи, используя закон Ома для участка цепи в последовательном и параллельном соединении проводников. 8.4.3.2 – применять условные обозначения элементов электрической цепи и объяснять их назначение.
Цели урока:	Закрепить ранее изученный материал и решить задачи (уметь сравнивать два вида соединения и делать вычисления; уметь самостоятельно рисовать электрические схемы и собирать цепь; использовать закон Ома для участка цепи в последовательном и параллельном соединении).
Критерии успеха:	Учащийся достиг цели обучения, если правильно собирает последовательные и параллельные цепи; выполняет расчеты для тока и напряжения, используя закон Ома для участка цепи; вычисляет общее сопротивление цепи; делает правильные выводы.
Языковые цели:	Учащиеся могут: — устно рассказать о различиях последовательного и параллельного соединения; — объяснить, где используется параллельное и последовательное соединение, и выразить свои мысли, используя физические термины.
Привитие ценностей:	Воспитание ценностей (уважение, глобальное гражданство) посредством рассмотрения вопроса, влияющего на взаимодействие и взаимосвязь общин на местном уровне.
Межпредметные связи:	Химия.
Предварительные знания:	Учащиеся знают понятия электрический ток, сила тока, напряжение, сопротивление. Они знакомы с законом Ома для участка цепи, умеют собирать простые схемы электрических цепей.

Ход урока

Запланированные этапы урока

Запланированная деятельность на уроке

Ресурсы

Начало 1 урока
2 мин.

5–7 мин.

Организационный момент.
В начале урока сделать акценты на:
— концентрацию внимания учащихся;
— совместно с учащимися определить цели урока/ЦО;
— определить «зону ближайшего развития» учащихся, ожидания к концу урока.
Сегодня наш урок на тему: «Решение на последовательное и параллельное соединение проводников».
Наш урок будет в форме аукциона. Аукцион («auctio» (лат.) – продажа на открытом аукционе) – это метод продажи, при котором товары предварительно выставляются на проверку. Я выставляю типы заданий на аукцион, объявляю количество баллов за каждый тип. Вы предлагаете ответы, получаете за них баллы, которые будут суммироваться индивидуально для каждого из вас. В конце урока сумма баллов будет определять ваши достижения цели.

Разминка. Игра «Рулетка»
http://www.classtools.net/random-name-picker/

Учитель заранее в поле игры вписывает имена учащихся.
Правила игры: Включают рулетку, и она выбирает ученика, который должен ответить на вопрос. Если ученик отвечает неверно, то он выбывает. Выигрывает оставшийся ученик.
ЦО:
— 8.4.3.1 объяснять возникновение и условия существования электрического тока;
— 8.4.3.4 объяснять физический смысл напряжения и применять формулу при решении задач;
— 4.3.6 объяснять физический смысл сопротивления, его единицы измерения.

Критерии успеха
Учащийся достиг цели, если…
— верно отвечает на вопросы;
— знает различия между силой тока, напряжением и сопротивлением;
— знает, чем обусловлен электрический ток в металлах;
— знает условия существования электрического тока;
— знает закон Ома;
— не шумит и не мешает ответам других учеников.
Вопросы для аудитории
1. Чем обусловлен электрический ток в металлах?
2. Почему проводники нагреваются?
3. От чего зависит нагревание металлического проводника?

Далее для продолжения хода игры учитель раздает карточки и применяет метод «Иерархии бриллиантов» (можно применять при объяснении темы на уроке для лучшего понимания и усвоения ключевых моментов. Он формирует навыки: совместной работы, критического мышления, принятия решений, ранжирования определенных вопросов и его обоснования). В данном случае метод направлен на определение приоритетов в выборе информации и идей на поставленный вопрос:

4. Какие условия необходимы для существования в цепи электрического тока?
Далее:
1. Ученики разрабатывают или предварительно записывают на карточке или стикере девять идей в отношении определенного вопроса.
2. Ученики отбирают и располагают в верхнем поле одну наиболее приоритетную карточку. Далее, на последующих местах располагают карточки в следующем порядке: на втором месте – две карточки, на третьем – три карточки, на четвертом – две и на пятом, внизу – одна карточка, представляющая наименьший приоритет. Карточки образуют форму бриллианта.
3. Ученики должны стремиться к согласованности мнений, которая достигается совместным обсуждением порядка расположения карточек и его обоснования.

Например,
на 1 месте – наличие свободных электронов;
на 2 месте – свободные электроны движутся упорядоченно, наличие электрического поля осуществляется источником тока;
на 3 месте – разность потенциалов;
на 4 месте – замкнутость электрической цепи;
на 5 месте, внизу – нагревание проводника.

Учебный план и ИОП по предмету физика.

Карточки
Презентация

Середина 1 урока

20 мин.

Основная часть. Аукционные задания.
ЦО: рассчитывать электрические цепи, используя закон Ома для участка цепи в последовательном и параллельном соединении проводников.
Форма деятельности: Индивидуальная работа.
Дифференциация: Ученики решают задания из карточки и презентации, каждая задача оценивается в определенный балл (1 уровень – 0. 5–1 б; 2 уровень – 2 б; 3 уровень – 5 б).
Оценивание: Ученики выполняют 80 % заданий из сборника задач.

Начнем с «аукциониста» электрических соединений. (на экране интерактивной доски слайды со схемами соединений).

Задание №1: На аукцион выставлены на выбор задачи пунктов А, Б по цене 0,5 балла и задача пункта В (достаточный уровень) по цене 1 балл. Решения этих задач потребуются в дальнейшем при рассмотрении более сложных задач. Время выполнения каждого задания не более 2 мин.
А) Разобрать схемы по типу соединений

Б) На какой схеме все лампочки соединены параллельно? (упр.1 из сайта https://bilimland.kz)

Презентация

https://bilimland.kz/ru/courses/physics-ru/ehlektrodinamika/postoyannyj-ehlektricheskij-tok/lesson/provodniki-v-ehlektricheskoi-czepi

карточки с заданием

Конец 1 урока
11 мин.

В) Решите, какие из утверждений обеспечивают правильное описание системы, представленной ниже.
(упр.1) https://bilimland.kz/ru/courses/physics-ru/ehlektrodinamika/postoyannyj-ehlektricheskij-tok/lesson/provodniki-v-ehlektricheskoi-czepi

Учащиеся выполняют задачи в тетрадях и, получив ответ, поднимают руку. Учитель подходит к ним, проверяет и выставляет баллы за правильный ответ. Два ученика в это время решают задачи у доски. Через 2 мин проверяем решения на доске. Ученики у доски получают баллы в случае правильного решения.
Итоги «аукциончика».

Задачи «Аукцион хороших задач»

Ученики вытягивают по жребию пункт задачи и решают (за каждую верно решенную задачу пунктов А-Б по 2 балла; пунктов С-Д по 3 балла). Время выполнения всех пунктов – 15 мин.

Учащиеся выполняют задачу в тетрадях и, получив ответ, поднимают руку. Учитель подходит, проверяет и выставляет 2 балла за правильный ответ.

Задание №2
А) Три проводника А, В и С, по которым протекают токи IА,IВ,IС, включены в цепь параллельно. По графику определите соотношения между токами, протекающими через эти проводники и сопротивлениями этих проводников (упр.2). https://bilimland.kz/ru/courses/physics-ru/ehlektrodinamika/postoyannyj-ehlektricheskij-tok/lesson/provodniki-v-ehlektricheskoi-czepi

Б) Определите общее соединение проводников.
Сопротивление одного резистора равно 1 Ом.

3. Мы продолжаем и у нас «Аукцион сложных задач». Это задание №3 на карточке, лежащей на столе. Правильное решение задачи оценивается в 5 баллов. Время решения 5–7 мин.
Задание №3 ( схема в презентации)
А) При напряжении в сети 180 В в люстре горит три лампочки, две из которых выключаются одним выключателем, а третья – другим выключателем. Сопротивление третьей лампочки – 300 Ом, а сопротивление двух других – 150 Ом.
Б) Рассчитайте сопротивления в схемах. Выберите их из представленных и вставьте на соответствующие места.
( упр.1) https://bilimland.kz/ru/courses/physics-ru/ehlektrodinamika/postoyannyj-ehlektricheskij-tok/lesson/provodniki-v-ehlektricheskoi-czepi

После выполнения учениками задания на доске показывается его решение.
Наконец, самое сложное задание для сегодняшнего урока выставлено на аукцион.

4. «Аукцион конкурсных заданий». Это задание №4 на карточке, лежащей на столе. (Заявка). Правильное решение каждого пункта задачи оценивается в 5 + 5 баллов (каждая верно собранная схема).
Время выполнения – 15 мин.
Формы и методы: Эксперимент. Выполнение практической работы. Учащиеся собирают схемы соединений.
Форма деятельности: Работа в парах или группах.
Формативное оценивание: Комментарий учителя.
В зависимости от оснащения приборами, учитель в праве выбрать способ выполнения задания: либо с приборами, либо виртуально.
Задание №4. Выполнение виртуального задания – https://bilimland.kz/ru/courses/simulyaczii/fizika

А) Соберите цепь по схеме. Замыкая и размыкая ключи, выясните, как работает эта цепь.

Б) Соберите схему соединения батарейки, двух лампочек и двух ключей, при которой включение и выключение каждой лампочки производится «своим» ключом, и начертите электрическую схему.
В) Нарисуйте, а затем соберите схему соединения батарейки, лампочки, звонка и двух ключей, при которой лампочка загорается при включении звонка, но может быть включена и при неработающем звонке.
Окончательные итоги. Максимальное количество решенных задач за урок.

Раздаточный материал: источники тока, ключи, электрические звонки, электронные платы, лампочки, соединительные провода, ноутбуки с подключением в сеть интернет

Конец урока

В конце урока учащиеся проводят рефлексию:
— Что узнал, чему научился?
— Что осталось непонятным?
— Над чем необходимо работать?
Домашнее задание: придумать задачу на смешанное соединение проводников.

Дифференциация – каким образом Вы планируете оказать больше поддержки? Какие задачи Вы планируете поставить перед более способными учащимися?	Оценивание – как Вы планируете проверить уровень усвоения материала учащимися?	Здоровье и соблюдение техники безопасности

Рефлексия по уроку

Используйте данный раздел для размышлений об уроке. Ответьте на самые важные вопросы о Вашем уроке из левой колонки.

Общая оценка

Какие два аспекта урока прошли хорошо (подумайте как о преподавании, так и об обучении)?
1:

Что могло бы способствовать улучшению урока (подумайте как о преподавании, так и об обучении)?
1:

Что я выявил(а) за время урока о классе или достижениях/трудностях отдельных учеников, на что необходимо обратить внимание на последующих уроках?

Приложение 1.

Проводники в электрических цепях могут соединяться последовательно и параллельно.

При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:

I₁ = I₂ = I.

Рисунок 1.9.1.
Последовательное соединение проводников

По закону Ома, напряжения U₁ и U₂ на проводниках равны:
U₁ = IR₁, U₂ = IR₂.
Общее напряжение U на обоих проводниках равно сумме напряжений U₁ и U₂:
U = U₁ + U₂ = I(R₁ + R₂) = IR,
где R – электрическое сопротивление всей цепи. Отсюда следует:

R = R₁ + R₂.

При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U₁ и U₂ на обоих проводниках одинаковы:
U₁ = U₂ = U.
Сумма токов I₁ + I₂, протекающих по обоим проводникам, равна току в неразветвленной цепи:
I = I₁ + I₂.

Рисунок 1.9.2.
Параллельное соединение проводников

Записывая на основании закона Ома

Приложение 2.

Класс: 8

Лаб. 6. Изучение параллельного соединения проводников

1. Сборка электрической цепи и измерение ее основных параметров.
1. Соберите электрическую цепь согласно рисунку, не включая вольтметр.

После проверки цепи учителем замкните ключ. Занесите в таблицу показание II амперметра. Можно ли утверждать, что ток силой II протекает по каждому из резисторов? Почему?
I₀ =;
U₀ =.
2. Подключите вольтметр поочередно в начале к одному из резисторов, потом к другому. Составьте таблицу измерений и запишите в нее показание U вольтметра обоих резисторов. Изобразите схему полной цепи.
3. Подключите вольтметр к обоим резисторам сразу. Напряжение на каком из резисторов измеряет вольтметр? Запишите показания вольтметра.
4. Применяя закон Ома к разветвленному участку, определите и занесите в таблицу его сопротивление.

2. Проверка закономерностей параллельного соединения.
1. Занесите в таблицу паспортные значения R₁ и R₂ резисторов, указанные на их панельках, и по формуле вычислите и занесите в таблицу значение сопротивления разветвленного участка.
R=R₁⋅R₂ /R₁+R₂.
2. Сравните рассчитанное значение R с сопротивлением участка, найденным по результатам измерений. Сделайте вывод.
R₁ (больше/меньше) R₀
3. Сравните значения силы токов I1, I2 в отдельных резисторах и значение силы тока II в неразветвленной части цепи. Сделайте вывод.
I₀ =

Контрольные вопросы:
1. Как соединены потребители электрической энергии в вашей квартире? Почему?
Электрическая энергия в квартире соединена параллельно, т. к. такое соединение позволяет подключить к источнику не зависимо друг от друга различные потребительские приборы, несмотря на их рабочий ток.
Чему равно сопротивление участка цепи, содержащего N параллельно соединенных одинаковых резисторов с сопротивлением каждый?
Сопротивление участка цепи, содержащего N параллельно соединенных резисторов сопротивлением: R₀=R₁/N.
Почему параллельное присоединение к участку цепи дополнительного резистора уменьшает сопротивление участка?
Потому что работа электрического тока на участке цепи зависит от перенесенного заряда и напряжения на этом участке. Ток начинает идти еще и по дополнительному резистору, что и уменьшает сопротивление. (Присоединение увеличивает площадь поперечного сечения участка цепи).

Суперзадание
Объясните, как переносом только одного провода с клеммы на клемму превратить параллельное соединение резисторов в последовательное. Какую роль в такой измененной цепи играет ключ?
Нужно перенести клемму с одного из резисторов на место перед ключом. Ключ играет роль включателя цепи.

Параллельное и последовательное соединение — законы и примеры

Как после перегорания одной лампочки в гирлянде можно определить способ соединения и починить ее? Попробуем разобраться.

Анфиса обнаружила на балконе старую гирлянду. Включив ее в розетку, девочка заметила, что горят все лампочки, кроме зеленых. Внимательно изучив провода, Анфиса увидела, что все зеленые лампочки соединены последовательно друг за другом.

Последовательное соединение проводников

При последовательном соединении конец первого проводника соединяют с началом второго, конец второго — с началом третьего и т. д.

Последовательное подключение обычно используется в тех случаях, когда необходимо целенаправленно включать или выключать определенный электроприбор. Например, для работы школьного электрического звонка требуется соединить его последовательно с источником тока и ключом.

Вот некоторые примеры использования схемы последовательного соединения:

освещение в вагонах поезда или трамвая;
простейшие елочные гирлянды;
карманный фонарик;
амперметр для измерения силы тока в цепи.

Законы последовательного соединения проводников

При последовательном соединении сила тока в любых частях цепи одна и та же:
I = I₁ = I₂ = … = I_n.
Если в цепи с последовательным способом соединения одна из ламп выйдет из строя и через нее не будет протекать электрический ток, то и через оставшиеся лампы ток проходить не будет. Вспомним Анфису и ее гирлянду: когда одна из зеленых лампочек перегорела, то ток, проходящий через нее, стал равен нулю. Следовательно, и другие зеленые лампочки, включенные последовательно, не загорелись. Чтобы починить гирлянду, нужно определить перегоревшую лампочку и заменить ее.
При последовательном соединении общее сопротивление цепи равно сумме сопротивлений отдельных проводников:
R_экв = R₁ + R₂ + … + R_n.
При последовательном соединении общее напряжение цепи равно сумме напряжений на отдельных участках:
U_экв = U₁ + U₂ + … + U_n.

Пример решения задачи

В цепь с напряжением 220 В включена лампа, через нее протекает ток силой 20 А. Когда к лампе последовательно подключили реостат, сила тока в цепи уменьшилась до 11 А. Чему равно сопротивление реостата?

Решение.

По закону Ома определим сопротивление лампы:
R₁ = U / I₁ = 220 / 20 = 11 Ом.
Также по закону Ома определим общее сопротивление цепи при включенном реостате:
R = U / I₂ = 220 / 11 = 22 Ом.
При последовательном соединении сопротивления лампы и реостата складываются:
R = R₁ + R₂.
Зная общее сопротивление цепи и сопротивление лампы, определим искомое сопротивление реостата:
R₂ = R − R₁ = 22 − 11 = 11 Ом.

Ответ: сопротивление реостата равно 11 Ом.

К сожалению, последовательное соединение не всегда оказывается удобным. Например, в торговом центре «Ашан» работает с 9:00 до 23:00, кинотеатр — с 10:00 до 02:30, а магазины — с 10:00 до 22:00. При последовательном соединении цепи свет должен будет гореть во всем ТЦ с 9:00 до 02:30. Согласитесь, что такой режим работы экономически невыгоден даже при минимальном тарифе на электроэнергию. В этом случае удачным решением будет использование параллельного соединения.

Практикующий детский психолог Екатерина Мурашова

Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков

Параллельное соединение проводников

При параллельном соединении начала всех проводников соединяются в одной общей точке электрической цепи, а их концы — в другой.

Параллельное соединение используют в тех случаях, когда необходимо подключать электроприборы независимо друг от друга. Например, если отключить чайник, то холодильник будет продолжать работать. А когда в люстре перегорает одна лампочка, остальные все так же освещают комнату.

Приведем еще несколько примеров применения параллельного способа соединения:

освещение в больших торговых залах;
бытовые электроприборы в квартире;
компьютеры в кабинете информатики;
вольтметр для измерения напряжения на участке цепи.

Параллельное соединение проводников: формулы

Напряжение при параллельном соединении в любых частях цепи одинаково:
U = U₁ = U₂ = … = U_n.
Как вы помните, все бытовые электроприборы рассчитаны на одинаковое номинальное напряжение 220 В. Да и согласитесь, куда проще делать все розетки одинаковыми, а не рассчитывать напряжение для каждого прибора при их последовательном соединении.
Сила тока при параллельном соединении (в неразветвленной части цепи) равна сумме сил тока в отдельных параллельно соединенных проводниках:
I_экв = I₁ + I₂ + … + I_n.
Электрический ток растекается по ветвям обратно пропорционально их сопротивлениям. Если сопротивления в ветвях равны, то и ток при параллельном соединении делится между ними поровну.
Общее сопротивление цепи определяется по формуле:
1 / R_экв = 1 / R₁ + 1 / R₂ + … + 1 / R_n.
Для двух параллельно соединенных проводников формулу можно записать иначе:
R_экв = (R₁ · R₂) / (R₁ + R₂).

Если n одинаковых проводников, каждый из которых имеет сопротивление R₁, соединены параллельно, то общее сопротивление участка цепи можно найти, разделив сопротивление одного из проводников на их количество:

R_экв = R₁ / n.

Вернемся к Анфисе и ее гирлянде. Мы уже разобрались, почему перестали гореть все зеленые лампочки. Пришло время узнать, почему продолжили гореть все остальные. В современных гирляндах используют параллельное и последовательное соединение одновременно. Например, лампочки одного цвета соединяют последовательно, а с другими цветами — параллельно. Таким образом, отключение ветви с зелеными лампочками не повлияло на работу остальной части цепи.

Пример решения задачи

Два резистора с сопротивлениями 10 Ом и 11 Ом соответственно соединены параллельно и подключены к напряжению 220 В. Чему равна сила тока в неразветвленной части цепи?

Решение.

Определим общее сопротивление при параллельном соединении проводников:
R = (R₁ · R₂) / (R1 + R2) = (10 · 11) / (10 + 11) = 110 / 21 Ом ≈ 5,24 Ом.
По закону Ома определим силу тока в цепи:
I = U / R = 220 / (110 / 21) = 42 А.

Ответ: сила тока в неразветвленной части цепи равна 42 А.

Смешанное соединение проводников

Зачастую реальные электрические схемы оказываются сложнее, поэтому используют различные комбинации последовательного и параллельного способов соединения. Такой способ соединения называется смешанным. Смешанное соединение проводников предполагает использование последовательного и параллельного способов соединения в одной цепи.

Алгоритм решения задач со смешанным соединением проводников:

Прочитать условие задачи, начертить схему электрической цепи, при необходимости пронумеровать проводники.
Проанализировать схему, т. е. найти участки, где используется только последовательное или только параллельное соединение проводников. Определить сопротивление на этих участках.
Выяснить вид соединения участков между собой. Найти общее сопротивление всей цепи.
С помощью закона Ома и законов последовательного и параллельного соединения проводников найти распределения токов и напряжений в цепи.

Пример решения задачи

На рисунке показана схема электрической цепи. Сопротивления резисторов одинаковы и равны 12 Ом. Напряжение источника — 100 В. Какова сила тока, протекающего через резистор R₄?

Решение.

Проанализируем данную схему. Резисторы R₂ и R₃ соединены между собой последовательно, а с резистором R₄ — параллельно. Весь этот участок соединен последовательно с источником тока и резистором R₁.
Определим сопротивление последовательно соединенных резисторов R₂ и R₃:
R₂₃ = R₂ + R₃ = 12 + 12 = 24 Ом.
Найдем общее сопротивление резистора R₄ и участка 2–3, соединенных параллельно:
R₂₃₄ = (R₂₃ · R₄) / (R₂₃ + R₄) = (24 · 12) / (24 + 12) = 8 Ом.
Определим общее сопротивление всей цепи как сумму включенных последовательно резистора R₁ и участка 2–3–4:
R_экв = R₁ + R₂₃₄ = 12 + 8 = 20 Ом.
По закону Ома найдем силу тока в неразветвленной части цепи:
I = U / R_экв = 200 / 20 = 5 А.
По закону Ома определим напряжение на участке, состоящем из резисторов R₂, R₃, R₄:
U_экв1 = I · R₂₃₄ = 5 · 8 = 40 В.
Поскольку при параллельном соединении напряжение одинаково, то напряжение на резисторе R₄ также равно 40 В. По закону Ома найдем силу тока, протекающего через резистор R₄:
I₄ = U_экв1 / R₄ = 40 / 12 ≈ 3,3 А.

Ответ: через резистор R₄ протекает ток силой приблизительно 3,3 А.

Мы разобрали довольно много формул последовательного и параллельного подключения проводников. А запомнить их можно с помощью вот таких схем:

Скачать шпаргалку

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи. На уроках вы научитесь составлять самые разнообразные электрические цепи и решать задачи с ними, а также узнаете об их применении в жизни. Ждем вас!

Задачи на последовательное соединение проводников

Репетитор
по физике

916 478 1032

П
Р
О
Г
Р
А
М
М
И
Р
О
В
А
Н
И
Е
Репетитор
916 478 1032

Репетитор
по физике

916 478 1032

Репетитор
по алгебре

916 478 1032

Репетитор
по физике

916 478 1032

\( I_{общ}=I_1=I_2=I_3 \)
\( U_{общ}=U_1+U_2+U_3 \)
\( R_{общ}=R_1+R_2+R_3 \)

Пройти тест на эту тему

Задача 1. (Последовательное соединение проводников)
Сопротивления \(R_1=2 \ \ Ом \) и \(R_2=3 \ \ Ом \) соединены последовательно.
Найти сопротивление цепи.

Показать ответ Показать решение Видеорешение

Ответ: \(R_{общ}=5 \ \ Ом \)

Дано: \( R_1=2 \ \ Ом \)

\( R_2=3 \ \ Ом \)

\(R_{общ}-?\)

\( R_{общ}=R_1+R_2=2 \ \ Ом + 3 \ \ Ом=5 \ \ Ом \)

Ответ: \( R_{общ}= 5 \ Ом \)

Задача 2. (Последовательное соединение проводников)
Напряжение на контактах батарейки \(U_{общ}=15 \ В \; \), \(R_1=2 \ Ом \), \(R_2=3 \ Ом \). Вычислить силу тока цепи.

Показать ответ Показать решение Видеорешение

Ответ: \( I_{общ}=3 \ А\)

Дано:
\( U_{общ}=15 \ В \)

\( R_1=2 \ Ом \)

\( R_2=3 \ Ом \)

\(I_{общ}-?\)

\( R_{общ}=R_1+R_2 \)

\( I_{общ}=\dfrac{U_{общ}}{R_{общ}}=\dfrac{U_{общ}}{R_1+R_2}=\dfrac{15 В}{2 \ Ом + 3 \ Ом}=3 А\)

Ответ: \( I_{общ}=3 \ А \)

Задача 3. (Последовательное соединение проводников)
Напряжение на контактах батарейки \(U_{общ}=15 \ В \; \), \(R_1=2 \ Ом \), \(R_2=3 \ Ом \). Вычислить напряжение на каждом из сопротивлений.

Показать ответ Показать решение Видеорешение

Ответ: \(U_1=6 \ В, \;\; U_2=9 \ В\)

Дано:
\( U_{общ}=15 \ В \)

\( R_1=2 \ Ом \)

\( R_2=3 \ Ом \)

\(U_1-?\)

\(U_2-?\)

\( R_{общ}=R_1+R_2 \)

\( I_{общ}=\dfrac{U_{общ}}{R_{общ}}=\dfrac{U_{общ}}{R_1+R_2}=\dfrac{15 \ В}{2 \ Ом + 3 \ Ом}=3 А\)

\( I_1=I_2=I_{общ}= 3 \ А \)

\( U_1=I_1R_1=3 \ А \cdot 2 \ Ом=6 \ В\)

\( U_2=I_2R_2=3 \ А \cdot 3 \ Ом=9 \ В\)

Ответ: \(U_1=6 \ В, \;\; U_2=9 \ В\)

Заметим, что \(6 \ В+9 \ В=15 \ В\)

Задача 4. (Последовательное соединение проводников)

Напряжение на контактах батарейки \(U_{общ}=12 \ В \; \), \(R_1=1 \ Ом \), \(R_2=2 \ Ом ,\;\;\;R_3=3 \ Ом \). Вычислить напряжение на каждом из сопротивлений.

Показать ответ Показать решение Видеорешение

Ответ: \(U_1=2 \ В, \;\; U_2=4 \ В, \;\; U_3=6 \ В\)

Дано:
\( U_{общ}=12 \ В \)

\( R_1=1 \ Ом \)

\( R_2=2 \ Ом \)

\( R_2=3 \ Ом \)

\(U_1-?\)

\(U_2-?\)

\(U_3-?\)

\( R_{общ}=R_1+R_2 +R_3\)

\( I_{общ}=\dfrac{U_{общ}}{R_{общ}}=\dfrac{U_{общ}}{R_1+R_2+R_3}=\dfrac{12 В}{1Ом+2 Ом + 3 Ом}=2 А\)

\( I_1=I_2=I_3=I_{общ}= 2 \ А\)

\( U_1=I_1R_1=2 \ А\cdot 1 \ Ом=2 \ В\)

\( U_2=I_2R_2=2 \ А\cdot 2 \ Ом=4 \ В\)

\( U_3=I_3R_3=2 \ А\cdot 3 \ Ом=6 \ В\)

Ответ: \(U_1=2 \ В, \;\; U_2=4 \ В,\;\; U_2=6 \ В\)

Заметим, что \(2 \ В+4 \ В+6 \ В=12 \ В\)

Задача 5. (Последовательное соединение проводников)

Напряжение на контактах батарейки \(U_{общ}=12 \ В \; \), \(R_1=0,5 \ Ом \), \(R_2=1,5 \ Ом ,\;\;\;R_3=1 \ Ом,\;\;\;R_4=2 \ Ом \). Вычислить напряжение на резисторе \(R_1 \) .

Показать ответ Показать решение Видеорешение

Ответ: \(U_1=1,2 \ В\)

Дано:
\( U_{общ}=12 \ В \)

\( R_1=0,5 \ Ом \)

\( R_2=1,5 \ Ом \)

\( R_3=1 \ Ом \)

\( R_4=2 \ Ом \)

\(U_1-?\)

\( R_{общ}=R_1+R_2 +R_3+R_4\)

\( I_{общ}=\dfrac{U_{общ}}{R_{общ}}=\dfrac{U_{общ}}{R_1+R_2+R_3+R_4}=\dfrac{12 В}{0,5 \ Ом+1,5 \ Ом + 1 \ Ом+ 2 \ Ом}=2,4 \ А\)

\( I_1=I_{общ}= 2,4 \ А\)

\( U_1=I_1R_1=2,4 А\cdot 0,5 \ Ом=1,2 \ В\)

Ответ: \(U_1=1,2 \ В\)

Задача 6. (Последовательное соединение проводников)

Напряжение цепи \(U_{цепи}=120 \ В \; \), \(R_1=2,5 \ Ом \), \(R_2=1,5 \ Ом ,\;\;\;R_3=1 \ Ом \). Вычислить напряжение на резисторе \(R_2 \) .

Показать ответ Показать решение Видеорешение

Ответ: \(U_2=36 \ В\)

Дано:
\( U_{общ}=120 \ В \)

\( R_1=2,5 \ Ом \)

\( R_2=1,5 \ Ом \)

\( R_3=1 \ Ом \)

\(U_2-?\)

\( R_{общ}=R_1+R_2 +R_3\)

\( I_{общ}=\dfrac{U_{общ}}{R_{общ}}=\dfrac{U_{общ}}{R_1+R_2+R_3}=\dfrac{120 \ В}{2,5 \ Ом+1,5 \ Ом + 1 \ Ом}=24 \ А\)

\( I_2=I_{общ}= 24 \ А\)

\( U_2=I_2R_2=24 \ А\cdot 1,5 \ Ом=36 \ В\)

Ответ: \(U_2=36 \ В\)

Задача 7. (Последовательное соединение проводников)

Амперметр А показывает силу тока \(I_{общ}=4 \ А \; \), \(R_1=1,5 \ Ом \), \(R_2=2,5 \ Ом \). Вычислить напряжение на каждом из сопротивлений и напряжение цепи (общее)

Показать ответ Показать решение Видеорешение

Ответ: \(U_1=6 \ В, \;\; U_2=10 \ В ,\;\; U_{общ}=16 \ В\)

Дано:
\( I_{общ}=4 \ А \)

\( R_1=1 \ Ом \)

\( R_2=2,5 \ Ом \)

\(U_1-?\)

\(U_2-?\)

\(U_{общ}-?\)

\( I_1=I_2=I_{общ}= 4 \ А\)

\( U_1=I_1R_1=4 \ А\cdot 1,5 Ом=6 \ В\)

\( U_2=I_2R_2=4 \ А\cdot 2,5 Ом=10 \ В\)

\( U_{общ}= U_1+U_2=6 \ В+4 \ В=10 \ В \)

Ответ: \(U_1=6 \ В, \;\; U_2=10 \ В,\;\; U_{общ}=16 \ В \)

Задача 8. (Последовательное соединение проводников)

Амперметр А показывает силу тока \(I_{общ}=0,7 \ А \; \), \(R_1=1,5 \ Ом, \;R_2=2,5 \ Ом , \;R_3=3 \ Ом \). Вычислить напряжение цепи (общее)

Показать ответ Показать решение Видеорешение

Ответ: \(U_{общ}=4,9В\)

Дано:
\( I_{общ}=0,7 А \)

\( R_1=1,5 \ Ом \)

\( R_2=2,5 \ Ом \)

\( R_3= 3 \ Ом \)

\(U_{общ}-?\)

\( I_1=I_2=I_3=I_{общ}= 0,7 А\)

\( U_1=I_1R_1=0,7 А\cdot 1,5 Ом=1,05 \ В\)

\( U_2=I_2R_2=0,7 А\cdot 2,5 Ом=1,75 \ В\)

\( U_3=I_3R_3=0,7 А\cdot 3 Ом=2,1 \ В\)

\( U_{общ}= U_1+U_2+U_3=1,05 В+1,75 В+2,1 В=4,9 \ В\)

Ответ: \( U_{общ}=4,9 \ В \)

Задача 9. (Последовательное соединение проводников)

Амперметр показывает силу тока \(I_{общ}=1,7 \ А \; \), \(R_1=1 \ Ом, \;R_2=2,5 \ Ом , \;R_3=31 \ Ом \). Вычислить напряжение на резисторе \( R_2 \)

Показать ответ Показать решение Видеорешение

Ответ: \(U_2=4,25В\)

Дано:
\( I_{общ}=1,7 А \)

\( R_1=1 \ Ом \)

\( R_2=2,5 \ Ом \)

\( R_3= 31 \ Ом \)

\(U_2-?\)

\( I_2=I_{общ}= 1,7 А\)

\( U_2=I_2R_2=1,7 А\cdot 2,5 Ом=4,25 В\)

Ответ: \( U_2=4,25В \)

Задача 10. (Последовательное соединение проводников)

Амперметр показывает силу тока \(I_{общ}=1,7 А \; \), \(R_1=1 \ Ом, \;R_2=2,5 \ Ом , \;R_3=31 \ Ом \). Какое напряжение показывает вольтметр \( V \; \) ?

Показать ответ Показать решение Видеорешение

Ответ: \(U_2=4,25В\)

Дано:
\( I_{общ}=1,7 А \)

\( R_1=1 \ Ом \)

\( R_2=2,5 \ Ом \)

\( R_3= 31 \ Ом \)

\(U_2-?\)

Вольтметр показывает напряжение на втором сопротивлении

\( I_2=I_{общ}= 1,7 А\)

\( U_2=I_2R_2=1,7 А\cdot 2,5 Ом=4,25 В\)

Ответ: \( U_2=4,25В \)

Задача 11. (Последовательное соединение проводников)

Ответ: \(U_2=58,65 \ В\)

Дано:
\( I_{общ}=1,7 \ А \)

\( R_1=1 \ Ом \)

\( R_2=2,5 \ Ом \)

\( R_3= 31 \ Ом \)

\(U_2-?\)

Вольтметр показывает напряжение цепи

\( U_{общ}= I_{общ}\cdot R_{общ}=I_{общ}\cdot(R_1+R_2+R_3) \)
\( U_{общ}=1,7 \ А\cdot(1 \ Ом+2,5 \ Ом +31 \ Ом)= 58,65 \ В \)

Ответ: \( U_2=58,65 \ В \)

Задача 12. (Последовательное соединение проводников)

Амперметр показывает силу тока \(I_{общ}=3 \ А \; \), \(R_1=1 \ Ом, \;R_2=2 \ Ом , \;R_3=3 \ Ом \). Какое напряжение показывает вольтметр \( V \; \) ?

Показать ответ Показать решение Видеорешение

Ответ: \( U_{12}=9 \ В \)

Дано:
\( I_{общ}=3 \ А \)

\( R_1=1 \ Ом \)

\( R_2=2 \ Ом \)

\( R_3= 3 \ Ом \)

\(U_{12}-?\)

Вольтметр показывает сумму напряжений на первом и втором сопротивлении

\( I_1= I_2=I_{общ}=3А \)

\( U_1= I_1\cdot R_1=3А\cdot 1 \ Ом= 3В \)
\( U_2=I_2\cdot R_2=3А\cdot 2 \ Ом= 6В \)
\( U_{12}=3В+ 6В =9В\)

Ответ: \( U_{12}=9В \)

Задача 13. (Последовательное соединение резисторов)

Сила тока цепи, изображенной на рисунке \(I_{общ}=0,3 \ А \; \), а ее напряжение \(U_{общ}=9\ В . \) Сопротивления резисторов \(R_1=12 \ Ом, \;R_2=2 \ Ом . \) Найти сопротивление третьего резистора.

Показать ответ Показать решение Видеорешение

Ответ: \( R_3= 16 \ Ом \)

Сначала запишем закон Ома для всей цепи,

а потом из него найдем общее сопротивление цепи :

Дано:
\( I_{общ}=0,3 \ А \)

\( R_1=12 \ Ом \)

\( R_2=2 \ Ом \)

\( U_{общ}= 9 \ В \)

\(R_3-?\)

\(I_{общ}= \dfrac{U_{общ}}{R_{общ}} \)

\(R_{общ}= \dfrac{U_{общ}}{I_{общ}} \)

\(R_{общ}= \dfrac{9 \ В}{ 0,3 \ А } =30 \ Ом \)

\( R_{общ}= R_1+R_2+R_3 \)

\( R_{общ}- R_1-R_2=R_3 \)

\( R_3=R_{общ}- R_1-R_2=30 \ Ом — 12 \ Ом- 2 \ Ом =16 \ Ом \)

Ответ: \( R_3= 16 \ Ом \)

1. Контрольный 4,4А
Напряжение на контактах батарейки \(U_{общ}=22 В \; \), \(R_1=2 \ Ом \), \(R_2=3 \ Ом \). Найти силу тока цепи.

2. Контрольный 8,8В
Напряжение на контактах батарейки \(U_{общ}=22 В \; \), \(R_1=2 \ Ом \), \(R_2=3 \ Ом \). Найти напряжение на первом резисторе.

3. Контрольный 18В
Напряжение на контактах батарейки \(U_{общ}=42 В \; \), \(R_1=2 \ Ом \), \(R_2=3 \ Ом \), \(R_3=2 \ Ом \) Найти напряжение на резисторе \(R_2\).

4. Контрольный 33В
Напряжение на контактах батарейки \(U_{общ}=66 В \; \), \(R_1=1 \ Ом \), \(R_2=1 \ Ом \;\; R_3=1 \ Ом\;\; R_4=3 \ Ом. \) Найти напряжение на резисторе \(R_4\).

5. Контрольный 1,6В
Амперметр А показывает силу тока \(I_{общ}=0,2 А \; \), \(R_1=3,5 \ Ом \), \(R_2=4,5 \ Ом \). Вычислить напряжение цепи (общее)

6. Контрольный 0,2В
Амперметр А показывает силу тока \(I_{общ}=2 \ мА \; \), \(R_1=35 \ Ом \), \(R_2=45 \ Ом \),\(R_3=20 \ Ом \). Вычислить напряжение цепи (общее)

7. Контрольный 24,5В
Амперметр А показывает силу тока \(I_{общ}=700 \ мА \; \), \(R_1=20 \ Ом \), \(R_2=5 \ Ом \),\(R_3=10 \ Ом \). Вычислить напряжение цепи (общее)

Резисторы в цепях — Практика — Гиперучебник по физике

[закрыть]

практическая задача 1

Определите следующие величины для каждой из двух цепей, показанных ниже…

эквивалент сопротивления
ток от блока питания
ток через каждый резистор
падение напряжения на каждом резисторе
мощность, рассеиваемая на каждом резисторе

раствор

Соблюдайте правила для последовательных цепей.

Сопротивления последовательно складываются.
Р _Т = Р ₁ + Р ₂ + Р ₃
Р _Т = 20 Ом + 30 Ом + 50 Ом
R _T = 100 Ом
Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи.
I _T = V _T / R _T
I _T = 125 V/100 Ω
I _T = 1.25 A
Постоянный ток через резисторы, соединенные последовательно.
I _T = I ₁ = I ₂ = I ₃ = 1,25 A
Падение напряжения можно найти по закону Ома.
V ₁ = I ₁ R ₁
V ₁ = (1.25 A) (20 ω) ₁ = (1.25 A) (20 ω)0115 В ₁ = 25,0 В
V ₂ = I ₂ R ₂
V ₂ = (1,25 A) (30.
59.

. В
V ₃ = I ₃ R ₃
V ₃ = (1,25 A) (50’115) ₃ = (1,25 A) (50.11) ₃ = (1,25 A) (50.11) ₃ = (1,25 A) (5015) ₃ = (1,25 A) (5015) ₃.0087 В ₃ = 62,5 В
Проверьте свои расчеты, добавив падение напряжения. В последовательной цепи они должны равняться увеличению напряжения источника питания.
В _Т = В ₁ + В ₂ + В ₃
125 В = 25,0 В + 37,5 В + 62,5 В
125 В = 125 В
Мы в порядке, так что давайте закончим.

Есть три уравнения для определения мощности. Поскольку у нас есть три резистора, давайте в качестве упражнения применим к каждому отдельное уравнение.

P ₁ = В ₁ I ₁
P ₁ = (25,0 В) (1,25 A)
P ₁ = 31,250 W

P ₂ = I ₂ ² R ₂
P ₂
P ₂
P ₂
P ₂.

₂ = 46,875 Вт

П ₃ = V ₃ ² / R ₃
P ₃ = (62,5 В) ² / (50 Ω)
7 9999999999. 99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999979.
8 2 / (50 Ω)
7777777999.
8 2 /.

В последовательной цепи элемент с наибольшим сопротивлением потребляет наибольшую мощность.

Соблюдайте правила для параллельных цепей.

Параллельные сопротивления объединяются по правилу суммы обратных величин.

1	=	1	+	1	+	1
Р _Т		Р ₁		Р ₂		Р ₃
1	=	1	+	1	+	1
Р _Т		20 Ом		100 Ом		50 Ом
1	=	5	+	1	+	2
Р _Т		100 Ом		100 Ом		100 Ом
1	=	8
Р _Т		100 Ом
Р _Т	=	100 Ом	= 12,5 Ом
		8

Суммарный ток определяется напряжением источника питания и эквивалентным сопротивлением цепи.
I _T = V _T / R _T
I _T = 125 V/12.5 Ω
I _T = 10 А
(Примечание: мы ответим на часть 4 перед частью 3.) В параллельной цепи каждая ветвь испытывает одинаковое падение напряжения.
V _T = V ₁ = V ₂ = V ₃ = 125 В
Ток в каждой ветви можно найти по закону Ома.
I ₁ = V ₁ / R ₁
I ₁ = (125 В) / (20 Ом)
I ₁ = 6.25 A
I ₂ = V ₂ / R ₂
I ₂ = (125 V)/(100 Ω)
I ₂ = 1,25 А
I ₃ = V ₃ / R ₃
I ₃ = (125 В) / (50 Ом)
I ₃ = 2. 50 A I ₃ = 2.50 A I ₃ = 2,50 A I ₃ = 2,50 A I
Проверьте свои расчеты, добавив токи. При параллельной схеме они должны суммироваться с током от источника питания.
I _Т = I ₁ + я ₂ + I ₃
10 А = 6,25 А + 1,25 А + 2,50 А
10 А = 10 А
Хорошо, работает.
Снова в качестве упражнения используйте другое уравнение для определения электрической мощности каждого резистора.
P ₁ = V ₁ I ₁
P ₁ = (125 В) (6,25 A)
1 P 41414141414141414141414141414141414141414141. 900 40041414141414141414141414141414141414141414.900.
P ₂ = I ₂ ² R ₂
P ₂
P ₂
P ₂
P ₂ 9035 .
.9001,1,1,1,1,1,1,1,9035
9.. ₂ = 156,25 Вт
P ₃ = V ₃ ² / R ₃
P ₃
P _{3 ₃
P ₃
. P ₃ = 312,50 Вт}
В параллельной цепи элемент с наименьшим сопротивлением потребляет наибольшую мощность.

практическая задача 2

На кухне в Северной Америке есть три прибора, подключенных к сети 120 В с автоматическим выключателем на 15 А: кофеварка на 850 Вт, микроволновая печь на 1200 Вт и 900 Вт тостер.

Нарисуйте принципиальную схему этой цепи.
Какие из этих приборов могут работать одновременно без срабатывания автоматического выключателя?

раствор

Розетки подключены параллельно , так что приборы в цепи независимы друг от друга. Выключение кофеварки не приведет к отключению тостера (при условии, что оба были включены одновременно). Каждый прибор также получит одинаковое регулируемое напряжение, что упрощает конструкцию электрических устройств. Недостатком этой схемы является то, что параллельные токи могут составлять опасно высокие уровни. А 9Автоматический выключатель 0087 в серии перед параллельными ответвлениями может предотвратить перегрузку, автоматически размыкая цепь.

Цепь 15 А, работающая при напряжении 120 В, потребляет 1800 Вт общей мощности.

P = VI = (120 В)(15 А) = 1800 Вт

Полная мощность в параллельной цепи представляет собой сумму мощности, потребляемой на отдельных ветвях.

Кофеварка	+	микроволновая печь
850 Вт	+	1200 Вт
2050 Вт

микроволновая печь	+	тостер
1200 Вт	+	900 Вт
2100 Вт

тостер	+	кофеварка
900 Вт	+	850 Вт
1750 Вт

В этом контуре одновременно могут работать только кофеварка и тостер . Все другие комбинации вызовут размыкание автоматического выключателя.

практическая задача 3

На приведенной ниже схеме показана схема с одной батареей и 10 резисторами; 5 слева и 5 справа. Определять…

ток через
падение напряжения на
мощность, рассеиваемая каждым резистором

раствор

Чтобы решить сложную проблему, нужно разбить ее на ряд более простых задач. Однако будьте осторожны, чтобы не упустить из виду свою цель среди всех кусочков. Перед началом проложите свой курс. В этом случае мы начнем с нахождения эффективного сопротивления всей цепи и тока от батареи. Это позволяет нам получить ток во всех различных сегментах цепи. (Ток делится и снова делится, пытаясь следовать по пути наименьшего сопротивления.) После этого легко рассчитать падение напряжения на каждом резисторе, используя В = IR и мощность, рассеиваемая при использовании P = VI . Никакая часть этой задачи не является сложной сама по себе, но поскольку схема очень сложна, мы некоторое время будем очень заняты.

Начнем процесс с объединения резисторов. В этой цепи четыре последовательных пары.

левый
R _с = 3 Ом + 1 Ом R _с = 4 Ом R _с = 4 Ом + 2 Ом Ч _с = 6 Ом

справа
R _S = 2 ω+3 ω R _S = 5 Ом R _S = 1 Ом+4 0115 R S = 1 Ом+40115 R S = 4 ω .

Эти пары образуют две параллельные цепи, одну слева и одну справа.

левый

1	=	1	+	1
Р _р	=	4 Ом	+	6 Ом

1	=	5
Р _р	=	12 Ом

Р _р =	12 Ом	= 2,4 Ом
	5

справа

1	=	1	+	1
Р _р	=	5 Ом	+	5 Ом

1	=	2
Р _р	=	5 Ом

Ч _р =	5 Ом	= 2,5 Ом
	2

Каждая группа из четырех резисторов соединена последовательно с другой.

левый
R _с = 2,4 Ом + 0,6 Ом R _с = 3 Ом

справа
R _с = 2,5 Ом + 0,5 Ом Ч _с = 3 Ом

Левая и правая половины схемы параллельны друг другу и батарее.

1	=	1	+	1	=	2
Р _р	=	3 Ом	+	3 Ом	=	3 Ом

Р _р =	3 Ом	= 1,5 Ом
	2

Теперь, когда у нас есть эффективное сопротивление всей цепи, определим ток от источника питания по закону Ома.

I _всего =	В _Всего	+	24 В	= 16 А
	R _Всего		1,5 Ом

Теперь пройдемся по цепи (не буквально, конечно). В каждом соединении ток будет делиться на большее количество проводников по пути с меньшим сопротивлением и на меньшее количество по пути с большим сопротивлением. Поскольку заряд нигде не вытекает из полной цепи, ток будет одинаковым для всех элементов, соединенных последовательно друг с другом.

Левая и правая половины цепи имеют одинаковое общее сопротивление, а значит, ток будет делиться между ними поровну.

8 A для резистора 0,6 Ом
на слева .

8 A для резистора 0,5 Ом
на справа .

С каждой стороны ток снова разделяется на две параллельные ветви.

Ответвления на слева имеют сопротивления в соотношении…

Р _{1 и 3}	=	4 Ом	+	2
Р _{2 и 4}	=	6 Ом	+	3

что означает, что токи будут делить в соотношении…

Р _{1 и 3}	=	3
Р _{2 и 4}	=	2

3	8А = 4,8А
5

для резисторов 1 Ом и 3 Ом
на слева .

2	8А = 3,2 А
5

для резисторов 2 Ом и 4 Ом
на слева .

Ответвления на справа идентичны, поэтому ток разделяется на две равные половины.

☟

1	8А = 4,0 А
2

для резисторов 2 Ом и 3 Ом
на справа .

1	8А = 4,0 А
2

для резисторов 1 Ом и 4 Ом
на справа .

Используйте В = IR снова и снова, чтобы определить падение напряжения. (См. таблицы в конце этого решения.)
ИСПОЛЬЗОВАНИЕ P = VI (или P = I ² R или P = V ² / R ). Более PELOCE SIGH . Эти последние две задачи настолько утомительны, что вам следует использовать какое-нибудь приложение для работы с электронными таблицами. Введите заданные значения сопротивления и текущие значения, только что рассчитанные, в столбцы и дайте указание выбранному электронному устройству умножить их соответствующим образом. Как-то так…

Левая сторона
сопротивление (Ом)	ток (А)	напряжение (В)	мощность (Вт)
0,6	8,0	04.8	38,40
1,0	4,8	04.8	23.04
2,0	3,2	06.4	20,48
3,0	4,8	14,4	69.12
4,0	3,2	12,8	40,96

Правая сторона
сопротивление (Ом)	ток (А)	напряжение (В)	мощность (Вт)
0,5	8	04	32
1,0	4	04	16
2,0	4	08	32
3,0	4	12	48
4,0	4	16	64

практическая задача 4

Учитывая схему ниже…

Рассчитайте эквивалентное сопротивление цепи.
Рассчитайте ток через батарею.
Нарисуйте график зависимости напряжения от положения в цепи, предполагая, что В _a = 0 В на отрицательном полюсе аккумулятора.
График тока в зависимости от положения в цепи.

раствор

Вот решения…

Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений…
Р _Т = Р ₁ + R ₂ + R ₃
R _T = 3 Ω + 9 Ω + 6 Ω
R _T = 18 Ω

Полный ток можно найти из закона Ома…

I _T = V _T / R _T
I _T = (12 V) / (18 ω) = ⅔ _T = (12 V) / (18 ω) = ⅔
9003 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008 9008.

= 0,667 А

Напряжение в цепи возрастает в батарее и падает в резисторе (когда мы следим за течением обычного тока). Повышение напряжения в батарее указано как 12 В, а падение напряжения на каждом резисторе можно найти, многократно применяя закон Ома…
V ₁ = I ₁ R ₁
V ₁ = (⅔ a) (3 ω)
.0042 ₁ = 2 В
V ₂ = I ₂ R ₂
V ₂ = (⅔ A) (
5
.
V ₃ = I ₃ R ₃
V ₃ = (⅔ A)(6 Ω)
V ₃ = 4 V
Начиная с нуля вольт на отрицательной клемме аккумулятора, напряжение повышается на 12 В, затем падает на 2 В, 6 В и 4 В, что возвращает нас к нулю. (Мы предполагаем, что батарея и провода имеют незначительное сопротивление.) Вот как это выглядит на графике.
Вот как это выглядит при наложении графика на схему.
Ток в последовательной цепи везде одинаков. Мы уже определили, что это 0,667 А. Осталось провести горизонтальную линию на уровне двух третей ампера.
Вот как это выглядит при наложении графика на схему.

Резисторы | Закон Ома | Учебник по электронике

Поскольку зависимость между напряжением, током и сопротивлением в любой цепи очень регулярна, мы можем надежно контролировать любую переменную в цепи, просто контролируя две другие. Возможно, самой легкой для управления переменной в любой цепи является ее сопротивление. Это можно сделать, изменив материал, размер и форму его проводящих компонентов (помните, как тонкая металлическая нить накала лампы создавала большее электрическое сопротивление, чем толстая проволока?).

Что такое резистор?

Специальные компоненты, называемые резисторами, изготавливаются специально для создания точного сопротивления для включения в цепь. Обычно они изготавливаются из металлической проволоки или углерода и спроектированы так, чтобы поддерживать стабильное значение сопротивления в широком диапазоне условий окружающей среды.

В отличие от ламп, они не излучают свет, но производят тепло, так как электрическая мощность рассеивается ими в рабочей цепи. Однако обычно целью резистора является не производство полезного тепла, а просто обеспечение точного электрического сопротивления.

Обозначения и номиналы резисторов на схеме

Наиболее распространенным символом резистора на схеме является зигзагообразная линия:

присутствуют в цепи, они будут помечены уникальным идентификационным номером, таким как R ₁ , R ₂ , R ₃ и т. д. Как видите, символы резисторов могут отображаться как горизонтально, так и вертикально:

Реальные резисторы совсем не похожи на зигзагообразный символ. Вместо этого они выглядят как небольшие трубки или цилиндры с двумя выступающими проводами для подключения к цепи. Вот выборка резисторов различных типов и размеров:

Чтобы больше соответствовать их внешнему виду, альтернативный схематический символ для резистора выглядит как маленькая прямоугольная коробка:

Можно также показать, что резисторы имеют переменное, а не постоянное сопротивление. Это может быть описание фактического физического устройства, предназначенного для обеспечения регулируемого сопротивления, или может быть показано, что какой-то компонент имеет нестабильное сопротивление. диагональная стрелка через него означает, что этот компонент имеет переменное, а не фиксированное значение. Этот символ «модификатор» (диагональная стрелка) является стандартным соглашением об электронных символах.

Переменные резисторы

Переменные резисторы должны иметь какие-либо физические средства регулировки, либо вращающийся вал, либо рычаг, который можно перемещать для изменения величины электрического сопротивления. Вот фотография, показывающая некоторые устройства, называемые потенциометрами, которые можно использовать в качестве переменных резисторов: резисторы также оцениваются с точки зрения того, сколько тепловой энергии они могут рассеять без перегрева и повреждения. Естественно, эта номинальная мощность указывается в физических единицах «ватт». Большинство резисторов в небольших электронных устройствах, таких как портативные радиоприемники, имеют мощность 1/4 (0,25) Вт или меньше.

Номинальная мощность любого резистора примерно пропорциональна его физическому размеру. Обратите внимание на первую фотографию резистора, как номинальная мощность связана с размером: чем больше резистор, тем выше его номинальная рассеиваемая мощность. Также обратите внимание, что сопротивление (в омах) никак не связано с размером! Хотя сейчас может показаться бессмысленным иметь устройство, которое ничего не делает, кроме сопротивления электрическому току, резисторы являются чрезвычайно полезными устройствами в цепях.

Поскольку они просты и широко используются в мире электричества и электроники, мы потратим значительное количество времени на анализ цепей, состоящих только из резисторов и батарей.

Чем полезны резисторы?

Для практической иллюстрации полезности резисторов рассмотрите фотографию ниже. Это изображение печатной платы, или печатной платы: сборка, состоящая из прослоенных слоев изолирующей фенольно-волокнистой плиты и проводящих медных полос, в которые можно вставлять и закреплять компоненты с помощью процесса низкотемпературной сварки, называемого «пайкой».

Различные компоненты на этой печатной плате обозначены печатными этикетками. Резисторы обозначаются любой маркировкой, начинающейся с буквы «R».

Эта конкретная печатная плата является компьютерным аксессуаром, называемым «модем», который позволяет передавать цифровую информацию по телефонным линиям. На плате этого модема можно увидеть не менее дюжины резисторов (все рассчитаны на рассеиваемую мощность 1/4 Вт). Каждый из черных прямоугольников (называемых «интегральными схемами» или «чипами») также содержит собственный набор резисторов для своих внутренних функций. Другой пример печатной платы показывает резисторы, упакованные в еще меньшие блоки, называемые «устройствами для поверхностного монтажа».

Эта конкретная печатная плата является нижней частью жесткого диска персонального компьютера, и снова припаянные к ней резисторы обозначены этикетками, начинающимися с буквы «R»:

резисторы для поверхностного монтажа на этой печатной плате, и в это число, конечно же, не входит количество резисторов, встроенных в черные «микросхемы». Эти две фотографии должны убедить любого, что резисторы — устройства, которые «просто» препятствуют протеканию электрического тока, — очень важные компоненты в области электроники!

«Нагрузка» на принципиальных схемах

На принципиальных схемах символы резисторов иногда используются для иллюстрации любого общего типа устройства в цепи, выполняющего какую-либо полезную функцию с использованием электроэнергии. Любое неспецифическое электрическое устройство обычно называется нагрузкой, поэтому, если вы видите схематическую диаграмму, показывающую символ резистора, помеченный как «нагрузка», особенно в учебной принципиальной схеме, объясняющей какую-либо концепцию, не связанную с фактическим использованием электроэнергии, этот символ может просто быть своего рода сокращенным представлением чего-то более практичного, чем резистор.

Анализ резисторных цепей

Чтобы обобщить то, что мы узнали в этом уроке, давайте проанализируем следующую схему, определяя все, что мы можем из предоставленной информации:

здесь для начала это напряжение батареи (10 вольт) и ток цепи (2 ампера). Мы не знаем ни сопротивления резистора в омах, ни рассеиваемой им мощности в ваттах. Просматривая наш массив уравнений закона Ома, мы находим два уравнения, которые дают нам ответы на основе известных величин напряжения и тока:

Подставляя известные величины напряжения (E) и тока (I) в эти два уравнения, мы можем определить сопротивление цепи (R) и рассеиваемую мощность (P): Для условий цепи 10 вольт и 2 ампера сопротивление резистора должно быть 5 Ом. Если бы мы разрабатывали схему для работы при этих значениях, нам пришлось бы указать резистор с минимальной номинальной мощностью 20 Вт, иначе он перегреется и выйдет из строя.

Материалы для резисторов

Резисторы могут быть изготовлены из различных материалов, каждый из которых имеет свои свойства и определенные области применения. Большинство инженеров-электриков используют следующие типы:

Резисторы с проволочной обмоткой (WW)

Резисторы с проволочной обмоткой изготавливаются путем намотки проволоки сопротивления на непроводящий сердечник по спирали. Обычно они производятся для высокоточных и мощных приложений. Сердечник обычно изготавливается из керамики или стекловолокна, а резистивная проволока — из никель-хромового сплава. Они не подходят для приложений с частотами выше 50 кГц.

Низкий уровень шума и устойчивость к колебаниям температуры являются стандартными характеристиками резисторов с проволочной обмоткой. Доступны значения сопротивления от 0,1 до 100 кОм с точностью от 0,1% до 20%.

Металлопленочные резисторы

Нихром или нитрид тантала обычно используются для металлопленочных резисторов. Комбинация керамического материала и металла обычно составляет резистивный материал. Величина сопротивления изменяется путем вырезания на пленке спирального узора, подобно углеродной пленке с помощью лазера или абразива. Металлопленочные резисторы обычно менее устойчивы к температуре, чем резисторы с проволочной обмоткой, но лучше справляются с более высокими частотами.

Металлооксидно-пленочные резисторы

Металлооксидные резисторы используют оксиды металлов, такие как оксид олова, что делает их немного отличными от металлопленочных резисторов. Эти резисторы надежны и стабильны и работают при более высоких температурах, чем металлопленочные резисторы. Из-за этого металлооксидные пленочные резисторы используются в приложениях, требующих высокой износостойкости.

Фольговые резисторы

Фольговые резисторы, разработанные в 1960-х годах, по-прежнему являются одним из самых точных и стабильных типов резисторов, которые вы найдете, и используются для приложений с высокими требованиями к точности. Керамическая подложка, на которую наклеена тонкая объемная металлическая фольга, образует резистивный элемент. Фольговые резисторы имеют очень низкотемпературный коэффициент сопротивления.

Резисторы из углеродного состава (CCR)

До 1960-х годов резисторы из углеродного состава были стандартом для большинства применений. Они надежны, но не очень точны (их погрешность не может быть лучше, чем около 5%). Смесь мелких частиц углерода и непроводящего керамического материала используется для резистивного элемента резисторов CCR.

Вещество формуется в форме цилиндра и запекается. Размеры корпуса и соотношение углеродного и керамического материала определяют величину сопротивления. Больше углерода, используемого в процессе, означает более низкое сопротивление. Резисторы CCR по-прежнему полезны для определенных приложений из-за их способности выдерживать импульсы высокой энергии, хорошим примером применения может быть источник питания.

Резисторы из углеродной пленки

Резисторы из углеродной пленки имеют тонкую углеродную пленку (со спиральным разрезом в пленке для увеличения резистивного пути) на изолирующем цилиндрическом сердечнике. Это позволяет сделать значение сопротивления более точным, а также увеличивает значение сопротивления. Резисторы из углеродной пленки намного более точны, чем резисторы из углеродного состава. Специальные углеродные пленочные резисторы используются в приложениях, требующих высокой импульсной стабильности.

Ключевые показатели эффективности (КПЭ)

Ниже приведены ключевые показатели эффективности для каждого материала резистора:

Характеристика	Металлическая пленка	Толстая металлическая пленка	Прецизионная металлическая пленка	Состав углерода	Углеродная пленка
Темп. диапазон	от -55 до +125	от -55 до +130	от -55 до +155	от -40 до +105	от -55 до +155
Макс. темп. коэфф.	100	100	15	1200	250-1000
Вмакс	200-350	250	200	350-500	350-500
Шум (мкВ на вольт приложенного постоянного тока)	0,5	0,1	0,1	4 (100К)	5 (100К)
Р Инсул.	10000	10000	10000	10000	10000
Припой (% изменения значения сопротивления)	0,20%	0,15%	0,02%	2%	0,50%
Влажное тепло (% изменения значения сопротивления)	0,50%	1%	0,50%	15%	3,50%
Срок годности (% изменения значения сопротивления)	0,10%	0,10%	0,00%	5%	2%
Полная мощность (2000 ч при 70°C)	1%	1%	0,03%	10%	4%

ОБЗОР:

Устройства, называемые резисторами, предназначены для обеспечения точного значения сопротивления в электрических цепях. Резисторы оцениваются как по сопротивлению (Ом), так и по способности рассеивать тепловую энергию (Вт).
Номинальные значения сопротивления резистора не могут быть определены исходя из физического размера рассматриваемого резистора(ов), хотя приблизительная номинальная мощность может быть определена. Чем больше резистор, тем большую мощность он может рассеять без повреждений.
Любое устройство, которое выполняет какую-либо полезную работу с помощью электроэнергии, обычно называется нагрузкой. Иногда символы резисторов используются на принципиальных схемах для обозначения неспецифической нагрузки, а не фактического резистора.

СВЯЗАННЫЕ РАБОЧИЕ ТАБЛИЦЫ:

Резисторы Рабочий лист

Попробуйте наш калькулятор цветового кода резистора в нашем разделе Инструменты .

Электрическое сопротивление

Эта идея фокуса исследуется через:

Противопоставление студенческих и научных взглядов
Критические идеи обучения
Педагогическая деятельность

Противопоставление студенческих и научных взглядов

Повседневный опыт студентов

Неудивительно, что студенты путают значения слов, используемых для разговоров об электричестве. Когда ученые впервые пытались понять электрические цепи, они использовали слова, уже имеющиеся в нашем языке, для понятий, которые они конструировали в своих объяснениях, т.е. «ток», «мощность». Но, конечно, значения этих слов, когда их использовали ученые, отличались от уже существовавших повседневных значений. Позже слова, созданные учеными для таких понятий, как «напряжение», медленно перешли в повседневный язык и приобрели в нашей повседневной речи значения, отличные от точных значений, используемых учеными. Итак, как описано в обоих Электрические цепи и Что касается напряжения, различия между значениями слов в повседневном употреблении и их научным использованием очень часто являются источником значительной концептуальной путаницы для студентов, когда они изучают электричество.

Основная идея Введение в научный язык также исследует вопросы повседневного и научного использования языка.

С точки зрения языка научная идея «электрического сопротивления» представляет собой несколько иной случай по двум основным причинам.

Во-первых, учащиеся почти никогда не задумываются об «электрическом сопротивлении» до того, как им официально представят ту или иную форму этой идеи. В тех редких случаях, когда учащиеся используют некоторое понятие, которое они называют «сопротивлением», для интерпретации повседневного опыта, это почти всегда будет сопровождаться их размышлениями об «электрическом токе» (и/или очень редко о каком-либо понятии «напряжение»).

Во-вторых, если у них и есть понятие сопротивления, оно обычно в целом согласуется с приемлемой научной точкой зрения — понятие «сопротивление», включающее форму «трения», которое каким-то образом влияет на «ток».

Некоторые студенты пытаются интерпретировать свой ограниченный опыт работы с электрическими цепями только с точки зрения электрического тока. Эти студенты интерпретируют высокий ток в цепи как означающий, что «ток течет легко» по цепи, а не как «низкое электрическое сопротивление» или каким-либо образом учитывают влияние напряжения в цепи.

Другая проблема (описанная в основной идее Электрические цепи), который также важен для понимания учащимися электрического сопротивления, часто называют «локальным рассуждением». То есть их размышления о том, что происходит в электрической цепи (с вопросами электрического сопротивления, а также тока), часто сосредоточены только на одной небольшой части цепи, полностью игнорируя все другие особенности цепи.

Учащиеся также часто думают, что если изменение внесено в одну часть электрической цепи, потребуется некоторое время, чтобы его эффект «переместился» по цепи, а не мгновенно повлиял на каждый компонент в цепи.

Исследования: Чой, Ли и Квон (2004 г.), Коэн, Эйлон и Ганиэль (1983 г.), Льежуа и Маллет (2002 г.), Райнер, Слотте, Чи и Резник (2000 г.), Шипстоун и Ганстоун (1985 г.) и Виар и Хантине-Ланглуа (2001).

Scientific view

Модели играют важную роль, помогая нам понять то, чего мы не видим, и поэтому они особенно полезны при попытке разобраться в электрических цепях. Модели ценятся как за их объяснительную способность, так и за их предсказательную способность. Однако модели также имеют ограничения.

Модель, используемая сегодня учеными для электрических цепей, использует идею о том, что все вещества содержат электрически заряженные частицы (см. Макроскопические и микроскопические свойства). Согласно этой модели электрические проводники, такие как металлы, содержат заряженные частицы, которые относительно легко могут перемещаться от атома к атому, тогда как в плохих проводниках, изоляторах, таких как керамика, заряженные частицы перемещаются гораздо труднее.

В научной модели электрический ток представляет собой общее движение заряженных частиц по непрерывному проводящему пути. Причиной этого движения обычно является источник энергии, такой как батарея, которая обеспечивает силу, необходимую для перемещения заряженных частиц. Электрический ток может возникнуть только тогда, когда существует полная проводящая «цепь», в которой заряженные частицы движутся от одного вывода батареи к другому (см. Электрические цепи), как показано стрелками, указывающими путь проводника на схеме ниже.

Заряженные частицы могут относительно легко проходить через материалы, являющиеся хорошими проводниками; относительно небольшая электрическая энергия необходима для создания этого движения заряда (тока) в таких материалах. С другой стороны, изоляторы требуют значительного количества электроэнергии для производства подобных токов. Свойство материалов, которое приводит к разнице в энергии, необходимой для создания одинаковых электрических токов, называется «электрическим сопротивлением» и измеряется в единице, называемой Ом. Электрическое сопротивление различных материалов может сильно различаться; сопротивление наиболее распространенных проводящих материалов (металлов) изменяется при изменении их температуры.

Научная модель электрического сопротивления представляет собой движущиеся заряженные частицы, сталкивающиеся с частицами, составляющими структуру материала, через который проходит ток. Для поддержания тока необходим ввод энергии, потому что во время этих столкновений частиц энергия непрерывно преобразуется в тепло. Там, где природа материала такова, что столкновения происходят гораздо чаще, выделяется больше тепла и выше электрическое сопротивление.

Существуют некоторые электрические устройства, функционирование которых зависит от этого преобразования энергии, в первую очередь это тепловентиляторы и световые шары (где нить накала шара должна раскаляться добела, чтобы в результате преобразования энергии возникал свет, а также тепло). Для этих устройств нам нужен материал со «средним» электрическим сопротивлением — достаточно низким, чтобы через материал проходил электрический ток соответствующего размера, и достаточно высоким, чтобы соответствующее количество энергии преобразовывалось в необходимую форму. Когда мы подключаем такие устройства к электрическим цепям, мы стремимся к как можно меньшему преобразованию энергии (как можно меньшему сопротивлению) в проводах, по которым ток проходит к устройству и обратно, и чрезвычайно высокому сопротивлению для таких материалов, как пластиковая изоляция вокруг токопроводящих проводов, через которые не проходит ток.

«Сталкивающиеся частицы» или механическая модель сопротивления, описанная выше, полезна при рассмотрении токов в простых проводниках. Это бесполезно пытаться объяснить гораздо более сложное функционирование токов в люминесцентных лампах, светоизлучающих диодах (СИД) и многих сложных электронных компонентах. Все модели/метафоры/аналогии имеют свои ограничения. Для механической модели наиболее очевидным ограничением является то, что она предполагает, что все частицы по существу идентичны и ведут себя так же, как крошечные шарикоподшипники или шарики.

Критические идеи обучения

Понятия электрического сопротивления и электрического тока тесно переплетены, и их необходимо преподавать одновременно.
Электрическое сопротивление — это свойство материалов, в результате которого для поддержания электрического тока в материале требуется энергия. Все материалы, с которыми мы сталкиваемся в повседневной жизни, обладают электрическим сопротивлением; это сопротивление может сильно варьироваться.
Различные материалы требуют разного количества энергии для достижения эквивалентных токов. Материалы, которые требуют очень мало энергии для обеспечения протекания тока, называются проводниками; они имеют очень низкое электрическое сопротивление. Материалы, которым требуется много энергии для протекания тока, называются изоляторами; они имеют очень высокое электрическое сопротивление.

При проектировании электрических цепей, позволяющих нам использовать электрические устройства для преобразования электрической энергии, нам нужны:

материалы с как можно более низким электрическим сопротивлением для токопроводящих проводов
материалы с как можно более высоким электрическим сопротивлением для частей цепи где требуется электрическая изоляция
материалы с электрическим сопротивлением, которое не является ни очень низким, ни очень высоким для преобразователей энергии частей устройства, для которого предназначена схема.

Предложения в этой основной идее были написаны таким образом, что предполагается, что сначала было введено понятие «электрический ток» (см. Электрические цепи), Дополнительные концепции и предложения затем тесно переплетаются с этими идеями.

Аналогично обоим Электрические цепи и Разбираясь в напряжении, очень важно отметить, что использование количественных подходов для обучения этим идеям (например, с использованием закона Ома) часто будет препятствовать развитию концептуального понимания и развитию способности объяснять электрические явления.

Это связано с тем, что когда основное внимание уделяется использованию формулы, представляющей закон Ома (V = IR), характер обучения учащихся совершенно не связан с какими-либо концепциями, которые представляют термины в формуле. Подход, который с большей вероятностью будет способствовать пониманию учащимися, — это качественный подход, основанный на использовании общих вопросов, таких как:

Каковы здесь основные понятия?
Как эти концепции можно использовать для объяснения некоторых простых электрических явлений?
Как правильно описательно описать взаимосвязь понятий?

Исследуйте отношения между представлениями об электрическом токе, сопротивлении и напряжении в Карты развития концепции – Электричество и магнетизм

Преподавательская деятельность

Сбор фактов/данных для анализа

Предоставьте учащимся ряд подготовленных материалов для измерения электрического сопротивления с помощью лампочки, батареи и подключенных измерительных проводов, как показано здесь. Эти предметы должны быть выбраны таким образом, чтобы предоставить учащимся две отдельные группы предметов для изучения: либо очень хорошие изоляторы, либо очень хорошие проводники. Цель состоит в том, чтобы учащиеся проверили каждый материал, используя свою лампочку и батарею, чтобы установить, горит лампочка или нет (т. е. сделать выводы, что материал является хорошим проводником или хорошим изолятором). Цель состоит в том, чтобы учащиеся увидели, что большинство металлов являются очень хорошими проводниками и что пластик и керамика широко используются в конструкции ручных электрических инструментов из-за их очень хороших изоляционных свойств.

Эти предметы могут включать: дерево, керамику, пластик, полистирол, резину, бумагу, стекло, медную проволоку, алюминиевую фольгу, железные/стальные гвозди, угольные/графитовые стержни*, латунные ключи и цинковые накладки.

*Графитовые стержни можно получить, заточив черный графитовый карандаш с обоих концов и подключив его к цепи с помощью зажимов типа «крокодил» (то, что мы называем «грифелем» в черном карандаше, на самом деле является графитом).

Обсудите с учащимися, почему материалы выбираются с учетом их изоляционных свойств. Вопросы для обсуждения могут включать:

Почему электрики должны использовать деревянные или стеклопластиковые лестницы, а не алюминиевые?
Почему токопроводящие провода покрыты изоляционным пластиком?
Каким образом конструкция электрических ручных инструментов и фенов с формованными пластиковыми корпусами позволит избежать поражения электрическим током при возможной неисправности?

Альтернативный подход к этой задаче показан на виньетке, Выведите практический дизайн из ограниченной информации , которая выступает за использование меньшего количества указаний учителя, поощряя учащихся к более активному принятию решений.

Открытое обсуждение на основе общего опыта

Выберите вторую группу проводников, чтобы обеспечить диапазон электрических сопротивлений от высокого до низкого, чтобы учащиеся могли снова провести тестирование с батареей, лампой и тестовыми проводами (т. е. яркость тестовой лампы будет варьироваться от от тусклого до яркого). Цель состоит в том, чтобы дать учащимся более сложную задачу сравнения относительного сопротивления каждого материала, чтобы они могли ранжировать их от плохих до очень хороших проводников. Эти элементы следует выбирать с осторожностью, чтобы они имели необходимое сопротивление для изменения яркости лампы и соответствовали напряжению используемой батареи. Не забудьте попробовать каждый из них, прежде чем давать их своим ученикам для тестирования.

Эти предметы могут включать в себя: припой, свинцовую фольгу, нихром (включая различные куски нихромовой проволоки совершенно разной длины; катушка радиатора является отличным источником) и медную проволоку.

Предложите учащимся протестировать каждый образец и попытаться ранжировать их по шкале от высокого сопротивления (плохой проводник, тусклая лампочка) до низкого сопротивления (хороший проводник, яркая лампочка).

Практика использования научных моделей и формирование предполагаемой полезности научных моделей

Создайте простую физическую симуляцию, подобную приведенной ниже, или используйте одну из множества компьютерных симуляций (например, представленных на веб-сайте Interactive Simulations ниже), чтобы помочь учащимся понять модели электрического сопротивления «столкновение частиц».

Университет Колорадо в Boulder Interactive Simulations

Простая физическая симуляция может состоять из мяча для настольного тенниса, катящегося по слегка наклонному столу с рядом препятствий (например, латунных гирь весом 50 г), расположенных для замедления движения мяча. Ограничьте боковое движение мяча, разместив несколько предметов с каждой стороны стола. (например, измерительные линейки, поднятые на несколько грузов на каждом конце).

Скорость мяча вниз по склону можно изменить, изменив количество препятствующих грузов на пути мяча или наклон стола. Дополнительное размещение большего количества грузов увеличит количество отклонений, с которыми сталкивается мяч, и, следовательно, замедлит движение мяча по мере его скатывания по склону. Увеличенное количество столкновений моделирует материал с высоким сопротивлением и низкой проводимостью. После демонстрации и обсуждения этой симуляции со студентами попросите их подготовить список допущений, прогностических способностей и недостатков модели. Затем их идеи могут быть представлены с использованием информационной таблицы, подобной приведенной ниже, в которой перечислены сильные и слабые стороны простого механического моделирования в точном моделировании электрического сопротивления.

Механическая модель — сильные стороны	Механическая модель — слабые стороны
Движение мяча подобно протеканию электрического тока по проводнику.	Мяч и грузы не «нагреваются» больше, когда происходит большее количество «столкновений частиц».
Чем больше число «столкновений частиц», тем медленнее ток («шарик») движется по проводнику.	Все относительные размеры частиц неверны.
Мы можем придать движущемуся мячу больше энергии и, следовательно, ускорить его движение, увеличив наклон стола.	Если имеется действительно большое количество препятствующих грузов, катящийся шар может застрять и не сможет двигаться. В электрическом токе скорость движущихся частиц в целом постоянна; изменения в токах связаны с изменениями в количестве движущихся частиц, а не в скорости, с которой они движутся.

В качестве дополнительного задания попросите учащихся поработать в небольших группах над созданием плакатных диаграмм, которые помогут лучше понять работу модели «столкновения частиц». Предложите учащимся обсудить и нарисовать особенности, указанные в их таблице сильных и слабых сторон, которые будут влиять на эффективность модели, например. относительный размер движущихся частиц по сравнению с неподвижными частицами, изменение количества движущихся частиц, изменение размеров длины пути или поперечного сечения. Предложите учащимся представить их своим сверстникам в малых группах для обсуждения.

Другую задачу, в которой также обсуждается использование аналогий с понятиями электрических цепей, см. виньетку. Использование бортовых журналов в 10 классе Электричество.

Способствовать осмыслению и уточнению существующих идей

Используя структуру POE (Предсказать, Наблюдение, Объяснить), разбейте учащихся на группы по 2–3 человека (или более, если не хватает оборудования):

а) Соедините электрическую цепь, состоящую из батареи, лампочки и выключателя, так, чтобы ток в цепи протекал только по одному пути. Это называется последовательной цепью. Предложите учащимся наблюдать за горящим земным шаром, когда выключатель замкнут.
б) Сформировать прогноз одной группы о том, что произойдет с яркостью земного шара (в качественном отношении – увеличится, уменьшится, останется прежним), когда второй глобус будет соединен также последовательно с другими компонентами, один за другим.
в) Согласуйте и запишите наблюдение, что происходит с яркостью глобуса, когда второй глобус включается в цепь.
г) Напишите одно групповое объяснение своего наблюдения.

Теперь обсудите с классом модель сопротивления как возникающего в результате столкновений между движущимися зарядами и частицами в проводах, по которым движется ток (то есть модель электрического сопротивления «столкновение частиц»). Как введение второй лампочки повлияет на ток и яркость первой лампочки?

Предложите учащимся в их первоначальных группах переписать свои первоначальные объяснения POE, чтобы теперь они были основаны на модели сопротивления частиц.

Помощь учащимся в самостоятельной разработке некоторых «научных» объяснений

Предложите учащимся снова соединить первоначальную схему батареи и одиночного светового шара и выключить.

Предложите учащимся наблюдать и записывать, что происходит с яркостью шара, когда ряд различных материалов соединяются (по одному за раз) таким образом, что ток имеет два возможных пути – либо через шар, либо через другой объект который добавляется (это называется параллельной схемой).

Например, на схеме показана вторая лампочка, подключенная к цепи с помощью зажимов типа «крокодил».

Возможные материалы:

еще один световой шар, как показано на схеме выше
короткий кусок медного провода (который может быть частью цепи только при кратковременном замыкании выключателя!)
a очень длинная катушка провода (предназначенная для добавления сопротивления в электрическую цепь)
графит в карандаше (как уже отмечалось, заострите карандаш с обоих концов и используйте зажимы типа «крокодил» для подключения карандаша к цепи)

Для каждого материала учащиеся должны составить групповое объяснение своих наблюдений того, что происходит с яркостью земного шара при добавлении материала, с точки зрения модели сопротивления частиц.

Консолидация идей учащихся посредством обсуждения всем классом ряда полученных объяснений.

Предложите открытую проблему для изучения в игровой форме или путем решения задач

В качестве исследовательского задания в библиотеке/интернете предложите учащимся изучить природу и использование сверхпроводников с помощью структуры обучающей процедуры, называемой Что? И что? Что дальше? Учащиеся изучают возможные ответы на следующие вопросы:

Что? – Какие факты могут найти учащиеся в ответ на вопрос «Что такое сверхпроводники и что они делают?»
И что? – Для каждого факта, который учащиеся приводят в ответ на вопрос «Что?», они должны написать как можно больше следствий этого факта; серия ответов на вопрос «Ну и что?»
Что дальше? – Для каждого факта, указанного в ответе на вопрос «Что?», и последствиях, приведенных в ответе на вопрос «И что?», учащиеся пишут, что может произойти или произойти в результате этого.

Предложите учащимся записать свои ответы в таблицу, например:

ЧТО?	И ЧТО?	ЧТО ДАЛЬШЕ?
Что такое сверхпроводники и для чего они?	Что из этого следует?	Что может произойти в результате этого?
Сверхпроводники — это материалы, которые при достаточном охлаждении проводят электрический ток без какого-либо сопротивления.	Если в сверхпроводнике без сопротивления пустить ток, этот ток будет продолжать течь вечно без каких-либо затрат энергии.	Электрический ток можно было бы накопить, просто запустив ток в сверхпроводнике, а затем оставив его.

19.3 Параллельные схемы — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

Интерпретировать принципиальные схемы с параллельными резисторами
Расчет эквивалентного сопротивления комбинаций резисторов, содержащих последовательные и параллельные резисторы

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

(5) Научные понятия. Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ф) дизайн. построить и рассчитать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как в последовательных, так и в параллельных комбинациях.

Кроме того, руководство по физике для средней школы обращается к содержанию этого раздела лабораторной работы под названием «Схемы», а также к следующим стандартам:

(5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
- (Ф) проектировать, конструировать и рассчитывать с точки зрения сквозного тока, разности потенциалов, сопротивления и мощности, используемой элементами электрической цепи, соединенными как последовательно, так и параллельно.

Основные термины раздела

параллельно

Параллельные резисторы

В предыдущем разделе мы узнали, что последовательно соединенные резисторы — это резисторы, соединенные один за другим. Если вместо этого мы объединим резисторы, соединив их рядом друг с другом, как показано на рис. 19.16, то говорят, что резисторы соединены параллельно . Резисторы параллельны, когда оба конца каждого резистора соединены напрямую друг с другом.

Обратите внимание, что все верхние части резисторов подключены к одному и тому же проводу, поэтому напряжение в верхней части каждого резистора одинаково. Точно так же все основания резисторов подключены к одному и тому же проводу, поэтому напряжение внизу каждого резистора одинаково. Это означает, что падение напряжения на каждом резисторе одинаково. В этом случае падение напряжения равно номинальному напряжению В аккумулятора, потому что верхний и нижний провода подключаются к положительному и отрицательному полюсам аккумулятора соответственно.

Хотя падение напряжения на каждом резисторе одинаково, мы не можем сказать то же самое о токе, протекающем через каждый резистор. Таким образом, I1, I2 и I3 I1, I2 и I3 не обязательно одинаковы, поскольку резисторы R1, R2 и R3 R1, R2 и R3 не обязательно имеют одинаковое сопротивление.

Обратите внимание, что три резистора на рис. 19.16 обеспечивают три различных пути, по которым может протекать ток. Это означает, что эквивалентное сопротивление этих трех резисторов должно быть меньше наименьшего из трех резисторов. Чтобы понять это, представьте, что наименьший резистор — это единственный путь, по которому может протекать ток. Теперь добавьте альтернативные пути, подключив другие резисторы параллельно. Поскольку у тока больше путей, общее сопротивление (т. Е. Эквивалентное сопротивление) уменьшится. Следовательно, эквивалентное сопротивление должно быть меньше наименьшего сопротивления параллельных резисторов.

Рисунок 19.16 На левой принципиальной схеме показаны три резистора, соединенные параллельно. Напряжение В батареи приложено ко всем трем резисторам. Токи, протекающие через каждую ветвь, не обязательно равны. На правой принципиальной схеме показано эквивалентное сопротивление, которое заменяет три параллельных резистора.

Поддержка учителей

Подчеркните, что напряжение на каждом параллельном резисторе одинаково, тогда как ток может различаться; то же самое будет, если пара резисторов имеет одинаковое сопротивление.

Чтобы найти эквивалентное сопротивление RequivRequiv трех резисторов R1, R2 и R3 R1, R2 и R3, применим закон Ома к каждому резистору. Поскольку падение напряжения на каждом резисторе составляет В , мы получаем

V=I1R1, V=I2R2, V=I3R3V=I1R1, V=I2R2, V=I3R3

19,21

или

I1=VR1, I2=VR2, I3=VR3.I1=VR1, I2=VR2, I3=VR3.

19.22

Мы также знаем из закона сохранения заряда, что три тока I1, I2 и I3 I1, I2 и I3 должны складываться, чтобы дать ток я который идет через батарею. Если бы это было не так, ток должен был бы таинственным образом создаваться или уничтожаться где-то в цепи, что физически невозможно. Таким образом, у нас есть

I=I1+I2+I3.I=I1+I2+I3.

19,23

Подстановка выражений для I1, I2 и I3 I1, I2 и I3 в это уравнение дает

I=VR1+VR2+VR3=V(1R1+1R2+1R3)I=VR1+VR2+VR3=V(1R1+1R2+1R3)

19,24

или

V=I(11/R1+1/R2+1/R3).V=I(11/R1+1/R2+1/R3).

19,25

Эта формула представляет собой просто закон Ома, где множитель в скобках означает эквивалентное сопротивление.

V=I(11/R1+1/R2+1/R3)=IRэкв. V=I(11/R1+1/R2+1/R3)=IRэкв.

19,26

Таким образом, эквивалентное сопротивление трех резисторов, включенных параллельно, равно

Треб.=11/R1+1/R2+1/R3. Треб.=11/R1+1/R2+1/R3.

19,27

Та же логика работает для любого числа параллельно соединенных резисторов, поэтому общая форма уравнения, которая дает эквивалентное сопротивление N резисторов, соединенных параллельно, составляет

Requiv=11/R1+1/R2+⋯+1/RN. Requiv=11/R1+1/R2+⋯+1/RN.

19,28

Рабочий пример

Найдите ток через параллельные резисторы

Три приведенные ниже цепи эквивалентны. Если номинальное напряжение батареи Vbattery=3VVbattery=3V, каково эквивалентное сопротивление цепи и какой ток протекает через цепь?

Стратегия

Три резистора соединены параллельно, и падение напряжения на них равно В _{аккумулятор} . Таким образом, мы можем применить уравнение для эквивалентного сопротивления параллельных резисторов, которое принимает вид

Requiv=11/R1+1/R2+1/R3.Requiv=11/R1+1/R2+1/R3.

19,29

Схема с эквивалентным сопротивлением показана ниже. Зная эквивалентное сопротивление, мы можем использовать закон Ома, чтобы найти ток в цепи.

Решение

Подстановка заданных значений сопротивления в уравнение для эквивалентного сопротивления дает

Треб. =11/R1+1/R2+1/R3=11/10 Ом+1/25 Ом+1/15 Ом=4,84 Ом. Треб.=11/R1+1/R2+1/R3=11/10 Ом+1 /25 Ом+1/15 Ом=4,84 Ом.

19,30

Таким образом, ток в цепи равен

V=IRI=VR=3V4,84Ω=0,62A.V=IRI=VR=3V4,84Ω=0,62A.

19,31

Обсуждение

Хотя через всю цепь протекает ток 0,62 А, обратите внимание, что этот ток протекает не через каждый резистор. Однако, поскольку в цепи должен сохраняться электрический заряд, сумма токов, проходящих через каждую ветвь цепи, должна в сумме равняться току, проходящему через батарею. Другими словами, мы не можем волшебным образом создать заряд где-то в цепи и добавить этот новый заряд к току. Давайте проверим это рассуждение, используя закон Ома, чтобы найти ток через каждый резистор.

I1=VR1=3V10Ω=0,30AI2=VR2=3V25Ω=0,12AI3=VR3=3V15Ω=0,20AI1=VR1=3V10Ω=0,30AI2=VR2=3V25Ω=0,12AI3=VR3=3V15Ω=0,20A

900,32 Как и ожидалось, эти токи в сумме дают 0,62 А, то есть общий ток, проходящий через эквивалентный резистор. Также обратите внимание, что через самый маленький резистор протекает наибольший ток, и наоборот.

Рабочий пример

Рассуждение с параллельными резисторами

Чему равно эквивалентное сопротивление трех одинаковых резисторов без проведения расчетов R параллельно?

Стратегия

Три одинаковых резистора R , соединенные параллельно, образуют три одинаковых пути, по которым может протекать ток. Таким образом, току через эти резисторы протекать в три раза легче, чем через один из них.

Раствор

Если через три одинаковых резистора R протекать в три раза легче, чем через один из них, то эквивалентное сопротивление должно быть в три раза меньше: Р /3.

Обсуждение

Проверим наши рассуждения, рассчитав эквивалентное сопротивление трех одинаковых резисторов R , включенных параллельно. Уравнение для эквивалентного сопротивления параллельных резисторов дает

Requiv=11/R+1/R+1/R=13/R=R3.Requiv=11/R+1/R+1/R=13/R =R3.

19.33

Таким образом, наши рассуждения были верны. В общем, когда доступно больше путей, по которым может протекать ток, эквивалентное сопротивление уменьшается. Например, если у нас есть одинаковые резисторы R параллельно, эквивалентное сопротивление будет R /10.

Практические задачи

10.

Три резистора, 10, 20 и 30 Ом, соединены параллельно. Чему равно сопротивление?

Эквивалентное сопротивление 5,5 Ом
Эквивалентное сопротивление 60 Ом
Эквивалентное сопротивление 6 × 103 Ом
Эквивалентное сопротивление 6 × 104 Ом

11.

Часы Физика: Параллельные резисторы. Это видео представляет и объясняет, как резисторы работают при параллельном соединении.

Нажмите, чтобы просмотреть содержимое

Если на R_1 происходит падение напряжения 5\text{-V}, а R_1 подключен параллельно R_2, каково падение напряжения на R_2?

Падение напряжения на проводе равно 0\,\text{В}.
Падение напряжения на проводе 2,5\,\text{В}.
Падение напряжения на проводе 5\,\text{В}.
Падение напряжения на проводе 10\,\text{В}.

Резисторы параллельно и последовательно

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного соединения. Комбинации последовательных и параллельных резисторов можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рис. 19.17. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее сокращаются до тех пор, пока не останется единственное сопротивление. Процесс скорее трудоемкий, чем сложный.

Рисунок 19.17 Эта комбинация семи резисторов имеет как последовательные, так и параллельные части. Каждое идентифицируется и приводится к эквивалентному сопротивлению, а затем они уменьшаются до тех пор, пока не будет достигнуто единственное эквивалентное сопротивление.

Поддержка учителей

Предупреждение о заблуждении

У учащихся может возникнуть соблазн сразу сложить вместе R1R1 и R7R7, поскольку они выглядят последовательно. Обратите внимание, что R1R1 включен последовательно с параллельной комбинацией R7R7 и всех резисторов справа от R7R7. Таким образом, необходимо найти эквивалентное сопротивление этой параллельной комбинации, прежде чем ее можно будет добавить к R1R1.

Поддержка учителей

Поработайте с учащимися над этим примером, чтобы убедиться, что они понимают сокращение, которое происходит на каждом шаге.

Давайте выполним четыре шага на рис. 19.17, чтобы уменьшить количество резисторов до одного эквивалентного резистора. Чтобы не отвлекаться на алгебру, мы будем считать, что сопротивление каждого резистора равно 10 Ом. На шаге 1 мы уменьшаем два набора параллельных резисторов, обведенных синей пунктирной петлей. Верхний набор имеет три параллельных резистора и будет уменьшен до одного эквивалентного резистора RP1RP1. Нижний набор имеет два параллельных резистора и будет уменьшен до одного эквивалентного резистора RP2RP2. Используя уравнение для эквивалентного сопротивления параллельно включенных резисторов, получаем

RP1=11/R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 Ом RP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.RP1=11 /R2+1/R3+1/R4=11/10 Ом+1/10 Ом+1/10 Ом=103 Ом RP2=11/R5+1/R6=11/10 Ом+1/10 Ом=5 Ом.

19,34

Эти два эквивалентных сопротивления обведены красным пунктиром после шага 1. Они соединены последовательно, поэтому мы можем использовать уравнение для эквивалентного сопротивления последовательных резисторов, чтобы свести их к одному эквивалентному сопротивлению RS1RS1 . Это делается на шаге 2, в результате получается

RS1=RP1+RP2=103 Ом+5 Ом=253 Ом. RS1=RP1+RP2=103 Ом+5 Ом=253 Ом.

19,35

Эквивалентный резистор RS1RS1 появляется в зеленой пунктирной петле после шага 2. Этот резистор включен параллельно резистору R7R7, поэтому пара может быть заменена эквивалентным резистором RP3RP3, который определяется как

RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.RP3=11/RS1+1/R7=13/25 Ом+1/10 Ом=5011 Ом.

19,36

Это делается на шаге 3. Резистор RP3RP3 включен последовательно с резистором R1R1, как показано фиолетовым пунктиром после шага 3. Эти два резистора объединяются на последнем шаге, чтобы сформировать окончательный эквивалентный резистор RequivRequiv , то есть

Requiv=R1+RP3=10Ω+5011Ω=16011Ω.Requiv=R1+RP3=10Ω+5011Ω=16011Ω.

19,37

Таким образом, всю комбинацию из семи резисторов можно заменить одним резистором с сопротивлением около 14,5 Ом.

Это было много работы, и вы можете спросить, почему мы это делаем. Нам важно знать эквивалентное сопротивление всей цепи, чтобы мы могли рассчитать ток, протекающий по цепи. Закон Ома говорит нам, что ток, протекающий по цепи, зависит от сопротивления цепи и напряжения в цепи. Но чтобы узнать ток, надо сначала узнать эквивалентное сопротивление.

Вот общий подход к поиску эквивалентного резистора для любой произвольной комбинации резисторов:

Определите группу резисторов, которые включены только параллельно или только последовательно.
Для резисторов, соединенных последовательно, используйте уравнение для эквивалентного сопротивления последовательно соединенных резисторов, чтобы привести их к одному эквивалентному сопротивлению. Для параллельных резисторов используйте уравнение для эквивалентного сопротивления параллельных резисторов, чтобы привести их к одному эквивалентному сопротивлению.
Нарисуйте новую принципиальную схему, заменив резисторы из шага 1 эквивалентными им резисторами.
Если в цепи осталось более одного резистора, вернитесь к шагу 1 и повторите. В противном случае вам конец.

Веселье в физике

Робот

Роботы захватывают наше коллективное воображение уже более века. Теперь эта мечта о создании умных машин для выполнения нашей грязной работы, а иногда и просто для того, чтобы составить нам компанию, становится реальностью. Робототехника стала огромной областью исследований и разработок, причем некоторые технологии уже коммерциализированы. Вспомните, например, маленькие автономные пылесосы.

На рис. 19.18 показаны лишь некоторые из множества различных форм, которые могут принимать роботы. Самые продвинутые человекоподобные роботы умеют ходить, разливать напитки, даже танцевать (хотя и не очень грациозно). Другие роботы созданы на основе биологии, например собачий робот , показанный на средней фотографии рис. 19.18. Этот робот может перевозить сотни фунтов груза по пересеченной местности. Фотография справа на рисунке 19.18 показано внутреннее устройство М-блока , , разработанного Массачусетским технологическим институтом. Эти простые на вид блоки содержат инерционные колеса и электромагниты, которые позволяют им вращаться и подбрасываться в воздух, а также соединяться в различные формы. Общаясь по беспроводной связи между собой, они самособираются в различные формы, такие как столы, стулья, а когда-нибудь, возможно, даже здания.

Все роботы включают в себя огромное количество физики и техники. Роботы освоили простое действие по наливанию напитка лишь недавно, после более чем 30 лет исследований и разработок! Баланс и время, которые мы, люди, считаем само собой разумеющимися, на самом деле являются очень сложными действиями, требующими отличного баланса, ловкости и обратной связи. Чтобы справиться с этим, требуются датчики для определения баланса, вычислительная мощность для анализа данных и передачи соответствующих компенсационных действий, а также соединения и приводы для выполнения необходимых действий.

Помимо определения гравитации или ускорения, роботы могут иметь несколько различных датчиков для обнаружения света, звука, температуры, запаха, вкуса и т. д. Все эти устройства основаны на физических принципах, которые вы изучаете в этом тексте. Например, оптика, используемая для роботизированного зрения, аналогична той, что используется в ваших цифровых камерах: пиксельные полупроводниковые детекторы, в которых свет преобразуется в электрические сигналы. Для определения температуры можно использовать простые термисторы, представляющие собой резисторы, сопротивление которых изменяется в зависимости от температуры.

Создание робота сегодня намного проще, чем несколько лет назад. Сейчас многие компании предлагают комплекты для сборки роботов. По сложности они варьируются от подходящих для детей начальной школы до задач, которые могут бросить вызов лучшим профессиональным инженерам. Если интересно, вы можете легко найти их в Интернете и начать делать своего собственного робота уже сегодня.

Рисунок 19.18 Роботы бывают разных форм и размеров, от классического гуманоида типа до робот-собака в маленькие кубики, которые самостоятельно собираются для выполнения различных задач.

Смотреть физику

Резисторы параллельно

В этом видео лектор обсуждает простую схему с батареей и парой резисторов, соединенных параллельно. Он подчеркивает, что электроны движутся в направлении, противоположном направлению положительного тока, а также использует тот факт, что напряжение одинаково во всех точках идеального провода. Вывод очень похож на то, что сделано в этом тексте, но лектор хорошо его проходит, объясняя каждый шаг.

Проверка захвата

Верно или неверно — на принципиальной схеме мы можем предположить, что напряжение одинаково в каждой точке данного провода.

ложный
правда

Смотреть физику

Резисторы последовательно и параллельно

В этом видеоролике показано, как рассчитать эквивалентное сопротивление цепи, содержащей резисторы, соединенные параллельно и последовательно. Лектор использует тот же подход, что и изложенный выше, для нахождения эквивалентного сопротивления.

Проверка захвата

Представьте, что N одинаковых резисторов соединены параллельно. Каждый резистор имеет сопротивление Ом. Каково эквивалентное сопротивление этой группы параллельных резисторов?

Эквивалентное сопротивление ( R ) ^Н .
Эквивалентное сопротивление NR.
Эквивалентное сопротивление РН.РН.
Эквивалентное сопротивление NR.NR.

Рабочий пример

Найдите ток через сложную цепь резистора

Аккумулятор в схеме ниже имеет номинальное напряжение 10 В. Какой ток течет по цепи и в каком направлении?

Стратегия

Примените стратегию нахождения эквивалентного сопротивления, заменив все резисторы одним эквивалентным сопротивлением, затем используйте закон Ома, чтобы найти ток через эквивалентный резистор.

Решение

Комбинация резисторов R4R4 и R5R5 может быть уменьшена до эквивалентного сопротивления 9 Ом. 0003

RP1=11/R4+1/R5=11/45 Ом+1/60 Ом=25,71 ОмR.RP1=11/R4+1/R5=11/45 Ом+1/60 Ом=25,71 Ом.

19,38

Замена R4R4 и R5R5 этим эквивалентным сопротивлением дает приведенную ниже схему.

Теперь заменим два верхних резистора R2R2 и R3R3 эквивалентным резистором RS1RS1, а два нижних резистора RP1RP1 и R6R6 эквивалентным резистором RS2RS2. Эти резисторы включены последовательно, поэтому мы складываем их вместе, чтобы найти эквивалентное сопротивление. 100003

19,39

Замена соответствующих резисторов эквивалентными им резисторами дает следующую схему.

Теперь замените два резистора RS1 и RS2RS1 и RS2, включенных параллельно, на эквивалентный им резистор RP2RP2. Сопротивление RP2RP2 составляет

RP2=11/RS1+1/RS2=11/80Ω+1/45,71Ω=29,09Ω.RP2=11/RS1+1/RS2=11/80Ω+1/45,71Ω=29,09Ω. .

19,40

Обновление электрической схемы путем замены RS1 и RS2RS1 и RS2 этим эквивалентным сопротивлением дает приведенную ниже схему.

Наконец, мы объединяем резисторы R1 и RP2R1 и RP2, которые включены последовательно. Эквивалентное сопротивление: RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. RS3=R1+RP2=75 Ом+29,09 Ом=104,09 Ом. Окончательная схема показана ниже.

Теперь воспользуемся законом Ома, чтобы найти силу тока в цепи.

V=IRS3I=VRS3=10V104,09Ω=0,096AV=IRS3I=VRS3=10V104,09Ω=0,096A

19,41

Ток идет от положительной клеммы батареи к отрицательной клемме батареи, поэтому течет по часовой стрелке в этой цепи.

Обсуждение

Этот расчет может показаться довольно длинным, но немного потренировавшись, вы сможете комбинировать некоторые шаги. Обратите также внимание на то, что в расчетах учитывались дополнительные значащие цифры. Только в конце окончательный результат округлялся до двух значащих цифр.

Рабочий пример

Странно выглядящие принципиальные схемы

Иногда вы можете столкнуться с схемами, которые не очень аккуратно нарисованы, например, схема, показанная ниже. Эта принципиальная схема больше похожа на то, как реальная схема может выглядеть на лабораторном столе. Каково эквивалентное сопротивление резисторов на этой диаграмме, если предположить, что сопротивление каждого резистора равно 10 Ом, а номинальное напряжение батареи равно 12 В?

Стратегия

Давайте перерисуем эту принципиальную схему, чтобы она была понятнее. Затем мы применим описанную выше стратегию для расчета эквивалентного сопротивления.

Решение

Чтобы перерисовать диаграмму, рассмотрите рисунок ниже. В верхней схеме синие резисторы образуют путь от положительной клеммы батареи к отрицательной клемме. Параллельно этой цепи расположены красные резисторы, которые образуют еще один путь от положительного к отрицательному выводу батареи. Синие и красные пути показаны более четко на нижней принципиальной схеме. Обратите внимание, что как на верхней, так и на нижней принципиальных схемах синяя и красная дорожки соединяют положительную клемму батареи с отрицательной клеммой батареи.

Теперь легче увидеть, что R1 и R2R1 и R2 параллельны, а параллельная комбинация последовательно с R4R4 . Эта комбинация, в свою очередь, параллельна последовательной комбинации R3 и R5R3 и R5. Сначала мы вычисляем синюю ветвь, которая содержит R1, R2 и R4, R1, R2 и R4. Эквивалентное сопротивление

Rсиний=11/R1+1/R2+R4=11/10Ом+1/10Ом+10Ом=15Ом. 10 Ом=15 Ом.

19,42

где мы показываем вклад параллельного соединения резисторов и последовательного соединения резисторов. Теперь рассчитаем эквивалентное сопротивление красной ветви, которое равно

Rкрасный=R3+R5=10Ом+10Ом=20Ом.Rкрасный=R3+R5=10Ом+10Ом=20Ом.

19,43

Включение этих эквивалентных резисторов в схему дает следующую схему.

Эти два резистора включены параллельно, поэтому их можно заменить одним эквивалентным резистором с сопротивлением

Requiv=11/Rblue+1/Rred=11/15Ω+1/20Ω=8,6Ω. Requiv=11/ Rсиний+1/Rкрасный=11/15 Ом+1/20 Ом=8,6 Ом.

19,44

Окончательная эквивалентная схема показана ниже.

Обсуждение

Найти эквивалентное сопротивление было проще при наличии четкой электрической схемы. Вот почему мы пытаемся сделать четкие принципиальные схемы, где параллельно подключенные резисторы выстроены параллельно друг другу и в одном и том же горизонтальном положении на схеме.

Теперь мы можем использовать закон Ома, чтобы найти ток, проходящий через каждую ветвь этой цепи. Рассмотрим принципиальную схему с RblueRblue и RredRred. Напряжение на каждой из этих ветвей составляет 12 В (т. е. номинальное напряжение батареи). Ток в синей ветке

Iсиний=VRсиний=12В15Ом=0,80А.Iсиний=VRсиний=12В15Ом=0,80А.

19,45

Ток в красной ветви равен

Ired=VRred=12V20Ω=0,60A.Ired=VRred=12V20Ω=0,60A.

19,46

Ток, проходящий через батарею, должен быть суммой этих двух токов (понимаете, почему?), или 1,4 А.

Практические задачи

12.

Какова формула эквивалентного сопротивления двух параллельных резисторов с сопротивлением R ₁ и R ₂ ?

Эквивалентное сопротивление двух параллельных резисторов Reqv=R1+R2Reqv=R1+R2
Эквивалентное сопротивление двух параллельных резисторов Reqv=R1×R2Reqv=R1×R2
Эквивалентное сопротивление двух параллельных резисторов Reqv=R1-R2Reqv=R1-R2
Эквивалентное сопротивление двух параллельных резисторов Reqv=11/R1+1/R2Reqv=11/R1+1/R2

13.

Рисунок 19.19

Каково эквивалентное сопротивление двух показанных резисторов?

Эквивалентное сопротивление 20 Ом
Эквивалентное сопротивление 21 Ом
Эквивалентное сопротивление 90 Ом
Эквивалентное сопротивление 1925 Ом

Проверьте свое понимание

14.

Падение напряжения на параллельных резисторах ________.

одинаковы для всех резисторов
больше для больших резисторов
меньше для больших резисторов
больше для меньших резисторов

15.

Рассмотрим цепь из параллельных резисторов. Минимальный резистор 25 Ом. Каков верхний предел эквивалентного сопротивления?

Верхний предел эквивалентного сопротивления составляет 2,5 Ом.
Верхний предел эквивалентного сопротивления составляет 25 Ом.
Верхний предел эквивалентного сопротивления составляет 100 Ом.
Нет верхнего предела.

Серия
и параллельные цепи — Learn.sparkfun.com
Дом
Учебники
Серийные и параллельные цепи
≡ Страниц
Авторы: Пит-О
Избранное Любимый 56
Последовательные и параллельные схемы
Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками. Но все может стать затруднительным, когда на вечеринку приходят другие компоненты. Куда течет ток? Что делает напряжение? Можно ли это упростить для лучшего понимания? Не бойся, бесстрашный читатель. Далее следует ценная информация.
В этом уроке мы сначала обсудим разницу между последовательными и параллельными цепями, используя схемы, содержащие самые основные компоненты — резисторы и батареи — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях при объединении различных типов компонентов, таких как конденсаторы и катушки индуктивности.
Описано в этом руководстве
Как выглядят последовательные и параллельные схемы
Как пассивные компоненты действуют в этих конфигурациях
Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях
Рекомендуемая литература
Вы можете просмотреть эти руководства по основным компонентам, прежде чем углубляться в построение схем в этом руководстве.
Что такое электричество
Напряжение, ток, сопротивление и закон Ома
Что такое цепь?
Конденсаторы
Катушки индуктивности
Резисторы
Как пользоваться макетной платой
Как пользоваться мультиметром
Видео

Цепи серии
Узлы и ток
Прежде чем мы углубимся в это, нам нужно упомянуть, что такое узел . Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда цепь моделируется на схеме, эти узлы представляют собой провода между компонентами.
Пример схемы с четырьмя узлами уникального цвета.
Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также необходимо понять , как ток течет по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи. Некоторое количество тока будет протекать по каждому пути, который может пройти, чтобы добраться до точки с самым низким напряжением (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет протекать ток, когда он проходит от положительной клеммы батареи к отрицательной:
Ток (обозначен синей, оранжевой и розовой линиями), протекающий по той же схеме, что и выше. Разные токи обозначены разными цветами.
Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂ ) ток на входе такой же, как и на выходе. В других узлах (в частности, в трехстороннем соединении между R ₂ , R ₃ и R ₄ ) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным!
Определены последовательные цепи
Два компонента соединены последовательно, если они имеют общий узел и если через них протекает один и тот же ток . Вот пример цепи с тремя последовательными резисторами:
В приведенной выше цепи ток может протекать только одним способом. Начиная с положительной клеммы аккумулятора, ток сначала встретится с R ₁ . Оттуда ток будет течь прямо к R ₂, затем на R ₃ и, наконец, обратно на отрицательную клемму аккумулятора. Обратите внимание, что ток может следовать только по одному пути. Эти компоненты расположены последовательно.
Параллельные цепи
Параллельные цепи определены
Если компоненты совместно используют два общих узла , они параллельны. Вот пример схемы трех резисторов, подключенных параллельно к батарее:
От положительной клеммы батареи ток течет к R ₁ … и R ₂ и R ₃ . Узел, который соединяет батарею с R ₁, также связан с другими резисторами. Другие концы этих резисторов аналогичным образом соединяются вместе, а затем снова соединяются с отрицательным полюсом батареи. Есть три различных пути, по которым ток может пройти, прежде чем вернуться в батарею, и говорят, что соответствующие резисторы включены параллельно.
Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — последовательно:ток::параллельно:напряжение.
Последовательные и параллельные цепи работают вместе
Отсюда мы можем смешивать и сочетать. На следующей картинке мы снова видим три резистора и батарейку. С положительной клеммы аккумулятора ток сначала встречается с R ₁ . Но на другой стороне R ₁ узел разделяется, и ток может идти как на R ₂, так и на R ₃ . Пути тока через R ₂ и R ₃ затем снова соединяются вместе, и ток возвращается к отрицательной клемме аккумулятора.
В этом примере R ₂ и R ₃ параллельны друг другу, а R ₁ последовательно соединены с параллельной комбинацией R ₂ и R ₃ .
Расчет эквивалентных сопротивлений в последовательных цепях
Вот некоторая информация, которая может оказаться для вас более полезной. Когда мы соединяем резисторы вместе, последовательно и параллельно, мы меняем способ прохождения через них тока. Например, если у нас есть питание 10 В через 10 кОм; резистор, закон Ома говорит, что у нас есть ток 1 мА.
Если потом поставить еще 10кОм резистор последовательно с первым и оставить питание без изменений, мы сократили ток наполовину, потому что сопротивление удвоилось.
Другими словами, у тока по-прежнему есть только один путь, и мы только усложнили течение тока. Насколько сложнее? 10 кОм + 10 кОм = 20 кОм. И вот как мы вычисляем резисторы последовательно — просто добавляем их значения .
Если выразить это уравнение в более общем виде: общее сопротивление N — произвольное количество — резисторов это их общая сумма.
Расчет эквивалентных сопротивлений в параллельных цепях
Как насчет параллельных резисторов? Это немного сложнее, но ненамного. Рассмотрим последний пример, где мы начали с источника питания 10 В и резистора 10 кОм. резистор, но на этот раз мы добавляем еще 10 кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, по закону Ома первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть в общей сложности 2 мА, поступающие от источника питания, что вдвое превышает исходный 1 мА. Это означает, что мы сократили общее сопротивление вдвое.
Пока можно сказать, что 10кОм; || 10 кОм = 5 кОм («||» примерно переводится как «параллельно с»), у нас не всегда будет 2 одинаковых резистора. Что тогда?
Уравнение для параллельного добавления произвольного числа резисторов:
Если вам не нравятся обратные величины, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два резистора, соединенных параллельно:
Однако это Метод хорош только для двух резисторов в одном расчете. С помощью этого метода мы можем комбинировать более 2 резисторов, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (опять же как произведение на сумму), но обратный метод может быть менее трудоемким.
Время эксперимента. Часть 1 резисторы
Мультиметр
Макет
Давайте проведем простой эксперимент, чтобы доказать, что эти вещи работают именно так, как мы говорим.
Во-первых, мы собираемся подключить 10 кОм. резисторы последовательно и наблюдайте, как они складываются самым незагадочным образом. С помощью макетной платы поместите один 10кОм; сопротивление, как показано на рисунке, и измерить мультиметром. Да, мы уже знаем, что это будет 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности». Как только мы убедим себя, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один таким же образом, но с проводами от каждого резистора, электрически подключенными через макетную плату, и измерьте снова. Теперь измеритель должен показать что-то близкое к 20 кОм.
Вы можете заметить, что измеренное вами сопротивление может не совпадать с тем, каким должен быть резистор. Резисторы имеют определенный допуск , что означает, что они могут быть отклонены на определенный процент в любом направлении. Таким образом, вы можете прочитать 9,99 кОм; или 10,01 кОм. Пока оно близко к правильному значению, все должно работать нормально.
Читатель должен продолжать это упражнение до тех пор, пока не убедится, что он знает, каков будет результат, прежде чем повторить его снова, или пока у него не закончатся резисторы, чтобы воткнуть их в макетную плату, в зависимости от того, что наступит раньше.
Время эксперимента. Часть 2
Теперь давайте попробуем с резисторами в конфигурации параллельно . Поместите один 10кОм; резистор на макетной плате, как и раньше (надеемся, что читатель уже полагает, что одиночный резистор 10 кОм будет измерять что-то близкое к 10 кОм на мультиметре). Теперь поместите второй 10кОм. резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но прежде чем измерять комбинацию, рассчитайте либо методом произведения на сумму, либо обратным методом, каким должно быть новое значение (подсказка: оно будет 5 кОм). Затем измерьте. Это что-то близкое к 5кОм? Если это не так, дважды проверьте отверстия, в которые подключены резисторы.
Повторите упражнение с резисторами 3, 4 и 5. Расчетные/измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли вышло так, как планировалось? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Иди выпей молочный коктейль, прежде чем мы продолжим. Ты заслужил это.
Практические рекомендации для последовательных и параллельных резисторов
Есть несколько ситуаций, которые могут потребовать некоторых творческих комбинаций резисторов. Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень конкретное соотношение резисторов, значения которых вряд ли будут «стандартными». И хотя мы можем получить очень высокую степень точности в значениях резисторов, мы, возможно, не захотим ждать X дней, необходимых для отправки чего-либо, или платить цену за нестандартные значения, которых нет в наличии. Так что в крайнем случае мы всегда можем создать свои собственные номиналы резисторов.
Совет №1: Одинаковые резисторы в параллельном соединении
Добавление N резисторов с одинаковыми номиналами R в параллельном соединении дает нам R/N Ом. Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм/4 = 2,5 кОм.
Совет № 2: Терпимость
Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3,2 кОм; резистор, можно поставить 3 10кОм резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% допуска от необходимого вам значения. Но если схема, которую вы строите, должна иметь допуск ближе 4%, мы можем измерить наш запас 10 кОм, чтобы увидеть, какие из них являются самыми низкими значениями, потому что у них тоже есть допуск. По идее, если заначка 10кОм; все резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители деталей, как известно, допускают именно такие ошибки, так что стоит немного поковыряться.
Совет № 3: номинальная мощность при последовательном/параллельном соединении
Такое последовательное и параллельное сочетание резисторов работает и для номинальной мощности. Допустим, нам нужен 100 Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это куча 1 кОм; резисторы на четверть ватта (¼ Вт) (и сейчас 3 часа ночи, вся горная роса закончилась, а кофе остыл). Вы можете комбинировать 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм/10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Некрасиво, но это поможет нам завершить финальный проект и может даже принести нам дополнительные баллы за способность думать на ходу.
Нам нужно быть немного более осторожными, когда мы соединяем параллельно резисторы разных номиналов, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Это должно быть совершенно очевидно для читателя, но…
Совет № 4: Параллельное подключение разных резисторов
Суммарное сопротивление двух резисторов разного номинала всегда меньше резистора наименьшего номинала. Читатель был бы поражен тем, сколько раз кто-то комбинирует значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм; || 10 кОм; НЕ равняется ничему около 5 кОм!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет № 4 10 раз.
Совет № 5: Рассеиваемая мощность при параллельном подключении
Мощность, рассеиваемая при параллельном соединении резисторов разного номинала, распределяется между резисторами неравномерно, поскольку токи не равны. Используя предыдущий пример (1 кОм; || 10 кОм), мы можем видеть, что 1 кОм; будет потреблять в 10 раз больше тока, чем 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор будет рассеивать в 10 раз больше мощности, чем 10 кОм.
В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных сокращений, когда значения совпадают.
Последовательные и параллельные конденсаторы
Объединение конденсаторов аналогично объединению резисторов, только наоборот. Как ни странно это звучит, это абсолютно верно. С чего бы это?
Конденсатор — это всего лишь две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую кучу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически появляется больше места для электронов. И если пластины раздвинуты дальше друг от друга, емкость уменьшается, потому что напряженность электрического поля между ними уменьшается по мере увеличения расстояния.
Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и допустим, они оба заряжены и готовы разрядиться на друга, сидящего рядом с вами.
Помните, что в последовательной цепи есть только один путь для протекания тока. Из этого следует, что количество электронов, выходящих из нижней крышки, будет равно количеству электронов, выходящих из верхней части. Значит, емкость не увеличилась?
На самом деле все еще хуже. Поместив конденсаторы последовательно, мы фактически разнесли пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов суммируется. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас есть 5 мкФ. Результатом этого является то, что мы добавляем значения последовательных конденсаторов так же, как мы добавляем значения параллельных резисторов. Для последовательного добавления конденсаторов применимы как метод произведения на сумму, так и обратный метод.
Может показаться, что нет смысла добавлять последовательно конденсаторы. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.
Добавление конденсаторов параллельно похоже на последовательное добавление резисторов: значения просто складываются, никаких ухищрений. Почему это? Параллельное размещение эффективно увеличивает размер пластин без увеличения расстояния между ними. Чем больше площадь, тем больше емкость. Простой.
Время эксперимента. Часть 3
Что вам понадобится: резистор
Три конденсатора по 100 мкФ
A Держатель 3-элементной батарейки AA
Три элемента типа АА
Макет
Мультиметр
Зажимы-провода
Давайте посмотрим на некоторые последовательно и параллельно соединенные конденсаторы в действии. Это будет немного сложнее, чем примеры резисторов, потому что сложнее измерить емкость напрямую с помощью мультиметра.
Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается от нуля вольт. Когда ток начинает идти в одном из выводов, равное количество тока выходит из другого. А если последовательно с конденсатором сопротивления нет, то может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, более медленно стекая до тех пор, пока напряжения не сравняются, когда ток полностью прекращается.
Как указано выше, потребляемый ток может быть довольно большим, если последовательно с конденсатором отсутствует сопротивление, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядкой конденсатора, поэтому мы собираемся использовать 10 кОм; резистор последовательно, чтобы замедлить действие до точки, где мы можем легко это увидеть. Но сначала нам нужно поговорить о том, что такое постоянная времени RC.
Приведенное выше уравнение говорит о том, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Простой? Нет? Мы продемонстрируем на следующей странице.
Время эксперимента. Часть 3, продолжение…
В первой части этого эксперимента мы будем использовать один резистор на 10 кОм и один на 100 мкФ (что соответствует 0,0001 фарад). Эти две части создают постоянную времени, равную 1 секунде:
резистора, мы можем ожидать, что напряжение на крышке поднимется примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду. После 5 постоянных времени (в данном случае 5 секунд) максимальное значение составляет около 99% заряда до напряжения питания, и он будет следовать кривой заряда, примерно как на графике ниже.
Теперь, когда мы это знаем, мы собираемся соединить цепь на схеме (убедитесь, что на этом конденсаторе указана полярность!).
С помощью нашего мультиметра, настроенного на измерение напряжения, проверьте выходное напряжение батареи при включенном выключателе. Это наше напряжение питания, и оно должно быть около 4,5 В (будет немного больше, если батареи новые). Теперь подключите цепь, позаботившись о том, чтобы переключатель на батарейном блоке находился в положении «ВЫКЛ», прежде чем подключать его к макетной плате. Кроме того, позаботьтесь о том, чтобы красный и черный провода находились в правильных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы было проще).
Когда мы убедимся, что схема выглядит правильно, а наш измеритель включен и настроен на считывание напряжения, переведите переключатель на батарейном блоке в положение «ВКЛ». Примерно через 5 секунд показания счетчика должны быть близки к напряжению аккумуляторной батареи, что свидетельствует о правильности уравнения и о том, что мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что ток не может разрядить конденсатор; у нас разомкнутая цепь. Для разрядки конденсатора можно параллельно подключить еще один резистор 10К. Примерно через 5 секунд он вернется к довольно близкому к нулю.
Время эксперимента.
Часть 3, еще больше…
Теперь мы переходим к интересным частям, начиная с последовательного соединения двух конденсаторов. Помните, что мы сказали, что результат будет аналогичен соединению двух резисторов параллельно. Если это правда, мы можем ожидать (используя произведение на сумму)
Что это сделает с нашей постоянной времени?
Имея это в виду, подключите еще один конденсатор последовательно к первому, убедитесь, что счетчик показывает ноль вольт (или около того), и переведите переключатель в положение «ВКЛ». Потребовалось ли примерно в два раза меньше времени, чтобы зарядить аккумуляторную батарею до напряжения? Это потому, что емкость в два раза меньше. Электронный бензобак стал меньше, поэтому для его зарядки требуется меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель увидит надпись на стене.
Теперь попробуем подключить конденсаторы параллельно, помня, что мы сказали ранее, что это будет похоже на добавление резисторов последовательно. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет
. Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4,5 В.
Для проверки начните с нашей оригинальной схемы на 10 кОм; резистор и один конденсатор на 100 мкФ последовательно, как показано на первой схеме для этого эксперимента. Мы уже знаем, что конденсатор зарядится примерно через 5 секунд. Теперь добавьте второй конденсатор параллельно. Убедитесь, что показания мультиметра близки к нулю вольт (разрядите через резистор, если показания не равны нулю), и переведите переключатель на батарейном блоке в положение «ON». Занимает много времени, не так ли? Разумеется, мы увеличили резервуар для электронного газа, и теперь его заполнение занимает больше времени. Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение длительного времени.
Серийные и параллельные катушки индуктивности
Серийные и параллельные катушки индуктивности
Случаи, когда катушки индуктивности необходимо добавлять последовательно или параллельно, довольно редки, но не являются чем-то исключительным. В любом случае, давайте обратимся к ним, чтобы быть полным.
В двух словах, они складываются так же, как резисторы, то есть они складываются со знаком плюс при последовательном соединении и с произведением на сумму при параллельном. Сложность возникает, когда они расположены близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, а не два или более, хотя большинство катушек индуктивности экранированы для предотвращения взаимодействия магнитных полей.
В любом случае достаточно сказать, что они складываются подобно резисторам. Дополнительная информация, касающаяся катушек индуктивности, выходит далеко за рамки данного руководства.
Хотите узнать больше об основных темах?
См. нашу страницу Engineering Essentials , где представлен полный список краеугольных тем, связанных с электротехникой.
Отведи меня туда!
Ресурсы и продолжение
Теперь, когда вы знакомы с основами последовательных и параллельных схем, почему бы не ознакомиться с некоторыми из этих руководств?
Делители напряжения. Одной из самых основных и повторяющихся схем является делитель напряжения. Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
Что такое Ардуино? — Теперь, когда вы освоили основы схемотехники, вы можете перейти непосредственно к изучению микроконтроллеров на одной из самых популярных платформ: Arduino.
Основы коммутатора
. В этом руководстве мы говорили о некоторых основных элементах схемы, но этот не был одним из них. Переключатели являются важнейшим компонентом практически любого электронного проекта. Узнайте все о переключателях в этом руководстве
Шитье с помощью токопроводящей нити. Цепи не обязательно должны состоять только из макетных плат и проволоки. E-textiles использует проводящую нить для вшивания света и другой электроники в одежду или другую ткань.
Power Tool: Flow vs.
Среди трудностей лежит возможность. Альберт Эйнштейн
В физике закон Ома описывает, как ток течет через материал. Поток может быть замедлен материалом, оказывающим сопротивление, или, в некоторых случаях, поток может быть почти полностью перекрыт.
Тот же самый закон физики можно применить к нашей жизни и, в данном конкретном случае, к построению бизнеса.
Представьте, что вы строите бизнес как одну большую электрическую цепь. Вы можете видеть конец цепи — видение того, где вы хотите быть. Когда вы путешествуете по трассе, ваше путешествие может казаться легким и легким, а иногда ваше продвижение может быть замедлено или почти полностью остановлено.
Мы можем назвать это потоком и сопротивлением.
Поток
Те, кто течет, как течет жизнь, знают, что им не нужна никакая другая сила. Лао-цзы
Бывают моменты, когда кажется, что построить свой бизнес совсем несложно. Вы чувствуете связь с тем, чего хотите достичь, и своей целью, и сосредоточены на своих повседневных действиях для достижения своих целей. Вы видите, как открываются возможности, чувствуете себя в соответствии со своей интуицией и предпринимаете вдохновенные действия.
Когда вы находитесь в потоке, вы чувствуете связь с настоящим моментом. Вы можете погрузиться в задачу с полной концентрацией, и в результате ваша производительность взлетит до небес.
Поток легче всего достигается, когда вы выполняете задачи, которые задействуют ваши уникальные сильные стороны и способности. Гей Хендрикс (2010) называет этот поток вашей Зоной Гениальности.
Сопротивление
Чему вы сопротивляетесь – сохраняется. Карл Юнг
В других случаях при построении бизнеса вы встречаете сопротивление — как внутри себя, так и во внешнем мире, — что может замедлить ваш прогресс.
Сопротивление естественному течению может проявляться по-разному:
Ограничивающие убеждения — убеждения, которые не служат вам, а, скорее, мешают вам реализовать свой потенциал, например, убеждение, что вы недостаточно хороши, или страх осуждения со стороны других. Эти убеждения могут, например, помешать вам стать заметным и расширить свою аудиторию.
Опыт — сложный опыт, такой как неудачные отношения с клиентами, баланс между работой и личной жизнью или выполнение чего-то, чего вы никогда раньше не делали, например, проведение семинара или создание веб-сайта. Негативные отношения с клиентом могут помешать вам давать честную обратную связь другим клиентам или заставить вас обвинять клиента.
Отвлекающие факторы или «синдром блестящего предмета» — постоянно следовать новым идеям и начинать новые проекты вместо того, чтобы просматривать начатые проекты. Это может привести к отсутствию приверженности вашей цели и держать вас в «зоне попыток».
Успех и самосаботаж — В книге «Большой скачок» (2010) Хендрикс обсуждает, как, когда дела идут хорошо, вы можете достичь верхнего предела того, с каким успехом, по вашему мнению, вы можете справиться. Когда вы достигаете этого потолка, обычная практика состоит в том, чтобы начать заниматься самосаботажем. Например, вы можете начать критиковать или привносить негативные чувства в отношения с клиентами, потому что в глубине души вы сомневаетесь, сможете ли вы им действительно помочь.
Сопротивление связано со многими негативными установками, такими как обвинение, отсутствие обязательств и прокрастинация. Когда вы чувствуете сопротивление, ваше продвижение к цели замедляется.
Сопротивление часто можно спутать с несоосностью. Несоответствие возникает, когда вы не чувствуете связи с тем путем, на котором идете, — что-то кажется неправильным. Это может быть выбранная вами ниша, услуга или продукт, который вы продаете, или то, чем вы занимаетесь большую часть своего времени. Возможно, вы не чувствуете связи со своей целью или проводите большую часть своего времени, занимаясь тем, что вам не нравится.
Вы можете определить, сталкиваетесь ли вы с сопротивлением или смещением, оттачивая, где в вашем теле вы это испытываете. Сопротивление часто происходит в голове и связано с вашим эго. Мы можем признать, что слишком много думаем или что у нас есть скрытое убеждение, которое влияет на наше поведение. Несоосность — это то, что вы чувствуете всем телом или сердцем — это всеохватывающее чувство, что что-то не так.
Несоответствие можно легко спутать с сопротивлением при открытии бизнеса, поскольку есть много занятий, которые вы, возможно, не выбрали бы и не находитесь в зоне своей гениальности. Когда вы начинаете бизнес, вы обычно несете ответственность за все, от создания веб-сайта до написания блогов для рассылки по электронной почте вашего списка. Многие из этих действий могут показаться вам неудобными. Вы можете почувствовать сопротивление в виде страха, ограничивающих убеждений или прокрастинации. Нежелание что-то делать или сомнение в том, сможете ли вы это сделать, обычно является сопротивлением, а не рассогласованием. Тем не менее, когда вы довели свой бизнес до определенного прибыльного уровня, именно эти менее чем приятные действия, которые вас не освещают, вы бы сначала отдали на аутсорсинг. Это позволяет вам уделить внимание вашей истинной зоне гениальности и тратить больше времени на приток.
Поддержание потока
Поток — это не отсутствие сопротивления, а способность присутствовать и двигаться вперед с полным принятием и ответственностью за то, что есть.
10 шагов к достижению потока
Выберите свою нишу разумом и сердцем. С кем ты хочешь проводить дни? Для кого ты хочешь быть героем? Часто в бизнесе есть много проблем, которые мы могли бы решить, многим клиентам мы могли бы помочь. Выберите нишу, которая позволит вам окружить себя людьми, которые зажигают вас и заряжают энергией.
Прикоснитесь к своей зоне гениальности. Определите, какие виды деятельности задействуют ваши уникальные способности, не кажутся работой и приносят вам наивысшее соотношение изобилия и удовлетворения.
Отдайте на аутсорсинг деятельность за пределами вашей Зоны Гениальности. Как можно скорее (и, возможно, раньше, чем кажется возможным) отдайте на аутсорсинг повторяющиеся задачи, отнимающие много времени и отвлекающие вас от того, что вы делаете лучше всего.
Ставьте цели. Четко определите, чего вы хотите достичь и почему. Если вы не знаете, куда идете, вы не будете связаны со своей целью и упустите возможность быстрее добраться туда.
Устраните отвлекающие факторы и не работайте одновременно. Полностью посвятите себя каждой задаче и предпримите простые шаги, чтобы устранить отвлекающие факторы, например закройте электронную почту и отключите уведомления.
Воспринимайте сопротивление как возможность. В отличие от электрического тока, у нас есть выбор. Когда мы сталкиваемся с сопротивлением, у нас есть возможность превратить это сопротивление в проводник, который движет нас вперед. Склонитесь к сопротивлению и дискомфорту, поймите и примите. Найдите подарок в ситуации. Например, неудачные отношения с клиентом открывают место для нового клиента.
Подготовьте себя к успеху. Ежедневно работайте над своим мышлением и вырабатывайте полезные привычки, которые помогут вам в развитии вашего бизнеса.
Сначала выполняйте любые упражнения с сопротивлением. Начните свой день с самых важных дел.
Оставьте место для творчества.
No related posts.

В _Т	=	В ₁	+	В ₂	+	В ₃
125 В	=	25,0 В	+	37,5 В	+	62,5 В
125 В	=	125 В