Применение векторов к решению задач 8 класс онлайн-подготовка на Ростелеком Лицей
Выражение вектора через два неколлинеарных
Напомним, что мы уже изучили некоторые факты о векторах, и теперь умеем определять равные векторы, коллинеарные векторы, сонаправленные и противоположно направленные. Также мы умеем складывать векторы по правилу треугольника и параллелограмма, складывать несколько векторов по правилу многоугольника, умеем умножать вектор на число. Решение задач с векторами использует все эти знания. Перейдем к решению некоторых примеров.
Пример 1 – задача 769: отрезок ВВ1 – медиана треугольника . Выразите через векторы и векторы , , и .
Отметим, что векторы и неколлинеарны, то есть прямые АВ и АС не параллельны.
В дальнейшем мы узнаем, что любой вектор может быть выражен через два неколлинеарных вектора.
Выразим первый вектор (см. Рис. 1): , т. к. по условию ВВ1 – медиана треугольника, значит, векторы и имеют равные модули, кроме того, очевидно, что они коллинеарны и при этом сонаправлены, значит, данные вектора равны.
Рис. 1
Для выражения следующего вектора воспользуемся правилом параллелограмма для вычитания. Мы помним, что одна из диагоналей параллелограмма, построенного на двух векторах, соответствует сумме этих векторов, а вторая – их разности. Диагональ, соответствующая разности векторов, следует от конца к началу, таким образом, если построить на заданных векторах и параллелограмм, то его диагональ будет соответствовать разности .
Вектор является противоположным к заданному вектору , отсюда .
Вектор аналогично вектору можно представить в виде разности векторов . При выражении следует учесть тот факт, что точка В1 является серединой отрезка АС, значит, векторы и равны, значит, вектор можно представить как удвоенное произведение вектора .
Перед решением задачи мы сказали, что через заданные два неколлинеарных вектора можно выразить любой вектор. Выразим, например, медиану АА1 (см. Рис. 2).
Получили систему уравнений, выполним их сложение:
Векторы в сумме составляют нулевой вектор, так как они коллинеарны и противонаправлены, а модули их равны, таким образом получаем:
Рис.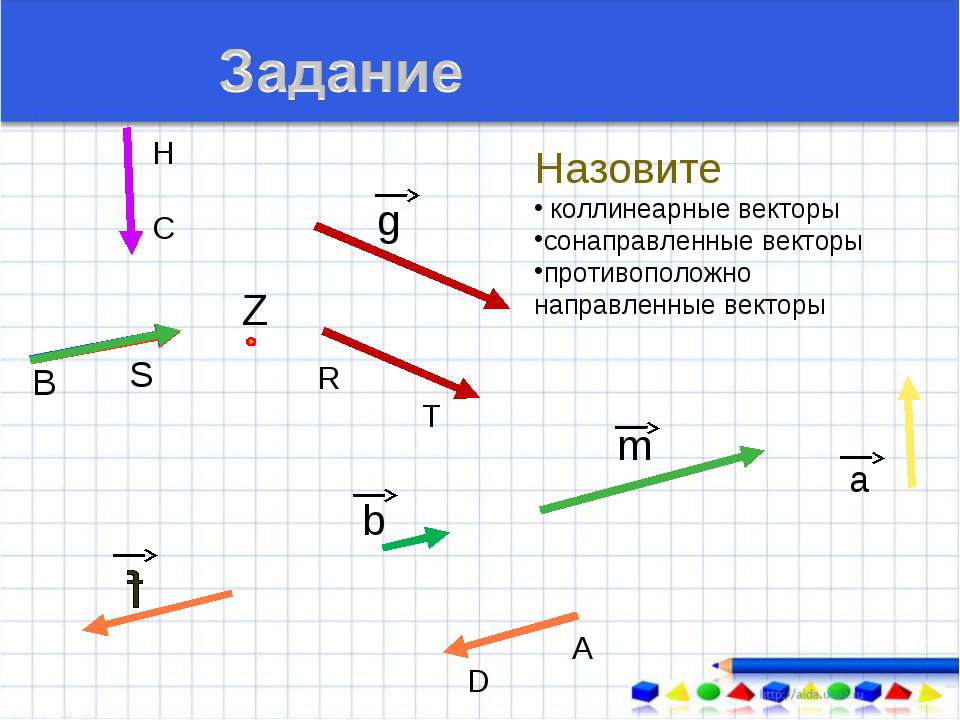 2
2
Поделим обе части уравнения на два, получим:
Из данной задачи можно сделать вывод, что если заданы два неколлинеарных вектора, то любой третий вектор на плоскости можно однозначно выразить через эти два вектора. Для этого необходимо применить правило сложения векторов, либо методом треугольника, либо параллелограмма, и правило умножения вектора на число.
Свойство средней линии треугольника
Пример 2: доказать с помощью векторов свойство средней линии треугольника (см. Рис. 3).
Задан произвольный треугольник , точки M и N – середины сторон АВ и АС соответственно, MN – средняя линия треугольника. Свойство средней линии: средняя линия параллельна основанию треугольника и равна его половине.
Доказательство данного свойства аналогично для треугольника и трапеции.
Рис. 3
Выразим вектор двумя способами:
Получили систему уравнений:
Выполним сложение уравнений системы:
Сумма векторов – это нулевой вектор, длины этих векторов равны по условию, кроме того, они очевидно коллинеарны и противонаправлены.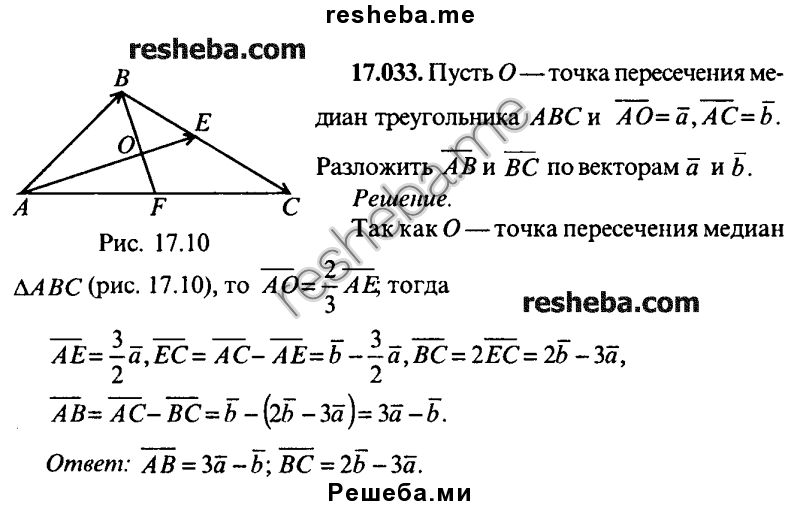 Аналогично суммой векторов будет нулевой вектор. Получаем:
Аналогично суммой векторов будет нулевой вектор. Получаем:
Поделим обе части уравнения на два:
Таким образом, мы получили, что средняя линия треугольника равна половине его основания. Кроме того, из равенства вектора половине вектора следует, что эти векторы коллинеарны и сонаправлены, а значит, прямые MN и ВС параллельны.
Таким образом, мы доказали свойство средней линии трапеции при помощи векторов.
Свойство точки пересечения медиан треугольника
Пример 3: задан произвольный треугольник (см. Рис. 4). В нем проведены медианы АА1, ВВ1, СС1. Точка пересечения медиан – М. Вектор соответствует силе , – силе , – силе . Доказать, что .
Напомним, что медианы треугольника пересекаются в одной точке и этой точкой делятся в отношении 2:1, считая от вершины.
Иногда точку пересечения медиан называют центром тяжести треугольника.
Выполним сложение векторов , воспользуемся для этого правилом параллелограмма (см. Рис. 5).
Рис. 5).
Рис. 4
Получаем:
С другой стороны, , так как BMCD – параллелограмм, диагонали параллелограмма точкой пересечения делятся пополам, А1 – точка пересечения диагоналей параллелограмма, значит, отрезки МА1 и А1D равны, отсюда, по свойству точки пересечения медиан, длины векторов и равны, но данные векторы противонаправлены, а значит, их сумма
Рис. 5
равна нулевому вектору. Мы помним, что вектор , а вектор , таким образом, , что и требовалось доказать.
Неравенство треугольника
Пример 4 – задача 773: докажите, что для любых векторов и справедливо следующее неравенство:
Решение: представим разность векторов в виде суммы: . Также обратим внимание на тот факт, что длины противонаправленных векторов и равны: . Таким образом, можно переписать исходное выражение:
Для удобства введем новую переменную: и перепишем выражение:
. А данное неравенство – неравенство треугольника – было доказано в предыдущем уроке. Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Отметим, что равенство наблюдается в том случае, когда треугольник вырождается в отрезок.
Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Cleverstudents.ru (Источник).
Домашнее задание
- Задание 1: заданы два неколлинеарных вектора и . Постройте векторы: ; ; .
- Задание 2: заданы два коллинеарных вектора и . Постройте векторы: ; ; .
- Задание 3: докажите, что для любого вектора справедливы равенства: ; .

| Интегрированный урок по физике и математике «Векторы». 9 класс Повторение и закрепление основных понятий в математике и физике, связанных с векторами. Повторить и закрепить основные понятия, связанные с векторами, закрепить умение решать задачи, применяя теоретический материал геометрии и физики. Применение темы «Векторы» при решении задач практического содержания. Цель урока:
Задачи урока:
Ученик должен знать:
Ученик должен уметь:
Тип урока: Личностно-ориентированная, информационно-коммуникативная. КЭС: векторы, сумма, разность, умножение вектора на число, координаты вектора, скалярное произведение двух векторов, вычисление значений угла между векторами, радиус-вектор, практическая значимость понятия «вектор».
Сценарий урока: 1. Подготовка к восприятию материала: Вступительное слово учителя математики: «…нет ни одной области в математике, которая когда-либо не окажется применимой к явлениям действительного мира…» Н.И.Лобачевский -Мы изучаем векторы. А где это применяется? Векторная история это пограничная история, между математикой и физикой. Геометрический подход к физическим задачам наследуется еще от древних греков. Смещение от числовых, или скалярных, координат из аналитической геометрии к житейскому понятию «направление», смешанному с иллюстративно-художественным подходом, постепенно трансформировало образы мышления физиков. Прежде, чем говорить об использовании векторов при решении физических задач, вспомним действия, которые можно выполнять с векторами. (Задавая вопросы, учитель может использовать игровой компонент: бросая мячик, формулировать вопрос, принимая его, получать ответ). — Какие способы сложения векторов вам известны? (Правило треугольника и правило параллелограмма) — В чем принципиальное отличие этих правил? ( При сложении по правилу треугольника начало второго вектора совмещается с концом первого (слайд 2), а при сложении по правилу параллелограмма начала обоих векторов совпадают (слайд 3).) — Что будет вектором суммы при сложении векторов по правилу треугольника? (Вектор, берущий начало в начале первого и заканчивающийся в конце второго вектора.) — Что будет вектором суммы при сложении векторов по правилу параллелограмма? (Вектор, являющийся диагональю параллелограмма, построенного на исходных векторах, исходящий из общего начала слагаемых векторов. — Что будет вектором разности двух векторов? (Вектор, соединяющий концы векторов и идущий в направлении уменьшаемого (слайд 4)). — А если нужно выполнить действие с векторами, которые не выходят из одной точки? (Один из векторов параллельным переносом перенести так, чтобы начала их совпали.) — Что происходит при умножении вектора на положительное число? (Длина вектора изменяется во столько раз, на какое число выполняется умножение, а направление не изменяется). — А если выполняем умножение на отрицательное число? (Направление меняется на противоположное (слайд 5)). — Как называются получившиеся векторы? (Коллинеарные (сонаправленные и противоположно направленные)). Задача 1. Построить вектор , равный сумме трех заданных векторов (слайд 6). Решение (слайд 7): Задача 2. Построить вектор . (слайд 8). Решение (слайд 9). Задача 3 (слайд 10). Решение (слайд 11). Задача 4 (слайд 12). Решение (слайд 13). — Как найти координаты вектора, зная координаты его начала и его конца (слайд 14)? (Чтобы найти координаты вектора, нужно из координат конца вычесть соответствующие координаты начала вектора (слайд 15)). — Как найти длину вектора, зная координаты его начала и его конца (слайд 16)? ( Длина вектора равна корню из суммы квадратов разностей соответствующих координат начала и конца вектора) . Задача 5(слайд 17). Решение (слайд 18). — Как найти координаты суммы двух векторов? (Найти сумму соответствующих координат (слайд 19)). — Как найти координаты разности двух векторов? (Найти разность соответствующих координат (слайд 20)). — Что называют «скаляром»? (Скаляр – это физический термин, обозначающий число). -Почему умножение векторов называется скалярным? (Потому что в результате умножения двух векторов получается число). — А что получается при умножении вектора на число (скаляр)? (Вектор). — Как найти в этой ситуации координаты нового вектора? (Координаты исходного вектора умножить на скаляр (слайд 21)). — Модуль вектора – это скаляр или вектор? (Скаляр, так как модуль – это длина вектора). — Чему равен модуль вектора? (Корню из квадрата этого вектора (слайд 22)). — Как найти модуль вектора, если нам известны его координаты? (Извлечь корень из суммы квадратов координат этого вектора (слайд 23)). — Как найти скалярное произведение векторов, зная их координаты? (Сложить произведения соответствующих координат этих векторов (слайд 24)). — Как найти скалярное произведение векторов другим способом? (Умножить произведение длин этих векторов на косинус угла между ними (слайд 25)). В физике дается определение радиус-вектора. Радиус-вектор – это направленный отрезок, проведенный из начала координат в данную точку пространства. Если противоречие между двумя определениями, сформулированными в математике и физике? (В любом случае, сделать акцент на идею направления в обоих определениях) Многие физические величины характеризуются подобно радиус-вектору не только числовым значением, но и направлением. Например: скорость, перемещение, импульс, напряженность электрического поля, сила и др. Эти физические величины называют векторными. Длину такого вектора называют модулем вектора. Законы сложения и вычитания векторов мы будем использовать с вами на уроках физики неоднократно, изучая разные темы. Сейчас мы рассматриваем задачи по теме «Относительность механического движения, законы сложения скоростей и перемещений». Данные задачи обязательно встретятся вам на ГИА в этом году и при сдаче ЕГЭ по физике в 11 классе. Рассмотрим сегодня на уроке задачи практического содержания по этой теме. Парашютист опускается вертикально вниз со скоростью 4 м/с в безветренную погоду. С какой скоростью он будет двигаться при горизонтальном ветре, скорость которого относительно Земли 3 м/с. На какое расстояние отнесет его от места падения, если он спускается с высоты 2км? Работа над задачей.
Задача 2. Штурман пытается провести судно в тумане через узкий проход между рифами. Представьте себе, что проход между рифами идет в северном направлении, Скорость океанского течения равна 5м/с, направлено оно на восток, а скорость, сообщаемая винтом судну 9 м/с. Идет аналогичная работа над задачей. (Слайды 30 – 32) Задача 3. Скорость лодки 4 м/с, скорость течения 2 м/с. Под каким углом к береговой линии должен лодочник вести лодку, чтобы попасть на противоположный берег строго против того места, от которого он отплыл? Сделайте чертеж. (Слайды 33 – 35) В конце урока предлагается тест по материалам урока. Вопросы теста по карточкам, которые выдают каждому обучающемуся. Тест на тему «Векторы» ученика 9 класса гимназии №1799 «Экополис» _______________________________________________.
3. Лодка должна попасть на противоположный берег реки кратчайшим путем в системе отсчета, связанной с берегом.  Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен Скорость течения реки, а скорость лодки относительно воды . Модуль скорости лодки относительно берега должен быть равен1) 2) 3) 4) Ответ: 4 4. Два автомобиля движутся по прямой дороге: один — со скоростью (–10 м/с), другой – со скоростью (–25 м/с). Скорость второго автомобиля относительно первого равна 1) –35 м/с 2) –15 м/с 3) –20 м/с 4) 35 м/с Ответ: 2 5. Пилот поднялся на воздушном шаре на высоту 800м, за это время шар был отнесен ветром в горизонтальном направлении на 600м. Найдите перемещение шара относительно земли? 1) 1400м 2)200м 3)1000м 4) 800м Ответ: 3 Заключительная часть урока. Подводится итог. Выставляются оценки за урок. Идет обобщение материала. Домашнее задание. 1. Лодка с туристами потерпела крушение в 40 м от берега, налетев на пороги. Туристы поплыли к берегу со скоростью 2 м/с, относительно воды перпендикулярно линии берега, но быстрое течение со скоростью 10 м/с сносило их в сторону. 2. Вертолет летел на юг со скоростью 20 м/с. С какой скоростью и под каким углом к меридиану будет лететь вертолет, если подует восточный ветер со скоростью 10 м/с? 3. Задачник Степановой Г.Н. №№ 61, 60,59. Интегрированные уроки имеют огромное значение для создания предметных, метапредметных и личностных компетенции обучающихся, являются мощным мотивом к интеллектуальному труду, способствуют более глубокому усвоению материала, расширению границ изученного материала, развитию творческих способностей учащихся, которые развиваются в рамках двух дисциплин, умению логично, научно и доступно излагать свои мысли, математически грамотно говорить. Литература:
|
векторных путешествий! — Деятельность — TeachEngineering
Quick Look
Уровень: 9 (8-10)
Необходимое время: 30 минут
Расходные материалы Стоимость/группа:
0,00 долл. СШАРазмер группы: 1
Зависит от деятельности энти: Нет
предметных областей: Земля и Космос, Геометрия, Измерение
Поделиться:
TE Информационный бюллетень
Краткое содержание
Учащиеся используют векторный анализ, чтобы понять концепцию счисления пути. Они используют векторы для построения курса на основе времени и скорости. Затем они корректируют положения с помощью векторов, представляющих ветры и течения.
Они используют векторы для построения курса на основе времени и скорости. Затем они корректируют положения с помощью векторов, представляющих ветры и течения.Инженерное подключение
Несмотря на то, что впервые они были описаны математиками, сегодня почти каждая отрасль техники использует векторы в качестве инструмента, особенно для расчета силы и напряжения. Инженеры-механики, аэрокосмические, гражданские и химические инженеры, которые проектируют с использованием концепций гидродинамики, используют векторы в своих расчетах для описания реальных сил, таких как ветер и движение воды. Инженеры-электрики также используют их для описания сил магнитных и электрических полей.
Цели обучения
После этого задания учащиеся должны уметь:
- Объясните , что векторы могут отображать расстояния и направления и являются хорошим способом отслеживания перемещений на картах.

- Используйте векторы, чтобы понимать направления, расстояния и время, связанные с движением и скоростью.
Образовательные стандарты
Каждый урок или занятие TeachEngineering соотносится с одной или несколькими науками K-12, технологические, инженерные или математические (STEM) образовательные стандарты.
Все более 100 000 стандартов K-12 STEM, включенных в TeachEngineering , собираются, поддерживаются и упаковываются сетью стандартов достижений (ASN) , проект D2L (www.achievementstandards.org).
В ASN стандарты структурированы иерархически: сначала по источнику; напр. по штатам; внутри источника по типу; напр. , естествознание или математика; внутри типа по подтипу, затем по классам, и т.д. .
Общие базовые государственные стандарты — математика
- (+) Признать, что векторные величины имеют как величину, так и направление.

Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- (+) Решайте задачи, связанные со скоростью и другими величинами, которые могут быть представлены векторами.
 (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- (+) Сложение и вычитание векторов. (Оценки 9 — 12) Подробнее
Посмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
- Сложите векторы встык, по компонентам и по правилу параллелограмма.
 Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее
Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) ПодробнееПосмотреть согласованную учебную программу
Согласны ли вы с таким раскладом? Спасибо за ваш отзыв!
Международная ассоциация преподавателей технологий и инженерии — Технология
ГОСТ
Предложите выравнивание, не указанное вышеСписок материалов
Каждому ученику нужно:
- Рабочий лист Vector Voyage 1
- Рабочий лист векторного путешествия 2
- 3 карандаша разного цвета (синий, зеленый и красный соответствуют инструкциям на рабочем листе)
Рабочие листы и вложения
Vector Voyage Worksheet 1 (pdf)
Vector Voyage Worksheet 2 (pdf)
Пустой рабочий лист векторного путешествия (pdf)
Vector Voyage Worksheet 1 Ключ ответа (pdf)
Vector Voyage Worksheet 2 Ключ ответа (pdf)
Vector Voyage Worksheet 3 Ключ ответа (pdf)
Посетите [www. teachengineering.org/activities/view/cub_navigation_lesson02_activity1], чтобы распечатать или загрузить.
teachengineering.org/activities/view/cub_navigation_lesson02_activity1], чтобы распечатать или загрузить.Введение/Мотивация
Можете описать скорость и расстояние? (Ответ: расстояние = скорость x время; запишите это на доске.) Помните, что для того, чтобы это соотношение работало, единицы измерения должны совпадать. Например, если скорость измеряется в милях в час, то время необходимо преобразовать в часы, чтобы ответ был правильным.
Как древние морские капитаны удерживали свои корабли на курсе во время своих путешествий? (Посмотрите, есть ли у студентов какие-либо идеи.) Они использовали счисления , чтобы выяснить, куда они направляются. Как вы думаете, они следовали за солнцем, береговой линией или даже за звездами? (Подождите, что ответят некоторые ученики.) Да, так и было. Однако, зная скорость, время и курс своего путешествия, они могли определить, где и примерно когда они прибудут, что было большим преимуществом!
Колумб — и большинство других моряков его эпохи — использовали для навигации счисление пути. С точным счислением навигаторы определяют свои позиции, оценивая курс и расстояние, которое они прошли от известных точек. Начиная с известной точки, например порта, навигатор измеряет курс и расстояние от этой точки на карте, прокалывая карту булавкой, чтобы отметить новое положение. Эти ранние мореплаватели использовали математику, чтобы помочь им найти свой путь и не сбиться с курса, когда на их путешествия влияли ветер, течение и другие факторы. К сожалению, Колумб так и не достиг места назначения, где, как он думал, он окажется. Как вы думаете, почему это произошло? Насколько точен счисление?
С точным счислением навигаторы определяют свои позиции, оценивая курс и расстояние, которое они прошли от известных точек. Начиная с известной точки, например порта, навигатор измеряет курс и расстояние от этой точки на карте, прокалывая карту булавкой, чтобы отметить новое положение. Эти ранние мореплаватели использовали математику, чтобы помочь им найти свой путь и не сбиться с курса, когда на их путешествия влияли ветер, течение и другие факторы. К сожалению, Колумб так и не достиг места назначения, где, как он думал, он окажется. Как вы думаете, почему это произошло? Насколько точен счисление?
Процедура
Счисление пути — это процесс навигации путем продвижения на известное положение с использованием курса, скорости, времени и пройденного расстояния. Другими словами, выяснение, где вы будете в определенное время, если вы держите скорость , время и курс , который вы планируете путешествовать.
Рис. 1. Графическое изображение рейса судна с использованием векторов. авторское право
Copyright © 2003 Matt Lippis, Программа ITL, Инженерный колледж, Колорадский университет в Боулдере
Курс — это направление, в котором вы собираетесь вести судно. В этом упражнении «курс» или курс всегда строго на запад (270 градусов по часовой стрелке от 0 градусов северной широты). Направление — это направление, в котором судно движется в данной точке. Путь, по которому фактически следовали, может быть очень кривым из-за действия волн, течения, ветра и рулевого (лица, ответственного за управление судном). «Прекрасный курс» — это фактически пройденный курс.
Векторы — это стрелки, представляющие две части информации: значение величины (длина стрелки) и значение направления (направление стрелки). С точки зрения движения информация, содержащаяся в векторе, представляет собой пройденное расстояние и пройденное направление. Векторы дают нам графический метод для расчета суммы нескольких одновременных движений. Если на движение влияет только одна переменная (представленная вектором A или B), то судно прибывает в конец этого вектора. Если на движение влияют две переменные (представленные суммой A и B), то конечное положение судна можно найти, соединив два вектора вместе.
Если на движение влияет только одна переменная (представленная вектором A или B), то судно прибывает в конец этого вектора. Если на движение влияют две переменные (представленные суммой A и B), то конечное положение судна можно найти, соединив два вектора вместе.
Рис. 2. Векторы иллюстрируют конечный пункт рейса судна. авторское право
авторское право © 2003 Matt Lippis, программа ITL, инженерный колледж, Университет Колорадо в Боулдере
Перед занятием
- Сделайте копии рабочего листа «Векторное путешествие 1» и рабочего листа «Векторное путешествие 2», по одной на каждого учащегося.
- Распечатайте для себя лист ответов 1, 2 и 3 «Векторное путешествие».
- Познакомьте учащихся с векторами.
Со студентами
Спросите учащихся: Должны ли моряки беспокоиться о ветре и течении при путешествии на большие расстояния? (Ответ: Да. Ветер и течения могут увести корабль далеко от курса, которым он следовал бы в противном случае. Если навигатор не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Если навигатор не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Спросите учащихся: как векторы связаны со скоростью? (Ответ: вектор [скорости] сообщает как скорость, так и направление [N, S, E, W], в то время как скорость сама по себе не указывает вам направление.)
- Раздайте каждому учащемуся рабочий лист Vector Voyage 1.
- С помощью карандаша указанного цвета попросите учащихся нарисовать 10 квадратных векторов движения прямо по карте и ответить на вопросы рабочего листа.
- Предложите учащимся перерисовать 10 квадратных векторов движения на карте, добавляя поправки на вектор ветра для каждого месяца. Вектор движения каждого месяца должен начинаться с конца вектора ветра предыдущего месяца (см. Рабочий лист 1 «Векторное путешествие»). Предложите учащимся ответить на вопросы рабочего листа.
- Предложите учащимся перерисовать 10 квадратных векторов движения и векторов поправок на ветер на карте, добавляя текущие векторные поправки для каждого месяца.
 Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2.
Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2. - Когда они закончат, укажите, как бы они приземлились в США без воздействия ветра или океанских течений. Однако из-за ветра и океанских течений они оказались на Кубе.
- Сообщите учащимся, что каждый квадрат имеет длину 100 миль. Затем попросите их рассчитать расстояние для Части 1. (Ответ: 3500 миль.)
Словарь/Определения
счисление пути : процесс навигации путем расчета текущего положения с использованием ранее определенного положения и продвижения этого положения на основе известных или расчетных скоростей за истекшее время и курс.
Оценка
Предварительная оценка
Вопрос для обсуждения: Запрашивайте, объединяйте и обобщайте ответы учащихся.
- Должны ли моряки беспокоиться о ветре и течении при путешествии на большие расстояния? (Ответ: Да. Ветер и течения могут увести корабль далеко от курса, которым он следовал бы в противном случае.
- Должен ли штурман обращать внимание на ветер? К текущему? (Ответ: Да. Если штурман не уследит за влиянием ветра и течения, корабль может безнадежно заблудиться.)
Встроенная оценка активности
Рабочие листы: Как указано в разделе «Процедура > Со учащимися», попросите учащихся заполнить рабочие листы и ответить на вопросы из них. Просмотрите их ответы, чтобы оценить их мастерство в предмете.
Оценка после активности
Вопросы, созданные учащимися: Попросите каждого учащегося выбрать место на африканском побережье, а затем определить векторы поправок на ветер и течение, которые приведут туда корабль после 1 месяца плавания на восток на 10 квадратов. Предложите им обменяться этими исправлениями с партнером (не позволяя партнерам видеть свои листы) и рассчитать, куда они прибудут в Африку, используя исправления своего партнера на своих листах.
Советы по устранению неполадок
Приступая к рисованию векторов, учащиеся могут запутаться. При необходимости помогите им, нарисовав первые два вектора на доске так, чтобы их мог видеть весь класс или небольшие группы.
Вектор поправки на ветер добавляется к концу первой стрелки вектора для месяца 1. Векторы для Части 3 рабочих листов должны основываться на добавленных векторах в Части 2. И ветер, и океан влияют на выход на сушу; это точно представлено только путем построения векторов поправок на ветер.
Vector Voyage Worksheet 3 Ключ к ответу предлагает краткое изложение этой деятельности и четко иллюстрирует непосредственно движение вектора. Этот ключ к ответам – отличный справочник для учителей, у которого возникли трудности с этим упражнением.
Расширения деятельности
Предложите учащимся, использующим пустой рабочий лист векторного путешествия, построить свои собственные курсы, записывая движения, направления и исправления по пути. Попросите их дать инструкции по новому курсу партнеру, чтобы определить, могут ли они плыть к новому месту.
Попросите их дать инструкции по новому курсу партнеру, чтобы определить, могут ли они плыть к новому месту.
Масштабирование активности
- Учащиеся младших классов выполняйте часть задания по поправке на ветер всем классом. Затем предложите учащимся попробовать текущее исправление самостоятельно.
- Для старшеклассников попросите учащихся подсчитать фактическое общее расстояние, пройденное кораблем по пути на Кубу. Фактическое расстояние, пройденное кораблем, является результирующим вектором суммы трех векторов движения за каждый месяц. Учащиеся могут нарисовать эти векторы на своих картах, начав с начала сплошного вектора из 10 квадратов для каждого месяца и нарисовав стрелку прямо до конечного положения корабля в этом месяце. Используйте теорему Пифагора (a 2 +b 2 =c 2 ), чтобы найти длины этих векторов. (Ответ: расстояние от Испании до Кубы составляет 3683 мили.
 ) Ожидайте, что учащиеся также смогут рассчитать расстояние от Испании до Флориды таким же образом. (Ответ: 3940 миль.)
) Ожидайте, что учащиеся также смогут рассчитать расстояние от Испании до Флориды таким же образом. (Ответ: 3940 миль.) - Для учащихся старших классов попросите учеников рассчитать скорость корабля в милях в месяц и милях в час. (скорость = расстояние/время) (Ответ: Флорида — 1,37 мили в час или 985 миль в месяц, Куба — 1,7 мили в час или 1228 миль в месяц, а Нью-Йорк — 1,39.миль в час или 1000 миль в месяц.) Эти скорости высокие или низкие? Как насчет корабля без двигателей? Что случилось бы с запасами продовольствия, если бы корабль всегда сталкивался с ветром на 6 квадратов на восток?
Подписаться
Подпишитесь на нашу рассылку новостей, чтобы получать внутреннюю информацию обо всем, что связано с TeachEngineering, например, о новых функциях сайта, обновлениях учебных программ, выпусках видео и многом другом!PS: Мы никому не передаем личную информацию и электронные письма.
Больше учебных программ, подобных этому
Урок средней школы Навигация на суше, на море, в воздухе и в космосе Студенты узнают, что методы навигации меняются, когда люди путешествуют по разным местам — по суше, морю, воздуху и космосу. Например, путешественник, путешествующий по суше, использует другие методы и средства навигации, чем моряк или космонавт.
Например, путешественник, путешествующий по суше, использует другие методы и средства навигации, чем моряк или космонавт.
Методы навигации по суше, морю, воздуху и космосу
Урок средней школы Как стать великим навигатором!На этом уроке студенты узнают, как великие мореплаватели прошлого не сбивались с курса, то есть исторические методы навигации. Обсуждаются концепции счисления пути и астронавигации.
Как стать Великим Навигатором!
Урок средней школы Навигация со скоростью спутниковНа этом уроке учащиеся изучают фундаментальные концепции технологии GPS — трилатерацию и использование скорости света для расчета расстояний.
Навигация со скоростью спутников
Авторские права
© 2004 Регенты Университета КолорадоАвторы
Джефф Уайт; Мэтт Липпис; Пенни Аксельрад; Джанет Йоуэлл; Малинда Шефер ЗарскеПрограмма поддержки
Комплексная программа преподавания и обучения, Инженерный колледж Колорадского университета в БоулдереБлагодарности
Содержание этой учебной программы цифровой библиотеки было разработано в рамках грантов Фонда улучшения высшего образования (FIPSE), Министерства образования США и Национального научного фонда (грант GK-12 № 0338326). Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Однако это содержание не обязательно отражает политику Министерства образования или Национального научного фонда, и вы не должны исходить из того, что оно одобрено федеральным правительством.
Последнее изменение: 21 октября 2020 г.
Добавление вектора: метод «голова к хвосту» Ресурсы для учителей
Класс физики помогает учащимся, учителям и классам с 1990-х годов. Мы так же увлечены этой миссией сейчас, как и раньше. Если вы учитель физики или физических наук, мы рекомендуем вам использовать наш видеоурок со своими учениками. И мы также рекомендуем вам рассмотреть возможность использования других ресурсов на нашем веб-сайте, которые согласуются с видео. Мы перечислили несколько ниже, чтобы помочь вам начать работу.
У нас много ресурсов по векторам и их сложению! И поскольку этот видеоурок, вероятно, является отправной точкой для нескольких уроков по добавлению векторов, мы определили несколько ресурсов, которые будут полезны учителям, планирующим уроки и модули, относящиеся к этому видеоуроку и последующим.
Наборы инструментов для учителей: Vectors
Планируете раздел или серию уроков по Vectors? Мы можем помочь. Попробуйте набор инструментов — набор проверенных ресурсов, которые зависят от мультимедиа и основаны на стандартах. Этот на Векторах должен стимулировать несколько хороших идей.
Учебный уголок: Векторы и снаряды
Наш Учебный уголок состоит из большой коллекции аналитических листов по различным темам. Они обеспечивают систематический и развивающий подход к концепциям физики. Эти три будут особенно полезны для любого модуля, который начинается с сложения векторов:
Сложение векторов || Компоненты вектора, разрешение вектора и сложение вектора || Сложение векторов по компонентам
Физические интерактивы: сложение векторов
Экспериментируйте с векторами, результантами и многим другим в этом интерактивном рабочем пространстве. Перетащите на него вектор, измените его размер и положение. Добавьте к нему второй или третий вектор и наблюдайте за результатом. Экспериментируйте, пока вам не надоест… или пока вам не нужно будет ложиться спать.
Добавьте к нему второй или третий вектор и наблюдайте за результатом. Экспериментируйте, пока вам не надоест… или пока вам не нужно будет ложиться спать.
Physics Interactives: Name That Vector
Это инструмент для развития навыков, который предлагает пользователям 12 задач на сложение векторов. Двадцать пять векторов отображаются на сетке; каждая задача включает сложение трех векторов вместе для определения результирующего. Акцент деятельности делается на добавлении компонентов. Встроенная система подсчета очков делает этот интерактив идеальным кандидатом для занятий в классе.
Интерактивные занятия по физике: игра на угадывание вектора
Отображаются два случайных вектора, и учащиеся должны выбрать размер и направление равнодействующей. Будьте быстры, потому что таймер отсчитывает время. Задача состоит в том, чтобы решить как можно правильно за 20 секунд. Повторите процесс и побейте свой высокий балл.
Справка по физике: Сложение векторов
Состоит из 12 задач на сложение двух векторов. Используйте точно нарисованную масштабированную векторную диаграмму, чтобы определить результирующую; затем проверьте свои ответы. Отличная практика. Отличный отзыв.
Используйте точно нарисованную масштабированную векторную диаграмму, чтобы определить результирующую; затем проверьте свои ответы. Отличная практика. Отличный отзыв.
Концептуальные конструкторы: сложение векторов с головы до хвоста
Учащиеся любят Концептуальные конструкторы! Они одинаково хорошо работают как упражнения в классе или (если у вас есть зарегистрированная учетная запись учителя) как назначенная внеклассная работа. Это конкретное видео идеально подходит для видео и является отличным продолжением того, что вы узнали.
Концептуальные конструкторы: сложение векторов
Их никогда не бывает слишком много. Они отлично подходят для занятий в классе и (с Конструкторами концепций версии 2) внеклассной работы. Это упражнение можно использовать для поддержки прямых графических подходов или аналитического метода сложения векторов.
Разработчики концепций: добавление компонентов
Это один из наших фаворитов.




 )
) 
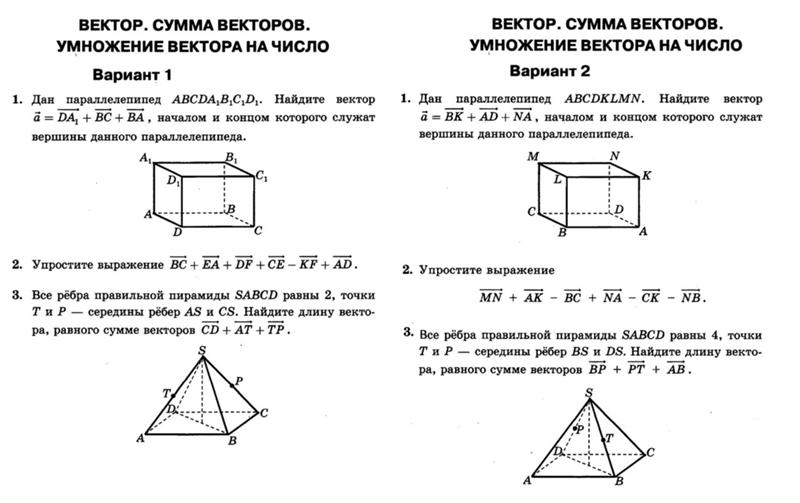


 Выполните построение и покажите в каком направлении штурман должен вести судно по компасу.
Выполните построение и покажите в каком направлении штурман должен вести судно по компасу. С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи.
С какой реальной скоростью относительно берега двигались туристы? На какое расстояние их снесло, когда они выплыли на берег? Сделайте чертежи. Дидактические материалы для 8 класса. Просвещение,2006
Дидактические материалы для 8 класса. Просвещение,2006

 (Оценки
9 —
12) Подробнее
(Оценки
9 —
12) Подробнее Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее
Поймите, что величина суммы двух векторов обычно не является суммой величин.
(Оценки
9 —
12) Подробнее Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2.
Текущий вектор каждого месяца теперь начинается с конца вектора ветра предыдущего месяца. Вектор движения каждого месяца теперь должен начинаться с конца текущего вектора предыдущего месяца (см. Рабочий лист 2 «Векторное путешествие», ключ к ответам). Попросите учащихся ответить на вопросы из рабочего листа Vector Voyage 2. ) Ожидайте, что учащиеся также смогут рассчитать расстояние от Испании до Флориды таким же образом. (Ответ: 3940 миль.)
) Ожидайте, что учащиеся также смогут рассчитать расстояние от Испании до Флориды таким же образом. (Ответ: 3940 миль.)