Объем усеченной трапеции: Формула нахождения объема усеченной пирамиды онлайн

Ошибки в математических рассуждениях

Ошибки в математических рассуждениях

Брадис В.М., Минковский В.Л., Харчева А.К. Ошибки в математических рассуждениях. Москва: Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1959. — 178 с. Об упражнениях на опровержение ошибочных математических рассуждений и их классификации. Математические софизмы и их педагогическая роль. Классификация упражнений на опровержение ложных математических рассуждений. Арифметика. Примеры ложных рассуждений. Анализ примеров. Алгебра. Примеры ложных рассуждений. Анализ примеров. Геометрия. Примеры ложных рассуждений. Анализ примеров. Рассказы-объяснения по поводу ошибочных рассуждений. Тригонометрия. Примеры ложных рассуждений. Анализ примеров. Приближенные вычисления. Рассказы-объяснения по поводу ошибочных рассуждений. Оглавление ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ Глава I. ОБ УПРАЖНЕНИЯХ НА ОПРОВЕРЖЕНИЕ ОШИБОЧНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ И ИХ КЛАССИФИКАЦИИ 1. МАТЕМАТИЧЕСКИЕ СОФИЗМЫ И ИХ ПЕДАГОГИЧЕСКАЯ РОЛЬ. II. КЛАССИФИКАЦИЯ УПРАЖНЕНИЙ НА ОПРОВЕРЖЕНИЕ ЛОЖНЫХ МАТЕМАТИЧЕСКИХ РАССУЖДЕНИЙ. 2. Распространение на исключительные случаи. 3. Приписывание свойств определенного вида всему роду. 4. Неправильное применение принципа непосредственных умозаключений путем обращения. 5. Подмена точных определений геометрической интуицией. 6. Ошибки построения. 7. Ошибки, являющиеся следствием буквального толкования сокращенной (условной) формулировки некоторых геометрических утверждений. 2? 32. Еще одно «доказательство» равенства нулю произвольно взятого числа. 33. Число не изменяется, если в нем переставить любые цифры! 34. Что говорит теорема о существовании корня в алгебре комплексных чисел? 35. Об одном спэсобе получать правильные результаты, применение которого требует большой осторожности. 36. О сумме 1-1+1-1 + … 37. Всегда ли целое больше своей части? 38. Еще одно «доказательство» равенства двух произвольно взятых чисел. 39. Сумма двух произвольных одинаковых чисел равна нулю. 40. Число не изменится, если к нему прибавить 1. 41. Ахиллес и черепаха. 42. О некоторых ученических ошибках. II. АНАЛИЗ ПРИМЕРОВ. Глава IV. ГЕОМЕТРИЯ. 1. ПРИМЕРЫ ЛОЖНЫХ РАССУЖДЕНИЙ. 44. Отрезок прямой равен своей правильной части. 45. Все треугольники равновелики. 46. Сумма оснований любой трапеции равна нулю. 47. Объемлемая и объемлющая. 48. Еще о пропорциональности. 49. Две окружности разного радиуса имеют одну и ту же длину. 50. Сумма катетов равна гипотенузе. 51. Длина полуокружности равна ее диаметру. 52. Боковая поверхность круглого прямого конуса с радиусом основания r и высотой h выражается формулой P=pi*r(r+h). 53. В данной точке на прямой можно восставить два перпендикуляра к этой прямой. 54. Через одну точку можно провести две прямые, параллельные данной прямой. 55. Окружность имеет два центра. 56. Из точки на прямую можно опустить два перпендикуляра. 57. Через две данные точки можно провести две прямые. 58. Любой треугольник — равнобедренный. 59. Катет прямоугольного треугольника равен его гипотенузе. 60. Прямой угол равен тупому (планиметрический вариант). 61. 64 кв. см = 65 кв. см. 62. Задача о заплате. II. АНАЛИЗ ПРИМЕРОВ. III. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ. 64. Трисекция угла. 65. Еще о трисекции угла. 66. Квадратура круга. 67. Об одном доказательстве теоремы о сумме внутренних углов треугольника. 2 74. Площадь прямоугольника равна нулю. 75. Существуют равные треугольники, у которых не все стороны равны. 76. Каждый треугольник — прямоугольный. II. АНАЛИЗ ПРИМЕРОВ Глава VI. ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ. РАССКАЗЫ-ОБЪЯСНЕНИЯ ПО ПОВОДУ ОШИБОЧНЫХ РАССУЖДЕНИЙ 78. Все большие числа приближенно равны между собой. 79. О точности произведения приближенных чисел. 80. Верна ли формула … 81. Сколько цифр надо знать в подкоренном числе, чтобы получить корень с заданной точностью? 82. Зачем освобождаются от иррациональности в знаменателе?

Формула расчета объема усеченной пирамиды четырехгранной. Формулы объема пирамиды полной и усеченной

Пирамидой называется многогранник, одна из граней которого многоугольник (основание ), а все остальные грани – треугольники с общей вершиной (боковые грани ) (рис. 15). Пирамида называется правильной , если ее основанием является правильный многоугольник и вершина пирамиды проектируется в центр основания (рис.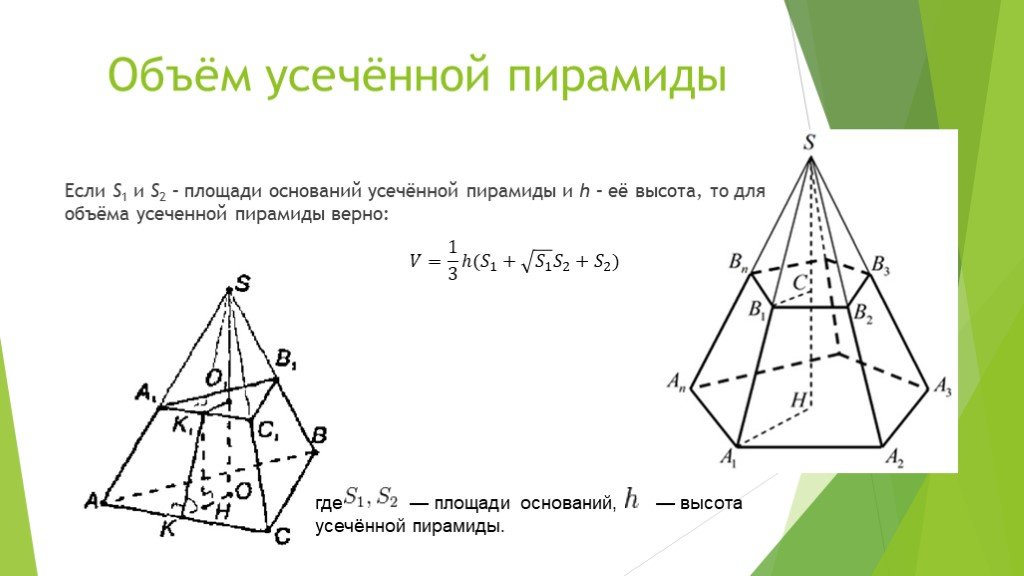 16). Треугольная пирамида, у которой все ребра равны, называется тетраэдром .

Боковым ребром пирамиды называется сторона боковой грани, не принадлежащая основанию Высотой пирамиды называется расстояние от ее вершины до плоскости основания. Все боковые ребра правильной пирамиды равны между собой, все боковые грани – равные равнобедренные треугольники. Высота боковой грани правильной пирамиды, проведенная из вершины, называется

апофемой . Диагональным сечением называется сечение пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Площадью боковой поверхности пирамиды называется сумма площадей всех боковых граней. Площадью полной поверхности называется сумма площадей всех боковых граней и основания.

Теоремы

1. Если в пирамиде все боковые ребра равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности описанной около основания.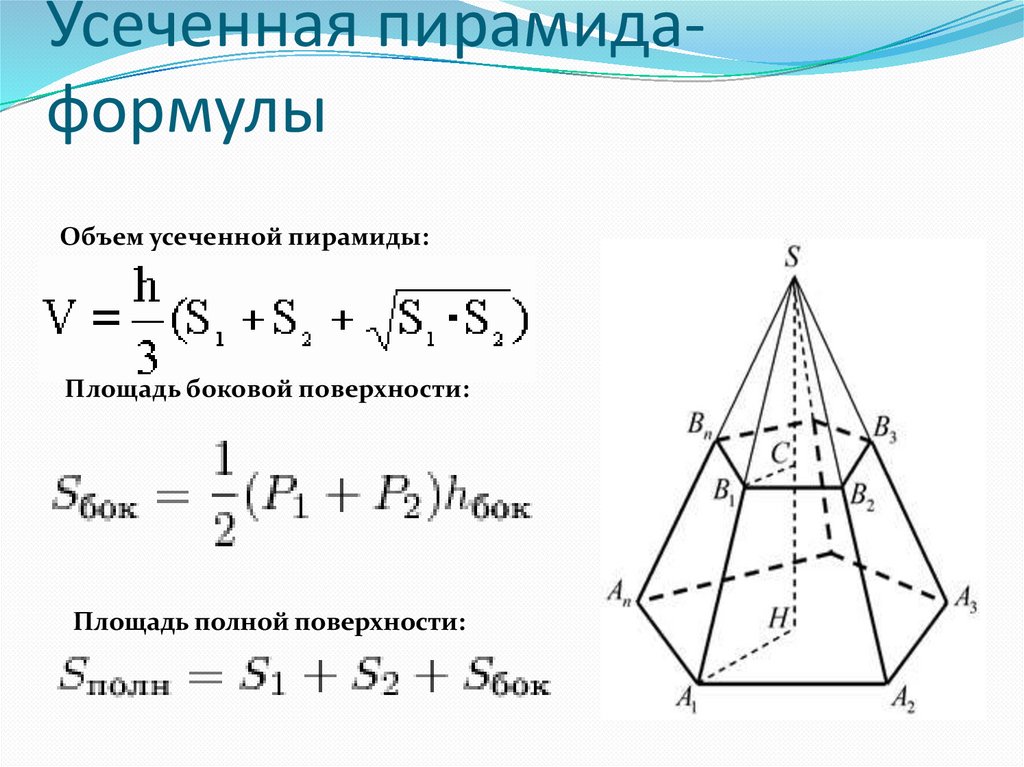

2. Если в пирамиде все боковые ребра имеют равные длины, то вершина пирамиды проектируется в центр окружности описанной около основания.

3. Если в пирамиде все грани равнонаклонены к плоскости основания, то вершина пирамиды проектируется в центр окружности вписанной в основание.

Для вычисления объема произвольной пирамиды верна формула:

где V – объем;

S осн – площадь основания;

H – высота пирамиды.

Для правильной пирамиды верны формулы:

где p – периметр основания;

h а – апофема;

H – высота;

S полн

S бок

S осн – площадь основания;

V – объем правильной пирамиды.

Усеченной пирамидой называется часть пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды (рис. 17). Правильной усеченной пирамидой называется часть правильной пирамиды, заключенная между основанием и секущей плоскостью, параллельной основанию пирамиды.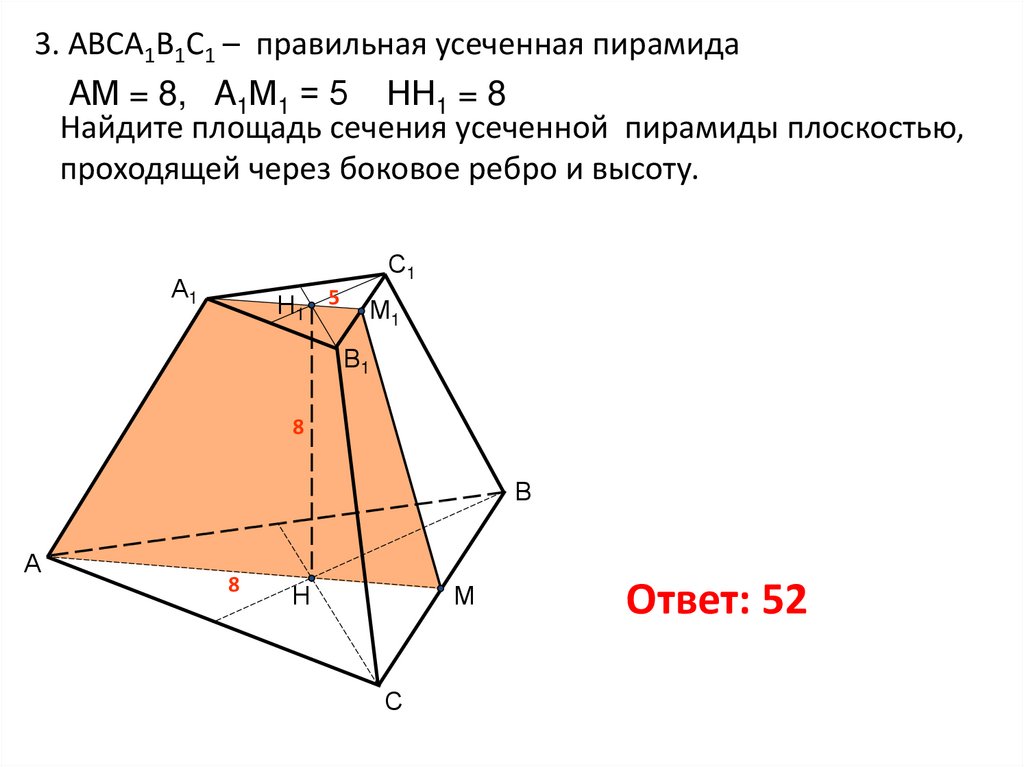

Основания усеченной пирамиды – подобные многоугольники.

Боковые грани – трапеции. Высотой усеченной пирамиды называется расстояние между ее основаниями. Диагональю усеченной пирамиды называется отрезок, соединяющий ее вершины, не лежащие в одной грани. Диагональным сечением называется сечение усеченной пирамиды плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

Для усеченной пирамиды справедливы формулы:

(4)

где S 1 , S 2 – площади верхнего и нижнего оснований;

S полн – площадь полной поверхности;

S бок – площадь боковой поверхности;

H – высота;

V – объем усеченной пирамиды.

Для правильной усеченной пирамиды верна формула:

где p 1 , p 2 – периметры оснований;

h а – апофема правильной усеченной пирамиды.

Пример 1. В правильной треугольной пирамиде двугранный угол при основании равен 60º.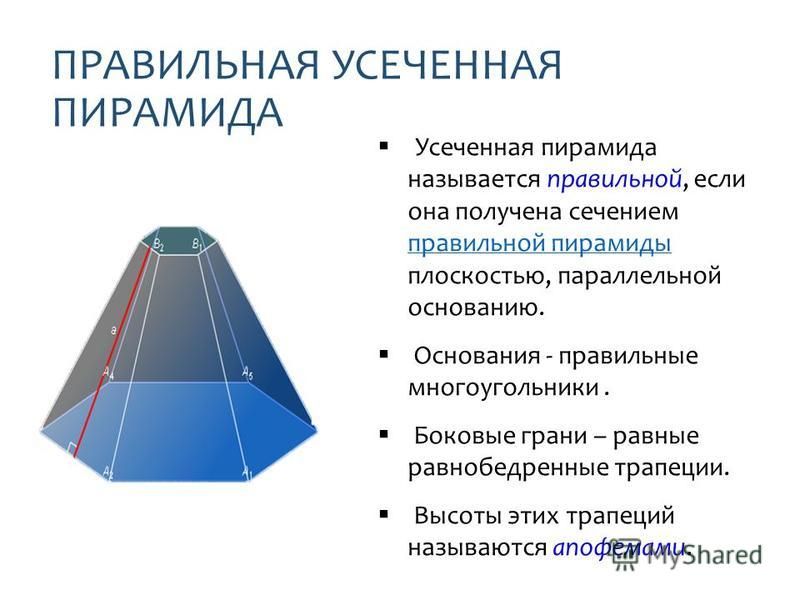

Найти тангенс угла наклона бокового ребра к плоскости основания.

Решение. Сделаем рисунок (рис. 18).

Пирамида правильная, значит в основании равносторонний треугольник и все боковые грани равные равнобедренные треугольники. Двугранный угол при основании – это угол наклона боковой грани пирамиды к плоскости основания. Линейным углом будет угол a между двумя перпендикулярами: и т.е. Вершина пирамиды проектируется в центре треугольника (центр описанной окружности и вписанной окружности в треугольник АВС ). Угол наклона бокового ребра (например SB ) – это угол между самим ребром и его проекцией на плоскость основания. Для ребра SB этим углом будет угол SBD . Чтобы найти тангенс необходимо знать катеты SO и OB . Пусть длина отрезка

BD равна 3а . Точкой О отрезок BD делится на части: и Из находим SO : Из находим:

Ответ:

Пример 2.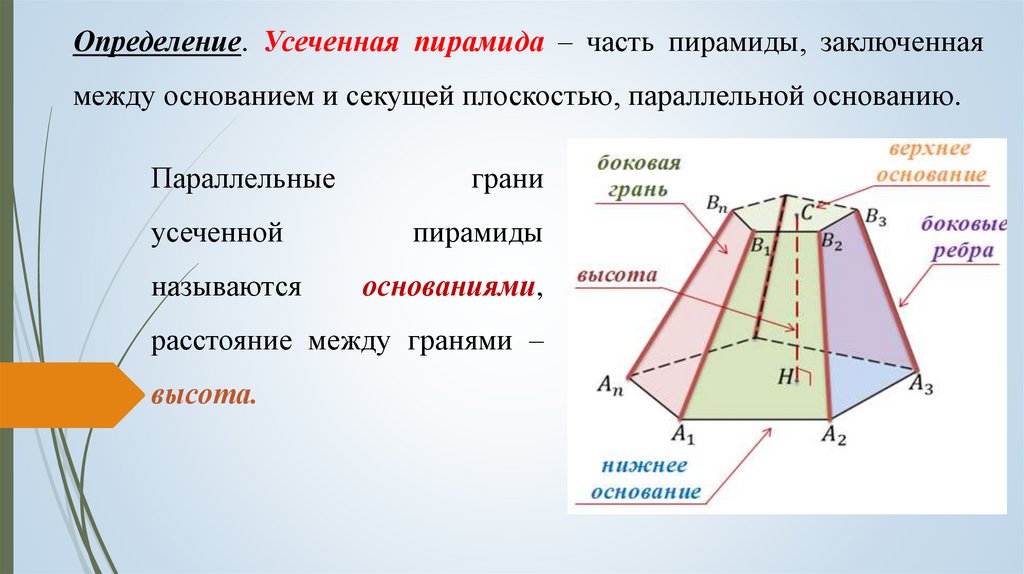 Найти объем правильной усеченной четырехугольной пирамиды, если диагонали ее оснований равны см и см, а высота 4 см.

Решение. Для нахождения объема усеченной пирамиды воспользуемся формулой (4). Чтобы найти площади оснований необходимо найти стороны квадратов-оснований, зная их диагонали. Стороны оснований равны соответственно 2 см и 8 см. Значит площади оснований и Подставив все данные в формулу, вычислим объем усеченной пирамиды:

Ответ: 112 см 3 .

Пример 3. Найти площадь боковой грани правильной треугольной усеченной пирамиды, стороны оснований которой равны 10 см и 4 см, а высота пирамиды 2 см.

Решение. Сделаем рисунок (рис. 19).

Боковая грань данной пирамиды является равнобокая трапеция. Для вычисления площади трапеции необходимо знать основания и высоту. Основания даны по условию, остается неизвестной только высота. Ее найдем из где А 1 Е перпендикуляр из точки А 1 на плоскость нижнего основания, A 1 D – перпендикуляр из А 1 на АС .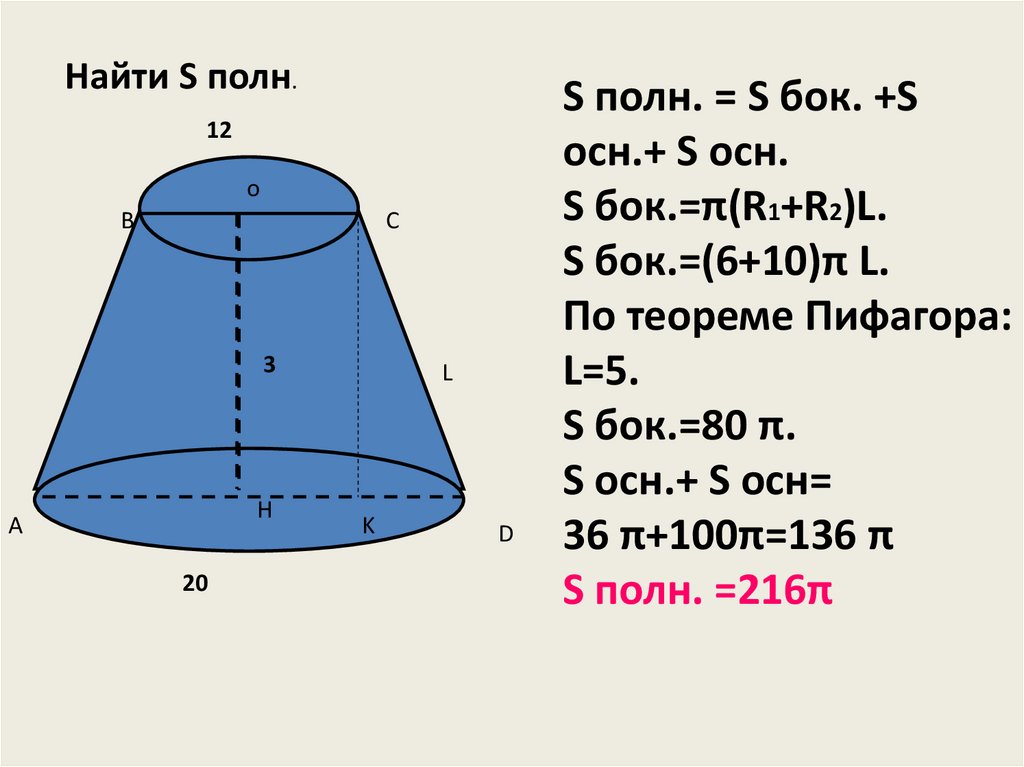 А 1 Е = 2 см, так как это высота пирамиды. Для нахождения DE сделаем дополнительно рисунок, на котором изобразим вид сверху (рис. 20). Точка О – проекция центров верхнего и нижнего оснований. так как (см. рис. 20) и С другой стороны ОК – радиус вписанной в окружности и ОМ – радиус вписанной в окружности:

MK = DE .

По теореме Пифагора из

Площадь боковой грани:

Ответ:

Пример 4. В основании пирамиды лежит равнобокая трапеция, основания которой а и b (a > b ). Каждая боковая грань образует с плоскостью основания пирамиды угол равный j . Найти площадь полной поверхности пирамиды.

Решение. Сделаем рисунок (рис. 21). Площадь полной поверхности пирамиды SABCD равна сумме площадей и площади трапеции ABCD .

Воспользуемся утверждением, что если все грани пирамиды равнонаклонены к плоскости основания, то вершина проектируется в центр вписанной в основание окружности. Точка О – проекция вершины S на основание пирамиды. Треугольник SOD является ортогональной проекцией треугольника CSD на плоскость основания. По теореме о площади ортогональной проекции плоской фигуры получим:

Аналогично и значит Таким образом задача свелась к нахождению площади трапеции АВСD . Изобразим трапецию ABCD отдельно (рис.22). Точка О – центр вписанной в трапецию окружности.

Так как в трапецию можно вписать окружность, то или Из по теореме Пифагора имеем

Умение вычислять объем пространственных фигур является важным при решение ряда практических задач по геометрии. Одной из распространенных фигур является пирамида. В данной статье рассмотрим пирамиды как полной, так и усеченной.

Пирамида как объемная фигура

Каждый знает о египетских пирамидах, поэтому хорошо представляет, о какой фигуре пойдет речь. Тем не менее египетские каменные сооружения являются лишь частным случаем огромного класса пирамид.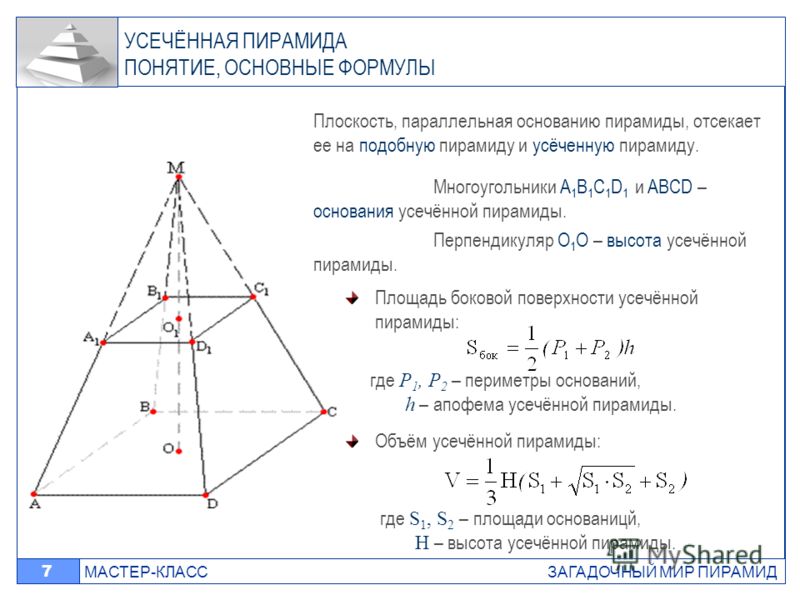

Рассматриваемый геометрический объект в общем случае представляет собой многоугольное основание, каждая вершина которого соединена с некоторой точкой в пространстве, не принадлежащей плоскости основания. Данное определение приводит к фигуре, состоящей из одного n-угольника и n треугольников.

Любая пирамида состоит из n+1 граней, 2*n ребер и n+1 вершины. Поскольку рассматриваемая фигура является совершенным полиэдром, то числа отмеченных элементов подчиняются равенству Эйлера:

2*n = (n+1) + (n+1) — 2.

Многоугольник, находящийся в основании, дает название пирамиды, например, треугольная, пятиугольная и так далее. Набор пирамид с разными основаниями приведен на фото ниже.

Точка, в которой n треугольников фигуры соединяются, называется вершиной пирамиды. Если из нее опустить на основание перпендикуляр и он пересечет его в геометрическом центре, тогда такая фигура будет называться прямой. Если это условие не выполняется, то имеет место наклонная пирамида.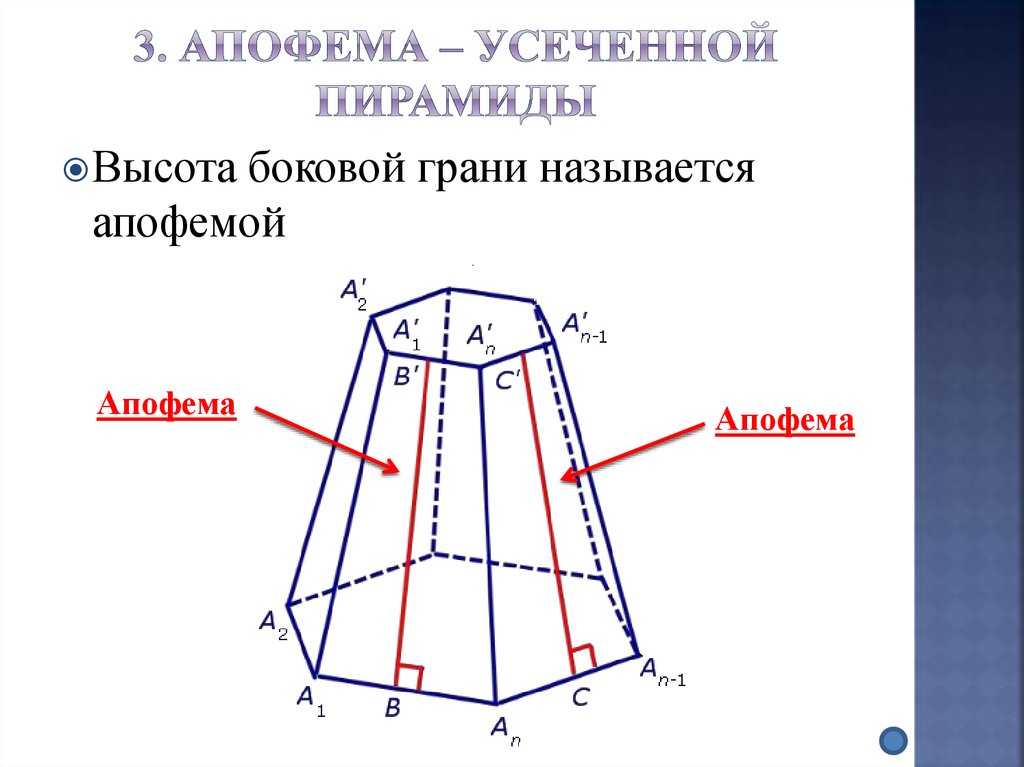

Прямая фигура, основание которой образовано равносторонним (равноугольным) n-угольником, называется правильной.

Формула объема пирамиды

Для вычисления объема пирамиды воспользуемся интегральным исчислением. Для этого разобьем фигуру параллельными основанию секущими плоскостями на бесконечное число тонких слоев. Рисунок ниже показывает четырехугольную пирамиду высотой h и длиной стороны L, в которой четырехугольником отмечен тонкий слой сечения.

Площадь каждого такого слоя можно вычислить по формуле:

A(z) = A 0 *(h-z) 2 /h 2 .

Здесь A 0 — площадь основания, z — значение вертикальной координаты. Видно, что если z = 0, то формула дает значение A 0 .

Чтобы получить формулу объема пирамиды, следует вычислить интеграл по всей высоте фигуры, то есть:

V = ∫ h 0 (A(z)*dz).

Подставляя зависимость A(z) и вычисляя первообразную, приходим к выражению:

V = -A 0 *(h-z) 3 /(3*h 2)| h 0 = 1/3*A 0 *h.

Мы получили формулу объема пирамиды. Чтобы найти величину V, достаточно умножить высоту фигуры на площадь основания, а затем результат поделить на три.

Заметим, что полученное выражение справедливо для вычисления объема пирамиды произвольного типа. То есть она может быть наклонной, а ее основание представлять собой произвольный n-угольник.

и ее объем

Полученную в пункте выше общую формулу для объема можно уточнить в случае пирамиды с правильным основанием. Площадь такого основания вычисляется по следующей формуле:

A 0 = n/4*L 2 *ctg(pi/n).

Здесь L является длиной стороны правильного многоугольника с n вершинами. Символ pi — это число пи.

Подставляя выражение для A 0 в общую формулу, получаем объем правильной пирамиды:

V n = 1/3*n/4*L 2 *h*ctg(pi/n) = n/12*L 2 *h*ctg(pi/n).

Например, для треугольной пирамиды эта формула приводит к следующему выражению:

V 3 = 3/12*L 2 *h*ctg(60 o) = √3/12*L 2 *h.

Для правильной четырехугольной пирамиды формула объема приобретает вид:

V 4 = 4/12*L 2 *h*ctg(45 o) = 1/3*L 2 *h.

Определение объемов правильных пирамид требует знания стороны их основания и высоты фигуры.

Пирамида усеченная

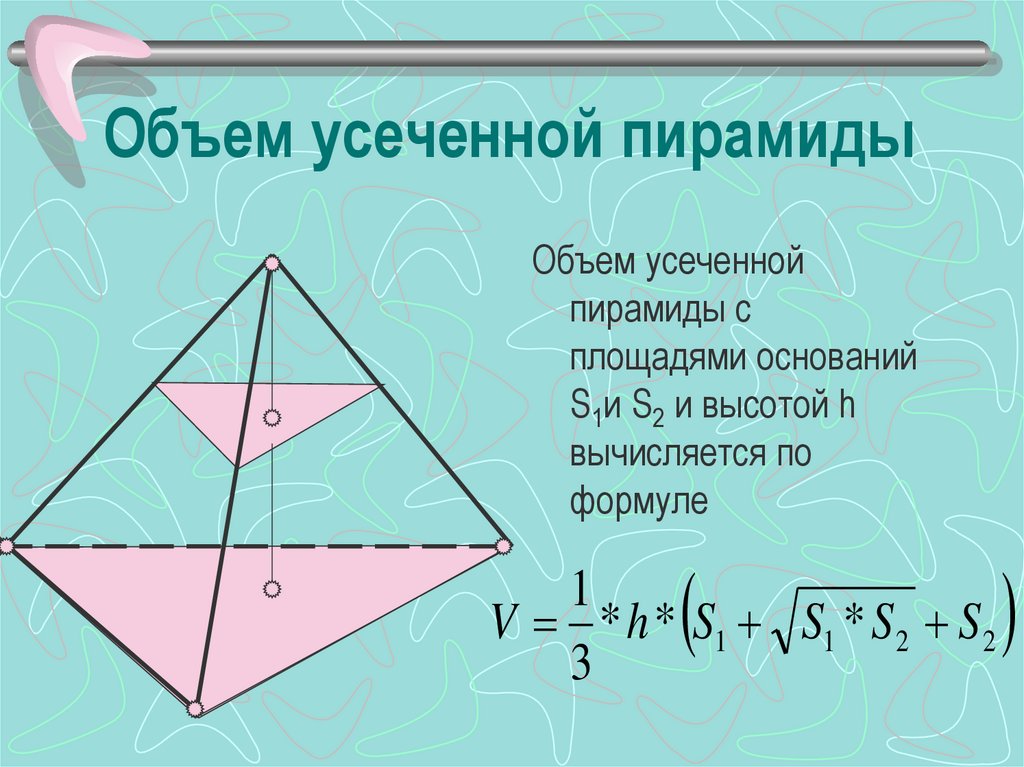
Предположим, что мы взяли произвольную пирамиду и отсекли у нее часть боковой поверхности, содержащей вершину. Оставшаяся фигура называется усеченной пирамидой. Она состоит уже из двух n-угольных оснований и n трапеций, которые их соединяют. Если секущая плоскость была параллельна основанию фигуры, тогда образуется усеченная пирамида с параллельными подобными основаниями. То есть длины сторон одного из них можно получить, умножая длины другого на некоторый коэффициент k.

Рисунок выше демонстрирует усеченную правильную Видно, что верхнее основание ее так же, как и нижнее, образовано правильным шестиугольником.

Формула которую можно вывести, используя подобное приведенному интегральное исчисление, имеет вид:

V = 1/3*h*(A 0 + A 1 + √(A 0 *A 1)).

Где A 0 и A 1 — площади нижнего (большого) и верхнего (маленького) оснований соответственно. Переменной h обозначается высота усеченной пирамиды.

Объем пирамиды Хеопса

Любопытно решить задачу на определение объема, который заключает внутри себя самая большая египетская пирамида.

В 1984 году британские египтологи Марк Легнер (Mark Lehner) и Джон Гудман (Jon Goodman) установили точные размеры пирамиды Хеопса. Ее первоначальная высота равнялась 146,50 метра (в настоящее время около 137 метров). Средняя длина каждой из четырех сторон сооружения составила 230,363 метра. Основание пирамиды с высокой точностью является квадратным.

Воспользуемся приведенными цифрами для определения объема этого каменного гиганта. Поскольку пирамида является правильной четырехугольной, тогда для нее справедлива формула:

Подставляем цифры, получаем:

V 4 = 1/3*(230,363) 2 *146,5 ≈ 2591444 м 3 .

Объем пирамиды Хеопса равен практически 2,6 млн м 3 .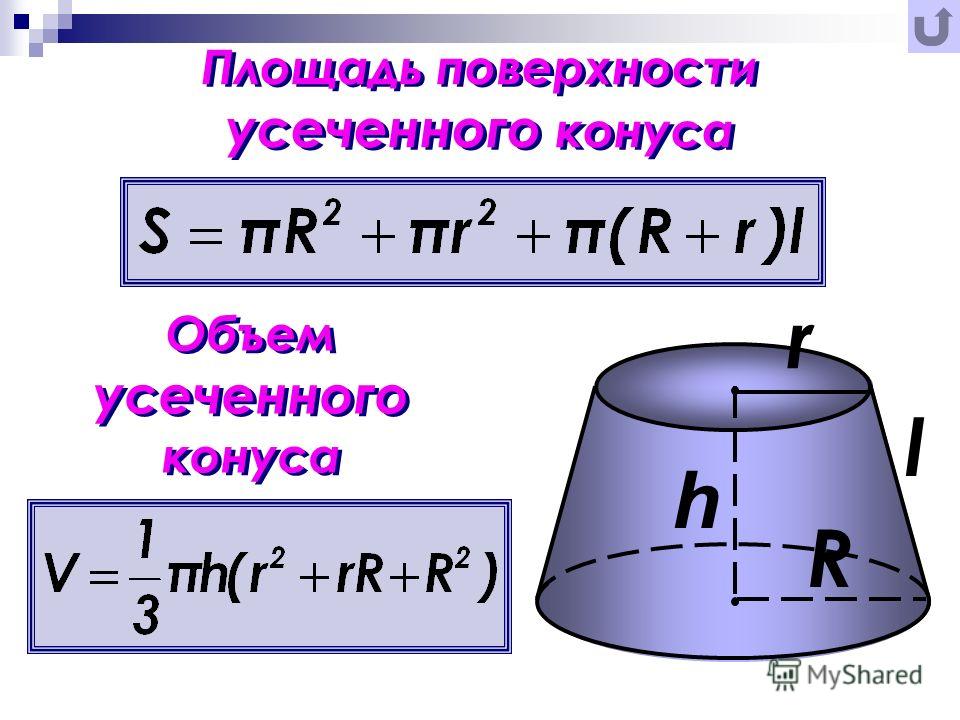 Для сравнения отметим, что олимпийский бассейн имеет объем 2,5 тыс. м 3 . То есть для заполнения всей пирамиды Хеопса понадобится больше 1000 таких бассейнов!

– это многогранник, который образуется основанием пирамиды и параллельным ему сечением. Можно сказать, что усеченная пирамида – это пирамиду со срезанной верхушкой. Эта фигура обладает множеством уникальных свойств:

• Боковые грани пирамиды являются трапециями;
• Боковые ребра правильной усеченной пирамиды одинаковой длины и наклонены к основанию под одинаковым углом;
• Основания являются подобными многоугольниками;
• В правильной усеченной пирамиде, грани представляют собой одинаковые равнобедренные трапеции, площадь которых равна. Также они наклонены к основанию под одним углом.

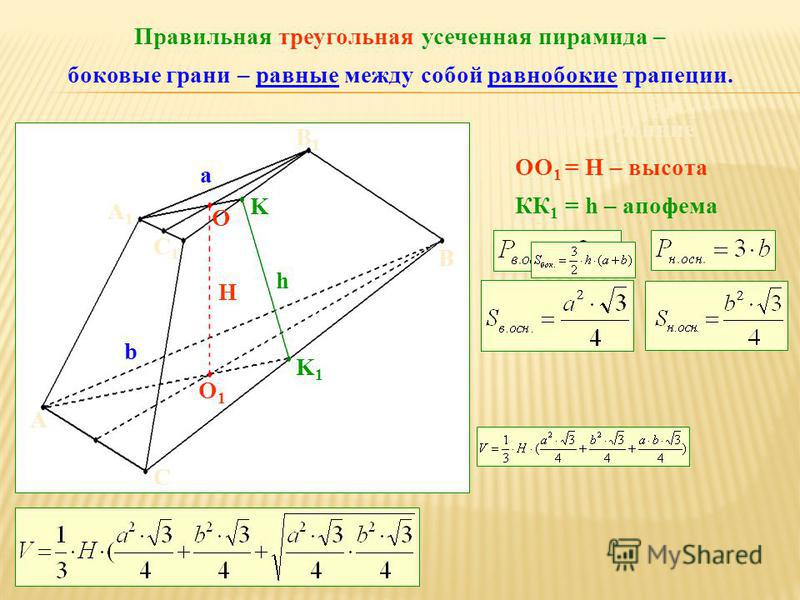
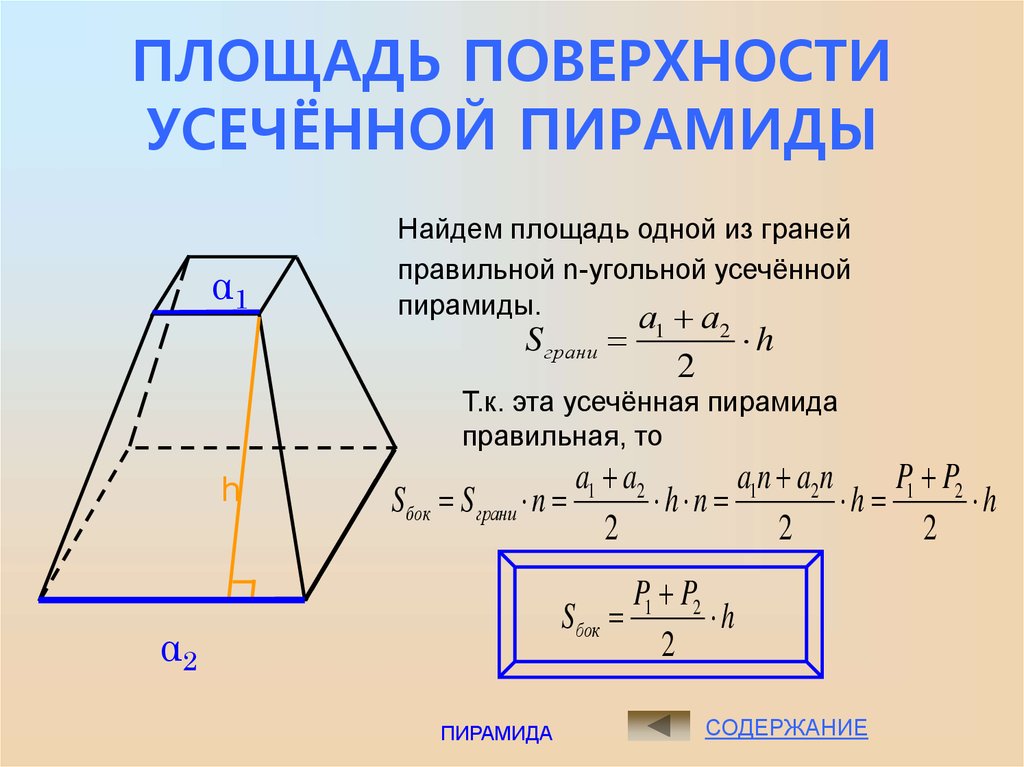
Формула площади боковой поверхности усеченной пирамиды представляет собой сумму площадей ее сторон:

Так как стороны усеченной пирамиды представляют собой трапеции, то для расчета параметров придется воспользоваться формулой площади трапеции .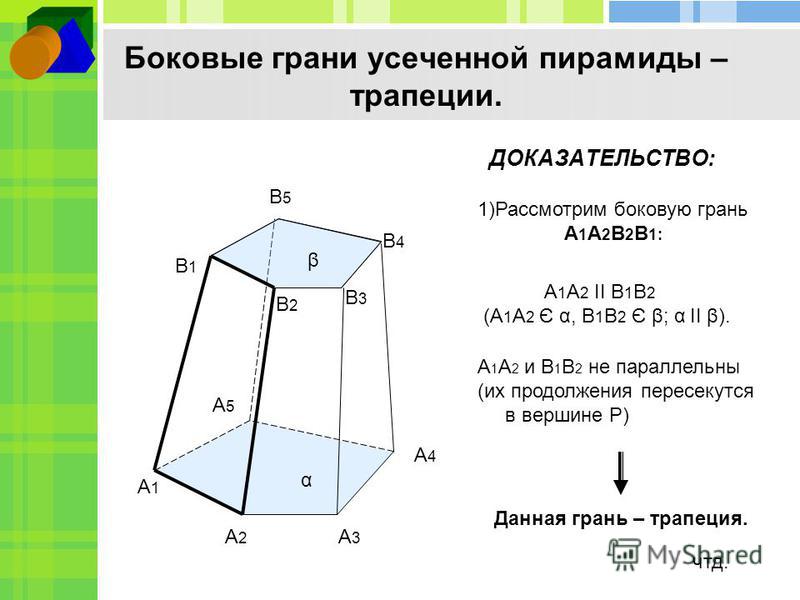 Для правильной усеченной пирамиды можно применить другую формулу расчета площади. Так как все ее стороны, грани, и углы при основании равны, то можно применить периметры основания и апофему, а также вывести площадь через угол при основании.

Если по условиям в правильной усеченной пирамиде даны апофема (высота боковой стороны) и длины сторон основания, то можно произвести расчет площади через полупроизведение суммы периметров оснований и апофемы:

Давайте рассмотрим пример расчета площади боковой поверхности усеченной пирамиды.
Дана правильная пятиугольная пирамида. Апофема l = 5 см, длина грани в большом основании равна a = 6 см, а грань в меньшем основании b = 4 см. Рассчитайте площадь усеченной пирамиды.

Для начала найдем периметры оснований. Так как нам дана пятиугольная пирамида, мы понимаем, что основания представляют собой пятиугольники. Значит, в основаниях лежит фигура с пятью одинаковыми сторонами. Найдем периметр большего основания:

Таким же образом находим периметр меньшего основания:

Теперь можем рассчитывать площадь правильной усеченной пирамиды. Подставляем данные в формулу:

Таким образом, мы рассчитали площадь правильной усеченной пирамиды через периметры и апофему.

Еще один способ расчета площади боковой поверхности правильной пирамиды, это формула через углы у основания и площадь этих самых оснований .

Давайте рассмотрим пример расчета. Помним, что данная формула применяется только для правильной усеченной пирамиды.

Пусть дана правильная четырехугольная пирамида. Грань нижнего основания a = 6 см, а грань верхнего b = 4 см. Двухгранный угол при основании β = 60°. Найдите площадь боковой поверхности правильной усеченной пирамиды.

Для начала рассчитаем площадь оснований. Так как пирамида правильная, все грани оснований равны между собой. Учитывая, что в основании лежит четырехугольник, понимаем, что нужно будет рассчитать площадь квадрата . Она представляет собой произведение ширины на длину, но в квадрате эти значения совпадают. Найдем площадь большего основания:


Теперь используем найденные значения для расчета площади боковой поверхности.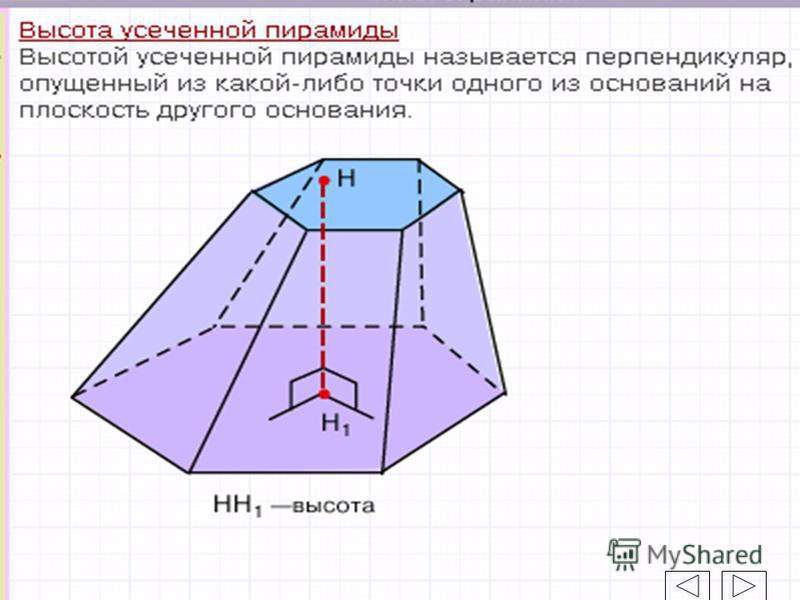

Зная несколько несложных формул, мы легко рассчитали площадь боковой трапеции усеченной пирамиды через различные значения.

• 09.10.2014

  Показанный на рисунке предварительный усилитель предназначен для использования с 4-я видами источников звука, например микрофон, CD-проигрыватель, магнитола и др. При этом у предварительно усилителя один вход, который может менять чувствительность от 50 мВ до 500мВ. выходное напряжение усилителя 1000мВ. Подключая разные источники сигнала при переключении переключателя SA1, мы всегда получим …

• 20.09.2014

  БП рассчитан на нагрузку мощностью 15…20 Вт. Источник выполнен по схеме однотактного импульсного высокочастотного преобразователя. На транзисторе собран автогенератор, работающий на частоте 20…40кГц. Частота настраивается емкостью С5. Элементы VD5,VD6 и С6 образуют цепь запуска автогенератора. Во вторичной цепи после мостового выпрямителя стоит обычный линейный стабилизатор на микросхеме, что позволяет иметь …

• 28.

  09.2014

  На рисунке представлен генератор на микросхеме К174ХА11, частота которого управляется напряжением. При изменении емкости С1 от 560 до 4700пФ можно получить широкий диапазон частот, при этом настройка частоты производится изменением сопротивления R4. Так например автор выяснил что, при С1=560пФ частоту генератора можно изменять при помощи R4 от 600Гц до 200кГц, …

• 03.10.2014

  Блок предназначен для питания мощного УНЧ, он рассчитан на выходное напряжение ±27В и так нагрузки до 3А на каждое плече. БП двух полярный, выполнен на комплектарных составных транзисторах КТ825-КТ827. Оба плеча стабилизатора выполнены по одной схеме, но в другом плече (он не показан) изменена полярность конденсаторов и использованы транзисторы другой …

Творческий проект для классов К-8

---

Креатив Проекты для К-12

Урок Планы

• 1869 Задача вступительного теста MIT
• Проблема «3N+1»
• Корзина, полная яиц
• Геометрическое доказательство теоремы Пифагора 9 «вырезать и вставить»0022
• Проблема для Молодые и старые ученики
• Проблема от русского Математическая олимпиада
• Доказательство Пифагора теорема с использованием подобных треугольников
• Головоломка с целыми числами от одного до шестнадцати
• Головоломка с номером 1089
• «Струнный рисунок», который мы можем нарисовать: ромб внутри шестиугольника
• Трехсторонний кот для рисования
• Путешественник на сетке 6 на 6
• Дополнительная плата
• Прибавление в детском саду и первый класс
• Арифметическое чудо из 1899 года
• Старый купец и его четверо детей
• Древний узел
• Анимации на TI
• Углы треугольника: геометрическое свойство посредством складывания бумаги
• Районы и границы
• Площадь и Периметр
• Арифметика с манипуляциями
• Средний балл за тест
• Мяч в коробке
• Банан
• Бочки, Бочки и другие фигурные контейнеры
• Большие числа АКА Зерна риса на шахматная доска
• Блочные дома
• Сборка собачьей будки в масштабе
• Создание ящика со скелетом в соответствии с к Спецификации
• Свечи
• Корзины для конфет
• Емкость
• Наутилус с камерой
• Проверка, является ли число простым номер
• Коробка с китайским календарем
• Хорды ​​по кругу
• Круг, квадрат и треугольник
• Часы и время
• Монеты
• Раскрашивание линий в шестиугольнике
• Красочный Треугольники
• Конгруэнтность Треугольники
• Подсчет
• Счетная доска для детей учащиеся
• Счет до 100
• Бумага для биговки По кривым
• Кубики
• Куб со срезанным краем
• Кухня полоски
• Вырезание прямоугольника
• Вырезание треугольника
• Разрезание треугольника на две части куски равной площади и равного периметра
• Вырезание равностороннего треугольника
• Резка многогранников
• Цилиндр и конус одинаковой высоты и диаметра основания
• Вывод формулы для площадь треугольника
• Диагональ площади
• Разделение квадрата
• Деление с остатком на ТИ-108: Два экземпляра
• Собаки, кошки и мыши
• Точка за точкой
• Удвоение и деление пополам
• Чертеж прямоугольник
• Рисование простой фигуры из устных указаний
• Рисование треугольников
• Легкие квадраты
• Яичная дилемма (Часть 1)
• Возведение в степень
• Факторинг
• фантазии Конверты
• Нахождение дроби между двумя дроби
• Пятиконечный 3D Звезда
• переворачивание монеты
• Сложенный бумажный цветок С шестью лепестками
• Четыре жука
• Четыре карты
• Четыре кубика
• От миллиарда до нуля
• От одного до одного триллиона
• Игра кругов и звезд
• Игра в десятки
• Гигантская энчилада
• Шапка для Хэллоуина
• Орел или решка?
• Шестиугольная головоломка
• Праздник Орнамент
• Лошадь на продажу
• Как работает Калькулятор Вычислить квадратный корень из числа?
• Сколько пентамино?
• Сколько клеток на шахматной доске?
• Сколько треугольников? (Части 1 и 2)
• Сколько треугольников в этом треугольнике?
• Как измерить угол без транспортира
• Как превратить прямоугольник в другой прямоугольник
• Гиперболы и Эллипсы
• Я могу угадать твой возраст!
• Я могу угадать ваш возраст и номер дома!
• Невозможный объект
• Вписанный треугольник
• Проценты
• Введение в измерения (первый класс)
• Неправильные многоугольники
• Юлекурв АКА Валентайн Корзина
• Прыжок: игра в пасьянс с десятью жетонами
• Воздушные змеи
• Умножение решетки
• Дырявая крыша
• Ушастые твари
• Волшебные бобы
• Волшебный складной кубик
• Магический квадрат
• Создание животных Режущие полигональные пазлы
• Создание блоков из четырех Кубики
• Изготовление коробок
• Изготовление эвольвенты
• Лабиринт
• Мини-слот-машина
• Луны
• Больше задач «точка-точка»
• Больше старых словесных задач
• Умножения «Готово по Адаму Рису»
• Натан подбрасывает монету 20 раз
• Игра в числа с Кости
• Головоломка с числами
• Воля старого пастуха
• Олимпийские кольца
• Одна треть
• Покраска домов (и другие «рабочие» задачи)
• Парадокс средних
• Разделение квадрата
• Пентагон Пазлы
• Алгебра телефонных номеров
• Копилка
• Игра с формами
• Powerball 55
• Красивая подарочная коробка
• Простые числа: сито Эратосфена
• Свойства коробки
• Тыквы
• Пазл с камешками
• Пирамида на четверти
• Пирамида из кубиков
• Пирамида из мрамора
• Четырехугольники
• Прямоугольники
• Правильные многоугольники с равными Районы
• Связанные проблемы
• Прямоугольный треугольник
• Последовательности составных номера: конкурс
• Фигуры цифр
• Формы чисел с использованием треугольники
• Делиться хлебом
• Овца: Старая головоломка
• Шесть пирамид
• Шестнадцать Квадратные дюймы
• Печать Соломона
• Сортировочная игра
• Спираль (марки К-4)
• Спираль (5-8 классы)
• Спираль Феодора на Калькуляторе ТИ-83/84
• Квадратные и кубические единицы
• Квадрат в треугольнике
• Соломенные многогранники
• Алгоритм вычитания
• Вычитание со счетчиками
• Сумма всех 100 чисел в таблице умножения
• Сумма первых N целых чисел
• Сумма двух квадратов
• Выживший на шестиугольном острове
• Татами
• Чайные коробки
• Преобразование температуры
• Мозаика круга
• Задача о лестнице и ящике
• Сыр «Смеющаяся корова» Клиновые контейнеры
• Практическая ценность Доказательства
• Рейнберд Зуни
• Три четверти
• Круг из трех частей Пазл
• Бросание одного кубика
• Треугольник в квадрат: A шарнирный разборный
• Превращение прямоугольника в квадрат путем вскрытия
• Двенадцать простых фигур
• Двадцать четыре кубика
• Две старые проблемы
• Два брата-пастуха
• Понимание Длинная дивизия
• Необычный Контейнеры
• Что дальше?
• Что это за прямоугольник?
• Инь Ян

Отрыв | Примечания | Кредиты | Альбом | НМСУ Курсы для учителей | Контакт США
последнее изменение: 2 февраля 2022 г.

геометрия — Объем усеченной призмы

спросил 5 лет, 7 месяцев назад

Изменено 2 года назад

Просмотрено 9к раз

$\begingroup$

Мне нужно было найти объем того, что Википедия называет усеченной призмой, то есть призмой (с треугольным основанием), которая пересекается с полупространством таким образом, что граница полупространства пересекает три вертикальных ребра призмы на высотах $h_1 , ч_2, ч_3$.

Я смог найти формулу $$ V=A\frac{h_1+h_2+h_3}{3}, $$ (где $A$ — площадь основания треугольника) онлайн, но без доказательства.

Я тоже смог доказать эту формулу сам, но с очень неприятным доказательством. (Площади горизонтальных сечений я проинтегрировал; после прохождения первого пересечения с гиперплоскостью на высоте $h_1$ эти сечения имеют вид треугольника основания минус квадратично возрастающий треугольник, затем после пересечения первого пересечения на высоте $h_2$ имеют форму квадратично сужающегося треугольника)

Знаете изящное доказательство формулы объема?

PS: Википедия цитирует «William F. Kern, James R Bland, Solid Mesuration with proofs, 1938, p.81» для названия усеченная призма , но я не могу найти эту книгу.

• геометрия
• аналитическая геометрия
• объем

$\endgroup$

3

$\begingroup$

Существующие два ответа довольно хороши, так что вот мои пять копеек в виде доказательства без слов. . . Ладно, пару слов не помешает 🙂

Пусть $h_1$ — наименьшая высота (до фиолетового), $h_3$ — наибольшая высота до верха, а $h_2$ — промежуточная высота (до бирюзового).

$$\mathcal{V}_{\text{целое}} = \mathcal{V}_{\text{фиолетовый}} + \mathcal{V}_{\text{бирюзовый}} + \mathcal{V }_{\text{top}} $$

Площадь базового треугольника обозначается как $A$, как и в ОП.

\begin{выравнивание*} \mathcal{V}_{\text{фиолетовый}} &= h_1 A & &\text{как прямая призма} \\ \mathcal{V}_{\text{teal}} &= \frac23 (h_2 — h_1) A &&\text{как прямая призма с высотой $h_2-h_1$ минус} \\ &&&\text{перевернутый треугольный конус той же высоты} \\ \mathcal{V}_{\text{top}} &= \frac13 (h_3 — h_2) A & &\text{как треугольный конус, основание которого по-прежнему равно $A$ по принципу Кавальери} \конец{выравнивание*} Легко видеть, что коэффициент, связанный с каждой высотой, равен $1/3. \quad$ Q.E.D.

$\endgroup$

$\begingroup$

Вы видите это следующим образом:

Сначала мы можем свести к случаю, когда $h_1=0$, заметив, что объем куска до высоты $h_m=\min(h_1,h_2,h_3)$ равен точно $h_m \cdot А$.

Предположим теперь, что $h_0=0$ и $h_1, h_2 \geq 0$. Это обозначает углы треугольника $D,E,F$, где $D$ — это угол, к которому не присоединено вертикальное ребро.

Обозначим грань, окаймленную ребрами с длинами $h_2$ и $h_3$, через $B$. Заметим, что оставшаяся усеченная призма на самом деле является пирамидой над $B$ с вершиной $D$.

Это основное наблюдение, остальное — относительно простые расчеты.

Обозначим теперь высоту треугольника $A$ при вершине $D$ через $h_D$ и сторону треугольника, противоположную $D$, через $d$. Получаем площадь $A = \tfrac{1}{2} d h_D$. Заметим, что $h_D$ перпендикулярно $B$

Для объема $V$ имеем $$ V = \tfrac{1}{3} B h_D = \tfrac{1}{3} \frac{d (h_2 + h_3)}{2} h_D = \tfrac{1}{3} \frac{d h_D}{2} (h_2 + h_3) = \tfrac{1}{3} A (h_2 + h_3) $$

$\endgroup$

$\begingroup$

Обратите внимание, что если вы поместите поверх усеченной призмы другую усеченную призму с тем же основанием и вертикальными ребрами $x-h_1$, $x-h_2$, $x-h_3$ (где $x\ge\max (h_1,h_2,h_3)$), то вы получите призму с основанием $A$ и высотой $x$.