Пересечение множеств примеры: Пересечение и объединение множеств — урок. Алгебра, 9 класс.

Математический анализ. (Виленкин)

Виленкин Н.Я., Шварцбурд С.И. Математический анализ. Учебное пособие для IX—X классов средних школ с математической специализацией. M., Просвещение, 1969 г. Учебное пособие для школ с математической специализацией, снабженное большим количеством задач и упражнений. Как и вышедшая ранее (1968 г.) книга «Алгебра» того же авторского коллектива, может быть использована преподавателями и учащимися общеобразовательной школы. Оглавление ПРЕДИСЛОВИЕ ДЛЯ УЧИТЕЛЯ ВВЕДЕНИЕ 2. Числовые множества. 3. Пустое множество. 4. Подмножество. 5. Пересечение множеств. 6. Сложение множеств. 7. Разбиение множеств. 8. Вычитание множеств. 9. Отображение множеств. 10. Краткие исторические сведения. Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО § 1. Тождественные преобразования многочленов 2. Целые рациональные выражения и функции. 3. Степень с натуральным показателем и ее свойства. 4. Многочлены. 5. Умножение многочленов. 6. Числовые кольца и поля. 7. Кольцо многочленов над данным числовым полем. 8. Бином Ньютона. § 2. Деление многочленов. Корни многочленов 2. Теорема Безу. Схема Горнера. 3. Корни многочлена. 4. Интерполяционные формулы. 5. Кратные корни. 6. Многочлены второй степени. 7. Многочлены с целыми коэффициентами. 8. Краткие исторические сведения. Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА § 1. Общая теория уравнений 2. Область допустимых значений. 3. Уравнения. 4. Совокупности уравнений. 5. Преобразования уравнений. 6. Теоремы о равносильности уравнений. § 2. Уравнения с одним неизвестным 2. Метод разложения на множители. 3. Метод введения нового неизвестного. 4. Биквадратные уравнения. 5. Возвратные уравнения 3-й и 4-й степеней. § 3. Функциональные неравенства 2. Равносильные неравенства. 3. Доказательство неравенств. 4. Линейные неравенства. 5. Решение неравенств второй степени. 6. Решение алгебраических неравенств высших степеней. 7. Краткие исторические сведения. Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ § 1. Степени с целым показателем 2. Степень с нулевым показателем. 3. Степень с целым отрицательным показателем. § 2. Корни. Степени с рациональными показателями 2. Степени с рациональными показателями. 3. Свойства степеней с рациональными показателями. § 3. Иррациональные алгебраические выражения 2. Одночленные иррациональные выражения. 3. Сокращение показателей и приведение корней к общему показателю. 4. Извлечение корня из произведения и степени. 5. Вынесение алгебраических выражений из-под корня и внесение их под корень. 6. Возведение корня в степень. 7. Извлечение корня из корня. 8. Подобные корни. 9. Сложение и вычитание корней. 10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби. 11. Преобразование выражений вида … 12. Смешанные задачи на преобразование иррациональных выражений. § 4. Иррациональные уравнения и неравенства 2. Сведение иррациональных уравнений к рациональным. 3. Уединение радикала. 4. Введение нового неизвестного. 5. Особые случаи решения иррациональных уравнений. 6. Иррациональные неравенства. 7. Краткие историчесие сведения. Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ § 1. Системы алгебраических уравнений 2. Системы уравнений. 3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными. 4. Совокупность уравнений. 5. Равносильные системы уравнений. 6. Метод подстановки. 7. Метод алгебраического сложения уравнений. 8. Метод введения новых неизвестных. 9. Системы однородных уравнений. 10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными. § 2. Системы линейных уравнений 2. Теоремы о равносильности систем линейных уравнений. 3. Пример решения системы линейных уравнений методом Гаусса. 4. Метод Гаусса (приведение системы к обобщенно-треугольному виду). 5. Решение обобщенно-треугольной системы линейных уравнений. 6. Системы однородных линейных уравнений. § 3. Симметрические многочлены и их приложения к решению систем уравнений 2. Выражение степенных сумм 3. Основная теорема о симметрических многочленах от двух переменных. 4. Системы симметрических алгебраических уравнений. 5. Применение симметрических многочленов к решению иррациональных уравнений. § 4. Неравенства с многими переменными 2. Среднее арифметическое и среднее геометрическое трех чисел. 3. Неравенство Коши (двумерный вариант). 4. Задачи на наибольшие и наименьшие значения. § 5. Решение неравенств 2. Неравенства с двумя переменными. 3. Задание областей неравенствами и системами неравенств. 4. Понятие о линейном программировании. 5. Краткие исторические сведения. Глава V. КОМПЛЕКСНЫЕ ЧИСЛА § 1. Комплексные числа в алгебраической форме 2. Комплексные числа. 3. Сложение комплексных чисел; умножение на действительные числа. 4. Умножение комплексных чисел. 5. Квадратные уравнения с действительными коэффициентами. 6. Деление комплексных чисел. 7. Сопряженные комплексные числа. 8. Извлечение квадратных корней из комплексных чисел. § 2. Тригонометрическая форма комплексных чисел 2. Полярная система координат. 3. Тригонометрическая форма комплексного числа. 4. Умножение и деление комплексных чисел в тригонометрической форме. 5. Возведение комплексных чисел в степень. Формула Муавра. 6. Извлечение корня из комплексного числа. 7. Функции комплексного переменного и преобразования комплексной плоскости. 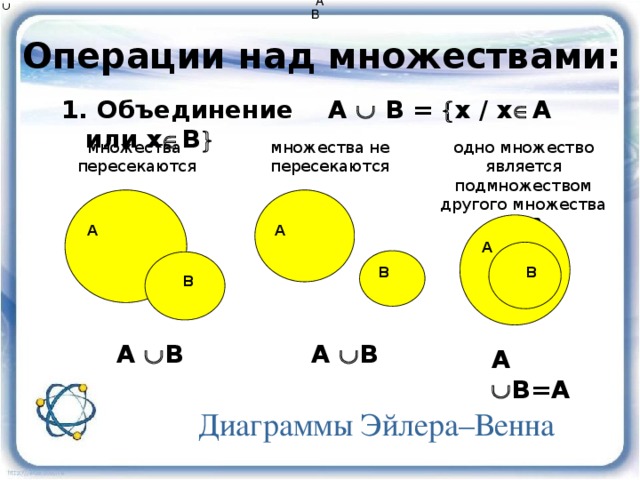§ 3. Некоторые виды алгебраических уравнений 2. Двучленные уравнения. 3. Корни из единицы и построение правильных многоугольников. 4. Трехчленные уравнения. § 4. Основная теорема алгебры многочленов и ее следствия 2. Многочлены с действительными коэффициентами. 3. Разложение на множители многочленов с действительными коэффициентами. 4. Краткие исторические сведения. Глава VI. ЦЕПНЫЕ ДРОБИ § 1. Конечные цепные дроби 2. Пример цепной дроби. 3. Определение цепной дроби. 4. Представление рациональных чисел в виде конечной цепной дроби. 5. Подходящие дроби. 6. Свойства подходящих дробей. 8. Подходящие дроби и календарь. 9. Приближение цепной дроби подходящими дробями. § 2. Бесконечные цепные дроби 2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными. 3. Цепные дроби как вычислительный инструмент. 4. Краткие исторические сведения. Глава VII. КОМБИНАТОРИКА § 1. Комбинаторные задачи § 2. Комбинаторные задачи. Продолжение § 3. Определения и формулы § 4. Соединения с повторениями § 5. Комбинаторные задачи. Окончание § 6. Бином Ньютона и его обобщения § 7. Краткие исторические сведения Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ § 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности § 3. Примеры вычисления вероятностей § 4. Полная вероятность. Формула Байеса § 5. Повторение испытаний § 6. Примеры вычисления вероятностей. Окончание § 7. Краткие исторические сведения

НОУ ИНТУИТ | Лекция | Математические методы описания моделей конструкций РЭС. Некоторые понятия теории множеств

< Лекция 21 || Лекция 16: 1234

Аннотация: Рассматривается методика использования основных понятий теории множеств при решении задач конструкторского проектирования.

Ключевые слова: знание, алгоритмическая, конструирование, входной, выходная информация, множества, свойства множества, элементы множества, способы задания множеств, список, бесконечное множество, произвольное, запись, непротиворечивость, равенство, интегральная схема, объект, мощность множества, Пустое множество, специальный символ, связь, место, пересечение множеств, объединение, вычитание, Дополнение, декартово произведение, пересечение, операции, объединение множеств, операция пересечения, разность множеств, отрицание, дополнение множества, декартово произведение множества, Паросочетание, прямое произведение множеств, композиция, разбиение множества, алгебра, Универсальное множество, очередь, операция дополнения, транзитивность, квантор общности, квантор существования, высказывание, булева переменная, числовой функцией, функция, значение, булева функция, операция отрицания, конъюнкция, дизъюнкция, тождество, коммутативность, ассоциативность, дистрибутивность, предикат, отношение, бинарным отношением, размерность, отношение эквивалентности, функциональная группа, рефлексивность, подмножество, класс эквивалентности, отношение порядка, строгие порядки, антирефлексивность, антисимметричность, кортеж, отношение доминирования, отображение множества, отображение, выражение, область определения, координаты, значение функции, показатели качества, перестановка, Законы идемпотентности, Законы де Моргана

intuit.ru/2010/edi»>Изложить основные понятия теории множеств, знание которых является обязательным при современном конструкторском проектировании РЭС.

16.1. Определения

Математические методы, положенные в основу алгоритмических процессов конструирования РЭС, а также процессы организации входной и выходной информации о проектируемом объекте широко используют понятия и символы теории множеств.

Под множеством понимают совокупность объектов любой природы, называемых элементами данного множества, обладающих каким-либо общим для множества свойством.

В множестве, по определению, все элементы различны, а порядок перечисления элементов множества произвольный. Следовательно, совокупность элементов не является множеством.

Существует два основных способа задания множеств: перечисление и описание.

Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств.

Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов.

Множество считается заданным, если указано свойство которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству , не обладают.

Если — произвольное множество, а — некоторое свойство, то запись

означает множество тех и только тех элементов , которые обладают свойством

intuit.ru/2010/edi»>При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов.

Как основное понятие теории, понятие множества не подлежит логическому определению.

Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия.

Множества обозначают заглавными буквами латинского алфавита: и т.д., а элементы множества — соответствующими строчными буквами того же алфавита: или строчными буквами с индексами: и т.д.

Равенство свидетельствует о том, что элементы являются элементами множества .

Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества.

Например, если во всём множестве микросхем электронного блока сложной радиоаппаратуры есть некоторое множество гибридных интегральных схем, то это можно записать так:

Это читается так: множество состоит из элементов множества , обладающих тем свойством, что является гибридной интегральной схемой.

Здесь введено новое обозначение означающее, что объект является элементом множества . Если же некоторый объект не принадлежит множеству , то это условие записывают в виде .

В том случае, когда не вызывает сомнения, из какого множества берутся элементы , принадлежность их к множеству можно не указывать.

Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид

Число элементов множества называют мощностью этого множества и обозначают прямыми скобками, например, .

Если число элементов множества конечно, то такое множество называют конечным.В противном случае множество будет бесконечным.

В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента.

Пустое множество обозначают специальным символом Например, если множество пусто, то пишут

Последовательность из элементов множества называют n — строкой. В отличие от обычного множества, где порядок элементов безразличен, в — строке обязательно задаётся их определённая последовательность.

Множество равно множеству , если оба эти множества состоят из одних и тех же элементов.

Если множество полностью содержится во множестве и при этом то говорят, что множество является подмножеством множества Y:

Следовательно, мы рассмотрели два соотношения:

— принадлежность ;

— включение .

Первое определяет связь между множеством и его элементами, а второе — между двумя множествами.

В случае, когда и, одновременно, , имеет место равенство , т.е. множества и совпадают.

Символическая запись означает, что множество не совпадает с множеством .

Дальше >>

< Лекция 21 || Лекция 16: 1234

Python Set Intersection — Полное руководство для начинающих

Из статьи, опубликованной на прошлой неделе, вы узнали, что такое Python set Differention() .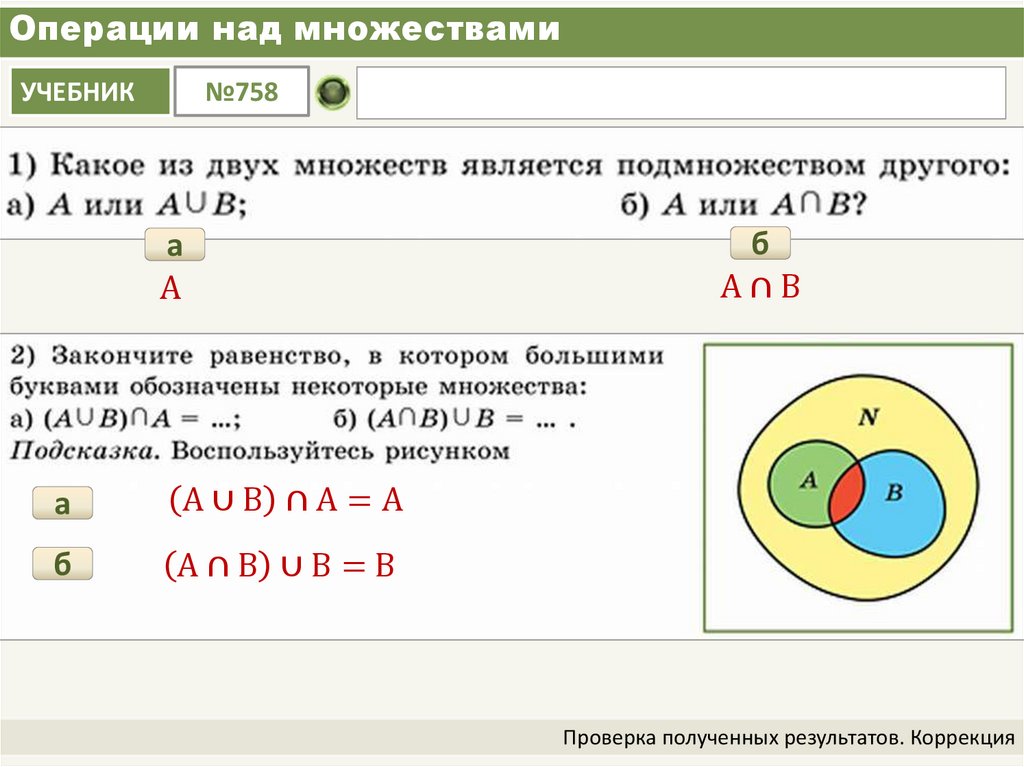 Теперь мы рассмотрим другую часто используемую функцию множества. Пересечение наборов Python позволяет найти общие элементы между двумя или более наборами. Он имеет много полезных приложений, таких как поиск общих навыков между кандидатами на работу.

Сегодня вы узнаете все о пересечении множеств Python. Вы будете готовы использовать его с уверенностью после прочтения статьи.

Лучшая часть? Вам вообще не нужно читать, так как я рассмотрел эту тему в формате видео:

Пересечение множества Python — основы

Итак, что такое пересечение множества Python? Вот что мы ответим в этом разделе. Вы получите полное представление об определении, синтаксисе и возвращаемых значениях с помощью наглядных примеров.

Определение и использование

Функция пересечения множеств возвращает общий элемент (элементы) двух или более множеств.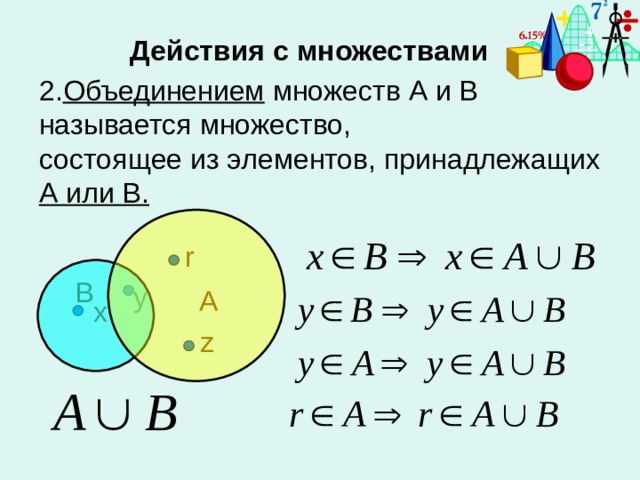 Например, мне нравится программировать на Python, JavaScript и PHP, а вы используете Java, Python и Ruby. У нас обоих есть общий Python. Мы будем работать с двумя множествами на протяжении всей статьи просто для простоты, но та же логика применима и при пересечении большего количества из них.

Взгляните на следующие два набора:

Вычисление пересечения между этими наборами означает, что мы получим новый набор с одним элементом — Python. Почему? Потому что это единственный элемент, общий для обоих наборов:

Пересечение множества в Python обычно представляется диаграммой Венна. Вот как это выглядит:

Общим для обоих наборов является только Python, поэтому область пересечения я выделил синим цветом.

Что делает метод пересечения в Python и как найти пересечение между множествами? Давайте рассмотрим синтаксис, чтобы ответить на эти вопросы.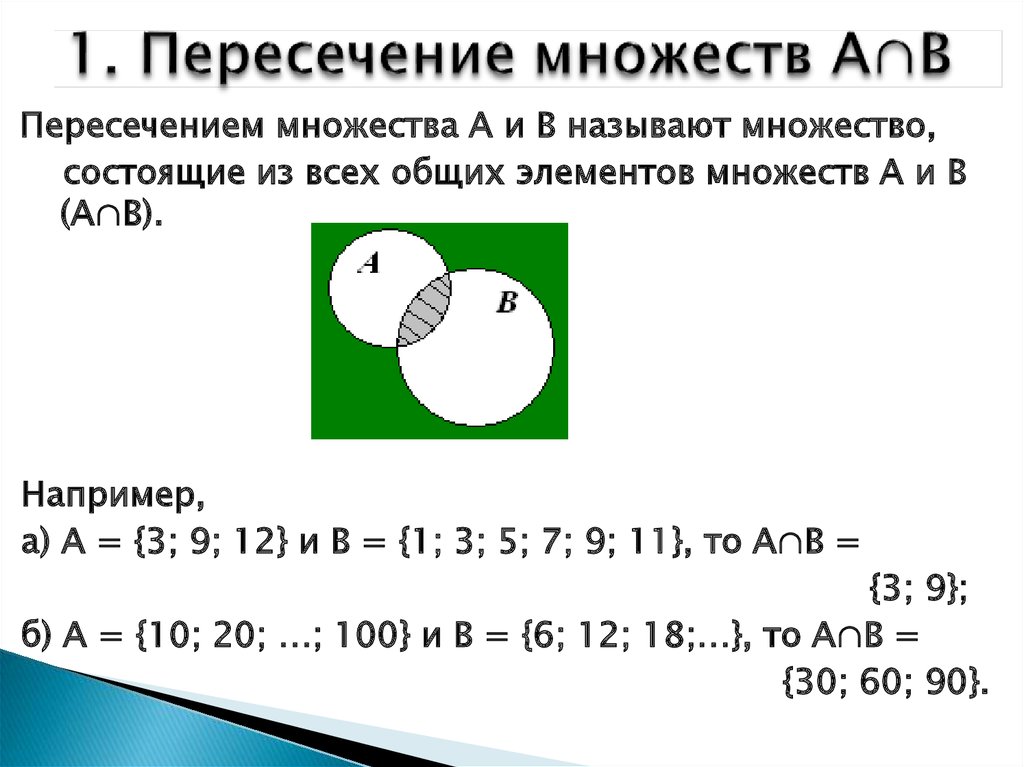

Синтаксис

 # Пересечение двух множеств
set1.intersection(set2)
# Пересечение между несколькими наборами
set1.intersection(set2, set3) 

Где:

• set1 — Итерация, из которой нужно найти пересечение.
• набор2 , набор3 — Другие наборы используются для расчета пересечения.

Возвращаемое значение

Функция пересечения возвращает новый набор, являющийся пересечением между первым набором и всеми остальными наборами, переданными в качестве аргументов, но только если в функцию были переданы наборы или итерируемые объекты.

Если в функцию пересечения() не были переданы аргументы, возвращается копия набора.

Пример функции пересечения набора Python

Мы объявим два набора, как и на изображение 1 :

• A : содержит Python , Javascript и Php
• B9004AV . и Ruby

В обоих наборах присутствует только Python, поэтому вычисление пересечения должно возвращать новый набор с единственным элементом Python:

 A = {'Python', 'JavaScript', 'PHP'}
B = {'Java', 'Python', 'Ruby'}
print(f"A ∩ B = {A.intersection(B)}") 

Вывод:

 A ∩ B = {'Python'} 

Если вы не укажете какие-либо параметры для функции пересечения, будет возвращена копия набора:

 print(f"A ∩ / = {A .intersection()}") 

Вывод:

 A ∩ / = {'JavaScript', 'PHP', 'Python'} 

Вы можете убедиться, что он был скопирован, напечатав адрес памяти:

 A = {' Python», «JavaScript», «PHP»}
A_copy = A.пересечение()
печать (шестнадцатеричный (идентификатор (A)))
print(hex(id(A_copy))) 

Вывод:

 0x108c68e40
0x108da5ac0 

Вы не увидите одинаковых значений, да и не в этом дело. Важно то, что они разные, что указывает на то, что набор был скопирован в другой адрес памяти.

 def list_intersection (l1: список, l2: список) -> список:
    вернуть [значение для значения в l1, если значение в l2]
def list_intersection2 (l1: список, l2: список) -> список:
    список возврата (набор (l1). пересечение (l2))
A = ['Python', 'JavaScript', 'PHP']
B = ['Java', 'Python', 'Ruby']
print(f"A ∩ B v1 = {list_intersection(A, B)}")
print(f"A ∩ B v2 = {list_intersection2(A, B)}") 

 A ∩ B v1 = ['Python']
A ∩ B v2 = ['Python'] 

 A = {'Python', 'JavaScript', 'PHP'}
B = {'Java', 'Python', 'Ruby'}
print(f"A ∩ B = {A & B}") 

 A ∩ B = {'Python'} 

Все остальное остается прежним. Помните, что оба операнда должны иметь тип, равный 9.Оператор 0003 и для работы.

Распространенные ошибки пересечения наборов Python

Вероятно, вы столкнетесь с ошибками, когда впервые начнете работать с наборами. Они распространены, но обычно их легко отлаживать.

AttributeError: «список» не имеет пересечения атрибутов

Это наиболее распространенная ошибка, которая возникает, когда вы вызываете функцию пересечения() для неверного типа данных. Эта функция встроена только в наборы.

Вот пример — при использовании списков возникает исключение:

 A = ['Python', 'JavaScript', 'PHP']
B = ['Java', 'Python', 'Ruby']
print(f"A ∩ B = {A.intersection(B)}") 

Вывод:

Убедитесь, что оба имеют установленный тип, и вы будете хорошо пойти.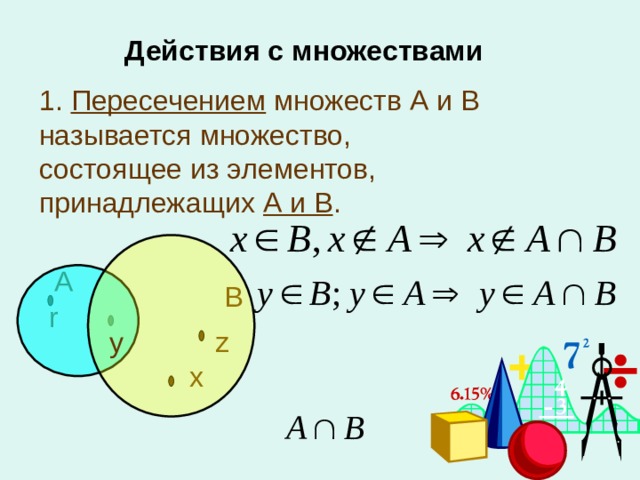

TypeError: неподдерживаемые типы операндов для &: ‘set’ и ‘list’

Эта ошибка возникает при попытке использовать сокращенную запись (знак и ) для недопустимых типов данных. Оба операнда должны иметь установленный тип, чтобы сокращенная запись работала. Вот пример:

 A = {'Питон', 'JavaScript', 'PHP'}
B = ['Java', 'Python', 'Ruby']
print(f"A ∩ B = {A & B}") 

Вывод:

Как видите, A — это множество, а B это список, поэтому знак и не работает.

Часто задаваемые вопросы о пересечении множеств Python

Теперь мы рассмотрим пару часто задаваемых вопросов (FAQ) относительно функции пересечения множеств Python.

Установить перекресток и обновить перекресток — в чем разница?

Функция cross_update() удаляет элементы, которые не найдены в обоих наборах (или нескольких наборах). Эта функция отличается от функции пересечения() тем, что она удаляет ненужные элементы из исходного набора и ничего не возвращает:

 A = {'Python', 'JavaScript', 'PHP'}
B = {'Java', 'Python', 'Ruby'}
A.intersection_update(B)
print(A) 

Вывод:

 {'Python'} 9B) 

Вывод:

 {'Ruby', 'Java', 'PHP', 'JavaScript'} 

Какова временная сложность пересечения множеств в Python?

Временная сложность пересечения набора в Python на наборе из n элементов и аргументе набора с m элементами составляет O(min(n, m)) , потому что вам нужно проверить для меньшего набора, каждый ли его элементов является членом большего множества. Проверка членства: O(1) , согласно finxter.com.

Заключение

Пересечение множества Python предельно просто для понимания. Мы рассмотрели интуицию и определение с наглядными примерами и построили свой путь к пониманию более сложного использования и типичных ошибок, с которыми вы столкнетесь. Мы также ответили на некоторые часто задаваемые вопросы.

Я надеюсь, что эта статья помогла вам лучше понять функцию пересечения множеств Python. Как всегда, если у вас есть какие-либо вопросы или комментарии, пожалуйста, не стесняйтесь задавать их в разделе комментариев ниже. Удачного кодирования!

Learn More

• Python Set Union
• Python Set Difference
• Python If-Else Statement in One Line — Ternary Operator Explained

Stay connected

• Hire me as a technical writer
• Subscribe on YouTube
• Подключиться к LinkedIn

Пересечение набора — определение, примеры, свойства

Пересечение множеств A и B содержит все элементы, общие для множества A и множества B.

Обозначается символом ∩

Пусть А = {1, 2, 3, 4 } , В = { 3, 4 , 5, 6}

А ∩ В = {3, 4}

Синяя область A ∩ B

1. A ∩ B = B ∩ A (коммутативный закон).
2. (A  ∩ B) ∩ C = A ∩ (B ∩ C) (Ассоциативный закон).
3. ∅ ∩ A = ∅, U ∩ A = A (закон ∅ и U).
4. A ∩ A = A (закон идемпотента)
5. A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) (дистрибутивное право) i. т. е., ∩ распределяет по ∪
   или мы также можем записать его как
   А ∪ (В ∩ С) = (А ∪ В) ∩ (А ∪ С)

Давайте обсудим эти законы

Возьмем наборы

Пусть А = {1, 2, 3, 4}, В = {3, 4, 5, 6}, С = {6, 7, 8}

и универсальное множество = U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

А ∩ В = {1, 2, 3, 4} ∩ {3, 4, 5, 6} = {3, 4}

В П А = {3, 4, 5, 6} ∩ {1, 2, 3, 4} = {3, 4}

∴ А ∩ В = В ∩ А

∩ C) (Ассоциативный закон).

А ∩ В = {3, 4}

(A ∩ B ) ∩ C = {3, 4} ∩ {6, 7, 8} = {} = ∅

В ∩ С = {3, 4, 5, 6} ∩ {6, 7, 8} = {6}

А ∩ (В ∩ С) = {1, 2, 3, 4} ∩ {6} = {} = ∅

∴ (A ∩ B) ∩ C = A ∩ (B ∩ C)

В пересечении у нас есть все элементы, которые являются общими

Поскольку ∅ не имеет элементов, между ∅ и A не будет общего элемента.

∴ Пересечение ∅ и A будет ∅

∅ ∩ А = {} ∩ {1, 2, 3, 4} = {}

∴ ∅ ∩ А = ∅

Поскольку U имеет все элементы, общими элементами между U и A будут все элементы множества A.