Закон распределения дискретной случайной величины
Skip to content
Artman Теория вероятностей
Закон распределения дискретной случайной величины (ДСВ) представляет собой соответствие между значениями х1, х2,…,хn этой величины и их вероятностями p1, p2,…,pn
Может быть задан аналитически, графически или таблично.
Самый простой способ представления закона распределения дискретной случайной величины — в виде таблицы ряда распределения, то есть
| X | x1 | x2 | …… | xn |
| P | p1 | p2 | …… | pn |
х1, х2,…,хn — значения дискретной случайной величины;
p1, p2,…,pn — вероятности значений X дискретной случайной величина.
Также должно выполняться условия, что сумма вероятностей равна 1, то есть
∑p=p1+p2+ … +pn=1
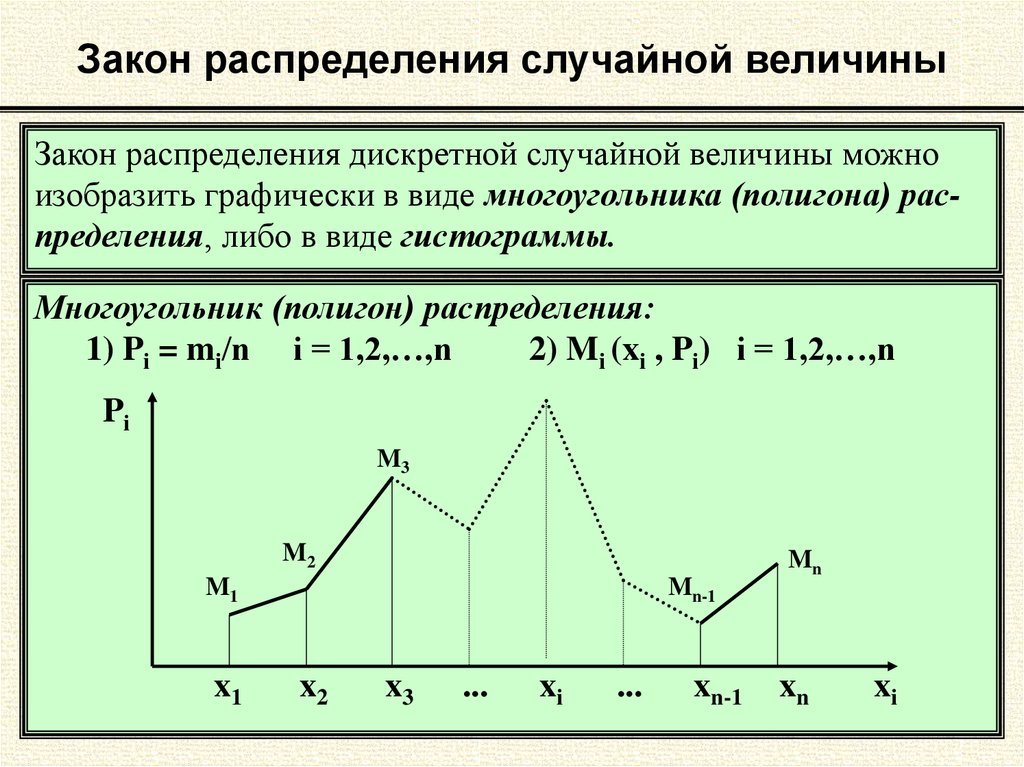
Графически закон распределения ДСВ задается в виде многоугольника распределения см. здесь., а аналитически, например, с применением формулы Бернулли.Рассмотрим примеры
Пример 1
Монета подбрасывается 10 раз, герб выпал 6 раз, а орел — 4 раза. Составить закон распределения дискретной случайной величины.
Решение
Вероятности равны:
p1(6)=6/10=0,6;
p2(4)=4/10=0,4
| X | 6 | 4 |
| P | 0.6 | 0.4 |
Пример 2
Из корзины извлечено 4 белых шара, 6 черных, 8 синих и 2 красных шара. Найти закон распределения случайной величины X возможного выигрыша на один билет.
Решение
Объем выборки равен
n=4+6+8+2=20
X принимает следующие значения:
x1=4; x2=6; x3=8; x1=2
Найдем их вероятности:
p1(4)=4/20=0,2;
p2(6)=6/20=0,3;
p3(8)=8/20=0,4;
p4(2)=2/20=0,1
Получаем таблицу закона распределения дискретной случайной величины
| X | 4 | 6 | 8 | 2 |
| P | 0.2 | 0.3 | 0.4 | 0.1 |
Пример 3
По контрольной работе по математике школьники получили оценки:
удовлетворительно — 5 человек;
хорошо — 13 человек;
отлично — 7 человек.
Составьте таблицу закона распределения ДСВ
Решение
n=5+13+7=26
Вычислим вероятности:
p1(5)=5/25=0,2;
p2(13)=13/25=0,52;
p3(7)=7/25=0,28
Таблица имеет вид:
| X | 5 | 13 | 8 | 2 |
| P | 0.2 | 0.52 | 0.28 | 0.1 |
Пример 4
Партия из 8 изделий содержит 5 стандартных. Наудачу отбираются 3 изделия. Составить таблицу закона распределения числа стандартных изделий среди отобранных.
Решение
Для составления закона распределения воспользуемся формулой комбинаторики сочетание без повторений, то есть всего 8 изделия, а отобрать необходимо 3 изделия получаем:
при P(X=0) — вероятность того, что среди трех отобранных изделий не окажется ни одного стандартного;
при P(X=1) — вероятность того, что среди трех отобранных изделий окажется одно стандартное и два нестандартных изделия;
при
при P(X=3) — вероятность того, что среди трех отобранных изделий все три изделия стандартные. {3 — x}$ — общее число способов отбора нестандартных деталей
{3 — x}$ — общее число способов отбора нестандартных деталей
Тогда вероятности события A вычисляются по формуле
Закон распределения дискретной случайной величины X для составления ряда распределения:
Получаем таблицу ряда распределения ДСВ
| X | 0 | 1 | 2 | 3 |
| P | 0 | 0.2 | 0.6 | 0.2 |
11996
Дискретные случайные величины. Биномиальное распределение, Геометрическое распределение, Математическое ожидание, Дисперсия
Основные понятия теории вероятностей | Основные теоремы | Повторение испытаний. Формула Бернулли, интегральная и локальная теоремы Лапласа. | Дискретные случайные величины | Закон больших чисел | Непрерывные случайные величины | Распределение функции случайных аргументов | Системы двух случайных величин | Онлайн калькуляторы
| Дискретные случайные величины | Закон больших чисел | Непрерывные случайные величины | Распределение функции случайных аргументов | Системы двух случайных величин | Онлайн калькуляторы
4. Дискретные случайные величины
4.1. Числовые характеристики дискретных случайных величин
Случайной величиной называется величина- которая в результате опыта может принять то или иное значение, неизвестно заранее – какое именно.
Случайная величина называется дискретной, если она принимает лишь отдельные, изолированные значения с определенными вероятностями. Число возможных значений может быть как конечным, так и бесконечным.
Математическое ожидание (M(x)).
Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности
Свойства математического ожидания
· , где C- постоянное число
·
·
· , для независимых случайных величин Х и Y
Математическое ожидание числа появлений события в независимых испытаниях
, где n- число испытаний, p- вероятность появления
интересующего нас события в одном испытании.
Дисперсия
Дисперсией дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
На практике чаще пользуются другой формулой
, где
Свойства дисперсии
· , где C- постоянное число
·
·
Дисперсия числа появлений события в независимых испытаниях
, где n- число испытаний, p- вероятность появления интересующего нас события в одном испытании.
Среднее квадратическое отклонение
4.2. Закон распределения вероятностей дискретной случайной величины.
Законом
распределения дискретной случайной величины называют соответствие между возможными значениями и их
вероятностями.
|
X |
|
|
… |
|
|
P |
|
|
… |
|
Сумма вероятностей всех событий должна равняться 1.
Некоторые законы распределения:
Биномиальное распределение
Биномиальным называют распределение вероятностей, определяемое формулой Бернулли
Математическое ожидание
Дисперсия
Среднее квадратическое отклонение
Вероятность Биномиального распределения рассчитать онлайн
Распределение Пуассона
Вероятность каждого значения находится по формуле Пуассона
, где
Пусть производится n независимых
испытаний, в каждом из которых вероятность появления события А равна р. Причем, число испытаний велико, а
вероятность появления события А в каждом испытании мала ( ). В
этом случае и прибегают в формуле Пуассона.
Формула Пуассона, как и теоремы Лапласа дают
приближенный результат, точной является только формула Бернулли.
Причем, число испытаний велико, а
вероятность появления события А в каждом испытании мала ( ). В
этом случае и прибегают в формуле Пуассона.
Формула Пуассона, как и теоремы Лапласа дают
приближенный результат, точной является только формула Бернулли.
Геометрическое распределение.
Случайная дискретная величина Х – число испытаний, которые нужно провести до первого появления события А. Случайная величина Х может принимать значения: 11.2.3….
Вероятность того, что для этого придется провести к испытаний
, где p –вероятность появления события А в одном испытании,
Ряд распределения имеет вид
|
X |
1 |
2 |
… |
|
… |
|
P |
|
|
… |
|
… |
Гипергеометрическое распределение
Распределение называется гипергеометрическим, если вероятность каждого значения Х находится по формуле
— вероятность
того, что из N элементов ,среди которых М обладает
определенным свойством, возьмут n элементов, причем к из них будут обладать данным свойством.
4.3. Теоретические моменты
Начальным моментом порядка к случайной величины Х называют математическое ожидание величины
В частности,
Тогда формулу для нахождения дисперсии можно представить в виде
Центральным моментом порядка к случайной величины Х называют математическое ожидание величины
В частности,
§2. Закон распределения дискретной случайной величины Многоугольник распределения
Пусть X – некоторая дискретная случайная величина, все значения которой , ,…, такие, что каждому значению соответствует вероятность , где .
Определение.
Закон распределения (ряд распределения) – соответствие,
устанавливающее связь между всеми
значениями
случайной величины и соответствующими
вероятностями
.
Способы задания закона распределения дискретной случайной величины:
1. Табличный.
В первой строке таблицы перечислены все возможные значения случайной величины (обычно – в порядке возрастания), во второй – соответствующие вероятности:
… | … | |||||
… | … |
Т.к. в результате опыта случайная величина X принимает только одно из значений , ,…, , то события, состоящие в появлении каждого из этих значений, являются несовместными и образуют полную группу событий, следовательно:
или .
2. Формулой.
(Вспомните, какие формулы для вычисления вероятности применяли ранее)
3. Графически.
На плоскости введем прямоугольную систему координат. Пара чисел на плоскости изображает точку.
Рис.7.
Определение. Ломаная, вершины которой имеют координаты , где , называется многоугольником распределения вероятностей дискретной случайной величины X (полигоном ДСВ Х) (рис.7).
Задача 1. Вероятность правильного решения задачи по теории вероятностей первым студентом – 0,7 , вторым – 0,8 . Составить закон распределения дискретной случайной величины X – число студентов, правильно решивших задачу (с первого раза). Записать ряд распределения.
Решение. Возможные значения случайной величины X: , , .
Вычислим
вероятность появления каждого из
значений случайной величины, используя
формулы сложения и умножения вероятностей.
1. , т.е. ни один из студентов не решит задачу.
– вероятность того, что первый студент не решит задачу.
– вероятность того, что второй студент не решит задачу.
.
2. , т.е. только один студент из двух решит задачу.
3. , т.е. оба студента решат задачу.
.
По результатам составим таблицу:
Х | 0 | 1 | 2 |
Р | 0,06 | 0,38 | 0,56 |
Графически
изобразим полученный ряд распределения
(построим многоугольник распределения,
рис. 8).
8).
Рис. 8.
Функция распределения вероятностей используется как способ задания случайной величины и как средство описания случайной величины.
Определение. Функция распределения вероятностей случайной величины X – функция , определяющая вероятность того, что случайная величина X примет значение меньше, чем x, т.е.
.
называется также интегральной функцией распределения вероятностей случайной величины X.
Эта формула выражает связь между двумя разделами математики: математическим анализом и теорией вероятностей, между функциями действительных переменных и случайными величинами, она дает возможность для вычисления вероятности появления случайной величины (вероятности появления события) применять аппарат математического анализа.
Геометрическая иллюстрация.
Х
х
Изобразим Х точкой на числовой оси, лежащей левее
некоторой точки x. Очевидно, вероятность того, что некоторая
точка будет находиться левее x, зависит от расположения точки x,
т.е. является функцией аргумента x.
Очевидно, вероятность того, что некоторая
точка будет находиться левее x, зависит от расположения точки x,
т.е. является функцией аргумента x.
Замечание: Для дискретной случайной величины, которая может принимать значение , ,…, , функция распределения имеет вид
.
(эта запись означает, что суммируются вероятности всех тех значений , величина которых меньше x).
Задача.2. Дискретная случайная величина задана рядом распределения
-2 | 1 | 3 | 5 | |
0,1 | 0,2 | 0,4 | 0,3 |
Записать
функцию распределения случайной величины X,
построить ее график.
Решение.
При ,
При ,
При ,
При ,
При ,
На основании полученных результатов построим график функции
И
Рис. 10.
з рис. 10 видно, что – разрывная, имеет четыре скачка по числу принимаемых случайной величиной X значений. Если увеличивать число значений случайной величины с одновременным уменьшением интервалов между ними, то дискретная случайная величина будет приближаться к непрерывной, а ее функция распределения – к непрерывной функции (рис. 11).
1
0
Рис.11.
Свойства функции F(x).
1. .
2. F(x) – неубывающая
функция, т. е., если ,
то
е., если ,
то
Из свойства 2 следует:
вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу равна разности значений функции распределения на концах этого полуинтервала . Причем, если F(x) – непрерывная функция, то (т.е. вероятность того, что НСВ X примет значение, принадлежащее полуинтервалу, интервалу, отрезку с одними и теми же концами, одинакова;
вероятность того, что НСВ примет какое-либо наперед заданное значение, равна 0, т.е. P(X=x)=0.
Если все значения СВ принадлежат (a;b), то (т.е. ).
Задача 3. Задана функция распределения вероятностей непрерывной СВ X:
Найти: 1) ; 2) .
Решение. 1) По следствию
из свойства 2:
1) По следствию
из свойства 2:
=F(1,3)—F(1)=
2) =F (2)—F (0,5)=
Распределения вероятностей для дискретных случайных величин
4.2 Распределения вероятностей дискретных случайных величин
Цели обучения
- Изучить концепцию распределения вероятностей дискретной случайной величины.
- Чтобы узнать о понятиях среднего значения, дисперсии и стандартного отклонения дискретной случайной величины, а также о том, как их вычислить.
Распределения вероятностей
Связано с каждым возможным значением х дискретной случайной величины х есть вероятность P(x) того, что х примет значение х в одном испытании эксперимента.
Определение
Распределение вероятностей Список всех возможных значений и их вероятности. дискретной случайной величины X представляет собой список всех возможных значений X вместе с вероятностью того, что X примет это значение в одном испытании эксперимента.
дискретной случайной величины X представляет собой список всех возможных значений X вместе с вероятностью того, что X примет это значение в одном испытании эксперимента.
Вероятности в распределении вероятностей случайной величины X должны удовлетворять следующим двум условиям:
- Каждая вероятность P(x) должна быть между 0 и 1: 0≤P(x)≤1.
- Сумма всех вероятностей равна 1: ΣP(x)=1.
Пример 1
Правильная монета подбрасывается дважды. Пусть X будет количеством наблюдаемых голов.
- Построить распределение вероятности х .
- Найти вероятность того, что будет замечена хотя бы одна голова.
Решение:
Возможные значения, которые может принимать X : 0, 1 и 2.
x012P(x)0.250.500.25 Каждое из этих чисел соответствует событию в выборочном пространстве S={hh,ht,th,tt} равновероятных результатов для этого эксперимента: X = от 0 до {tt}, X = от 1 до {ht,th} и X = от 2 до {hh}. Вероятность каждого из этих событий и, следовательно, соответствующего значения X можно найти, просто посчитав, чтобы получить
Каждое из этих чисел соответствует событию в выборочном пространстве S={hh,ht,th,tt} равновероятных результатов для этого эксперимента: X = от 0 до {tt}, X = от 1 до {ht,th} и X = от 2 до {hh}. Вероятность каждого из этих событий и, следовательно, соответствующего значения X можно найти, просто посчитав, чтобы получитьЭта таблица представляет собой распределение вероятностей X .
«По крайней мере одна голова» — это событие X ≥ 1, которое является объединением взаимоисключающих событий X = 1 и X = 2. Таким образом,
P(X≥1)=P(1)+P(2)=0,50+0,25=0,75Гистограмма, графически иллюстрирующая распределение вероятностей, представлена на рис. 4.1 «Распределение вероятностей двойного подбрасывания правильной монеты».
Рис. 4.1 Распределение вероятности двукратного подбрасывания правильной монеты
4.1 Распределение вероятности двукратного подбрасывания правильной монеты
Пример 2
Бросается пара правильных игральных костей. Пусть X обозначает сумму количества точек на верхних гранях.
- Построить распределение вероятностей X .
- Найти P ( X ≥ 9).
- Найдите вероятность того, что X примет четное значение.
Решение:
Выборочное пространство равновероятных исходов равно
Возможными значениями для X являются числа от 2 до 12. X = 2 — это событие {11}, поэтому P(2)=1∕36. X = 3 — это событие {12,21}, поэтому P(3)=2∕36. Продолжая таким образом, мы получаем таблицу
. x2345678Эта таблица представляет собой распределение вероятностей X .
Событие X ≥ 9 является объединением взаимоисключающих событий X = 9, X = 10, X = 11 и X = 12. Таким образом,
Таким образом,
Прежде чем мы сразу перейдем к выводу, что вероятность того, что X принимает четное значение, должно быть 0,5, обратите внимание, что X принимает шесть различных четных значений, но только пять различных нечетных значений. Мы вычисляем
P(X четный)=P(2)+P(4)+P(6)+P(8)+P(10)+P(12)=136+336+536+536+336+136=1836 =0,5Гистограмма, графически иллюстрирующая распределение вероятностей, приведена на рис. 4.2 «Распределение вероятностей для бросания двух честных игральных костей».
Рис. 4.2 Распределение вероятностей при бросании двух игральных костей
Среднее значение и стандартное отклонение дискретной случайной величины
Определение
СреднееЧисло Σx P(x), измеряющее его среднее значение при повторных испытаниях. (также называемое ожидаемым значением . Его среднее значение. ) дискретной случайной величины X число интерпретируется как среднее значений, принимаемых случайной величиной в повторных попытках эксперимента. 9Пример 3 =Σx P(x)=(−2)·0,21+(1)·0,34+(2)·0,24+(3,5)·0,21=1,135
(также называемое ожидаемым значением . Его среднее значение. ) дискретной случайной величины X число интерпретируется как среднее значений, принимаемых случайной величиной в повторных попытках эксперимента. 9Пример 3 =Σx P(x)=(−2)·0,21+(1)·0,34+(2)·0,24+(3,5)·0,21=1,135
Пример 4
месяц. Одна тысяча лотерейных билетов продается по 1 доллару каждый. У каждого равные шансы на победу. Первый приз — 300 долларов, второй — 200 долларов, третий — 100 долларов. Пусть X обозначают чистую прибыль от покупки одного билета.
- Построить распределение вероятностей X .
- Найти вероятность выигрыша любых денег при покупке одного билета.
- Найдите ожидаемое значение X и интерпретируйте его значение.
Решение:
Если билет выбран в качестве победителя первого приза, чистая прибыль для покупателя равна призу в размере 300 долларов за вычетом 1 доллара, уплаченного за билет, следовательно, X = 300 − 1 = 299.
x29919999−1P(x)0,0010,0010,0010,997 Такой билет один, поэтому P (299) = 0,001. Применение того же принципа «доход минус расход» к обладателям второго и третьего приза и к 997 проигравшим билетам дает распределение вероятностей:
Такой билет один, поэтому P (299) = 0,001. Применение того же принципа «доход минус расход» к обладателям второго и третьего приза и к 997 проигравшим билетам дает распределение вероятностей:Пусть W обозначает событие, когда выбирается билет, чтобы выиграть один из призов. Использование таблицы
Р(Вт)=Р(299)+Р(199)+Р(99)=0,001+0,001+0,001=0,003Использование формулы в определении ожидаемой стоимости,
E(X)=299·0,001+199·0,001+99·0,001+(−1)·0,997=−0,4Отрицательное значение означает, что в среднем человек теряет деньги. В частности, если бы кто-то неоднократно покупал билеты, то, хотя он время от времени выигрывал бы, в среднем он терял бы 40 центов за каждый купленный билет.
Концепция ожидаемой стоимости также является базовой для страховой отрасли, как показывает следующий упрощенный пример.
Пример 5
Компания по страхованию жизни продает полис страхования жизни сроком на один год на сумму 200 000 долларов США лицу, относящемуся к определенной группе риска, с премией в размере 195 долларов США. Найдите ожидаемую ценность для компании одного полиса, если вероятность того, что человек из этой группы риска проживет один год, составляет 99,97%.
Решение:
Пусть X обозначает чистую прибыль компании от продажи одного такого полиса. Есть две возможности: застрахованное лицо живет целый год или застрахованное лицо умирает до истечения года. Применяя принцип «доход минус расход», в первом случае значение х равно 195 — 0; в последнем случае это 195−200 000 = −199 805. Поскольку вероятность в первом случае равна 0,9997, а во втором случае 1−0,9997=0,0003, распределение вероятностей для X будет следующим: )=Σx P(x)=195·0,9997+(−199,805)·0,0003=135
Иногда (фактически, 3 раза из 10 000) компания теряет большую сумму денег по полису, но обычно она получает 195 долларов, что, исходя из нашего расчета E(X), дает в среднем чистую прибыль в размере 135 долларов на проданный полис.
Definition
The variance , σ2 , of a discrete random variable X is the number
σ2=Σ(x−μ)2 P(x)
which by algebra эквивалентна формуле
σ2=Σx2 P(x)−µ2
Определение
Стандартное отклонение ), измеряя его изменчивость при повторных испытаниях., σ , дискретной случайной величины X представляет собой квадратный корень из ее дисперсии, поэтому определяется формулами
Дисперсия и стандартное отклонение дискретной случайной величины X могут быть интерпретированы как меры изменчивости значений, принятых случайной величиной в повторных испытаниях эксперимента. Единицы стандартного отклонения соответствуют единицам X .
Пример 6
Дискретная случайная величина X имеет следующее распределение вероятностей: «.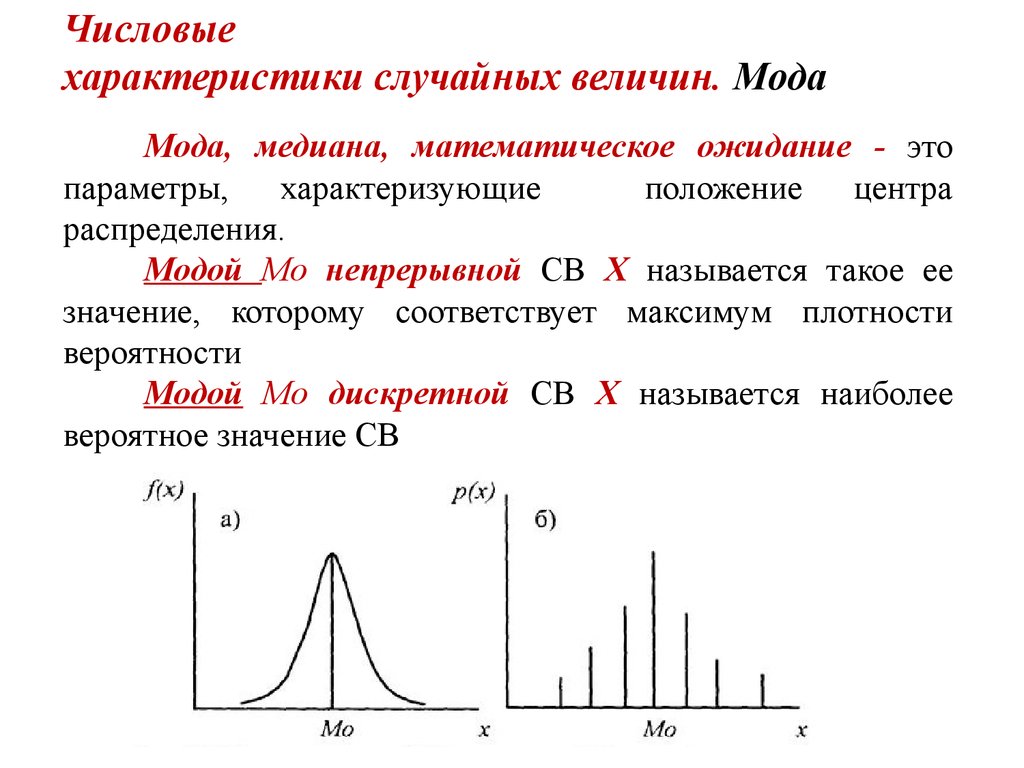
Рис. 4.3 Вероятностное распределение дискретной случайной величины
Вычислите каждую из следующих величин.
- и .
- Р(0).
- P ( X > 0).
- P ( X ≥ 0).
- P(X≤−2).
- Среднее μ из X .
- Дисперсия σ2 X .
- Стандартное отклонение σ от X .
Решение:
- Поскольку сумма всех вероятностей должна составлять 1, a=1−(0,2+0,5+0,1)=0,2.
- Непосредственно из таблицы, P(0)=0,5.
- Из таблицы P(X>0)=P(1)+P(4)=0,2+0,1=0,3.
- Из таблицы P(X≥0)=P(0)+P(1)+P(4)=0,5+0,2+0,1=0,8.
- Поскольку ни одно из чисел, перечисленных в качестве возможных значений для X , не меньше или равно -2, событие X ≤ -2 невозможно, поэтому P ( X ≤ -2) = 0,
Использование формулы в определении μ ,
μ=Σx P(x)=(−1)·0,2+0·0,5+1·0,2+4·0,1=0,4Используя формулу определения σ2 и только что вычисленное значение μ ,
σ2=Σ(x−μ)2 P(x)=(−1−0,4)2·0,2+(0−0,4)2·0,5+(1−0,4)2·0,2+(4−0,4)2·0,1 =1,84- Используя результат части (g), σ=1,84=1,3565.

Ключевые выводы
- Распределение вероятностей дискретной случайной величины X представляет собой список всех возможных значений x , взятых X , вместе с вероятностью P(x), что X примет это значение в одной попытке эксперимента. .
- Среднее значение μ дискретной случайной величины X — это число, указывающее среднее значение X по многочисленным испытаниям эксперимента. Он вычисляется по формуле μ=Σx P(x).
- Дисперсия σ2 и стандартное отклонение σ дискретной случайной величины X — это числа, указывающие на изменчивость X в ходе многочисленных испытаний эксперимента. Их можно вычислить по формуле σ2=[Σx2 P(x) ]−µ2, взяв квадратный корень, чтобы получить σ .
Упражнения
Определите, является ли таблица допустимым распределением вероятностей дискретной случайной величины.
 Объясните полностью.
Объясните полностью.х-2024P(х)0.30.50.20.1
x0.50.250.25P(x)−0.40.60.8
x1.12.54.14.65.3P(x)0.160.140.110.270.22
Определите, является ли таблица допустимым распределением вероятностей дискретной случайной величины. Объясните полностью.
x01234P(x)−0,250,500,350,100,30
x123P(x)0.
 3250.4060.164
3250.4060.164x2526272829P(x)0.130.270.280.180.14
Дискретная случайная величина X имеет следующее распределение вероятностей:
x7778798081P(x)0.150.150.200.400.10
Вычислите каждое из следующих значений.
- Р(80).
- P ( X > 80).
- P ( X ≤ 80).
- Среднее μ из X .
- Дисперсия σ2 X .
- Стандартное отклонение σ из X .
Дискретная случайная величина X имеет следующее распределение вероятностей:
x1318202427P(x)0,220,250,200,170,16
Вычислите каждую из следующих величин.

- П(18).
- P ( X > 18).
- Р ( X ≤ 18).
- Среднее μ из X .
- Дисперсия σ2 X .
- Стандартное отклонение σ от X .
Если каждая кость в паре «нагружена» так, что одна выпадает вдвое реже, чем должна, шестерка выпадает вдвое реже, чем должна, а вероятности остальных граней не меняются, то распределение вероятностей для сумма X количества точек на верхних гранях, если прокатить два, равно
x234567P(x)114441448144121441614422144×8
- 12P(x)241442014416144121449144
4
.
- P(5≤X≤9).

- P ( X ≥ 7).
- Среднее μ из X . (Для честных костей это число равно 7.)
- Стандартное отклонение σ из X . (Для честных костей это число составляет около 2,415.)
- P(5≤X≤9).
Базовый
Борачио работает на заводе по производству автомобильных шин. Число X исправных, но дефектных шин, которые он производит в случайный день, имеет распределение вероятностей
x 2345P(x)0,480,360,120,04
- Найдите вероятность того, что завтра Борачио произведет более трех дефектных шин.
- Найдите вероятность того, что завтра Борачио произведет не более двух шин с дефектами.

- Вычислить среднее значение и стандартное отклонение X . Интерпретируйте среднее значение в контексте проблемы.
По опыту заводчика хомяков число X живых детенышей в помете самки в возрасте не старше двенадцати месяцев, не родившей помет за последние шесть недель, имеет распределение вероятностей
x3456789P(x)0.040.100.260.310.220.050.02
- Найдите вероятность того, что в следующем помете родится от пяти до семи живых детенышей.
- Найдите вероятность того, что в следующем помете родится не менее шести живых щенков.
- Вычислить среднее значение и стандартное отклонение X . Интерпретируйте среднее значение в контексте проблемы.
Число X дней в летние месяцы, когда строительная бригада не может работать из-за погодных условий, имеет распределение вероятностей вероятность того, что следующим летом будет потеряно не более десяти дней.

- Найти вероятность того, что следующим летом будет потеряно от 8 до 12 дней.
- Найдите вероятность того, что следующим летом не будет пропущено ни одного дня.
- Вычислить среднее значение и стандартное отклонение X . Интерпретируйте среднее значение в контексте проблемы.
Приложения
. Пусть X обозначает количество мальчиков в случайно выбранной семье из трех детей. Предполагая, что мальчики и девочки равновероятны, постройте распределение вероятностей X .
. Пусть X обозначает количество раз, когда честная монета выпадает орлом при трех подбрасываниях. Постройте распределение вероятностей X .
Продано пять тысяч лотерейных билетов по 1 доллару каждый. Один билет принесет 1000 долларов, два билета — 500 долларов каждый, а десять билетов — 100 долларов каждый. Пусть X обозначает чистую прибыль от покупки случайно выбранного билета.
Один билет принесет 1000 долларов, два билета — 500 долларов каждый, а десять билетов — 100 долларов каждый. Пусть X обозначает чистую прибыль от покупки случайно выбранного билета.
- Построить распределение вероятностей X .
- Вычислить ожидаемое значение E(X) для X . Интерпретируйте его значение.
- Вычислить стандартное отклонение σ от X .
Продано семь тысяч лотерейных билетов по 5 долларов каждый. Один билет принесет 2000 долларов, два билета — 750 долларов каждый, а пять билетов — 100 долларов каждый. Пусть X обозначают чистую прибыль от покупки случайно выбранного билета.
- Построить распределение вероятностей X .
- Вычислить ожидаемое значение E(X) для X .
 Интерпретируйте его значение.
Интерпретируйте его значение. - Вычислить стандартное отклонение σ от X .
Страховая компания продаст $
полисов страхования жизни сроком на один год для лица, относящегося к определенной группе риска, с премией в размере 478 долларов США. Найдите ожидаемую ценность для компании одного полиса, если вероятность того, что человек из этой группы риска проживет один год, составляет 99,62%.
Страховая компания продает полис страхования жизни сроком на один год на сумму 10 000 долларов США лицу, относящемуся к определенной группе риска, с премией в размере 368 долларов США. Найдите ожидаемую ценность для компании одного полиса, если человек в этой группе риска имеет 97,25% шанс прожить один год.
По оценкам страховой компании, вероятность того, что человек, относящийся к определенной группе риска, проживет один год, составляет 0,9825. Такой человек хочет купить полис страхования жизни сроком на один год на сумму 150 000 долларов. Пусть C обозначает, сколько страховая компания взимает с такого человека за такой полис.
Такой человек хочет купить полис страхования жизни сроком на один год на сумму 150 000 долларов. Пусть C обозначает, сколько страховая компания взимает с такого человека за такой полис.
- Построить распределение вероятностей X . (Две записи в таблице будут содержать С .)
- Вычислить ожидаемое значение E(X) для X .
- Определите значение C , которое должно быть у компании, чтобы обеспечить безубыточность по всем таким политикам (то есть чтобы получить в среднем нулевую чистую прибыль на политику по таким политикам).
- Определите значение C , чтобы компания могла получить в среднем чистую прибыль в размере 250 долларов США на полис по всем таким полисам.
По оценкам страховой компании, вероятность того, что человек, относящийся к определенной группе риска, проживет один год, составляет 0,99. Такой человек хочет купить полис страхования жизни сроком на 75 000 долларов на один год. Пусть C обозначает, сколько страховая компания взимает с такого человека за такой полис.
Такой человек хочет купить полис страхования жизни сроком на 75 000 долларов на один год. Пусть C обозначает, сколько страховая компания взимает с такого человека за такой полис.
- Построить распределение вероятностей X . (Две записи в таблице будут содержать С .)
- Вычислить ожидаемое значение E(X) для X .
- Определите значение C , которое должно быть у компании, чтобы обеспечить безубыточность по всем таким политикам (то есть чтобы получить в среднем нулевую чистую прибыль на политику по таким политикам).
- Определите значение C , чтобы компания могла получить в среднем чистую прибыль в размере 150 долларов США на полис по всем таким полисам.
Колесо рулетки имеет 38 слотов. Тридцать шесть слотов пронумерованы от 1 до 36; половина из них красные, а половина черные. Оставшиеся два слота пронумерованы 0 и 00 и окрашены в зеленый цвет. При ставке 1 доллар на красное игрок платит 1 доллар за игру. Если шарик попадает в красную щель, он получает обратно доллар, который поставил, плюс дополнительный доллар. Если мяч не приземлится на красное, он теряет свой доллар. Пусть х обозначают чистую прибыль игрока за одну игру.
Тридцать шесть слотов пронумерованы от 1 до 36; половина из них красные, а половина черные. Оставшиеся два слота пронумерованы 0 и 00 и окрашены в зеленый цвет. При ставке 1 доллар на красное игрок платит 1 доллар за игру. Если шарик попадает в красную щель, он получает обратно доллар, который поставил, плюс дополнительный доллар. Если мяч не приземлится на красное, он теряет свой доллар. Пусть х обозначают чистую прибыль игрока за одну игру.
- Построить распределение вероятностей X .
- Вычислите ожидаемое значение E(X) для X и интерпретируйте его значение в контексте задачи.
- Вычислить стандартное отклонение X .
Колесо рулетки имеет 38 слотов. Тридцать шесть слотов пронумерованы от 1 до 36; оставшиеся два слота пронумерованы 0 и 00. Предположим, что «число» 00 считается нечетным, а число 0 все же четным. При ставке в 1 доллар на чет игрок платит 1 доллар за игру. Если шарик попадает в слот с четным номером, он получает обратно доллар, который поставил, плюс дополнительный доллар. Если шарик не попадает в слот с четным номером, он теряет свой доллар. Пусть X обозначают чистую прибыль игрока за одну игру.
Предположим, что «число» 00 считается нечетным, а число 0 все же четным. При ставке в 1 доллар на чет игрок платит 1 доллар за игру. Если шарик попадает в слот с четным номером, он получает обратно доллар, который поставил, плюс дополнительный доллар. Если шарик не попадает в слот с четным номером, он теряет свой доллар. Пусть X обозначают чистую прибыль игрока за одну игру.
- Построить распределение вероятностей X .
- Вычислите ожидаемое значение E(X) для X и объясните, почему эта игра не предлагается в казино (где 0 не считается четным).
- Вычислить стандартное отклонение X .
Время с точностью до целой минуты, которое требуется городскому автобусу, чтобы пройти от одного конца маршрута до другого, имеет вероятностное распределение. Как иногда бывает с вероятностями, вычисленными как эмпирические относительные частоты, вероятности в таблице составляют в сумме только значение, отличное от 1,00, из-за ошибки округления.
Как иногда бывает с вероятностями, вычисленными как эмпирические относительные частоты, вероятности в таблице составляют в сумме только значение, отличное от 1,00, из-за ошибки округления.
x424344454647P(x)0.100.230.340.250.050.02
- Найдите среднее время, затрачиваемое автобусом на проезд по маршруту.
- Найдите стандартное отклонение времени, за которое автобус проезжает весь маршрут.
Тибальт получает по почте предложение принять участие в национальном розыгрыше. Призы и шансы на победу указаны в предложении следующим образом: 5 миллионов долларов, один шанс из 65 миллионов; 150 000 долларов, один шанс из 6,5 миллионов; 5000 долларов, один шанс из 650 000; и 1000 долларов, один шанс из 65000. Если Тибальту нужно 44 цента, чтобы отправить его по почте, какова ожидаемая ценность лотереи для него?
Для числа X гвоздей в случайно выбранной 1-фунтовой коробке показано распределение вероятностей.
 Найдите среднее количество гвоздей на фунт.
Найдите среднее количество гвоздей на фунт.x100101102P(x)0.010.960.03
Одновременно бросаются три игральные кости. Пусть X обозначает количество кубиков, выпавших на вершине с тем же количеством точек, что и хотя бы на одном другом кубике. Распределение вероятностей для X равно
x0u3P(x)p1536136
- Найдите недостающее значение u из X .
- Найти недостающую вероятность p .
- Вычислить среднее значение X .
- Вычислить стандартное отклонение X .
Одновременно бросаются две игральные кости. Пусть X обозначают разницу в количестве точек, выпавших на верхних гранях двух игральных костей.
 Так, например, если выпали единица и пятерка, X = 4, а если выпали две шестерки, X = 0.
Так, например, если выпали единица и пятерка, X = 4, а если выпали две шестерки, X = 0.- Постройте распределение вероятностей для X .
- Вычислить среднее μ из X .
- Вычислить стандартное отклонение σ из X .
Честная монета подбрасывается несколько раз до тех пор, пока не выпадет орел или не будет сделано пять подбрасываний, в зависимости от того, что произойдет раньше. Пусть X обозначает количество сделанных бросков.
- Построить распределение вероятностей для X .
- Вычислить среднее μ из X .
- Вычислить стандартное отклонение σ от X .

Производитель получает определенный компонент от поставщика партиями по 100 единиц. Две единицы в каждой партии выбираются случайным образом и тестируются. Если хотя бы одна из единиц неисправна, поставка отклоняется. Предположим, что в поставке 5 дефектных единиц.
- Построить распределение вероятностей для числа X бракованных единиц в такой выборке. (Древовидная диаграмма полезна.)
- Найти вероятность того, что такая посылка будет принята.
Шейлок входит в местное отделение банка в 16:30. каждый день выплаты жалованья, в это время всегда дежурят два кассира. Число X клиентов в банке, которые либо стоят у окна кассира, либо ждут в одной очереди следующего доступного кассира, имеет следующее распределение вероятностей.

x0123P(x)0.1350.1920.2840.230x456P(x)0.1030.0510.005
- Какое количество клиентов Шейлок чаще всего видит в банке, когда входит в него?
- Какое количество клиентов, стоящих в очереди, чаще всего видит Шейлок, когда входит?
- Каково среднее количество клиентов, ожидающих своей очереди в тот момент, когда входит Шейлок?
Владелец предлагаемого театра под открытым небом должен решить, включать ли в него покрытие, которое позволит проводить представления в любых погодных условиях. Основываясь на предполагаемом размере аудитории и погодных условиях, вероятностное распределение дохода X за ночь, если покрытие не установлено, составляет покрытия составляет 410 000 долларов. Владелец построит его, если эти затраты могут быть возмещены за счет увеличения дохода, который дает покрытие в первые десять 9 лет.
 0-ночные сезоны.
0-ночные сезоны.- Рассчитайте средний доход за ночь, если покрытие не установлено.
- Используйте ответ на вопрос (а), чтобы вычислить прогнозируемый общий доход за сезон из 90 ночей, если покрытие не установлено.
- Рассчитайте прогнозируемый общий доход за сезон, когда покрытие установлено. Для этого предположим, что если бы покрытие было на месте, доход каждую ночь сезона был бы таким же, как доход в ясную ночь.
- Используя ответы на вопросы (b) и (c), решите, будут ли возмещены дополнительные затраты на установку покрытия за счет увеличения доходов в течение первых десяти лет. Будет ли владелец устанавливать крышку?
Дополнительные упражнения
Ответы
- нет: сумма вероятностей превышает 1
- нет: отрицательная вероятность
- нет: сумма вероятностей меньше 1
- 0,4
- 0,1
- 0,9
- 79,15
- σ2=1,5275
- σ = 1,2359
- 0,6528
- 0,7153
- мк = 7,8333
- σ2=5,4866
- σ = 2,3424
- 0,79
- 0,60
- мк = 5,8, σ = 1,2570
x0123P(x)1/83/83/81/8
х−199949999P(x)498750001500025000105000
- −0,4
- 17.
 8785
8785
136
xCC−150 000P(x)0,98250,0175
- С-2625
- С ≥ 2625
- С ≥ 2875
х-11Р(х)20381838
- E(X)=-0,0526.
 Во многих ставках игрок терпит средний проигрыш около 5,25 цента на ставку.
Во многих ставках игрок терпит средний проигрыш около 5,25 цента на ставку. - 0,9986
- 43,54
- 1.2046
101.02
x012345P(x)6361036836636436236
- 1,9444
- 1.
 4326
4326
х012Р(х)0.9020.0960.002
- 0,902
- 2523.25
- 227,092,5
- 270 000
- Крышку установит владелец.
статистика | Определение, типы и значение
гистограмма
Посмотреть все СМИ
- Ключевые люди:
- Карл Пирсон
Сэр Рональд Эйлмер Фишер
Молли Оршанский
Ричард фон Мизес
ПК.
 Махаланобис
Махаланобис
- Похожие темы:
- Парадокс Симпсона кластерный анализ регрессия к среднему шкала измерения закон больших чисел
Просмотреть весь связанный контент →
Резюме
Прочтите краткий обзор этой темы
статистика , наука о сборе, анализе, представлении и интерпретации данных. Потребность правительства в данных переписи, а также в информации о различных видах экономической деятельности во многом послужила толчком для развития области статистики на раннем этапе. В настоящее время необходимость превращения больших объемов данных, доступных во многих прикладных областях, в полезную информацию стимулировала как теоретические, так и практические разработки в статистике.
Данные — это факты и цифры, которые собираются, анализируются и обобщаются для представления и интерпретации. Данные могут быть классифицированы как количественные или качественные. Количественные данные измеряют количество или количество чего-либо, а качественные данные предоставляют ярлыки или имена для категорий подобных предметов. Например, предположим, что конкретное исследование интересует такие характеристики, как возраст, пол, семейное положение и годовой доход для выборки из 100 человек. Эти характеристики будут называться переменными исследования, и значения данных для каждой из переменных будут связаны с каждым человеком. Таким образом, значения данных 28, мужчина, холост и 30 000 долларов будут записаны для 28-летнего холостого мужчины с годовым доходом 30 000 долларов. При наличии 100 человек и 4 переменных набор данных будет состоять из 100 × 4 = 400 элементов. В этом примере возраст и годовой доход являются количественными переменными; соответствующие значения данных указывают, сколько лет и сколько денег для каждого человека. Пол и семейное положение являются качественными переменными. Ярлыки «мужской» и «женский» предоставляют качественные данные о поле, а ярлыки «холост», «замужем», «разведен» и «овдовевший» указывают на семейное положение.
Например, предположим, что конкретное исследование интересует такие характеристики, как возраст, пол, семейное положение и годовой доход для выборки из 100 человек. Эти характеристики будут называться переменными исследования, и значения данных для каждой из переменных будут связаны с каждым человеком. Таким образом, значения данных 28, мужчина, холост и 30 000 долларов будут записаны для 28-летнего холостого мужчины с годовым доходом 30 000 долларов. При наличии 100 человек и 4 переменных набор данных будет состоять из 100 × 4 = 400 элементов. В этом примере возраст и годовой доход являются количественными переменными; соответствующие значения данных указывают, сколько лет и сколько денег для каждого человека. Пол и семейное положение являются качественными переменными. Ярлыки «мужской» и «женский» предоставляют качественные данные о поле, а ярлыки «холост», «замужем», «разведен» и «овдовевший» указывают на семейное положение.
Методы выборочного обследования используются для сбора данных обсервационных исследований, а методы планирования эксперимента используются для сбора данных экспериментальных исследований. Область описательной статистики связана в первую очередь с методами представления и интерпретации данных с использованием графиков, таблиц и числовых сводок. Всякий раз, когда статистики используют данные из выборки, т. е. подмножества совокупности, чтобы делать выводы о совокупности, они выполняют статистический вывод. Оценка и проверка гипотезы — это процедуры, используемые для получения статистических выводов. Такие области, как здравоохранение, биология, химия, физика, образование, инженерия, бизнес и экономика, широко используют статистические выводы.
Область описательной статистики связана в первую очередь с методами представления и интерпретации данных с использованием графиков, таблиц и числовых сводок. Всякий раз, когда статистики используют данные из выборки, т. е. подмножества совокупности, чтобы делать выводы о совокупности, они выполняют статистический вывод. Оценка и проверка гипотезы — это процедуры, используемые для получения статистических выводов. Такие области, как здравоохранение, биология, химия, физика, образование, инженерия, бизнес и экономика, широко используют статистические выводы.
Вероятностные методы первоначально были разработаны для анализа азартных игр. Вероятность играет ключевую роль в статистическом выводе; он используется для измерения качества и точности выводов. Многие из методов статистического вывода описаны в этой статье. Некоторые из этих методов используются в основном для исследований с одной переменной, в то время как другие, такие как регрессионный и корреляционный анализ, используются для получения выводов о взаимосвязях между двумя или более переменными.
Викторина по Британике
Дайте определение: математические термины
Вот ваша миссия, если вы решите ее принять: Дайте определение следующим математическим терминам до того, как истечет время.
Описательная статистика представляет собой табличные, графические и числовые сводки данных. Цель описательной статистики — облегчить представление и интерпретацию данных. Большинство статистических материалов, публикуемых в газетах и журналах, носят описательный характер. Одномерные методы описательной статистики используют данные для улучшения понимания одной переменной; многомерные методы сосредоточены на использовании статистики для понимания взаимосвязей между двумя или более переменными. Чтобы проиллюстрировать методы описательной статистики, рассмотрим предыдущий пример, в котором были собраны данные о возрасте, поле, семейном положении и годовом доходе 100 человек.
Табличные методы
Наиболее часто используемая табличная сводка данных для одной переменной представляет собой частотное распределение. Распределение частоты показывает количество значений данных в каждом из нескольких непересекающихся классов. Другая табличная сводка, называемая относительным частотным распределением, показывает долю или процент значений данных в каждом классе. Наиболее распространенная табличная сводка данных для двух переменных представляет собой перекрестную таблицу, аналог частотного распределения с двумя переменными.
Распределение частоты показывает количество значений данных в каждом из нескольких непересекающихся классов. Другая табличная сводка, называемая относительным частотным распределением, показывает долю или процент значений данных в каждом классе. Наиболее распространенная табличная сводка данных для двух переменных представляет собой перекрестную таблицу, аналог частотного распределения с двумя переменными.
Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас
Для качественной переменной частотное распределение показывает количество значений данных в каждой качественной категории. Например, переменная «пол» имеет две категории: «мужской» и «женский». Таким образом, частотное распределение по полу будет иметь два непересекающихся класса, чтобы показать количество мужчин и женщин. Распределение относительной частоты для этой переменной покажет долю лиц мужского пола и долю лиц женского пола.
Построение частотного распределения для количественной переменной требует большей осторожности при определении классов и точек разделения между соседними классами. Например, если возрастные данные в приведенном выше примере находятся в диапазоне от 22 до 78 лет, можно использовать следующие шесть непересекающихся классов: 20–29, 30–39, 40–49, 50–59, 60–69 и 70–70 лет. 79. Распределение частоты покажет количество значений данных в каждом из этих классов, а распределение относительной частоты покажет долю значений данных в каждом из этих классов.
Например, если возрастные данные в приведенном выше примере находятся в диапазоне от 22 до 78 лет, можно использовать следующие шесть непересекающихся классов: 20–29, 30–39, 40–49, 50–59, 60–69 и 70–70 лет. 79. Распределение частоты покажет количество значений данных в каждом из этих классов, а распределение относительной частоты покажет долю значений данных в каждом из этих классов.
Перекрестная таблица представляет собой двустороннюю таблицу, в которой строки таблицы представляют классы одной переменной, а столбцы таблицы представляют классы другой переменной. Чтобы построить перекрестную таблицу с использованием переменных «пол» и «возраст», пол можно показать в двух строках, мужской и женский, а возраст можно показать в шести столбцах, соответствующих возрастным классам 20–29, 30–39, 40–49, 50 лет. –59, 60–69 и 70–79. Запись в каждой ячейке таблицы будет указывать количество значений данных с полом, указанным в заголовке строки, и возрастом, указанным в заголовке столбца. Такая перекрестная таблица может быть полезна для понимания взаимосвязи между полом и возрастом.
Для описания данных доступно несколько графических методов. Гистограмма — это графическое устройство для изображения качественных данных, которые были суммированы в частотном распределении. Метки категорий качественной переменной показаны на горизонтальной оси графика. Полоса над каждой меткой построена таким образом, что высота каждой полосы пропорциональна количеству значений данных в категории. Гистограмма семейного положения для 100 человек в приведенном выше примере показана на рисунке 1. На графике есть 4 столбца, по одному для каждого класса. Круговая диаграмма — еще одно графическое средство для обобщения качественных данных. Размер каждого фрагмента круговой диаграммы пропорционален количеству значений данных в соответствующем классе. Круговая диаграмма семейного положения 100 человек показана на рисунке 2.
Гистограмма является наиболее распространенным графическим представлением количественных данных, которые были обобщены в частотном распределении. Значения количественной переменной показаны на горизонтальной оси. Прямоугольник рисуется над каждым классом таким образом, что основание прямоугольника равно ширине интервала класса, а его высота пропорциональна количеству значений данных в классе.
Прямоугольник рисуется над каждым классом таким образом, что основание прямоугольника равно ширине интервала класса, а его высота пропорциональна количеству значений данных в классе.
2.1 Случайные величины и распределения вероятностей
Эта книга находится в Открыть обзор . Мы хотим, чтобы ваши отзывы сделали книгу лучше для вас и других учащихся. Вы можете аннотировать некоторый текст, выделив его курсором, а затем щелкнув во всплывающем меню. Вы также можете увидеть аннотации других: нажмите в правом верхнем углу страницы
Кратко остановимся на некоторых основных понятиях теории вероятностей.
- Взаимоисключающие результаты случайного процесса называются исходами . «Взаимоисключающий» означает, что можно наблюдать только один из возможных результатов.
- Мы называем вероятностью исхода пропорцию того, что исход произойдет в долгосрочной перспективе, то есть если эксперимент будет повторяться много раз.

- Набор всех возможных исходов случайной величины называется пространством выборки .
- Событие является подмножеством выборочного пространства и состоит из одного или нескольких результатов.
Эти идеи объединены в концепции случайной величины , которая представляет собой числовую сводку случайных результатов. Случайных величин может быть дискретный или непрерывный .
- Дискретные случайные величины имеют дискретные результаты, например, \(0\) и \(1\).
- Непрерывная случайная величина может принимать континуум возможных значений.
Вероятностные распределения дискретных случайных величин
Типичным примером дискретной случайной величины \(D\) является результат игры в кости
roll: с точки зрения случайного эксперимента это не что иное, как случайный выбор
выборка размера \(1\) из набора чисел, которые являются взаимоисключающими результатами.
Здесь выборочное пространство равно \(\{1,2,3,4,5,6\}\), и мы можем думать о многих различных
событий, например, «наблюдаемый результат лежит между \(2\) и \(5\)».
Базовой функцией для получения случайных выборок из заданного набора элементов является функция sample(), см. ?sample . Мы можем использовать его для имитации случайного результата броска костей. Давайте бросим кости!
образец (1:6, 1) #> [1] 3
Распределение вероятностей дискретной случайной величины представляет собой список всех возможных значений переменной и их вероятностей, сумма которых равна \(1\). Кумулятивная функция распределения вероятностей дает вероятность того, что случайная величина меньше или равна определенному значению.
Для броска костей распределение вероятностей и кумулятивное распределение вероятностей приведены в таблице 2.1.
| Исход | 1 | 2 | 3 | 4 | 5 | 6 |
| Вероятность | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
| Кумулятивная вероятность | 1/6 | 2/6 | 3/6 | 4/6 | 5/6 | 1 |
Мы можем легко построить обе функции, используя R. Поскольку вероятность равна \(1/6\) для каждого результата, мы устанавливаем векторную вероятность, используя функцию rep(), которая повторяет заданное значение заданное количество раз.
Поскольку вероятность равна \(1/6\) для каждого результата, мы устанавливаем векторную вероятность, используя функцию rep(), которая повторяет заданное значение заданное количество раз.
# сгенерировать вектор вероятностей
вероятность <- rep (1/6, 6)
# построить вероятности
сюжет (вероятность,
xlab = "результаты",
main = "Распределение вероятностей") Для кумулятивного распределения вероятностей нам нужны кумулятивные вероятности, т. е. нам нужны кумулятивные суммы векторных вероятностей. Эти суммы можно вычислить с помощью cumsum().
# сгенерировать вектор кумулятивных вероятностей
cum_probability <- cumsum(вероятность)
# построить вероятности
сюжет (cum_probability,
xlab = "результаты",
main = "Распределение кумулятивных вероятностей") Испытания Бернулли
Набор элементов, из которых sample() извлекает результаты, не обязательно должен состоять из чисел
Только. С тем же успехом мы могли бы имитировать подбрасывание монеты с исходами \(H\) (орел) и \(T\)
(хвосты).
образец (с ("Н", "Т"), 1)
#> [1] "H" Результатом одного подбрасывания монеты является распределенная Бернулли случайная величина, т. е. переменная с двумя возможными различными исходами.
Представьте, что вы собираетесь подбросить монету \(10\) раз подряд и задаетесь вопросом, насколько это вероятно. состоит в том, чтобы получить \(5\) орлов. Это типичный пример того, что мы называем экспериментом Бернулли , поскольку он состоит из \(n=10\) испытаний Бернулли, которые независимы друг от друга, и нас интересует вероятность наблюдения \(k=5\) успехов \(H\), которые происходят с вероятностью \(p=0,5\) (при условии честной монеты) в каждом испытании. Обратите внимание, что порядок результатов здесь не имеет значения. 9{n-k}\]
с \(\begin{pmatrix}n\\ k \end{pmatrix}\) биномиальным коэффициентом.
В R мы можем решать задачи, подобные указанной выше, с помощью функции dbinom(), которая вычисляет \(P(k\vert n, p)\) вероятность биномиального распределения при заданных параметрах x (\( к\))
size (\(n\)) и prob (\(p\)), см.
?dbinom . Вычислим \(P(k=5\vert n = 10, p = 0,5)\) (мы запишем это кратко как \(P(k=5)\).)
dbinom(x = 5,
размер = 10,
вероятность = 0,5)
#> [1] 0,2460938 Мы заключаем, что \(P(k=5)\) вероятность увидеть решку \(k=5\) раз при подбрасывании правильной монеты \(n=10\) раз примерно \(24,6\% \).
Теперь предположим, что нас интересует \(P(4 \leq k \leq 7)\), т. е. вероятность наблюдая \(4\), \(5\), \(6\) или \(7\) успехов для \(B(10, 0,5)\). Это можно вычислить, предоставив вектор в качестве аргумента x в нашем вызове dbinom() и просуммировав с помощью sum().
# вычислить P(4 <= k <= 7) с помощью 'dbinom()' сумма (dbinom (x = 4: 7, размер = 10, вероятность = 0,5)) #> [1] 0,7734375
Альтернативный подход заключается в использовании pbinom(), функции распределения биномиального распределения для вычисления \[P(4 \leq k \leq 7) = P(k \leq 7) - P(k\leq3 ).\ ]
# вычислить P(4 <= k <= 7) с помощью 'pbinom()' pbinom (размер = 10, вероятность = 0,5, q = 7) - pbinom (размер = 10, вероятность = 0,5, q = 3) #> [1] 0.7734375
Вероятностное распределение дискретной случайной величины есть не что иное, как список всех возможных результатов, которые могут произойти, и их соответствующих вероятностей. В примере с подбрасыванием монеты у нас есть \(11\) возможных исходов для \(k\).
# установить вектор возможных исходов к <- 0:10 к #> [1] 0 1 2 3 4 5 6 7 8 9 10
Чтобы визуализировать функцию распределения вероятностей \(k\), мы можем сделать следующее:
# присвоить вероятности
вероятность <- dbinom(x = k,
размер = 10,
вероятность = 0,5)
# построить результаты в зависимости от их вероятностей
график (х = к,
у = вероятность,
main = "Функция распределения вероятностей") Аналогичным образом мы можем построить кумулятивную функцию распределения \(k\) по формуле выполнение следующего фрагмента кода:
# вычисление совокупных вероятностей
prob <- pbinom(q = k,
размер = 10,
вероятность = 0,5)
# построить кумулятивные вероятности
график (х = к,
у = вероятность,
main = "Функция кумулятивного распределения") Ожидаемое значение, среднее значение и дисперсия
Ожидаемое значение случайной величины, грубо говоря, представляет собой долгосрочное среднее значение ее результатов при большом количестве повторных испытаний. 6 d_i = 3,5 \]
6 d_i = 3,5 \]
\(E(D)\) - это просто среднее арифметическое натуральных чисел от \(1\) до \(6\), поскольку все веса \(p_i\) равны \(1/6\). Это можно легко вычислить с помощью функции mean(), которая вычисляет среднее арифметическое числового вектора.
# вычислить среднее натуральных чисел от 1 до 6 среднее (1:6) #> [1] 3.5
Примером выборки с заменой является бросание игральной кости три раза подряд.
# набор семян для воспроизводимости set.seed(1) # бросаем кубик три раза подряд образец (1: 6, 3, заменить = T) #> [1] 1 4 1
Обратите внимание, что каждый вызов sample(1:6, 3, replace = T) дает другой результат, так как мы рисуем с заменой случайным образом. Чтобы вы могли воспроизвести результаты вычислений со случайными числами, мы будем использовать set.seed() для установки генератора случайных чисел R в определенное состояние. Вы должны убедиться, что это действительно работает: установите начальное число в сеансе R на 1 и убедитесь, что вы получаете те же три случайных числа!
Последовательности случайных чисел, сгенерированные R, являются псевдослучайными числами, т. е. они не являются «настоящими» случайными, но аппроксимируют свойства последовательностей случайных чисел. Поскольку это приближение достаточно хорошо для наших целей, в этой книге мы будем называть псевдослучайные числа случайными числами.
е. они не являются «настоящими» случайными, но аппроксимируют свойства последовательностей случайных чисел. Поскольку это приближение достаточно хорошо для наших целей, в этой книге мы будем называть псевдослучайные числа случайными числами.
Как правило, последовательности случайных чисел генерируются функциями, называемыми «генераторами псевдослучайных чисел» (PRNG). PRNG в R работает, выполняя некоторую операцию над детерминированным значением. Как правило, это значение является предыдущим числом, сгенерированным PRNG. Однако при первом использовании PRNG предыдущего значения нет. «Семя» — это первое значение последовательности чисел — оно инициализирует последовательность. Каждое начальное значение будет соответствовать другой последовательности значений. В R начальное число можно установить с помощью set.seed().
Нам удобно:
Если мы предоставим одно и то же начальное число дважды, мы получим одну и ту же последовательность чисел дважды. Таким образом, установка начального числа перед выполнением кода R, который использует случайные числа, делает результат воспроизводимым!
Таким образом, установка начального числа перед выполнением кода R, который использует случайные числа, делает результат воспроизводимым!
Конечно, мы могли бы также рассмотреть гораздо большее количество испытаний, скажем, \(10000\). При этом было бы бессмысленно просто выводить результаты на консоль: по умолчанию R отображает до \(1000\) записей больших векторов и опускает остаток (попробуйте). Цифры на глаз мало что дают. Вместо этого давайте вычислим среднее значение выборки результатов, используя mean(), и посмотрим, близок ли результат к ожидаемому значению \(E(D)=3,5\).
# установить семена для воспроизводимости
set.seed(1)
# вычислить выборочное среднее из 10000 бросков игральных костей
среднее (выборка (1: 6,
10000,
заменить = Т))
#> [1] 3.5138 Мы обнаружили, что выборочное среднее довольно близко к ожидаемому значению. Этот результат будет обсуждаться в главе 2.2 более подробно.
Другими часто встречающимися показателями являются дисперсия и стандартное отклонение. Оба являются мерами дисперсии случайной величины.
Оба являются мерами дисперсии случайной величины.
Ключевая концепция 2.2 92\) как вычислено var().
вар(1:6) #> [1] 3.5
Выборочная дисперсия, вычисленная функцией var(), является оценкой дисперсии генеральной совокупности. Вы можете проверить это, используя виджет ниже.
Вероятностные распределения непрерывных случайных величин
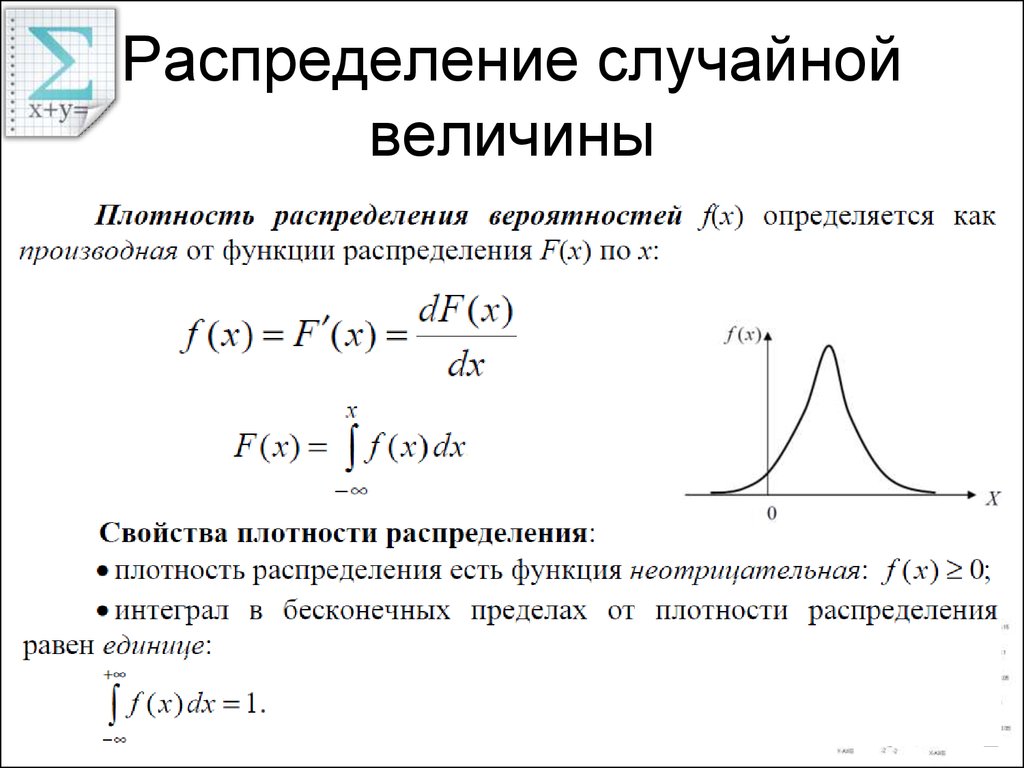
Поскольку непрерывная случайная величина принимает континуум возможных значений, мы не может использовать концепцию распределения вероятностей, используемую для дискретных случайных переменные. Вместо этого распределение вероятностей непрерывной случайной величины резюмируется его Функция плотности вероятности (PDF) .
Кумулятивная функция распределения вероятностей (CDF) для непрерывной случайной величины определяется так же, как и в дискретном случае. Следовательно, CDF непрерывных случайных величин устанавливает вероятность того, что случайная величина меньше или равна определенному значению.
Для полноты картины мы представляем пересмотренные Ключевые понятия 2.1 и 2.2 для непрерывного случая.
Ключевая концепция 2.3
Вероятности, ожидаемое значение и дисперсия непрерывной случайной величины 9{\ бесконечность} \\ =& -3 \left( \lim_{t \rightarrow \infty} \frac{1}{t} - 1 \right) \\ =& 3 \end{align}\]
Итак, мы показали, что площадь под кривой равна единице, что математическое ожидание равно \(E(X)=\frac{3}{2}\), и мы обнаружили, что дисперсия равна \(\text{Var}(X) = \frac{3}{4}\). Однако это было утомительно, и, как мы увидим, аналитический подход неприменим для некоторых ФПВ, например, если интегралы не имеют решений в замкнутой форме.
К счастью, R также позволяет нам легко найти результаты, полученные выше. Инструмент, который мы используем для этого, — функция интегрировать(). Во-первых, мы должны определить функции, для которых мы хотим вычислить интегралы, как R-функции, то есть PDF \(f_X(x)\), а также выражения \(x\cdot f_X(x)\) и \(x ^2\cdot f_X(x)\). 92 * f(x)
92 * f(x)
Далее, мы используем интегрировать() и устанавливаем нижний и верхний пределы интегрирования равными \(1\) и \(\infty\), используя аргументы нижний и верхний. По умолчанию интегрировать() выводит результат вместе с оценкой ошибки аппроксимации на консоль. Однако результат не является числовым значением, с которым можно легко произвести дальнейшие вычисления. Чтобы получить только числовое значение интеграла, нам нужно использовать оператор $ вместе со значением. Оператор $ используется для извлечения элементов по имени из объекта типа список. 92 ВарХ #> [1] 0.75
Несмотря на большое разнообразие дистрибутивов, наиболее часто в эконометрике встречаются нормальные, хи-квадрат, Стьюдента \(t\) и \(F\) дистрибутивы. Поэтому мы обсудим некоторые основные функции R, которые позволяют расчеты, включающие плотности, вероятности и квантили этих дистрибутивы.
Каждое распределение вероятностей, которое обрабатывает R, имеет четыре основные функции, имена которых состоят из префикса, за которым следует корневое имя. В качестве примера возьмем нормальное распределение. Корневое имя всех четырех функций, связанных с нормальным распределением, — норма. Четыре префикса
В качестве примера возьмем нормальное распределение. Корневое имя всех четырех функций, связанных с нормальным распределением, — норма. Четыре префикса
- d для «плотности» - функция вероятности / функция плотности вероятности
- p для «вероятности» - кумулятивная функция распределения
- q for «quantile» - функция квантиля (обратная кумулятивная функция распределения)
- р за «рандом» - генератор случайных чисел
Таким образом, для нормального распределения у нас есть функции R dnorm(), pnorm(), qnorm() и rnorm().
Нормальное распределение
Возможно, наиболее важным рассматриваемым здесь распределением вероятностей является нормальное
распределение. Не в последнюю очередь это связано с особой ролью стандартного нормального распределения и центральной предельной теоремы, которую мы вскоре рассмотрим. Нормальные распределения симметричны и имеют колоколообразную форму. Нормальное распределение характеризуется своим средним значением \(\mu\) и стандартным отклонением \(\sigma\), кратко выражаемыми формулой
\(\mathcal{N}(\mu,\sigma^2)\). Нормальное распределение имеет PDF 92)}.
\end{align}\]
Нормальное распределение имеет PDF 92)}.
\end{align}\]
Для стандартного нормального распределения мы имеем \(\mu=0\) и \(\sigma=1\). Стандартные нормальные переменные часто обозначаются \(Z\). Обычно стандартный нормальный PDF обозначается \(\phi\), а стандартный нормальный CDF обозначается \(\Phi\). Следовательно, \[ \phi(c) = \Phi'(c) \ \ , \ \ \Phi(c) = P(Z \leq c) \ \ , \ \ Z \sim \mathcal{N}(0,1) .\] Обратите внимание, что обозначение X \(\sim\) Y читается как «X распространяется как Y». В R мы можем удобно получать плотности нормальных распределений, используя функцию dnorm(). Давайте нарисуем график стандартной функции нормальной плотности, используя функцию curve() вместе с dnorm().
# нарисовать график N(0,1) PDF
кривая (dnorm (x),
хлим = с(-3,5, 3,5),
ylab = "Плотность",
main = "Стандартная нормальная функция плотности") Мы можем получить плотность в различных положениях, передав вектор в dnorm().
# плотность вычислений при x=-1,96, x=0 и x=1,96 dnorm(x = c(-1,96, 0, 1,96)) #> [1] 0.05844094 0.39894228 0.05844094
Подобно PDF, мы можем построить стандартный нормальный CDF, используя функцию curve(). Мы могли бы использовать для этого dnorm(), но гораздо удобнее полагаться на pnorm().
# построить стандартный нормальный CDF
кривая (pnorm (x),
хлим = с(-3,5, 3,5),
ylab = "Вероятность",
main = «Стандартная нормальная кумулятивная функция распределения») Мы также можем использовать R для расчета вероятности событий, связанных со стандартной нормальной переменной.
Допустим, нас интересует \(P(Z \leq 1.337)\). Для некоторой непрерывной случайной величины \(Z\) на \([-\infty,\infty]\) с плотностью \(g(x)\) нам пришлось бы определить \(G(x)\), анти- производная от \(g(x)\), так что 9{1,337} г(х) \mathrm{d}х. \]
Если \(Z \sim \mathcal{N}(0,1)\), то \(g(x)=\phi(x)\). Приведенный выше интеграл не имеет аналитического решения. К счастью, R предлагает хорошие приближения. Первый подход использует функцию интегрировать(), которая позволяет решать задачи одномерного интегрирования численным методом. Для этого мы сначала определяем функцию, для которой мы хотим вычислить интеграл, как R-функцию f. В нашем примере f — стандартная нормальная функция плотности и, следовательно, принимает один аргумент x. Следуя определению \(\phi(x)\), мы определяем f как 92)
}
Для этого мы сначала определяем функцию, для которой мы хотим вычислить интеграл, как R-функцию f. В нашем примере f — стандартная нормальная функция плотности и, следовательно, принимает один аргумент x. Следуя определению \(\phi(x)\), мы определяем f как 92)
}
Давайте проверим, вычисляет ли эта функция стандартные нормальные плотности, передавая вектор.
# определить вектор вещественных чисел кванты <- c(-1,96, 0, 1,96) # плотность вычислений f (кванты) #> [1] 0,05844094 0,39894228 0,05844094 # сравнить с результатами, полученными с помощью 'dnorm()' f(кванты) == dnorm(кванты) #> [1] TRUE TRUE TRUE
Результаты, полученные с помощью f(), действительно эквивалентны результатам, полученным с помощью dnorm().
Далее мы вызываем интегрировать() для f() и указываем аргументы нижний и верхний, нижний и верхний пределы интегрирования.
# интегрировать f()
интегрировать (f,
нижний = -Inf,
верхний = 1,337)
#> 0,87 с абсолютной ошибкой < 1,7e-07
Мы находим, что вероятность наблюдения \(Z \leq 1,337\) составляет примерно \(90,94\%\).
Второй и гораздо более удобный способ — использовать функцию pnorm(), стандартную функцию нормального кумулятивного распределения.
# вычислить вероятность с помощью pnorm() пнорм(1.337) #> [1] 0.87
Результат соответствует результату подхода, использующего интеграцию().
Обсудим еще несколько примеров:
Общеизвестный результат состоит в том, что \(95\%\) вероятностная масса стандартной нормали лежит в интервале \([-1,96, 1,96]\), то есть в расстояние около \(2\) стандартных отклонений от среднего. Мы можем легко подтвердить это, вычислив \[ P(-1,96 \leq Z \leq 1,96) = 1-2\times P(Z \leq -1,96) \] из-за симметрии стандартной нормальной PDF. Благодаря R мы можем отказаться от таблицы стандартной нормальной CDF, найденной во многих других учебниках, и вместо этого решить ее быстро, используя pnorm(). 92)\] Тогда \(Y\) стандартизируется вычитанием его среднего значения и
деление на его стандартное отклонение: \[ Z = \frac{Y -\mu}{\sigma} \] Пусть \(c_1\)
и \(c_2\) обозначают два числа, где \(c_1 < c_2\) и далее \(d_1 = (c_1 - \mu)/\sigma\) и \(d_2 = (c_2 - \mu)/\sigma\) . Затем
Затем
\[\begin{align*} P(Y \leq c_2) =& \, P(Z \leq d_2) = \Phi(d_2), \\ P(Y \geq c_1) =& \, P(Z \geq d_1) = 1 - \Phi(d_1), \\ P(c_1 \leq Y \leq c_2) =& \, P(d_1 \leq Z \leq d_2) = \Phi(d_2) - \Phi(d_1). \end{выравнивание*}\]
Теперь рассмотрим случайную величину \(Y\) с \(Y \sim \mathcal{N}(5, 25)\). Функции R, обрабатывающие нормальное распределение, могут выполнять стандартизацию. Если нас интересует \(P(3 \leq Y \leq 4)\), мы можем использовать pnorm() и настроить среднее значение и/или стандартное отклонение, которые отклоняются от \(\mu=0\) и \( \sigma = 1\), указав соответственно аргументы mean и sd. Внимание : аргумент sd требует стандартного отклонения, а не дисперсии!
pnorm(4, среднее = 5, sd = 5) - pnorm(3, среднее = 5, sd = 5)
#> [1] 0,07616203 92 \справа] \справа\}.
\end{split} \tag{2.1}
\end{align}\] Уравнение (2.1) содержит двумерную нормальную PDF. Довольно сложно понять это сложное выражение. Вместо этого рассмотрим частный случай, когда \(X\) и \(Y\) являются некоррелированными стандартными нормальными случайными величинами с плотностями \(f_X(x)\) и \(f_Y(y)\) с совместным нормальным распределением. Тогда у нас есть параметры \(\sigma_X = \sigma_Y = 1\), \(\mu_X=\mu_Y=0\) (из-за маргинальной стандартной нормальности) и \(\rho_{XY}=0\) (из-за независимость). Совместная плотность \(X\) и \(Y\) тогда становится равной 92 \right] \right\}, \tag{2.2} \]
Тогда у нас есть параметры \(\sigma_X = \sigma_Y = 1\), \(\mu_X=\mu_Y=0\) (из-за маргинальной стандартной нормальности) и \(\rho_{XY}=0\) (из-за независимость). Совместная плотность \(X\) и \(Y\) тогда становится равной 92 \right] \right\}, \tag{2.2} \]
PDF двумерного стандартного нормального распределения. Виджет ниже предоставляет интерактивный трехмерный график (2.2).
Наводя курсор на график, можно увидеть, что плотность вращательно-инвариантна, т. е. плотность в точке \((a, b)\) зависит исключительно от расстояния \((a, b)\) до происхождение: геометрически области равной плотности представляют собой края концентрических окружностей в плоскости XY с центром в точке \((\mu_X = 0, \mu_Y = 0)\).
Нормальное распределение имеет некоторые замечательные характеристики. Например, для двух совместно нормально распределенных переменных \(X\) и \(Y\) условная функция ожидания является линейной: можно показать, что \[ E(Y\vert X) = E(Y) + \rho \ frac{\sigma_Y}{\sigma_X} (X - E(X)). \] Интерактивный виджет ниже показывает стандартные двумерные нормально распределенные выборочные данные вместе с функцией условного ожидания \(E(Y\vert X)\) и предельной плотностью \(X\) и \(Y\). Все элементы корректируются соответствующим образом по мере изменения параметров. 92_3\) случайная величина на одном графике. Это достигается установкой аргумента add = TRUE во втором вызове кривой(). Далее мы настраиваем пределы обеих осей с помощью xlim и ylim и выбираем разные цвета, чтобы обе функции были лучше различимы. Сюжет завершается добавлением легенды с помощью legend().
\] Интерактивный виджет ниже показывает стандартные двумерные нормально распределенные выборочные данные вместе с функцией условного ожидания \(E(Y\vert X)\) и предельной плотностью \(X\) и \(Y\). Все элементы корректируются соответствующим образом по мере изменения параметров. 92_3\) случайная величина на одном графике. Это достигается установкой аргумента add = TRUE во втором вызове кривой(). Далее мы настраиваем пределы обеих осей с помощью xlim и ylim и выбираем разные цвета, чтобы обе функции были лучше различимы. Сюжет завершается добавлением легенды с помощью legend().
# построить PDF
кривая (dchisq (x, df = 3),
хлим = с(0, 10),
улим = с(0, 1),
столбец = "синий",
илаб = "",
main = "PDF и CDF распределения хи-квадрат, M = 3")
# добавляем CDF на график
кривая (pchisq (x, df = 3),
хлим = с(0, 10),
добавить = ИСТИНА,
столбец = "красный")
# добавить легенду к сюжету
легенда("слева вверху",
с("PDF", "CDF"),
col = c ("синий", "красный"),
лти = с(1, 1)) 92_M\) распределенная случайная величина всегда положительна, поддержка связанных PDF и CDF равна \(\mathbb{R}_{\geq0}\). 2\) на интервале \([0,15]\) с помощью кривой(). На следующем шаге мы перебираем степени свободы \(M=2,...,7\) и добавляем на график кривую плотности для каждого \(M\). Мы также настраиваем цвет линии для каждой итерации цикла, устанавливая col = M. Наконец, мы добавляем легенду, отображающую степени свободы и соответствующие цвета.
2\) на интервале \([0,15]\) с помощью кривой(). На следующем шаге мы перебираем степени свободы \(M=2,...,7\) и добавляем на график кривую плотности для каждого \(M\). Мы также настраиваем цвет линии для каждой итерации цикла, устанавливая col = M. Наконец, мы добавляем легенду, отображающую степени свободы и соответствующие цвета. # построить плотность для M=1
кривая (dchisq (x, df = 1),
хлим = с(0, 15),
xlab = "х",
ylab = "Плотность",
main = "Распределенные случайные величины хи-квадрат")
# добавить плотности для M=2,...,7 на график, используя цикл for()
для (М в 2:7) {
кривая (dchisq (x, df = M),
хлим = с(0, 15),
добавить = Т,
столбец = М)
}
# добавить легенду
легенда("вверху",
как.символ(1:7),
цвет = 1:7,
лты = 1,
title = "DF") 92_M\), форма распределения \(t_M\) зависит от \(M\). Распределения \(t\) симметричны, колоколообразны и похожи на нормальное распределение, особенно когда \(M\) велико. Это не случайно: при достаточно большом \(M\) распределение \(t_M\) можно аппроксимировать стандартным нормальным распределением. Это приближение работает достаточно хорошо для \(M\geq 30\). Как мы проиллюстрируем позже с помощью небольшого исследования моделирования, распределение \(t_{\infty}\) равно стандартное нормальное распределение.
Это не случайно: при достаточно большом \(M\) распределение \(t_M\) можно аппроксимировать стандартным нормальным распределением. Это приближение работает достаточно хорошо для \(M\geq 30\). Как мы проиллюстрируем позже с помощью небольшого исследования моделирования, распределение \(t_{\infty}\) равно стандартное нормальное распределение. Распределенная случайная величина \(t_M\) \(X\) имеет математическое ожидание, если \(M>1\), и дисперсию, если \(M>2\).
\[\begin{выравнивание}
Е(Х)=&0, \М>1\\
\text{Var}(X) =& \frac{M}{M-2}, \ M>2
\end{align}\]
Построим несколько распределений \(t\) с разными \(M\) и сравним их со стандартным нормальным распределением.
# построить стандартную нормальную плотность
кривая (dnorm (x),
хлим = с(-4, 4),
xlab = "х",
лты = 2,
ylab = "Плотность",
main = "Плотности распределений t")
# построить плотность t для M=2
кривая (dt (x, df = 2),
хлим = с(-4, 4),
столбец = 2,
добавить = Т)
# построить плотность t для M=4
кривая (dt (x, df = 4),
хлим = с(-4, 4),
столбец = 3,
добавить = Т)
# построить плотность t для M=25
кривая (dt (x, df = 25),
хлим = с(-4, 4),
столбец = 4,
добавить = Т)
# добавить легенду
легенда("вверху",
с("N(0, 1)", "М=2", "М=4", "М=25"),
цвет = 1:4,
лти = с(2, 1, 1, 1)) График иллюстрирует сказанное в предыдущем абзаце: по мере увеличения степеней свободы форма распределения \(t\) приближается к форме стандартной нормальной колоколообразной кривой. 2\) распределенных случайных величин, которые делятся своими степенями свободы \(M\) и \(n\ ). Количество 92_н \]
следует распределению \(F\) со степенями свободы в числителе \(M\) и степенями свободы в знаменателе \(n\), обозначаемыми \(F_{M,n}\). Распределение было впервые получено Джорджем Снедекором, но названо в честь сэра Рональда Фишера.
2\) распределенных случайных величин, которые делятся своими степенями свободы \(M\) и \(n\ ). Количество 92_н \]
следует распределению \(F\) со степенями свободы в числителе \(M\) и степенями свободы в знаменателе \(n\), обозначаемыми \(F_{M,n}\). Распределение было впервые получено Джорджем Снедекором, но названо в честь сэра Рональда Фишера.
По определению поддержка как PDF, так и CDF распределенной случайной величины \(F_{M,n}\) равна \(\mathbb{R}_{\geq0}\).
Допустим, у нас есть \(F\) распределенная случайная величина \(Y\) со степенями свободы в числителе \(3\) и степенями свободы в знаменателе \(14\) и нас интересует \(P(Y \geq 2)\). Это можно вычислить с помощью функции pf(). Установив для аргумента lower.tail значение FALSE, мы гарантируем, что R вычислит \(1-P(Y \leq 2)\), т. е. вероятностную массу в конце справа от \(2\).
pf(2, df1 = 3, df2 = 14, нижний.хвост = F)
#> [1] 0.1603538
Мы можем визуализировать эту вероятность, нарисовав линейный график соответствующей плотности и добавив заливку цветом с помощью polygon().

 Каждое из этих чисел соответствует событию в выборочном пространстве S={hh,ht,th,tt} равновероятных результатов для этого эксперимента: X = от 0 до {tt}, X = от 1 до {ht,th} и X = от 2 до {hh}. Вероятность каждого из этих событий и, следовательно, соответствующего значения X можно найти, просто посчитав, чтобы получить
Каждое из этих чисел соответствует событию в выборочном пространстве S={hh,ht,th,tt} равновероятных результатов для этого эксперимента: X = от 0 до {tt}, X = от 1 до {ht,th} и X = от 2 до {hh}. Вероятность каждого из этих событий и, следовательно, соответствующего значения X можно найти, просто посчитав, чтобы получить Такой билет один, поэтому P (299) = 0,001. Применение того же принципа «доход минус расход» к обладателям второго и третьего приза и к 997 проигравшим билетам дает распределение вероятностей:
Такой билет один, поэтому P (299) = 0,001. Применение того же принципа «доход минус расход» к обладателям второго и третьего приза и к 997 проигравшим билетам дает распределение вероятностей:
 Объясните полностью.
Объясните полностью. 3250.4060.164
3250.4060.164


 Интерпретируйте его значение.
Интерпретируйте его значение. Найдите среднее количество гвоздей на фунт.
Найдите среднее количество гвоздей на фунт. Так, например, если выпали единица и пятерка, X = 4, а если выпали две шестерки, X = 0.
Так, например, если выпали единица и пятерка, X = 4, а если выпали две шестерки, X = 0.

 0-ночные сезоны.
0-ночные сезоны. 8785
8785 Во многих ставках игрок терпит средний проигрыш около 5,25 цента на ставку.
Во многих ставках игрок терпит средний проигрыш около 5,25 цента на ставку. 4326
4326 Махаланобис
Махаланобис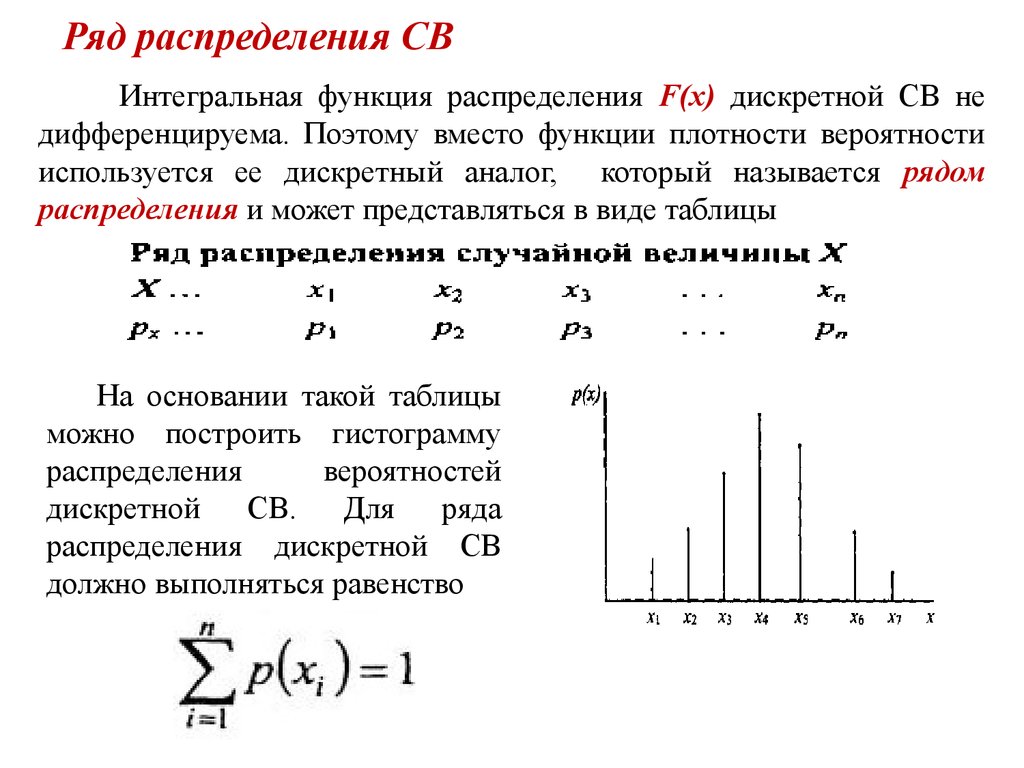
 7734375
7734375