Формула по которой можно найти площадь параллелограмма. Как найти площадь параллелограмма, треугольника, трапеции
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
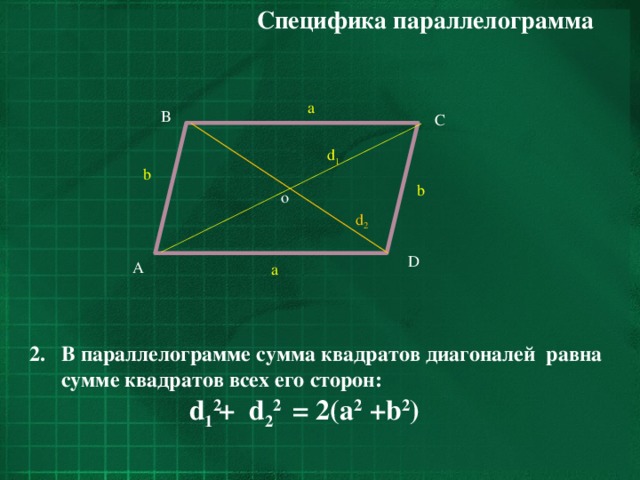
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.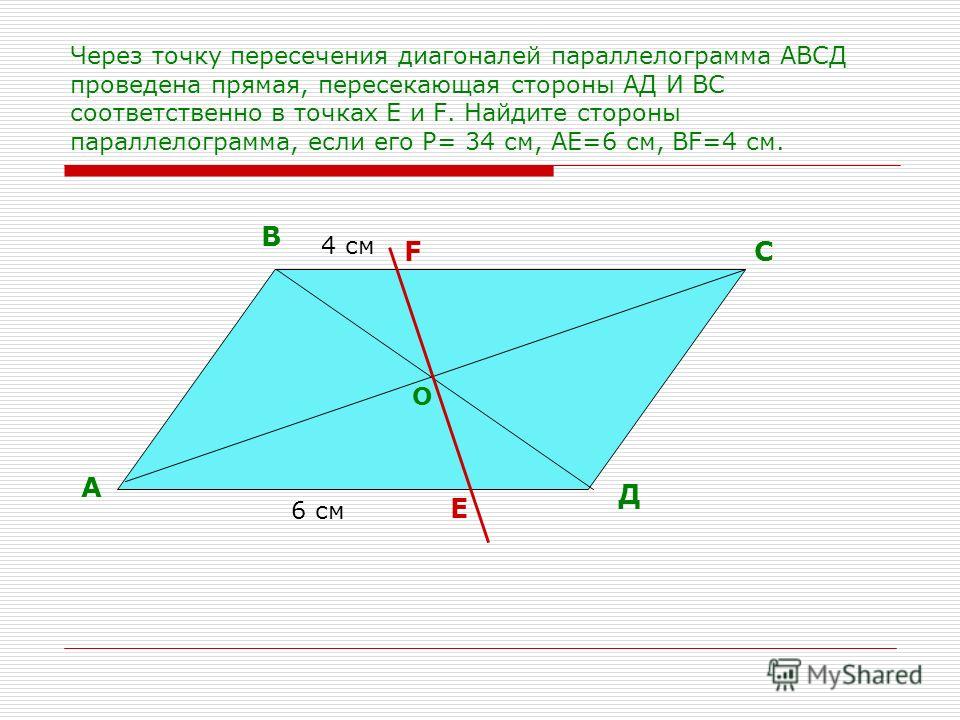
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
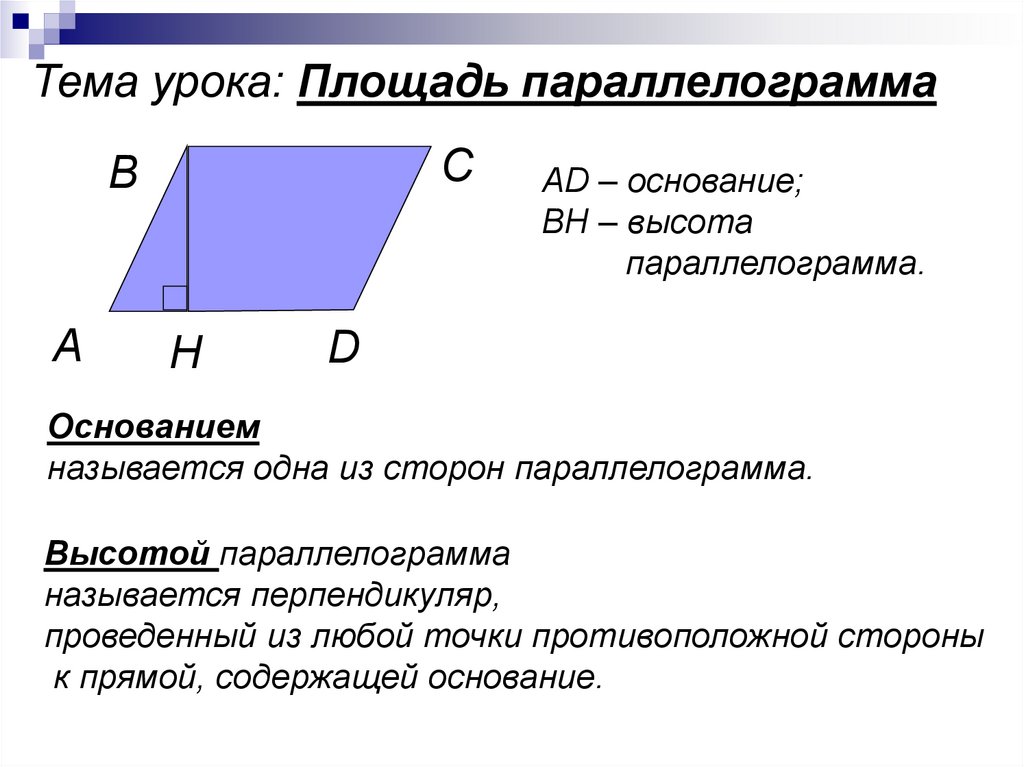
Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.
Площадь параллелограмма обозначается как (S).
Формулы нахождения площади параллелограмма
S=a*h , где а – это основание, h – это высота, которая проведена к основанию.
S=a*b*sinα , где a и b – это основания, а α — угол между основаниями а и b.
S =p*r , где р – это полупериметр, r – это радиус окружности, которая вписана в параллелограмм.
Площадь параллелограмма, который образован векторами a и b равна модулю произведения заданных векторов, а именно:
Рассмотрим пример №1: Дан параллелограмм, сторона которого равна 7 см, а высота 3 см. Как найти площадь параллелограмма, формула для решения нам необходима.
Таким образом, S= 7×3. S=21. Ответ: 21 см 2 .
Рассмотрим пример №2: Даны основания 6 и 7 см, а также дан угол между основаниями 60 градусов. Как найти площадь параллелограмма? Формула, используемая для решения:
Таким образом, сначала найдем синус угла. Синус 60 = 0,5, соответственно S = 6*7*0,5=21 Ответ: 21 см 2 .
Надеюсь, что эти примеры Вам помогут при решении задач.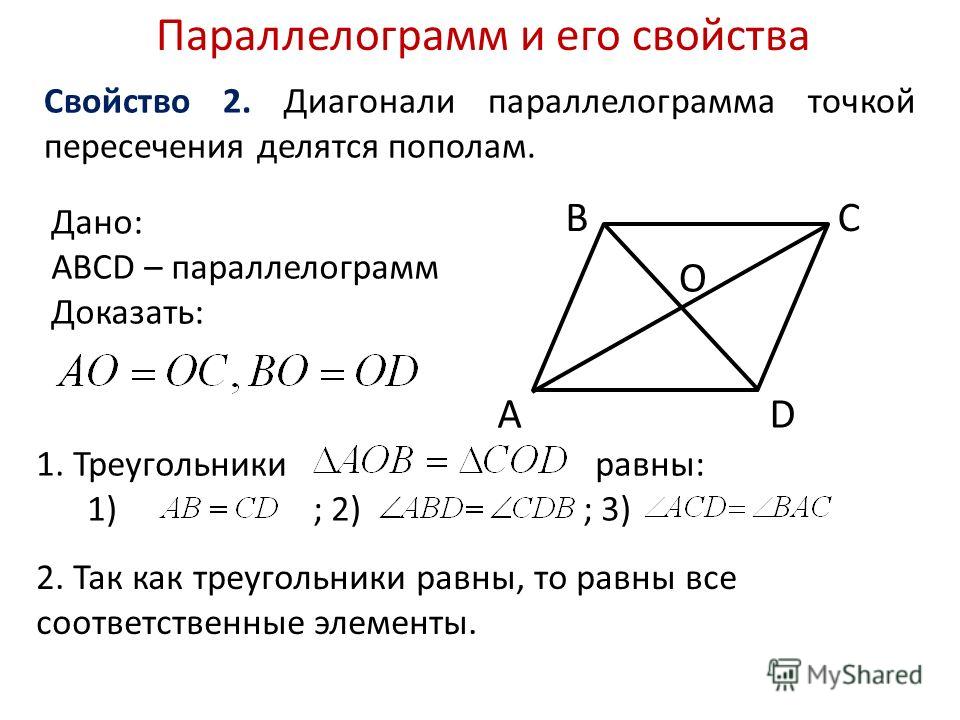 И помните, главное – это знание формул и внимательность
И помните, главное – это знание формул и внимательность
Что такое параллелограмм? Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
1. Площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot h_{a}\]
где:
a – сторона параллелограмма,
h a – высота, проведенная к этой стороне.
2. Если известны длины двух смежных сторон параллелограмма и угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]
3. Если заданы диагонали параллелограмма и известен угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = \frac{1}{2} \cdot d_{1} \cdot d_{2} \cdot sin(\alpha) \]
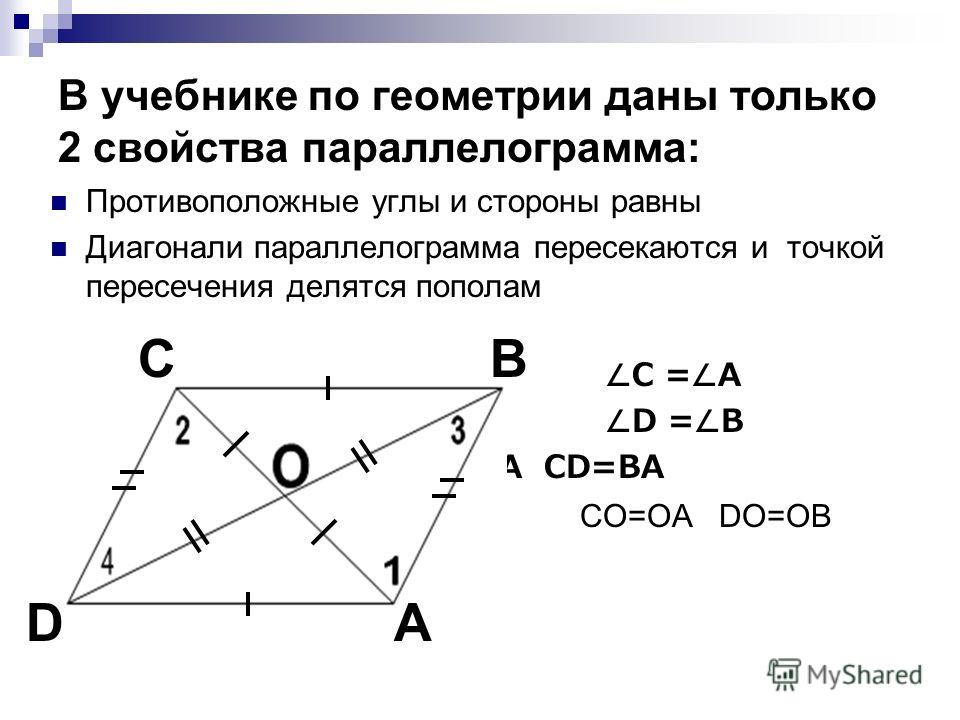
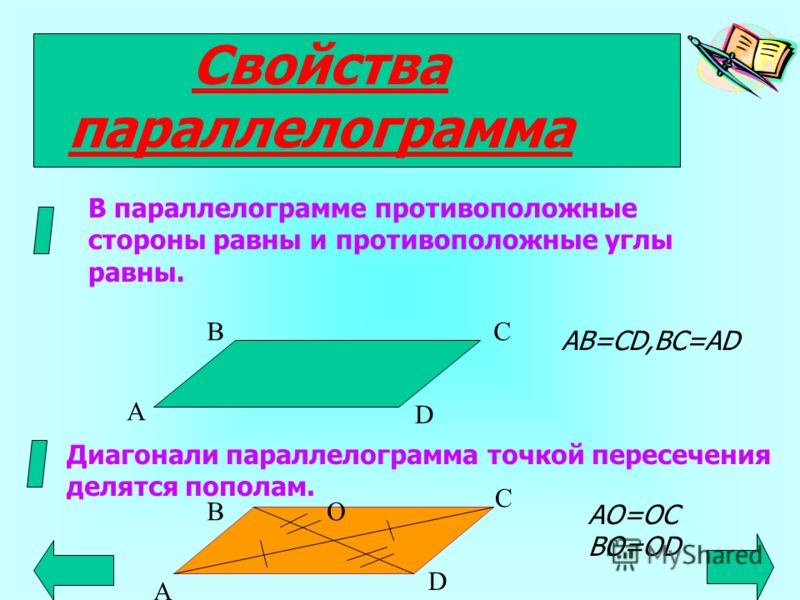
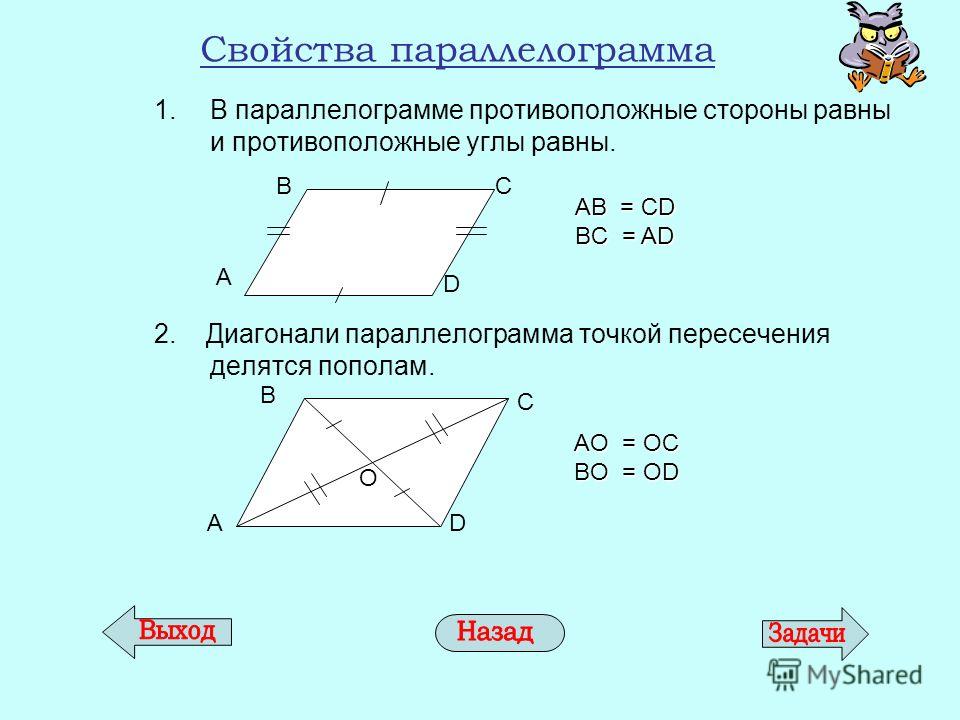
Свойства параллелограмма
В параллелограмме противоположные стороны равны: \(AB = CD \) , \(BC = AD \)
В параллелограмме противоположные углы равны: \(\angle A = \angle C \) , \(\angle B = \angle D \)
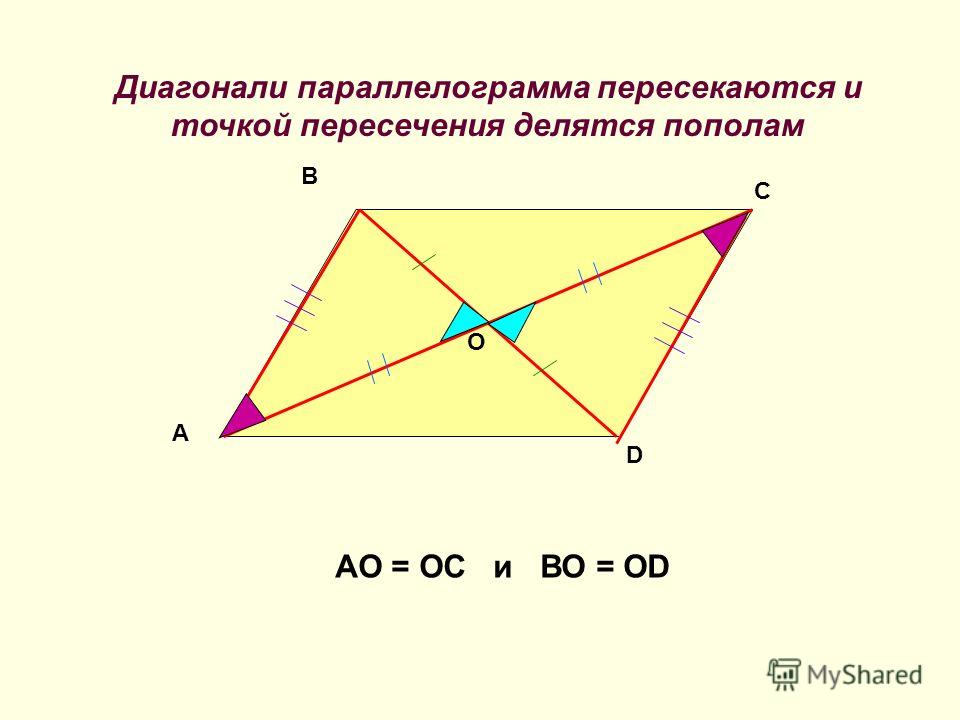
Диагонали параллелограмма в точке пересечения делятся пополам \(AO = OC \) , \(BO = OD \)
Диагональ параллелограмма делит его на два равных треугольника.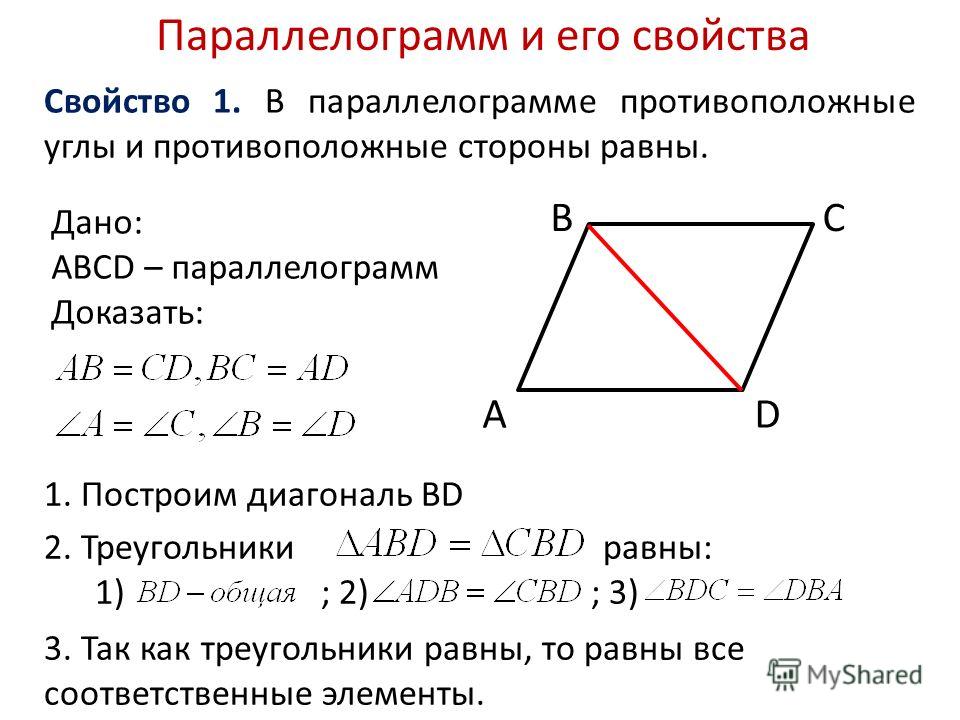
В параллелограмме угол между высотами равен его острому углу: \(\angle K B H =\angle A \) .
Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
Биссектрисы двух противоположных углов параллелограмма параллельны.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
\(AB = CD \) и \(AB || CD \)
\(AB = CD \) и \(BC = AD \)
\(AO = OC \) и \(BO = OD \)
\(\angle A = \angle C \) и \(\angle B = \angle D \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Определение параллелограмма
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением.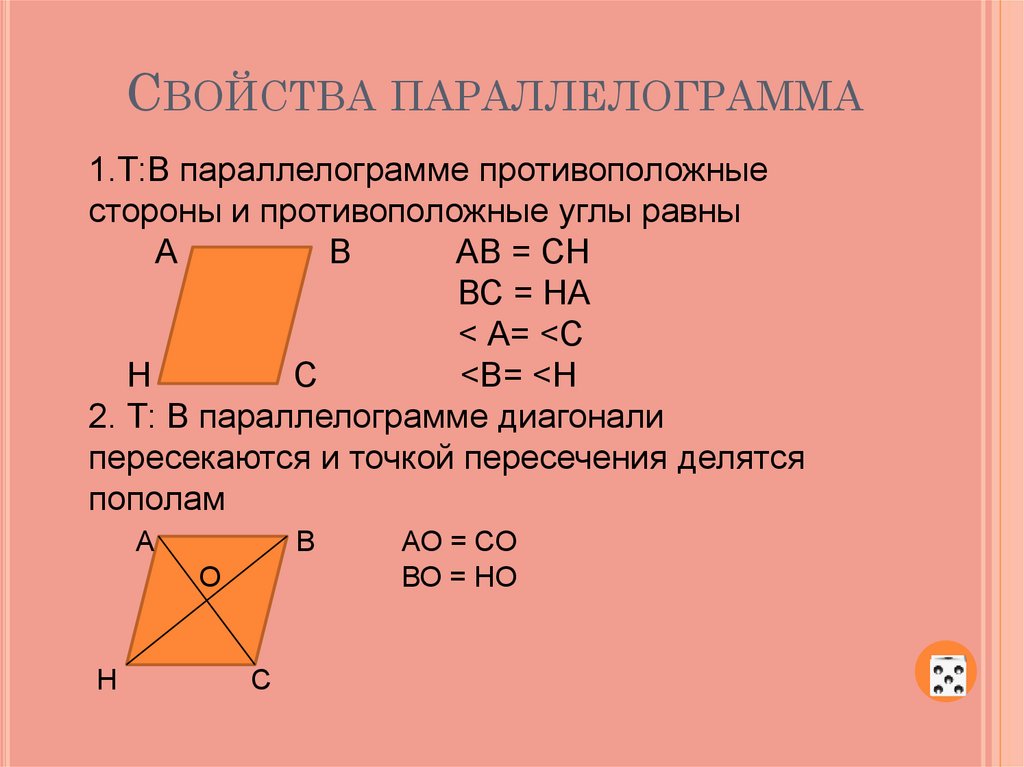 Для начала разберем обобщенный случай без использования чисел.
Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием a a a , боковой стороной b b b и высотой h h h , проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S = a ⋅ h S=a\cdot h S = a ⋅ h
A a
a
— основание;
h h
h
— высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
Пример
Найти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
A = 10 a=10
a
=
1
0
h = 5 h=5
h
=
5
Подставляем в нашу формулу. Получаем:
S = 10 ⋅ 5 = 50 S=10\cdot 5=50
S
=
1
0
⋅
5
=
5
0
(см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S = a ⋅ b ⋅ sin (α) S=a\cdot b\cdot\sin(\alpha) S = a ⋅ b ⋅ sin (α )
A , b a, b
a
,
b
— стороны параллелограмма;
α \alpha
α
— угол между сторонами a a
a
и b b
b
. {\circ})=12.5
S
=
2
1
⋅
1
0
⋅
5
⋅
sin
(3
0
∘
)
=
1
2
.
5
(см. кв.)
{\circ})=12.5
S
=
2
1
⋅
1
0
⋅
5
⋅
sin
(3
0
∘
)
=
1
2
.
5
(см. кв.)
Угол между сторонами параллелограмма. Свойство диагоналей параллелограмма
Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т.е. лежат на параллельных прямых
Свойства параллелограмма:
Теорема 22. Противоположные стороны параллелограма равны.
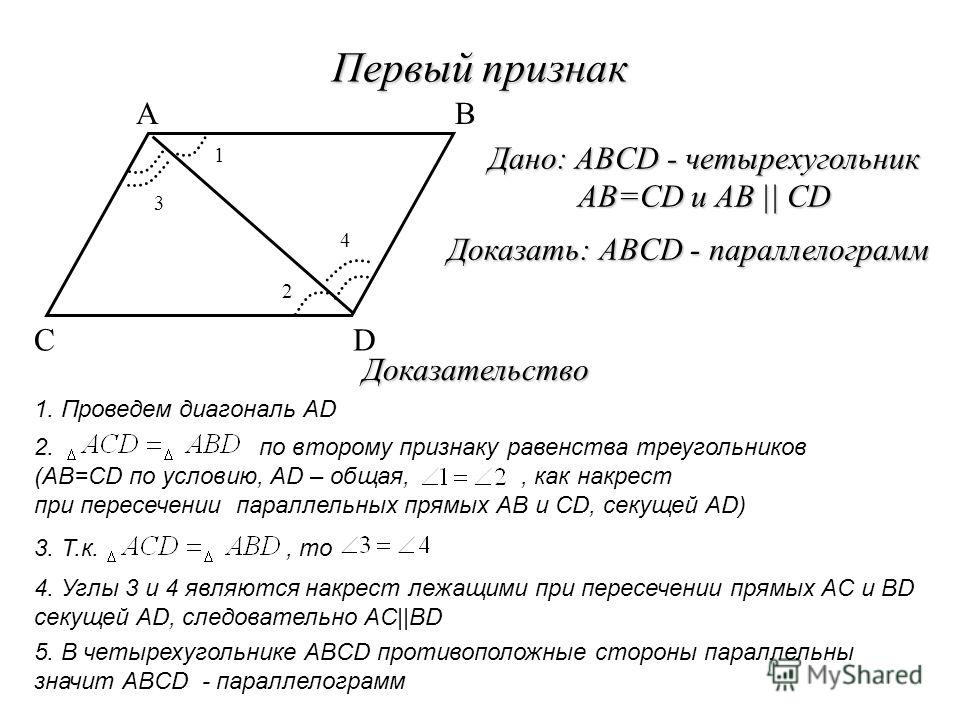
Доказательство. В параллелограмме АВСD проведем диагональ АС. Треугольники АСD и АСВ равны, как имеющие общую сторону АС и две пары равных углов. прилежащих к ней: ∠
САВ=∠
АСD, ∠
АСВ=∠
DAC (как накрест лежащие углы при параллельных прямых AD и ВС). Значит, АВ=CD и ВС=AD, как соответственные стороны равных треугольников, ч.т.д. Из равенства этих треугольников также следует равенство соответственных углов треугольников:
Теорема 23. Противоположные углы параллелограмма равны: ∠
А=∠
С и ∠
В=∠
D.
Равенство первой пары идет из равенства треугольников АВD и CBD, а второй — АВС и ACD.
Теорема 24. Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Соседние углы параллелограмма, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов.
Это так, потому что они являются внутренними односторонними углами.
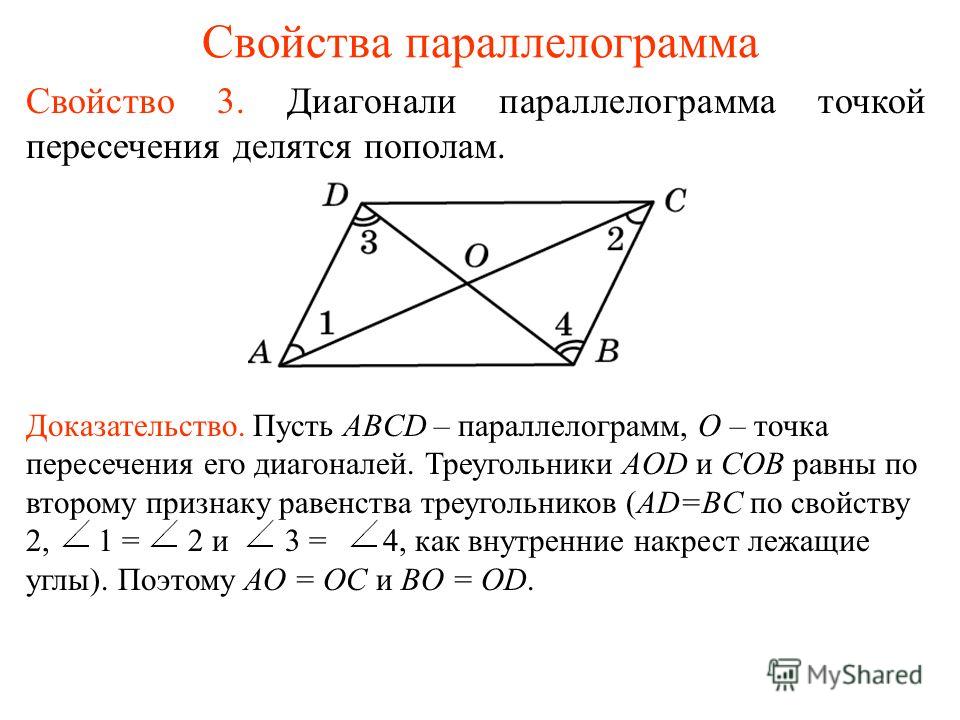
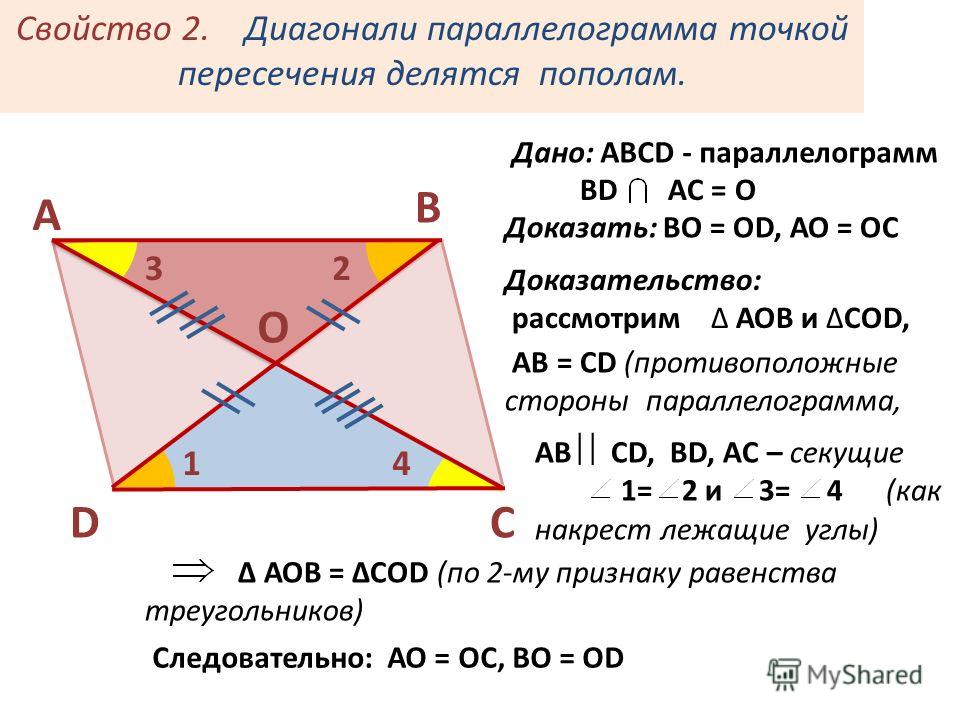
Теорема 25. Диагонали параллелограмма делят друг друга в точке их пересечения пополам.
Доказательство. Рассмотрим треугольники ВОС и АОD. По первому свойству AD=ВС ∠
ОАD=∠
ОСВ и ∠
ОDА=∠
ОВС как накрест лежащие при параллельных прямых AD и ВС. Поэтому треугольники ВОС и АОD равны по стороне и прилежащим к ней углам. Значит, ВО=ОD и АО=ОС, как соответственные стороны равных треугольников, ч.т.д.
Признаки параллелограмма
Теорема 26. Если противоположные стороны четырехугольника попарно равны, то он является параллелограммом.
Доказательство. Пусть у четырехугольника АВСD стороны AD и ВС, АВ и CD соответственно равны (рис2). Проведем диагональ АС. Треугольникик АВС и ACD равны по трем сторонам. Тогда углы ВАС и DСА равны и, следовательно, АВ параллельна CD. Параллельность сторон ВС и AD следует из равенства углов CAD и АСВ.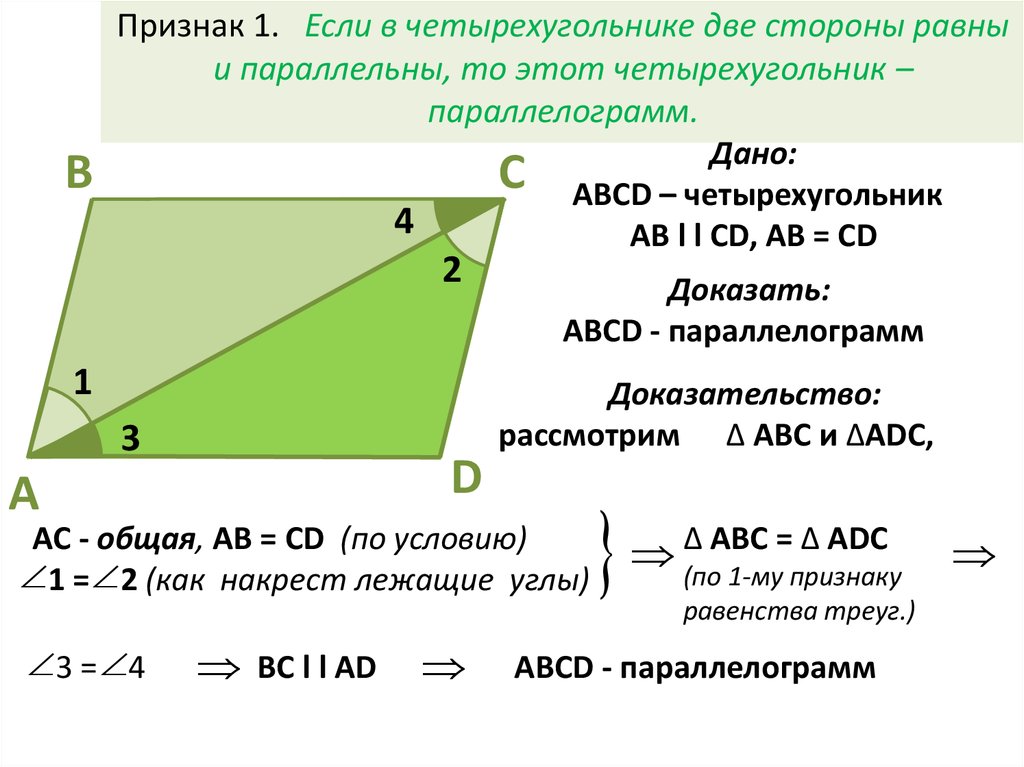
Теорема 27. Если противоположные углы четырехугольника попарно равны, то он является параллелограммом.
Пусть ∠
А=∠
С и ∠
В=∠
D. Т.к. ∠
А+∠
В+∠
С+∠
D=360 о, то ∠
А+∠
В=180 о и стороны AD и ВС параллельны (по признаку параллельности прямых). Также докажем и параллельность сторон АВ и CD и заключим, что АВСD является параллелограммом по определению.
Теорема 28. Если соседние углы четырехугольника, т.е. углы, прилежащие к одной стороне, составляют в сумме 180 градусов, то он является параллелограммом.
Если внутренние односторонные углы в сумме составляют 180 градусов, то прямые праллельны. Значит АВ парал CD и ВС парал AD. Четырехугольник оказывается параллелограммом по определению.
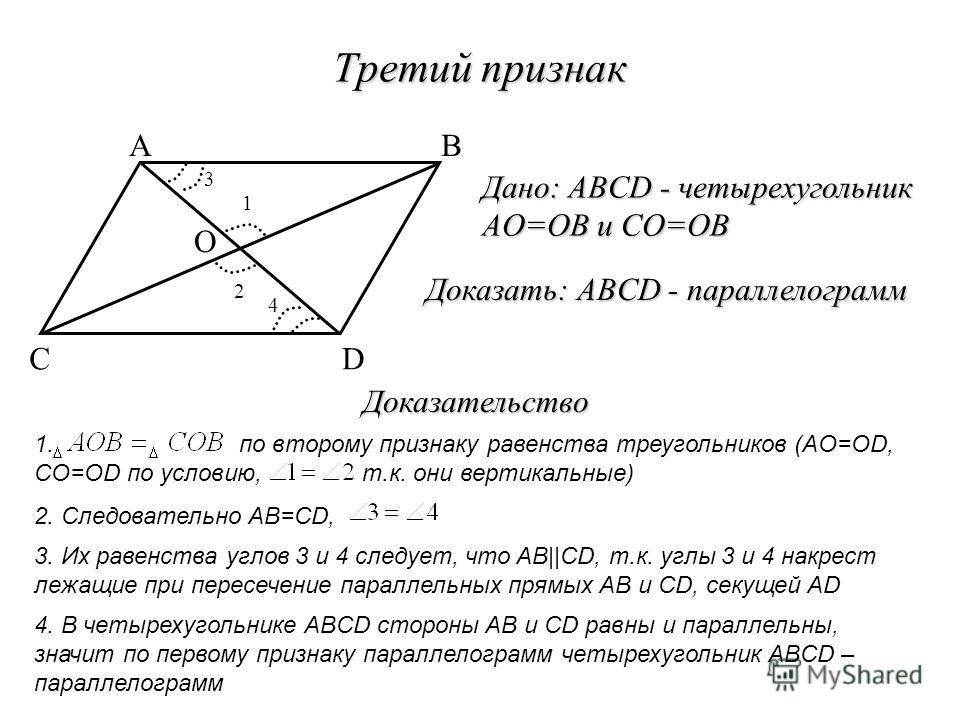
Теорема 29. Если диагонали четырехугольника взаимно делятся в точке пересечения пополам, то четырехугольник — параллелограмм.
Доказательство. Если АО=ОС, ВО=ОD, то треугольники АOD и ВОС равны, как имеющие равны углы (вертикальные) при вершине О, заключенные между парами равных сторон.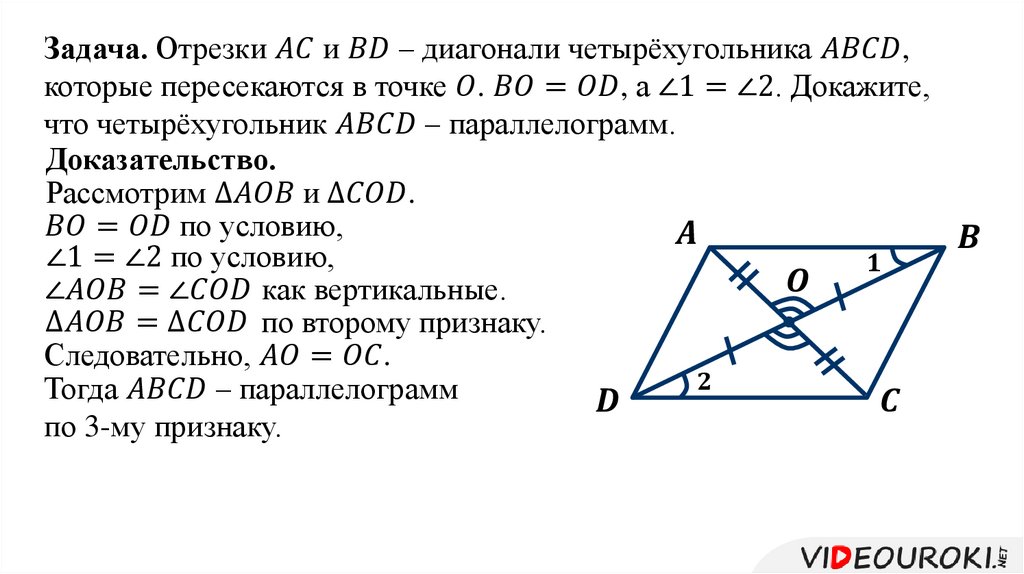 Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Из равенства треугольников заключаем, что AD и ВС равны. Также равны стороны АВ и CD, и четырехугольник оказывается параллелограммом по признаку 1.
Теорема 30. Если четырехугольник имеет пару равных, параллельных между собой сторон, то он является параллелограммом.
Пусть в четырехугольнике АВСD стороны АВ и CD параллельны и равны. Проведем диагонали АС и ВD. Из параллельности этих прямых следует равенство накрест лежащих углов АВО=СDО и ВАО=ОСD. Треугольники АВО и CDО равны по стороне и прилежащим к ней углам. Поэтому АО=ОС, ВО=ОD, т.е. диагонали точкой пересечения делятся пополам и четырехугольник оказывается параллелограммом по признаку 4.
В геометрии рассматривают частные случаи параллелограмма.
Понятие параллелограмма
Определение 1
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
Рисунок 1.
Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Признаки параллелограмма
Рассмотрим три признака параллелограмма и представим их в виде теорем.
Теорема 1
Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
\[\angle CAB=\angle DCA\]
как накрест лежащие углы.
По $I$ признаку равенства треугольников,
так как $AC$ — их общая сторона, а $AB=CD$ по условию. Значит
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. }Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Теорема 2
Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).
Рисунок 3.
Так как $AD=BC$, $AB=CD$, а $AC$ — общая сторона, то по $III$ признаку равенства треугольников,
\[\triangle DAC=\triangle ACB\]
\[\angle DAC=\angle ACB\]
Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
\[\angle DCA=\angle CAB\]
Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$.
Следовательно, по определению 1, данный четырехугольник является параллелограммом.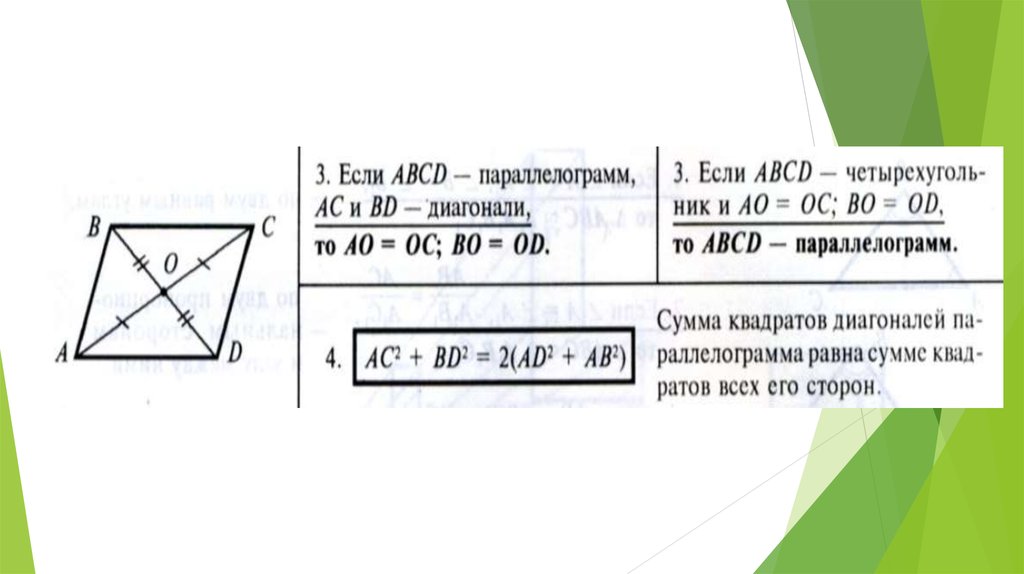
Теорема доказана.
Теорема 3
Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).
Рисунок 4.
Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,
\[\triangle BOC=\triangle AOD\]
\[\angle DBC=\angle BDA\]
Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.
Параллелограмм — это четырехугольник, у которого противоположные стороны попарно параллельны. На следующем рисунке представлен параллелограмм ABCD. У него сторона AB параллельна стороне CD, а сторона BC параллельна стороне AD.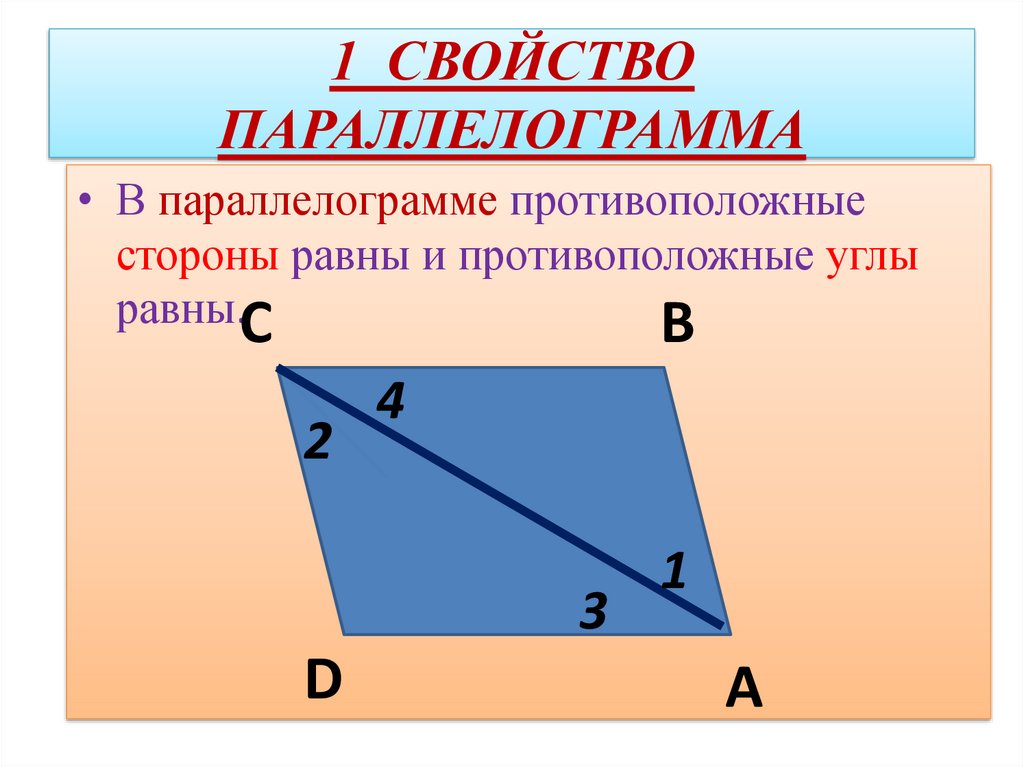
Как вы уже успели догадаться, параллелограмм является выпуклым четырехугольником. Рассмотрим основные свойства параллелограмма.
Свойства параллелограмма
1. В параллелограмме противоположные углы и противоположные стороны равны. Докажем это свойство — рассмотрим параллелограмм, представленный на следующем рисунке.
Диагональ BD разделяет его на два равных треугольника: ABD и CBD. Они равны по стороне BD и двум прилежащим к ней углам, так как углы накрест лежащие при секущей BD параллельных прямых BC и AD и AB и CD соответственно. Следовательно, AB = CD и
BC = AD. А из равенства углов 1, 2 ,3 и 4 следует, что угол A = угол1 +угол3 = угол2 + угол4 = угол С.
2. Диагонали параллелограмма точкой пересечения делятся пополам. Пусть точка О есть точка пересечения диагоналей AC и BD параллелограмма ABCD.
Тогда треугольник AOB и треугольник COD равны между собой, по стороне и двум прилежащим к ней углам. (AB=CD так как это противоположные стороны параллелограмма. А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
А угол1 = угол2 и угол3 = угол4 как накрест лежащие углы при пересечении прямых AB и CD секущими AC и BD соответственно.) Из этого следует, что AO = OC и OB = OD, что и требовалось доказать.
Все основные свойства проиллюстрированы на следующих трех рисунках.
Доказательство
Первым делом проведем диагональ AC . Получаются два треугольника: ABC и ADC .
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: и AC — общая).
И, значит, \triangle ABC = \triangle ADC , то AB = CD и AD = BC .
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4
. Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4
. Учитывая, что \triangle ABC = \triangle ADC
получаем \angle A = \angle C
, \angle B = \angle D
.
Учитывая, что \triangle ABC = \triangle ADC
получаем \angle A = \angle C
, \angle B = \angle D
.
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD . Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1 ) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).
Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?» . То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD ; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC ?
\triangle ABC = \triangle ADC по свойству 1 : AB = CD , AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC .
Но если \triangle ABC = \triangle ADC , то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.
AB = CD , AD = BC \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC .
По свойству 1 \triangle ABC = \triangle ACD .
Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC
и \angle 3 = \angle 4 \Rightarrow AB || CD
, то есть ABCD
— параллелограмм. {\circ}
говорит и о том, что AD || BC
.
{\circ}
говорит и о том, что AD || BC
.
При этом \alpha и \beta — внутренние односторонние при секущей AD . И это значит AB || CD .
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.
AO = OC ; BO = OD \Rightarrow параллелограмм.
Доказательство
BO = OD ; AO = OC , \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD , \Rightarrow \angle 3 = \angle 4 , и \Rightarrow AB || CD .
Аналогично BO = OD ; AO = OC , \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 , и \Rightarrow AD || BC .
Четвертый признак верен.
Конспект урока.
Алгебра 8 класс
Учитель Сысой А.К.
Школа 1828
Тема урока: «Параллелограмм и его свойства»
Тип урока: комбинированный
Цели урока:
1) Обеспечить усвоение нового понятия – параллелограмм и его свойств
2) Продолжить развитие навыков и умений решения геометрических задач;
3) Развитие культуры математической речи
План урока:
1. Организационный момент
Организационный момент
(Слайд 1)
На слайде демонстрируется высказывание Льюиса Кэрролла. Ученикам сообщается о цели урока. Проверяется готовность учеников к уроку.
2. Актуализация знаний
(Слайд 2)
На доске задачи для устной работы. Учитель предлагает ученикам подумать над этими задачами и поднять руку тем, кто понял, как задачу решать. После решения двух задач, на доказательство теоремы о сумме углов вызывается к доске ученик, который самостоятельно делает дополнительные построения на чертеже и доказывает устно теорему.
Учениками используется формула суммы углов многоугольника:
3. Основная часть
(Слайд 3)
На доске определение параллелограмма. Учитель говорит о новой фигуре и формулирует определение, делая с помощью чертежа необходимые пояснения. Затем на клетчатой части презентации, с помощью маркера и линейки, показывает, как можно рисовать параллелограмм (возможно несколько случаев)
(Слайд 4)
Учитель формулирует первое свойство параллелограмма. Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
Предлагает ученикам сказать, по рисунку, что дано и что необходимо доказать. После этого на доске появляется дано задачи. Ученики догадываются (может быть при помощи учителя) что искомые равенства надо доказать через равенства треугольников, которые можно получить проведя диагональ (на доске появляется диагональ). Далее ученики догадываются почему треугольники равны и называют признак равенства треугольников (появляется соответствующая форма). Устно сообщают факты, которые необходимы для равенства треугольников (по мере того как они их называют, появляется соответствующая визуализация). Далее ученики формулируют свойство равных треугольников, оно появляется в виде пункта 3 доказательства и затем самостоятельно завершают доказательство теоремы устно.
(Слайд 5)
Учитель формулирует второе свойство параллелограмма. На доске появляется рисунок параллелограмма. Учитель предлагает по рисунку сказать что дано, что необходимо доказать. После того как ученики правильно сообщают о том, что дано и что необходимо доказать, появляется условие теоремы. Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
Ученики догадываются, что равенство частей диагоналей можно доказать через равенство треугольников
AOB
и
COD
. С помощью предыдущего свойства параллелограмма догадываются о равенстве сторон
AB
и
CD
. Затем понимают, что надо найти равные углы и с помощью свойств параллельных прямых доказывают равенство прилежащих к равным сторонам углов. Данные этапы визуализируются на слайде. Из равенства треугольников следует и истинность теоремы – проговаривают ученики на слайде появляется соответствующая визуализация.
(Слайд 6)
Учитель формулирует третье свойство параллелограмма. В зависимости от времени, которое остаётся до конца урока, учитель может дать возможность ученикам самостоятельно доказать это свойство, или ограничится его формулировкой, а само доказательство оставить ученикам в качестве домашней работы. Доказательство может опираться на сумму углов вписанного многоугольника, которая повторялась в начале урока, или на сумму внутренних односторонних углов при двух параллельных прямых
AD
и
BC
, и секущей, например
AB
.
4. Закрепление материала
На этом этапе учащиеся, используя ранее изученные теоремы, решают задачи. Идеи к решению задачи подбирают ученики самостоятельно. Так как возможных вариантов оформления немало и все они зависят от того каким образом ученики будут искать решение задачи, визуализации решения задач нет, а ученики самостоятельно оформляют каждый этап решения на отдельной доске с записью решения в тетрадь.
(Слайд 7)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После того, как ученики, верно составят краткую запись условия на доске появляется «Дано». Ход решения задачи может выглядеть следующим образом:
Проведём высоту BH (визуализировано)
Треугольник AHB – прямоугольный. Угол A равен углу C и равен 30 0 (по свойству о противоположных углах в параллелограмме). 2BH =AB (по свойству катета, лежащего напротив угла в 30 0 в прямоугольном треугольнике). Значит AB = 13 см.
AB
= CD
, BC
= AD
(по свойству противоположных сторон в параллелограмме) Значит AB
=CD
=13см. Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Так как периметр параллелограмма равен 50 см, то BC
=AD
=(50 – 26):2=12см.
Ответ: AB = CD = 13 см, BC = AD = 12 см.
(Слайд 8)
Появляется условие задачи. Учитель предлагает по условию сформулировать «Дано». После появляется «Дано» на экране. С помощью красных линий выделяется четырёхугольник, про который нужно доказать, что он параллелограмм. Ход решения задачи может выглядеть следующим образом:
Т.к. BK и MD перпендикуляры к одной прямой, то прямы BK и MD параллельны.
Через смежные углы можно показать, что сумма внутренних односторонних углов при прямых BM и KD и секущей MD равна 180 0 . Поэтому данные прямые параллельны.
Так как у четырехугольника BMDK противоположные стороны попарно параллельны, то данный четырехугольник параллелограмм.
5. Окончание урока. Поведение итогов.
(Слайд 8)
На слайде появляются вопросы по новой теме, на которые ученики отвечают.
Формула нахождения параллелограмма.
 Периметр и площадь параллелограмма
Периметр и площадь параллелограммаПримечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно. Большая диагональ 15 см.Найти площадь параллелограмма.
Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.
Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.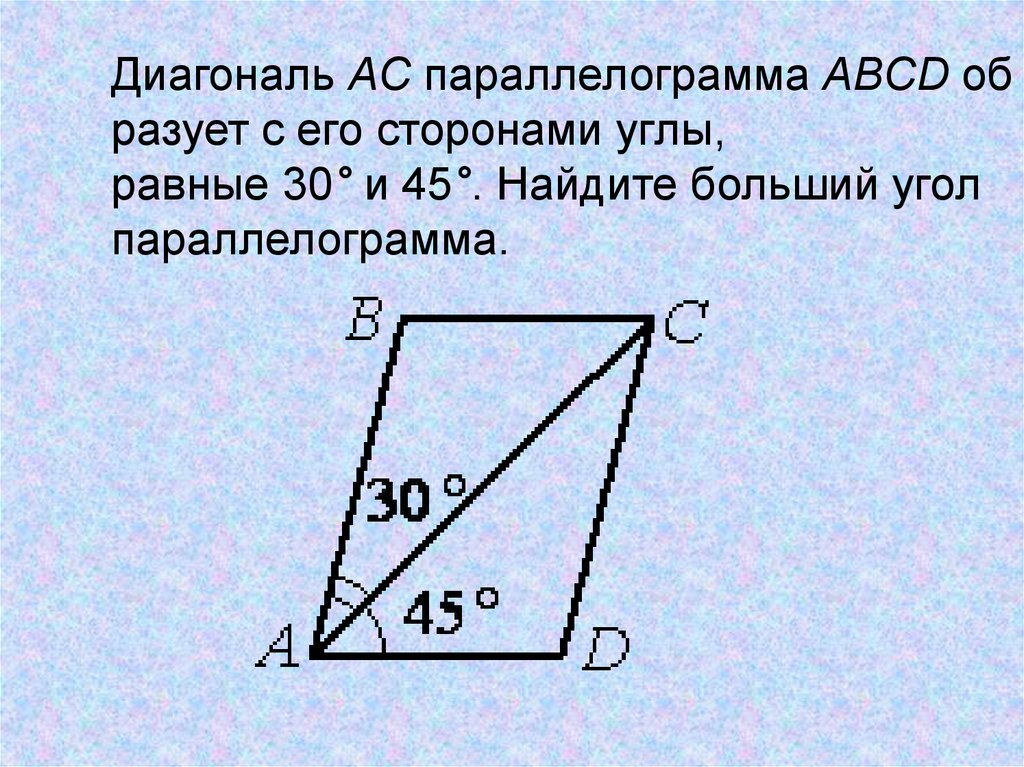
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD.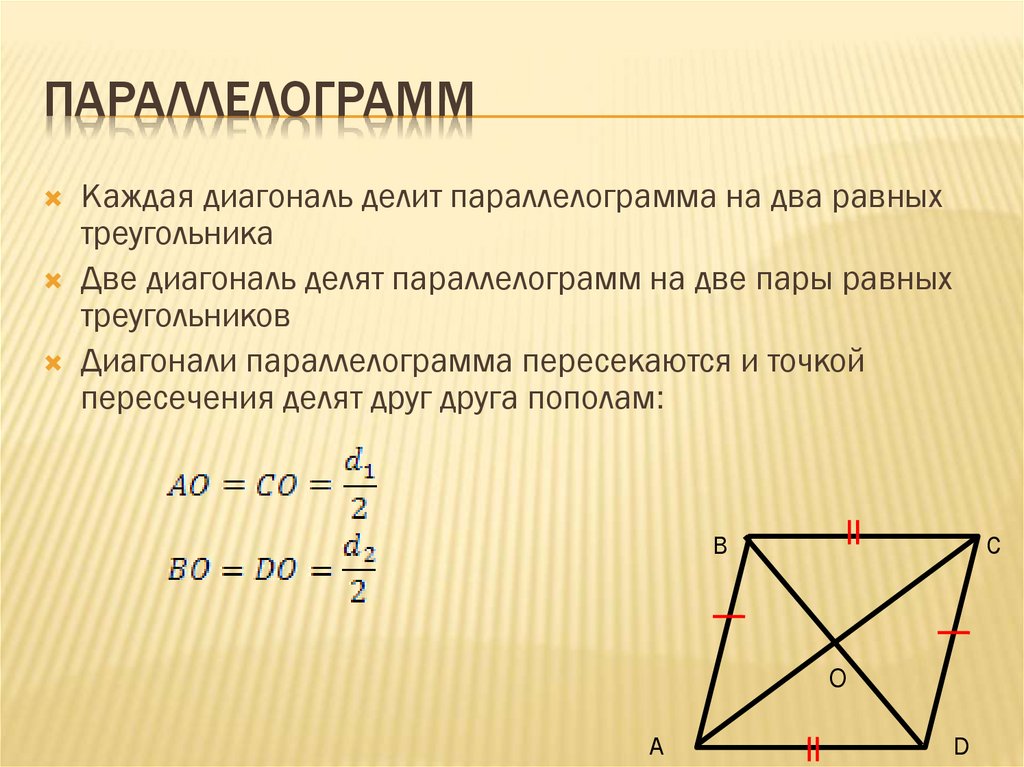 ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры.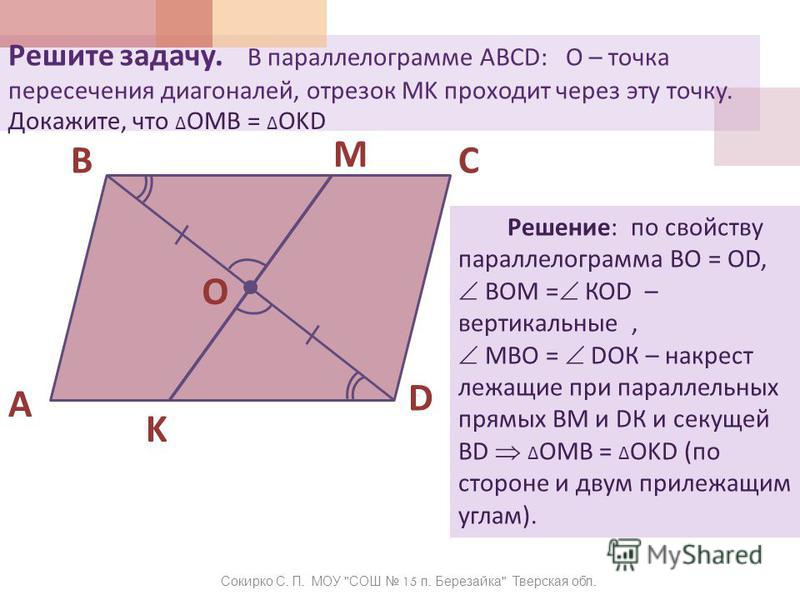 Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
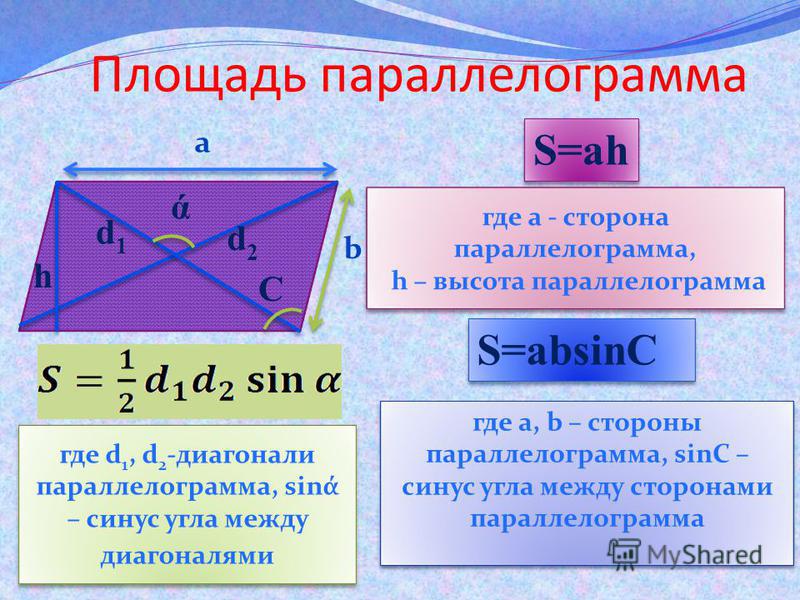
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник.
 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. - Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinα
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
- Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 2 2 где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Варенье из бузины: польза и вред
Узнать встретимся ли мы.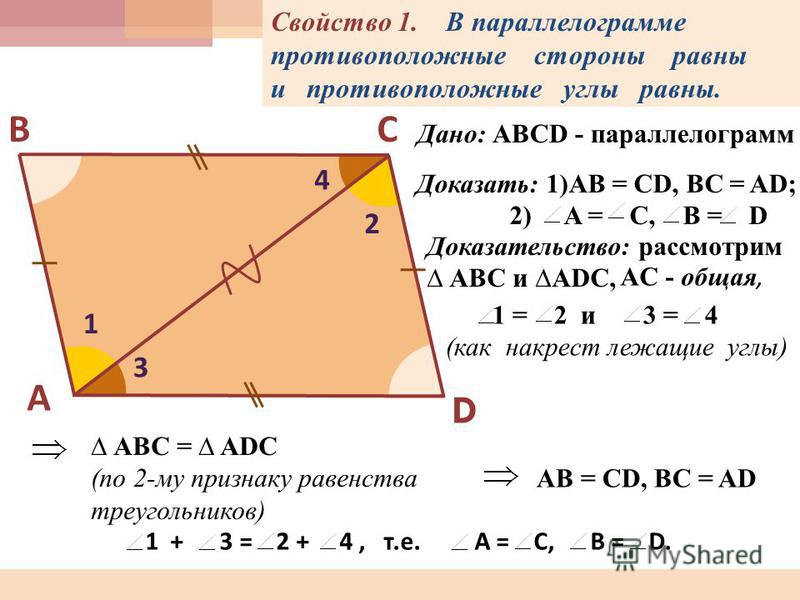 Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
Сонник дома солнца. Как правильно сформулировать вопрос в процессе гадания
✅ Диагональ формулы параллелограмма ⭐️⭐️⭐️⭐️⭐
5/5 — (1 bình chọn)
Mục Lục
Диагональ формулы параллелограмма параллелограмм. Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма. Используя эту формулу, мы можем узнать длины диагоналей, только используя длину сторон и любой из известных углов. Давайте узнаем больше о диагоналях параллелограмма вместе с решенными примерами в следующем разделе.
Что такое диагональ формулы параллелограмма?
Диагонали формулы параллелограмма помогают вычислить длину диагоналей данного параллелограмма. Эту формулу можно использовать для нахождения длин диагоналей, используя длину сторон и любой из известных углов.
Диагональ параллелограмма Формула
Формула 1: Для любого параллелограмма abcd формула для длины диагоналей:
Где,
- p и q — длина диагонали соответственно.

- х и у — стороны параллелограмма.
Формула 2: Еще одна специальная формула, связывающая длины диагоналей и сторон параллелограмма:
Где
- p и q — длины диагоналей соответственно.
- х и у — стороны параллелограмма.
Давайте быстро рассмотрим пару примеров, чтобы лучше понять диагонали формулы параллелограмма.
Примеры с использованием формулы диагонали параллелограмма
Пример 1: Найдите длину диагоналей ромба со стороной 4 дюйма, если внутренние углы равны 120° и 60°.
Решение:
Дано, внутренний угол A = 120°, а угол B = 60°.
x = 4, y = 4
Используя формулу диагонали параллелограмма,
Ответ: Длина диагоналей 4 дюйма и 6,92 дюйма.
Пример 2: Для параллелограмма ABCD, если длина смежных сторон составляет 35 футов и 82 фута. Если один из внутренних углов равен 37°.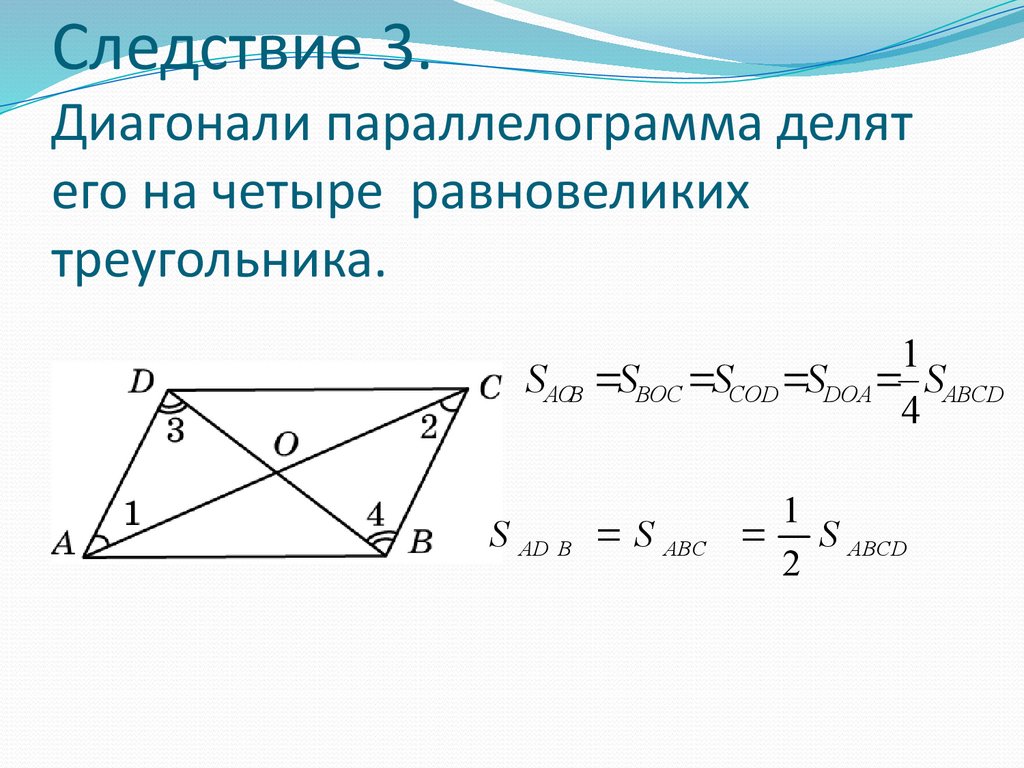 Найдите длину любой диагонали.
Найдите длину любой диагонали.
Решение:
Дано, внутренний угол A = 37°
x = 35 футов, y = 82 фута
Используя формулу диагонали параллелограмма,
Ответ:8 5 8 9 футов. Длина диагонали равна
. Пример 3: Вычислить длину диагонали параллелограмма со сторонами 4 единицы, 6 единиц и углом 60 градусов? Решение: Дано, a = 4 единицы, b = 6 единиц, угол A = 60° Используя формулу диагонали параллелограмма, Ответ: Диагональ параллелограмма = 5,291 единицы. Формула диагоналей параллелограмма дает длину диагоналей параллелограмма. Для любого параллелограмма abcd формула для длин диагоналей: Для любого параллелограмма пусть p и q – длины диагоналей, а x и y – стороны параллелограмма, тогда Формула диагонали параллелограмма помогает найти длины диагоналей, используя длину сторон и любой из известных углов. Таким образом, его составляющие включают в себя стороны параллелограмма и соответствующие им углы. Формула диагонали параллелограмма для обеих диагоналей выглядит следующим образом: Когда учащиеся узнают о четырехугольниках, они узнают о их различных типах и названиях. Четырехугольники или многоугольники — это геометрические фигуры на плоскости с 4 сторонами, 4 вершинами и 4 углами. В зависимости от длины сторон и степени угла, который они образуют в их соединяющихся вершинах, они классифицируются и называются по-разному. Квадрат: Имея равные стороны и угол 90 градусов, это самый распространенный и простой четырехугольник, с которым мы все знакомы. Прямоугольник: Похож на квадрат тем, что имеет равные все 5 углов по 90 градусов, но отличается неравными сторонами. Противоположные стороны равны, а соседние стороны не равны. Неправильный четырехугольник: Это самая неправильная форма с неравными сторонами и углами. Параллелограмм: В параллелограмме смежные стороны и углы не равны, а противоположные стороны и углы равны друг другу. Ромб: Две смежные стороны попарно равны. И равны только два угла, противоположные друг другу. Трапеция или трапеция: Это четырехугольник с одной парой сторон, противоположных друг другу, разной длины и параллельных друг другу. Равнобедренная трапеция: Это особый тип трапеции с непараллельными сторонами, имеющими одинаковую длину. Вот некоторые из простых четырехугольников, которые мы изучали в предыдущем классе. Каждый четырехугольник имеет две диагонали, которые делят друг друга пополам в центре четырехугольника. Точно так же диагонали параллелограмма делят друг друга пополам, но не равны по длине. Учащиеся могут легко найти диагонали параллелограмма или любого другого четырехугольника, соединив противоположные вершины. У квадрата и ромба они всегда пересекаются перпендикулярно друг другу, а у других не перпендикулярно. Также обратите внимание, что большая диагональ противоположна большему из углов параллелограмма, что является прямым следствием правила косинуса. В случае прямоугольника, который является типом параллелограмма, в котором внутренние углы равны 90°, диагональная формула сводится к следующему. Следующий результат можно также получить, применяя теорему Пифагора к прямоугольнику. Давайте рассмотрим следующий пример, чтобы понять, как использовать эти формулы. Вопрос: Если один из углов параллелограмма равен 60°, а его смежные стороны равны 4 см и 6 см, то вычислите длины его диагоналей. Решение: Почему бы вам не попробовать решить следующую задачу, чтобы проверить, усвоили ли вы эти формулы? Вопрос: Теперь мы можем решить эти два уравнения, чтобы вычислить a и b. Решая этот квадрат и игнорируя отрицательные ответы (потому что длины не могут быть отрицательными), мы получаем следующие значения. 1. Как найти длину диагоналей четырехугольника? Чтобы вычислить и найти длину диагоналей, мы должны сначала узнать меру сторон и углов, образованных сторонами и диагоналями. Затем мы можем применить тригонометрические правила, чтобы узнать длину диагоналей. Если диагонали образуют прямоугольный треугольник с любыми двумя сторонами треугольника, то для нахождения длины диагонали также можно использовать правило теоремы о гипотенузе. 2. Как узнать площадь параллелограмма? Параллелограмм – это четырехугольник с одной парой параллельных сторон. Он отличается от прямоугольной формы тем, что в его четырех вершинах нет прямых углов. Итак, чтобы узнать площадь, покрытую параллелограммом, вам нужно найти высоту или высоту параллелограмма. после нахождения высоты она умножается на основание параллелограмма. Другой метод состоит в том, чтобы сначала узнать перпендикулярное расстояние диагонали от одной вершины, отличной от двух на обоих ее концах. Затем это расстояние умножается на длину диагонали, чтобы найти площадь. 3. Какие все типы четырехугольников изучаются в высшей школе математики? Четырехугольники, имеющие четыре стороны и четыре вершины, делятся на две большие категории: простые и сложные. Кроме того, простые четырехугольники могут быть как вогнутыми, так и выпуклыми. 4. Сколько проблемных вопросов по главе должен решить студент для достаточной практики? Тема о диагоналях параллелограмма входит в главу о четырехугольнике в программе математики для старших классов. Таким образом, любой студент, который хочет попрактиковаться в вопросах, чтобы лучше понять главу, может решить задачи, представленные в упражнениях каждой главы. Если учащийся хочет получить больше вопросов, он может воспользоваться книгой Р. Д. Шармы или Р. 5. Как проверить правильность ответов на решенные вопросы? Решение проблемных вопросов к главам по геометрии иногда может сбивать с толку. Это может произойти даже после того, как у вас будет четкое понимание концепций. Так что лучше проверить доступные решения вопросов и лучше попрактиковаться. Vedantu предоставляет все ответы в виде решений на своем портале для студентов, которые готовятся самостоятельно. Решения доступны для всех популярных наборов вопросов, таких как NCERT Textbooks, RD Sharma, RS Aggarwal, а также для различных практических наборов вопросов, доступных на этом веб-сайте. Диагональ формулы параллелограмма: Название параллелограмм происходит от греческого слова parallelogrammon, что означает ограниченный параллельными линиями. Мы можем вычислить длины диагоналей параллелограмма, если нам известны меры его смежных сторон и смежных углов. В этой статье мы подробно обсудим диагональ формулы параллелограмма. Параллелограмм представляет собой четырехугольник, образованный параллельными прямыми. Противоположные стороны параллелограмма параллельны и равны. Угол параллелограмма между соседними сторонами может быть разным, но противоположные углы равны. Изучите приведенную ниже диаграмму, на которой представлены три вида параллелограммов. Это частные случаи параллелограммов. Диагональ — это отрезок, соединяющий два угла многоугольника, не являющегося ребром. Для nn-стороннего правильного многоугольника количество диагоналей можно получить по следующей формуле: Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма. В параллелограмме ABCD диагонали – AC и BD. Диагонали формулы параллелограмма используются для определения длины диагоналей параллелограмма. Используя длины сторон и меру углов, мы можем вычислить длины диагоналей. Параллелограмм можно разделить на несколько видов в зависимости от его различных свойств. В основном он подразделяется на три отдельные категории: Прямоугольник представляет собой параллелограмм с четырьмя прямыми углами и двумя наборами равных и параллельных противоположных сторон. ✅ Математические формулы ⭐️⭐️⭐️⭐️⭐ Открытый справочник по математике Главная
Контакт
О
Тематический указатель Четырехугольник, у которого обе пары противоположных сторон параллельны и
конгруэнтный,
и чье расположение на
координатная плоскость
определяется
координаты
из четырех
вершины (углы). Попробуйте это
Перетащите любую вершину параллелограмма ниже. В координатной геометрии параллелограмм подобен обычному параллелограмму.
(См. определение параллелограмма)
с добавлением того, что его положение на
координатная плоскость
известен.
Каждая из четырех вершин (углов) имеет известные
координаты.
По этим координатам можно найти различные свойства, такие как высота. Он обладает всеми теми же свойствами, что и знакомый нам параллелограмм: Длины четырех сторон и двух диагоналей можно найти, используя метод, описанный в
Расстояние между двумя точками, чтобы найти расстояние между парами точек. Например, на рисунке выше нажмите «Сброс» и выберите «показать диагонали» в меню параметров. Точно так же можно найти сторону AB, используя координаты точек A и B: Высота параллелограмма — это расстояние по перпендикуляру от вершины до противоположной стороны
(база).
На рисунке выше выберите «Показать высоту» в меню параметров. Он покажет высоту от B до противоположной стороны AB. Чтобы вычислить длину высоты, нам нужно найти перпендикулярное расстояние от точки до прямой.
На приведенном выше рисунке нам нужно расстояние от B до линии AD. Когда выбранная базовая сторона точно горизонтальна, высота — это просто разница в координатах y точек B и
любая точка на базе, скажем A. На рисунке выше нажмите «Сброс» и выберите «Показать высоту» в меню параметров.
Координаты B равны (18,26), поэтому его координата y — это второе число, 26.
Выберите точку на стороне основания, скажем, A. Другую высоту можно найти таким же образом, если другие стороны точно вертикальны, используя x-координаты соответствующих точек. Если параллелограмм повернут так, что ни одна из его сторон не является строго вертикальной или горизонтальной, то используйте любой из способов, описанных в п.
Расстояние от точки до прямой. В интересах ясности в приведенном выше апплете координаты округлены до целых чисел, а длины округлены до одного десятичного знака. Подробнее см.
Учебные заметки (C) 2011 Copyright Math Open Reference. Предыдущий 7.2 Треугольники Следующий 7.4 Теорема о средней точке Четырехугольник – это замкнутая фигура, состоящая из четырех отрезков прямой линии. Сумма внутренних углов четырехугольника равна °. В Mathopenref есть несколько полезных моделей четырехугольников различных типов. Нажав на любой из названных четырехугольников, вы попадете на страницу, относящуюся к этому четырехугольнику. Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны. — параллелограмм с и . Покажите, что: и и Перерисовать схему и провести линию. На вашей диаграмме отметьте все равные углы. В и : Противоположные стороны параллелограмма имеют одинаковую длину. Мы уже показали и . Следовательно, Кроме того, Следовательно, противоположные углы параллелограмма равны. Краткое описание свойств параллелограмма: Обе пары противоположных сторон параллельны. Обе пары противоположных сторон равны по длине. Обе пары противоположных углов равны. Обе диагонали делят друг друга пополам. Докажите, что если обе пары противоположных углов в четырехугольнике равны, то этот четырехугольник является параллелограммом. В : Но это совнутренние углы между прямыми и . Следовательно . Аналогично. Это ко-внутренние углы между прямыми и . Следовательно . Обе пары противоположных сторон четырехугольника параллельны, следовательно, это параллелограмм. Докажите, что если обе пары противоположных сторон четырехугольника равны, то этот четырехугольник является параллелограммом. Докажите, что если диагонали четырехугольника делят друг друга пополам, то этот четырехугольник является параллелограммом. Докажите, что если одна пара противоположных сторон четырехугольника равна и параллельна, то этот четырехугольник является параллелограммом. Четырехугольник является параллелограммом, если: Обе пары противоположных сторон параллельны. Обе пары противоположных сторон равны. Обе пары противоположных углов равны. Диагонали делят друг друга пополам. Одна пара противоположных сторон равна и параллельна. Упражнение 7.3 См. решения Найдите аргументами два других угла, равных . (альт с; ). (с равными сторонами). Следовательно, и оба равны . Пишите в терминах . Рассчитать значение . Докажите, что диагонали параллелограмма делят друг друга пополам в точке . Подсказка: используйте конгруэнтность. Первый номер каждого угла на данной схеме: В и : Следовательно (ААС). Теперь мы знаем, что это середина . Аналогично в и : Следовательно (ААС). Теперь мы знаем, что это середина . Следовательно, диагонали параллелограмма делят друг друга пополам. См. решения Прямоугольник – это параллелограмм, у которого все четыре угла равны . Прямоугольник обладает всеми свойствами параллелограмма: Обе пары противоположных сторон параллельны. Обе пары противоположных сторон равны по длине. Обе пары противоположных углов равны. Обе диагонали делят друг друга пополам. Он также обладает следующим особым свойством: является прямоугольником. Докажите, что диагонали имеют одинаковую длину. Часто задаваемые вопросы о диагонали формулы параллелограмма
Что такое диагональ формулы параллелограмма?
Как использовать формулу диагонали параллелограмма?
 Проверьте заданные параметры, значения сторон параллелограмма и соответствующие углы.
Проверьте заданные параметры, значения сторон параллелограмма и соответствующие углы. Каковы компоненты диагонали формулы параллелограмма?
Формула диагонали параллелограмма одинакова для обеих диагоналей?
 Различают следующие типы четырехугольников:
Различают следующие типы четырехугольников: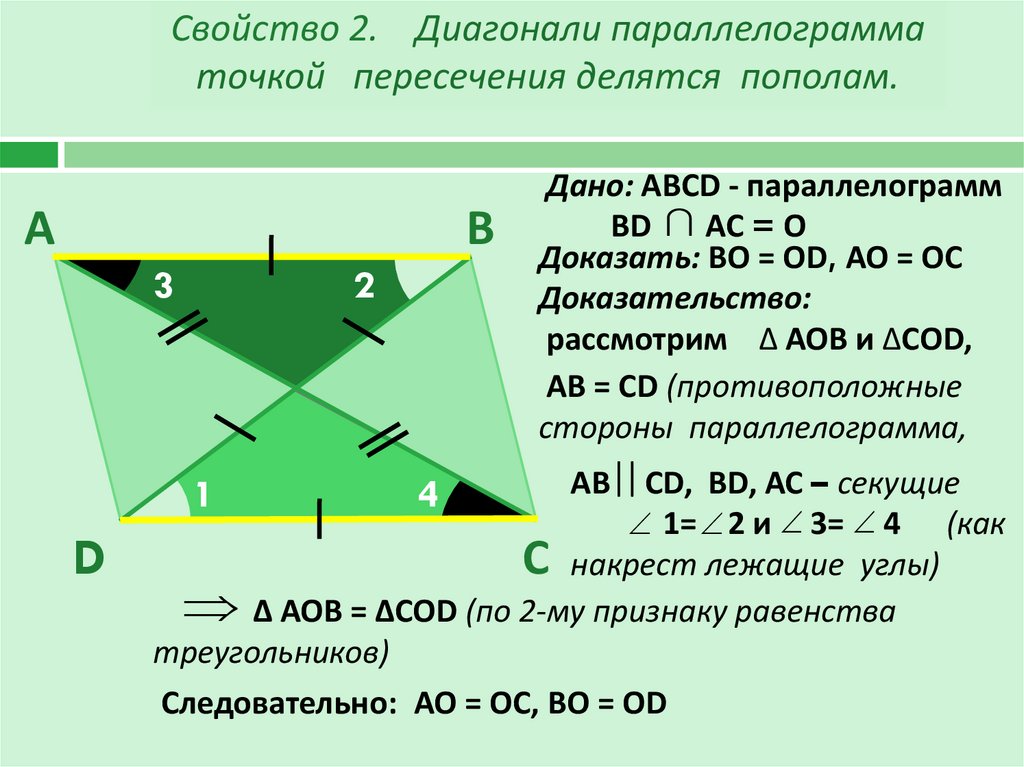

FAQs (Часто задаваемые вопросы)
 В некоторых случаях также может помочь формула равносторонних треугольников.
В некоторых случаях также может помочь формула равносторонних треугольников. Уже упоминались различные типы простых выпуклых четырехугольников. Этот список также включает продолговатый, воздушный змей, касательный четырехугольник, касательную трапецию, внекасательный четырехугольник, циклический четырехугольник, бицентрический четырехугольник, гармонический четырехугольник, ортогональный четырехугольник и равнодиагональный четырехугольник. В вогнутом четырехугольнике один внутренний угол больше 180 градусов. В таком четырехугольнике одна диагональ лежит вне четырехугольника.
Уже упоминались различные типы простых выпуклых четырехугольников. Этот список также включает продолговатый, воздушный змей, касательный четырехугольник, касательную трапецию, внекасательный четырехугольник, циклический четырехугольник, бицентрический четырехугольник, гармонический четырехугольник, ортогональный четырехугольник и равнодиагональный четырехугольник. В вогнутом четырехугольнике один внутренний угол больше 180 градусов. В таком четырехугольнике одна диагональ лежит вне четырехугольника. С. Аггарвала, доступной на рынке. Вопросы также доступны на веб-сайте Vedantu. Студенты могут скачать этот документ бесплатно после регистрации на портале.
С. Аггарвала, доступной на рынке. Вопросы также доступны на веб-сайте Vedantu. Студенты могут скачать этот документ бесплатно после регистрации на портале. Диагональ формулы параллелограмма – определение и примеры
 В результате параллелограмм представляет собой четырехугольник с параллельными прямыми на противоположных сторонах. Противоположные стороны параллелограмма будут параллельны и равны. Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма.
В результате параллелограмм представляет собой четырехугольник с параллельными прямыми на противоположных сторонах. Противоположные стороны параллелограмма будут параллельны и равны. Диагонали параллелограмма — это отрезки, соединяющие противоположные вершины параллелограмма. Что такое параллелограмм?
Диагональ
 В результате мы можем сделать диагональ, соединив любые два угла (вершины), которые ранее не были соединены ребром.
В результате мы можем сделать диагональ, соединив любые два угла (вершины), которые ранее не были соединены ребром. Количество диагоналей параллелограмма
Диагонали параллелограмма
Параллелограмм имеет две пары противоположных вершин и, следовательно, две диагонали. Диагонали формулы параллелограмма
Соотношение между сторонами и диагоналями параллелограмма
Типы параллелограмма
1. Прямоугольник
Прямоугольник
2. Квадрат
3. Ромб Формулы и свойства параллелограмма
Характеристики параллелограмма
Основные свойства параллелограмма
Стороны параллелограмма
Стороны параллелограмма формулы:
 Он останется параллелограммом, и его размеры будут рассчитаны по его координатам.
Вы также можете перетащить исходную точку в (0,0).
Он останется параллелограммом, и его размеры будут рассчитаны по его координатам.
Вы также можете перетащить исходную точку в (0,0).
См. определение параллелограмма для получения дополнительной информации. Стороны и диагонали
 Используя метод расстояния между двумя точками, диагональ AC равна
расстояние между точками А и С:
Используя метод расстояния между двумя точками, диагональ AC равна
расстояние между точками А и С: Высота над уровнем моря
Простой кейс
 Ее координата y равна 7.
Разница между ними в высоте:
Ее координата y равна 7.
Разница между ними в высоте: Поворотный корпус
Площадь параллелограмма
Отзыв от
Площадь параллелограмма
что площадь равна высоте, умноженной на основание. Оба они могут быть найдены с помощью методов, показанных выше. Что попробовать
На рисунке вверху страницы нажмите «скрыть подробности».
Затем перетащите углы, чтобы создать произвольный параллелограмм.
Вычислите длины сторон, диагонали и высоты фигуры.
Нажмите «показать детали», «показать диагонали» и «показать высоту», чтобы проверить свой ответ. Ограничения
 Это может привести к тому, что расчеты будут немного неверными. Например, если вы нажмете «повернутый» в меню параметров, форма останется той же, но будет отображаться немного другая высота. Это связано с тем, что координаты округляются немного по-разному, а высота рассчитывается из 90 337 отображаемых координат 90 338.
Это может привести к тому, что расчеты будут немного неверными. Например, если вы нажмете «повернутый» в меню параметров, форма останется той же, но будет отображаться немного другая высота. Это связано с тем, что координаты округляются немного по-разному, а высота рассчитывается из 90 337 отображаемых координат 90 338. Другие темы координатной геометрии
в координатной геометрии
Все права защищены 7.3 Четырехугольники | Евклидова геометрия
7.3 Четырехугольник
Параллелограмм
Подключиться к форме и
Используйте свойства параллельных прямых, чтобы указать на диаграмме все равные углы
Докажите

Найдите соотношение между и
Найти параллельные прямые

Прямоугольник
Подключение к и к форме и
Используйте определение прямоугольника, чтобы заполнить на диаграмме все равные углы и стороны.

Сводка свойств прямоугольника:
Обе пары противоположных сторон параллельны.
Обе пары противоположных сторон имеют одинаковую длину.
Обе пары противоположных углов равны.
Обе диагонали делят друг друга пополам.
Диагонали равны по длине.
Все внутренние углы равны
Упражнение 7.4 См. решения
— параллелограмм
(дано)
делит пополам
и (дано)
делит пополам
, поэтому прямоугольник 90 м — параллелограмм0003
(дан).
Следовательно, это прямоугольник (диаграммы прямоугольника).
См. решения
Ромб
- Ромб
Ромб – это параллелограмм, у которого все четыре стороны имеют одинаковую длину.

Ромб обладает всеми свойствами параллелограмма:
Обе пары противоположных сторон параллельны.
Обе пары противоположных сторон равны по длине.
Обе пары противоположных углов равны.
Обе диагонали делят друг друга пополам.
Он также имеет два особых свойства:
— ромб. Докажите, что:
диагонали делят друг друга пополам перпендикулярно;
диагонали делят внутренние углы пополам.
Используйте определение ромба, чтобы заполнить на диаграмме все равные углы и стороны
Докажите
Далее мы можем заключить, что .
Следовательно, диагонали делятся пополам перпендикулярно.
Используйте свойства конгруэнтных треугольников, чтобы доказать, что диагонали делят внутренние углы пополам
Следовательно, диагональ делит пополам . Точно так же мы можем показать, что также делит пополам ; и что диагональ делит пополам и .
Точно так же мы можем показать, что также делит пополам ; и что диагональ делит пополам и .
Мы заключаем, что диагонали ромба делят внутренние углы пополам.
Чтобы доказать, что параллелограмм является ромбом, нам нужно показать одно из следующего:
Все стороны равны по длине.
Диагонали пересекаются под прямым углом.
Диагонали делят внутренние углы пополам.
Краткое описание свойств ромба:
Обе пары противоположных сторон параллельны.
Обе пары противоположных сторон равны по длине.
Обе пары противоположных углов равны.
Обе диагонали делят друг друга пополам.
Все стороны равны по длине.
Диагонали делятся пополам в точке
.
Диагонали делят пополам обе пары противоположных углов.
Квадрат
- Квадрат
Квадрат – это ромб, у которого все четыре внутренних угла равны
.ИЛИ
Квадрат — это прямоугольник, у которого все четыре стороны равны по длине.
Квадрат обладает всеми свойствами ромба:
Обе пары противоположных сторон параллельны.
Обе пары противоположных сторон равны по длине.
Обе пары противоположных углов равны.
Обе диагонали делят друг друга пополам.
Все стороны равны по длине.
Диагонали делятся пополам в точке
.Диагонали делят пополам обе пары противоположных углов.
Также обладает следующими особыми свойствами:
Все внутренние углы равны.

Диагонали равны по длине.
Диагонали делят пополам обе пары внутренних противоположных углов (т.е. все равны ).
Чтобы доказать, что параллелограмм является квадратом, нам нужно показать одно из следующего:
Трапеция
- Трапеция
Трапеция – четырехугольник, у которого одна пара противоположных сторон параллельна.
В британском английском трапеция используется для обозначения четырехугольника с одной парой параллельных противоположных сторон, в то время как в американском английском трапеция представляет собой четырехугольник без пар противоположных параллельных сторон. В этой книге мы будем использовать британско-английское определение трапеции.
В британском английском языке трапеция используется для обозначения четырехугольника, у которого нет пар параллельных противоположных сторон, в то время как в американском английском трапеция представляет собой четырехугольник с одной парой параллельных противоположных сторон.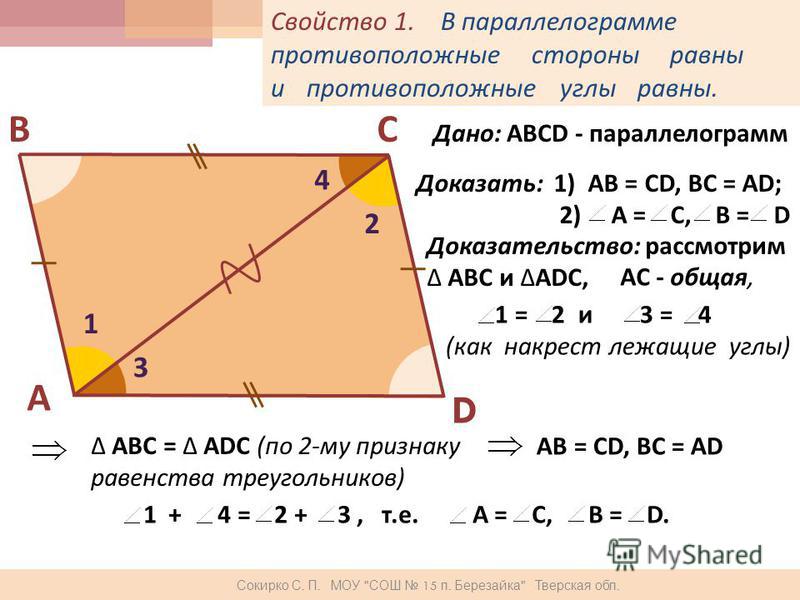
Трапецию иногда называют трапецией.
Ниже приведены некоторые примеры трапеций:
Воздушный змей
- Воздушный змей
Воздушный змей – это четырехугольник, у которого две пары смежных сторон равны.
— воздушный змей с и . Докажи, что:
Диагональные биссектрисы и
Докажите
В и :
Следовательно, у воздушного змея одна пара противоположных углов равна.
Используйте свойства конгруэнтных треугольников, чтобы доказать биссектрисы и
Следовательно, диагонали биссектрисы и .
Мы заключаем, что диагональ между равными сторонами воздушного змея делит два внутренних угла пополам и является осью симметрии.
Краткое описание свойств воздушного змея:
Диагональ между равными сторонами делит другую диагональ пополам.

Одна пара противоположных углов равна (углы между неравными сторонами).
Диагональ между равными сторонами делит внутренние углы пополам и является осью симметрии.
Диагонали пересекаются в точке
Упражнение 7.5 См. решения
Используйте набросок четырехугольника, чтобы доказать, что диагонали воздушного змея перпендикулярны друг другу.
Сначала пронумеруйте углы:
В и :
В :
Далее отметим, что:
Следовательно, диагонали воздушного змея перпендикулярны друг другу.
Объясните, почему четырехугольник — воздушный змей. Запишите все свойства четырехугольника.
Четырехугольник является воздушным змеем, потому что он имеет две пары смежных сторон, которые равны по длине.
Диагональ между равными сторонами делит другую диагональ пополам: .

Одна пара противоположных углов равна: .
Диагональ между равными сторонами делит внутренние углы пополам и является осью симметрии: .
Диагонали пересекаются в точке: .
См. решения
В этом видеоролике представлен обзор различных типов четырехугольников и их свойств.
Видео: 2G77
Хизер нарисовала следующую диаграмму, чтобы проиллюстрировать свое понимание отношений между различными четырехугольниками. Следующая диаграмма суммирует различные типы специальных четырехугольников.
Объясните ей возможную причину построения схемы, как показано на рисунке.
Создайте свою собственную диаграмму, чтобы показать взаимосвязь между различными четырехугольниками, и напишите краткое объяснение своей схемы.

Упражнение 7.6 См. решения
Нарисована следующая фигура в масштабе :
Дайте наиболее конкретное имя для фигуры.
Начнем с подсчета сторон. На этой фигуре четыре стороны, так что это либо просто четырехугольник, либо один из особых типов четырехугольника.
Далее мы спрашиваем себя, есть ли на рисунке параллельные прямые. Вы можете посмотреть на рисунок, чтобы увидеть, выглядят ли какие-либо из линий параллельными, или сделать быстрый набросок изображения и посмотреть, встречаются ли какие-либо пары противоположных линий в одной точке.
Обе пары противоположных сторон параллельны. Это означает, что фигура может быть только одной из следующих: параллелограмм, прямоугольник, ромб или квадрат.
Затем мы спросим себя, все ли внутренние углы равны 90°. Все внутренние углы равны 90°, поэтому это должен быть квадрат или прямоугольник. Наконец, мы проверяем, все ли стороны равны по длине. У этой фигуры длины сторон не равны, значит, это прямоугольник.
У этой фигуры длины сторон не равны, значит, это прямоугольник.
Следовательно, это прямоугольник.
Форма также является параллелограммом и четырехугольником. Этот вопрос, однако, требовал наиболее конкретного названия формы.
Нарисована следующая фигура в масштабе :
Дайте наиболее конкретное имя для формы.
Начнем с подсчета сторон. На этой фигуре четыре стороны, так что это либо просто четырехугольник, либо один из особых типов четырехугольника.
Далее мы спрашиваем себя, есть ли на рисунке параллельные прямые. Вы можете посмотреть на рисунок, чтобы увидеть, выглядят ли какие-либо из линий параллельными, или сделать быстрый набросок изображения и посмотреть, встречаются ли какие-либо пары противоположных линий в одной точке.
Обе пары противоположных сторон параллельны. Это означает, что фигура может быть только одной из следующих: параллелограмм, прямоугольник, ромб или квадрат.
Затем мы спросим себя, все ли внутренние углы равны 90°. Все внутренние углы не равны 90°, значит, это параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. У этой фигуры стороны равны по длине, значит, это ромб.
Все внутренние углы не равны 90°, значит, это параллелограмм или ромб. Наконец, мы проверяем, все ли стороны равны по длине. У этой фигуры стороны равны по длине, значит, это ромб.
Следовательно, это ромб.
Форма также является параллелограммом и четырехугольником. Этот вопрос, однако, требовал наиболее конкретного названия формы.
На основе формы, которую вы видите, перечислите все имена формы. Фигура нарисована в масштабе
Обе пары противоположных сторон не параллельны. Это означает, что фигура может быть только комбинацией следующих элементов: трапеция, воздушный змей или четырехугольник.
Форма определенно является четырехугольником, потому что у него четыре стороны. У него нет особых свойств: у него нет ни параллельных сторон, ни прямых углов, ни сторон, равных по длине. Следовательно, это всего лишь четырехугольник.
На основе формы, которую вы видите, перечислите все имена формы. Фигура нарисована в масштабе
Обе пары противоположных сторон не параллельны.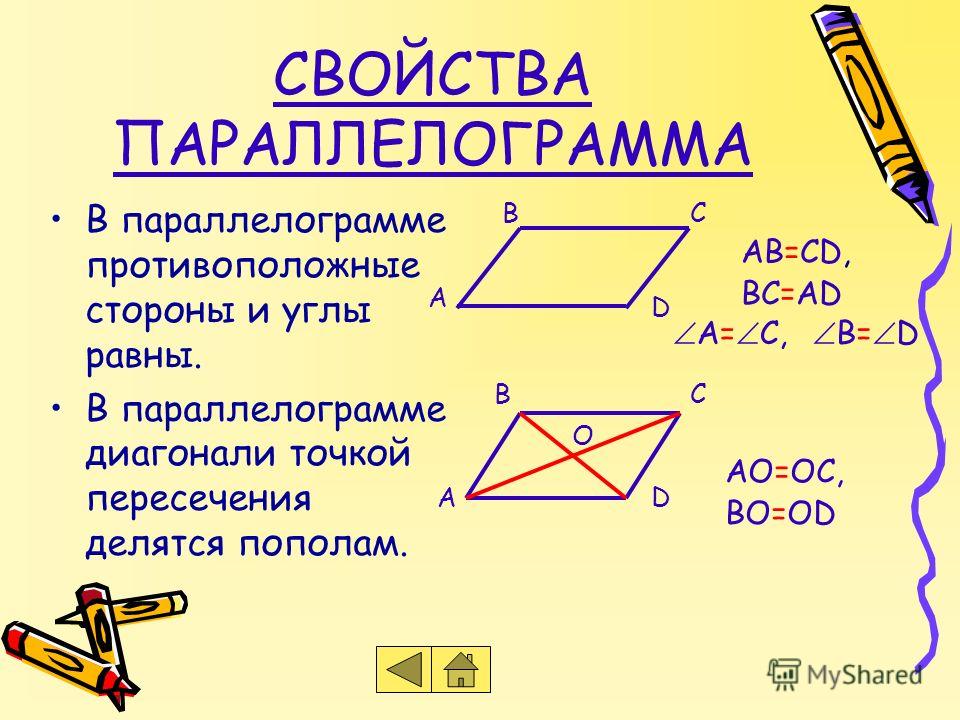 Это означает, что фигура может быть только комбинацией следующих элементов: трапеция, воздушный змей или четырехугольник.
Это означает, что фигура может быть только комбинацией следующих элементов: трапеция, воздушный змей или четырехугольник.
Форма определенно является четырехугольником, потому что у него четыре стороны. Это также воздушный змей, потому что у него две пары смежных сторон одинаковой длины. Это не может быть квадрат или прямоугольник, потому что у него нет прямых углов. Он не может быть параллелограммом или трапецией, потому что у него нет параллельных сторон. И это не ромб, потому что четыре стороны не имеют одинаковой длины.
Следовательно, правильный ответ: воздушный змей и четырехугольник.
На основе формы, которую вы видите, перечислите все имена формы. Фигура нарисована в масштабе
Обе пары противоположных сторон параллельны. Это означает, что эта фигура может принадлежать к одной или нескольким из следующих групп: квадрат, ромб, прямоугольник или параллелограмм.
Данная форма является квадратом. Тем не менее, это также прямоугольник. Квадрат также является параллелограммом, потому что у него параллельные стороны; и это тоже ромб, просто у него прямые углы. Квадрат — это еще и воздушный змей, трапеция и, конечно же, четырехугольник.
Квадрат также является параллелограммом, потому что у него параллельные стороны; и это тоже ромб, просто у него прямые углы. Квадрат — это еще и воздушный змей, трапеция и, конечно же, четырехугольник.
Следовательно, правильный ответ: квадрат, прямоугольник, ромб, параллелограмм, воздушный змей, трапеция и четырехугольник.
Найдите площадь
Постройте так, чтобы
был ромбом (диагонали делят пополам под прямым углом)
Так как ромб . Мы построили так, что . Следовательно .
В и :
Следовательно (правая сторона)
Следовательно и так прямоугольник (обе пары противоположных сторон равны по длине и все внутренние углы равны 90°).
Нам дана длина и . Поскольку он прямоугольный, мы можем использовать теорему Пифагора, чтобы найти длину :
Мы также знаем, что и так .
Следовательно, площадь прямоугольника:
Мы почти у цели. Теперь нам нужно вычислить площадь треугольника и вычесть ее из площади прямоугольника, чтобы получить площадь .

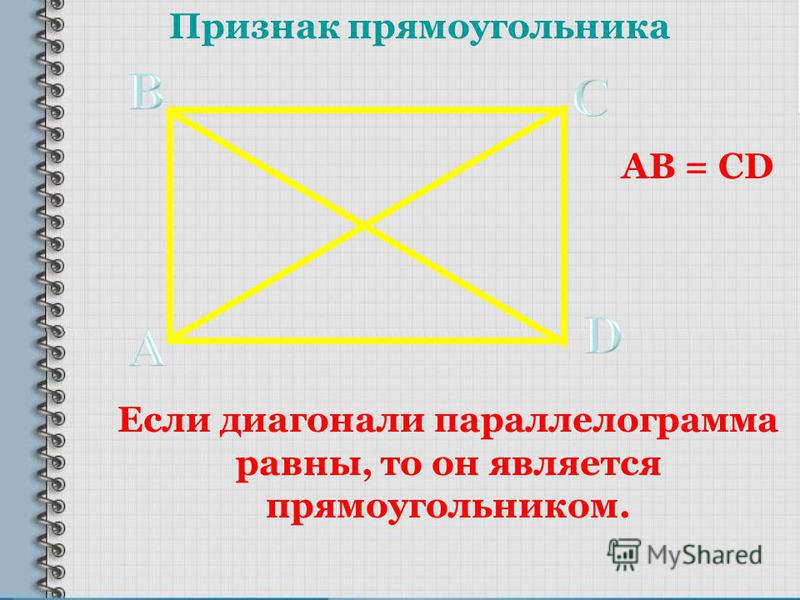

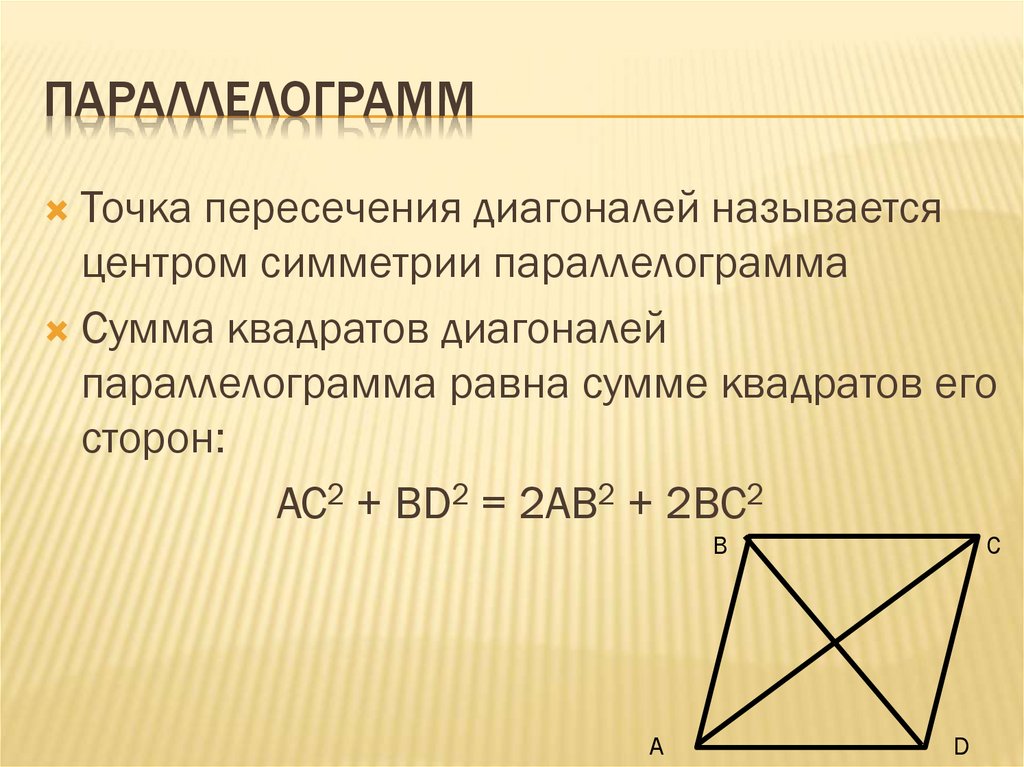 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.