| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град.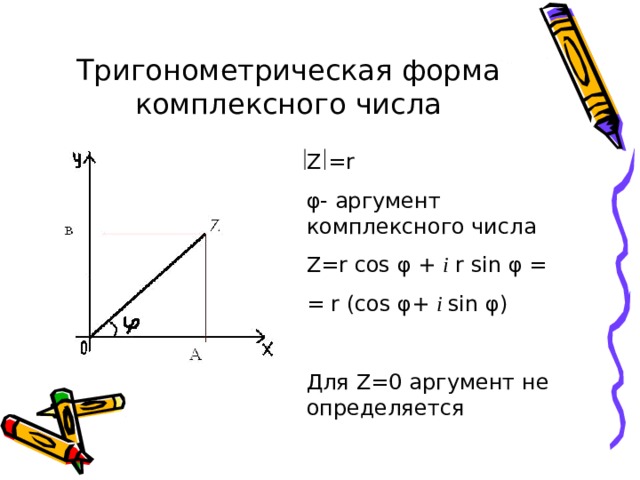 ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Урок 40. тригонометрическая форма комплексного числа — Алгебра и начала математического анализа — 11 класс
Алгебра и начала математического анализа, 11 класс
Урок №40. Тригонометрическая форма комплексного числа.
Перечень вопросов, рассматриваемых в теме
1) понятие модуля комплексного числа;
2) понятие тригонометрической формы комплексного числа;
3) перевод комплексного числа в тригонометрическую форму.
Глоссарий по теме
Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.
Для этого рассмотрим формулы для нахождения в зависимости от а и b.
1.
2.
3.
4.
5.
6.
7.
8.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н. Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Е. и др., Учебник комплект под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е.Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл.– М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Комплексные числа имеют три формы, две из них мы уже изучили — алгебраическую и геометрическую.
Но в электротехнике, электрооборудовании, электронике, автоматике и других дисциплинах комплексное число записывается в тригонометрической форме.
Например: при работе трансформатора идет нагрев обмоток — активное сопротивление R, катушка выделяет электромагнитные волны — реактивное сопротивление. Сняли замеры трансформатора
2 + 7 i ,
где 2 Ом — активное сопротивление,
7 Ом — реактивное сопротивление
Тригонометрическая форма комплексного числа r(cos φ+sin φ).
На любом трансформаторе стоит маркировка cos φ=. Это энергетический показатель ГОС стандартов. Он показывает эффективность работы, КПД, cos φ- активный показатель мощности, тока, напряжения. sin φ- реактивный показатель.
Любое комплексное число (кроме нуля) z=a+bi можно записать в тригонометрической форме: z=|z|∙(cosφ+isinφ), где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа.
Изобразим на комплексной плоскости число z=a+bi . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что a>0, b>0 :
Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа z стандартно обозначают: |z| или r.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедлива для любых значений a и b.
Данная формула справедлива для любых значений a и b.
Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.
Аргумент комплексного числа z стандартно обозначают: φ или arg z.
Из геометрических соображений получается следующая формула для нахождения аргумента:
Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
Для этого рассмотрим формулы для нахождения в зависимости от а и b.
1.
2.
3.
4.
5.
6.
7.
8.
Пример Представим в тригонометрической форме число z= -2+4i. Найдем его модуль и аргумент.
Поскольку a<0, b>0, то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
— число z в тригонометрической форме.
Разбор решения заданий тренировочного модуля
№1. Тип задания: единичный выбор
Представить в тригонометрической форме число z= -1+2i.
Найдем его модуль и аргумент.
Поскольку a<0, b>0, то – вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение arctg 2, поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:
— число z в тригонометрической форме.
Значит, верный ответ 1
№2. Тип задания: ввод с клавиатуры пропущенных элементов в тексте.
Найдите куб суммы z= (3+4i)3=_____________
Решение:
Возведем данное выражение в третью степень
Упрощаем полученное выражение, учитывая, что i2=-1
Ответ:
1.
 4.3. Тригонометрическая форма записи комплексных чисел
4.3. Тригонометрическая форма записи комплексных чисел
Глава 1. Арифметика
1.4.
1.4.3.
Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть
и φ = arg z. Тогда по определению аргумента имеем:
| z = a + bi = r(cos φ + i sin φ). |

Пример 1
Записать число в тригонометрической форме.
Показать решение
Арифметические действия над комплексными числами, записанными в тригонометрической форме, производятся следующим
образом. Пусть z1 = r1(cos φ1 + i sin φ1) и z2 = r2(cos φ2 + i sin φ2). Имеем:

Отсюда следует, что для того чтобы перемножить n комплексных чисел, нужно перемножить их модули и сложить аргументы: если φ1, φ2, …, φn – аргументы чисел z1, z2, …, zn, то
В частности, если все эти числа равны между собой, то получим формулу, позволяющую возводить комплексное число в любую натуральную степень.
Первая формула Муавра:
|
Пример 2
Вычислить если
Показать решение
Число z называется корнем степени
из комплексного числа w, если
Корень степени
обозначается
Пусть теперь число w фиксировано. Найдём z из уравнения
Найдём z из уравнения
Если w = 0, то у уравнения существует единственное решение z = 0.
Если w ≠ 0, то положим, что нам известно тригонометрическое представление числа w = r0(cos φ0 + i sin φ0), и будем искать число z также в тригонометрической форме: z = r(cos φ + i sin φ). Из определения аргумента и геометрической интерпретации комплексных чисел следует, что два комплексных числа, записанных в тригонометрической форме, равны тогда и только тогда, когда равны их модули, а аргументы отличаются на угол, кратный 2π. Имеем:
 .., n мы будем получать разные комплексные числа, а при k = n имеем:
.., n мы будем получать разные комплексные числа, а при k = n имеем:
Вторая формула Муавра:
|
Пример 3
Найти
Показать решение
Главная Онлайн учебники База репетиторов России Тренажеры по математике Подготовка к ЕГЭ 2017 онлайн |
|||||
|
|||||
|
|
|||||
Как записать комплексное число в алгебраической и тригонометрической форме
- Альфашкола
- Статьи
- Как записать комплексное число в алгебраической и тригонометрической форме
Комплесное число имеет три формы записи: алгебраическую, показательную и тригонометрическую. Проиллюстрируем на примере методы записи комплексного числа в алгебраической и тригонометрической форме и их использование для решения уравнений. 2}}\) и j=\(arctg {b \over a}\)
2}}\) и j=\(arctg {b \over a}\)
Для тог чтобы записать \({z}={{-2{\sqrt2}}\over1+i}\) в алгебраической форме, умножим числитель и знаменатель на сопряженное к знаменателю, т. е. на 1- i.
.
\(z=-{\sqrt2}+{\sqrt2}i\)- алгебраическая форма.
\(z=2{(cos{3π\over4}}+i sin{{3π\over4}})\)- тригонометрическая форма.
Применяя формулу для извлечения корня из комплексного числа:
Автор: Дмитрий Айстраханов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Лариса Александровна Новакова
Репетитор по математике
Стаж (лет)
Образование:
Амурский педагогический колледж, ООО «Издательство «Учитель»
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-8 класса. Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Люблю математику за то, что она воспитывает человека, приучая его к точности , учит логично мыслить, и в какой-то степени она способна привести ум в порядок. В своей работе использую не только традиционные формы и методы преподавания математики, но и новые современные технологии. Моя цель прежде всего, усилить мотивацию ребенка к познанию окружающего мира, продемонстрировать ему, что занятия математикой – это не получение отвлеченных от жизни знаний, а необходимая подготовка к жизни, поиск полезной информации и навыки ее применения в реальной жизни. Учитель пения, музыки.
Виктория Анатольевна Луковская
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский педагогический институт им. А.П. Чехова
А.П. Чехова
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 4-11 классов. Математика дисциплинирует и воспитывает ум, это основа для всех наук. Очень люблю работать с детьми! Уроки проходят в комфортной обстановке, к каждому ученику подхожу индивидуально, объясняю доступно и понятно. На занятиях применяю игровые приемы, схемы, графики и презентации, для того, чтобы учащимся было интересно.
Елизавета Бимбетовна Тулемисова
Репетитор по математике
Стаж (лет)
Образование:
Астраханский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Сердечно всех приветствую! Меня зовут Елизавета Бимбетовна, учитель высшей категории, Почетный работник воспитания и образования РФ, 2020 г. . Имею большой опыт обучения иностранным языкам (немецкий
и английский), последние 18 лет работала учителем в лингвистической гимназии. Есть богатый опыт работы с учебными пособиями иностранных издательств Hueber, Oxford, Cambridge, подготовки учеников к международным экзаменам. Владею коммуникативной методикой обучения и ориентируюсь на личность ученика, его пожелания, цели, уровень владения иностранным языком. Готовлю к ЕГЭ, ОГЭ, ВПР, результаты от 65 до 100 баллов. Выпускники успешно обучаются в ведущих вузах страны, а также за рубежом.
Буду рада сотрудничеству! До встречи!
. Имею большой опыт обучения иностранным языкам (немецкий
и английский), последние 18 лет работала учителем в лингвистической гимназии. Есть богатый опыт работы с учебными пособиями иностранных издательств Hueber, Oxford, Cambridge, подготовки учеников к международным экзаменам. Владею коммуникативной методикой обучения и ориентируюсь на личность ученика, его пожелания, цели, уровень владения иностранным языком. Готовлю к ЕГЭ, ОГЭ, ВПР, результаты от 65 до 100 баллов. Выпускники успешно обучаются в ведущих вузах страны, а также за рубежом.
Буду рада сотрудничеству! До встречи!
Похожие статьи
- Теорема Виета
- Одночлены
- Многоугольники
- Как легко разделить на 0,2
- ЕГЭ по математике, базовый уровень. Планиметрия.
 Равнобедренный треугольник (вариант 2)
Равнобедренный треугольник (вариант 2) - Полезные упражнения для тех, кто долго сидит за учебниками: зарядка для глаз
- Школьная газета: для кого, про что и зачем?
- Комплексы из-за внешности: учимся любить себя на примере звезд
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Тригонометрическая форма комплексных чисел. Комплексные числа в тригонометрической форме Тригонометрическая форма комплексного числа свойства
КОМПЛЕКСНЫЕ ЧИСЛА XI
§ 256. Тригонометрическая форма комплексных чисел
Пусть комплексному числу а + bi соответствует вектор OA > с координатами (а, b ) (см. рис. 332).
Обозначим длину этого вектора через r , а угол, который он образует с осью х , через φ . По определению синуса и косинуса:
По определению синуса и косинуса:
a / r = cos φ , b / r = sin φ .
Поэтому а = r cos φ , b = r sin φ . Но в таком случае комплексное число а + bi можно записать в виде:
а + bi = r cos φ + ir sin φ = r (cos φ + i sin φ ).
Как известно, квадрат длины любого вектора равен сумме квадратов его координат. Поэтому r 2 = a 2 + b 2 , откуда r = √a 2 + b 2
Итак, любое комплексное число а + bi можно представить в виде :
а + bi = r (cos φ + i sin φ ), (1)
где r = √a 2 + b 2 , а угол φ определяется из условия:
Такая форма записи комплексных чисел называется тригонометрической .
Число r в формуле (1) называется модулем , а угол φ — аргументом , комплексного числа а + bi .
Если комплексное число а + bi не равно нулю, то модуль его положителен; если же а + bi = 0, то а = b = 0 и тогда r = 0.
Модуль любого комплексного числа определен однозначно.
Если комплексное число а + bi не равно нулю, то аргумент его определяется формулами (2) однозначно с точностью до угла, кратного 2π . Если же а + bi = 0, то а = b = 0. В этом случае r = 0. Из формулы (1) легко понять, что в качестве аргумента φ в данном случае можно выбрать любой угол: ведь при любом φ
0 (cos φ + i sin φ ) = 0.
Поэтому аргумент нуля не определен.
Модуль комплексного числа r иногда обозначают | z |, а аргумент arg z . Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.
Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.
Пример. 1 . 1 + i .
Найдем модуль r и аргумент φ этого числа.
r = √ 1 2 + 1 2 = √ 2 .
Следовательно, sin φ = 1 / √ 2 , cos φ = 1 / √ 2 , откуда φ = π / 4 + 2n π .
Таким образом,
1 + i = √ 2 ,
где п — любое целое число. Обычно из бесконечного множества значений аргумента комплексного числа выбирают то, которое заключено между 0 и 2π . В данном случае таким значением является π / 4 . Поэтому
1 + i = √ 2 (cos π / 4 + i sin π / 4)
Пример 2. Записать в тригонометрической форме комплексное число √ 3 — i . Имеем:
r = √ 3+1 = 2, cos φ = √ 3 / 2 , sin φ = — 1 / 2
Поэтому с точностью до угла, кратного 2π , φ = 11 / 6 π ; следовательно,
√ 3
— i = 2(cos 11 / 6 π + i sin 11 / 6 π ).
Пример 3 Записать в тригонометрической форме комплексное число i .
Комплексному числу i соответствует вектор OA > , оканчивающийся в точке А оси у с ординатой 1 (рис. 333). Длина такого вектора равна 1, а угол, который он образует с осью абсцисс, равен π / 2 . Поэтому
i = cos π / 2 + i sin π / 2 .
Пример 4. Записать в тригонометрической форме комплексное число 3.
Комплексному числу 3 соответствует вектор OA > х абсциссой 3 (рис. 334).
Длина такого вектора равна 3, а угол, который он образует с осью абсцисс, равен 0. Поэтому
3 = 3 (cos 0 + i sin 0),
Пример 5. Записать в тригонометрической форме комплексное число -5.
Комплексному, числу -5 соответствует вектор OA >
, оканчивающийся в точке оси х с абсциссой -5 (рис. 335). Длина такого вектора равна 5, а угол, который он образует с осью абсцисс, равен π . Поэтому
335). Длина такого вектора равна 5, а угол, который он образует с осью абсцисс, равен π . Поэтому
5 = 5(cos π + i sin π ).
Упражнения
2047. Данные комплексные числа записать в тригонометрической форме, определив их модули и аргументы:
1) 2 + 2√3 i , 4) 12i — 5; 7).3i ;
2) √3 + i ; 5) 25; 8) -2i ;
3) 6 — 6i ; 6) — 4; 9) 3i — 4.
2048. Указать на плоскости множества точек, изображающих комплексные числа, модули г и аргументы ф которых удовлетворяют условиям:
1) r = 1, φ = π / 4 ; 4) r φ π / 6 ;
2) r =2; 5) 2 r φ
3) r 3; 6) φ = π / 3 ; 9) 1 r
10) 0 φ π / 2 .
2049. Могут ли модулем комплексного числа одновременно быть числа r и — r ?
2050. Могут ли аргументом комплексного числа одновременно быть углы φ и — φ ?
Могут ли аргументом комплексного числа одновременно быть углы φ и — φ ?
Данные комплексные числа представить в тригонометрической форме, определив их модули и аргументы:
2051*. 1 + cos α + i sin α . 2054*. 2(cos 20° — i sin 20°).
2052*. sin φ + i cos φ . 2055*. 3(- cos 15° — i sin 15°).
3.1. Полярные координаты
На плоскости часто применяется полярная система координат . Она определена, если задана точка O, называемая полюсом , и исходящий из полюса луч (для нас это ось Ox) – полярная ось. Положение точки M фиксируется двумя числами: радиусом (или радиус-вектором) и углом φ между полярной осью и вектором . Угол φ называется полярным углом; измеряется в радианах и отсчитывается от полярной оси против часовой стрелки.
Положение точки в полярной системе координат задается упорядоченной парой чисел (r; φ). У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r 1 ; φ 1) сопоставляется одна и та же точка, если .
У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r 1 ; φ 1) сопоставляется одна и та же точка, если .
Для прямоугольной системы координат xOy декартовы координаты точки легко выражаются через ее полярные координаты следующим образом:
3.2. Геометрическая интерпретация комплексного числа
Рассмотрим на плоскости декартову прямоугольную систему координат xOy .
Любому комплексному числу z=(a, b) ставится в соответствие точка плоскости с координатами (x, y ), где координата x = a, т.е. действительной части комплексного числа, а координата y = bi – мнимой части.
Плоскость, точками которой являются комплексные числа – комплексная плоскость.
На рисунке комплексному числу z = (a, b) соответствует точка M(x, y) .
Задание. Изобразите на координатной плоскости комплексные числа:
3. 3. Тригонометрическая форма комплексного числа
3. Тригонометрическая форма комплексного числа
Комплексное число на плоскости имеет координаты точки M (x; y) . При этом:
Запись комплексного числа — тригонометрическая форма комплексного числа.
Число r называется модулем комплексного числа z и обозначается . Модуль – неотрицательное вещественное число. Для .
Модуль равен нулю тогда и только тогда, когда z = 0, т.е. a = b = 0 .
Число φ называется аргументом z и обозначается . Аргумент z определен неоднозначно, как и полярный угол в полярной системе координат, а именно с точностью до слагаемого кратного 2π.
Тогда принимаем: , где φ – наименьшее значение аргумента. Очевидно, что
.
При более глубоком изучении темы вводится вспомогательный аргумент φ*, такой, что
Пример 1 . Найти тригонометрическую форму комплексного числа .
Решение. 1) считаем модуль: ;
2) ищем φ: ;
3) тригонометрическая форма:
Пример 2. Найти алгебраическую форму комплексного числа .
Найти алгебраическую форму комплексного числа .
Здесь достаточно подставить значения тригонометрических функций и преобразовать выражение:
Пример 3. Найти модуль и аргумент комплексного числа ;
1) ;
2) ; φ – в 4 четверти:
3.4. Действия с комплексными числами в тригонометрической форме
· Сложение и вычитание удобнее выполнять с комплексными числами в алгебраической форме:
· Умножение – при помощи несложных тригонометрических преобразований можно показать, что при умножении модули чисел перемножаются, а аргументы складываются: ;
В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. Показательная форма в практических заданиях встречается значительно реже. Рекомендую закачать и по возможности распечатать тригонометрические таблицы , методический материал можно найти на странице Математические формулы и таблицы. Без таблиц далеко не уехать.
Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:
Где
–
этомодуль комплексного числа ,
а
–аргумент комплексного числа .
Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:
Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря,модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа стандартно обозначают:или
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедливадля любых значений «а» и «бэ».
Примечание : модуль комплексного числа представляет собой обобщение понятия модуля действительного числа , как расстояния от точки до начала координат.
Аргументом
комплексного числа называетсяугол между положительной
полуосью действительной оси
и
радиус-вектором, проведенным из начала
координат к соответствующей точке. Аргумент не определён для единственного
числа:.
Аргумент не определён для единственного
числа:.
Рассматриваемый принцип фактически схож с полярными координатами, где полярный радиус и полярный угол однозначно определяют точку.
Аргумент комплексного числа стандартно обозначают:или
Из геометрических соображений получается следующая формула для нахождения аргумента:
. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.
Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.
Пример 7
Представить в тригонометрической форме комплексные числа: ,,,. Выполним чертёж:
На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:
Запомним намертво, модуль – длина (которая всегда неотрицательна ), аргумент – угол
1)
Представим в тригонометрической форме
число
. Найдем его модуль и аргумент. Очевидно,
что.
Формальный расчет по формуле:.
Очевидно,
что(число
лежит непосредственно на действительной
положительной полуоси). Таким образом,
число в тригонометрической форме:.
Найдем его модуль и аргумент. Очевидно,
что.
Формальный расчет по формуле:.
Очевидно,
что(число
лежит непосредственно на действительной
положительной полуоси). Таким образом,
число в тригонометрической форме:.
Ясно, как день, обратное проверочное действие:
2) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:.
Используя , легко обратно получить алгебраическую форму числа (заодно выполнив проверку):
3) Представим в тригонометрической форме число . Найдем его модуль и
аргумент. Очевидно, что . Формальный расчет по формуле:
Очевидно, что (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:.
Проверка:
4) И четвёртый интересный случай. Очевидно, что. Формальный расчет по формуле:.
Аргумент
можно записать двумя способами: Первый
способ:
(270
градусов), и, соответственно:. Проверка:
Проверка:
Однако более стандартно следующее правило: Если угол больше 180 градусов , то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить,
что и– это один и тот же угол.
Таким образом, запись принимает вид:
Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:
Кстати, полезно вспомнить внешний вид и свойства тригонометрических и обратных тригонометрических функций, справочные материалы находятся в последних параграфах страницы Графики и свойства основных элементарных функций. И комплексные числа усвоятся заметно легче!
В оформлении простейших примеров так и следует записывать: «очевидно, что модуль равен… очевидно, что аргумент равен…» . Это действительно очевидно и легко решается устно.
Перейдем
к рассмотрению более распространенных
случаев. C
модулем проблем не возникает, всегда
следует использовать
формулу
.
А вот формулы для нахождения аргумента
будут разными, это зависит от того, в
какой координатной четверти лежит число.
При этом возможны три варианта (их
полезно переписать):
C
модулем проблем не возникает, всегда
следует использовать
формулу
.
А вот формулы для нахождения аргумента
будут разными, это зависит от того, в
какой координатной четверти лежит число.
При этом возможны три варианта (их
полезно переписать):
1) Если (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле.
2) Если (2-ая координатная четверть), то аргумент нужно находить по формуле.
3) Если (3-я координатная четверть), то аргумент нужно находить по формуле.
Пример 8
Представить в тригонометрической форме комплексные числа: ,,,.
Коль скоро есть готовые формулы, то чертеж выполнять не обязательно. Но есть один момент: когда вам предложено задание представить число в тригонометрической форме, то чертёж лучше в любом случае выполнить . Дело в том, что решение без чертежа часто бракуют преподаватели, отсутствие чертежа – серьёзное основание для минуса и незачета.
Представляем
в комплексной форме числа
и,
первое и третье числа будут для
самостоятельного решения.
Представим в тригонометрической форме число . Найдем его модуль и аргумент.
Поскольку (случай 2), то
–вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:– числов тригонометрической форме.
Представим в тригонометрической форме число . Найдем его модуль и аргумент.
Поскольку (случай 1), то(минус 60 градусов).
Таким образом:
–число в тригонометрической форме.
А вот здесь, как уже отмечалось, минусы не трогаем .
Кроме забавного графического метода проверки, существует и проверка аналитическая, которая уже проводилась в Примере 7. Используем таблицу значений тригонометрических функций , при этом учитываем, что угол – это в точности табличный угол(или 300 градусов):– числов исходной алгебраической форме.
Числа
ипредставьте
в тригонометрической форме самостоятельно.
Краткое решение и ответ в конце урока.
В конце параграфа кратко о показательной форме комплексного числа.
Любое комплексное число (кроме нуля) можно записать в показательной форме:
Где – это модуль комплексного числа, а– аргумент комплексного числа.
Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде .
Например, для числа предыдущего примера у нас найден модуль и аргумент:,. Тогда данное число в показательной форме запишется следующим образом:.
Число в показательной форме будет выглядеть так:
Число – так:
Единственный совет – не трогаем показатель экспоненты, там не нужно переставлять множители, раскрывать скобки и т.п. Комплексное число в показательной форме записывается строго по форме .
Действия над комплексными числами, записанными в алгебраической форме
Алгебраической формой комплексного числа z = (a , b ). называется алгебраическое выражение вида
называется алгебраическое выражение вида
z = a + bi .
Арифметические операции над комплексными числами z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i , записанными в алгебраической форме, осуществляются следующим образом.
1. Сумма (разность) комплексных чисел
z 1 ± z 2 = (a 1 ± a 2) + (b 1 ±b 2)∙i ,
т.е. сложение (вычитание) осуществляются по правилу сложения многочленов с приведением подобных членов.
2. Произведение комплексных чисел
z 1 ∙z 2 = (a 1 ∙a 2 — b 1 ∙b 2) + (a 1 ∙b 2 + a 2 ∙b 1)∙i ,
т.е. умножение производится по обычному правилу умножения многочленов, с учетом того, что i 2 = 1.
3. Деление двух комплексных чисел осуществляется по следующему правилу:
, (z 2 ≠ 0),
т. е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.
е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.
Возведение в степень комплексных чисел определяется следующим образом:
Легко показать, что
Примеры .
1. Найти сумму комплексных чисел z 1 = 2 – i и z 2 = – 4 + 3i.
z 1 + z 2 = (2 + (–1)∙i )+ (–4 + 3i ) = (2 + (–4)) + ((–1) + 3) i = –2+2i.
2. Найти произведение комплексных чисел z 1 = 2 – 3i и z 2 = –4 + 5i.
= (2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i )+ 2∙5i – 3i∙ 5i = 7+22i.
3. Найти частное z от деления z 1 = 3 – 2на z 2 = 3 – i.
z = .
4. Решить уравнение: , x и y Î R .
(2x + y ) + (x + y )i = 2 + 3i.
В силу равенства комплексных чисел имеем:
откуда x = –1 , y = 4.
5. Вычислить: i 2 , i 3 , i 4 , i 5 , i 6 , i -1 , i -2 .
6. Вычислить , если .
.
7. Вычислить число обратное числу z =3-i .
Комплексные числа в тригонометрической форме
Комплексной плоскостью называется плоскость с декартовыми координатами (x, y ), если каждой точке с координатами (a, b ) поставлено в соответствие комплексное число z = a + bi . При этом ось абсцисс называется действительной осью , а ось ординат – мнимой . Тогда каждое комплексное число a + bi геометрически изображается на плоскости как точка A (a, b ) или вектор .
Следовательно, положение точки А (и, значит, комплексного числа z ) можно задать длиной вектора | | = r и углом j , образованным вектором | | с положительным направлением действительной оси. Длина вектора называется модулем комплексного числа и обозначается | z |=r , а угол j называется аргументом комплексного числа и обозначается j = arg z .
Ясно, что | z | ³ 0 и | z | = 0 Û z = 0.
Из рис. 2 видно, что .
Аргумент комплексного числа определяется неоднозначно, а с точностью до 2pk, k Î Z .
Из рис. 2 видно также, что если z=a+bi и j=arg z, то
cosj = , sinj = , tgj = .
Если zÎ R и z > 0,то arg z = 0 +2pk ;
если z Î R и z 0,то arg z = p + 2pk ;
если z = 0, arg z не определен.
Главное значение аргумента определяется на отрезке 0 £ arg z £ 2p,
либо -p £ arg z £ p .
Примеры:
1. Найти модуль комплексных чисел z 1 = 4 – 3i и z 2 = –2–2i.
2. Определить на комплексной плоскости области, задаваемые условиями:
1) | z | = 5; 2) | z | £ 6; 3) | z – (2+i ) | £ 3; 4) 6 £ | z – i | £ 7.
Решения и ответы:
1) | z | = 5 Û Û — уравнение окружности радиусом 5 и с центром в начале координат.
2) Круг радиусом 6 с центром в начале координат.
3) Круг радиусом 3 с центром в точке z 0 = 2 + i .
4) Кольцо, ограниченное окружностями с радиусами 6 и 7 с центром в точке z 0 = i .
3. Найти модуль и аргумент чисел: 1) ; 2) .
1) ; а = 1, b = Þ ,
Þ j 1 = .
2) z 2 = –2 – 2i ; a = –2, b = -2 Þ ,
.
Указание: при определении главного аргумента воспользуйтесь комплексной плоскостью.
Таким образом: z 1 = .
2) , r 2 = 1, j 2 = , .
3) , r 3 = 1, j 3 = , .
4) , r 4 = 1, j 4 = , .
Лекция
Тригонометрическая форма комплексного числа
План
1.Геометрическое изображение комплексных чисел.
2. Тригонометрическая запись комплексных чисел.
Тригонометрическая запись комплексных чисел.
3.Действия над комплексными числами в тригонометрической форме.
Геометрическое изображение комплексных чисел.
а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M ( a ; b ) (рис.1).
Рисунок 1
б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис.2).
Рисунок 2
Пример 7. Постройте точки, изображающие комплексные числа: 1; — i ; — 1 + i ; 2 – 3 i (рис.3).
Рисунок 3
Тригонометрическая запись комплексных чисел.
Комплексное число z = a + bi можно задать с помощью радиус – вектора с координатами ( a ; b ) (рис.4).
Рисунок 4
Определение . Длина вектора
, изображающего комплексное число z , называется модулем этого числа и обозначается
или r .
Длина вектора
, изображающего комплексное число z , называется модулем этого числа и обозначается
или r .
Для любого комплексного числа z его модуль r = | z | определяется однозначно по формуле .
Определение . Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументом этого комплексного числа и обозначается А rg z или φ .
Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа
z
≠ 0 – величина многозначная и определяется с точностью до слагаемого 2πк (к = 0; — 1; 1; — 2; 2; …): Arg z = arg z + 2πк , где arg z – главное значение аргумента, заключенное в промежутке (-π; π] , то есть -π arg z ≤ π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку .
Эту формулу при r =1 часто называют формулой Муавра:
(cos φ + i sin φ) n = cos (nφ) + i sin (nφ), n N .
Пример 11. Вычислите (1 + i ) 100 .
Запишем комплексное число 1 + i в тригонометрической форме.
a = 1, b = 1 .
cos φ = , sin φ = , φ = .
(1+i) 100 = [ (cos + i sin )] 100 = ( ) 100 (cos ·100 + i sin ·100) = = 2 50 (cos 25π + i sin 25π) = 2 50 (cos π + i sin π) = — 2 50 .
4) Извлечение квадратного корня из комплексного числа.
При извлечении квадратного корня из комплексного числа a + bi имеем два случая:
если b > о , то ;
Формы записи комплексного числа: тригонометрическая, показательная
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel. ru Математика Алгебра Формы записи комплексного числа: тригонометрическая, показательная
ru Математика Алгебра Формы записи комплексного числа: тригонометрическая, показательная
В данной публикации рассмотрена тригонометрическая форма комплексного числа с интерпретацией на коордлинатной плоскости, формулами расчета аргумента и примером для лучшего понимания изложенного материала. Также представлена базовая информация по показательной форме данного типа числа.
- Тригонометрическая форма комплексного числа
- Показательная форма комплексного числа
Тригонометрическая форма комплексного числа
Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в тригонометрической форме следующим образом:
z = |z| ⋅ (cos φ + i ⋅ sin φ)
Чтобы было понятнее, покажем комплексное число на координатной плоскости. При этом, в качестве примера будем исходить из того, что a и b больше нуля.
Модуль комплексного числа |z| – это расстояние от начала координат до соответствующей точки на комплексной плоскости, другими словами, это длина зеленого вектора на чертеже выше.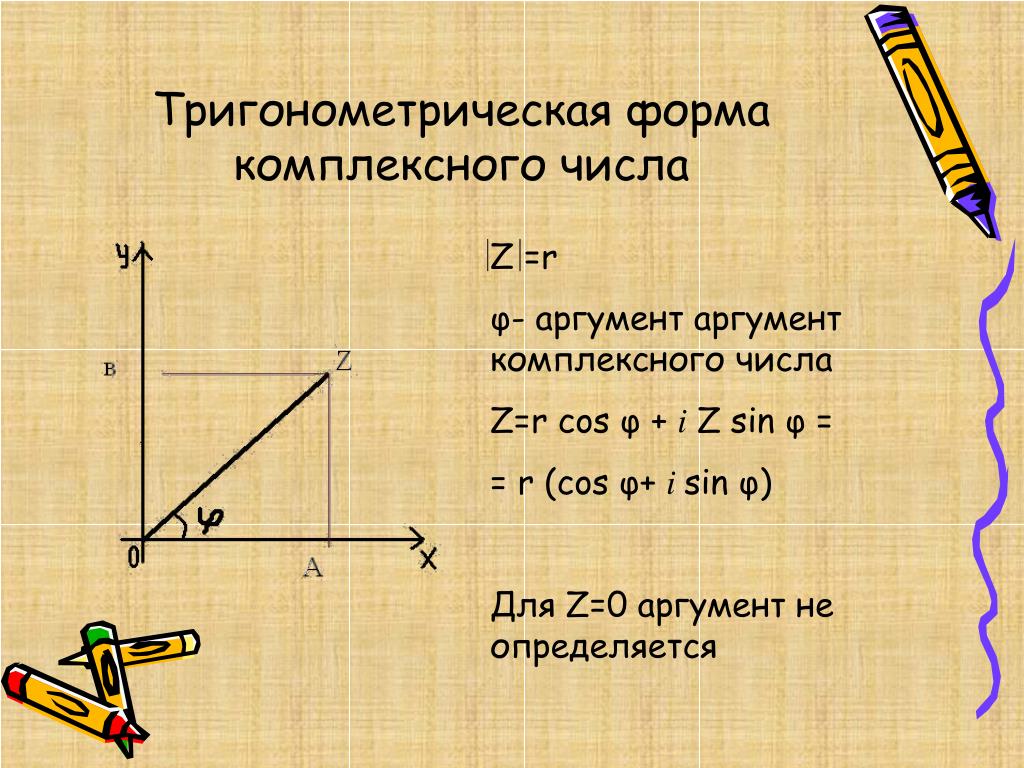
Исходя из теоремы Пифагора модуль вычисляется так:
Аргумент комплексного числа (φ) – угол между положительной полуосью действительной оси (RE) и вектором, который проведен из начала координат. Аргумент не существует для z = 0, может обозначаться как arg z.
Формула для расчета аргумента зависит от того, какие значения принимают a и b.
| a > 0 | 1-ая и 4-ая координатные четверти | ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-3.png" class="stbSkipLazy aligncenter size-full" width="120" height="271" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-3.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-3.png" class="stbSkipLazy aligncenter size-full" width="120" height="271" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-3.png" />»> |
| a < 0, b > 0 | 2-ая координатная четверть | ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-4.png" class="stbSkipLazy aligncenter size-full" width="156" height="345" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-4.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-4.png" class="stbSkipLazy aligncenter size-full" width="156" height="345" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-4.png" />»> |
| a < 0, b < 0 | 3-ая координатная плоскость | ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-5.png" class="stbSkipLazy aligncenter size-full" width="174" height="387" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-5.png" />» data-order=»<img src="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-5.png" class="stbSkipLazy aligncenter size-full" width="174" height="387" data-full="https://microexcel.ru/wp-content/uploads/2021/06/kompleksnye-chisla-trigonometriya-5.png" />»> |
Пример: представим в тригонометрической форме комплексное число z = 3i.
Решение:
a = 0, b = 3, следовательно:
Т.к. a = 0, значит вектор совпадает с осью ординат (направлен вверх), следовательно φ = 90°.
Таким образом, тригонометрическая форма числа z = 3i выглядит так:
z = 3 ⋅ (cos 90° + i ⋅ sin 90°)
Показательная форма комплексного числа
Любое комплексное число (за искл. нуля) вида z = a + bi можно записать в показательной форме:
нуля) вида z = a + bi можно записать в показательной форме:
z = |z| ⋅ e iφ, где:
- |z| – модуль комплексного числа;
- φ – его аргумент.
Примечание: показательная форма используется намного реже, чем тригонометрическая, поэтому базовой информации выше в большинстве случаев должно быть достаточно.
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Тригонометрическая форма – определение, пример и объяснение
Мы можем записать комплексные числа в терминах $r$ и $\theta$. Эта форма называется тригонометрической формой и является важной формой комплексных чисел, потому что намного легче найти корни и степени комплексных чисел, когда они находятся в их тригонометрических формах.
Эта форма называется тригонометрической формой и является важной формой комплексных чисел, потому что намного легче найти корни и степени комплексных чисел, когда они находятся в их тригонометрических формах.
Тригонометрическая форма комплексных чисел содержит расстояние координаты комплексного числа от начала координат и угол, образованный действительной осью, а также отрезок, соединяющий комплексное число и начало координат.
Мы часто используем тригонометрическую форму комплексных чисел, чтобы проиллюстрировать их как величины с расстоянием и направлением. Когда мы хотим найти степени и корни комплексных чисел, их также легче найти, когда комплексные числа представлены в тригонометрической форме.
В этой статье мы узнаем следующее:
- Два важных компонента комплексных чисел в тригонометрической или полярной форме.
- Преобразование комплексных чисел из стандартной формы в тригонометрическую форму.
- Нахождение частного и произведения двух комплексных чисел в тригонометрических формах.

Давайте продолжим и углубимся в определение комплексных чисел в тригонометрических формах.
Что такое тригонометрическая форма?
Тригонометрическая форма комплексных чисел также называется полярной формой комплексных чисел. Поэтому обязательно проверьте свои знания о полярных формах.
Тригонометрическая форма комплексного числа содержит модуль $r$ и аргумент $\theta$, представляющий комплексное число. Общая тригонометрическая форма комплексных чисел: $r(\cos\theta + i\sin\theta)$.
Из графика видно, как были получены тригонометрические или полярные формы комплексных чисел. Поскольку $a = r \cos\theta$ и $b = r \sin\theta$, $a + bi = r(\cos \theta + i\sin \theta)$.
Отсюда $r$ представляет модуль, а $\theta$ показывает угол (или аргумент), образованный $r$ и действительной осью.
Эти два компонента являются важными при представлении комплексных чисел в тригонометрической форме.
Как записать комплексные числа в тригонометрической форме? 9{\circ})$ в полярной или тригонометрической форме.

Мы можем использовать аналогичный процесс при записи других комплексных чисел в их соответствующих тригонометрических формах, поэтому обязательно попробуйте приведенный выше пример самостоятельно?
Как умножать и делить комплексные числа в тригонометрической форме?
Мы также можем умножать и делить комплексные числа в тригонометрической форме. Допустим, у нас есть два комплексных числа, $z_1 = r_1(\cos \theta_1 + i\sin \theta_1)$ и $z_2 = r_2(\cos \theta_2 + i\sin \theta_2)$, мы можем найти их произведение по формуле : 92$ как $-1$.
$ \begin{align} [r_1(\cos \theta_ 1 + i\sin \theta_1)][r_2(\cos \theta_2 + i\sin \theta_2) ] &= (r_1r_2)[(\cos \ theta_1 + i \sin \theta_1)(\cos \theta_2 + i \sin \theta_2)] \\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ (i\sin \theta_1 i \sin \theta_2)]\\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i \sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ (i^2\sin \theta_1 \sin \theta_2)]\\&= (r_1r_2)[(\cos \theta_1\cos \theta_2) + (\cos \theta_1i\sin\theta_2) + (i\sin\theta_1\cos \theta_2)+ -\sin \theta_1 \sin \theta_2] \\&=(r_1r_2)[(\cos \theta_1\cos \ theta_2-\sin \theta_1 \sin \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) ]\\&=(r_1r_2)[\cos(\theta_1 + \theta_2) + i(\cos \theta_1\sin\theta_2 + \sin\theta_1\cos \theta_2) \\&=(r_1r_2)[(\cos \theta_1\cos \theta_2-\sin \theta_1 \sin \theta_2) + i \sin (\theta_1 + \theta_2) ] \end{выровнено}$
Мы можем применить аналогичный процесс, чтобы вывести формулу для отношения $z_1$ и $z_2$. Но мы оставим это для вас, чтобы вы могли попробовать сами. ( Подсказка : используйте метод ФОЛЬГИ и разностные свойства синуса и косинуса).
Но мы оставим это для вас, чтобы вы могли попробовать сами. ( Подсказка : используйте метод ФОЛЬГИ и разностные свойства синуса и косинуса).
На данный момент имеем $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$.
Это означает, что нам не нужно преобразовывать комплексное число в тригонометрической форме в стандартную форму, чтобы найти их произведение или частное. 9{-1} \dfrac{b}{a}\phantom{x}\end{aligned}$
Мы также научились умножать и делить два комплексных числа в тригонометрической форме. Для двух комплексных чисел $z_1 = r_1(\cos\theta_1 + i\sin\theta_1)$ и $z_2 = r_2(\cos\theta_2+ i\sin\theta_2)$ произведение и частное будут такими, как показано ниже:
- $z_1 z_2 = r_1r_2 [\cos(\theta_1 + \theta_2) + i\sin(\theta_1 + \theta_2)]$
- $\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} [\cos(\theta_1 – \theta_2) + i\sin(\theta_1 – \theta_2)]$
Давайте воспользуемся этими свойствами для решения некоторых примеров, показанных ниже. 2}$. Между тем аргумент или $\theta$ можно определить, взяв тангенс, обратный $\dfrac{b}{a}$. 9{\circ})\end{align}$
2}$. Между тем аргумент или $\theta$ можно определить, взяв тангенс, обратный $\dfrac{b}{a}$. 9{\circ})\end{align}$
5.2: Тригонометрическая форма комплексного числа
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7125
- Тед Сандстром и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Основные вопросы
Следующие вопросы предназначены для того, чтобы направлять наше изучение материала в этом разделе. Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
Изучив этот раздел, мы должны понять концепции, мотивированные этими вопросами, и быть в состоянии написать точные, связные ответы на эти вопросы.
- Что такое полярная (тригонометрическая) форма комплексного числа?
- Как умножить два комплексных числа в полярной форме? 909:20
- Как разделить одно комплексное число в полярной форме на ненулевое комплексное число в полярной форме?
Начало занятия
Если \(z = a + bi\) комплексное число, то мы можем нанести \(z\) на плоскость, как показано на рисунке \(\PageIndex{1}\). В этой ситуации пусть \(r\) будет величиной \(z\) (то есть расстоянием от \(z\) до начала координат), а \(\theta\) — углом \(z\). ) делает с положительной действительной осью, как показано на рисунке \(\PageIndex{1}\).
Используйте тригонометрию прямоугольного треугольника, чтобы записать \(a\) и \(b\) через \(r\) и \(\theta\).
Объясните, почему мы можем записать \(z\) как
\[z = r(\cos(\theta) + i\sin(\theta)). \]
\]
Когда мы пишем \(z\) в форме, заданной уравнением \(\PageIndex{1}\):, мы говорим, что \(z\) записывается в тригонометрической форме (или полярной форме).
Угол \(\theta\) называется аргументом аргумента комплексного числа \(z\), а действительное число \(r\) равно 9{2}}\]
\[a = r\cos(\theta)\]
\[b = r\sin(\theta)\]
Умножение комплексных чисел сложнее, чем сложение комплексных чисел. Чтобы лучше понять произведение комплексных чисел, мы сначала исследуем тригонометрическую (или полярную) форму комплексного числа. Эта тригонометрическая форма связывает алгебру с тригонометрией и будет полезна для быстрого и простого нахождения степеней и корней комплексных чисел.
Примечание
Слово полярный здесь исходит из того, что этот процесс можно рассматривать как происходящий с полярными координатами.
Рисунок \(\PageIndex{1}\): тригонометрическая форма комплексного числа.
Чтобы найти \(\theta\), мы должны рассмотреть случаи.
- Если \(z = 0 = 0 + 0i\), то \(r = 0\) и \(\theta\) могут иметь любое действительное значение.
- Если \(z \neq 0\) и \(a \neq 0\), то \(\tan(\theta) = \dfrac{b}{a}\).
- Если \(z \neq 0\) и \(a = 0\) (поэтому \(b \neq 0\)), то 9{2}} = \sqrt{2}\), а аргумент \(z\) равен \(\arctan(\dfrac{-1}{1}) = -\dfrac{\pi}{4}\) .
Итак, \[z = \sqrt{2}(\cos(-\dfrac{\pi}{4}) + \sin(-\dfrac{\pi}{4})) = \sqrt{2}(\ cos(\dfrac{\pi}{4}) — \sin(\dfrac{\pi}{4})\]
2. Напомним, что \(\cos(\dfrac{\pi}{6}) = \dfrac{\sqrt{3}}{2}\) и \(\sin(\dfrac{\pi}{6} ) = \dfrac{1}{2}\). Итак, \[3(\cos(\dfrac{\pi}{6} + i\sin(\dfrac{\pi}{6})) = 3(\dfrac{\sqrt{3}}{2} + \ dfrac{1}{2}i) = \dfrac{3\sqrt{3}}{2} + \dfrac{3}{2}i\]
9{i\theta} = r(\cos(\theta) + i\sin(\theta))\]Произведения комплексных чисел в полярной форме
Существует важная формула произведения комплексных чисел, которую дает полярная форма.
 Проиллюстрируем на примере.
Проиллюстрируем на примере.Пример \(\PageIndex{1}\): произведения комплексных чисел в полярной форме
Пусть \(w = -\dfrac{1}{2} + \dfrac{\sqrt{3}}{2}i \) и \(z = \sqrt{3} + i\). Используя наше определение произведения комплексных чисел, мы видим, что
\[wz = (\sqrt{3} + i)(-\dfrac{1}{2} + \dfrac{\sqrt{3}}{2} i) = -\sqrt{3} + i.\] 9{2}} = 2\) и аргумент \(z\) удовлетворяет \(\tan(\theta) = \dfrac{1}{\sqrt{3}}\).
Поскольку \(z\) находится в первом квадранте, мы знаем, что \(\theta = \dfrac{\pi}{6}\) и полярная форма \(z\) равна \[z = 2[ \cos(\dfrac{\pi}{6}) + i\sin(\dfrac{\pi}{6})]\]
Мы также можем найти полярную форму комплексного произведения \(wz\). Здесь мы имеем \(|wz| = 2\), а аргумент \(zw\) удовлетворяет условию \(\tan(\theta) = -\dfrac{1}{\sqrt{3}}\). Поскольку \(wz\) находится в квадранте II, мы видим, что \(\theta = \dfrac{5\pi}{6}\) и полярная форма \(wz\) равна \[wz = 2[\cos (\dfrac{5\pi}{6}) + i\sin(\dfrac{5\pi}{6})].\]
Когда мы сравниваем полярные формы \(w, z\) и \(wz\), мы можем заметить, что \(|wz| = |w||z|\) и что аргумент \(zw\ ) равно \(\dfrac{2\pi}{3} + \dfrac{\pi}{6}\) или сумме аргументов \(w\) и \(z\).
 Это оказывается правдой в целом.
Это оказывается правдой в целом.Как мы покажем, результат примера \(\PageIndex{1}\) не случаен. В общем, у нас есть следующий важный результат о произведении двух комплексных чисел.
Умножение комплексных чисел в полярной форме
Пусть \(w = r(\cos(\alpha) + i\sin(\alpha))\) и \(z = s(\cos(\beta) + i\sin(\beta))\) быть комплексными числами в полярной форме. Тогда полярная форма комплексного произведения \(wz\) определяется как
\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]
Это утверждает, что для умножения двух комплексных чисел в полярной форме мы умножаем их нормы и складываем их аргументы.
Чтобы понять, почему этот результат в целом верен, пусть \(w = r(\cos(\alpha) + i\sin(\alpha))\) и \(z = s(\cos(\beta) + i\sin(\beta))\) — комплексные числа в полярной форме. Мы будем использовать тождества косинуса и синуса суммы углов, чтобы найти \(wz\):
\[w = [r(\cos(\alpha) + i\sin(\alpha))][s(\cos(\beta) + i\sin(\beta))] = rs([\cos (\alpha)\cos(\beta) — \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) + \cos(\beta)\sin( \alpha)]\]
Теперь воспользуемся тождествами косинуса и суммы и увидим, что
\(\cos(\alpha + \beta) = \cos(\alpha)\cos(\beta) — \sin(\ альфа)\sin(\beta)\) и \(\sin(\alpha + \beta) = \cos(\alpha)\sin(\beta) + \cos(\beta)\sin(\alpha)\) .

Используя уравнение (1) и эти тождества, мы видим, что
\[w = rs([\cos(\alpha)\cos(\beta) — \sin(\alpha)\sin(\beta)]) + i[\cos(\alpha)\sin(\beta) ) + \cos(\beta)\sin(\alpha)] = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta))\]
Иллюстрация этого дается в Рисунок \(\PageIndex{2}\). Формула умножения комплексных чисел в полярной форме говорит нам, что для умножения двух комплексных чисел мы складываем их аргументы и умножаем их нормы.
Рисунок \(\PageIndex{2}\): Геометрическая интерпретация умножения комплексных чисел.
Упражнение \(\PageIndex{2}\)
Пусть \(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3} )]\) и \(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).
- Что такое \(|wz|\)?
- Каков аргумент \(wz\)?
- В каком квадранте находится \(wz\)? Объяснять.
- Определите полярную форму wz.
- Нарисуйте рисунок \(w\), \(z\) и \(wz\), иллюстрирующий действие сложного произведения.

- Ответить
1. Поскольку \(|w| = 3\) и \(|z| = 2\), мы видим, что
\[|wz| = |ш||г| = (3)(2) = 6\]
2. Аргумент \(w\) равен \(\dfrac{5\pi}{3}\), а аргумент \(z\) равен \(-\dfrac{\pi}{4}\) , мы видим, что аргумент \(wz\) равен \[\dfrac{5\pi}{3} — \dfrac{\pi}{4} = \dfrac{20\pi — 3\pi}{12} = \dfrac{17\pi}{12}\]
3. Конечная сторона угла \(\dfrac{17\pi}{12} = \pi + \dfrac{5\pi}{12}\) радиан находится в третьем квадранте.
4. Мы знаем величину и аргумент \(wz\), поэтому полярная форма \(wz\) равна
.\[wz = 6[\cos(\dfrac{17\pi}{12}) + \sin(\dfrac{17\pi}{12})]\]
5. Ниже приведено изображение \(w, z\) и \(wz\), иллюстрирующее действие сложного произведения.
Частные комплексных чисел в полярной форме
Мы видели, что мы умножаем комплексные числа в полярной форме, умножая их нормы и складывая их аргументы. Существует аналогичный метод деления одного комплексного числа в полярной форме на другое комплексное число в полярной форме.

Деление комплексных чисел в полярной форме
Пусть \(w = r(\cos(\alpha) + i\sin(\alpha))\) и \(z = s(\cos(\beta) + i \sin(\beta))\) — комплексные числа в полярной форме с \(z \neq 0\). Тогда полярная форма комплексного частного \(\dfrac{w}{z}\) определяется выражением \[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha — \ beta) + i\sin(\alpha — \beta)).\]
Итак, чтобы разделить комплексные числа в полярной форме, мы делим норму комплексного числа в числителе на норму комплексного числа в знаменателе и вычесть аргумент комплексного числа в знаменателе из аргумента комплексного числа в числителе.
Доказательство этого аналогично доказательству умножения комплексных чисел и включено в качестве дополнения к этому разделу.
Упражнение \(\PageIndex{3}\)
Пусть \(w = 3[\cos(\dfrac{5\pi}{3}) + i\sin(\dfrac{5\pi}{3} )]\) и \(z = 2[\cos(-\dfrac{\pi}{4}) + i\sin(-\dfrac{\pi}{4})]\).
- Что такое \(|\dfrac{w}{z}|\)?
- Каков аргумент \(|\dfrac{w}{z}|\)?
- В каком квадранте находится \(|\dfrac{w}{z}|\)? Объяснять.

- Определите полярную форму \(|\dfrac{w}{z}|\).
- Нарисуйте рисунок \(w\), \(z\) и \(|\dfrac{w}{z}|\), иллюстрирующий действие сложного произведения.
- Ответить
1. Поскольку \(|w| = 3\) и \(|z| = 2\), мы видим, что
\[|\dfrac{w}{z}| = \dfrac{|w|}{|z|} = \dfrac{3}{2}\]
2. Аргумент \(w\) равен \(\dfrac{5\pi}{3}\), а аргумент \(z\) равен \(-\dfrac{\pi}{4}\) , мы видим, что аргумент \(\dfrac{w}{z}\) равен
\[\dfrac{5\pi}{3} — (-\dfrac{\pi}{4}) = \dfrac{20\pi + 3\pi}{12} = \dfrac{23\pi}{ 12}\]
3. Конечная сторона угла \(\dfrac{23\pi}{12} = 2\pi — \dfrac{\pi}{12}\) радиан находится в четвертом квадранте.
4. Мы знаем величину и аргумент \(wz\), поэтому полярная форма \(wz\) имеет вид \[\dfrac{w}{z} = \dfrac{3}{2}[\cos( \dfrac{23\pi}{12}) + \sin(\dfrac{23\pi}{12})]\]
5. Ниже приведено изображение \(w, z\) и \(wz\), иллюстрирующее действие сложного произведения.

Доказательство правила деления комплексных чисел в полярной форме
Пусть \(w = r(\cos(\alpha) + i\sin(\alpha))\) и \(z = s(\cos(\ beta) + i\sin(\beta))\) — комплексные числа в полярной форме с \(z \neq 0\). Итак,
\[\dfrac{w}{z} = \dfrac{r(\cos(\alpha) + i\sin(\alpha))}{s(\cos(\beta) + i\sin(\ бета)} = \dfrac{r}{s}\left [\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)} \ right ]\]
Мы будем работать с дробью \(\dfrac{\cos(\alpha) + i\sin(\alpha)}{\cos(\beta) + i\sin(\beta)}\) и следуйте обычной практике умножения числителя и знаменателя на \(\cos(\beta) — i\sin(\beta)\). Итак, 9{2}(\бета) = 1\)
Используя эти тождества с последним уравнением для \(\dfrac{w}{z}\), мы видим, что
\[\dfrac{w}{z} = \dfrac{r}{s}[\dfrac {\cos(\alpha — \beta) + i\sin(\alpha- \beta)}{1}].\]
Резюме
В этом разделе мы изучили следующие важные понятия и идеи:
Если \(z = a + bi\) комплексное число, то мы можем нанести \(z\) на плоскость. Если \(r\) является величиной \(z\) (то есть расстоянием от \(z\) до начала координат) и \(\theta\) угол \(z\) образует с положительным действительным ось, затем 9{2}}, \cos(\theta) = \dfrac{a}{r}\]
Если \(r\) является величиной \(z\) (то есть расстоянием от \(z\) до начала координат) и \(\theta\) угол \(z\) образует с положительным действительным ось, затем 9{2}}, \cos(\theta) = \dfrac{a}{r}\]
и \[\sin(\theta) = \dfrac{b}{r}\]
Угол \( \тета\) называется аргументом комплексного числа \(z\), а действительное число \(r\) является модулем или нормой \(z\).
Если \(w = r(\cos(\alpha) + i\sin(\alpha))\) и \(z = s(\cos(\beta) + i\sin(\beta))\) являются комплексными числами в полярной форме, то полярная форма комплексного произведения \(wz\) определяется как
\[wz = rs(\cos(\alpha + \beta) + i\sin(\alpha + \beta ))\] и \(z \neq 0\), полярная форма комплексного частного \(\dfrac{w}{z}\) равна
\[\dfrac{w}{z} = \dfrac{r}{s}(\cos(\alpha — \beta) + i\sin(\alpha — \beta)),\]
Это состояние что для умножения двух комплексных чисел в полярной форме мы умножаем их нормы и складываем их аргументы, а для деления двух комплексных чисел мы делим их нормы и вычитаем их аргументы.
Эта страница под названием 5.2: Тригонометрическая форма комплексного числа распространяется под лицензией CC BY-NC-SA 3.0, автором, ремиксом и/или куратором являются Тед Сандстром и Стивен Шликер (ScholarWorks @Grand Valley State University) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Тед Сандстром и Стивен Шликер
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу Оглавление
- нет
- Теги
- модуль (комплексное число)
- норма (комплексный номер)
- источник@https://scholarworks.
 gvsu.edu/books/12
gvsu.edu/books/12
Полярная форма комплексного числа
Горячая математикаПолярная форма комплексное число это еще один способ представления комплексного числа. Форма г знак равно а + б я называется прямоугольной формой координат комплексного числа.
Горизонтальная ось — это реальная ось, а вертикальная ось — воображаемая ось. Находим вещественные и комплексные компоненты в терминах р а также θ куда р длина вектора и θ это угол, составленный с действительной осью.
Из Теорема Пифагора :
р 2 знак равно а 2 + б 2
С помощью основных тригонометрические отношения :
потому что
θ
знак равно
а
р
а также
грех
θ
знак равно
б
р
.
Умножая каждую сторону на р :
р потому что θ знак равно а а также р грех θ знак равно б
Прямоугольная форма комплексного числа определяется выражением
г знак равно а + б я .
Подставьте значения а а также б .
г знак равно а + б я знак равно р потому что θ + ( р грех θ ) я знак равно р ( потому что θ + я грех θ )
В случае комплексного числа
р
представляет
абсолютная величина
или модуль и угол
θ
называется аргументом комплексного числа.
Это можно резюмировать следующим образом:
Полярная форма комплексного числа
г
знак равно
а
+
б
я
является
г
знак равно
р
(
потому что
θ
+
я
грех
θ
)
, куда
р
знак равно
|
г
|
знак равно
а
2
+
б
2
,
а
знак равно
р
потому что
θ
а также
б
знак равно
р
грех
θ
, а также
θ
знак равно
загар
−
1
(
б
а
)
за
а
>
0
а также
θ
знак равно
загар
−
1
(
б
а
)
+
π
или же
θ
знак равно
загар
−
1
(
б
а
)
+
180
°
за
а <
0
.
Пример:
Выразите комплексное число в полярной форме.
5 + 2 я
Полярная форма комплексного числа г знак равно а + б я является г знак равно р ( потому что θ + я грех θ ) .
Итак, сначала найдите абсолютное значение р .
р знак равно | г | знак равно а 2 + б 2 знак равно 5 2 + 2 2 знак равно 25 + 4 знак равно 29 ≈ 5,39
Теперь найдите аргумент
θ
.
С а > 0 , воспользуйтесь формулой θ знак равно загар − 1 ( б а ) .
θ знак равно загар − 1 ( 2 5 ) ≈ 0,38
Обратите внимание, что здесь θ измеряется в радианах.
Поэтому полярная форма 5 + 2 я около 5,39 ( потому что ( 0,38 ) + я грех ( 0,38 ) ) .
Грунтовка комплексного номера
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Большинство людей знакомы с комплексными числами в форме \(z = a + bi\), однако есть несколько альтернативных форм, которые иногда бывают полезны. В этом разделе мы рассмотрим оба из них, а также пару интересных фактов, которые вытекают из них.
Геометрическая интерпретация
Прежде чем перейти к альтернативным формам, мы должны сначала очень кратко рассмотреть естественную геометрическую интерпретацию комплексных чисел, так как это приведет нас к нашей первой альтернативной форме.
Рассмотрим комплексное число \(z = a + bi\). Мы можем думать об этом комплексном числе либо как о точке \(\left( {a,b} \right)\) в стандартной декартовой системе координат, либо как о векторе, который начинается в начале координат и заканчивается в точке \(\left ( {яркий)\). Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\).
Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\).
Полярная форма
Теперь рассмотрим первую альтернативную форму комплексного числа. Если мы представим ненулевое комплексное число \(z = a + bi\) как точку \(\left( {a,b} \right)\) в \(xy\)-плоскости, мы также знаем, что мы можем представить эту точку полярными координатами \(\left({r,\theta} \right)\), где \(r\) — расстояние точки от начала координат, а \(\theta \) — угол в радианах от положительной оси \(x\) до луча, соединяющего начало координат с точкой.
При работе с комплексными числами мы предполагаем, что \(r\) положительно и что \(\theta \) может быть любым из возможных (как положительных, так и отрицательных) углов, оканчивающихся на луче. Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \).
Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \).
Мы исключили \(z = 0\), так как \(\theta \) не определено для точки (0,0). Поэтому мы будем рассматривать только полярную форму ненулевых комплексных чисел.
У нас есть следующие формулы преобразования для преобразования полярных координат \(\left( {r,\theta} \right)\) в соответствующие декартовы координаты точки, \(\left( {a,b} \Правильно)\).
\ [a = r \ cos \ theta \ hspace {0,75 дюйма} b = r \ sin \ theta \]
Если мы подставим их в \(z = a + bi\) и разложим на множители \(r\), мы получим полярную форму комплексного числа,
\begin{equation}z = r\left( {\cos\theta + i\sin\theta} \right) \label{eq:eq1}\end{equation}
Обратите внимание, что у нас также есть следующая формула из полярных координат, связывающая \(r\) с \(a\) и \(b\). 92}} \]
92}} \]
, но правая часть это не что иное, как определение модуля, и мы видим, что
\begin{уравнение}r = \left| z \right|\label{eq:eq2} \end{уравнение}
Итак, иногда полярная форма записывается как
\begin{уравнение}z = \left| z \ right | \ left ( {\ cos \ theta + i \ sin \ theta } \ right) \ label {eq: eq3} \ end {equation}
Угол \(\theta \) называется аргумент из \(z\) и обозначается как,
\[\тета = \аргумент z\]
Аргументом \(z\) может быть любое из бесконечных возможных значений \(\theta \), каждое из которых может быть найдено путем решения
\begin{уравнение}\tan \theta = \frac{b}{a}\label{eq:eq4}\end{equation}
и убедитесь, что \(\theta \) находится в правильном квадранте.
Также обратите внимание, что любые два значения аргумента будут отличаться друг от друга на целое число, кратное \(2\pi \). Это имеет смысл, если учесть следующее.
Это имеет смысл, если учесть следующее.
Для заданного комплексного числа \(z\) выберите любое из возможных значений аргумента, скажем, \(\theta \). Если вы теперь увеличите значение \(\theta\), что на самом деле просто увеличивает угол, который точка образует с положительной осью \(x\), вы вращаете точку вокруг начала координат против часовой стрелки. . Поскольку для совершения одного полного оборота требуется \(2\pi \) радиан, вы вернетесь в исходную точку, когда достигнете \(\theta + 2\pi \) и, таким образом, получите новое значение аргумента. См. рисунок ниже.
Если вы продолжите увеличивать угол, вы снова вернетесь в исходную точку, когда достигнете \(\theta + 4\pi \), что снова является новым значением аргумента. Продолжая в том же духе, мы можем видеть, что каждый раз, когда мы достигаем нового значения аргумента, мы просто будем добавлять кратные \(2\pi \) к исходному значению аргумента.
Аналогичным образом, если вы начнете с \(\theta \) и уменьшите угол, вы будете вращать точку вокруг начала координат по часовой стрелке и вернетесь в исходную начальную точку, когда достигнете \(\theta — 2\pi \). Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента.
Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента.
Итак, мы можем видеть, что если \({\theta _1}\) и \({\theta _2}\) являются двумя значениями \(\arg z\), то для некоторого целого числа \(k\) мы будем у,
\begin{equation}{\theta _1} — {\theta _2} = 2\pi k\label{eq:eq5}\end{equation}
Обратите внимание, что мы также показали здесь, что \(z = r\left ({\cos \theta + i\sin \theta} \right)\) является параметрическим представлением для окружности радиуса \(r\) с центром в начале координат и что он будет описывать полный круг против часовой стрелки по мере увеличения угла от \(\theta\) до \(\theta + 2\pi \).
главное значение аргумента (иногда называемое основным аргументом ) является уникальным значением аргумента, которое находится в диапазоне \( — \pi < \arg z \le \pi \) и обозначается \({\mathop{\rm Arg}\nolimits} z\). Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \).
Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \).
Вспоминая отмеченное выше, что любые два значения аргумента будут отличаться друг от друга на кратное \(2\pi \), мы приходим к следующему факту.
\begin{equation}\arg z = {\mathop{\rm Arg}\nolimits} z + 2\pi n \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \label{eq :eq:6}\end{уравнение}
Нам, вероятно, следует сделать пару быстрых числовых примеров, прежде чем мы перейдем к рассмотрению второй альтернативной формы комплексного числа.
Пример 1 Запишите полярную форму каждого из следующих комплексных чисел.
- \(z = — 1 + i\,\sqrt 3 \) 909:20
- \(г = — 9 \)
- \(г = 12\,я\)
Показать все решения Скрыть все решения
a \(z = — 1 + i\,\sqrt 3 \) Показать решение
Сначала получим \(r\). \[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\]
\[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\]
Теперь давайте найдем аргумент \(z\). Это может быть любой угол, удовлетворяющий условию \(\eqref{eq:eq4}\), но обычно проще всего найти главное значение, поэтому мы найдем его. Главным значением аргумента будет значение \(\theta \), которое находится в диапазоне \( — \pi < \theta \le \pi \), удовлетворяет, 9{ - 1}}\влево( { - \sqrt 3 } \вправо)\]
и находится во втором квадранте, так как это расположение комплексного числа в комплексной плоскости.
Если вы используете калькулятор для нахождения значения этого арктангенса, убедитесь, что вы понимаете, что ваш калькулятор будет возвращать значения только в диапазоне \( — \frac{\pi }{2} < \theta < \frac{\ pi }{2}\), поэтому вы можете получить неверное значение. Напомним, что если ваш калькулятор возвращает значение \({\theta _1}\), то вторым значением, которое также будет удовлетворять уравнению, будет \({\theta _2} = {\theta _1} + \pi \). Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте.
Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте.
В нашем случае два значения:
\[{\ theta _1} = — \ frac {\ pi} {3} \ hspace {0,25 дюйма} {\ theta _2} = — \ frac {\ pi} {3} + \ pi = \ frac {{2 \ пи }}{3}\]
Первый находится в четвертом квадранте, а второй — во втором квадранте, как и тот, который нам нужен. Следовательно, главное значение аргумента равно
. \[{\mathop{\rm Arg}\nolimits} \,z = \frac{{2\pi}}{3}\]
и тогда все возможные значения аргумента равны
\[\arg z = \frac{{2\pi}}{3} + 2\pi n \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \]
Теперь давайте сделаем то, о чем нас изначально просили. Вот полярная форма \(z = — 1 + i\,\sqrt 3 \).
Вот полярная форма \(z = — 1 + i\,\sqrt 3 \).
\[z знак равно 2 \ влево ( {\ соз \ влево ( {\ гидроразрыва {{2 \ пи}} {3}} \ вправо) + я \ грех \ влево ( {\ гидроразрыва {{2 \ пи}}} {3 }} \верно-верно)\]
Теперь, для полноты картины, мы должны признать, что для этого комплексного числа есть много более равноправных полярных форм. Чтобы получить любую из других форм, нам просто нужно вычислить другое значение аргумента, выбрав \(n\). Вот несколько других возможных полярных форм.
\begin{align*}z & = 2\left( {\cos\left({\frac{{8\pi}}{3}} \right) + i\sin\left({\frac{{8\ pi }}{3}} \right)} \right) & \hspace{0.25in} & n = 1\\ z & знак равно 2 \ влево ( {\ cos \ влево ( { — \ гидроразрыва {{16 \ пи}} {3}} \ вправо) + я \ грех \ влево ( { — \ гидроразрыва {{16 \ пи}} { 3}} \right)} \right) & \hspace{0.25in} & n = — 3\end{align*}
b \(z = — 9 \) Показать решение
В этом случае мы уже отметили, что главное значение отрицательного действительного числа равно \(\pi \), поэтому нам не нужно его вычислять. Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа.
Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа.
\[\arg z = \pi + 2\pi n = \pi \left( {1 + 2n} \right) \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots \]
Теперь, \(r\) есть,
\[г = \влево| г \ справа | = \sqrt {81 + 0} = 9\]
Полярная форма (с использованием главного значения):
\[z = 9\left( {\cos\left(\pi\right) + i\sin\left(\pi\right)} \right)\]
Обратите внимание, что если бы у нас было положительное действительное число, то главное значение было бы \({\mathop{\rm Arg}\nolimits}\, z = 0\)
c \(z = 12\,i\) Показать решение
Еще один частный случай, очень похожий на действительные числа. Если бы мы использовали \(\eqref{eq:eq4}\) для поиска аргумента, то столкнулись бы с проблемами, поскольку действительная часть равна нулю, а это дало бы деление на ноль. Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части.
Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части.
В нашем случае мнимая часть положительна, поэтому это комплексное число будет лежать на положительной оси \(y\). Следовательно, главное значение и общий аргумент для этого комплексного числа:
. \[{\mathop{\rm Arg}\nolimits} z = \frac{\pi }{2} \hspace{0,5in} \arg z = \frac{\pi }{2} + 2\pi n = \ пи \ влево ( {\ гидроразрыва {1} {2} + 2n} \ справа) \ hspace {0,25 дюйма} n = 0, \ pm 1, \ pm 2, \ ldots \]
Кроме того, в этом случае \(r\) = 12 и поэтому полярная форма (опять же с использованием главного значения) будет, 9{i\,\left( {\theta + 2\pi n} \right)}} \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \]
где \(\theta \) — любое значение аргумента, хотя чаще всего это главное значение аргумента. 2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, — \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять}
2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, — \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять}
Полярные формы для обоих из них:
\begin{align}{z_1}{z_2} & = {r_1}\,{r_2}\left( {\cos \left({{\theta _{\,1}} + {\theta _{\,2 }}} \right) + i\sin \left( {{\theta _{\,1}} + {\theta _{\,2}}} \right)} \right)\label{eq:eq12} \\ & \номер \\ \frac{{{z_1}}}{{{z_2}}} & = \frac{{{r_1}}}{{{r_2}}}\left( {\cos \left({{\theta _{\ ,1}}\, — \,\,{\theta _{\,2}}} \right) + i\sin \left( {{\theta _{\,1}}\, — \,\, {\theta _{\,2}}} \right)} \right)\label{eq:eq13}\end{align}
Мы также можем использовать \(\eqref{eq:eq10}\) и \(\eqref{eq:eq11}\), чтобы получить интересные факты об аргументах произведения и частного комплексного числа. Поскольку \({\theta _1}\) — любое значение \(\arg {z_1}\), а \({\theta _2}\) — любое значение \(\arg {z_2}\), мы можем видеть, что ,
\begin{align}\arg \left( {{z_1}\,{z_2}} \right) & = \arg {z_1} + \arg {z_2}\label{eq:eq14} \\ & \номер \\ \arg \left( {\frac{{{z_1}}}{{{z_2}}}} \right) & = \arg {z_1} — \arg {z_2}\label{eq:eq15} \end{align }
Обратите внимание, что \(\eqref{eq:eq14}\) и \(\eqref{eq:eq15}\) могут работать или не работать, если вы используете главное значение аргумента, \({\rm{Arg } }\,г\). Например, рассмотрим \({z_1} = i\) и \({z_2} = — 1\). В этом случае мы имеем \({z_1}{z_2} = — i\) и главное значение аргумента для каждого равно
Например, рассмотрим \({z_1} = i\) и \({z_2} = — 1\). В этом случае мы имеем \({z_1}{z_2} = — i\) и главное значение аргумента для каждого равно
\[{\mathop{\rm Arg}\nolimits} \left( i \right) = \frac{\pi }{2} \hspace{0.5in} {\mathop{\rm Arg}\nolimits} \left( {- 1} \right) = \pi \hspace{0,5in} {\mathop{\rm Arg}\nolimits} \left( {-i} \right) = -\frac{\pi}{2}\]
Тем не менее,
\[{\mathop{\rm Arg}\nolimits} \left( i \right) + {\mathop{\rm Arg}\nolimits} \left({ — 1} \right) = \frac{{3\pi }}{2} \ne — \frac{\pi }{2}\]
и поэтому \(\eqref{eq:eq14}\) не выполняется, если мы используем главное значение аргумента. Обратите внимание, однако, если мы используем,
\[\ arg \left( i \right) = \ frac{\pi }{2} \hspace{0.5in}\arg \left( { — 1} \right) = \pi \]
затем
\[\arg \left( i \right) + \arg \left( { — 1} \right) = \frac{{3\pi}}{2}\]
действителен, поскольку \(\frac{{3\pi }}{2}\) является возможным аргументом для –\(i\), просто это не главное значение аргумента. {i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\]
{i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\]
Тогда мы будем иметь \({z_1} = {z_2}\) тогда и только тогда, когда
\begin{equation}{r_1} = {r_2} \hspace{0,25 дюйма} {\rm{и}} \hspace{0,25 дюйма} {\theta _2} = {\theta _1} + 2\pi k\,\ ,\,{\mbox{для некоторого целого числа}}k{\rm{}}\left( {т. е. \,\,k = 0, \pm 1, \pm 2, \ldots} \right)\label{eq :eq16}\end{уравнение}
Обратите внимание, что фраза «если и только если» — это причудливая математическая фраза, которая означает, что если \({z_1} = {z_2}\) верно, то верно и \(\eqref{eq:eq16}\), и аналогично , если \(\eqref{eq:eq16}\) истинно, то мы будем иметь \({z_1} = {z_2}\).
Это может показаться глупым фактом, но мы собираемся использовать его в следующем разделе, чтобы помочь нам найти степени и корни комплексных чисел.
6. Выражение в форме R sin(θ + α)
М. Борна
Борна
В электронике часто встречаются выражения включая сумму синусов и косинусов. это удобнее писать такие выражения, используя один термин.
Наша проблема:
Express a sin θ ± b cos θ в форме
R sin( θ ± α),
, где a , b , R и α – положительных констант.
Решение:
Сначала возьмем случай «плюс» ( θ + α), чтобы упростить задачу.
Пусть
a sin θ + b cos θ ≡ R sin ( θ + α)
(Символ «≡» означает: «тождественно равно»)
Используя приведенную выше формулу составного угла (Синус суммы углов),
sin(A + B) = sin A cos B + cos A sin B,
мы можем разложить R sin ( θ + α) следующим образом:
R sin ( θ + α)
≡ R (sin θ cos α + cos θ sin α)
≡ R sin θ cos α + R cos θ sin α
Так
a sin θ + b cos θ ≡ R cos α sin θ + R sin α 10910 cos Приравнивая коэффициенты sin θ и cos θ в этом тождестве,
у нас есть: Для sin θ : a = R cos α . Для cos θ : b = R sin α ……..(2) Уравнение (2) ÷ Уравнение (1): `b/a=(R sin alpha)/(R cos alpha)=tan alpha` Так `альфа=арктан\ б/а` (α — положительный острый угол и a и b являются положительными .) Теперь мы возводим в квадрат каждое уравнение. (1) и уравнение (2) и
добавьте их, чтобы найти выражение для R . [Ур. (1)] 2 + [уравнение. (2)] 2 : а 2 + б 2 = R 2 cos 2 α + R 2 sin 2 α = R 2 (cos 2 α + sin 2 α) = Р 2 (поскольку cos 2 A + sin 2 A = 1) 9092)` , то мы выразили a sin θ + b cos θ в требуемой форме: a sin θ + b cos θ = R sin( θ + α ) Вы заметите, что это очень похоже на
преобразование прямоугольной формы в полярную форму в полярную форму комплекса
Числа. Аналогично, для случая минус мы приравниваем a sin θ − b cos θ с разложением R sin ( θ минус ) следующим образом (обратите внимание на знаки α минус  ………(1)
………(1)
(зеленый выше)
(выделено красным выше) Мы можем получить α и R г. с использованием
калькулятор, похожий на то, как мы это делали с комплексными числами
раздел.
Мы можем получить α и R г. с использованием
калькулятор, похожий на то, как мы это делали с комплексными числами
раздел. Минус Дело
a sin θ − b cos θ ≡ R cos α sin θ 92)`
Наше уравнение для отрицательного случая:
a sin θ − b cos θ = R sin( θ − α)
Уравнения типа
a sin θ ± b cos θ = cЧтобы решить уравнение в форме
и sin θ ± b cos θ = c ,
выразить LHS в форма R sin( θ ± α) и затем решить
R sin( θ ± α) = c .

Упражнения — Синусоидальная форма
1. (a) Выразите 4 sin θ + 3 cos θ в виде R sin( θ + α).
(б) Используя свой ответ из части (а), решить уравнение 9@`:
4 sin θ + 3 cos θ = 5 sin( θ + 36,87°) (выделено красным)
Часть (b)
Из части (b)
4 sin θ + 3 cos θ = 5 sin( θ + 36,87°)
Итак,
5 sin( θ + 36,87°) = 2
sin( θ + 36,87°) = 0,4
Синус положителен в квадрантах I и II.
Решение sin 9@`
Верны ли эти ответы?
Из графика видно, что в области 0° ≤ θ < 360° единственные два угла, которые дают значение 2, это 119,6° и 346,7°. Так что наш ответ правильный.
2. Решить уравнение
`sin theta-sqrt2 cos theta=0,8`, для 0° ≤ θ < 360°.
Ответить
Сначала представим LHS в виде R sin( 9@`. Так что наш ответ правильный.
3. Ток i (в амперах) в момент времени t в конкретной цепи дается
i = 12 sin t + 5 cos t .
Найдите максимальный ток и время его первого появления.
Ответить
Обратите внимание, что обычно мы принимаем t ≥ 0. Для такого примера мы должны использовать радиан для угла.
У нас есть:
9092)=13` и «альфа=арктан(5/12)=0,39479».Итак, `12\ sin t+5\ cos t=` `13\ sin(t+0,39479)`
Итак, мы видим, что амплитуда равна 13 А, и это максимум ценность.
Чтобы найти первый раз, нужно решить
`13\ sin(t+0,39479)=13`
То есть
`sin(t+0,39479)=1`
Теперь sin θ = 1 впервые когда `тета=пи/2`. Значит надо решить:
`т+0,39479=пи/2`
`t=пи/2-0,39479=1,176`
Таким образом, максимальное значение 13 А впервые произойдет в момент времени t = 1,176 с.
Из графика видно, что это верно:
`i=12\ sin t+5\ cos t`
4. Решите 7 sin 3 θ − 6 cos 3 θ = 3,8 для 0° ≤ θ < 360°.
Ответить
Сначала представим LHS в виде R sin(3 9@`.
5. Сила тока и ампер в определенной цепи после t секунд предоставлено
`i=2\ sin(t-pi/3)-cos(t+pi/2)`
Найдите максимальный ток и самое раннее время его имеет место.
(Примечание: t > 0)
Ответить
Нам нужно получить это в более простой форме. В этом один, обратите внимание, что углы в скобках не совпадают с !
Сначала мы должны упростить их, чтобы углы в скобках были такой же. 92)=2,646`
`alpha=arctan(1.732/2)=` `0.714\ текст(радианы`
Так
`2\ sin t − 1,732\ cos t =` ` 2,646\ грех (т — 0,714)`
Таким образом, максимальное значение этого параметра равно `2,646\ «A»`.
Чтобы найти, когда это происходит, нам нужно решить:
`2,646\ sin(t − 0,714) = 2,646`
т. е. `sin(t − 0,714) = 1`
`t — 0,714 = π/2``t = 2,29`
Итак, `t = 2,29\ «с»` — это время, когда сначала достигается максимум.
Форма косинусаМы также можем выразить нашу сумму синуса и косинуса, используя косинус вместо синуса . В некоторых ситуациях это может быть удобнее.
Полученные выражения аналогичны тем, которые мы получили для синусоидального случая, но обратите внимание на различия по ходу дела.
Для a , b и R положительное и острое α, наше эквивалентное выражение задается следующим образом:
a sin θ + b cos θ ≡ R cos ( θ − α)
На этот раз способ получения α отличается от предыдущего.
Расширение R cos ( θ − α) с использованием нашего результата для расширения cos(A − B) дает нам:
R cos ( θ — α) = R cos θ cos α + R sin θ sin α
Перестановка и приравнивание коэффициентов дает нам
a sin θ + b cos θ ≡ R cos α cos θ + R 909 1966 sin α sin
Итак:
а = R sin α .
…. (1)
б = R cos α ….. (2)
Деление (1) на (2) дает нам: 92)`
Итак, сумма синуса и косинуса объединена в один косинус:
a sin θ + b cos θ ≡ R cos( θ − α)
Еще раз, a , b , R и α положительны константы, а α острая.
Косинус минус Дело
Если у нас есть a sin θ − b , потому что θ , и нам нужно выразить это в терминах одной функции косинуса, формула, которую мы должны использовать:
a sin θ − b cos θ ≡ − R cos ( θ + α)
Еще раз, a , b и R положительны.
`α` означает остроту и дается:
`альфа=арктан\ а/б`
R дает:
92`
Упражнения на косинус
1. Выразить 7 sin θ + 12 cos θ в виде R cos ( θ − α), где 0 ≤ α < π/2.
Выразить 7 sin θ + 12 cos θ в виде R cos ( θ − α), где 0 ≤ α < π/2.
Ответить
Находим α с помощью
`альфа=арктан\ а/б`
α должно быть в радианах для этого примера, так как нам говорят «0 ≤ α < π/2».
Так как `a = 7` и `b = 12`, мы имеем:
`α = арктангенс (7/12) = 0,528` 92)=13,892`
Следовательно, мы можем написать:
7 sin θ + 12 cos θ = 13,892 cos ( θ − 0,528)
Чтобы проверить наш ответ, мы рисуем графики как y = 7 sin θ + 12 cos θ , так и y = 13,892 cos ( θ − 0,528). Мы видим, что они абсолютно одинаковы. (показан только один).
Мы видим, что наш график косинуса имеет амплитуду «13,892» и сдвинут вправо на «0,528» радиан, что согласуется с полученным выражением: 13,892 cos ( θ − 0,528)
2.
Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ ), где 2,348 sin θ + α
Ответить
Мы находим α, используя
`a=текст(arctan)a/b`
Опять же, в этом примере `α` должен быть в радианах.
Так как `a = 2,348` и `b = 1,251`, мы имеем:
`α = арктангенс (2,348/1,251) = 1,081 `
Находим 92) = 2,660`
Таким образом, мы можем написать:
2,340 sin θ − 1,251 cos θ = -2,660 cos ( θ + 1,081)
Проверяя с помощью графика, мы получаем следующее для каждой стороны нашего ответа:
Мы видим, что наша кривая отрицательного косинуса имеет амплитуду 2,660 и смещена влево на 1,081 радиан, что согласуется с выражение -2,660 cos ( θ + 1,081).
Резюме
Вот сводка выражений и условий, которые мы нашли в этом разделе.

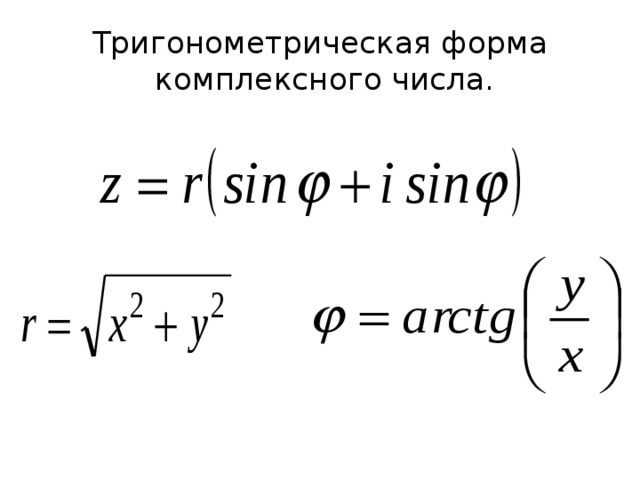
 Равнобедренный треугольник (вариант 2)
Равнобедренный треугольник (вариант 2)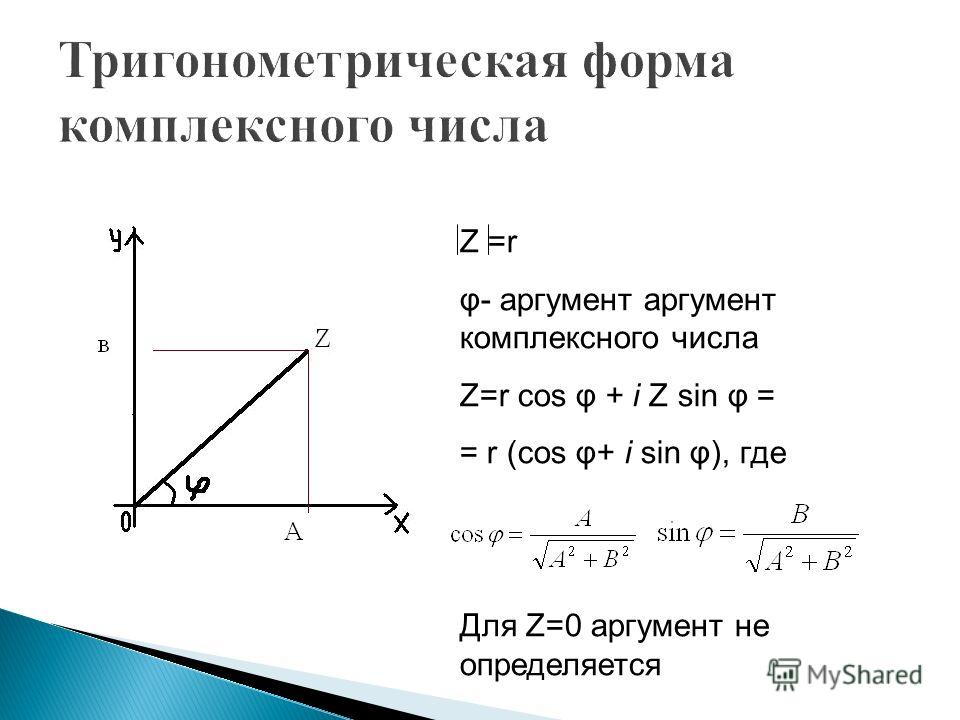
 Проиллюстрируем на примере.
Проиллюстрируем на примере. Это оказывается правдой в целом.
Это оказывается правдой в целом.




 gvsu.edu/books/12
gvsu.edu/books/12

 …. (1)
…. (1) Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ ), где 2,348 sin θ + α
Выразить 2,348 sin θ − 1,251 cos θ в виде −R cos ( θ ), где 2,348 sin θ + α