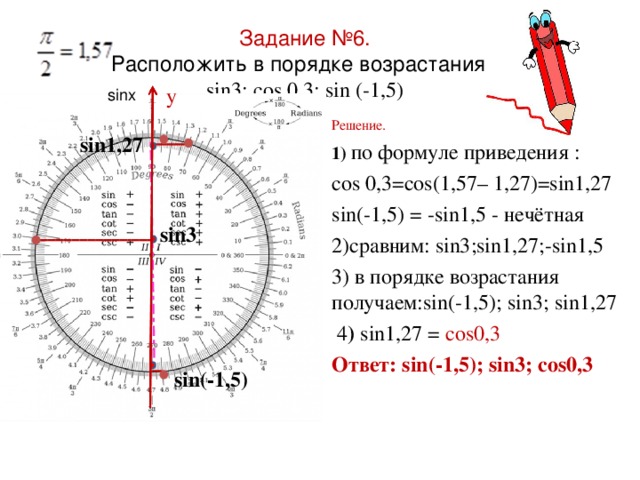
Нахождение значений синуса, косинуса, тангенса и котангенса, вычисление тригонометрических функций
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
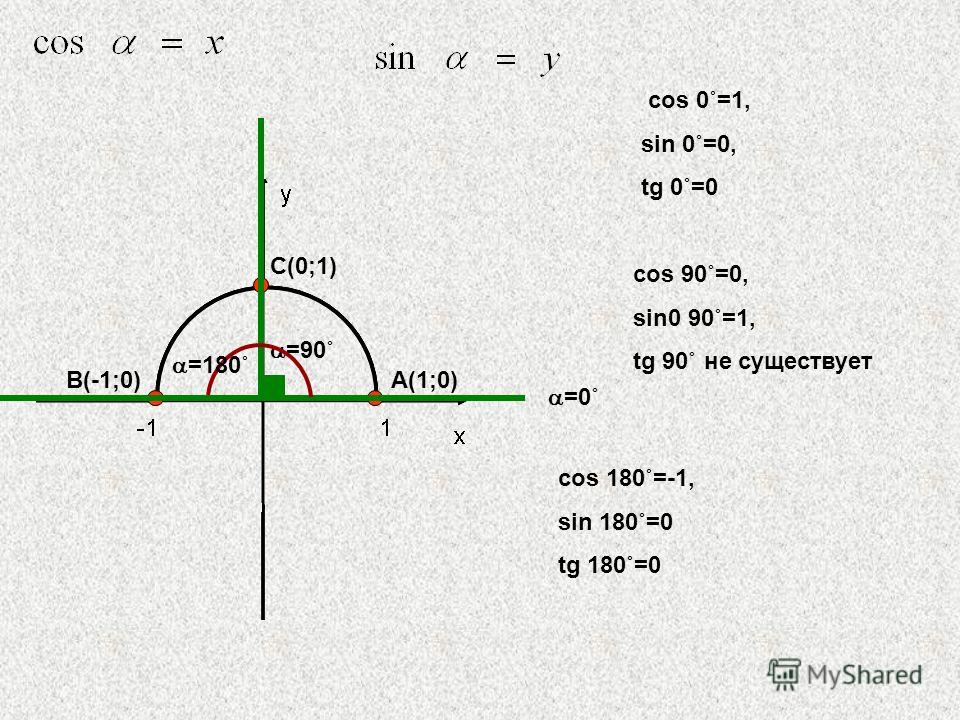
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Пример 2Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Пример 3Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0).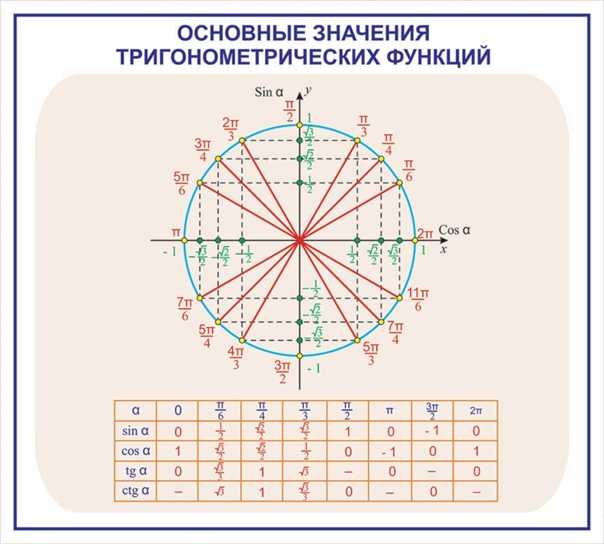
Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Пример 5Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу.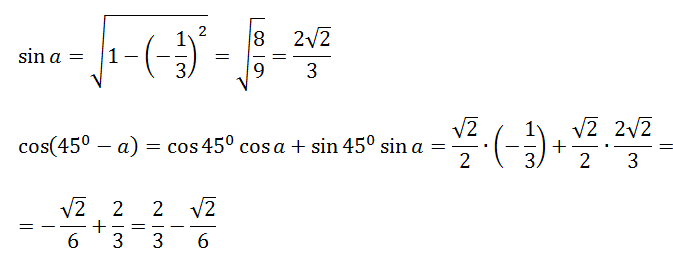 Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Определение 4Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Определение 6Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α .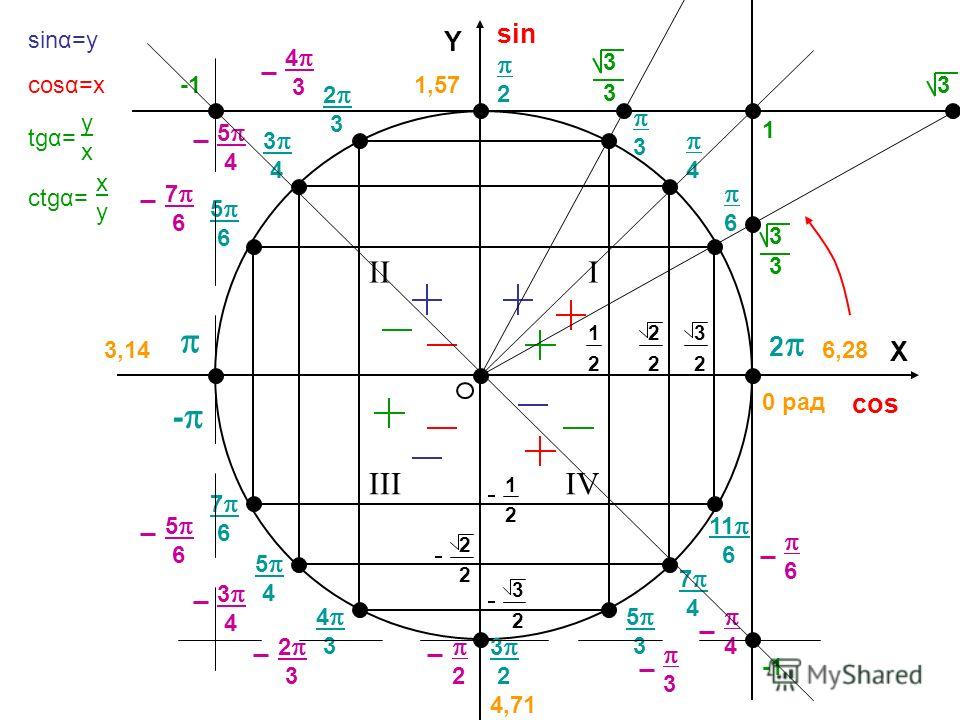 Благодаря этому мы вычисляем значение синуса. Имеем
Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Пример 7Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Пример 8Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Решение задач
от 1 дня / от 150 р. Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Нахождение значений синуса, косинуса, тангенса и котангенса, вычисление тригонометрических функций
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла.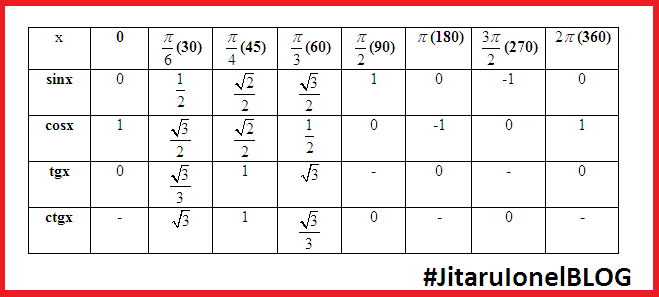 Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Пример 2Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Пример 3Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Пример 4Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины. Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 .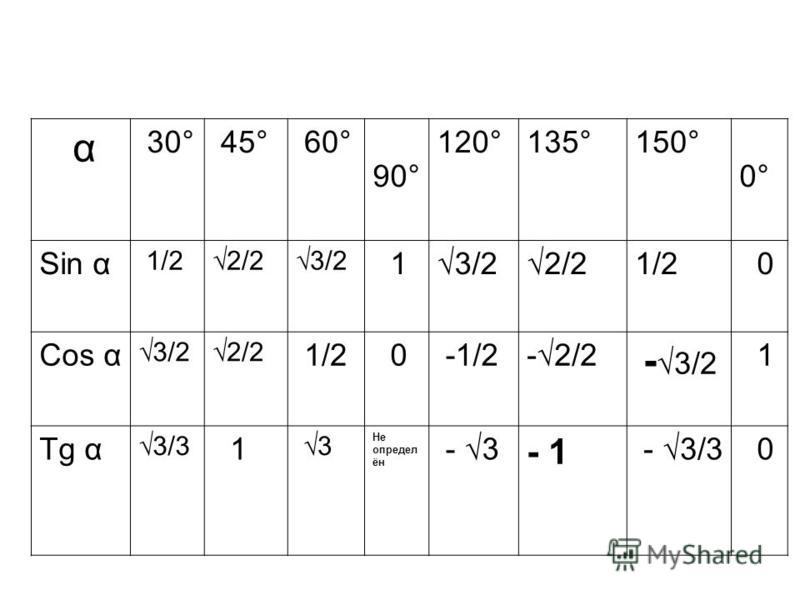 После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла.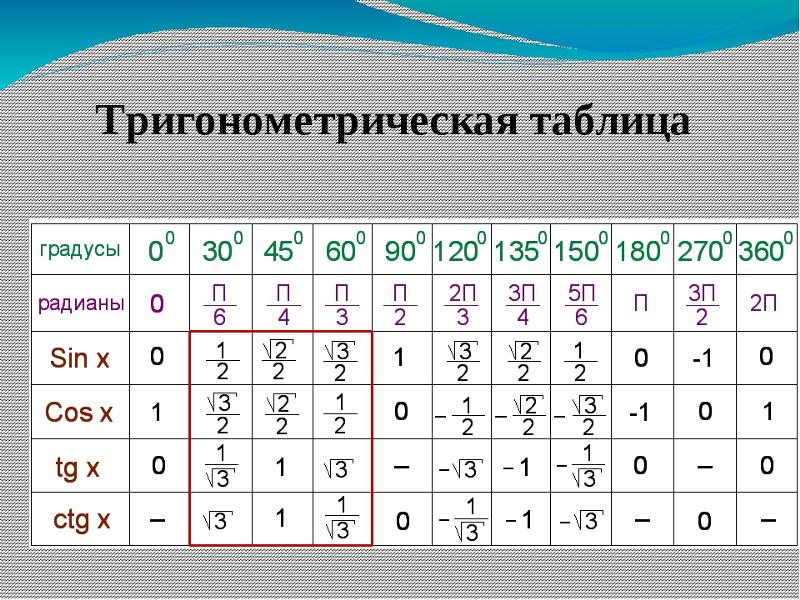 С помощью одной функции вы легко сможете найти другую.
С помощью одной функции вы легко сможете найти другую.
Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Определение 4Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Определение 6Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости.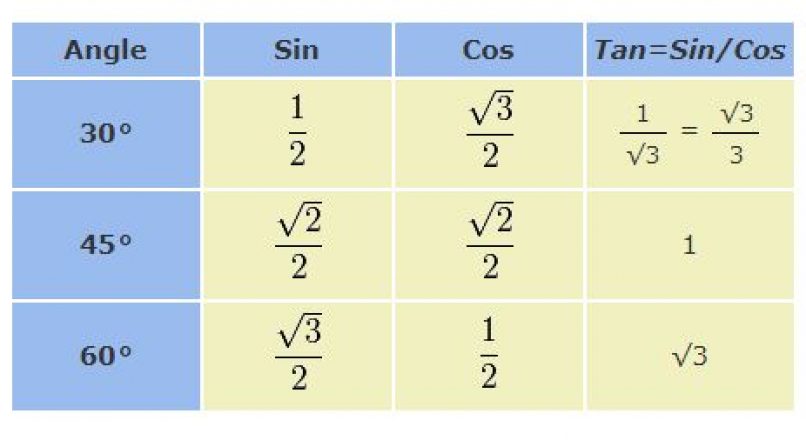 Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Пример 7Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии.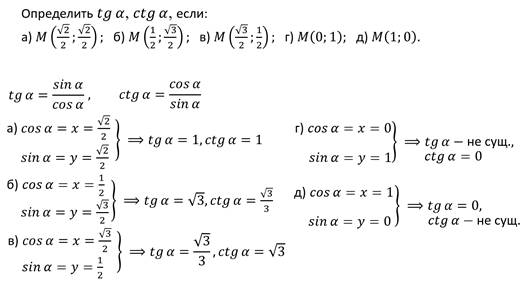 Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Пример 8Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность. Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р. Реферат
от 1 дня / от 700 р.
Реферат
от 1 дня / от 700 р.
Нахождение значений синуса, косинуса, тангенса и котангенса, вычисление тригонометрических функций
Для того, чтобы определить значение угла α, необходимо воспользоваться подходящей функции из тригонометрии. Во время решения задач постоянно возникает необходимость в том, чтобы узнать значение углов. Для некоторых углов можно найти точные значения, для других сложно определить точную цифру и можно вывести только приблизительное значение.
В этой статье мы подробно поговорим о функциях из тригонометрии. Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Мы не только расскажем о свойствах синуса, тангенса и других функций, но и узнаем, как правильно вычислять значения для каждого отдельного случая.
Рассмотрим подробно каждый случай.
Определение 1Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Соотношения сторон и углов фигуры используются для того, чтобы определить значения для 30°, 45°, 60°. Если угол выходит за пределы 90°, то перед вычислением значения следует воспользоваться специальной формулой для того, чтобы привести угол к нужному виду.
Если известно значение синуса для α, можно быстро узнать значение косинуса для этого же угла. Это легко выполнить с помощью основных тождеств, которые представлены в геометрии.
В некоторых случаях для того, чтобы узнать sin или cos угла, можно использовать подходящую тригонометрическую формулу. Например, по известному значению синуса 45°, мы сможем определить значение синуса 30°, воспользовавшись правилом из тригонометрии.
Если для примера не подходит ни одно из приведенных выше решений, можно найти приближенное значение. В этом вам помогут таблицы основных тригонометрических функций, которые легко можно найти.
Если взять за основу определения, возможно определить значения для определенного угла α. Также можно вычислить значения тангенса и котангенса для определенного случая. Можно найти значений основных функций из тригонометрии для частных вариантов. Это углы 0°, 90°, 180°, 270°, 360°.
Разобьем эти углы на четыре группы: 360·z градусов (2π·z рад), 90+360·z градусов (π2+2π·z рад), 180+360·z градусов (π+2π·z рад) и 270+360·z градусов (3π2+2π·z рад), где z- любое целое число.
Изобразим данные формулы на рисунке:
Для каждой группы соответствуют свои значения.
Пример 1При повороте из точки A на 360·z°, она переходит в себя. А1(1, 0). Синус 0°, 360°, 720° равен 0, а косинус равен 1. Представим это в виде формулы: sin (360°·z)=0 и cos (360°·z)=1 .
Можно определить, что tg (360°·z)=01=0 , а котангенс не определен.
Если А(1, 0) повернуть на 90+360·z°, то она перейдет в А1 (0, 1). По определению: sin (90°+360°·z) =1 и cos (90°+360°·z) =0 . Мы не сможем определить значение тангенса, но котангенс рассчитывается по данной формуле: ctg (90°+360°·z) =01=0 .
Пример 3Рассмотрим особенности для третьей группы углов. После поворота точки А(1, 0) на любой из углов 180+360·z°, она перейдет в A1(−1, 0). Мы находим значения функций кроме тангенса.
Пример 4Рассмотрим правила для четвертой группы углов. При повороте точки на 270+360·z° мы попадем в A1(0, −1). Мы находим значения всех функций кроме тангенса.
Для углов, которые не относятся к перечню от 0 °, 90 °, 180 °, 270 °, 360 °…, точных значений нет. Мы можем найти лишь приближенные значения. Рассмотрим пример. Условия – найти основные значения для угла −52 °. Выполним построения.
Согласно рисунку, абсцисса А1 ≈ 0,62, а ордината ≈ −0,78. Соответственно, sin(-52°)≈-0,78 и cos(-52°)≈0,62 . Осталось определиться с тангенсом и котангенсом.
Выполняем вычисления: tg(-52°)≈-0, 780, 62≈-1,26 и ctg(-52°)≈0,62-0,78≈-0,79.
Чем точнее выполняется чертеж, тем более точными будут значения для каждого индивидуального случая. Выполнять вычисления удобно только в теории, так как на практике довольно сложно и долго выполнять рисунки.
Линии тригонометрических функций
Определение 2Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Рассмотрим их на подробном рисунке
Как найти sin α, cos α, tg α, ctg α
Для тридцати-, сорокопяти-, шестидесятиградусных углов мы имеем определенные значения. Чтобы найти их, можно воспользоваться правилами о прямоугольном треугольнике с острыми углами. Для этого используется теорема Пифагора.
Пример 5Для того, чтобы узнать значения для углов тридцати- и шестидесятиградусных углов изображаем прямоугольный треугольник с углами данной величины.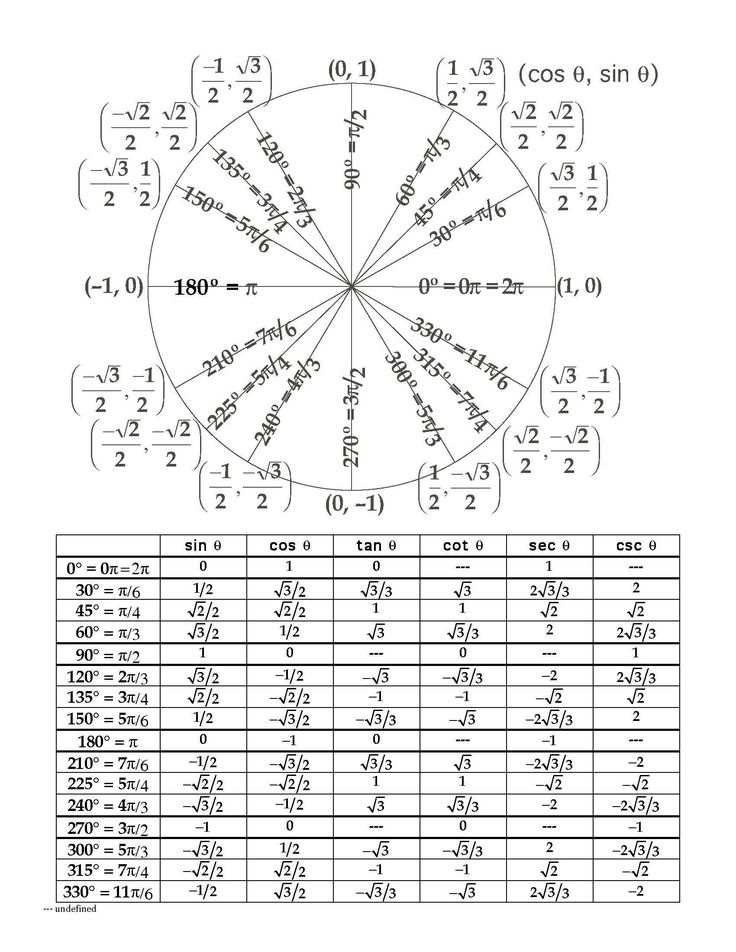 Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Длина гипотенузы должна быть равна 1. Согласно теореме Пифагора, катет, лежащий напротив тридцатиградусного угла, равен половине гипотенузы. Воспользуемся теоремой: 12-122=32 . Так как синус угла – это катет, деленный на гипотенузу, вычисляем, что sin 30°=121=12 и sin 60°=321=32 .
Косинус можно найти по формуле, которая предполагает деление прилежащего катета на гипотенузу. Вычисляем: cos 30°=321=32 и cos 60°=121=12 .
Тангенс можно найти по формуле, которая предполагает деление противолежащего катета на прилежащий. Котангенс находим по такой же схеме – делим прилежащий катет на противолежащий.
Вычисляем: tg 30°=1232=13=33 и tg 60°=3212=3 . Находим котангенс по подобной схеме: сtg 30°=3212=3 и сtg 60°=1232=13=33 . После этого приступаем к вычислению значений основных тригонометрических функций для сорока пятиградусного угла. Используем равнобедренный треугольник с углами 45° и гипотенузой, которая равна 1. Используем теорему Пифагора. Согласно формуле, длины катетов равны 22 . Т
Т
Теперь мы сможем найти значения для основных тригонометрических функций. Используем формулу, которая предполагает деление длин соответствующих сторон рассматриваемого треугольника.
Выводим формулу: ctg 45°=2222=1 .
Полученные значения для тридцати-, сорокапяти-, шестидесятиградусных углов будут использоваться для решения различных задач. Запишите их – они часто будут использоваться. Для удобства можно использовать таблицу значений.
Проиллюстрируем значения для тридцати-, сорокапяти-, шестидесятиградусных углов с использованием окружности и линий.
Значения основных функций тригонометрии
Основные тождества из геометрии связывают с собой sin α, cos α, tg α, ctg α для определенного угла. С помощью одной функции вы легко сможете найти другую.
Определение 3Для того, чтобы найти синус по известному косинусу, sin2α+cos2α=1 .
Определение 4Тангенс по известному косинусу tg2α+1=1cos2α .
Определение 5Котангенс по известному синусу или наоборот 1+ctg2α= 1sin2α .
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: tg α·ctg α=1 .
Для того, чтобы закрепить полученные знания, рассмотрим их на подробном примере
Пример 6Необходимо найти значение синуса угла π8, если tg π8=2-1 .
Сначала найдем котангенс угла: ctgπ8=1tgπ8=12-1=2+1(2-1)·(2+1)= 2+1(2)2-12=2+1 Воспользуемся формулой 1+ctg2α=1sin2α . Благодаря этому мы вычисляем значение синуса. Имеем
sin2π8=11+ctg2π8=11+(2+1)2=14+22=12·(2+2)=2-22·(2+2)·(2-2)==2-22·(22-(2)2)=2-24
Для завершения необходимо определить значение синуса. Угол π8 является углом первой четверти, то синус является положительным. Чтобы точно определить знак, вы можете воспользоваться таблицей, в которой определены знаки по четвертям координатной плоскости. Таким образом, sin π8=sin2π8=2-24=2-22 . sin π8=2-22.
Сведение к углу
Удобнее всего находить значения для угла от 0 до 90 °. Сведение к углу из интервала от 0 до 90 °. Если угол не соответствует заданному интервалу, можно использовать законы и тождества, которые мы учили на уроках геометрии. Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Тогда мы сможем найти значение, которое будет равно для угла указанных пределах.
Задача заключается в том, чтобы найти синус 210°. Представим 210 как разность или сумму, разложив число на несколько. Воспользуемся соответствующей формулой для приведения. Используем формулу для нахождения значения синуса 30°: sin 210°=sin(180°+30°)=-sin 30°=-12 , или косинуса 60 ° sin 210°=sin(270°-60°)=-cos 60°=-12.
Для того, чтобы решать задачи было намного проще, при нахождении значений переходите к углам из интервала от 0 до 90° с помощью формул приведения, если угол не находится в этих пределах.
Использование формул
Раннее мы рассмотрели подробности, касающиеся нахождению значений основных функций с использованием формул тригонометрии. Для того, чтобы определить значение для определенного угла, используйте формулы и значения основных функций для известных углов.
Для примера вычислим значение тангенса π8, который был использован в предыдущем примере. Возьмем за основу основные формулы тригонометрии.
Найдите значение tgπ8 .
Используя формулу тангенса, преобразуем уравнение до следующего равенства tg2π8=1-cosπ41+cosπ4 . Значения косинуса угла π4 известны из предыдущего примера. Благодаря этому мы быстро найдем значения тангенса.
tg2π8=1-cosπ41+cosπ4=1-221+22=2-22+2==(2-2)2(2+2)·(2-2)=(2-2)222-(2)2=(2-2)22
Угол π8 является углом первой четверти. Согласно таблице основных тригонометрических функций по четвертям координатной плоскости, тангенс этого угла положителен. Продолжаем вычисления для дальнейшего решения: tgπ8=tg2π8=(2-2)22=2-22=2-1
tgπ8=2-1.
Частные случаи
Тригонометрия – довольно сложная наука. Далеко не всегда можно найти формулы, используемые для вычисления. Существует множество уравнений, которые не поддаются стандартным формулам. Некоторые значения очень сложно обозначить точной цифрой. Это не так просто, как может показаться.
Однако точные значения не всегда нужны. Хватает и тех, что не претендуют на высокую точность.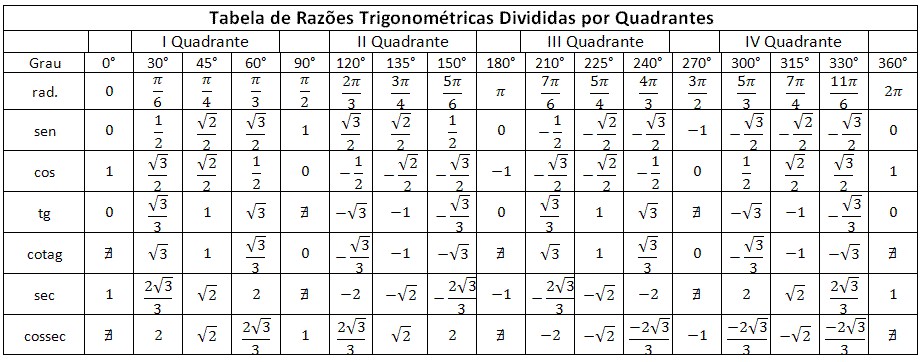 Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Благодаря существующим таблицам, которые можно найти в математических учебниках, можно найти любое приближенное значение основных функций. Благодаря справочным материалам вычислять формулы будет намного проще. В таблицах содержатся значения с высокой точностью.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Почему мы используем sin и cos в физике?
Почему мы используем sin и cos в физике? Он находится в кривом направлении, поэтому у него есть компонент по оси Y, а другой — по оси X. Вот почему вы используете синус и косинус. Вы вычисляете, какая часть этой силы находится в вертикальном направлении (проекция на ось Y) и какая в горизонтальном направлении (проекция на ось x).
Как sin и cos используются в реальной жизни? Функции синуса и косинуса используются для определения местоположения и расстояний в системе GPS мобильного телефона. В реальной жизни функции синуса и косинуса можно использовать в космических полетах и полярных координатах, музыке, баллистических траекториях, GPS и мобильных телефонах.
Какова цель использования тригонометрии в физике? В физике тригонометрия используется для нахождения компонент векторов, моделирования механики волн (как физических, так и электромагнитных) и колебаний, суммирования напряжённостей полей, использования скалярных и векторных произведений. Даже в движении снаряда у вас есть много применений тригонометрии.
Даже в движении снаряда у вас есть много применений тригонометрии.
Почему мы используем синус косинус и тангенс? Поскольку синус, косинус и тангенс являются функциями угла с, мы можем определить (измерить) отношения один раз и составить таблицы значений синуса, косинуса и тангенса для различных значений с. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти значение угла между сторонами.
Что такое sin Cos Tan в физике?
В тригонометрии значения sin cos и tan являются основными функциями, которые мы рассматриваем при решении тригонометрических задач. Эти значения тригонометрии используются для измерения углов и сторон прямоугольного треугольника. Помимо значений синуса, косинуса и тангенса, тремя другими основными значениями являются котангенс, секанс и косеканс.
Что такое cos в физике?
Функция косинуса (или функция косинуса) в треугольнике — это отношение прилежащей стороны к гипотенузе. Функция косинуса является одной из трех основных основных тригонометрических функций и сама является дополнением к синусу (ко+синус).
Кто является отцом тригонометрии?
Первая известная таблица аккордов была составлена греческим математиком Гиппархом примерно в 140 г. до н.э. Хотя эти таблицы не сохранились, утверждается, что двенадцать книг таблиц аккордов были написаны Гиппархом. Это делает Гиппарха основателем тригонометрии.
Кто изобрел тригонометрию?
Тригонометрия в современном понимании началась с греков. Гиппарх (ок. 190–120 до н. э.) первым составил таблицу значений тригонометрической функции.
Как НАСА использует тригонометрию?
Астрономы используют тригонометрию, чтобы рассчитать, насколько далеко звезды и планеты находятся от Земли. Несмотря на то, что мы знаем расстояния между планетами и звездами, этот математический метод также используется сегодня учеными НАСА, когда они проектируют и запускают космические челноки и ракеты.
Зачем нужна тригонометрия?
Тригонометрия, как следует из названия, касается треугольников. В частности, тригонометрия касается прямоугольных треугольников, один из внутренних углов которых равен 90°.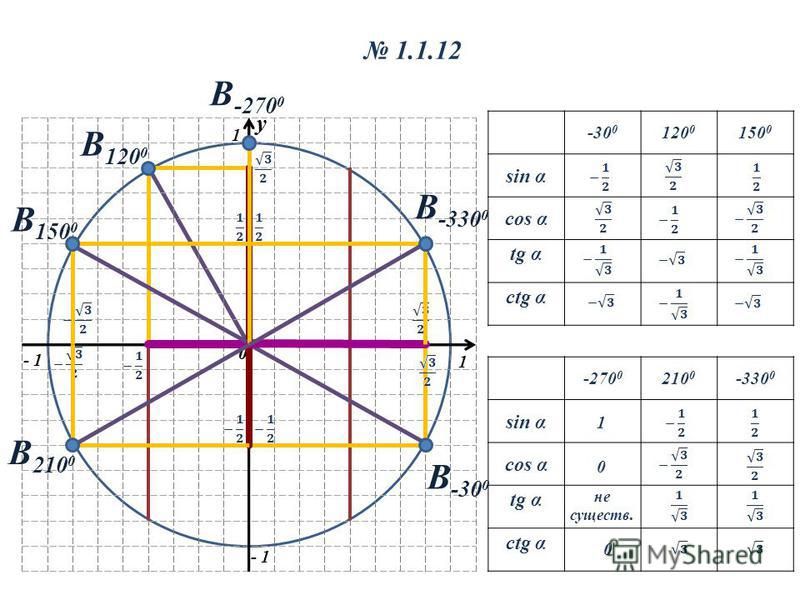 Тригонометрия — это система, которая помогает нам определить отсутствующие или неизвестные длины сторон или углов в треугольнике.
Тригонометрия — это система, которая помогает нам определить отсутствующие или неизвестные длины сторон или углов в треугольнике.
Есть ли триггер в физике?
Тригонометрия необходима для физики.
Почему тригонометрия так важна?
Отличные навыки тригонометрии позволяют учащимся определять сложные углы и размеры за относительно короткое время. Широко используемая в архитектуре, технике и многих других науках, тригонометрия является одним из наиболее ценных разделов математики.
Как рассчитывается синус?
Функция синуса (sin) – Тригонометрия. В прямоугольном треугольнике синус угла равен длине противолежащего катета, деленному на длину гипотенузы. В любом прямоугольном треугольнике синус угла x равен длине противоположной стороны (O), деленной на длину гипотенузы (H).
Что такое СОХ КАХ ТОА?
«SOHCAHTOA» — полезная мнемоника для запоминания определений тригонометрических функций синуса, косинуса и тангенса, т. е. синус равен противоположному по гипотенузе, косинус равен прилежащему по гипотенузе, а тангенс равен противоположному по отношению к прилежащему, (1) (2) (3) ) Другие мнемоники включают.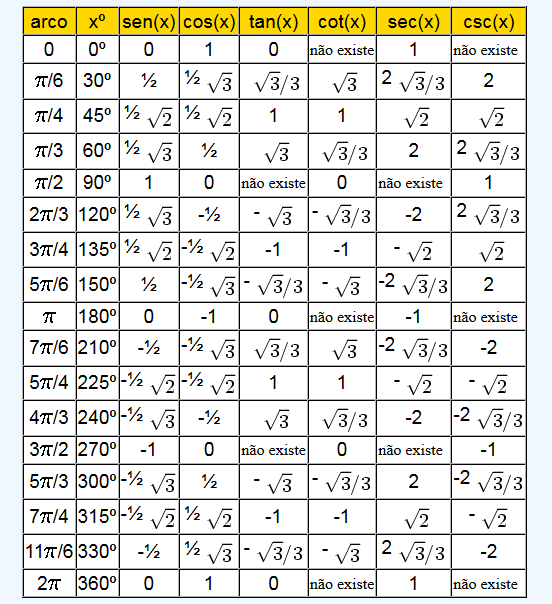
Каково назначение синуса?
Функция синуса обычно используется для моделирования периодических явлений, таких как звуковые и световые волны, положение и скорость гармонических осцилляторов, интенсивность солнечного света и продолжительность дня, а также колебания средней температуры в течение года.
Что такое формула кос?
Тогда формула косинуса: cos x = (прилежащая сторона) / (гипотенуза), где «прилежащая сторона» — это сторона, примыкающая к углу x, а «гипотенуза» — самая длинная сторона (сторона, противоположная прямому углу) треугольник.
Что такое формула тригонометрии?
В нем говорится, что c2, квадрат одной стороны треугольника, равен a2 + b2, сумме квадратов двух других сторон, минус 2ab cos C, удвоенное их произведение, умноженное на косинус противоположного угла. Когда угол С прямой, он становится формулой Пифагора.
Что такое формула загара?
Тангенс угла прямоугольного треугольника равен длине противолежащей стороны (О), деленной на длину прилежащей стороны (А).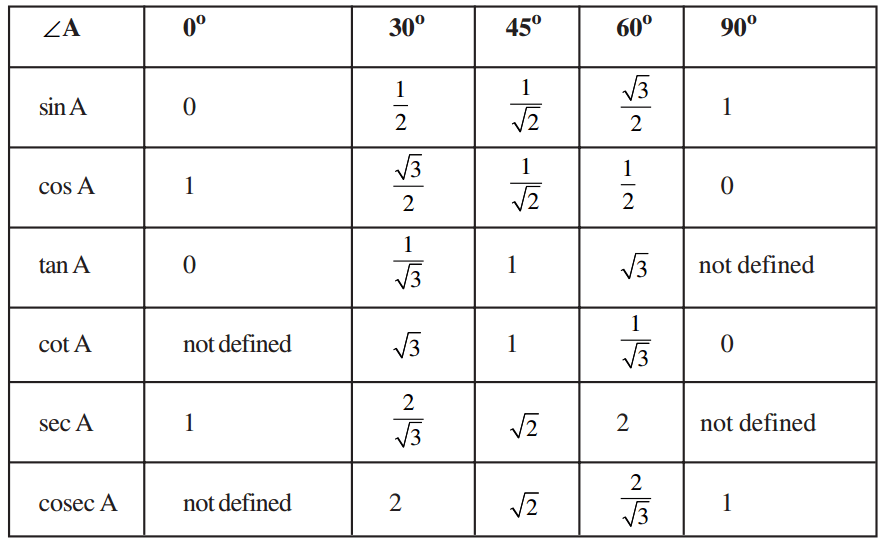 Это записывается просто как «загар» в формуле. tan(x) — это символ функции тангенса, который также называется формулой tan x.
Это записывается просто как «загар» в формуле. tan(x) — это символ функции тангенса, который также называется формулой tan x.
Что такое функция COS?
Функция косинуса является периодической функцией, которая очень важна в тригонометрии. Координата x точки, где другая сторона угла пересекает окружность, равна cos(θ) , а координата y равна sin(θ) .
Что такое cos в математике?
Косинус (часто сокращенно «cos») — это отношение длины стороны, примыкающей к углу, к длине гипотенузы. А тангенс (часто сокращенно «тан») — это отношение длины стороны, противоположной углу, к длине стороны, примыкающей.
Каково значение 1 cos тета?
Пояснение: 1+cos тета = sin тета/1 – cos тета. Muxakara и еще 15 пользователей считают этот ответ полезным. Спасибо 7.
Кто изобрел 0?
Первый современный эквивалент цифры ноль был придуман индийским астрономом и математиком Брахмагуптой в 628 году. Его символом для изображения цифры была точка под числом.
Кто изобрел число пи?
Египтяне рассчитывали площадь круга по формуле, которая давала приблизительное значение 3,1605 для π. Первое вычисление числа π было сделано Архимедом Сиракузским (287–212 гг. до н. э.), одним из величайших математиков древнего мира.
Первое вычисление числа π было сделано Архимедом Сиракузским (287–212 гг. до н. э.), одним из величайших математиков древнего мира.
Что такое 3 тригонометрических соотношения?
Три основных тригонометрических соотношения: синус, косинус и тангенс. Учитывая прямоугольный треугольник, вы можете найти синус (или косинус, или тангенс) любого из углов, отличных от 90°.
Как медсестры используют тригонометрию?
Получение степени младшего специалиста — это более короткий и более клинический подход к тому, чтобы стать медсестрой. Медсестры также интерпретируют графики во время компьютерной томографии и магнитно-резонансной томографии, могут использовать триггеры для обнаружения опухолей и определения частоты сердечных сокращений.
Точные значения sin, cos, tan (от 0 до 2pi, радианы)
- Бежать
- Сделать копию
- Скачать
- Добавить в очередь
- Добавить в корзину
Имя
Описание
Попробуйте ответить здесь на следующие вопросы:
- Для чего используется этот вопрос?
- Что оценивает этот вопрос?
- Что должен делать студент?
- Как рандомизируется вопрос?
- Есть ли какие-либо детали реализации, о которых следует знать редакторам?
Авторы
- Бен Браун
Обратная связь
От пользователей, являющихся членами Тригонометрии :
| Бен Браун | сказал | Готов к использованию | 5 лет, 3 месяца назад |
История
○
Бен Браун
5 лет, 3 месяца назад Опубликовал это.
○
Бен Браун
5 лет, 3 месяца назадДал отзыв: Готов к использованию
○
Бен Браун
5 лет, 3 месяца назад Создал это как копию точных значений для sin, cos, tan (от 0 до 330, градусов).| Имя | Статус | Автор | Последнее изменение | |
|---|---|---|---|---|
| Точные значения sin, cos, tan (острый, градусы) | Готов использовать | Бен Браун | 07.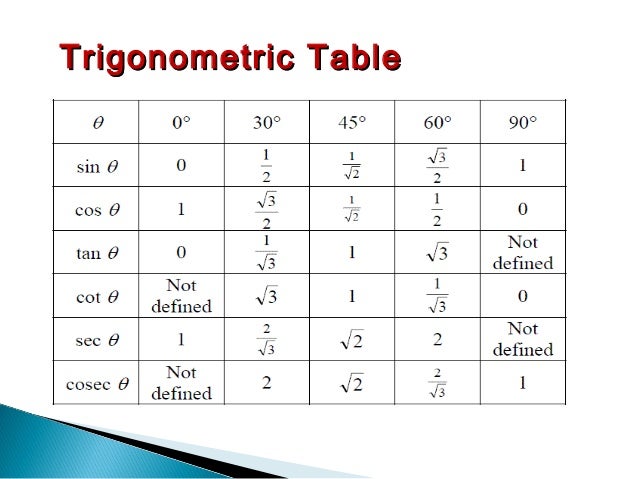 13.2017 14:57 13.2017 14:57 | |
| Точные значения для csc, sec, cot (acute, радианы) | Готов использовать | Бен Браун | 07.13.2017 14:56 | |
| Точные значения для csc, sec, cot (острая, градусы) | Готов использовать | Бен Браун | 07. 13.2017 14:56 13.2017 14:56 | |
| Точные значения sin, cos, tan (acute, радианы) | Готов использовать | Бен Браун | 07.13.2017 14:56 | |
| Точные значения sin, cos, tan (от 0 до 330, градусов) | Готов использовать | Бен Браун | 07. 13.2017 14:54 13.2017 14:54 | |
| Точные значения sin, cos, tan (от -1080 до 1080, градусов) | Готов использовать | Бен Браун | 23.10.2020 00:30 | |
| Точные значения sin, cos, tan (от 0 до 330, градусов) | черновик | Марлон Арсила | 31. 08.2016 17:41 08.2016 17:41 | |
| Точные значения для csc, sec, cot (acute, радианы) | черновик | Марлон Арсила | 19.09.2016 16:49 | |
| Точные значения sin, cos, tan (acute, радианы) | черновик | Марлон Арсила | 10. 19.2016 13:18 19.2016 13:18 | |
| Копия Питера Точные значения для sin, cos, tan (от 0 до 330, градусов) | черновик | Питер Джонстон | 30.03.2017 09:13 | |
| Точные значения sin, cos, tan (от 0 до 2pi, радианы) | Готов использовать | Бен Браун | 06. 07.2017 04:05 07.2017 04:05 | |
| Точные значения sin, cos, tan (от -6pi до 6pi, радианы) | Готов использовать | Бен Браун | 06.07.2017 04:04 | |
| Копия Терри Точные значения для sin, cos, tan (от -1080 до 1080, градусов) | черновик | Терри Янг | 04. 03.2019 17:51 03.2019 17:51 | |
| Копия Марии Точные значения для sin, cos, tan (от -6pi до 6pi, радианы) | черновик | Мария Анейрос | 25.05.2019 08:00 | |
| Копия Марии Точных значений sin, cos, tan (от 0 до 2pi, радианы) | черновик | Мария Анейрос | 25. 05.2019 08:01 05.2019 08:01 | |
| Копия Марии Точные значения для sin, cos, tan (острый, градусы) | черновик | Мария Анейрос | 29.05.2019 07:52 | |
| Точные значения sin, cos, tan (от -1080 до 1080, градусов) | черновик | Сяодань Ленг | 07.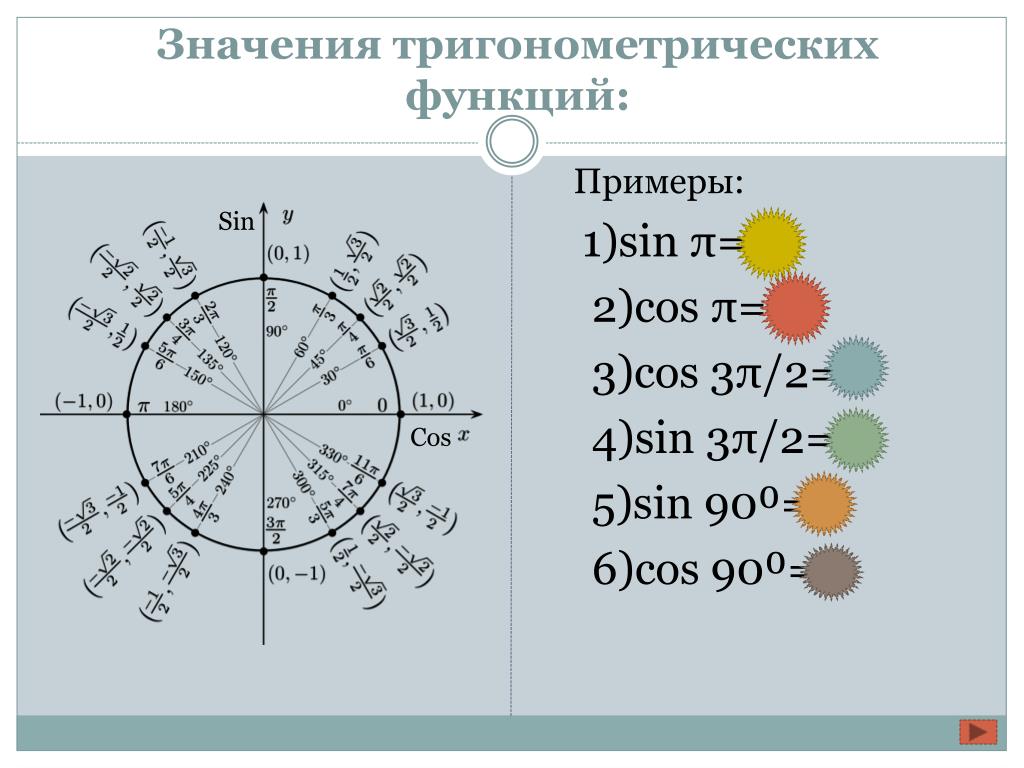 11.2019 01:05 11.2019 01:05 | |
| Точные значения sin, cos, tan (острый, градусы) | черновик | Сяодань Ленг | 07.11.2019 02:08 | |
| Точные значения для csc, sec, cot (острая, градусы) | черновик | Сяодань Ленг | 07.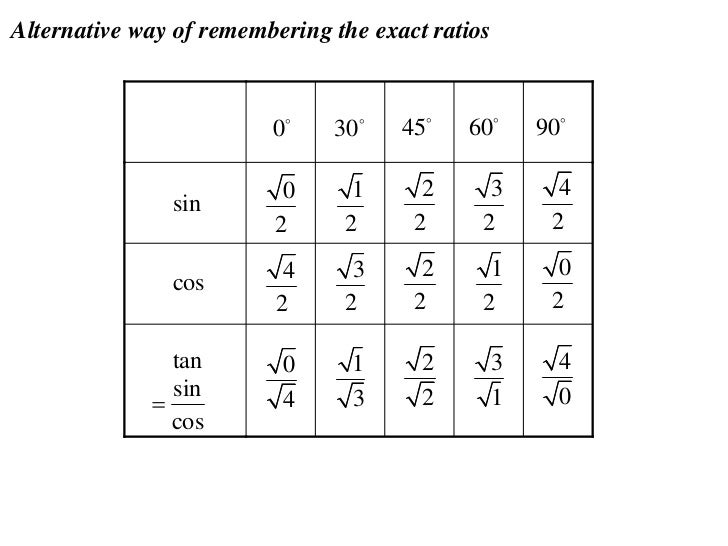 11.2019 02:08 11.2019 02:08 | |
| Точные значения для csc, sec, cot (acute, радианы) | черновик | Сяодань Ленг | 07.11.2019 02:09 | |
| Точные значения sin, cos, tan (acute, радианы) | черновик | Сяодань Ленг | 07.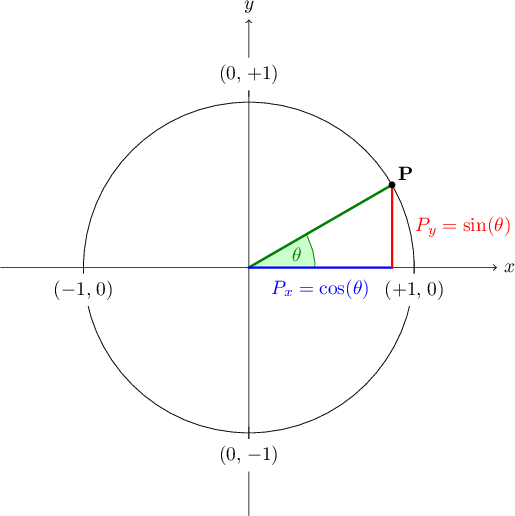 11.2019 02:09 11.2019 02:09 | |
| Точные значения sin, cos, tan (от 0 до 330, градусов) | черновик | Сяодань Ленг | 07.11.2019 02:10 | |
| Точные значения sin, cos, tan (от 0 до 2pi, радианы) | черновик | Сяодань Ленг | 07.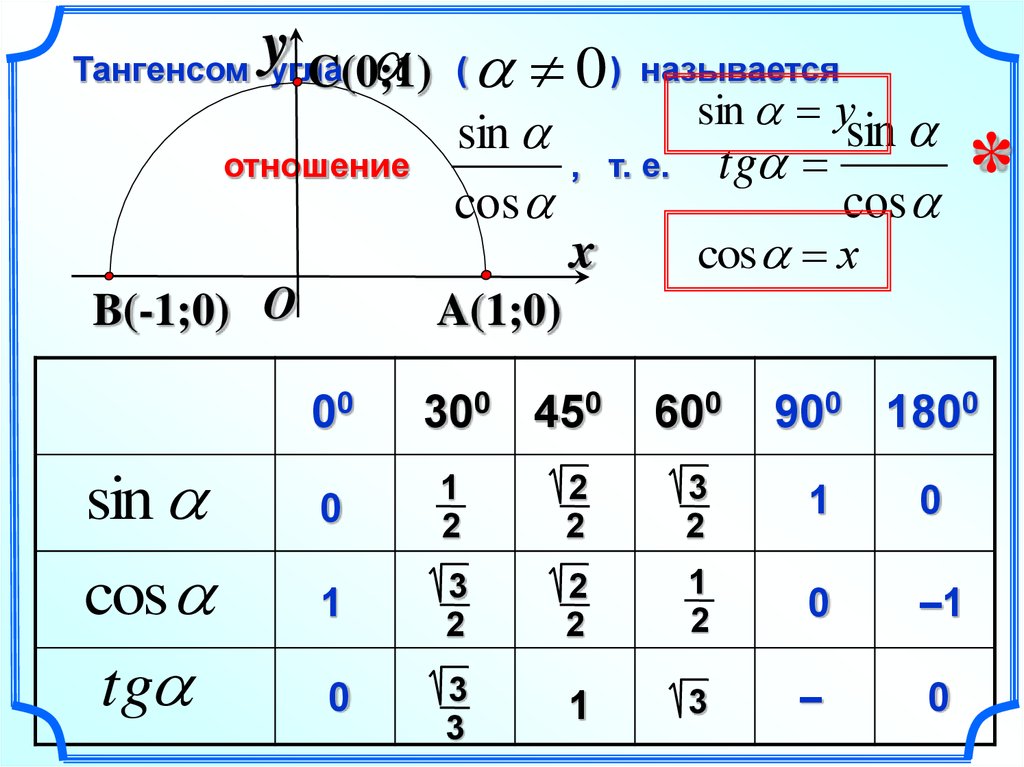 11.2019 02:24 11.2019 02:24 | |
| Точные значения sin, cos, tan (от -6pi до 6pi, радианы) | черновик | Сяодань Ленг | 07.11.2019 02:25 | |
| Копия Леонардо Точные значения для sin, cos, tan (от 0 до 330, градусов) | черновик | Леонардо Джулиано | 28. 08.2019 18:24 08.2019 18:24 | |
| Копия AJAY’s Exact values for sin, cos, tan (acute, Degrees) | черновик | АДЖАЙ ОТТА | 02.12.2020 11:31 | |
| Копия Яна Точные значения для sin, cos, tan (от -1080 до 1080, градусов) | черновик | Ян Хансен | 05. 03.2020 10:03 03.2020 10:03 | |
| Копия Пола Точные значения для sin, cos, tan (от 0 до 2pi, радианы) | черновик | Пол Хэнкок | 29.04.2020 02:50 | |
| Копия Абрари Точных значений sin, cos, tan (от 0 до 330, градусов) | черновик | Абрари Хасми | 19. 09.2020 17:27 09.2020 17:27 | |
| Копия Чон-Хвана Точных значений sin, cos, tan (от -1080 до 1080, градусов) | черновик | Чон-Хван До | 11.03.2020 21:54 | |
| Копия Джона Точные значения для sin, cos, (от -1080 до 1080, градусов) | черновик | Джон Харви | 02. 01.2021 13:53 01.2021 13:53 | |
| Точные значения sin, cos, tan (от 0 до 330 градусов) | Необходимо протестировать | Сьюзан МакГлинн | 30.09.2021 00:25 | |
| Копия Сьюзен Точные значения для sin, cos, tan (острый, градусы) | черновик | Сьюзан МакГлинн | 30. 09.2021 00:25 09.2021 00:25 | |
| Точные значения sin, cos, tan (острый, градусы) | Готов использовать | Сьюзан МакГлинн | 30.09.2021 00:25 | |
| Копия Сьюзен Точные значения для sin, cos, tan (от 0 до 330, градусов) | черновик | Сьюзан МакГлинн | 30. 09.2021 00:25 09.2021 00:25 | |
| Копия Лин Точные значения для sin, cos, tan (от 0 до 2pi, радианы) | Имеет некоторые проблемы | Лин Армстронг | 02.03.2021 06:09 | |
| Точные значения sin, cos, tan (острый, градусы) | черновик | Гизем Интепе | 30.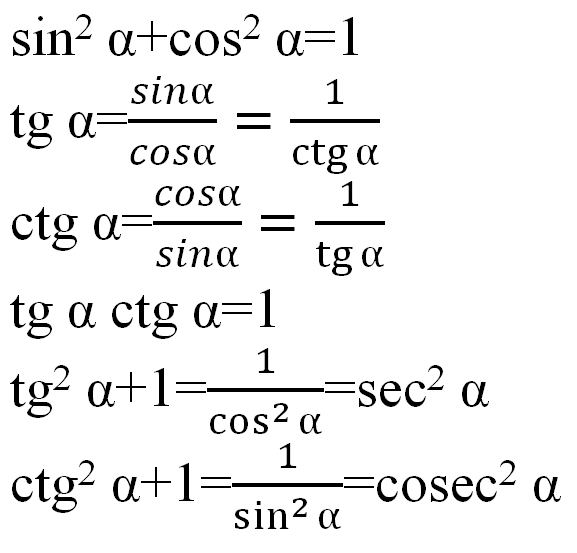 09.2021 00:25 09.2021 00:25 | |
| Точные значения sin, cos, tan (0, 90, 270, 360 градусов) | черновик | Сьюзан МакГлинн | 30.09.2021 00:25 | |
| Точные значения sin, cos, tan (от 0 до 330 градусов) | Необходимо протестировать | Сьюзан МакГлинн | 17. 02.2022 09:04 02.2022 09:04 | |
| Копия Лин Точные значения для sin, cos, tan (острый, градусы) | черновик | Лин Армстронг | 02.15.2021 02:58 | |
| Копия Лин Точные значения для sin, cos, tan (от 0 до 330 градусов) | черновик | Лин Армстронг | 02. 15.2021 03:01 15.2021 03:01 | |
| Копия Лин копии Лин Точные значения для sin, cos, tan (от 0 до 330 градусов) | черновик | Лин Армстронг | 30.09.2021 00:25 | |
| Копия черновика Лин Точные значения для sin, cos, tan (от 0 до 2pi, радианы) NO tan | Необходимо протестировать | Лин Армстронг | 20.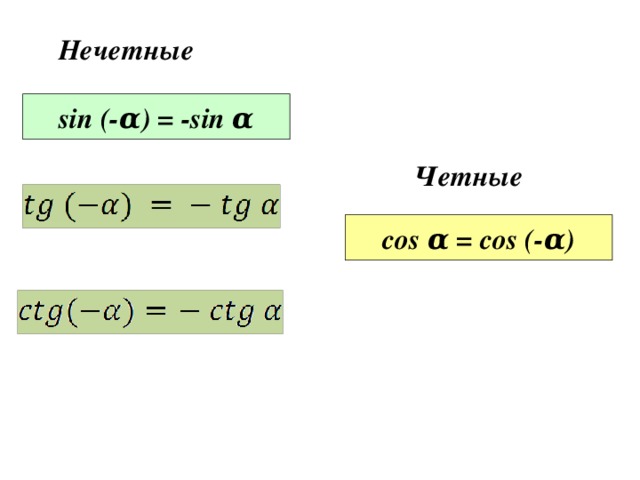 02.2022 11:07 02.2022 11:07 | |
| Копия Сьюзен Точные значения для sin, cos, tan (от 0 до 330 градусов) | черновик | Сьюзан МакГлинн | 30.09.2021 00:25 | |
| Копия Сьюзен Точные значения для sin, cos, tan (от 0 до 330 градусов) | черновик | Сьюзан МакГлинн | 30.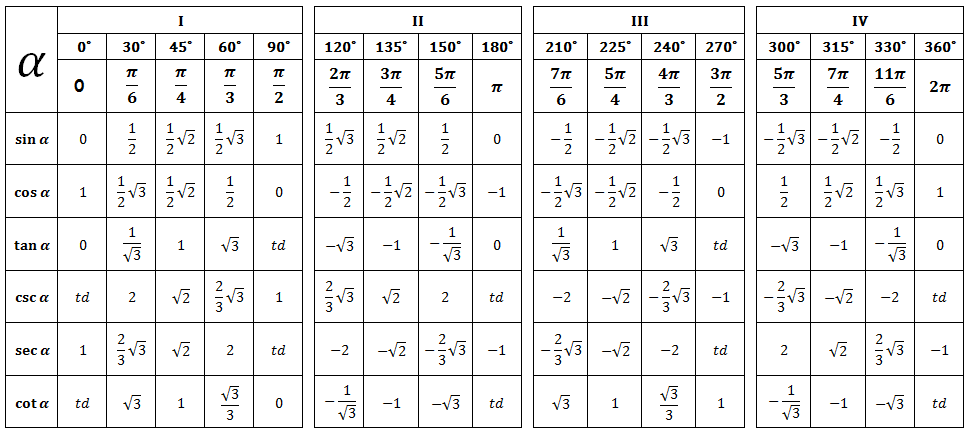 09.2021 00:25 09.2021 00:25 | |
| Копия Лин копии Лин Точные значения для sin, cos, tan (от 0 до 2pi, радианы) | Имеет некоторые проблемы | Лин Армстронг | 20.02.2022 11:09 | |
| Копия Джима Точные значения для sin, cos, tan (от 0 до 330 градусов) | черновик | Джим Петтигрю | 03. 01.2021 00:30 01.2021 00:30 | |
| Точные значения sin, cos, tan (острый, градусы) | черновик | Энтони Браун | 05.01.2021 13:16 | |
| Точные значения для csc, sec, cot (acute, радианы) | черновик | Энтони Браун | 05. 01.2021 13:45 01.2021 13:45 | |
| Точные значения для csc, sec, cot (acute, радианы) | черновик | Энтони Браун | 05.01.2021 14:28 | |
| Точные значения sin, cos, tan (от -1080 до 1080, градусов) | черновик | АДЖАЙ ОТТА | 06.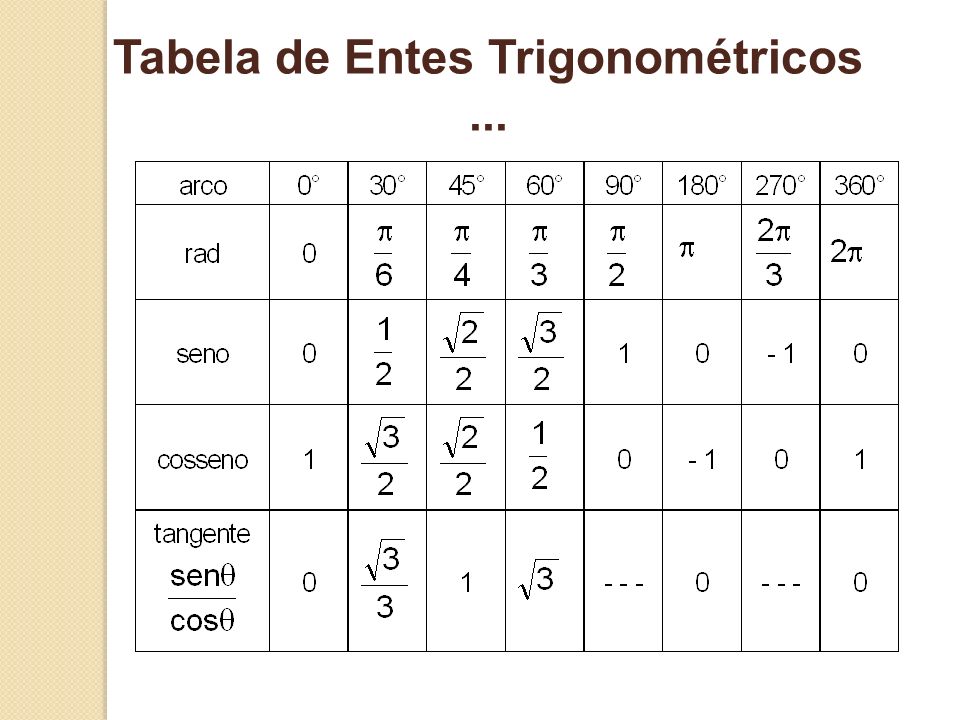 12.2021 16:52 12.2021 16:52 | |
| Точные значения sin, cos, tan (острый, градусы) | черновик | Таном Шоу | 29.07.2021 12:30 | |
| Точные значения просто sin и tan (острый, градусы) | черновик | Таном Шоу | 18. 08.2021 04:32 08.2021 04:32 | |
| Точные значения sin, cos, tan (острый, градусы) | Необходимо протестировать | Кошик Майсур | 09.12.2021 15:56 | |
| Точные значения sin, cos, tan (от 0 до 330, градусов) | Имеет некоторые проблемы | Кошик Майсур | 08.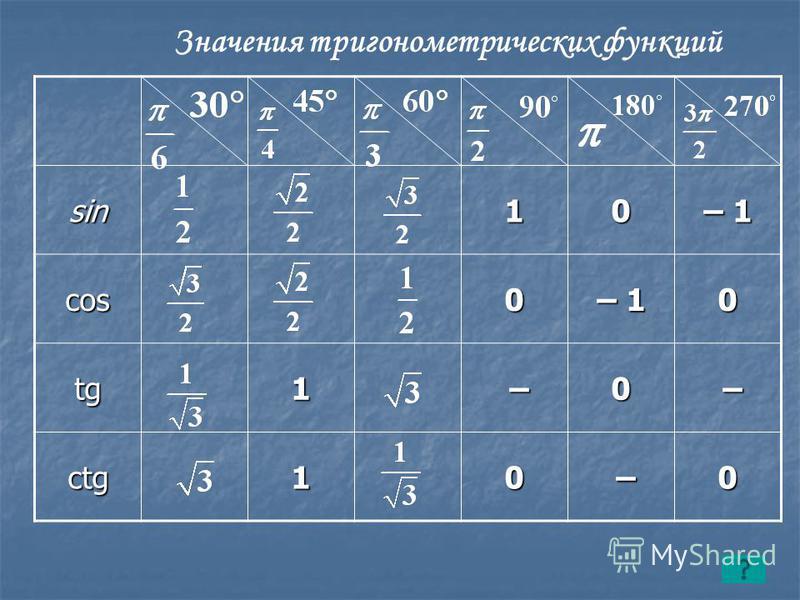 09.2021 10:20 09.2021 10:20 | |
| Точные значения sin, cos, tan (от 0 до 2pi, радианы) | Имеет некоторые проблемы | Кошик Майсур | 08.10.2021 11:35 | |
| Точные значения sin, cos, tan (acute, радианы) | Готов использовать | Стив Килгаллон | 28.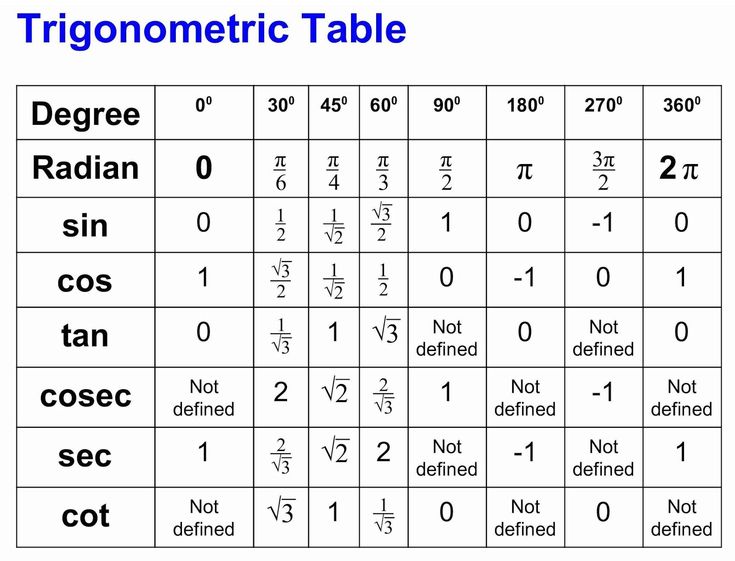 01.2022 14:13 01.2022 14:13 | |
| Точные значения sin, cos, tan (острый, градусы) | Готов использовать | Стив Килгаллон | 28.01.2022 14:14 | |
| Копия Лин Точные значения для sin, cos, tan (acute, градусы в радианах?) v2 | Не работает | Лин Армстронг | 02.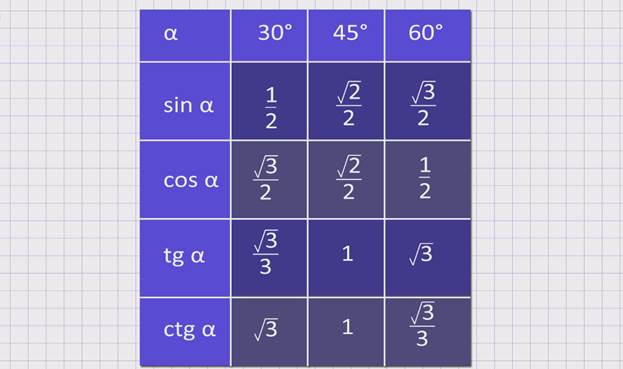 16.2022 22:57 16.2022 22:57 | |
| Копия Lyn копии Lyn Точные значения sin, cos, tan (от 0 до 2pi, радианы) NO tan | черновик | Лин Армстронг | 20.02.2022 11:07 | |
| Точные значения sin и cos (от 0 до 2pi, радианы) | Необходимо протестировать | Лин Армстронг | 20. 02.2022 11:05 02.2022 11:05 | |
| Точные значения sin, cos, tan (acute, радианы) | Готов использовать | Анна Картлидж | 05.05.2022 10:39 | |
| Точные значения sin, cos, tan (от 0 до 2pi, радианы) | Готов использовать | Анна Картлидж | 05.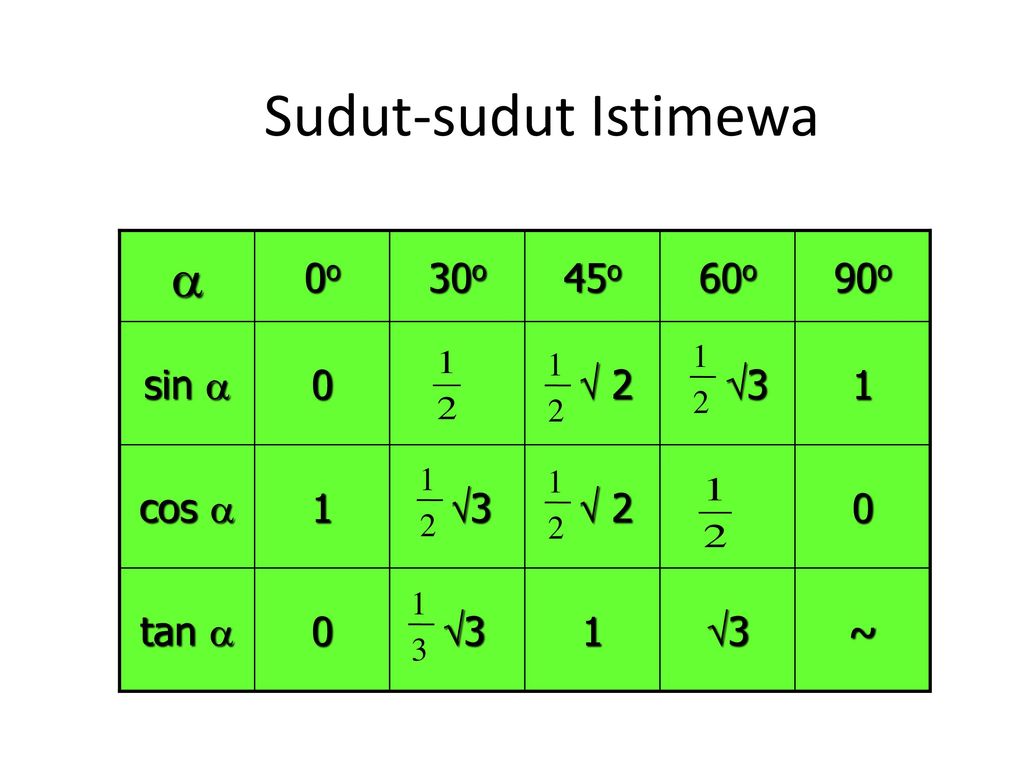 05.2022 10:39 05.2022 10:39 | |
| Копировать__to__see___of Точные значения sin, cos, tan (от 0 до 330, градусов) | черновик | Рауль Дуарте | 30.05.2022 22:50 | |
| Радианы — точные значения sin, cos, tan (acute) | Готов использовать | Анна Картлидж | 29. 07.2022 18:02 07.2022 18:02 |
Постановка вопроса
Дайте любую вводную информацию, которая нужна студенту.
В этом вопросе не определены переменные.
Имя
Тип данных
Ценность
Справочник по функциям JME
(номер)
Числа между а также (включительно) с размером шага
Случайное число между а также (включительно) с размером шага
(текстовая строка)
Это шаблон?
Это шаблон?
(цифры)
(текстовые строки)
Эта переменная была создана автоматически, поскольку где-то в этом вопросе есть ссылка на нее.
Предупреждение
Эта переменная является узлом HTML. Нельзя полагаться на то, что HTML-узлы будут работать правильно при возобновлении сеанса — например, прикрепленные обратные вызовы событий будут потеряны, а математическая запись, вероятно, также сломается.
Если это вызывает проблемы, попробуйте создать узлы HTML, где вы будете использовать их в областях содержимого, а не хранить их в переменных.
Описание
Опишите, что представляет эта переменная, и перечислите любые предположения, сделанные относительно ее значения.
Может ли экзамен переопределить значение этой переменной?
← Зависит от:
→ Используется:
Похоже, эта переменная нигде не используется.
Ошибка в условии, которое вы указали на вкладке Тестирование переменных. Значения переменных не могут быть сгенерированы, пока они не будут исправлены.
Автоматически регенерировать переменные?
Условие удовлетворить
Ошибка:
Максимальное количество запусков
в течение секунд
Работает в течение …
Помогите с режимом исследования
Максимальная отметка
(сумма объективных пределов)
Цели
Показать цели
| Имя | Ограничение | |
|---|---|---|
Штрафы
Показать пенальти
| Имя | Ограничение | |
|---|---|---|
В этом вопросе не определены части.
Выберите часть для редактирования.
Задайте учащемуся вопрос и дайте любые подсказки о том, как он должен ответить на эту часть.
Показать все отзывы?
Сообщение, если используется этот вариант
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Знаков
Правильный ответ
Правильный ответ — уравнение.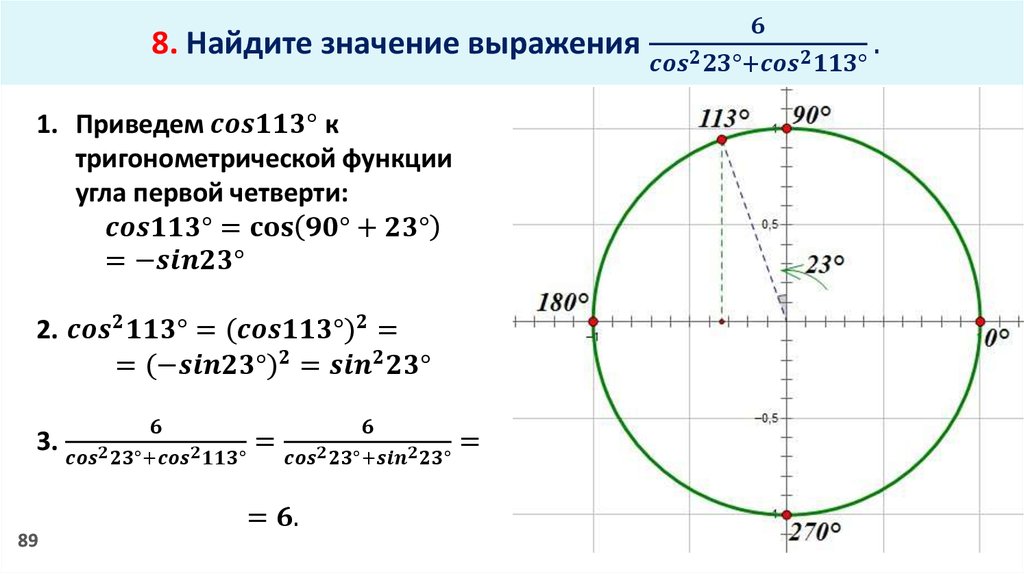 Используйте вкладку точности, чтобы сгенерировать значения переменных, удовлетворяющие этому уравнению, чтобы их можно было точно пометить.
Используйте вкладку точности, чтобы сгенерировать значения переменных, удовлетворяющие этому уравнению, чтобы их можно было точно пометить.
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Правила упрощения ответа
Показать предварительный просмотр ответа учащегося?
Выражение чувствительно к регистру?
Проверка точности
Определите диапазон баллов, по которому ответ учащегося будет сравниваться с правильным ответом, и метод, используемый для их сравнения.
Тип проверки
Проверка точности
Пункты для проверки
Максимальное количество неудач
Проверка начала диапазона
Проверка конца диапазона
Генераторы переменных значений
Приведите выражения, которые дают значения для каждой из переменных в ожидаемом ответе. Оставьте пустым, чтобы выбрать случайное значение из диапазона, определенного выше, в соответствии с предполагаемым типом переменной.
(это может быть )
Ограничение шаблона
Переменные
Предупреждать, если учащийся использует неожиданное имя переменной?
Инициировать однобуквенные имена переменных?
Разрешить неизвестные имена функций?
Использовать неявную композицию функций?
Строковые ограничения
Максимальная длина
(без максимума)
Частичный кредит за длинный ответ
Предупреждение
Требуемые строки
Частичный кредит за неиспользование всех необходимых строк
Показывать обязательные строки в предупреждении?
Предупреждение
Запрещенные строки:
Частичный кредит за использование любой запрещенной строки
Показывать запрещенные строки в предупреждении?
Предупреждение
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Сортировать ответы учащихся перед выставлением оценок?
Знаков
Минимальное допустимое значение
Максимально допустимое значение
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Ограничение точности
Разрешить ученику вводить дробь?
Нужно ли уменьшать дробь?
Показать подсказку по вводу дроби?
Частичный кредит для неуменьшенной дроби
Показать правильный ответ в виде дроби?
Требовать нули в конце?
Показать подсказку об ограничении точности?
Частичный кредит за неправильную точность
Сообщение, если неправильная точность
Допустимые обозначения
Правильный стиль ответа
Знаков
Матч-тест
Образец ответа
Показать ответ
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Ответ должен быть в правильном регистре?
Частичный зачет за ответ, не соответствующий случаю
Показать состояние обратной связи выбора?
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Тип выбора
Количество столбцов дисплея
(не отображается в столбцах)
Пользовательская матрица маркировки?
Пользовательское матричное выражение
Переменный список вариантов?
Список вариантов
Перетасовать порядок выбора?
Минимальные баллы
Максимальное количество баллов
(без максимума)
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Количество столбцов дисплея
(не отображается в столбцах)
Минимум ответов
Максимальное количество ответов
(без максимума)
Что делать, если выбрано неправильное количество ответов:
Пользовательская матрица маркировки?
Пользовательское матричное выражение
Показать состояние обратной связи выбора?
Метод маркировки
Для каждого варианта укажите количество баллов, которое будет добавлено или вычтено при выборе учащимся.
Для каждого варианта ответа напишите 1, если учащийся должен отметить его, или 0, если он не должен его отметить.
Вы должны установить максимальное количество оценок, чтобы использовать этот метод оценки.
Переменный список вариантов?
Список вариантов
Перетасовать порядок выбора?
Минимальные баллы
Максимальное количество баллов
(без максимума)
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Минимум ответов
Максимальное количество ответов
(без максимума)
Что делать, если выбрано неправильное количество ответов:
Тип выбора
Макет
Пользовательское выражение макета
Показать состояние обратной связи выбора?
Переменный список вариантов?
Список вариантов
Перетасовать порядок выбора?
Переменный список ответов?
Список ответов
Перемешать ответы?
Метод маркировки
Вы должны установить максимальное количество оценок, чтобы использовать этот метод оценки.
Пользовательская матрица маркировки?
Пользовательское матричное выражение
Для каждой комбинации ответа и выбора укажите количество баллов, которое нужно добавить или вычесть, когда учащийся выберет его.
Для каждой комбинации ответа и выбора напишите 1, если учащийся должен поставить галочку, или 0, если он не должен ставить галочку.
| ответы | |
|---|---|
| Выбор |
Для этой части должны быть определены как варианты, так и ответы.
Знаков
Правильный ответ
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Расширенные настройки
Количество рядов
Количество столбцов
Разрешить учащемуся изменять размер матрицы?
Минимальное количество строк
(Без ограничений)
Максимальное количество строк
(без ограничений)
Минимальное количество столбцов
(Без ограничений)
Максимальное количество столбцов
(Без ограничений)
Допустимая погрешность в каждой ячейке
Получить баллы за каждую правильную ячейку?
Ограничение точности
Требовать нули в конце?
Частичный кредит за неправильную точность
Сообщение, если неправильная точность
Разрешить ученику вводить дроби?
Отобразить числа в правильном ответе в виде дробей?
Знаков
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Помогите с этим типом детали
Штраф за обнаружение шагов
Показать правильный ответ при открытии?
Показать значок обратной связи с оценкой?
Оценка засчитывается для достижения цели
Использовать собственный алгоритм маркировки?
Расширить базовый алгоритм маркировки?
Базовый алгоритм маркировки
Пользовательский алгоритм маркировки
Проверка работы алгоритма маркировки
Убедитесь, что алгоритм выставления оценок работает с разными наборами переменных и ответов учащихся, используя приведенный ниже интерфейс.
Создайте модульные тесты, чтобы сохранить ожидаемые результаты и задокументировать, как должен работать алгоритм.
Произошла ошибка, означающая, что алгоритм маркировки не может работать:
| Зазор | Ожидаемый ответ | Ответ студента |
|---|---|---|
- id) == $data.id}»/>
Переменные вопроса
Эти переменные доступны в алгоритме маркировки.
| Имя | Значение | |
|---|---|---|
Параметры маркировки
Эти значения доступны как дополнительные переменные в алгоритме маркировки.
| Имя | Значение |
|---|---|
Настройки детали
Эти значения доступны в виде записей в переменной settings .
| Имя | Значение |
|---|---|
| г. |
Этот отзыв основан на вашем последнем ответе. Отправьте измененный ответ, чтобы получить обновленный отзыв.
Предупреждения:
Альтернативный вариант:
| Примечание | Значение | Обратная связь |
|---|---|---|
| toggle»> |
Нажмите на название заметки, чтобы показать или скрыть ее. При создании модульного теста будут включены только показанные заметки.
Модульные тесты
Модульные тесты не определены. Введите ответ выше, выберите одну или несколько заметок и нажмите кнопку «Создать модульный тест».
Следующие тесты проверяют правильность поведения вопроса.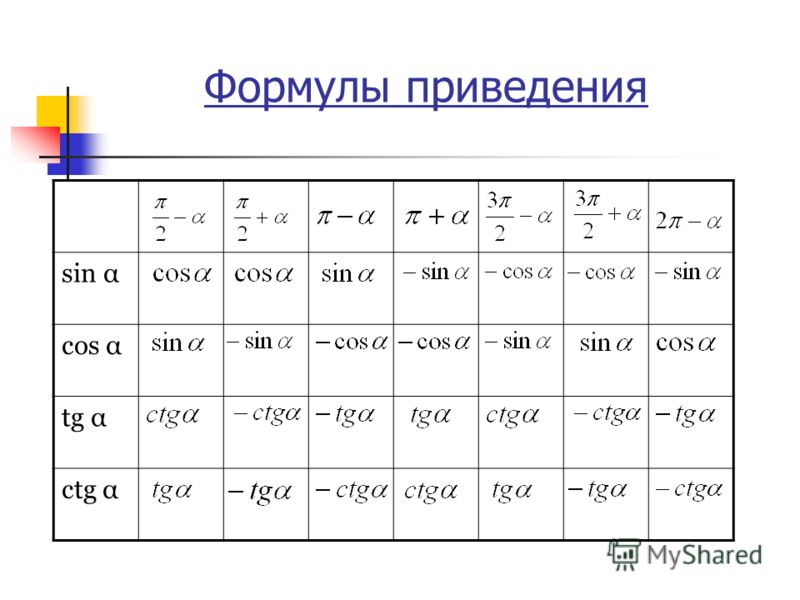
Этот тест еще не был запущен Этот тест дает ожидаемый результат Этот тест не дает ожидаемого результата
Этот тест в настоящее время не дает ожидаемого результата. Исправьте алгоритм маркировки для получения ожидаемых результатов, подробно описанных ниже, или, если этот тест устарел, обновите тест, чтобы принять текущие значения.
Одна или несколько нот в этом тесте больше не определены. Если эти примечания больше не нужны, вам следует удалить этот тест.
| Имя | Значение |
|---|---|
| goToVariable(name)}, text: name ? name : ‘Unnamed'»/> |
Ответ студента
| Примечание | Значение | Обратная связь | |||
|---|---|---|---|---|---|
| Эта заметка дает ожидаемый результат | Текущий: | ||||
| Ожидается: |
Этот тест еще не выполнялся.
Если вам нужно изменить способ работы этой части помимо доступных опций, вы можете написать код JavaScript, который будет выполняться в моменты времени, описанные ниже.
Чтобы учесть ошибки, допущенные учащимся в предыдущих расчетах, замените переменные вопроса ответами на более ранние части.
Чтобы создать замену переменной, вы должны определить хотя бы одну переменную и еще одну часть.
Выбранные вами замены переменных приведут к повторной генерации следующих переменных каждый раз, когда учащийся отправляет ответ на эту часть:
- 909:40
Эти переменные содержат некоторые случайные элементы, что означает, что они не гарантируют, что они будут иметь одно и то же значение каждый раз, когда учащийся отправляет ответ. Вы должны определить новые переменные для хранения случайных элементов, чтобы они оставались неизменными каждый раз, когда эта часть помечается.
Дополнительная информация об этой проблеме
Стратегия замены переменной
Штраф при использовании адаптивной маркировки
Студент не может добраться до этой части.
Добавьте ссылку «следующая часть» на эту часть из другой части.
Ни одна из частей, которые могут вести к этой части, также не достижима.
Предлагаете вернуться к предыдущей части?
Варианты следующей детали
Определите список частей, которые студент может посетить после этой.
Предыдущие детали
Эта часть может следовать из:
Эта часть не следует ни за какой другой.
к
Совет
Дайте проработанное решение всего вопроса.
Выберите расширения для использования в этом вопросе.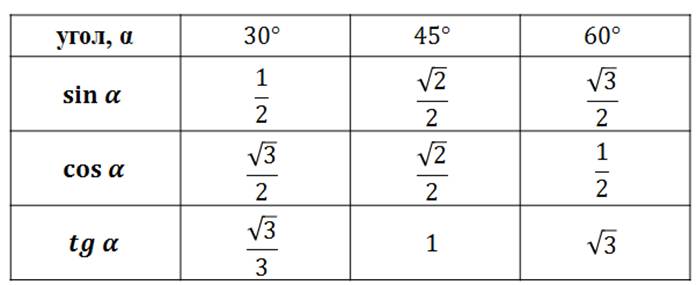
Определите наборы правил для упрощения и отображения математических выражений.
Имя
Определение
Определите функции для использования в выражениях JME.
Имя
Язык
Параметры
- : из
Тип выхода
Определение:
Встроенные константы
Отметьте встроенные константы, которые вы хотите включить в этот вопрос.
-
-
Пользовательские константы
Вы можете определять константы на основе встроенных констант, даже если они отключены.
| Имена | Значение | Латекс | |
|---|---|---|---|
Добавьте стиль к отображению вопроса и напишите скрипт, который будет запускаться при создании вопроса.
Javascript
Этот сценарий будет запущен после того, как будет сгенерирована переменная вопроса, но до прикрепления HTML.
CSS
Применение правил оформления к содержимому вопроса.
URL-адрес
Альтернативный текст
Этот вопрос используется на следующих экзаменах:
- Тригонометрия: точные значения и определения единичных окружностей (радианы) Бена Брауна
в тригонометрии.

- первый экзамен Сара Сантос в рабочем пространстве Сары.
- Тригонометрия Криса Темплета в рабочем пространстве Криса.
- (будет встроен в виде iframe)
Ширина
Высота
Текст заголовка
Альтернативный текст
Ширина
Высота
Numbas © Ньюкаслский университет.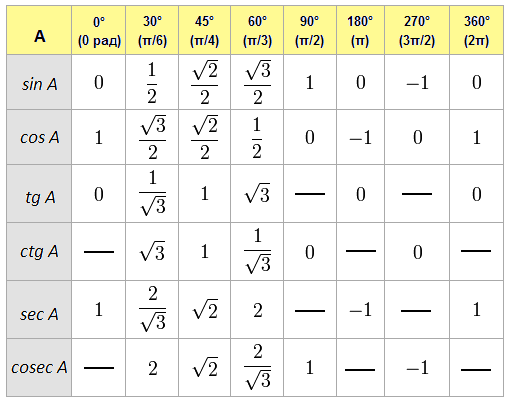 Условия использования и политика конфиденциальности.
Заявление о доступности.
Условия использования и политика конфиденциальности.
Заявление о доступности.позволяет вычислить $\\sin$, $\\cos$ и $\\tan$ для определенных углов независимо от того, в каком квадранте находится точка. Потому что, о каком бы угле нас ни спрашивали, мы всегда можем использовать треугольник в первый квадрант, чтобы определить длины сторон, а затем считать знаки координат отдельно.
Например, , чтобы определить $\\sin\\left(\\frac{7\\pi}{6}\\right)$, $\\cos\\left(\\frac{7\\ pi}{6}\\right)$ и $\\tan\\left(\\frac{7\\pi}{6}\\right)$ мы сначала нарисуем следующее:
Из этой диаграммы мы можем видим, что $\\cos\\left(\\frac{7\\pi}{6}\\right)=-\\cos\\left(\\frac{\\pi}{6}\\right) $ и $\\sin\\left(\\frac{7\\pi}{6}\\right)=-\\sin\\left(\\frac{\\pi}{6}\\right )$, так как треугольники конгруэнтны и мы находимся в 3-м квадранте, где оба значения $x$ и $y$ (и, следовательно, значения $\\cos$ и $\\sin$) отрицательны.
Но, зная эти точные значения, мы можем заключить, что \\[\\cos\\left(\\frac{7\\pi}{6}\\right)=-\\cos\\left(\\ frac{\\pi}{6}\\right)=-\\dfrac{\\sqrt{3}}{2},\\] \\[\\sin\\left(\\frac{7\\ pi}{6}\\right)=-\\sin\\left(\\frac{\\pi}{6}\\right)=-\\dfrac{1}{2},\\] и, наконец, \\[\\tan\\left(\\frac{7\\pi}{6}\\right)=\\dfrac{\\sin\\left(\\frac{7\\pi}{6} \\right)}{\\cos\\left(\\frac{7\\pi}{6}\\right)}=\\dfrac{-\\frac{1}{2}}{-\\ frac{\\sqrt{3}}{2}}=\\dfrac{1}{\\sqrt{3}}.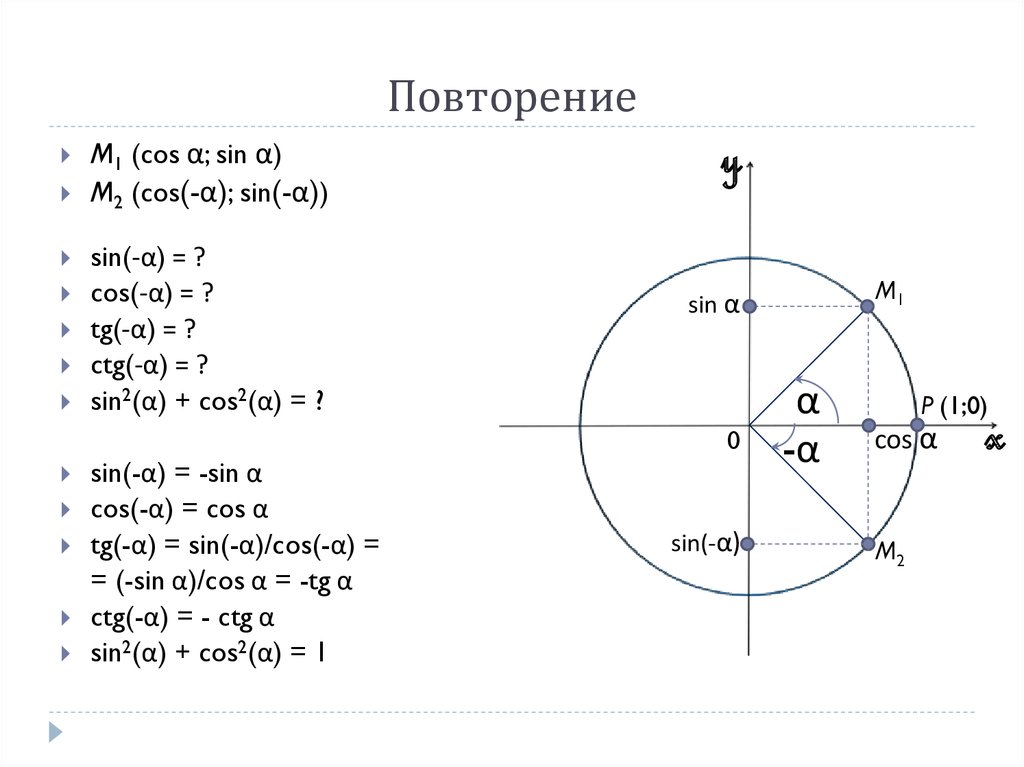 \\]
\\]
тестирование sin, cos, tan of random(0,90,120,135,150,180,210,225,240,270,300,315,330) градусов, но в радианах
Учащемуся показываются два варианта выбора: «Да» и «Нет». Один из них правильный.
Список считается правильным, если каждое число встречается столько же раз, сколько и в ожидаемом ответе, и в нем нет лишних чисел.
При желании вы можете рассматривать ответ как набор, поэтому количество вхождений не имеет значения, важно только, включено ли каждое число или нет.
Sin Cos Tan: формула, таблица значений, примеры
Значения Sin, Cos, Tan являются основными тригонометрическими отношениями для изучения отношения между углами и сторонами треугольника. Изучите формулы и значения с помощью простых примеров.
Sin, Cos и Tan — основные тригонометрические функции, учитываемые при решении тригонометрических задач. Sin, Cos и Tan сокращенно обозначают синус, косинус и тангенс соответственно. Эти математические функции используются для изучения соотношения между углами и сторонами треугольника.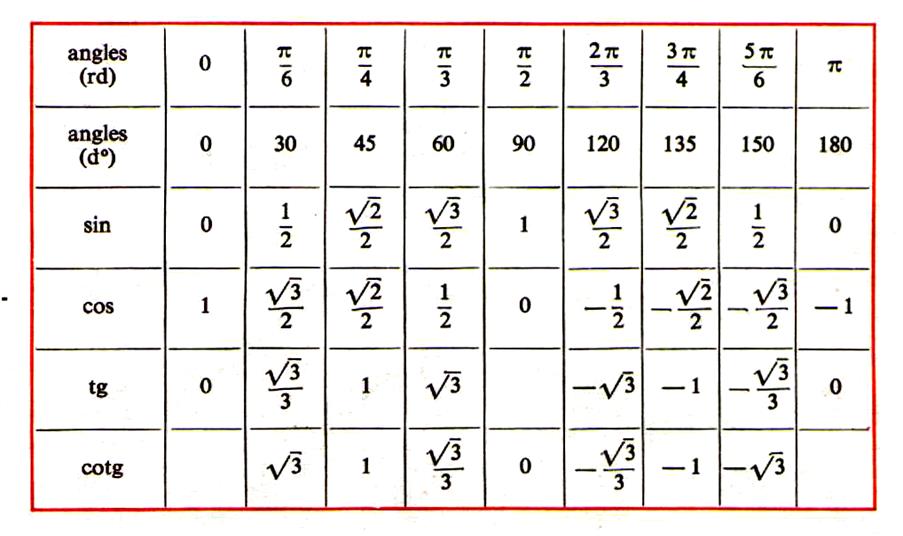
Что такое Sin, Cos и Tan в тригонометрии?
В то время как Пифагор установил связь между сторонами прямоугольного треугольника с помощью теоремы Пифагора, Гиппарк структурировал связь между сторонами и точками прямоугольного треугольника, используя идеи тригонометрии.
Однако sin, cos и tan являются важными тригонометрическими пропорциями. Каждое из которых дает пропорцию различных сторон прямоугольного треугольника. Самая длинная сторона треугольника называется гипотенузой, а две другие стороны называются смежной и противоположной сторонами.
Грех, Кос и Тан: Формула
Грех, Кос и Тан имеют свою формулу. Например, на диаграмме ниже показан прямоугольный треугольник. Самая длинная сторона - гипотенуза, а остальные стороны прилежащие и противоположные.
Формулы для sin, cos и tan следующие:
- Синус θ = противолежащая сторона/гипотенуза
- Cos θ = смежная сторона/гипотенуза
- Tan θ = Противоположная сторона/ Прилегающая сторона
Таким образом, мы установили связь между sin, cos и tan θ с помощью приведенных выше формул - Tan θ = Sin θ/Cos θ
Другие тригонометрические формулы
Поскольку мы установили связь между sin, cos и tan , вот другие формулы:
- Tan θ = Sin θ/Cos θ
- Кот θ = Cos θ/Sin θ
- Sin θ = Tan θ/с θ
- Cos θ = Sin θ/Tan θ
- Сек θ = Тангенс θ/Sin θ
- Cosec θ = Sec θ/Tan θ
Таблица значений Sin θ, Cos θ и Tan θ
В таблице ниже представлены тригонометрические функции относительно их степеней.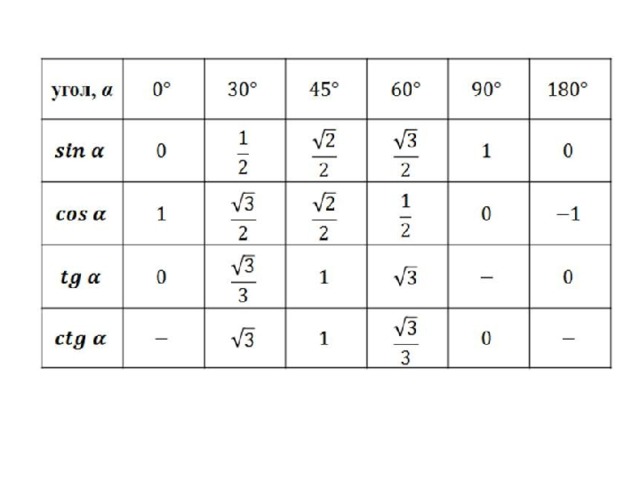 Градусы: 0°, 30°, 45°, 60° и 90°.
Градусы: 0°, 30°, 45°, 60° и 90°.
| Углы (в градусах) | 0° | 30° | 45° | 60° | 90° |
| углов (в радианах) | 0 | №/6 | №/4 | №/3 | №/2 |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Кос θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Желто-коричневый θ | 0 | 1/√3 | 1 | √3 | Не определено |
| Детская кроватка θ | Не определено | √3 | 1 | 1/√3 | 0 |
| сек θ | 1 | 2/√3 | √2 | 2 | Не определено |
| Косек θ | Не определено | 2 | √2 | 2/√3 | 1 |
Как найти значения Sin θ, Cos θ и Tan θ?
Иногда бывает сложно найти значения тригонометрических функций.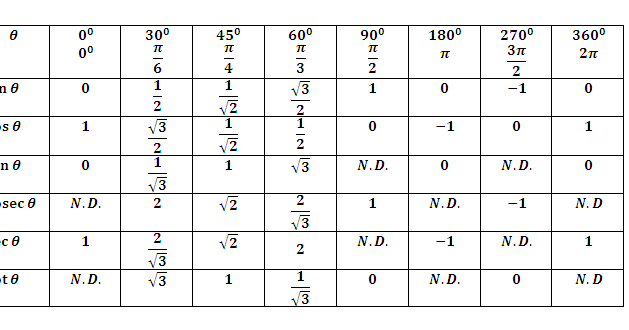 Итак, вот несколько простых шагов:
Итак, вот несколько простых шагов:
- Во-первых, мы можем разделить числа 0,1,2,3 и 4 на 4, а затем извлечь положительные корни из всех этих чисел.
- Затем мы можем найти значения sin, т. е. 0, ½, 1/√2, √3/2, 1, относительно их углов.
- Затем запишите те же значения в обратном формате, чтобы получить значения cos при 0°, 30°, 45°, 60° и 90°.
- Далее, тан есть отношение sin и cos. Таким образом, мы можем получить значения коэффициента тангенса для конкретных углов.
| Значения греха | Значения Cos | Значения тангенса |
| Sin 0° = √(0/4) = 0 | Кос 0° = √(4/4) = 1 | тангенс 0° = 0/1 = 0 |
| Sin 30° = √(1/4) = ½ | Cos 30° = √(3/4) = √3/2 | Тан 30° = (1/2) / (√3/2) = 1/√3 |
| Sin 45° = √(2/4) = 1/√2 | Cos 45° = √(2/4) = 1/√2 | Тан 45° = (1/√2) / (1/√2) = 1 |
| Sin 60° = √3/4 = √3/2 | Cos 60° = √(1/4) = 1/2 | Tan 60° = [(√3/2)/(½)] = √3 |
| Sin 90° = √(4/4) = 1 | Cos 90° = √(0/4) = 0 | Tan 90° = 1/0 = не определено |
Советы по запоминанию таблицы значений Sin θ, Cos θ и Tan θ
Вот несколько советов, которые могут помочь запомнить таблицу значений Sin θ, Cos θ и Tan θ:
- Во-первых, углы всегда находятся под углами 0°, 30°, 45°, 60° и 90°.

- Далее таблица sin θ выглядит как 0, ½, 1/√2, √3/2, 1. Непосредственно следующая таблица, cos θ, точно такая же, как sin θ в обратном формате – то же, что и остальная часть таблицы.
- Каждое значение в строке tan получается путем деления соответствующих значений sin на cos, поскольку tan = sin/cos.
Практическое использование значений Sin θ, Cos θ и Tan θ
Sin, cos и tan имеют большое значение при решении многочисленных жизненных трудностей. Ниже приведены некоторые идеалистические варианты использования функций:
- Используется для определения движения планет.
- Функции адаптированы для измерения угла возвышения, уклона и высоты зданий и гор.
- Далее, функции имеют практическое значение для оценки раскопок археологического отдела.
- Кроме того, он используется в бортовой технике для измерения изменения угла под действием ветра.

- Также используется в морской технике.
- Кроме того, применяется в гражданском строительстве для определения этажей, нагрузок, уклонов крыш.
Что следует помнить
Как упоминалось ранее, sin, cos и tan являются основными тригонометрическими функциями, используемыми для вычисления сторон прямоугольного треугольника.
- Sin θ определяется отношением противолежащего катета к гипотенузе.
- Sin θ= Противоположность/Гипотенуза = Tan θ/Сек θ
- Cos определяется отношением прилежащего катета к гипотенузе.
- Cos θ = Смежный/Гипотенуза = Sin θ/Tan θ
- Tan θ определяется отношением sin θ к cos θ.
- Tan θ = Sin θ/Cos θ = Противоположный/Смежный.
Примеры вопросов
1. Лестница прислонена к кирпичной стене под углом 50° к горизонтали. Если лестница находится на расстоянии 10 м от стены, то до какой высоты стены доходит лестница?
Лестница прислонена к кирпичной стене под углом 50° к горизонтали. Если лестница находится на расстоянии 10 м от стены, то до какой высоты стены доходит лестница?
Ответ:
Предположим, что лестница достигает x футов стены.
Используя предоставленную информацию:
Здесь мы знаем примыкающую сторону (которая равна 10 футам) и нам нужно найти противоположную сторону (которая равна x футам). Таким образом, мы используем отношение между противоположной и смежной сторонами, которое равно загару.
Tan 50° = x/10
x = 10 Tan 50°
x ≈ 11,9 футов
Здесь тангенс 50° рассчитывается с помощью калькулятора, а окончательный результат округляется до 1 десятичного знака. Таким образом, лестница достигает до 11,9 футов стены.
2. Артист цирка карабкается по веревке длиной 20 м, туго натянутой и привязанной к вершине вертикального шеста к земле. Найдите высоту шеста, если угол между канатом и землей равен 30°.
Ответ:
Длина веревки (AC) = 20 м и ∠ACB = 30º
Пусть высота стержня AB равна h м.
Длина веревки (AC) = 20 м и ACB = 30°
Тогда в треугольнике ABC
Sin 30 = AB/AC Значит, высота столба 10 м.
3. Если tan θ + cot θ = 5, найдите значение tan2θ + cotθ .
Ответ:
Tan θ + Cot θ = 5
Tan 2θ + Cot 2θ + 2 Tan θ Cot θ = 25 … (возведение в квадрат обеих сторон) 23
4.В прямоугольном треугольнике ABC с углом A, равным 90°, найдите углы B и C так, что sin(B) = cos(B)
Ответ:
Пусть b длина сторона, противоположная углу B, и c - длина стороны, противоположной углу C, а h - длина гипотенузы.
Sin(B) = b/h и Cos(B) = c/h
Sin(B) = Cos(B) означает b/h = c/h, что дает c = b
Две стороны равны по длине означает, что треугольник равнобедренный и углы B и C равны по величине 45 °.
5. Упростим тригонометрическое выражение: 2 cot (A)-2/1 - tan(-A)
Ответ:
2 Cot A-2/1 - Tan A
= (2 Cos A/Sin A)-2/1-(Sin A/Cos A)
= 2(Cos A- Sin A)/Sin A/(Cos A-Sin A)/Cos A
= 2 (Cos A- Sin A)/Sin A × Cos A/(Cos A-Sin A)
= 2 × Cos A/Sin A
= 2 × Cot A {Cot A=Cos A/Sin A}
= 2 Cot A
6. Решите данное выражение, используя значения sin cos tan: tan 60o (sec 60°/cosec 60°)
Ответ:
Мы знаем, Sec 60°/Cosec 60° = Sin 60°/Cos 60°
⇒ Tan 60°(sec 60°/Cosec 60°) = Tan 60°(Sin 60°/Cos 60°) = Tan 60° × Tan 60°
⇒ (√3)2 = 3
7. Найдите точную длину тени, отбрасываемой 15-футовым фонарным столбом, когда угол возвышения солнца 60º.
Ответ:
Предположим, что длина тени фонарного столба равна x футов.
Используя данную информацию:
x = 15/Tan 60°
x = 15/√3 (по таблице тригонометрии)
x = 15√3/3
Следовательно, длина тени фонарного столба равна 15√3/3 футов
8. Если sin θ = 2/3 и тангенс θ
Если sin θ = 2/3 и тангенс θ
Ответ :
Дано, что sin θ положительный, а tan θ отрицательный. Таким образом, θ должно быть в квадранте II, где cos θ отрицательно. Теперь sin θ = 2/3 = противоположность/гипотенуза.
Таким образом, мы можем предположить, что противоположность = 2k, гипотенуза = 3k. по теореме Пифагора = -√5/3
Что такое значение Sin Cos?
- 07.01.2022
- 17
Соммарио
- Что такое значение Sin Cos?
- Чему равен sin * cos?
- Как решить Sin Cos?
- Грех потому что грех?
- Как вычислить синус?
- Как сделать синус?
- Что такое OPP HYP?
- Что такое OPP вместо HYP?
- Как решить уравнение косинуса?
- Как найти грех?
- Что такое закон sin and cos?
- Как преобразовать sin в Cos?
- Что такое cos разделить на Sin?
- Чему равен косинус?
Что такое значение Sin Cos?
Глядя из вершины с углом θ, sin(θ) представляет собой отношение противолежащего катета к гипотенузе , а cos(θ) представляет собой отношение прилежащего катета к гипотенузе .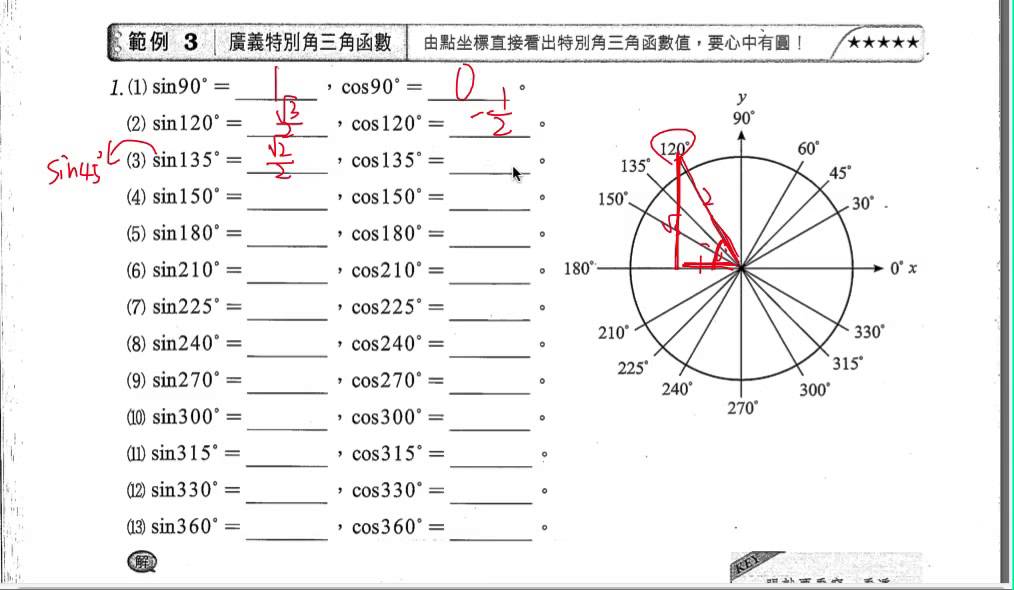 Независимо от размера треугольника значения sin(θ) и cos(θ) одинаковы для данного θ, как показано ниже.
Независимо от размера треугольника значения sin(θ) и cos(θ) одинаковы для данного θ, как показано ниже.
Чему равен sin * cos?
SINE, COSINE и TANGENT
| SINE функция: | SIN (θ) = противоположный / гипотенуза |
|---|---|
| Косинус. | tan(θ) = Противоположный / Смежный |
Как решить Sin Cos?
2:294:29Пример: Решить уравнение триггера: sin(x) = cos(x) и координаты y также равны, поэтому синус тета и косинус тета равны, поэтому от единичного круга. Мы легко можем видеть, что наши решения будут такими: x равно PI.
Грех потому что грех?
Sin и Cos — это основные коэффициенты триггера, которые говорят о форме прямоугольного треугольника. ... В любом прямоугольном треугольнике для любого угла: Синус угла ( sin A) = длина противоположной стороны / длина гипотенузы. Косинус угла (cos A) = длина прилежащей стороны / длина гипотенузы.
Косинус угла (cos A) = длина прилежащей стороны / длина гипотенузы.
Как вычислить синус?
0:242:19Как рассчитать Sin, Cos и Tan без калькулятора: уроки математики и советыYouTube
Как сделать синус?
Как вычислить синус угла
- Определите гипотенузу. Где правильный угол? ...
- Найдите противоположную сторону. Посмотрите на рассматриваемый угол, который есть. ...
- Промаркируйте соседнюю сторону. Единственная оставшаяся сторона, сторона k, должна быть соседним отрезком. ...
- Найдите две стороны, которые вы используете в коэффициенте срабатывания. ...
- Найдите синус.
Что такое OPP HYP?
Помните opp/hyp: противолежащая сторона равна b , а гипотенуза равна c, поэтому sin B = b/c. ... Помните adj/hyp: соседняя сторона равна a, поэтому cos B = a/c.
... Помните adj/hyp: соседняя сторона равна a, поэтому cos B = a/c.
Что такое OPP вместо HYP?
В прямоугольном треугольнике самая длинная сторона — это гипотенуза, «противоположная» сторона — это сторона, расположенная напротив данного угла , а «прилежащая» сторона — это ближайшая к данному углу сторона. Мы используем специальные слова для описания сторон прямоугольных треугольников. Гипотенуза прямоугольного треугольника всегда является стороной, противолежащей прямому углу.
Как решить уравнение косинуса?
1:5711:48Решение тригонометрических уравнений путем поиска всех решений - YouTubeYouTube
Как найти грех?
Как вычислить синус угла
- Определите гипотенузу. Где правильный угол? .
 ..
.. - Найдите противоположную сторону. Посмотрите на рассматриваемый угол, который есть. ...
- Промаркируйте соседнюю сторону. Единственная оставшаяся сторона, сторона k, должна быть соседним отрезком. ...
- Найдите две стороны, которые вы используете в коэффициенте срабатывания. ...
- Найдите синус.
Что такое закон sin and cos?
- Законы синуса и косинуса, также называемые правилами синуса и косинуса, используются для нахождения решения косоугольного треугольника. Это треугольник, который не является прямоугольным треугольником. В этом треугольнике все углы острые или только один тупой. Это правило гласит, что стороны данного треугольника пропорциональны синусу противоположных углов г. e
Как преобразовать sin в Cos?
- Как преобразовать синус в косинус угла? В радианах это π/2-x), поскольку сумма углов в треугольнике равна 180 градусам, и, делая то же самое, sin (90-x) — это длина, противоположная ей, а cos (90-x) — это длина, прилегающая к ней.
 Далее следует sin (90-x)=cos(x) и cos(90-x)=sin (x) (они эквивалентны; подставьте 90-x в любом из них) .
Далее следует sin (90-x)=cos(x) и cos(90-x)=sin (x) (они эквивалентны; подставьте 90-x в любом из них) .
Сколько cos делится на Sin?
- Нижняя часть, разделенная на прямую между углами (2) равно sin A. Прямая между двумя углами , деленная на гипотенузу (3), равна cos B. Умножьте два вместе. Средняя линия находится как в числителе, так и в знаменателе, поэтому каждая из них сокращается и оставляет нижнюю часть противоположной над гипотенузой (4).
Чему равен косинус?
- Обе функции являются тригонометрическими кофункциями друг друга, причем функция дополнительного угла, которая является «кофункцией», равна равно для другой функции: sin (x) = cos (90°-x) и. cos (x) = sin (90°-x).
⇐ Dove si Stampare i Biglietti da Visita?
Кабанери железной крепости закончен? ⇒
Пост корреляции:
Обзор, вопросы, простые приемы, правила, подготовка
Содержание
- scrollTo(duration=200)"> Введение
- Что такое значения греха?
- Что такое значения Cos?
- Каковы значения тангенса?
- Иллюстративные примеры
- Часто задаваемые вопросы
Мы изучаем различные стороны и углы прямоугольного треугольника в тригонометрии. В тригонометрии есть несколько основных функций: синус, косинус и тангенс.
Ниже перечислены некоторые важные тригонометрические функции:
Функция | Сокращение | Связь со стороной треугольника |
|---|---|---|
Синус | грех | Противоположная сторона/гипотенуза |
Тангенс | желтовато-коричневый | Противоположная сторона / Прилегающая сторона |
Косинус | Смежная сторона/гипотенуза | |
Косеканс | косек | Гипотенуза / Противоположная сторона |
Секущая | сек | Гипотенуза / Смежная сторона |
Котангенс | кроватка | Смежная сторона / Противоположная сторона |
При нахождении значений sin, cos и tan треугольника учитываются углы 00, 300, 450, 600 и 900. Формулы для расчета значений sin, cos и tan следующие:
Формулы для расчета значений sin, cos и tan следующие:
- Sin Ɵ = Противоположная сторона / Гипотенуза = BC / AC
- Cos Ɵ = Смежная сторона / Гипотенуза = AB / AC
- Tan Ɵ = Противоположная сторона / Смежная сторона = BC / AB
Таким образом, tan Ɵ = sin Ɵ / cos Ɵ
Диаграмма Sin Cos Tan
Углы в градусах | 0 0 | 30 0 | 45 0 | 60 0 | 90 0 |
|---|---|---|---|---|---|
Углы в радианах | 0 | π/6 | №/4 | π/3 | π/2 |
Син Ɵ | 0 | 1 / 2 | 1 / √2 | √3 / 2 | 1 |
Кос Ɵ | 1 | √3 / 2 | 1 / √2 | 1 / 2 | 0 |
Желто-коричневый Ɵ | 0 | 1 / √3 | 1 | √3 | ∞ |
Детская кроватка Ɵ | ∞ | √3 | 1 | 1 / √3 | 0 |
сек Ɵ | 1 | 2 / √3 | √2 | 2 | ∞ |
Косек Ɵ | ∞ | 2 | √2 | 2 / √3 | 1 |
Функции sin, cos и tan рассматриваются как первичные функции для решения различных тригонометрических задач. Тригонометрия является важным разделом математики для учащихся X класса. Этот раздел имеет вес около 6 баллов на экзамене.
Тригонометрия является важным разделом математики для учащихся X класса. Этот раздел имеет вес около 6 баллов на экзамене.
sin 00 = √(0/4) = 0
sin 300 = √(1/4) = 1/2
sin 450 = √(2/4) = 1/√2
sin 600 = √3/4 = √3/2
sin 900 = √(4/4) = 1
Каковы значения Cos?cos 00 = √(4/4) = 1
cos 300 = √(3/4) = √3/2
cos 450 = √(2/4) = 1/√2
cos 600 = √(1/4) = 1/2
cos 900 = √(0/4) = 0
Каковы значения тангенса?тангенс 00 = 0/1 = 0
тангенс 300 = [(√1/4) / (√3/4)] = 1/√3
тангенс 450 = √(2/4) = 1/ √2
tan 600 = [(√3/2) / (1/2)] = √3
tan 900 = 1/0 = ∞
Иллюстративные примеры Пример 3. A радиусом 3 см согнут и обрезан так, чтобы он мог лежать по окружности пяльца, который составляет около 48 см. Вычислите угол, который опирается на центр обруча.
Решение:
Длина = 2π x 3 = 6π см
Здесь s = 6π см (длина дуги) и r = 48 см (радиус окружности)
Таким образом, Ө = Дуга/Радиус = 6π/48 = π /8 = 22,50
Пример 2. Если A = cos2Ө + sin4Ө для всех значений Ө, то докажите, что 3/4 ≤ A ≤1
Решение:
A = cos2Ө + sin4Ө = sin2 sin2Ө ≤ cos2Ө + sin2Ө
Таким образом, A ≤ 1
Также A = cos2Ө + sin4Ө = ( 1 - sin2Ө) + sin4Ө
= (sin2Ө - 1/2)2 + (1 - 1/4) = ( sin2Ө - 1/2)2 + 3/4 ≥ ¾
Таким образом, 3/4 ≤ A ≤ 1
Пример 3. Если tan Ө = -4/3, то sinӨ равно
- -4/5, но не 4/5
- -4/5 или 4/5
- 4/5, но не -4/5
- Ничего из вышеперечисленного
Решение:
Поскольку тангенс Ө = -4/3 отрицателен, Ө лежит либо в третьем, либо в четвертом квадранте. Таким образом, sin Ө = 4/5, если Ө лежит во втором квадранте, и sin Ө = -4/5 , если Ө лежит в четвертом квадранте. Таким образом, правильным ответом будет вариант 2.
Таким образом, sin Ө = 4/5, если Ө лежит во втором квадранте, и sin Ө = -4/5 , если Ө лежит в четвертом квадранте. Таким образом, правильным ответом будет вариант 2.
В: Назовите основную функцию тригонометрии?
А: Тригонометрия выполняет три основные функции; а именно, функция синуса, функция косинуса и функция тангенса.
В: Где в жизни применяется тригонометрия?
А: Самое главное тригонометрия используется для расчета расстояния и высоты объекта. Некоторые из других отделов, в которых используется тригонометрия, - морская биология, отдел авиации, криминология и другие.
В: Кто основал тригонометрию?
А: Концепция тригонометрии была основана Гиппархом, греческим математиком.
В: Каковы основные тригонометрические функции?
А:
Тригонометрические функции представляют собой функцию синуса, функцию раскладушки, функцию косинуса, функцию косинуса, функцию тангенса и функцию сек.
В: Каково применение тригонометрии?
А: Тригонометрия применяется в различных областях, таких как сейсмология, физические науки, океанография, навигация, метеорология, электроника, акустика, астрономия и др. Тригонометрия также полезна для определения расстояния до длинных рек, оценки высоты гор и т. д.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек (30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек (45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразование из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразование из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктический(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразование из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | грех((5pi)/3) | |
| 43 | Найти точное значение | грех((3pi)/4) | |
| 44 | Найти точное значение | коричневый (пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | Кос(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек (60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразование из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразование из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразование из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | желтовато-коричневый ((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразование из радианов в градусы | (3 шт. )/4 )/4 | |
| 79 | Найти точное значение | грех((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | грех((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктангел (квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | грех((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразование из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | грех((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
Тригонометрические функции в Python - sin, cos, tan и т.
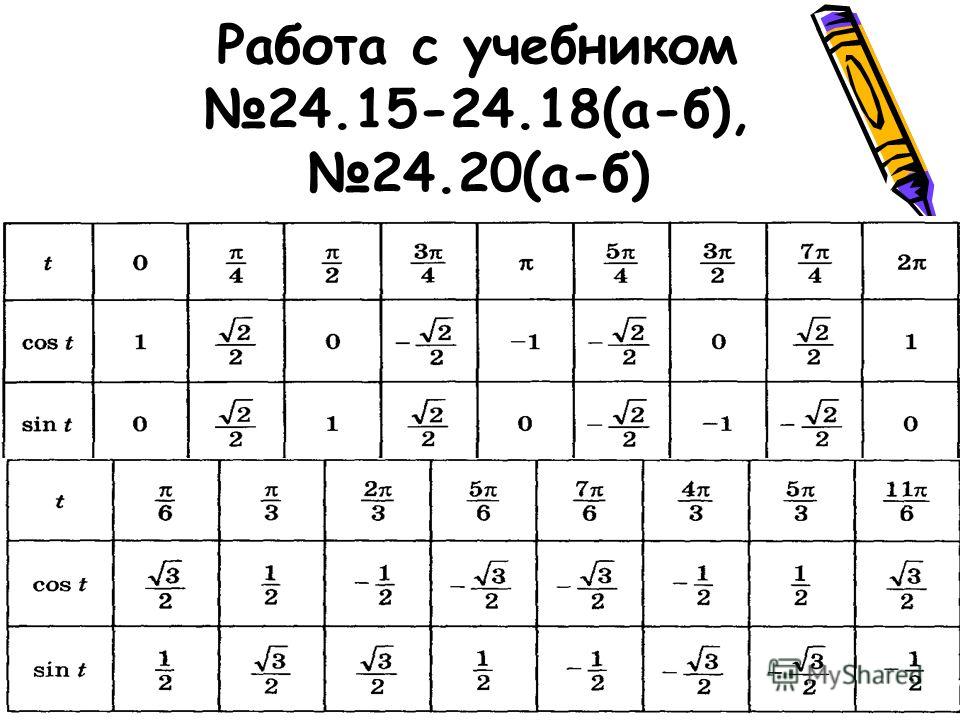 д.
д.Математическая библиотека в python имеет множество тригонометрических функций , которых достаточно для выполнения различных тригонометрических вычислений с минимальным количеством строк кода. Эти функции можно использовать после импорта математического модуля или путем ссылки на математическую библиотеку с оператором точка следующим образом:
math.function_name(parameter) # или импортировать математический модуль импорт математики
Есть 2 вспомогательных метода, которые помогают преобразовывать значения из радианов в градусы и наоборот, чтобы вы могли проверить значение в любом формате.
градусов(значение) : Этот метод преобразует переданное ему значение из радиан в градусы.
радианы(значение) : Этот метод преобразует переданное ему значение из градусов в радианы.
Краткий факт: Все тригонометрические функции в Python предполагают, что входной угол равен радиана .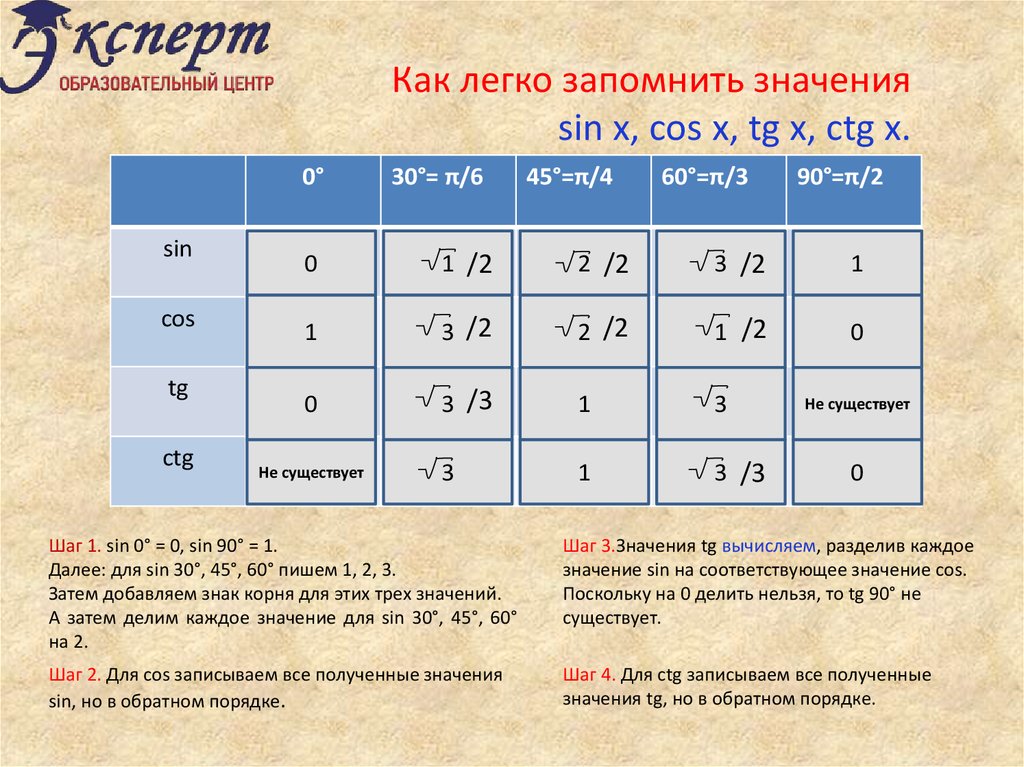
Кроме того, поскольку мы изучаем математику, pi/2 равно 90 градусов и pi/3 равно 60 градусам , модуль math в python предоставляет константу 97 pi 99222 который можно использовать с тригонометрической функцией.
| Тригонометрические функции | Описание |
| math.cos() | Возвращает косинус числа (в радианах). |
| math.sin() | Возвращает синус числа (в радианах). |
| мат.загар() | Возвращает тангенс числа в радианах. |
| math.acos() | Возвращает арккосинус числа в радианах. |
| math.asin() | Возвращает арксинус числа в радианах. |
| мат.атан() | Возвращает арктангенс числа в радианах. |
Пример:
В приведенном ниже примере кода мы использовали методы градусов() и радианов() ,
import math.print(math.степени((math.pi/2))) print(math.radians(60))
Вывод :
90,0 1.0471975511965976
Теперь давайте посмотрим на различные тригонометрические функции в действии, одну за другой.
sin(x) Функция Эта функция возвращает синус переданного значения (здесь x). Ввод x должен быть углом , упомянутым в терминах радиан (пи/2, пи/3/пи/6 и т. д.).
cos(x) Функция Эта функция возвращает косинус переданного значения (здесь x). Ввод x представляет собой угол, представленный в радианах .
желтовато-коричневый(х) Функция Эта функция возвращает тангенс переданного ей значения, то есть синус/косинус угла. Ввод здесь представляет собой угол в терминах радиан .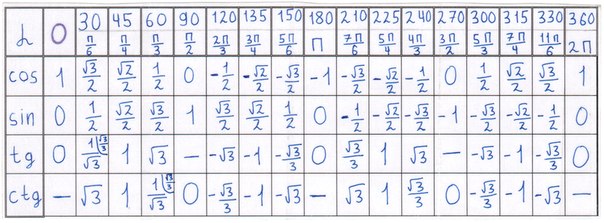
Пример кода для
sin , cos и tan :Ниже приведен простой пример кода для трех тригонометрических функций, определенных выше,
import math print(math.sin(math.pi/3)) #pi/3 радиан преобразуется в 60 градусов печать (math.tan (math.pi/3)) печать (math.cos (math.pi/6))
Выход:
0,8660254037844386 1.7320508075688767 0.8660254037844387
asin(x) ФункцияЭта функция возвращает значение , обратное синусу , который также известен как арксинус комплексного числа . Ввод осуществляется в радианах и должен находиться в диапазоне от -1 до 1 . Он возвращает число с плавающей запятой в качестве вывода .
acos(x) Функция Эта функция возвращает косинус , обратный параметра x в радианах. Это также известно как арккосинус комплексного числа .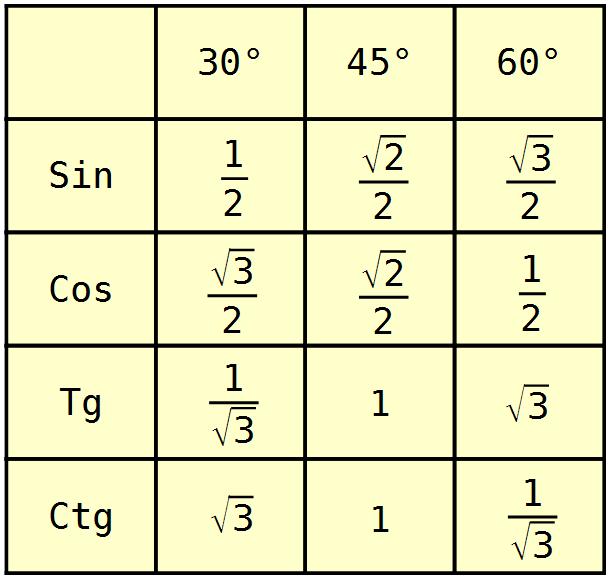 Значение
Значение x должно находиться в диапазоне от -1 до 1 . Он возвращает число с плавающей запятой в качестве вывода.
atan(x) Функция Эта функция возвращает значение , обратное тангенсу , в радианах. Он известен как арктангенс комплексного числа 909.37 . Значение параметра лежит в пределах -1 и 1 . Его также можно представить как (math.sin(math.pi / 4)) / (math.cos(math.pi / 4)) . Он возвращает число с плавающей запятой в качестве вывода.
Пример кода для
asin , acos и atan с углами в радианах:import math печать (математика. asin (1)) печать (math.acos (0)) print(math.atan(1))
Вывод:
1.57079632676 1.5707963267
6 0,7853981633974483
Пример ниже показывает, как функции asin , acos и atan могут использоваться с комплексными числами, имеющими формат x+iy .
импорт cmath
х = 1,0
у = 1,0
г = комплекс (х, у)
print ("Арксинус: ",cmath.asin(z))
print ("Арккосинус: ",cmath.acos(z))
print ("Арктангенс равен: ",cmath.atan(z)) Вывод:
Арксинус: (0,666233+1.061275061 57j) Арккосинус: (0,683814-1,06127506157j) Арктангенс: (1.0172219678978514+0.402350852507j)
sinh(x) ФункцияЭтот метод возвращает гиперболический синус переданного угла комплексного числа.
cosh(x) ФункцияЭтот метод возвращает гиперболический косинус угла переданного комплексного числа.
tanh(x) ФункцияЭтот метод возвращает гиперболический тангенс угла переданного комплексного числа.
Пример кода для
sinh , cosh и tanh с комплексными числами: import cmath
х = 1,0
у = 1,0
г = комплекс (х, у)
print ("Гиперболический синус: ",cmath. sinh(z))
print ("Гиперболический косинус: ",cmath.cosh(z))
print ("Гиперболический тангенс: ",cmath.tanh(z))
sinh(z))
print ("Гиперболический косинус: ",cmath.cosh(z))
print ("Гиперболический тангенс: ",cmath.tanh(z)) Выход:
Гиперболический синус: (0,63496347361+1,2984575814159773j) Гиперболический косинус: (0,8337300251311491+0,9888977057628651j) Гиперболический тангенс: (1.083
- 73386946+0.2717525853195118j)
asinh(x) ФункцияВозвращает обратное значение гиперболического синуса угла/комплексного числа.
acosh(x) ФункцияВозвращает обратную гиперболическому косинусу углового/комплексного числа.
atanh(x) ФункцияВозвращает инверсию гиперболического тангенса угла/комплексного числа.
Пример кода для методов
asinh , acosh и atanh с комплексными числами: import cmath
х = 1,0
у = 1,0
г = комплекс (х, у)
print ("Обратный гиперболический синус: ",cmath. asinh(z))
print ("Обратный гиперболический косинус: ",cmath.acosh(z))
print ("Арктический гиперболический тангенс: ",cmath.atanh(z))
asinh(z))
print ("Обратный гиперболический косинус: ",cmath.acosh(z))
print ("Арктический гиперболический тангенс: ",cmath.atanh(z)) Выход:
Обратный гиперболический синус: (1,06127506157+0,666233j) Арктический гиперболический косинус: (1,061275061 57+0,683813j) Арктический гиперболический тангенс: (0,402350852507+1,0172219678978514j)
atan2(y, x) Функция Возвращает значение, лежащее между -pi и 9.1972г.п. . Представляет собой угол между положительной осью x и координатами (x,y).
print(math.atan2(1.2,1.3))
Вывод:
0.74541741583
гипотенуза(х,у) Функция Эта функция возвращает гипотенузу , т.е. евклидову норму . Это означает, что он возвращает расстояние между началом координат и точками (x, y). Это указывает длину вектора в двумерном пространстве. Евклидова норма также известна как «величина» вектора. Это числовое значение вектора (поскольку векторы имеют не только направление, но и величину).
Евклидова норма также известна как «величина» вектора. Это числовое значение вектора (поскольку векторы имеют не только направление, но и величину).
Если передано более 2 аргументов, корректно возвращается TypeError .
print(math.hypot(2,2))
Вывод:
2,8284271247461903
ПРИМЕЧАНИЕ: При сравнении этих значений с числовыми значениями углов может быть несколько различий в десятичных разрядах, которые можно безопасно игнорировать. Например, tan(pi/3) преобразуется в tan 60 , что эквивалентно 9.1972 кв.(3) . Если используется функция tan , вывод равен 1.7320508075688767 , тогда как sqrt(3) дает 1.7320508075688772 .
Это так просто? Как насчет исключений и ошибок?
Вы абсолютно правы. Существует два типа исключений, которые потенциально могут возникнуть из-за неправильного использования этих методов:
TypeError : Этот тип ошибки возникает, когда значение, не являющееся числом, передается в качестве параметра одному из тригонометрических методов.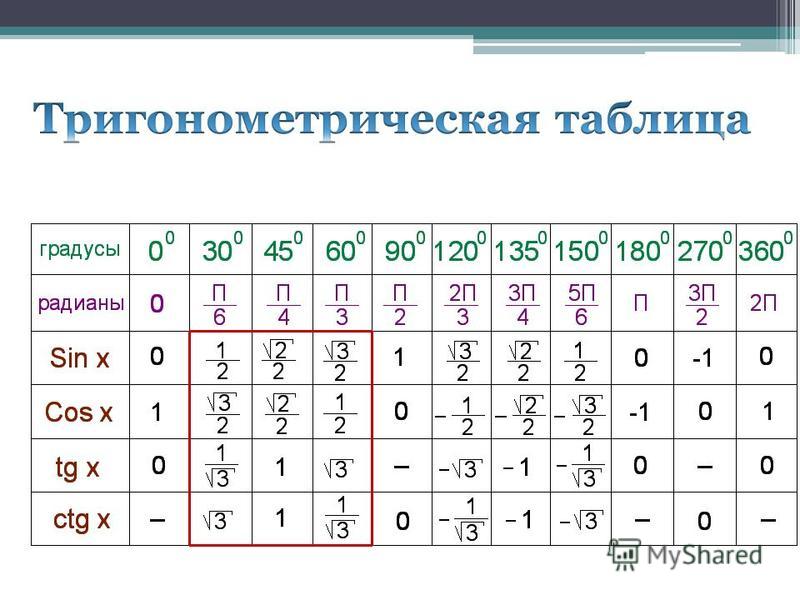

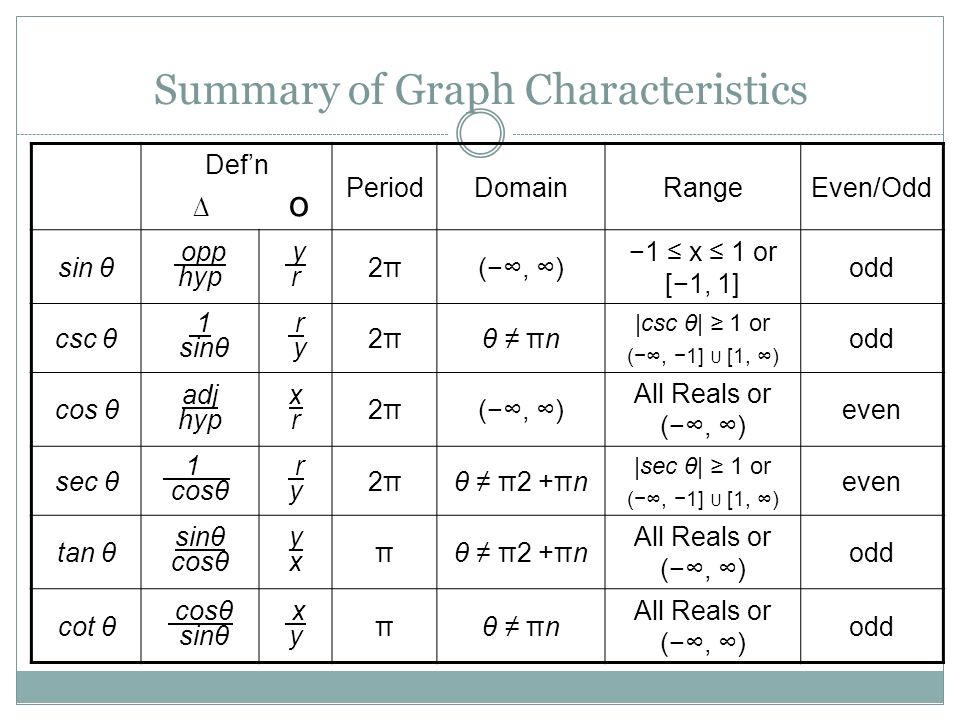
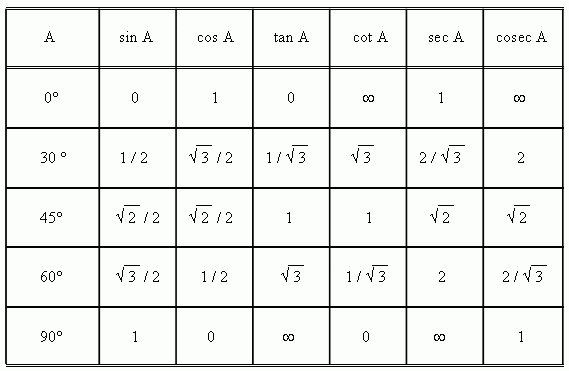

 ..
.. Далее следует sin (90-x)=cos(x) и cos(90-x)=sin (x) (они эквивалентны; подставьте 90-x в любом из них) .
Далее следует sin (90-x)=cos(x) и cos(90-x)=sin (x) (они эквивалентны; подставьте 90-x в любом из них) . print(math.степени((math.pi/2)))
print(math.radians(60))
print(math.степени((math.pi/2)))
print(math.radians(60)) 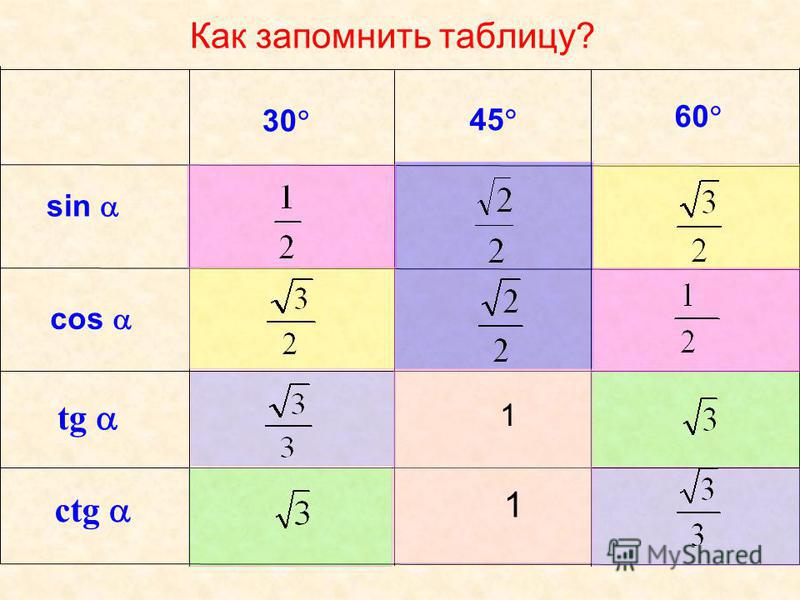 sinh(z))
print ("Гиперболический косинус: ",cmath.cosh(z))
print ("Гиперболический тангенс: ",cmath.tanh(z))
sinh(z))
print ("Гиперболический косинус: ",cmath.cosh(z))
print ("Гиперболический тангенс: ",cmath.tanh(z))  asinh(z))
print ("Обратный гиперболический косинус: ",cmath.acosh(z))
print ("Арктический гиперболический тангенс: ",cmath.atanh(z))
asinh(z))
print ("Обратный гиперболический косинус: ",cmath.acosh(z))
print ("Арктический гиперболический тангенс: ",cmath.atanh(z))