cosx = 0 частные случаи решения
Доброй всем ночи!
Вы уже, скорее всего, знакомы с основными понятиями о тригонометрических уравнениях. По-этому останавливаться на этом не вижу смысла. Вы просили продемонстрировать на уравнении: cosx = 0 частные случаи решения.
Давайте проясним, что здесь значит частные случаи. Это значит, что Вам упросили жизнь. Каким образом?! смотрите, Вы если запомните, чему равно это уравнение, то Вам не нужно вспоминать целую таблицу, придумывать из раза в раз велосипед. Помощь не большая, но иногда — это палочка-выручалочка.
Давайте разберём наше уравнение, чтоб Вы имел представление, что Вам вообще надо запоминать.
Прежде, чем разобраться с Вашей уравнением cosx = 0, нужно подумать, в каком виде можно представить данное уравнение, чтоб понять как его решать.
Вот так будет выглядеть Ваше условие на математическом языке:
Да, я понимаю, что это Вам особо не помогло. Но для этого есть определённое правило решения подобных уравнений, которое примет такой общий вид:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Так как с основным разобрались, то теперь можем и решить до конца Ваше уравнение:
Ответ:
ru.solverbook.com
Удобные случаи простейших тригонометрических уравнений
by Колпаков А.Н. on 14 сентября 2010
Частные случаи:
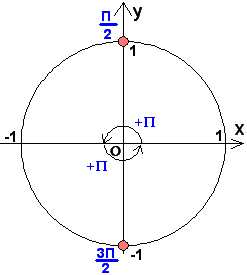1) Нули косинуса:
Уравнение можно решить
по общей формуле, однако наличие нуля в правой части делает ответ более удобным для дальнейшего отбора корней.
2) решение уравнения CosX=1
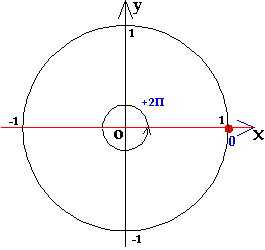
Уравнение можно решить
по общей формуле, однако наличие единицы в правой части делает ответ более удобным для дальнейшего отбора корней.
3)решение уравнения CosX=-1
Уравнение можно решить
по общей формуле, однако наличие единицы в правой части делает ответ более удобным для дальнейшего отбора корней.
Посмотреть тригонометрические формулы.
Колпаков Александр Николаевич, репетитор по математике
Метки: Пособия репетитора, Решение уравнений, Справочник репетитора, Тригонометрия
ankolpakov.ru
Решение тригонометрических уравнений. Тест — курсы по математике
Тестирование онлайн
Арксинус, арккосинус, арктангенс, арккотангенс
Арксинус
Если есть выражение sinx=a, то x=arcsina. То есть арксинусом числа а называется такое число x , что его синус равен а.
Ограничения:
Арккосинус
Если есть выражение cosx=a, то x=arccosa. То есть арккосинусом числа а называется такое число x , что его косинус равен а.
Ограничения:
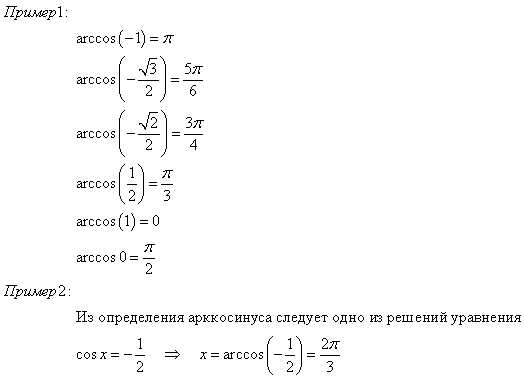
Арктангенс
Если есть выражение tgx=a, то x=arctga. То есть арктангенсом числа а называется такое число x , что его тангенс равен а.
Ограничения:
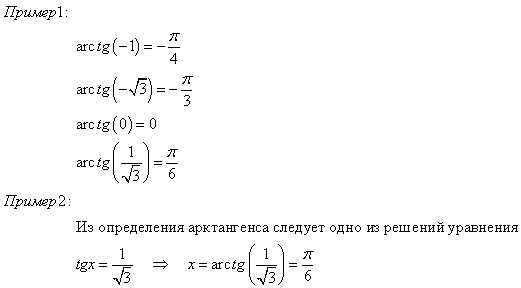
Арккотангенс
Если есть выражение сtgx=a, то x=arсctga. То есть арккотангенсом числа а называется такое число x , что его котангенс равен а.
Ограничения:
Не табличное значение «аркфункций» можно найти пользуясь калькулятором. Для того, чтобы понять почему у функций именно такие ограничения, необходимо изучить их графики.
Решение уравнения sinx=a
Общее решение уравнения
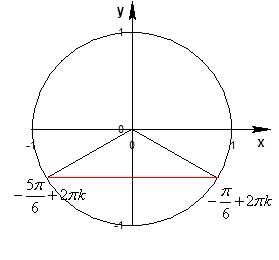
Частные случаи
Решение уравнения cosx=a
Общее решение уравнения
Частные случаи
Решение уравнения tgx=a, ctgx=a
Общее решение уравнения
Частные случаи для tgx=a
Частные случаи для ctgx=a
fizmat.by