Чему равен вертикальный угол – Смежные и вертикальные углы. Перпендикулярные прямые [wiki.eduVdom.com]

Справедлива следующая теорема.

Теорема 3. Из всякой точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.

Для проведения на чертеже перпендикуляра из точки к прямой используют чертежный угольник (рис.5).

Замечание. Формулировка теоремы обычно состоит из двух частей. В одной части говорится о том, что дано. Эта часть называется условием теоремы. В другой части говорится о том, что должно быть доказано. Эта часть называется заключением теоремы. Например, условие теоремы 2 — углы вертикальные; заключение — эти углы равны.

Всякую теорему можно подробно выразить словами так, что ее условие будет начинаться словом «если», а заключение — словом «то». Например, теорему 2 можно подробно высказать так: «Если два угла вертикальные, то они равны».

Пример 1. Один из смежных углов равен 44°. Чему равен другой?

Решение. Обозначим градусную меру другого угла через x, тогда согласно теореме 1.
44° + х = 180°.
Решая полученное уравнение, находим, что х = 136°. Следовательно, другой угол равен 136°.

Пример 2. Пусть на рисунке 21 угол COD равен 45°. Чему равны углы АОВ и АОС?

Решение. Углы COD и АОВ вертикальные, следовательно, по теореме 1.2 они равны, т. е. ∠ АОВ = 45°. Угол АОС смежный с углом COD, значит, по теореме 1.

Пример 3. Найти смежные углы, если один из них в 3 раза больше другого.

Решение. Обозначим градусную меру меньшего угла через х. Тогда градусная мера большего угла будет Зх. Так как сумма смежных углов равна 180° (теорема 1), то х + Зх = 180°, откуда х = 45°.
Значит, смежные углы равны 45° и 135°.

Пример 4. Сумма двух вертикальных углов равна 100°. Найти величину каждого из четырех углов.

Решение. Пусть условию задачи отвечает рисунок 2. Вертикальные углы COD к АОВ равны (теорема 2), значит, равны и их градусные меры. Поэтому ∠ COD = ∠ АОВ = 50° (их сумма по условию 100°). Угол BOD (также и угол АОС) смежный с углом COD, и, значит, по теореме 1
∠ BOD = ∠ АОС = 180° — 50° = 130°.

Вертикальные углы — это… Что такое Вертикальные углы?

В геометрии, два угла называются вертикальными, если они созданы пересечением двух прямых и не являются прилегающими. Такие углы имеют общую вершину. Они имеют одинаковую градусную меру и могут рассматриваться как равные.

Теорема о вертикальных углах

Если две прямые пересекаются в точке, образуются четыре угла. Несмежные углы называются вертикальными или противоположно вертикальными углами. Также, каждая пара прилегающих углов образует прямую, а эти углы называются смежными^[1]. Поскольку каждая пара вертикальных углов является смежными к прилегающим, то градусные меры вертикальных углов — равны.

Алгебраическое решение вертикальных углов

Например, угол A на рисунке — неизвестен. Обозначим A = x. Если два прилегающих угла образуют прямую, то они — смежные. Тогда, градусная мера C = 180 − x. Аналогично, градусная мера D = 180 − x. Углы C и D имеют одинаковую меру, которая равна 180 — x и являются вертикальными. Поскольку, угол B является смежным для обоих углов C и D, для того, чтобы вычислить размер B можно использовать градусную меру любого из них. Используя меру угла C или угла D, найдём градусную меру угла B = 180 — (180 — x) = 180—180 + x = x. Отсюда, оба угла A и B имеют г

См. также

Литература

1. ↑ Euclid The Elements. — c. 300 BC. Proposition I:13.

Ссылки

dic.academic.ru

Вертикальные углы | Треугольники

Какие углы вертикальные? Каким свойством обладают вертикальные углы?

Рассмотрим определение вертикальных углов и их свойство, а также применим свойство вертикальных углов для решения задач.

Определение.

Вертикальные углы — это пары углов с общей вершиной, которые образованы при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого.

При пересечении двух прямых образуется две пары вертикальных углов:

∠1 и ∠2  — вертикальные углы

∠3 и ∠4 — вертикальные углы

Свойство вертикальных углов.

Вертикальные углы равны.

∠AOC =∠BOD

∠AOD =∠BOC

Таким образом, при пересечении двух прямых образуется две пары равных межу собой углов.

Задачи.

1) Сумма вертикальных углов равна 140º. Найти эти углы.

Решение:

Так как вертикальные углы равны, а в условии сказано, что их сумма равна 140º, то каждый из них равен по 140:2=70º.

Ответ: 70º, 70º.

2) Сумма двух углов, образованных при пересечении двух прямых, равна 100º. Найти эти углы.

Решение:

При пересечении двух прямых образуются углы двух видов — вертикальные и смежные.

Так как сумма смежных углов равна 180º, а по условию, сумма углов равна 100º, то эти углы — вертикальные.

А так как вертикальные углы равны, то каждый из них равен по 100:2=50º.

Ответ: 50º, 50º.

Вертикальные углы во многих задачах — важный элемент при доказательстве  равенства треугольников и подобия треугольников.

www.treugolniki.ru

Смежные и вертикальные углы

1. Смежные углы.

Если мы продолжим сторону какого-нибудь угла за его вершину, то получим два угла (рис. 72): ∠АВС и ∠СВD, у которых одна сторона ВС общая, а две другие, АВ и ВD, составляют прямую линию.

Два угла, у которых одна сторона общая, а две другие составляют прямую линию, называются смежными углами.

Смежные углы можно получить и таким образом: если из какой-нибудь точки прямой проведём луч (не лежащий на данной прямой), то получим смежные углы.

Например, ∠АDF и ∠FDВ — углы смежные (рис. 73).

Смежные углы могут иметь самые разнообразные положения (рис. 74).

Смежные углы в сумме составляют развёрнутый угол, поэтому сумма двух смежных углов равна 180°

Отсюда прямой угол можно определить как угол, равный своему смежному углу.

Зная величину одного из смежных углов, мы можем найти величину другого смежного с ним угла.

Например, если один из смежных углов равен 54°, то второй угол будет равен:

180° — 54° = l26°.

2. Вертикальные углы.

Если мы продолжим стороны угла за его вершину, то получим вертикальные углы. На рисунке 75 углы EOF и АОС— вертикальные; углы АОЕ и СОF — также вертикальные.

Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого угла.

Пусть ∠1 = \(\frac{7}{8}\) ⋅ 90°(рис. 76). Смежный с ним ∠2 будет равен 180° — \(\frac{7}{8}\) ⋅ 90°, т. е. 1\(\frac{1}{8}\) ⋅ 90°.

Таким же образом можно вычислить, чему равны ∠3 и ∠4.

∠3 = 180° — 1\(\frac{1}{8}\) ⋅ 90° = \(\frac{7}{8}\) ⋅ 90°;

∠4 = 180° — \(\frac{7}{8}\) ⋅ 90° = 1\(\frac{1}{8}\) ⋅ 90° (рис. 77).

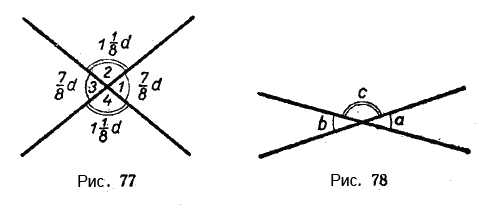
Мы видим, что ∠1 = ∠3 и ∠2 = ∠4.

Можно решить ещё несколько таких же задач, и каждый раз будет получаться один и тот же результат: вертикальные углы равны между собой.

Однако, чтобы убедиться в том, что вертикальные углы всегда равны между собой, недостаточно рассмотреть отдельные числовые примеры, так как выводы, сделанные на основе частных примеров, иногда могут быть и ошибочными.

Убедиться в справедливости свойства вертикальных углов необходимо путём доказательства.

Доказательство можно провести следующим образом (рис. 78):

∠a + ∠c = 180°;

∠b + ∠c = 180°;

(так как сумма смежных углов равна 180°).

Отсюда

∠a + ∠c = ∠b + ∠c

(так как и левая часть этого равенства равна 180°, и правая его часть тоже равна 180°).

В это равенство входит один и тот же угол с.

Если мы от равных величин отнимем поровну, то и останется поровну. В результате получится: ∠a = ∠b, т. е. вертикальные углы равны между собой.

3. Сумма углов, имеющих общую вершину.

На чертеже 79 ∠1, ∠2, ∠3 и ∠4 расположены по одну сторону прямой и имеют общую вершину на этой прямой. В сумме эти углы составляют развёрнутый угол, т. е.

∠1 + ∠2 + ∠3 + ∠4 = 180°.

На чертеже 80 ∠1, ∠2, ∠3, ∠4 и ∠5 имеют общую вершину. В сумме эти углы составляют полный угол, т. е. ∠1 + ∠2 + ∠3 + ∠4 + ∠5 = 360°.

razdupli.ru

Измерение вертикальных углов.

Вертикальным называется угол между направлением на предмет и горизонтальным направлением визирной оси трубы теодолита. Вертикальные углы могут быть заключены в пределах от 90^о до –90^о. Вертикальные углы измеряются для определения превышений между точками тригонометрическим нивелированием и для определения горизонтальных проложений наклонных линий местности. Измеряя вертикальные углы, можно также определить высоты объектов (зданий, водокачек, дымовых труб и т.д.).

Горизонтальное направление визирной оси определяется при помощи места нуля (МО) вертикального круга. Место нуля – это отсчет по вертикальному кругу при горизонтальном положении визирной оси и горизонтальном положении оси уровня при вертикальном или горизонтальном (у теодолита 4Т30) круге.

У разных теодолитов вертикальный круг имеет различное устройство и различную оцифровку. Поэтому формулы для определения вертикальных углов и места нуля вертикального круга у разных теодолитов различаются. Например, у теодолита 4Т30 оцифровка вертикального круга секторная, по 75^о в одну и в другую сторону от нуля, причем в одну сторону деления подписываются со знаком +, в другую – со знаком — . На рис.7 показаны отсчеты по вертикальному кругу теодолита 4Т30 для положительного вертикального угла при круг право (КП) и круге лево (КЛ).

Рис.7

Из рисунка очевидны формулы:

;; (3)

из этих формул можно вывести, что

13

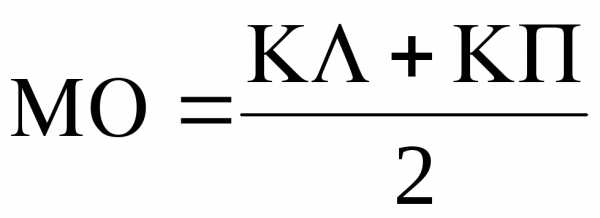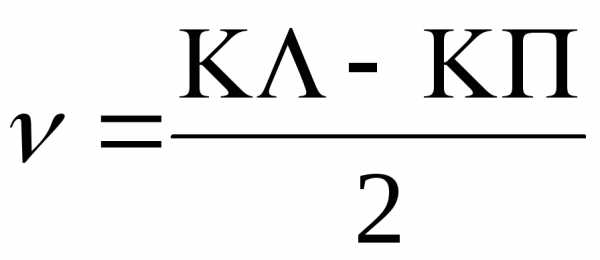; ; (4)

у теодолита 3Т30 (Т30) формула для определения вертикального угла и место нуля (МО) будут другие:

; ; (5)

; . (6)

Необходимо отметить, что отсчеты по вертикальному кругу у теодолита 4Т30 берутся по шкале, подписанной буквой В , равной 1^о вертикального круга и поделенной на 12 частей. Следовательно, цена деления шкалы равна 5’. Деля ее на глаз на 10 частей, мы можем брать отсчет с точностью 0,5’(30”). Слева направо шкала возрастает от 0’ до 60’ (подписано цифрой 6), справа налево шкала уменьшается от -0’ до –60’ (подписано –6). Отсчет по шкале берется следующим образом: количество градусов считывается с подписанного градусного штриха вертикального круга, который проектируется на шкалу; количество минут определяется по шкале от ее нуля до градусного штриха вертикального круга. Причем, если градусный штрих положителен, то количество минут считается слева направо от 0 шкалы до этого штриха, и прибавляется к градусам. Отсчет будет положительным. Например, на рис. 8 отсчет равен +2^о19’. Если градусный штрих вертикального круга отрицателен, то количество минут считается справа налево от –0 до градусного штриха и прибавляется к градусам; отсчет будет отрицательным. Например, на рис. 9 отсчет равен –-0^о52’.

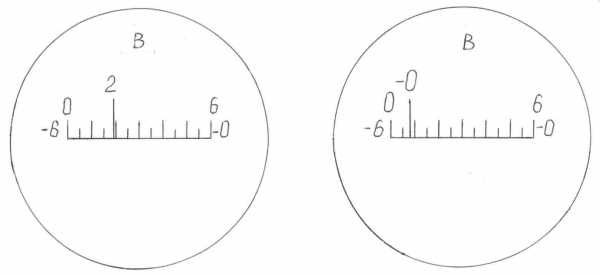
Рис. 8 Рис. 9

При измерении вертикальных углов теодолитом 4Т30 тщательно приводят ось теодолита в отвесное положение, затем зрительную трубу наводят на точку при круге право (КП). Перед взятием отсчета при необходимости нужно поправить уровень (пузырек вывести на середину) подъемными винтами. Затем берется и записывается отсчет КП по вертикальному кругу. Далее труба переводится через зенит и наводится на ту же точку при круге лево (КЛ). Подправив при необходимости уровень подъемными винтами, берут и записывают отсчет по вертикальному кругу КЛ. По формулам (4) определяют вертикальный угол и место нуля МО.

Место нуля следует определить повторно при наведении на другую точку, и из двух значений вычислить его среднее арифметическое, Если среднее значение МО больше 1’, его следует исправить. Для этого вычислить исправленные отсчеты для вертикального круга по формулам

КЛ_{исправ.}= КЛ – МО или КП_{исправ.}= КП – МО (7)

и установить исправленный отсчет на вертикальном круге наводящим винтом зрительной трубы. При этом крест сетки нитей сместится с изображения наблюдаемой точки. Отвинтить колпачок в окулярной части трубы, шпилькой ослабить на пол оборота боковые исправительные винты сетки нитей. Вращением верхнего и нижнего исправительных винтов сетки в одну сторону, навести крест сетки нитей на точку. Закрепив боковые винты сетки, еще раз определяем МО.

Если мы определили место нуля (МО), то другие вертикальные углы можем измерять однократным наведением зрительной трубы на цель при круге право (КП) или круге лево (КЛ) с одновременным снятием отсчетов по вертикальному кругу и подсчитывать углы по формулам (3).

Рекомендуемая литература.

Д.Ш.Михелев. Инженерная геодезия.- М.: Академия, 2004.

studfiles.net

Вертикальные углы равны

Сначала разберемся какие же углы можно назвать вертикальными.
Начертим две пересекающиеся прямые. Обозначим получившиеся углы одинарной и двойной дугами.

Вертикальными называют углы, которые имеют общую вершину, а стороны одного из углов продолжают стороны другого.
На данном рисунке есть две пары вертикальных углов. Первая пара вертикальных углов – это углы АОВ и COD, а вторая – углы АОС и BOD.
Вертикальные углы можно получить только при пересекающихся двух прямых.
Как видно из рисунка, вертикальные углы обозначены одинаковыми дугами, что обозначает их равенство. Относительно вертикальных углов существует теорема, которая гласит, что вертикальные углы равны.
Разберем на примере как можно использовать понятие вертикальных углов.

Задача.
Известно, что сумма двух вертикальных углов равна 100 градусов. Найти градусную меру всех четырех углов, которые были получены при пересечении данных прямых.

Решение.
Используем рисунок, представленный выше.
Пусть известна сумма двух вертикальных углов COD и АОВ, которая по условию равна 100 градусов.. из теоремы о вертикальных углах известно, что они равны между собой. Тогда получим, что:
уг. AOB = уг. COD.
Запишем выражение, которое известно из условия:
уг. AOB + уг. COD = 100.
Используя предыдущее условие последнее выражение можно переписать так:
уг. AOB + уг. AOB = 100.
Тогда получим:
2 * уг. AOB = 100
уг. AOB = 50.
Рассмотрим смежные углы АОВ и АОС. Известно, что их сумма равна 180 градусов:
уг. АОВ + уг.л АОС = 180.
Найдем угол АОС:
уг. АОС = 180 – уг. АОВ = 180 – 50 = 130.
Второй парой вертикальных углов будут углы АОС и BOD, а значит:
уг. АОС = уг. BOD = 130.

Ответ. 50, 50, 130, 130.

ru.solverbook.com

Вертикальные углы равны. Какие углы вертикальные. Определение вертикальных углов.

В геометрии пары углов могут относиться друг к другу разными способами, в этой статье мы объясним что такое вертикальные углы
Когда две линии пересекаются, противоположные углы образуют вертикальные углы или вертикально противоположные углы. Они называются вертикальными углами, так как имеют одну и ту же вершину. Снизу рисунок вертикальных углов \(y\) и \(y\), \(x\) и \(x\):

 
Вертикальные углы равны. Заметьте также, что сумма углов  \(x\) и \(y\)   равна \(180°\). Прокрутите страницу вниз для получения дополнительных примеров и решений.

Пример 1. Найти \(x\):

Решение:
           \( х + 65° = 180° ⇒ х = 180° – 65° = 115° \)

Найти \(z\):

 \(z\) и \(x\) — вертикальные углы, поэтому они равны 115° .

Найти y:           

 y и \(65°\) вертикальные углы.
            Поэтому \(y = 65°\)

Ответ: \(x = 115°, y = 65° , z = 115° \)

 Пример 1. \(AEC \) и \(DEB\) прямые линии, которые пересекаются в точке \(E\). \(∠DEC\) \(=135°\).  Найти  \(q\).

Решение:
 \(∠AEB\) = \(∠DEC\)  вертикальные углы \(—>\) \( q + 45= 135\)
  \(q=\) \( 135 – 45 = 90\)

Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!

Запишитесь на бесплатное тестирование знаний!

myalfaschool.ru