Что такое предел функции как его найти
Обобщённое понятие предела: число a есть предел некоторой переменной величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.
Поясним это на примере, который также проиллюстрируем. А после примера приведём общий алгоритм решения пределов.
Запишем приведённый пример на языке формул. Итак, номер окружности возрастает и стремится к бесконечности, то есть . Допустим, существует такой равнобедренный треугольник, что длина диаметра каждой вписанной в него окружности расчитывается по формуле
Величина, которую нам требуется найти, будет записана так:
Lim это и есть предел, а под ним указывается переменная, которая стремится к определённому значению – нулю, любому другому числу, бесконечности.
Теперь вычислим предел, присвоив переменной
С рассмотренной последовательностью окружностей свяжем другую переменную величину — последовательность сумм их диаметров:
Рассмотрев рисунок снова, обнаружим, что предел последовательности равен h – высоте равнобедренного треугольника. Вообще, предел может быть равен нулю, любому другому числу или бесконечности.
Теперь более строгие определения предела функции, которые Вас могут спросить на экзамене, и для понимания которых потребуется чуть больше внимания.
Предел функции при
Пусть функция f(x) определена на некотором множестве X и пусть дана точка . Возьмём из X последовательность точек, отличных от :
(1)
сходящуюся к . Значения функции в точках этой последовательности также образуют числовую последовательность
(2)
и можно ставить вопрос о существовании её предела.
Это означает: чтобы найти предел функции, нужно в функцию вместо x подставить то значение, к которому стремится x.
Пример 1. Найти предел функции при .
Решение. Подставляем вместо x значение 0. Получаем:
.
Итак, предел данной функции при равен 1.
Предел функции при , при и при
Кроме рассмотренного понятия предела функции при существует также понятие предела функции при стремлении аргумента к бесконечности.
Символически это записывается так: .
Определение 3. Число A называется пределом функции f(x) при (), если для любой бесконечно большой последовательности значений аргумента, элементы которой положительны (отрицательны), соответствующая последовательность (2) значений функции сходится к A.
Символически это записывается так: ().
Это, как и в случае определения 1, означает: чтобы найти предел функции, нужно в функцию вместо x подставить бесконечность, плюс бесконечность или минус бесконечность.
Пример 2.
Найти предел функции при .Решение. Подставляем вместо x бесконечность. Получаем, что последовательность значений функции является бесконечно малой величиной и поэтому имеет предел, равный нулю:
.
Для наглядности и убедительности, решая данный пример в черновике, можете подставить вместо x супербольшое число. При делении получите супермалое число.
Теорема 1. (о единственности предела функции). Функция не может иметь более одного предела.
Следствие. Если две функции f(x) и g(x) равны в некоторой окрестности точки , за исключением, может быть, самой точки , то либо они имеют один и тот же предел при , либо обе не имеют предела в этой точке.
Теорема 2. Если функции f(x) и g(x) имеют пределы в точке , то:
1) предел алгебраической суммы функций равен алгебраической сумме пределов слагаемых, т.е.
(3)
2) предел произведения функций равен произведению пределов сомножителей, т.е.
(4)
3)предел частного двух функций равен частному от деления предела делимого на предел делителя, если предел делителя не равен нулю, т.е.
(5)
Замечание. Формулы (3) и (4) справедливы для любого конечного числа функций.
Следствие 1. Предел постоянной равен самой постоянной, т.е.
Следствие 2. Постоянный множитель можно выносить за знак предела, т.е.
Пример 3. Найти предел:
Решение.
Пример 4. Найти предел:
Решение. Предварительно убедимся, что предел делителя не равен нулю:
Таким образом, формула (5) применима и, значит,
Теорема 3 (о пределе сложной функции). Если существует конечный предел
а функция f(u) непрерывна в точке , то
Другими словами, для непрерывных функций символы предела и функции можно поменять местами.
Непосредственное применение теорем о пределах, однако, не всегда приводит к цели. Например, нельзя применить теорему о пределе частного, если предел делителя равен нулю. В таких случаях необходимо предварительно тождественно преобразовать функцию, чтобы иметь возможность применить следствие из теоремы 1.
Пример 5. Найти предел:
Решение. Теорема о пределе частного здесь неприменима, так как
Преобразуем заданную дробь, разложив числитель и знаменатель на множители. В числителе получим
где
корни квадратного трёхчлена (если Вы забыли, как решать квадратные уравнения, то Вам сюда). Теперь сократим дробь и, используя следствие из теоремы 1, вычислим предел данной функции:
При решении примеров 5 и 8 нам уже встретилась неопределённость вида . Эта неопределённость и неопределённость вида — самые распространённые неопределённости, которые требуется раскрывать при решении пределов.
БОльшая часть задач на пределы, попадающихся студентам, как раз несут в себе такие неопределённости. Для их раскрытия или, точнее, ухода от неопределённостей существует несколько искусственных приёмов преобразования вида выражения под знаком предела. Эти приёмы следующие: почленное деление числителя и знаменателя на старшую степень переменной, домножение на сопряжённое выражение и разложение на множители для последующего сокращения с использованием решений квадратных уравнений и формул сокращённого умножения.
Освоим эти приёмы на примерах.
Для преобразования выражений потребуются пособия Действия со степенями и корнями и Действия с дробями.
Неопределённость вида
Пример 12. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной
.
Комментарий к правой части выражения. Стрелками и цифрами обозначено, к чему стремятся дроби после подстановки вместо n значения бесконечность. Здесь, как и в примере 2, степень n в знаменателя больше, чем в числителе, в результате чего вся дробь стремится к бесконечно малой величине или «супермалому числу».
Получаем ответ: предел данной функции при переменной, стремящейся к бесконечности, равен .
Пример 13. Раскрыть неопределённость и найти предел .
Решение. Здесь старшая степень переменной x равна 1. Поэтому почленно делим числитель и знаменатель на x:
.
Комментарий к ходу решения. В числителе загоняем «икс» под корень третьей степени, а чтобы его первоначальная степень (1) оставалась неизменной, присваиваем ему ту же степень, что и у корня, то есть 3. Стрелок и дополнительных чисел в этой записи уже нет, так что попробуйте мысленно, но по аналогии с предыдущим примером определить, к чему стремятся выражения в числителе и знаменателе после подстановки бесконечности вместо «икса».
Получили ответ: предел данной функции при переменной, стремящейся к бесконечности, равен нулю.
Неопределённость вида
Пример 14. Раскрыть неопределённость и найти предел .
Решение. В числителе — разность кубов. Разложим её на множители, применяя формулу сокращённого умножения из курса школьной математики:
.
В знаменателе — квадратный трёхчлен, который разложим на множители, решив квадратное уравнение (ещё раз ссылка на решение квадратных уравнений):
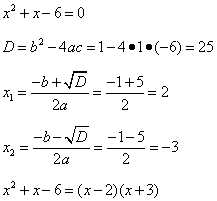
Запишем выражение, полученное в результате преобразований и найдём предел функции:
Пример 15. Раскрыть неопределённость и найти предел
Решение. Теорема о пределе частного здесь неприменима, поскольку
Поэтому тождественно преобразуем дробь: умножив числитель и знаменатель на двучлен, сопряжённый знаменателю, и сократим на x +1. Согласно следствию из теоремы 1, получим выражение, решая которое, находим искомый предел:
Пример 16. Раскрыть неопределённость и найти предел
Решение. Непосредственная подстановка значения x = 0 в заданную функцию приводит к неопределённости вида 0/0. Чтобы раскрыть её, выполним тождественные преобразования и получим в итоге искомый предел:
Продолжение темы «Предел»
Поделиться с друзьями
function-x.ru
Определение и нахождение пределов. Методы решения лимитов
Тестирование онлайн
Определение предела последовательности
Число a называется пределом числовой последовательности, если для любого существует число такое, что для всех n>N выполняется неравенство
Когда число a является пределом числовой последовательности (xn), то пишут:
Пример 1. Рассмотрим числовую последовательность . Найдем несколько первых элементов этой последовательности:
Элементы числовой последовательности будем отображать точками на координатной прямой:
Легко заметить, что пункты, которые отображают элементы данной числовой последовательности с нарастанием номера n все ближе и ближе приближаются к пункту a=1. Расстояние от xn до пункта а=1 может быть меньше или вообще любого положительного числа.
Когда последовательность имеет предел, то она называется сходящейся. Когда пределом последовательности является число a, то говорят, что последовательность (xn) сходится к a.
(В нашем примере последовательность сходится к 1).
Когда последовательность не имеет предела, то она называется расходящейся.
Из определения предела последовательности следует, что
Арифметические действия над сходящимися последовательностями

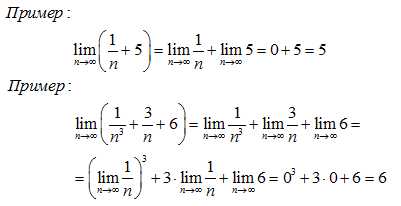
Определение предела функции
Число A называется пределом функции y=f(x) в пункте x0, когда для любого положительного числа существует такое положительное число , что для всех x, которые удовлетворяют неравенству выполняется неравенство:
Когда число A является пределом функции f(x), то пишут:
Обратите внимание! Здесь x стремится к некоторому числу, а не к бесконечности. Арифметические действия для пределов фунции аналогичные.
Методы решения пределов
При отыскании пределов отношения двух многочленов относительно x при оба члена отношения полезно разделить на xn, где n — наивысшая степень этих многочленов.
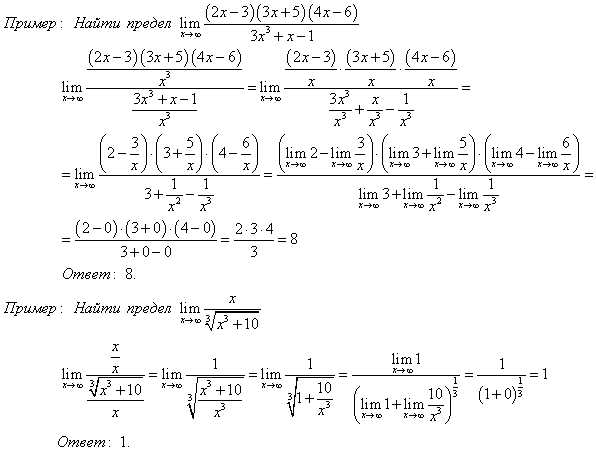
Решение пределов вида , где P(x) и Q(x) — целые многочлены. Если P(x0)=Q(x0)=0, то дробь рекомендуется сократить.
Выражения, содержащие иррациональности, приводятся к рациональному виду во многих случаях путем введения новой переменной.
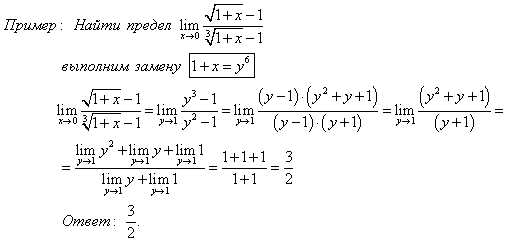
Еще один способ решения пределов с иррациональными выражениями — это перевод иррациональности из числителя в знаменатель или, наоборот, из знаменателя в числитель.
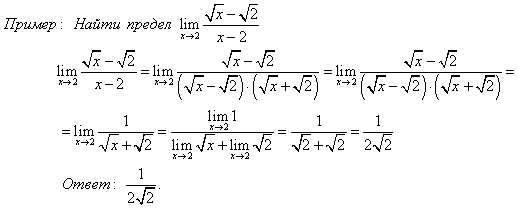
При вычислении пределов во многих случаях используется формула
Нахождение пределов вида
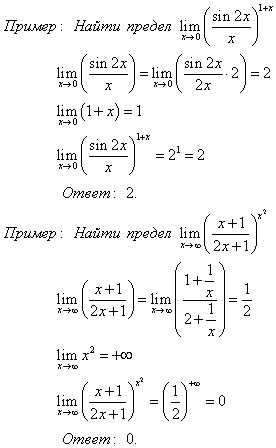
При решении подобных пределов часто используют формулу числа e:
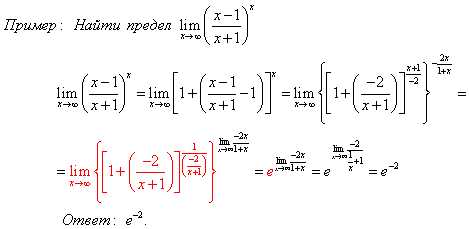
Некоторые важные пределы:

fizmat.by
Предел функции в точке
Сегодня рассмотрим подборку новых задач на нахождение предела в точке. Начнем с простых примеров на подстановку значения, чаще всего рассматривают в 11 классе школьной программы по математике.
Далее остановимся и проанализируем пределы с неопределенностями, методы раскрытия неопределенностей, применением первой и второй важных границ и их последствий.
Приведенные примеры полностью не охватят всей темы, но на многие вопросы внесут ясность.
Найти предел функции в точке:
Пример 46. Предел функции в точке определяем подстановкой
Так как знаменатель дроби не превращается в ноль то такую задача под силу решить каждому выпускнику школы.
Пример 47. Имеем долю полиномов, кроме того знаменатель не содержит особенности (не равен нулю).
Еще одна задача, фактически за 11 класс.
Пример 48. Методом подстановки определяем предел функции
Из условия следует, что граница функции равна двум, если переменная стремится к бесконечности.
Пример 49.Прямая подстановка x=2 показывает, что граница в точке имеет особенность {0/0}. Это означает, что и числитель и знаменатель скрыто содержат (x-2).
Выполняем разложение полиномов на простые множители, а потом сокращаем дробь на указанный множитель (x-2).
Предел дроби, которая останется, находим методом подстановки.
Пример 50.Предел функции в точке имеет особенность типа {0/0}.
Избавляемся разницы корней методом умножения на сумму корней (сопряженное выражение), полином раскладываем.
Далее, упростив функцию, находим значение предела в единице.
Пример 51.Рассмотрим задачу на сложные пределы.
До сих пор от иррациональности избавлялись методом умножения на сопряженное выражение.
Здесь же, в знаменателе, имеем корень кубический, поэтому нужно использовать формулу разности кубов.
Все остальные преобразования повторяются от условия к условию.
Полином раскладываем на простые множители,
далее сокращаем на множитель, который вносит особенность (0)
и подстановкой x=-3 находим предел функции в точке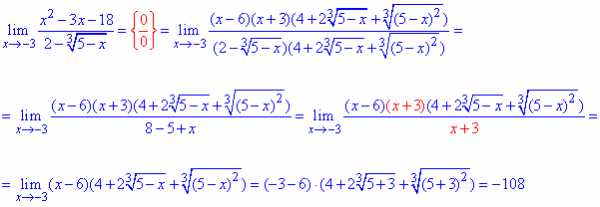
Пример 52.Особенность вида {0/0} раскрываем с помощью первого замечательного предела и его последствий.
Сначала разницу синусов распишем согласно тригонометрической формуле
sin(7x)-sin(3x)=2sin(2x)cos(5x).
Далее числитель и знаменатель дроби дополняем выражениями, которые необходимы для выделения важных пределов.
Переходим к произведению пределов и оцениваем вложение каждого множителя.
Здесь использовали первый замечательный предел:
и следствия из него
где a и b – произвольные числа.
Пример 53.Чтобы раскрыть неопределенность при переменной стремящейся к нулю, используем второй замечательный предел.
Чтобы выделить экспоненту, приводим показатель к 2-му замечательному пределу, а все остальное, что останется в предельном переходе, даст степень експоненты.
Здесь использовали следствие из второго замечатеьного предела:
Вычислить предел функции в точке:
Пример 54. Нужно найти предел функции в точке. Простая подстановка значения показывает, что имеем деление нулей.
Для ее раскрытия разложим на простые множители полиномы и выполним сокращение на множитель, который вносит особенность (х+2).
Однако числитель дальше содержит (x+2), а это значит, что при x=-2 граница равна нулю.
Пример 55.Имеем дробную функцию — в числителе разница корней, в знаменателе — поленом.
Прямая подстановка дает особенность вида {0/0}.
Переменная стремится к минус единице, а это значит, что следует искать и избавляться особенности вида (x+1).
Для этого избавляемся иррациональности умножением на сумму корней, а квадратичную функцию раскладываем на простые множители.
После всех сокращений методом подстановки определяем предел функции в точке
Пример 56.С виду подлимитной функции можно ошибочно заключить, что нужно применить первый предел, но вычисления показали, что все гораздо проще.
Сначала распишем сумму синусов в знаменателе sin(2x)+sin(6x)=2sin(4x)*cos(2x).
Далее расписываем tg(2x), и синус двойного угла sin(4x)=2sin(2x)cos (2x).
Синусы упрощаем и методом подстановки вычисляем предел дроби
Пример 57.Задача на умение использовать вторую замечательный предел:
суть заключается в том, что следует выделить ту часть, которая дает экспоненту.
Остальное, что останется в показателе в предельном переходе даст степень экспоненты.
На этом разбор задач на пределы функций и последовательностей не заканчивается.
В настоящее время подготовлено более 150 готовых ответов к пределам функций, поэтому изучайте и делитесь ссылками на материалы с однокласниками.
yukhym.com
Предел функции в точке, формулы и примеры
Определение предела функции в точке по Гейне
Это определение предела функции на языке последовательностей.
Определение предела функции в точке по Коши
Это определение предела функции на языке « — ».
Замечание 1. Из определения предела функции по Гейне следует, что функция не может иметь в точке двух разных пределов.
Замечание 2. Понятие предела функции в точке – локальное понятие: существование и значение предела полностью определяется значениями функции в как угодно малой окрестности этой точки.
Замечание 3. Геометрически существование предела функции в точке по Коши означает, что для любого числа можно указать на координатной плоскости такой прямоугольник с основанием и высотой , с точкой пересечения диагоналей , что все точки графика данной функции на интервале , за исключением, быть может, точки, лежат в этом прямоугольнике (рис. 1).
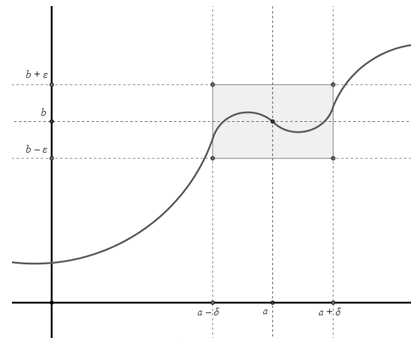
Рис. 1
Учитывая то, как будут раскрываться модули, а также тот факт, стремится слева или справа к значению , для записанных выше выражений можно построить следующую таблицу:
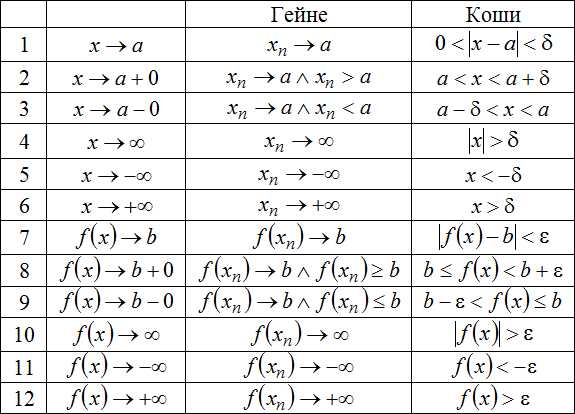
Во втором столбце записаны условия, накладываемые на переменную и функцию, а третий и четвертый столбцы соответствуют тому, как необходимо эти условия трактовать в определениях предела функции по Гейне и Коши соответственно.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Как находить пределы?
Существует в математике такое понятие, как предел функции. Чтобы понимать, как находить пределы, нужно помнить определение предела функции: функция f (x) имеет предел L в точке x = a, если для каждой последовательности значений х, сходящейся к точке a, последовательность значений у приближается к:
Понятие и свойства пределов
Что такое предел, можно понять из примера. Предположим, мы имеем функцию у=1/х. Если мы будем последовательно увеличивать значение х и смотреть, чему равен у, то получим всё уменьшающиеся значения: при х=10000 у=1/10000; при х=1000000 у=1/1000000. Т.е. чем больше х, тем меньше у. Если х=∞, у будет настолько мал, что его можно будет считать равным 0. Таким образом, предел функции у=1/х при х стремящемся к ∞ равен 0. Записывается это так:
Предел функции имеет несколько свойств, которые нужно помнить: это существенно облегчит решение задач на нахождение пределов:
- Предел суммы равен сумме пределов: lim(x+y)=lim x+lim y
- Предел произведения равен произведению пределов: lim(xy)=lim x*lim y
- Предел частного равен частному от пределов: lim(x/y)=lim x/lim y
- Постоянный множитель выносят за знак предела: lim(Cx)=C lim x
У функции у=1 /x, в которой x →∞, предел равен нулю, при x→0, предел равен ∞.
В статье Как решать пределы подробно рассказывается методика решения таких задач. А мы рассмотрим несколько примеров.
Решение примеров на пределы
Начинать находить пределы функций надо всегда с подстановки в функцию того значения х, к которому он стремится.
Пример 1
- Lim (х-3) = lim (3-3) = 0
- х→3
Пример 2
- Lim [х²/(1-х)]. Если подставить х=∞, получим
- х→∞
- ∞²/(1-∞) = ∞²/(-∞).
Одну бесконечность в числителе и знаменателе сокращаем:
- ∞/(-1) = -∞. Значит,
- Lim [х²/(1-х)] = -∞.
- х→∞
В этих примерах всё просто. Однако обычно пределы функций ищут при таких значениях х, которые создают неопределённость типа 0/0 или ∞/∞. Такие неопределённости нужно раскрывать.
Пример 3
- Lim [(2х² — 3х – 5)/(1 + х + 3х²)]
- х→∞
Подставляем х=∞ и получаем в числителе и знаменателе бесконечность, и там, и там в квадрате. Значит, получилась неопределённость типа ∞/∞.
Попробуем сначала разделить обе части дроби на старшую степень — х²:
- Lim {[(2х² — 3х – 5)/x²]/[(1 + х + 3х²)/x²]} =
- х→∞
- = Lim {[(2х²/x²) – (3х/x²) – (5/x²)]/[(1/x²) +( х/x²) + (3х²/x²)]} =
- х→∞
- Lim {[2 – (3/x) – (5/x²)]/[(1/x²) +(1/x) + 3]}
- х→∞
- При х = ∞ 3/х = 0; 5/х² = 0; 1/x² = 0; 1/x = 0.
Значит, из всей страшной четырёхэтажной дроби у нас остались:
Ответ:
- Lim [(2х² — 3х – 5)/(1 + х + 3х²)] = 2/3
- х→∞
В этом при
elhow.ru
Предел функции. Односторонний предел
Задачи на нахождение предела очень часто можно встретить в таких науках как механика, физика, высшая математика, прикладная математика и т.д. Суть таких задач заключается в отыскании значения функции при движении аргумента до некоторого значения при котором функция может быть и неопределена. Поведение функции в определенной точке и называется ее пределом. Он может принимать как постоянное значение так и быть равным бесконечности ().
ОПРЕДЕЛЕНИЕ ПРЕДЕЛА ФУНКЦИИ
Пусть имеем функцию которая определена в некоторой окрестности точки . Число называется пределом функции при , если для любого малого наперед заданного положительного числа можно найти такое положительное число что для всех удовлетворяющих неравенство
выполняется неравенство
В упрощенной форме определения записывают так
При функция является бесконечно большой, если для любого числа можно найти такое число что для всех , удовлетворяющих неравенство оправдывается неравенство
В краткой форме это определение примет вид
Функция является бесконечно малой при , если выполняется
ОДНОСТОРОННИЕ ГРАНИЦЫ
Запись можно понимать как приближение к точке слева, когда и дело, когда . аким образом, приближение точек до может быть двусторонним. На основе этого введены определения правой и левой границы.
Число есть пределом функции слева (левой границей), если для любого числа существует такое, что при выполняется неравенство
Число является пределом функции справа (правой границей) если для сколь угодно малого значения найдется такое что для всех из промежутка выполняется неравенство
Левая и правая границы называются односторонними границами.
Функция имеет предел в точке тогда и только тогда, когда существуют одновременно границы справа и слева и они равны между собой
Рассмотрим примеры из сборника задач Дубовика В.П., Юрика И.И. «Высшая математика» на нахождение границ.
————————————
Пример 1. Найти пределы.
1) (4. 331)
2) (4. 333)
3) (4. 337)
4) (4. 342)
5) (4. 348)
6) (4. 357)
Решение.
1) Первые примеры не являются сложными и их решения сводится к подстановки значения аргумента в функцию
2) Как и в предыдущем примере проводим подстановку
3) Выполняем подстановку переменной в предел
4) В такого типа примерах нужно знаменатель разложить по правилу разности квадратов, после этого выполнить подстановку
5) В таких примерах нужно числитель и знаменатель сократить на множитель, который вносит наибольший вклад
6) В подобных примерах ищут наибольший показатель переменной в числителе и знаменателе, а потом проводят анализ. При следовании корни ведут себя следующим образом
С оценки показателей видим что числитель быстрее растет чем знаменатель
следовательно функция бесконечно большая и ее предел бесконечный
На этом вводной урок нахождения пределов функций завершен. Другие примеры вычисления пределов и методику их нахождения Вы найдете в следующих материалах.
————————————
Посмотреть материалы:
yukhym.com
Односторонние пределы функции, формулы и примеры
Рис. 1
Рис. 2
Определение одностороннего предела функции по Гейне
Обозначение:
Итак,
Обозначение:
То есть
Определение одностороннего предела по Коши
Замечание. Основные свойства односторонних пределов схожи со свойствами обычных пределов.
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
