Что называется углом между двумя пересекающимися прямыми – Угол между пересекающимися прямыми: определение, примеры нахождения

Угол между пересекающимися прямыми: определение, примеры нахождения

Данный материал посвящен такому понятию, как угол между двумя пересекающимися прямыми. В первом пункте мы поясним, что он из себя представляет, и покажем его на иллюстрациях. Потом разберем, какими способами можно найти синус, косинус этого угла и сам угол (отдельно рассмотрим случаи с плоскостью и трехмерным пространством), приведем нужные формулы и покажем на примерах, как именно они применяются на практике.

Yandex.RTB R-A-339285-1

Что такое угол между пересекающимися прямыми

Для того чтобы понять, что такое угол, образующийся при пересечении двух прямых, нам потребуется вспомнить само определение угла, перпендикулярности и точки пересечения.

Определение 1

Мы называем две прямые пересекающимися, если у них есть одна общая точка. Эта точка называется точкой пересечения двух прямых.

Каждая прямая разделяется точкой пересечения на лучи. Обе прямые при этом образуют 4 угла, из которых два – вертикальные, а два – смежные. Если мы знаем меру одного из них, то можем определить и другие оставшиеся.

Допустим, нам известно, что один из углов равен α. В таком случае угол, который является вертикальным по отношению к нему, тоже будет равен α. Чтобы найти оставшиеся углы, нам надо вычислить разность 180°-α. Если α будет равно 90 градусам, то все углы будут прямыми. Пересекающиеся под прямым углом линии называются перпендикулярными (понятию перпендикулярности посвящена отдельная статья).

Взгляните на рисунок:

Перейдем к формулированию основного определения.

Определение 2

Угол, образованный двумя пересекающимися прямыми – это мера меньшего из 4-х углов, которые образуют две эти прямые.

Из определения нужно сделать важный вывод: размер угла в этом случае будет выражен любым действительным числом в интервале (0, 90]. Если прямые являются перпендикулярными, т

zaochnik.com

Угол между прямыми

Определение угла между прямыми

Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.

Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

Если две прямые заданы уравнениями с угловым коэффициентом

y = k₁x + b₁,
y = k₂x + b₂,

то угол между ними можно найти, используя формулу:

tg γ = k₁ — k₂

1 + k₁·k₂

Если знаменатель равен нулю (1 + k₁·k₂ = 0), то прямые перпендикулярны.

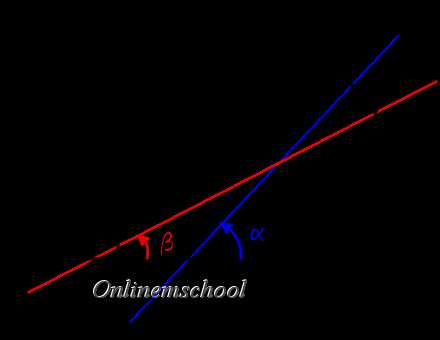Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX

tg α = k₁
tg β = k₂

Соответственно легко найти угол между прямыми

γ = α — β

tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k₁ — k₂1 + k₁·k₂

Угол между прямыми через направляющие векторы этих прямых

Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано параметрически

x = l t + ay = m t + b

то вектор направляющей имеет вид {l; m}

Если уравнение прямой задано как

A x + B y + C = 0

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m

то вектор направляющей имеет вид {l; m}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}

Угол между прямыми через векторы нормалей этих прямых

Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если уравнение прямой задано как

A x + B y + C = 0

то вектор нормали имеет вид {A; B}

Если задано уравнение прямой с угловым коэффициентом

y = kx + b

то вектор нормали имеет вид {1; -k}

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

sin φ = |a · b||a| · |b|

Примеры задач на вычисления угла между прямыми на плоскости

Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k₁ — k₂1 + k₁·k₂ = 2 — (-3)1 + 2·(-3) = 5-5 = 1

Ответ. γ = 45°

Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}

cos φ = |1 · 2 + 2 · 1|1² + 2² · 2² + 1² = 45 · 5 = 0.8

Ответ. φ ≈ 36.87°

Пример 3 Найти угол между прямыми 2x + 3y = 0 и x — 23 = y4.

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2x + 3y = 0 => y = -23x   (k₁ = -23)

x — 23 = y4 => y = 43x — 83   (k₂ = 43)

tg γ = k₁ — k₂1 + k₁·k₂ = -23 — 431 + (-23)·43 = -631 — 89 = 18

Ответ. γ ≈ 86.82°

Угол между прямыми в пространстве

Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:

cos φ = |a · b||a| · |b|

Если дано каноническое уравнение прямой

x — x₀l = y — y₀m = z — z₀n

то направляющий вектор имеет вид {l; m; n}

Если уравнение прямой задано параметрически

x = l t + ay = m t + bz = n t + c

то направляющий вектор имеет вид {l; m; n}

Пример 4. Найти угол между прямыми x = 2t + 1y = tz = -t — 1 и x = t + 2y = -2t + 1z = 1.

Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0|2² + 1² + (-1)² · 1² + (-2)² + 0² = 06 · 5 = 0

Ответ. φ = 90°

Пример 5 Найти угол между прямыми x — 23 = y4 = z — 35 и -x — 22 = 1 — 3y = 3z — 52.

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.

Преобразуем второе уравнение к каноническому вид.

-x — 22 = x — 2-2

1 — 3y = 1 + y-1/3 = y — 1/3-1/3

3z — 52 = z — 5/32/3

Получено уравнение второй прямой в канонической форме

x — 2-2 = y — 1/3-1/3 = z — 5/32/3

{-2; -13; 23} — направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(-13) + 5·233² + 4² + 5² · (-2)² + (-13)² + (23)² = -6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49 = -450 · 41/9 = 12582 = 682205

Ответ. φ ≈ 74.63°

ru.onlinemschool.com

Стереометрия. Скрещивающиеся прямые. | Подготовка к ЕГЭ по математике

Категория: Справочные материалы

Елена Репина 2013-08-11 2013-08-11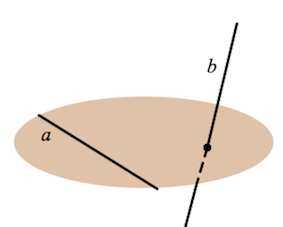

Скрещивающиеся прямые – прямые, которые невозможно поместить в одну плоскость, то есть они не параллельны и не пересекаются.

Признак скрещивающихся прямых

Если одна из прямых лежит в плоскости, а вторая пересекает эту плоскость в точке, отличной от точек первой прямой, то такие прямые – скрещивающиеся.

Расстояние между скрещивающимися прямыми

 

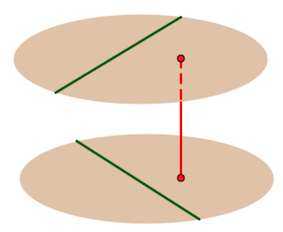
Через две скрещивающиеся прямые можно провести две параллельные плоскости (единственным образом).

Расстояние между скрещивающимися прямыми – есть расстояние между этими плоскостями.

 

Общий перпендикуляр к двум скрещивающимся прямым

Общим перпендикуляром к двум скрещивающимся прямым называется отрезок, перпендикулярный каждой из двух скрещивающихся прямых, концы которого лежат на этих прямых.

Длина общего перпендикуляра равна расстоянию между скрещивающимися прямыми.

 

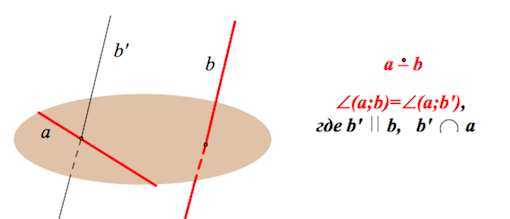
Угол между скрещивающимися прямыми

 

Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

(Одну из прямых можно  вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).

Автор: egeMax | Нет комментариев

egemaximum.ru

1. Взаимное расположение прямых в пространстве. Угол между двумя прямыми

Как известно из курса планиметрии, две прямые в плоскости могут пересекаться (имеют общую точку) или быть параллельными (не имеют общую точку).
В пространстве мы можем представить ситуацию, когда две прямые не пересекаются, но они и не параллельны.

Одна дорога проходит по эстакаде, а другая под эстакадой

 

Кабели моста

 

Горизонтальные линии крыши и вертикальные линии стен

 

Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема «Признак скрещивающихся прямых»

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).

Доказательство
Рассмотрим прямую \(AB\), лежащую в плоскости, и прямую \(CD\), которая пересекает плоскoсть в точке \(D\), не лежащей на прямой \(AB\).

 

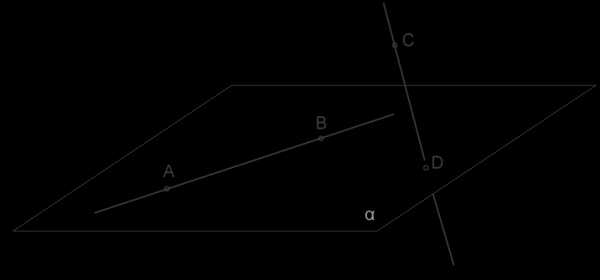
1. Допустим, что прямые \(AB\) и \(CD\) всё-таки лежат в одной плоскости.
2. Значит, эта плоскость идёт через прямую \(AB\) и точку \(D\), то есть, она совпадает с плоскостью \(α\).
3. Это противоречит условиям теоремы, по которым прямая \(CD\) не находится в плоскости \(α\), а пересекает её.
Теорема доказана.

 

В пространстве прямые расположены следующим образом:
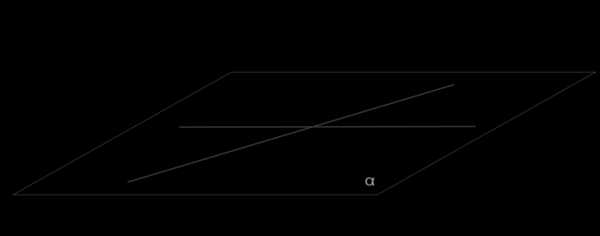
1. параллельные;

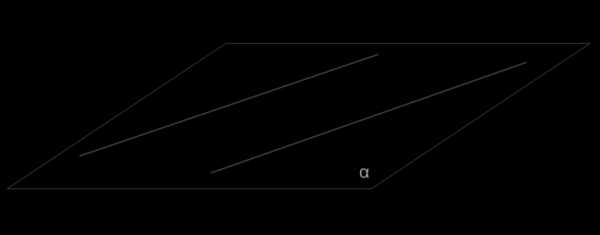
2. пересекающиеся;

3. скрещивающиеся.
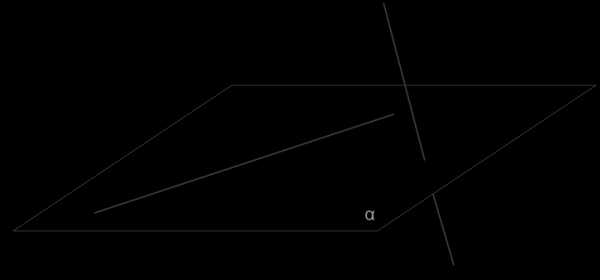Теорема

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство
Рассмотрим скрещивающиеся прямые \(AB\) и \(CD\).

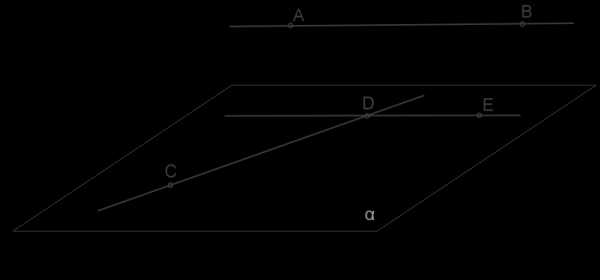
1. Через точку \(D\) можно провести прямую \(DE\), параллельную \(AB\).
2. Через пересекающиеся прямые \(CD\) и \(DE\) можно провести плоскость \(α\).
3. Так как прямая \(AB\) не лежит в этой плоскости и параллельна прямой \(DE\), то она параллельна плоскости.

4. Эта плоскость единственная, так как любая другая плоскость, проходящая через \(CD\), будет пересекаться с \(DE\) и \(AB\), которая ей параллельна.
 Теорема доказана.

Углы между прямыми

1. Если прямые параллельны, то угол между ними — 00.
2. Углом между двумя пересекающимися прямыми называют  величину меньшего из углов, образованных этими прямыми. Если все углы равны, то эти прямые перпендикулярны (образуют угол 900).
3. Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

 

Обрати внимание!

Провести соответственные прямые, параллельные данным скрещивающимся прямым, можно через любую точку. Иногда удобно выбрать эту точку на одной из данных скрещивающихся прямых и провести через эту точку прямую, параллельную другой из скрещивающихся прямых.

Пример:

дан куб ABCDA1B1C1D1.

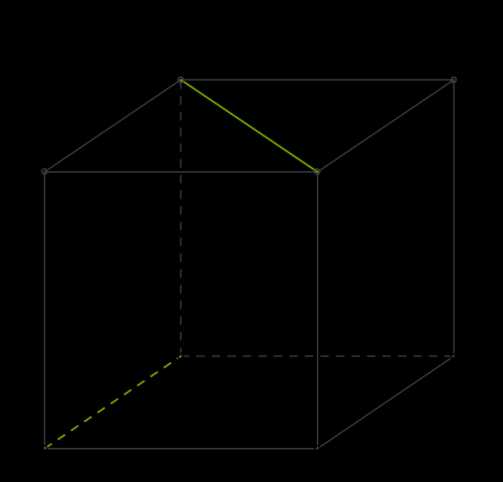
Найти угол между AB и B1D1.

Выберем точку B на прямой AB и проведём через B прямую BD параллельно B1D1.

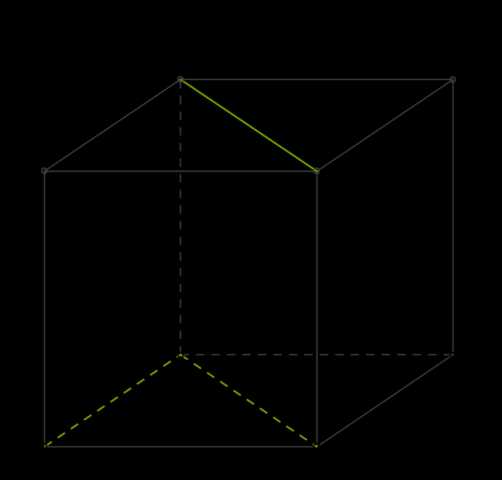
Угол между AB и BD — 450, так как ABCD — квадрат.

Соотвeтственно, угол между AB и B1D1 — тоже 450.

www.yaklass.ru

Угол между скрещивающимися прямыми

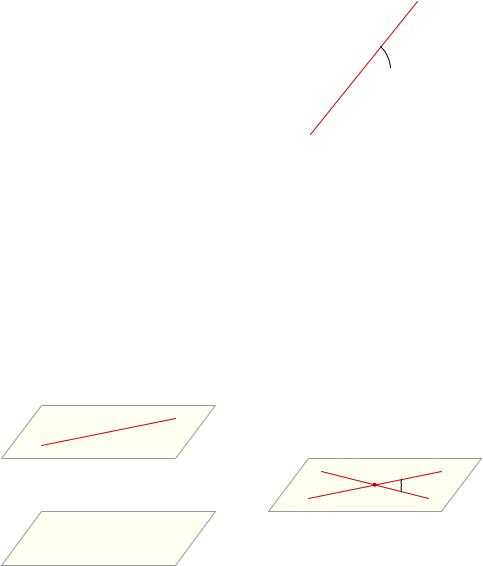
Скрещивающиеся прямые не пересекаются. Можно ли в таком случае говорить об угле между ними? Оказывается, можно.

4.1Угол между пересекающимися прямыми

Вспомним сначала, что такое угол между пересекающимися прямыми. Пусть прямые a и b пересекаются (рис. 23). При этом образуются четыре угла. Если все углы равны друг другу, то прямые a и b называются перпендикулярными (левый рисунок), и угол между этими прямыми равен 90 . Если не все углы равны друг другу (то есть образуются два равных острых угла и два равных тупых угла), то углом между прямыми a и b называется острый угол ‘ (правый рисунок).

	b			‘	b
		a			a

Рис. 23. Угол между пересекающимися прямыми

4.2Определение угла между скрещивающимися прямыми

Теперь введём понятие угла между скрещивающимися прямыми.

Пусть прямые a и b скрещиваются. Возьмём в пространстве произвольную точку M. Дальнейшие действия зависят от того, принадлежит точка M одной из наших прямых или нет.

1.Пусть точка M не принадлежит ни прямой a, ни прямой b. Проведём через M прямую a0, параллельную a, и прямую b0, параллельную b (рис.24). Прямые a0 и b0 пересекаются; тогда угол ‘ между этими прямыми и называется углом между прямыми a и b.

a

a0

‘

M b0

b

Рис. 24. Угол между скрещивающимися прямыми

Таким образом, угол между скрещивающимися прямыми a и b это угол между пересекающимися прямыми a0 и b0, такими, что a0 k a и b0 k b.

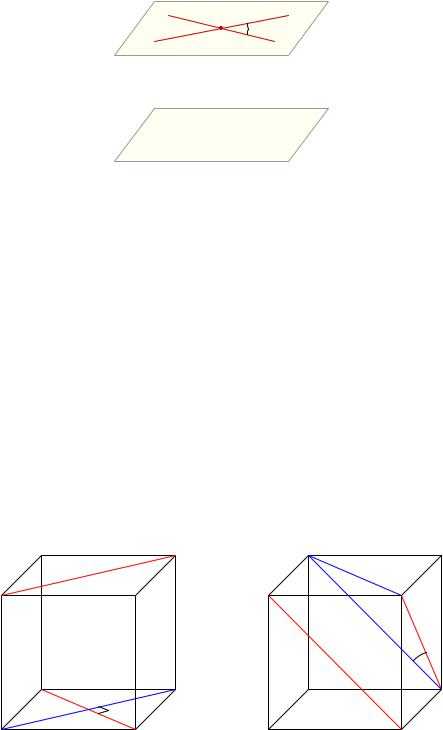
2.Пусть точка M принадлежит одной из прямых; например, пусть M 2 a. Проведём через точку M прямую b0, параллельную b (рис.25). Прямые a и b0 пересекаются; угол ‘ между этими прямыми и называется углом между прямыми a и b.

a

‘

Mb0

b

Рис. 25. Угол между скрещивающимися прямыми

Итак, угол между скрещивающимися прямыми a и b это угол между прямой a и прямой b0, параллельной b и пересекающей a.

Можно показать, что определение угла между скрещивающимися прямыми является корректным, то есть не зависит от конкретного выбора точки M (иными словами, как точку M ни выбирай, угол ‘ всегда получится одним и тем же). Поэтому в конкретных задачах выбор точки M диктуется исключительно соображениями удобства.

4.3Примеры решения задач

Разберём три задачи, расположенные по возрастанию сложности. Третья задача сопоставима с задачами C2, предлагающимися на ЕГЭ по математике.

Задача 1. В кубе ABCDA1B1C1D1 найти угол между прямыми: а) A1C1 и BD; б) A1B и B1C.

Решение. Делаем чертёж (рис. 26). Прямые, угол между которыми надо найти, изображены красным цветом.

D	C	D	C
A	B	A	B
	К пункту а)		К пункту б)

Рис. 26. К задаче 1

а) Проведём AC k A1C1. Угол между прямыми A1C1 и BD есть угол между прямыми AC и BD. Но AC ? BD как диагонали квадрата. Поэтому A1C1 ? BD.

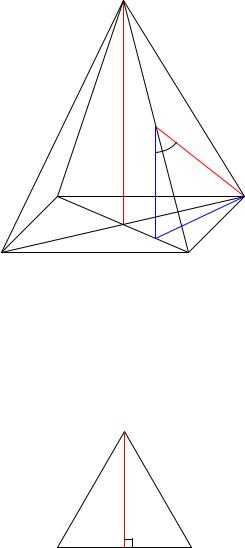
б) Проведём D1C k A1B. Угол между прямыми A1B и B1C есть угол между прямыми D1C и B1C (то есть угол D1CB1). Треугольник D1CB1 равносторонний: D1C = CB1 = B1D1 как диагонали равных квадратов, являющихся гранями куба. Следовательно, \D1CB1 = 60 .

Ответ: a) 90 ; б) 60 .

Задача 2. В правильной четырёхугольной пирамиде SABCD (с вершиной S) боковое ребро равно стороне основания. Точка M середина ребра SB. Найдите угол между прямыми CM и SO, где O центр основания пирамиды.

Решение. Пусть N середина отрезка BO (рис. 27). Тогда MN средняя линия треугольника SBO. Следовательно, MN k SO, и потому искомый угол есть ‘ = \CMN.

S

aM

Рис. 27. К задаче 2

Поскольку SO перпендикулярна плоскости основания, MN также перпендикулярна этой плоскости. Стало быть, треугольник CMN прямоугольный с гипотенузой CM.

Пусть каждое ребро пирамиды равно a. Длину отрезка CM найдём из равностороннего треугольника BCS (рис. 28).

C

a

B

a

M

S

2

Рис. 28. К задаче 2

По теореме Пифагора имеем:

a

2

a2

CM2 = BC2 BM2 = a2

=

3

;

2

4

откуда

p

CM =

a 3

:

2

Обязательно запомните это выражение для высоты равностороннего треугольника со сто-

роной a. Оно вам ещё неоднократно пригодится.

Для диагонали квадрата ABCD имеем: BD = ap

(почему?). Треугольник ASC равен

2

треугольнику ABC (по трём сторонам), то есть является равнобедренным прямоугольным.

Тогда

p

SO = BO =

a

2

:

2

Следовательно,

p

MN =

1

SO =

a

2

:

2

4

Из треугольника CMN теперь имеем:

MN ap

=4

2

1

cos ‘ =

=

ap

=2

= p

:

CM

3

6

Ответ: arccos 1 .

p

6

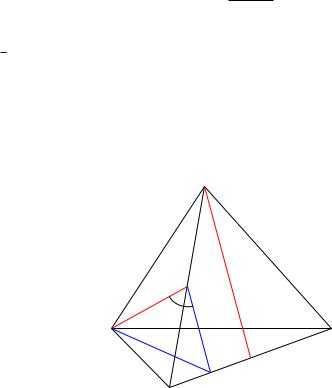
Задача 3. В правильном тетраэдре ABCD точка K середина BD, точка M середина BC. Найдите угол между прямыми AK и DM.

Решение. Пусть точка L середина BM (рис. 29). Тогда KL средняя линия треугольника BDM; значит, KL k DM, и потому искомый угол есть ‘ = \AKL.

D

		a
		K
		‘
A		C
	a	M

L

B

Рис. 29. К задаче 3

Величину ‘ мы вычислим по теореме косинусов из треугольника AKL. Предварительно найдём стороны этого треугольника.

Как и в предыдущей задаче, имеем:

p

AK =

a

3

;

2

где a ребро тетраэдра. Кроме того,

p

p

KL =

1

DM =

1 a 3

=

a 3

:

2

2

2

4

Остаётся найти сторону AL. Это можно сделать из треугольника ABL, в котором AB = a,

BL = a=4, \ABL = 60 . По теореме косинусов получим:

a

2

a

a2

a2

13a2

AL2

= a2

+

2a

cos 60 = a2 +

=

:

4

4

16

4

16

Теперь возвращаемся к треугольнику AKL. По теореме косинусов:

				AL2 = AK2 + KL2 2 AK AL cos ‘:
Подставляем сюда найденные длины сторон:
		13a2				ap				2			ap						2		ap				ap
									3							3						3						3
				=						! +								! 2												cos ‘:
16					2								4								2					4
Остаётся довести выкладки до конца:
13a2					3a2					3a2			3a2								15a2					3a2
				=				+								cos ‘ =														cos ‘;
16						4					16		4								16					4
откуда находим:																			1
												cos ‘ =								:
																			6

Ответ: arccos 16 .

studfiles.net

Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Стереометрия

Взаимное расположение двух прямых в пространстве

      Все возможные случаи взаимного расположения двух прямых в пространстве представлены в следующей таблице.

Фигура	Рисунок	Определение
Две пересекающиеся прямые		Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку.
Две параллельные прямые		Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек
Две скрещивающиеся прямые		Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые.

Две пересекающиеся прямые

Две прямые называют пересекающимися прямыми, если они имеют единственную общую точку.

Две параллельные прямые

Две прямые называют параллельными прямыми, если они лежат в одной плоскости и не имеют общих точек

Две скрещивающиеся прямые

Две прямые называют скрещивающимися прямыми, если не существует плоскости, содержащей обе прямые.

      С перечисленными в предыдущей таблице случаями взаимного расположения двух прямых в пространстве близко связаны утверждения, представленные в следующей таблице.

Фигура	Рисунок	Тип утверждения и формулировка
Две различные точки		Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.
Прямая линия и точка, не лежащая на этой прямой		Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.
Две пересекающиеся прямые		Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.
Две параллельные прямые		Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две различные точки

Аксиома о прямой линии, заданной двумя точками Через две различные точки проходит одна и только одна прямая линия.

Прямая линия и точка, не лежащая на этой прямой

Аксиома о параллельных прямых Через точку, не лежащую на прямой,проходит одна и только одна прямая, параллельная этой прямой.

Две пересекающиеся прямые

Теорема о плоскости, определяемой двумя пересекающимися прямыми Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Две параллельные прямые

Теорема о плоскости, определяемой двумя параллельными прямыми Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.

Признак скрещивающихся прямых

      Признак скрещивающихся прямых. Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются (рис.1).

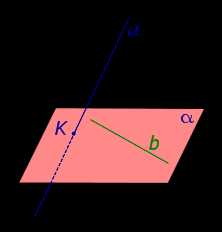
Рис.1

      Доказательство. Напомним, что две прямые называют скрещивающимися, если не существует плоскости, содержащей обе эти прямые, и будем доказывать признак скрещивающихся прямых методом «От противного».

      Для этого предположим, что прямая   a,   пересекающая плоскость в точке K, и прямая b, лежащая в плоскости   α  (рис. 1), не являются скрещивающимися. Из этого предположения следует, что существует плоскость, содержащая обе эти прямые. Обозначим эту плоскость буквой  β  и докажем, что плоскость  β  совпадает с плоскостью  α. Действительно, поскольку обе плоскости   α  и   β проходят через прямую b и точку K, не лежащую на этой прямой, то они совпадают. Следовательно, прямая a лежит в плоскости прямая a лежит в плоскости. Мы получили противоречие с тем, что по условию прямая a пересекает плоскость прямая a пересекает плоскость, а не лежит в ней. Доказательство признака скрещивающихся прямых завершено.

Угол между скрещивающимися прямыми

     Углом между скрещивающимися прямыми называют угол между пересекающимися прямыми пересекающимися прямыми, соответственно параллельными параллельными данным скрещивающимся прямым скрещивающимся прямым (рис. 2).

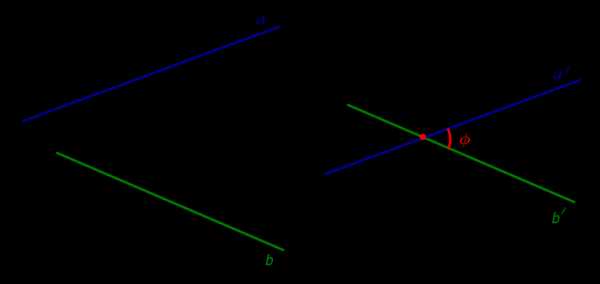
Рис.2

     На рисунке 2 изображены скрещивающиеся прямые   a  и   b. Прямая a’ параллельна прямой a, прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол   φ  и является углом между скрещивающимися прямыми   a  и   b.

      Задача. В кубе кубе   ABCDA₁B₁C₁D₁   найти угол между прямыми   AB₁   и   BC₁.

      Решение. Поскольку прямая   AB₁   пересекает плоскость   BB₁C₁   в точке   B₁,   которая не лежит на прямой   BC₁,   то по признаку скрещивающихся прямых прямые   AB₁   и   BC₁   скрещиваются (рис. 3).

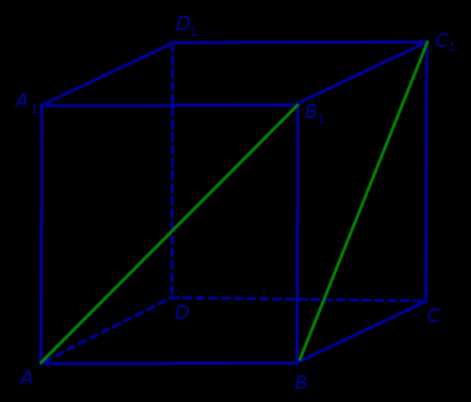
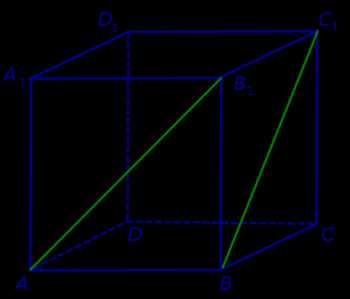
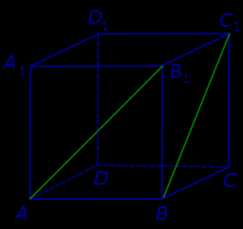
Рис.3

      Для того, чтобы найти угол между прямыми   AB₁   и   BC₁, проведем в кубе диагональ боковой грани   AD₁   и диагональ верхнего основания   D₁B₁   (рис. 4).

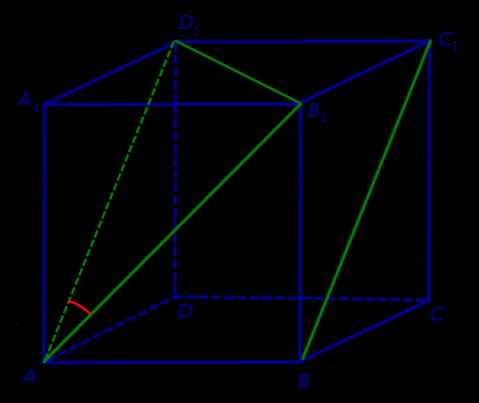
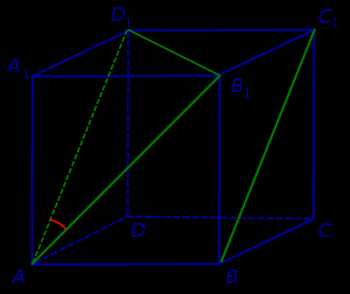
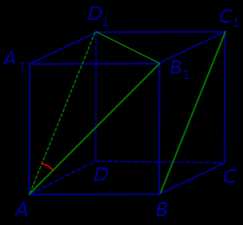
Рис.4

      По определению угла между скрещивающимися прямыми угол   D₁AB₁   и является углом между прямыми AB₁   и   BC₁.   Поскольку треугольник   AD₁B₁   равносторонний, угол   D₁AB₁   равен   60°.

      Ответ. 60°.

      Замечание. Для более глубокого усвоения понятия «Скрещивающиеся прямые» рекомендуем ознакомиться с разделами нашего сайта «Свойства скрещивающихся прямых» и «Взаимное расположение прямой и плоскости в пространстве. Признак параллельности прямой и плоскости».

      На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.

Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10

      Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит

      У нас также для школьников организованы

МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»

www.resolventa.ru

чему равен угол между скрещивающимися и пересекающимися прямыми?

А по конкретней никак нельзя? Что значит чему равен? 1. Между пересекающимися — непосредственно углу между ними 2. Для определения угла между скрещивающимися, нужно одну из прямых плоско-параллельным переносом совместить до пересечения со второй. И дальше смотри п. 1. Все вопросы в агент.

Углом между скрещивающимися прямыми называется угол межу пересекающимися прямыми, которые параллельны данным скрещивающимся прямым. Угол между двумя пересекающимися прямыми измеряется так же, как и в планиметрии ( так как через эти прямые можно провести плоскость

Если уравнения прямых записаны в виде (x-x1)/a=(y-y1)/b=(z-z1)/c, то угол между ними — угол между направляющими векторами, т. е. между векторами, координаты которых стоят в знаменателе указанного уравнения.

touch.otvet.mail.ru