Что такое смешанное произведение векторов – свойства примеры и решения, геометрический смысл смешанного произведения векторов

Смешанное произведение векторов, формула и примеры

Определение и формула смешанного произведения векторов

ОПРЕДЕЛЕНИЕ Смешанным произведением трех векторов и называется число, равное скалярному произведению вектора на векторное произведение векторов и :

   

Если векторы и заданы своими координатами: и , то их смешанное произведение равно определителю матрицы, составленной из этих векторов:

   

ПРИМЕР

Задание	Найти смешанное произведение векторов
Решение	Для нахождения смешанного произведения составляем определитель, по строкам которого записаны координаты заданных векторов:
Ответ

Свойства смешанного произведения векторов

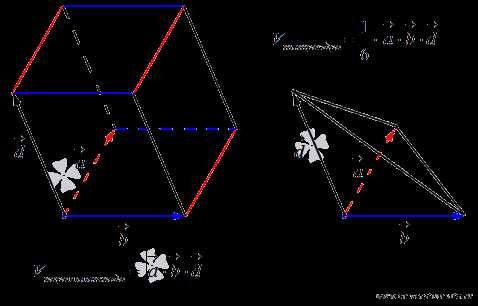
1. Геометрический смысл смешанного произведения. Модуль смешанного произведения трех векторов и равен объёму параллелепипеда, образованного этими векторами:

   

ЗАМЕЧАНИЕ Объем пирамиды, образованной тремя векторами и , равен одной шестой модуля смешанного произведения этих векторов:

   

2. Если смешанное произведение трех ненулевых векторов равно нулю, то эти векторы компланарны.

3. .

ЗАМЕЧАНИЕ Мнемоническое правило для запоминания этой формулы: смешанное произведение трех векторов и равно «бац минус цаб».

4. .

5. Тождество Якоби:

   

ПРИМЕР

Задание	Найти объем пирамиды построенной на векторах
Решение	Объем пирамиды, построенной на векторах и , равен одной шестой модуля смешанного произведения этих векторов:     Поэтому вначале найдем смешанное произведение заданных векторов. Для этого составим определитель, по строкам которого записаны координаты векторов и , и вычислим его, например, по правилу треугольника:     Тогда искомый объем (куб. ед.).
Ответ	(куб. ед.)

ru.solverbook.com

Смешанное произведение векторов и его свойства

Смешанным произведением векторов называется число, равное скалярному произведению векторана векторное произведение векторови. Смешанное произведение обозначается.

Геометрические свойства смешанного произведения

1. Модуль смешанного произведения некомпланарных векторов равен объемупараллелепипеда, построенного на этих векторах. Произведениеположительно, если тройка векторов— правая, и отрицательно, если тройка— левая, и наоборот.

2. Смешанное произведение равно нулю тогда и только тогда, когда векторыкомпланарны:

 векторы компланарны.

Докажем первое свойство. Найдем по определению смешанное произведение: , где— угол между векторамии. Модуль векторного произведения (по геометрическому свойству 1) равен площадипараллелограмма, построенного на векторахи: . Поэтому. Алгебраическое значениедлины проекции векторана ось, задаваемую вектором, равно по модулю высотепараллелепипеда, построенного на векторах(рис. 1.47). Поэтому модуль смешанного произведения равен объемуэтого параллелепипеда:

Знак смешанного произведения определяется знаком косинуса угла . Если тройкаправая, тои смешанное произведениеположительно. Если же тройкалевая, тои смешанное произведениеотрицательно.

Докажем второе свойство. Равенство возможно в трех случаях:или(т.е.),или(т.е. векторпринадлежит плоскости векторови). В каждом случае векторыкомпланарны (см. разд. 1.1).

Смешанным произведением трех векторов называется число, равное векторному произведению первых двух векторов,, умноженному скалярно на вектор. Векторами это можно представить так

Так как векторы на практике задают в координатной форме, то их смешанный произведение равен определитель, построенном на их координатамВ силу того, что векторное произведение антикомутативно, а скалярное произведение коммутативно, то циклическая перестановка векторов в смешанном произведении не изменяет его значение. Перестановка двух соседних векторов меняет знак на противоположный

Смешанный произведение векторов положительный, если они образуют правую тройку и отрицательный — если левую.

Геометрические свойства смешанного произведения1. Объем параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов.2. Объем четырехугольной пирамиды равен трети модуля смешанного произведения3. Объем треугольной пирамиды равен одной шестой модуля смешанного произведения4. Векторы планарных тогда и только тогда, когдаВ координатах условие компланарности означает равенство нулю определителяДля практического усвоения рассмотрим примеры.

Пример 1.

Определить, какой тройкой (правой или левой) являются векторы

Решение.

Найдем смешанное произведение векторов и по знаку выясним, какую тройку векторов они образуют

Векторы образуют правую тройку Векторы образуют правую тройкуВекторы образуют левую тройкуВекторы образуют правую тройкуВекторы образуют левую тройкуДанные векторы линейно зависимы.. Смешанным произведением трех векторов.  Смешанным произведением трех векторов называется число

Геометрическое свойство смешанного произведения:

Теорема 10.1.Объём параллелепипеда, построенного на векторах равен модулю смешанного произведения этих векторов

,

или объём тетраэдра (пирамиды), построенного на векторах равен одной шестой модуля смешанного произведения

.

Доказательство. Из элементарной геометрии известно, что объём параллелепипеда равен произведению высоты на площадь основания

Площадь основания параллелепипеда S равна площади параллелограмма, построенного на векторах (см. рис. 1). Используя

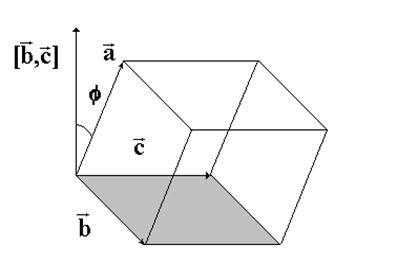Рис. 1. К доказательству теоремы 1. геометрический смысл векторного произведения векторов , получаем, что

.

Далее, если тройка векторов является правой (как на рис. 1), то высота параллелепипеда равна проекции векторана вектор, т.е.

Отсюда получаемЕсли тройка векторов левая, то вектор и вектор направлены противоположно, тогдаилиТаким образом, попутно доказано, что знак смешанного произведения определяет ориентацию тройки векторовтройка правая и ‑ тройка левая). Докажем теперь вторую часть теоремы. Из рис. 2 очевидно, что объем треугольной призмы, построенной на трех векторахравен половине объема параллелепипеда, построенного на этих векторах, то есть 

Рис. 2. К доказательству теоремы 1.

Но призма состоит из трех одинакового объема пирамид OABC, ABCD и ACDE. Действительно, объемы пирамид ABCD и ACDE равны, так как они имеют равные по площади основания BCD и CDE и одинаковую высоту, опущенную из вершины A. То же справедливо для высот и оснований пирамид OABC и ACDE. Отсюда

studfiles.net

Как найти смешанное произведение векторов

Предварительные сведения

Для того чтобы мы могли ввести понятие смешанного произведения векторов, нужно сначала вспомнить понятия скалярного и векторного произведений этих векторов.

Определение 1

Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

$\overline{α}\overline{β}=|\overline{α}||\overline{β}|cos⁡∠(\overline{α},\overline{β})$

Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.

Теорема 1

Скалярное произведение двух данных векторов $\overline{α}$ и $\overline{β}$ равняется сумме произведений их соответствующих координат.

Математически выглядит следующим образом

$\overline{α}\overline{β}=α_1 α_2+β_1 β_2$

Обозначение: $\overline{α}\cdot \overline{β}$.

Определение 2

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Обозначение: $\overline{α}х\overline{β}$.

Математически это выглядит следующим образом:

1. $|\overline{α}х\overline{β}|=|\overline{α}||\overline{β}|sin⁡∠(\overline{α},\overline{β})$
2. $\overline{α}х\overline{β}⊥\overline{α}$, $\overline{α}х\overline{β}⊥\overline{β}$
3. $(\overline{α}х\overline{β},\overline{α},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 1)

Понятие смешанного произведения векторов

Определение 3

Смешанным произведением векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $\overline{α}$ на вектор векторного произведения $\overline{β}х\overline{γ}$ двух других векторов.

Обозначение: $(\overline{α},\overline{β},\overline{γ})$.

Математически это выглядит следующим образом:

$(\overline{α},\overline{β},\overline{γ})=\overline{α}\cdot (\overline{β}х\overline{γ})$

Очевидно, что смешанное произведение будет равняться нулю в двух случаях:

1. Если длина одного или нескольких векторов равняется нулю.
2. Если эти векторы будут являться компланарными.

Пример 1

Найти значение смешанного произведения векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.

Решение.

Из определений 1, и 3 будем получать

$(\overline{α},\overline{β},\overline{γ})=\overline{α}\cdot (\overline{β}х\overline{γ})=|\overline{a}||\overline{β}х\overline{γ}|cos∠(\overline{α},\overline{β}х\overline{γ})$

Изобразим эти векторы в декартовом координатном пространстве (рис. 2):

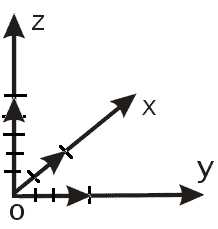
Найдем вначале длину вектора векторного произведения векторов $\overline{β}$ и $\overline{γ}$

Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:

$|\overline{β}|=\sqrt{0+16+0}=4$

$|\overline{γ}|=\sqrt{9+0+0}=3$

Тогда, по определению 2, получим

$|\overline{β}х\overline{γ}|=|\overline{α}||\overline{β}|sin90^\circ=4\cdot 3\cdot 1=12$

Из 3 части определения 2 очевидно, что вектор $\overline{β}х\overline{γ}$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $\overline{α}$ и $\overline{β}х\overline{γ}$ равняется $0^\circ$.

Длина вектора $\overline{α}$

$|\overline{α}|=\sqrt{0+0+25}=5$

Получим

$(\overline{α},\overline{β},\overline{γ})=|\overline{a}||\overline{β}х\overline{γ}|cos∠(\overline{α},\overline{β}х\overline{γ})=5\cdot 12\cdot cos0^\circ=60$

Ответ: $60$.

Вычисление смешанного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $\overline{α}$, $\overline{β}$ и $\overline{γ}$, которые будут иметь координаты $(α_1,α_2,α_3)$, $(β_1,β_2,β_3)$ и $(γ_1,γ_2,γ_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:

$(\overline{α},\overline{β},\overline{γ})=\begin{vmatrix}α_1&α_2&α_3\\β_1&β_2&β_3\\γ_1&γ_2&γ_3\end{vmatrix}$

Иначе, получим

$\overline{α}х\overline{β}=α_1 β_2 γ_3+α_3 β_1 γ_2+α_2 β_3 γ_1-α_3 β_2 γ_1-α_2 β_1 γ_3-α_1 β_3 γ_2$

Пример 2

Найти значение смешанного произведения векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.

Решение.

Воспользуемся формулой, приведенной выше. Получим

$(\overline{α},\overline{β},\overline{γ})=\begin{vmatrix}1&1&0\\0&3&3\\-1&2&6\end{vmatrix}=18+(-3)+0-0-6-0=18-9=9$

Ответ: $9$.

Свойства смешанного произведения векторов

Для произвольных четырех векторов $\overline{α}, $\overline{β}$, $\overline{γ}$ и $\overline{δ}$, а также $r∈R$ справедливы следующие свойства: справедливы следующие свойства:

1) При перестановке местами знаков произведений в смешанном произведении можно менять между собой

$(\overline{α},\overline{δ},\overline{γ})=\overline{α}\cdot (\overline{δ}х\overline{γ})=(\overline{α}х\overline{δ})\cdot \overline{γ}$

2) Векторы в смешанном произведении можно менять только циклически

$(\overline{α},\overline{δ},\overline{γ})=(\overline{δ},\overline{γ},\overline{α})=(\overline{γ},\overline{α},\overline{δ})$

3) Перемещение только одного вектора на другое место меняет знак

$(\overline{α},\overline{δ},\overline{γ})=-(\overline{β},\overline{α},\overline{γ})=-(\overline{γ},\overline{δ},\overline{α})=-(\overline{α},\overline{γ},\overline{δ})$

4) Из формулы выше, очевидны следующие равенства:

$(r\overline{α},\overline{δ},\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$

$(\overline{α},r\overline{δ},\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$

$(overlie{α},\overline{δ},r\overline{γ})=r(\overline{α},\overline{δ},\overline{γ})$

5) Справедливы равенства:

$(\overline{α}+\overline{β},\overline{δ},\overline{γ})=(\overline{α},\overline{δ},\overline{γ})+(\overline{β},\overline{δ},\overline{γ})$

$(\overline{α},\overline{δ}+\overline{β},\overline{γ})=(\overline{α},\overline{δ},\overline{γ})+(\overline{α},\overline{β},\overline{γ})$

$(\overline{α},\overline{δ},\overline{γ}+\overline{β})=(\overline{α},\overline{δ},\overline{γ})+(\overline{α},\overline{δ},\overline{β})$

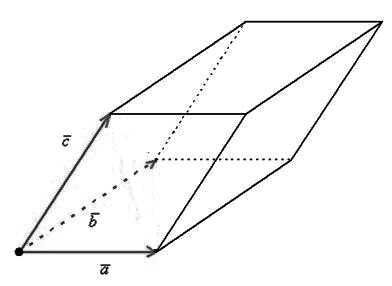
6) Геометрический смысл – площадь параллелепипеда (рис. 3):

$S=|(\overline{α},\overline{β},\overline{c})|$

spravochnick.ru

Смешанное произведение векторов — это… Что такое Смешанное произведение векторов?



Смешанное произведение векторов

Wikimedia Foundation. 2010.

• Смешанная эстафета 4х6 км
• Смешанное состояние

Смотреть что такое «Смешанное произведение векторов» в других словарях:

• Смешанное произведение — векторов   скалярное произведение вектора на векторное произведение векторов и …   Википедия

• СМЕШАННОЕ ПРОИЗВЕДЕНИЕ — трех векторов a b, c, результат скалярного умножения первого из этих векторов на векторное произведение второго вектора на третий; обозначается abc или (a, b, c). Смешанное произведение численно равно объему параллелепипеда, построенного на… …   Большой Энциклопедический словарь

• СМЕШАННОЕ ПРОИЗВЕДЕНИЕ (a, b, с) — векторов a, b, с скалярное произведение вектора а на векторное произведение векторов b и с: ( а, b, c) =(a,[b, с]). См. Векторная алгебра …   Математическая энциклопедия

• смешанное произведение — трёх векторов а, b, с, результат скалярного умножения первого из этих векторов на векторное произведение второго вектора на третий; обозначается abc или (а, b, с). Смешанное произведение численно равно объёму параллелепипеда, построенного на… …   Энциклопедический словарь

• Смешанное произведение —         трёх векторов а, b, с, результат скалярного умножения первого из этих Векторов на Векторное произведение второго вектора на третий; обозначается а b с. С. п. численно равно объёму параллелепипеда, построенного на сомножителях a, b, с,… …   Большая советская энциклопедия

• СМЕШАННОЕ ПРОИЗВЕДЕНИЕ — трёх векторов а, b, с, результат скалярного умножения первого из этих векторов на векторное произведение второго вектора на третий; обозначается аЪс или (а, Ь, с). С. п. численно равно объёму параллелепипеда, построенного на сомножителях а, b, с …   Естествознание. Энциклопедический словарь

• Векторное произведение векторов — Содержание 1 Правые и левые тройки векторов 2 Определение 3 Свойства …   Википедия

• Косое произведение векторов — Псевдоскалярное или косое произведение векторов и на плоскости называют число где   угол вращения (против часовой стрелки) от к …   Википедия

• Векторно-векторное произведение векторов — Тройное векторное произведение (другое название: двойное векторное произведение) векторов векторное произведение вектора на векторное произведение векторов и …   Википедия

• Векторное произведение — в трёхмерном пространстве. Векторное произведение  это псевдовектор, перпендикулярный плоскости, построенной по двум …   Википедия

dic.academic.ru

Смешанное произведение векторов и его свойства — Мегаобучалка

Определение. Смешанным произведением трёх векторов (обозначается называется скалярное произведение вектора на векторное произведение , т.е.

(17)

Из формулы (17) следует, что свойства смешанного произведения являются следствиями свойств скалярного и векторного произведений векторов. Перечислим их без доказательств.

Смешанное произведение не меняется при круговой перестановке сомножителей:

Геометрический смысл смешанного произведения. Модуль смешанного произведения численно равен объёму параллелепипеда, построенного на векторах:

Из свойства следует, что если векторы лежат в одной плоскости (параллельны одной плоскости, т.е. компланарны), то параллелепипеда на них построить нельзя (его объём равен нулю) и

Таким образом, равенство нулю смешанного произведения есть условие компланарности трёх векторов.

Смешанное произведение в координатной форме. Пусть

Тогда

(18)

Например, пусть тогда

т.е. эти три вектора параллельны одной плоскости (компланарны).

Пример 6. Даны три не компланарных вектора . Выяснить, компланарны ли векторы , ,

Решение. Векторы заданы в бескоординатной форме, поэтому пользуемся определением и правилами оперирования как с многочленами:

, т.к. — некомпланарны.

Ответ: Векторы некомпланарны.

Подводя итог и имея в виду геометрические приложения, запомним, что для вычисления углов и длин используем скалярное произведение; для вычисления площадей — векторное произведение; для вычисления объёмов – смешанное произведение.

Пример 7. Даны координаты вершин пирамиды . Найти: 1) угол между ребрами и ; 2) площадь грани ; 3) проекцию вектора на вектор ; 4) объём пирамиды ; 5) длину высоты пирамиды, проведённой из точки . .

Решение: Сделаем схематический чертёж.

Введём векторы , и и

вычислим их координаты, вычитая

из координат конца координаты начала:

.

 

1) Угол между рёбрами и найдём как угол между векторами и с помощью скалярного произведения:

следовательно

по таблицам находим

2) Площадь грани вычислим с помощью векторного произведения , точнее, с помощью его модуля: Сначала найдём само векторное произведение:

Тогда

21,6 ед.²

3) Проекцию вектора на вектор находим с помощью скалярного произведения:

4) Объём пирамиды равен объёма параллелепипеда, построенного на векторах , и , который равен модулю их смешанного произведения. Поэтому сначала находим смешанное произведение:

следовательно,

5) Объём пирамиды равен произведению площади основания на высоту:

 

megaobuchalka.ru

[Зачет 77] Определение смешанного произведения трёх векторов, его свойства и геометрический смысл.

Определение смешанного произведения трёх векторов, его свойства и геометрический смысл
Смешанным произведением трех векторов , ,  называется число, равное скалярному произведению вектора  на вектор : 

Геометрический смысл смешанного произведения

Геометрический смысл смешанного произведения: если тройка векторов  правая, то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: . В случае левой тройки  смешанное произведение указанных векторов равно объему параллелепипеда со знаком минус: . Если ,  и  компланарны, то их смешанное произведение равно нулю. Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах ,  и  равен модулю смешанного произведения этих векторов:

Объем пирамиды, построенной на этой тройке векторов равен

Свойства смешанного произведения:

1°     2°     3°    Три вектора компланарны тогда и только тогда, когда  4°    Тройка векторов является правой тогда и только тогда, когда . Если же , то векторы ,  и образуют левую тройку векторов. 5°     6°     7°     8°     9°     10°    Тождество Якоби:  Если векторы ,  и  заданы своими координатами, то их смешанное произведение вычисляется по формуле Пример Задание. Вычислить объем пирамиды, построенной на векторах , ,  Решение. Найдем смешанное произведение заданных векторов, для это составим определитель, по строкам которого запишем координаты векторов ,  и :

fizmatinf.blogspot.com

Лекция Векторное произведение векторов. Смешанное произведение векторов.

    Скачать с Depositfiles 

Лекция № 6. Тема 3 : Векторное произведение

3.1. Векторное произведение двух векторов и его основные свойства

Определение 1. Векторным произведением двух векторов  и  называется вектор , удовлетворяющий следующим условиям:

1. 

2. вектор  перпендикулярен векторам  и .

3. вектора      образуют правую тройку, т.е. из конца третьего вектора  кратчайший поворот от вектора  ко второму вектору  виден против часовой стрелки.

В противном случае тройка векторов называется левой.

 а) правая  б) левая

 

 

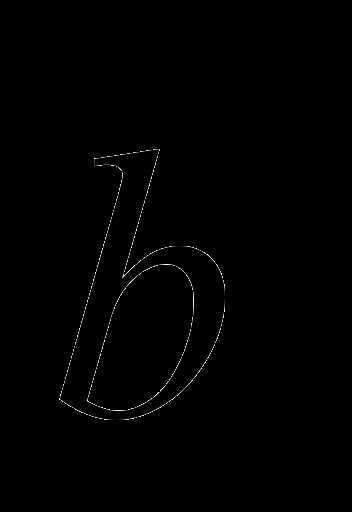
Обозначается векторное произведение: 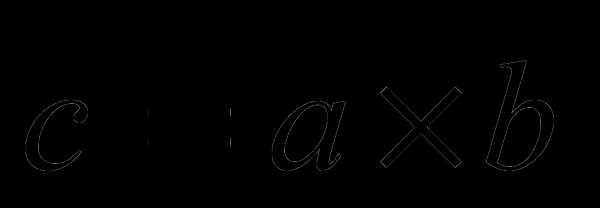 или 

Из определения векторного произведения следуют его свойства и геометрический смысл:

Модуль векторного произведения численно равен площади параллелограмма, построенного на этих векторах.

Основные свойства векторного произведения:

1.   векторное произведение антикоммутативно.

2. 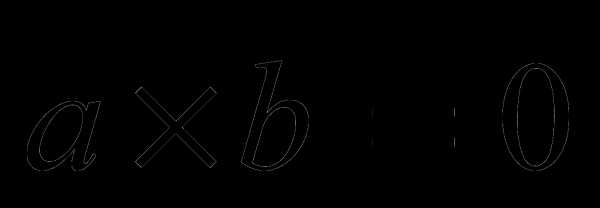, где , если  и 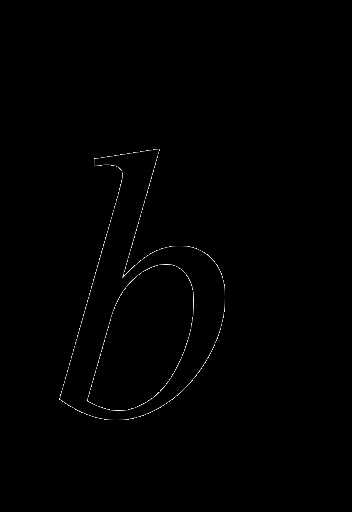 коллинеарные или по крайней мере один из сомножителей является нулевым вектором.

3. 

4. 

Замечание 1. Тройка базисных векторов  является правой.

3.2. Векторное произведение векторов, заданных своими координатами

Из определения векторного произведения следует, что:

 (1)

Тогда с учетом формул (1) и свойств векторного произведения получаем

 (2)

Пример 1. Заданы векторы  и 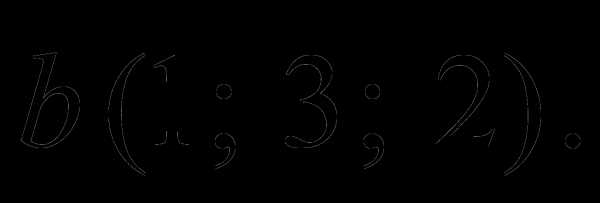 Найти площадь параллелограмма, построенного на этих векторах.

Исходя из геометрического смысла векторного произведения, получим

Тогда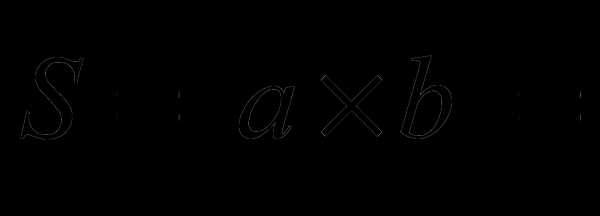 

Замечание 2. Площадь треугольника, построенного на векторах  и 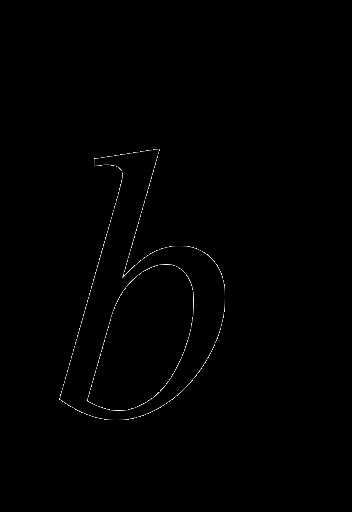 будет равна .

3.3.* Механический смысл векторного произведения

Если   радиус-вектор точки , к которой при-ложена сила , то момент этой силы относительно точки 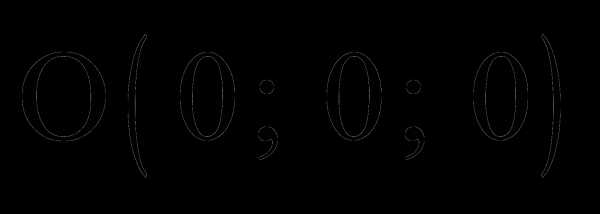вычисляется по формуле

 (3)

При этом   моменты силы 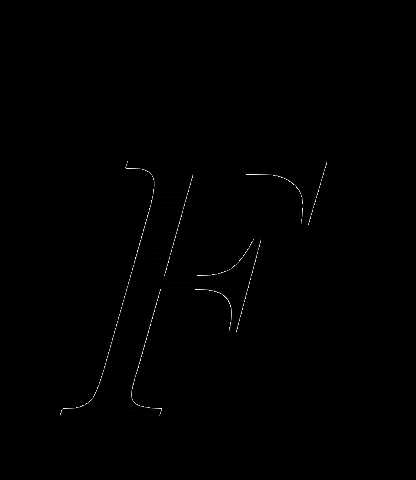 относительно координатных осей. z

Рассмотрим задачу из механики: 3 M

В точке  приложена сила 

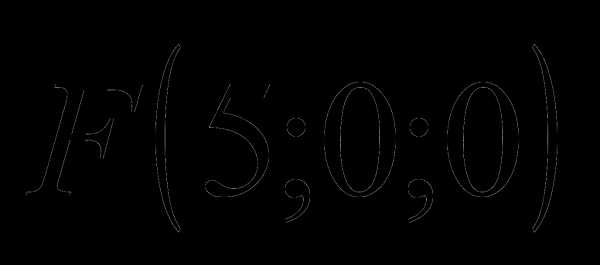. Требуется найти моменты

этой силы относительно координатных осей. 2 y

По формуле (3) получаем х

Полезно отметить тот факт, что значения этих моментов совпадают со школьным определением – «Момент равен произведению силы на плечо». См. рисунок!

Тема 4 : Смешанное произведение

4.1. Смешанное произведение и его основные свойства

Определение 2. Векторно–скалярное произведение 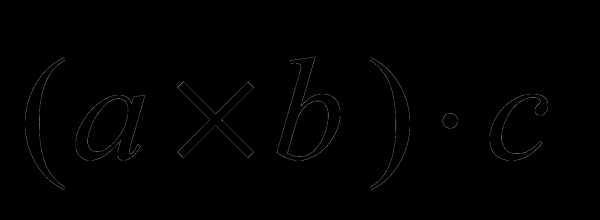 называется смешанным и обозначается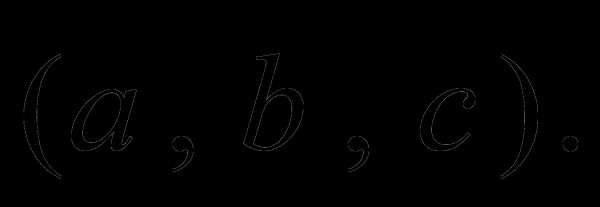 

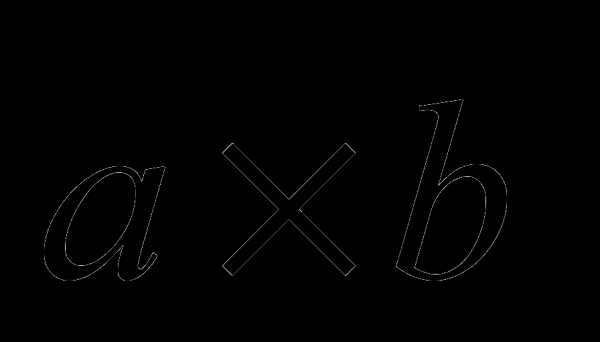
Рассмотрим его геометрический смысл.

Построим параллелепипед на векторах 

 Его объем равен  в 

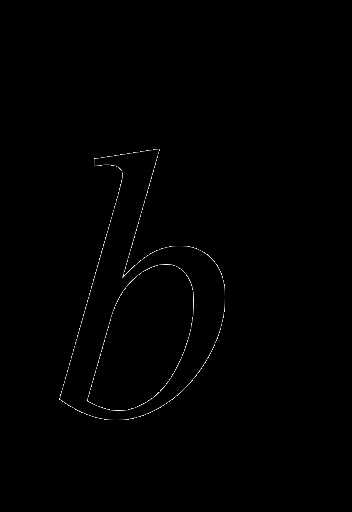
его основании лежит параллелограмм с  h

площадью  

Его высота  поэтому имеем 

 (4)

Знак в выражении 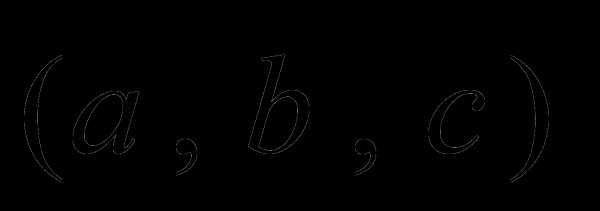 совпадает со знаком  и поэтому смешанное произведение положительно, если вектора 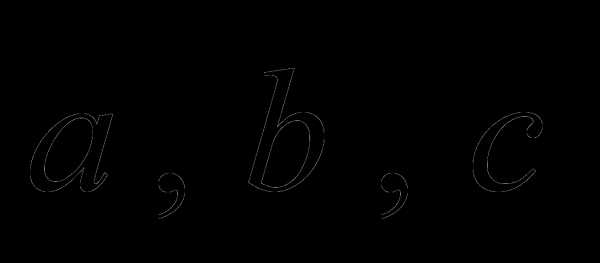 образуют правую тройку.

Таким образом, приходим к следующему правилу:

Смешанное произведение некомпланарных векторов 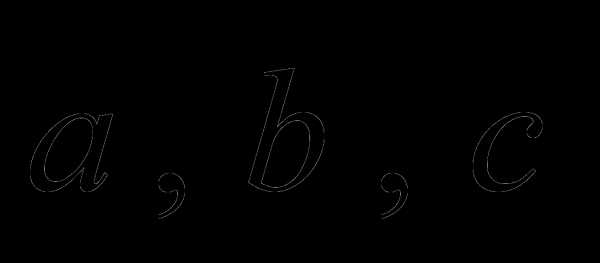 по модулю равно объёму параллелепипеда, построенного на этих векторах. Оно поло-жительно, если тройка векторов правая и отрицательно, если левая.

Рассмотрим основные свойства смешанного произведения:

1. Если смешанное произведение равно нулю, то векторы компланарны.

Верно и обратное, т.е., если сомножители компланарны, то смешанное произведение равно нулю.

Равенство  возможно в следую-щих случаях:

а) хотя бы один из векторов 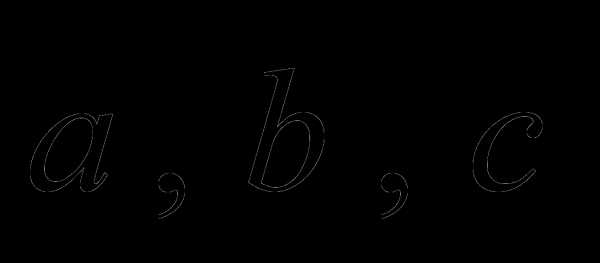 является нулевым, то векторы компланарны;

б)  и 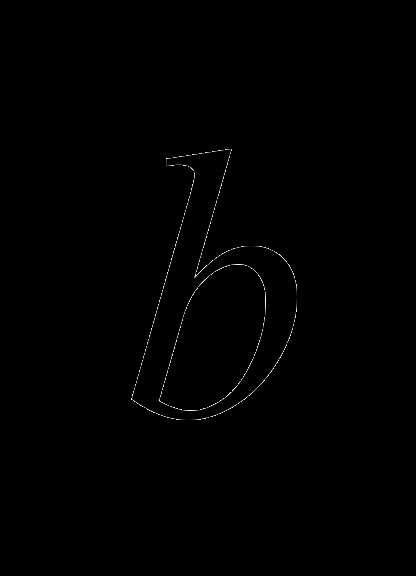 коллинеарны   компланарны;

в)   компланарны.

Аналогично доказывается обратное утверждение.

2. , т.е. при циклической перестановке сомножителей смешанное произведение знак не меняется. Это следует из того, что в данном случае ориентация тройки этих векторов сохраняется. В остальных случаях перестановки сомножителей ориентация векторов меняется и тогда

3.  где А и В константы.

Это свойство следует из свойств векторного и скалярного произведений.

4.2. Смешанное произведение векторов, заданных своими координатами

Пусть заданы векторы . Требуется найти их смешанное произведение.

Из определения скалярного и векторного произведений следует

Таким образом, получаем формулу

 

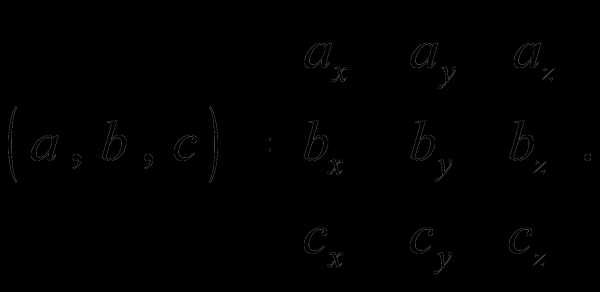 (5)

Пример 2: Проверить – лежат ли векторы , 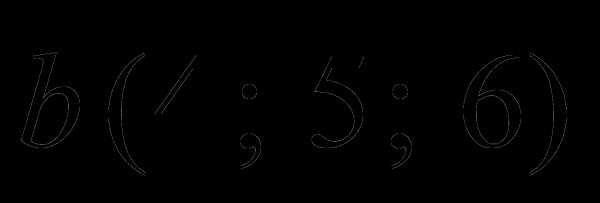 и  в одной плоскости, т.е. являются ли они компланарными.

По формуле смешанного произведения векторов имеем:

Поскольку , то данные векторы ,  и  лежат в одной плоскости, т.е. являются компланарными.

Пример 3. Пирамида задана координатами своих вершин   Найти высоту, проведённую из вершины D на грань АВС. D

Построим векторы 

 Н С

Из геометрии известно, что объем пирамиды равен трети произведения А площади основания  на ее высоту Н, т.е. В

, (6)

поскольку основанием пирамиды является треугольник (его площадь  равна половине площади параллелограмма 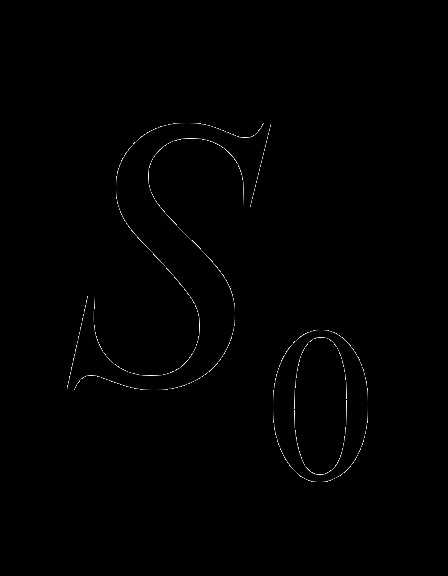), а высота пирамиды равна высоте соответствующего параллелепипеда.

Используя геометрический смысл смешанного произведения и форму-лы (5) и (6), получим

Из формулы (2) и геометрического смысла векторного произведения следуют

Снова воспользуемся известной из геометрии формулой

и тогда окончательно получим

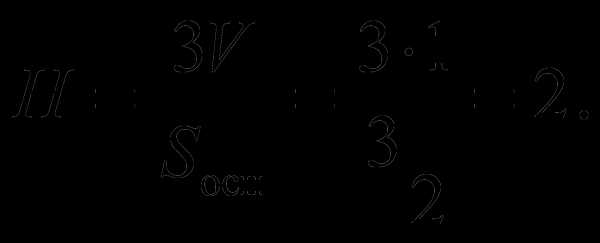
    Скачать с Depositfiles 

greleon.ru