Как графически решить уравнение? — Науколандия
Иногда уравнения решают графическим способом. Для этого надо преобразовать уравнение так (если оно уже не представлено в преобразованном виде), чтобы слева и справа от знака равенства стояли выражения, для которых легко можно нарисовать графики функций. Например, дано такое уравнение:
x² – 2x – 1 = 0
Если мы еще не изучали решение квадратных уравнений алгебраическим способом, то можем попробовать сделать это либо разложением на множители, либо графически. Чтобы решить подобное уравнение графически, представим его в таком виде:
x² = 2x + 1
Из такого представления уравнения следует, что требуется найти такие значения x, при которых левая часть будет равна правой.
Как известно, графиком функции y = x² является парабола, а y = 2x + 1 — прямая. Координата x точек координатной плоскости, лежащих как на первом графике, так и на втором (то есть точек пересечения графиков) как раз и являются теми значениями x, при которых левая часть уравнения будет равна правой. Другими словами, координаты x точек пересечения графиков являются корнями уравнения.
Графики могут пересекаться в нескольких точках, в одной точке, вообще не пересекаться. Отсюда следует, что уравнение может иметь несколько корней, или один корень, или вообще их не иметь.
Рассмотрим пример попроще:
x² – 2x = 0 или x² = 2x
Нарисуем графики функций y = x² и y = 2x: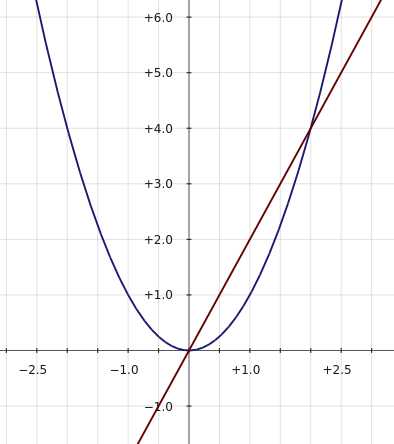
Как видно из чертежа, парабола и прямая пересекаются в точках (0; 0) и (2; 4). Координаты x этих точек соответственно равны 0 и 2. Значит, уравнение x² – 2x = 0 имеет два корня — x1 = 0, x2 = 2.
Проверим это, решив уравнение вынесением общего множителя за скобки:
x² – 2x = 0
x(x – 2) = 0
Ноль в правой части может получиться либо при x равном 0, либо 2.
Причина, по которой мы не стали графически решать уравнение x² – 2x – 1 = 0 в том, что в большинстве уравнений корнями являются вещественные (дробные) числа, а точно определить на графике значение x сложно. Поэтому для большинства уравнений графический способ решения не является лучшим. Однако знание этого способа дает более глубокое понимание связи между уравнениями и функциями.
scienceland.info
Решите графически уравнение
Иногда удобно решать уравнения графическим способом, то есть путем построения графика заданной кривой.
Прежде чем приниматься строить кривую, необходимо выполнить преобразования уравнения (если оно еще не преобразовано) в такой вид, для которого в левой и правой части уравнения будут стоять функции, которые можно легко построить на координатной плоскости.
Например, задано уравнение:
Преобразуем его следующим образом:
Теперь можно легко построить функцию и функцию .
Из такого вида уравнения вытекает, что необходимо найти те значения х, для которых левая часть уравнения будет равна правой части.
Искомыми значениями х будут те, при которых два данных графика будут пересекаться (точки пересечения графиков).
При решении графическим способом уравнений можно получить несколько вариантов: графики пересекаются в нескольких точках, не пересекаются вообще или пересекаются в одной точке.
Соответственно количеству точек пересечения будет и количество решений данного уравнения: несколько решений, ни одного решения или одно решение.
ru.solverbook.com
Как решать графические уравнения 🚩 Урок по математике для 9 класса «Графический способ решения 🚩 Образование 🚩 Другое
Пусть имеется полное квадратное уравнение: A*x2+B*x+C=0, где A, B и C — любые числа, причем A не равно нулю. Это общий случай квадратного уравнения. Существует также приведенный вид, в котором A=1. Чтобы решить графически любое уравнение, нужно перенести в другую часть слагаемое с наибольшей степенью и приравнять обе части к какой-либо переменной.
После этого в левой части уравнения останется A*x2, а в правой — B*x-C (можно предположить, что B — отрицательное число, сути это не меняет). Получится уравнение A*x2=B*x-C=y. Для наглядности в этом случае обе части приравнены к переменной y.
Теперь можно записать два уравнения: y=A*x2 и y=B*x-C. Далее необходимо построить график каждой из этих функций. График y=A*x2 представляет собой параболу с вершиной в начале координат, ветви которой направлены вверх или вниз, в зависимости от знака числа A. Если оно отрицательно, ветви направлены вниз, если положительно — вверх.
График y=B*x-C представляет собой обычную прямую линию. Если C=0, прямая проходит через начало координат. В общем случае она отсекает от оси ординат отрезок, равный С. Угол наклона этой прямой относительно оси абсцисс определяется коэффициентом B. Он равен тангенсу наклона этого угла.
После того как графики построены, будет видно, что они пересекутся в двух точках. Координаты этих точек по оси абсцисс определяют корни квадратного уравнения. Для их точного определения нужно четко строить графики и правильно выбрать масштаб.
Существует еще один способ графического решения квадратного уравнения. Необязательно переносить B*x+C в другую часть уравнения. Можно сразу построить график функции y=A*x2+B*x+C. Такой график представляет собой параболу с вершиной в произвольной точке. Этот способ сложнее предыдущего, зато можно построить только один график, чтобы решить уравнение.
Сначала нужно определить вершину параболы с координатами x0 и y0. Ее абсцисса вычисляется по формуле x0=-B/2*a. Для определения ординаты нужно подставить полученное значение абсциссы в исходную функцию. Математически это утверждение записывается так: y0=y(x0).
Затем требуется найти две точки, симметричные оси параболы. В них исходная функция должна обращаться в ноль. После этого можно строить параболу. Точки ее пересечения с осью Х дадут два корня квадратного уравнения.
www.kakprosto.ru
