cos п
Способов для вычисления значения выражения cos п достаточно, поэтому рассмотрим некоторые из них.
- По таблице значений косинуса
Один из самых простых способов — это использование таблицы, в которой собраны значения четырех основных тригонометрических функций от основных аргументов.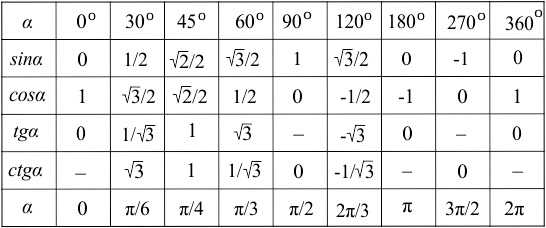
В таблице значения аргументов могут быть представлены в виде градусов или в виде радиан. Поскольку в задании аргументы даны в радианах, то по таблице найдем столбец, в котором находится значение Пи. В первом столбце обратим внимание на функции — нас интересует косинус. На пересечении этих двух данных получим результат — значение косинуса Пи.
Итак, косинус Пи согласно таблице равен —1:
- По тригонометрическому кругу
Можно вычислять значения тригонометрических функций по тригонометрическому кругу (или окружности).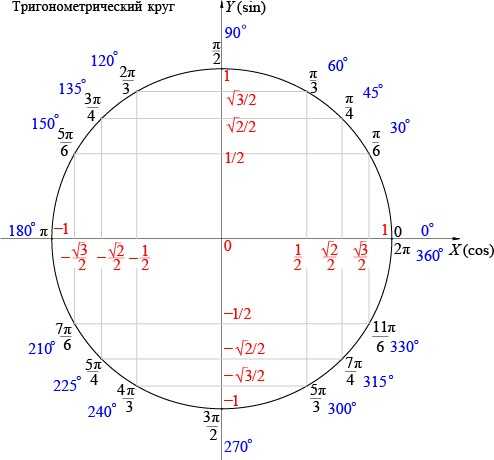
На осях круга содержаться значения двух тригонометрических функций: на оси Ох — значения косинусов, а на оси Оу — значения синусов.
Найдем на самой окружности значение, которое соответствует аргументу функции, то есть Пи. Число на оси Ох лежит в точке —1. Таким образом, косинус равен —1.
- По графику косинуса
Для основных углов удобно находить значения функций с помощью графика соответствующей функции.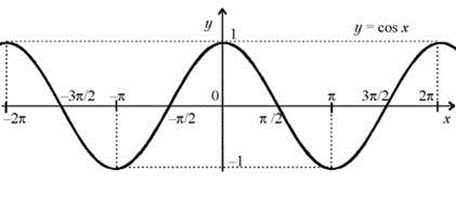
По косинусоиде (так называется график косинуса) отчетливо видно, что косинус равен —1.
ru.solverbook.com
cos п
Вы искали cos п? На нашем сайте вы можете получить ответ на любой математический вопрос. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и p cos, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «cos п».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как cos п,p cos,кос п 6,косинус 2п,косинус 2п 3,косинус п 2. На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и cos п. Просто введите задачу в окошко и нажмите «решить» здесь или введите в окно ввода ниже свой запрос (например, кос п 6).
Где можно решить любую задачу по математике, а так же cos п Онлайн?
Решить задачу cos п вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на этой странице.
www.pocketteacher.ru
cos (–pi)
Значение выражения cos (-pi) можно найти несколькими способами.
1-й способ.
Способ является самым простым из всех существующих, если у Вас под рукой есть таблица значений тригонометрических функций от основных углов.

Но перед использованием этой таблицы необходимо вспомнить и применить знание о том, что функция косинус является четной функцией, то есть косинус от отрицательного значения будет равен косинусу положительного значения того же угла:
А теперь можно воспользоваться таблицей и определить, что:
2-й способ.
Этот способ подойдет для тех, у кого нет возможности посмотреть в таблицу. Способ заключается в использовании тригонометрической окружности, с помощью которой можно определять значения и более сложных значений тригонометрических функций.
Посмотрим внимательно на тригонометрический круг. За значения косинуса отвечает ось абсцисс. Число совпадает с числом и на оси абсцисс совпадает с точкой —1. Следовательно, косинус от равен —1.
3-й способ.
Способ подойдет для тех, кто не умеет пользоваться тригонометрической окружностью, но помнит, как выглядит график косинуса.

На графике четко видно значение функции при .
ru.solverbook.com
cos 2п
Значение тригонометрической функции можно вычислить несколькими способами.
1-й способ.
Этот способ один из самых простых и распространенных. Для его использования необходима таблица значений тригонометрических функций от основных углов.
По таблице видно, что значение равно единице:
2-й способ.
Что делать, если такой таблицы под рукой нет? В таком случае пригодится второй способ, который заключается в использовании тригонометрического круга (или окружности). С ее помощью можно находить значения и других, более сложных значений тригонометрических функций.

Рассмотрим тригонометрический круг. Значения косинуса содержатся на оси абсцисс. Число совпадает с числом 0. Если спроецировать эту точку на ось абсцисс, то получим 1. Следовательно, косинус от равен 1.
3-й способ.
В случае, если нет под рукой таблицы или сложно ориентироваться по тригонометрической окружности, то можно использовать график косинуса.
Исходя из графика можно очень точно определить значение функции при . Для этого находим, в какой точке графика его аргумент равен и проецируем эту точку на ось ординат. Получаем значение 1.
ru.solverbook.com
cos (2п / 3)
Значение выражения cos (2п / 3) можно найти не одним способом. Рассмотрим основные.
Способ первый.
Этот способ — самый простой из существующих. Заключается в использовании таблицы значений тригонометрических функций от основных аргументов.

Часто перед использованием этой таблицы выполняется преобразование аргументов, представленных в радианах — в градусы. Бывает так легче понять значение функции косинус. Мы же используем таблицу, в которой можно определять значение тригонометрической функции как от аргумента в градусах, так и в радианах.
По таблице определим значение косинуса от 2Пи / 3 — это —1/2.
Математически записывается так:
Способ второй.
Его удобно использовать, когда нет таблицы. Способ использует для вычисления значения косинуса (или другой тригонометрической функции) тригонометрическую окружность.

При использовании тригонометрической окружности (или круга) необходимо помнить, что значения косинуса содержит ось абсцисс. Согласно заданию аргумент функции равен 2п / 3. На окружности данное значение соответствует 120 градусам. Чтобы вычислить значение функции косинус от этого аргумента нужно опустить перпендикуляр на ось абсцисс, после чего получим точку —1/2. Следовательно, косинус от 2п/3 равен —1/2.
Способ третий.
Если нет возможности посмотреть таблицу или использовать тригонометрическую окружность, то можно начертить график функции косинус. Необходимое значение можно определить по нему.

ru.solverbook.com
Ответы@Mail.Ru: cos 5п\6
корень из 3 делить на 2
cos(5п\6) = cos(п — п\6) = — cos(п\6) = — корень из 3 на 2 Я для таких вещей рисую окружность, помогает 🙂
Предыдущий ответ правильный, только он будет отрицателен (со знаком минус) я имела в виду первый ответ)touch.otvet.mail.ru
cos 2x = 1 – cos (п / 2 – x)
Задача.
Решить уравнение cos 2x = 1 — cos (п / 2 — x).
Решение.
Для того, чтобы решить данное уравнение его нужно преобразовать к более удобному виду. Начнем преобразование с правой части, в которой стоит косинус разности известного и неизвестного значений угла. В таком случае можно поступить двумя разными вариантами, которые приведут к одинаковым результатам. Первый вариант — использовать формулу косинуса разности, второй — формула приведения для косинуса разности п / 2 и неизвестного. Выберем второй вариант, поскольку он намного короче. Для этого по формуле приведения перейдем от косинуса к синусу:
Теперь разберемся с левой частью, в которой перейдем от косинуса двойного угла к синусу по формулам косинуса:
После перенесения всех слагаемых в одну сторону от знака равенства, получим:
Вынесем общий синус за скобки, тем самым сведя решение одного уравнения к решению двух простых равенств:
Полученное первое уравнение имеет решение в виде набора корней:
Полученное второе уравнение имеет следующее решение:
Переменные q и f — это любые целые числа.
Ответ. и , q и f —любые целые числа.
ru.solverbook.com
