Цпт что такое – ЦПТ — это… Что такое ЦПТ?

Центральная предельная теорема | Data Science

Практика изучения случайных явлений показывает, что хотя результаты отдельных наблюдений, даже проведенных в одинаковых условиях, могут сильно отличаться, в то же время средние результаты для достаточно большого числа наблюдений устойчивы и слабо зависят от результатов отдельных наблюдений. Теоретическим обоснованием этого замечательного свойства случайных явлений является закон больших чисел. Общий смысл закона больших чисел — совместное действие большого числа случайных факторов приводит к результату, почти не зависящему от случая.

Центральная предельная теорема

Теорема Ляпунова объясняет широкое распространение нормального закона распределения и поясняет механизм его образования. Теорема позволяет утверждать, что всегда, когда случайная величина образуется в результате сложения большого числа независимых случайных величин, дисперсии которых малы по сравнению с дисперсией суммы, закон распределения этой случайной величины оказывается практически нормальным законом. А поскольку случайные величины всегда порождаются бесконечным количеством причин и чаще всего ни одна из них не имеет дисперсии, сравнимой с дисперсией самой случайной величины, то большинство встречающихся в практике случайных величин подчинено нормальному закону распределения. (Источник)

Итак, нормальное распределение — наиболее распространенное в природе распределение непрерывных величин. Математическим обоснованием этого факта служит центральная предельная теорема:

Сумма большого числа как угодно распределенных независимых случайных величин распределена асимптотически нормально, если только слагаемые вносят равномерно малый вклад в сумму.

Это значит, что чем больше независимых слагаемых в сумме, тем ближе закон ее распределения к нормальному. Вместо суммы часто рассматривают среднее арифметическое большого числа случайных величин, оно отличается от суммы только множителем (1/n) , поэтому его распределение также стремится к нормальному с ростом числа n суммируемых величин. Поскольку случайные величины, с которыми мы сталкиваемся, например, при измерениях, есть результат действия множества независимых факторов, понятно, почему измеряемые значения, как правило, распределены нормально.

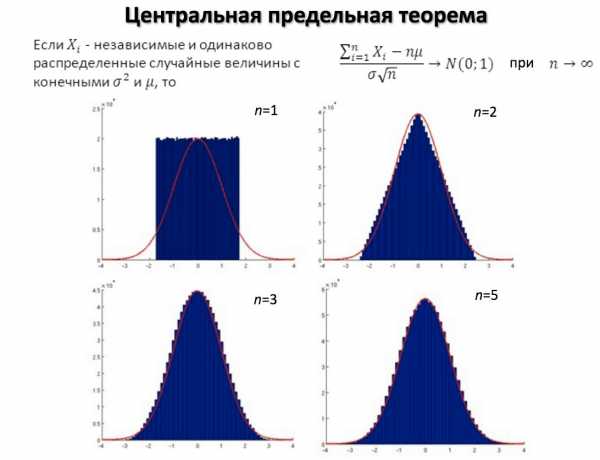
Следствием центральной предельной теоремы является широко применяемая при решении задач теорема Муавра-Лапласа.

Дополнительные тезисы:

• Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный. Но в среднем при грубом предположении распределение считают нормальным при n>=30.

• Закон больших чисел лежит в основе различных видов страхования (страхование жизни человека на всевозможные сроки, имущества, скота, посевов и др.).

• При планировании ассортимента товаров широкого потребления учитывается спрос на них населения. В этом спросе проявляется действие закона больших чисел.

• Широко применяемый в статистике выборочный метод находит свое научное обоснование в законе больших чисел. Например, о качестве привезенной из колхоза на заготовительный пункт пшеницы судят по качеству зерен, случайно захваченных в небольшую мерку. Зерна в мерке немного по сравнению со всей партией, но во всяком случае мерку выбирают такой, чтобы зерен в ней было вполне достаточно для проявления закона больших чисел с точностью, удовлетворяющей потребности. Мы вправе принять за показатели засоренности, влажности и среднего веса зерен всей партии поступившего зерна соответствующие показатели в выборке. (Источник)

datascientist.one

4. Центральная предельная теорема

Центральная предельная теорема (ЦПТ) представляет собой вторую группу предельных теорем, которые устанавливают связь между законом распределения суммы случайных величин и его предельной формой –нормальным законом распределения.

До сих пор мы часто говорили об устойчивости средних характеристик большого числа испытаний, говоря точнее, об устойчивости сумм вида

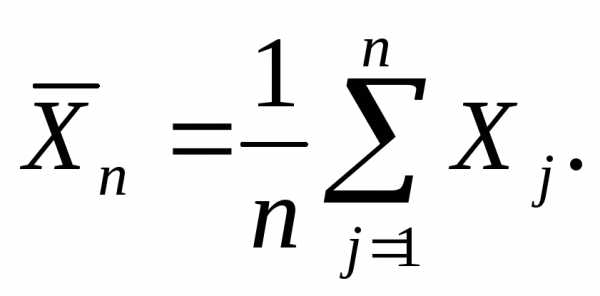
Однако следует обратить внимание, что величина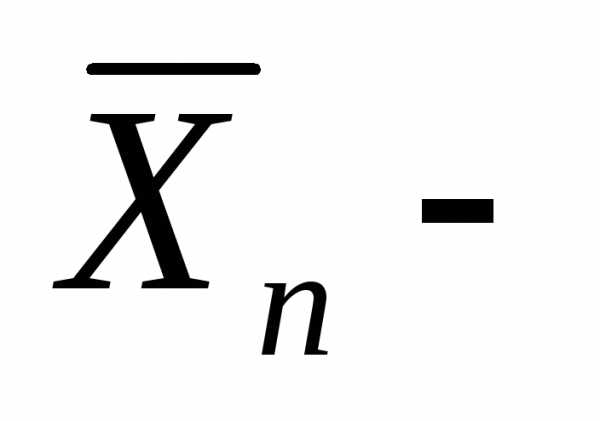случайная, а значить, она имеет некоторый закон распределения. Оказывается этот замечательный факт, составляет содержание

другой группы теорем, объединяемых под общим названием

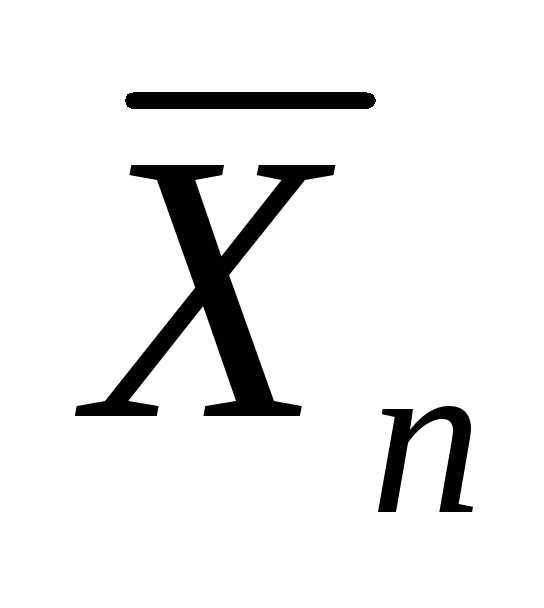центральная предельнаятеорема, что при досточно общих условиях закон распределенияблизок к нормальному закону.

Поскольку величина 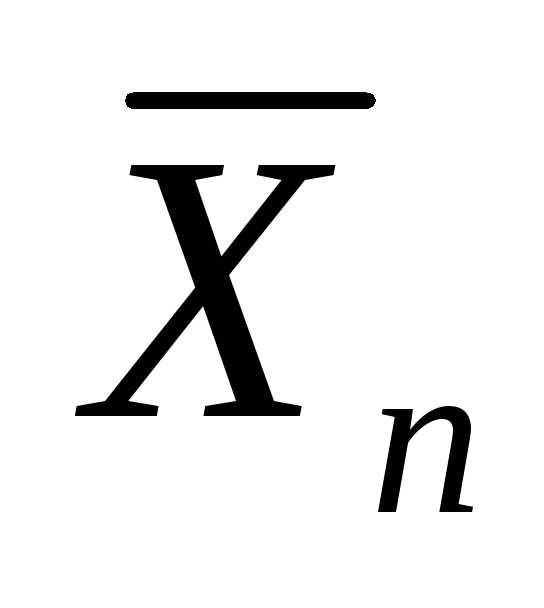отличается от суммы

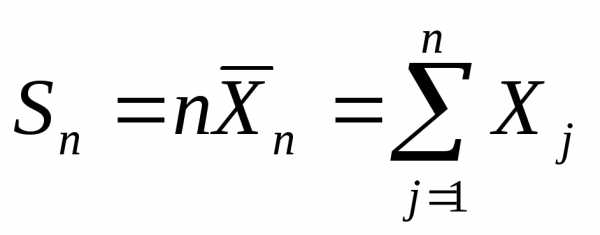
лишь постоянным множителем 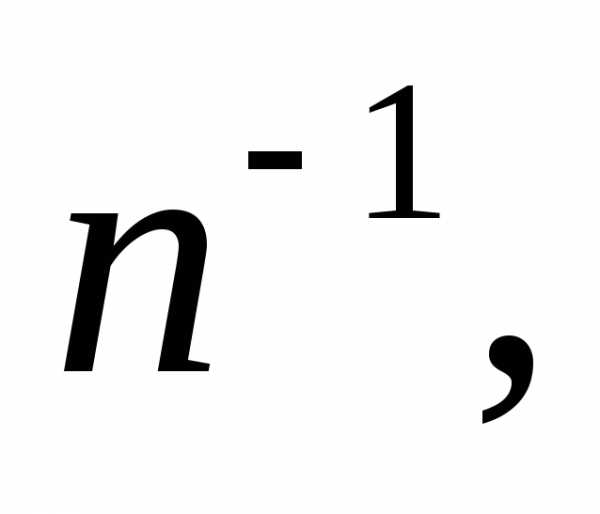то в общих чертах содержание ЦПТ может быть сформулировано следующим образом.

Распределение суммы большого числа независимых случайных величин при весьма

общих условиях близко к нормальному закону распределению.

Известно, что нормально распределенные случайные величины широко распространены на практике (не только в теории вероятностей, но и в её многочисленных приложениях). Чем такое явление объясняется? Ответ на такой «феномен» впервые был дан выдающимся русским математиком А.М. Ляпуновым в 1901году: «Центральная предельная теорема Ляпунова». Ответ Ляпунова заключается в его условии, при которых справедливо ЦПТ (см. далее).

В целях подготовки точной формулировки ЦПТ, поставим перед собой два вопроса:

1. Какой точный смысл содержит в себе утверждение о том, что «закон распределения суммы 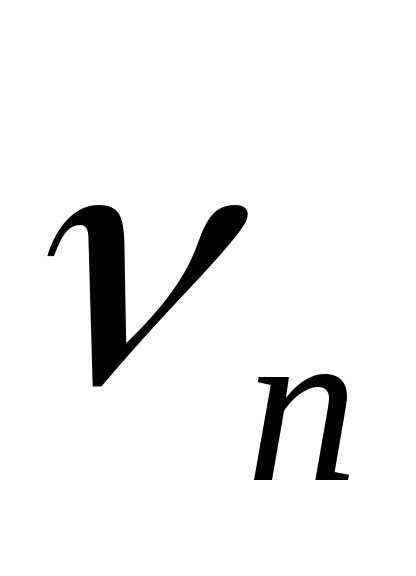«близка» к нормальному закону?».

2. При каких условиях справедлива эта близость?

Чтобы ответить на эти вопросы, рассмотрим бесконечную последовательность случайных величин: Составим «частичные суммы» нашей последовательности с.в.

(23)

От каждой случайных величин 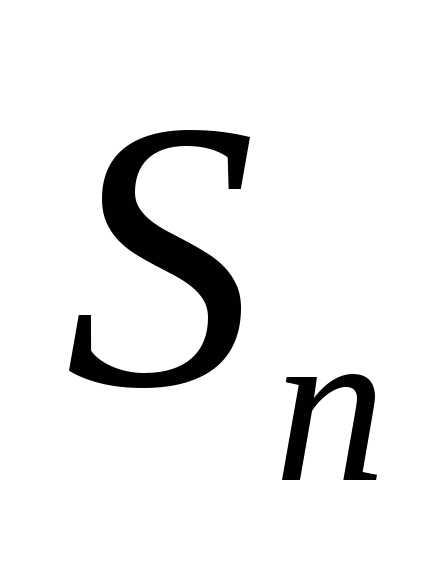перейдём к «нормированной» случайной величине

(24)

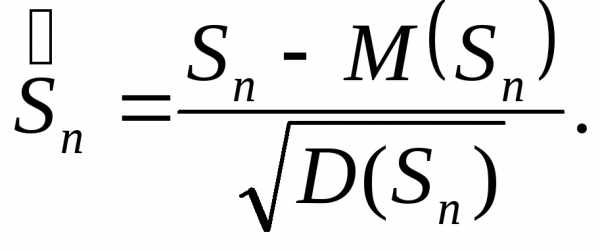
Нами было установлено (см.Т.8., п.3, равенства (19)), что .

Ответ на первый вопрос теперь можно сформулировать в виду предельного равенства

(25) , (,

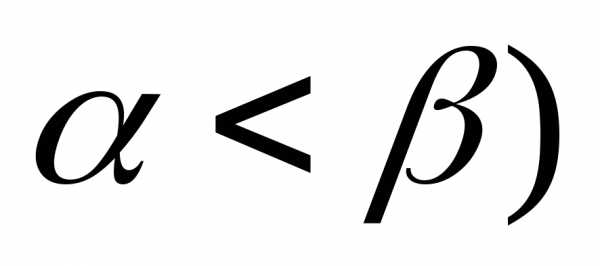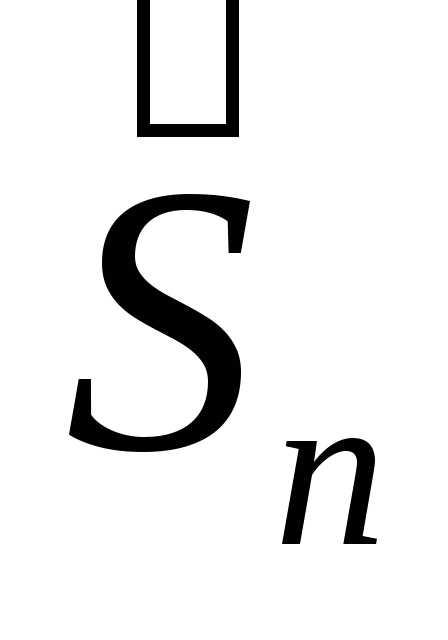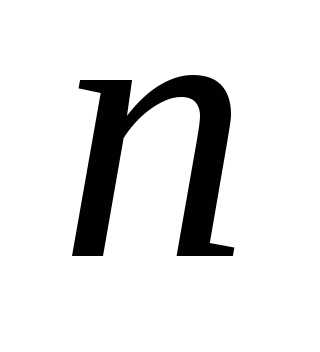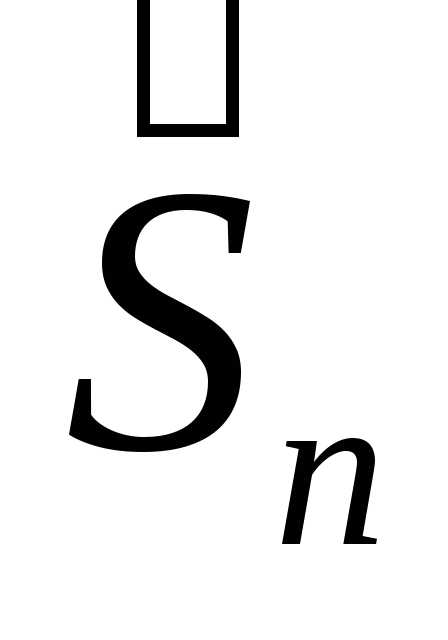означающего, что закон распределения с.в. с ростомприближается к нормальному закону с. Разумеется, из того факта, что величинаимеет приближенно нормальное распределение, следует, что и величина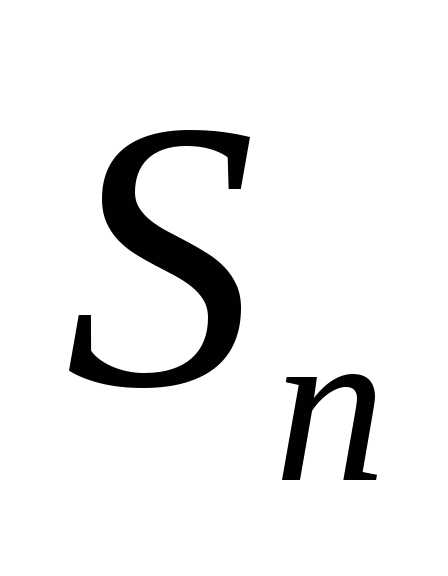распределена приближенно нормально,

или

(26)

— формула для определения вероятности того, что сумма нескольких с.в. окажется в заданных пределах. Часто ЦПТ используют при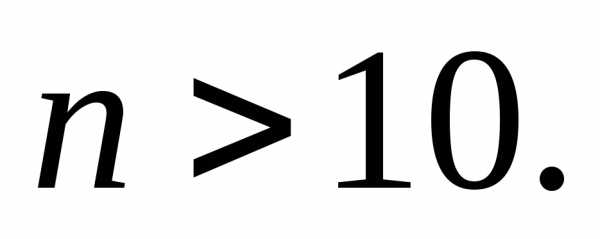

По поводу условий, которые следует наложить на величины можно высказать следующие соображения. Рассмотрим разностьПолучим отклонение с.в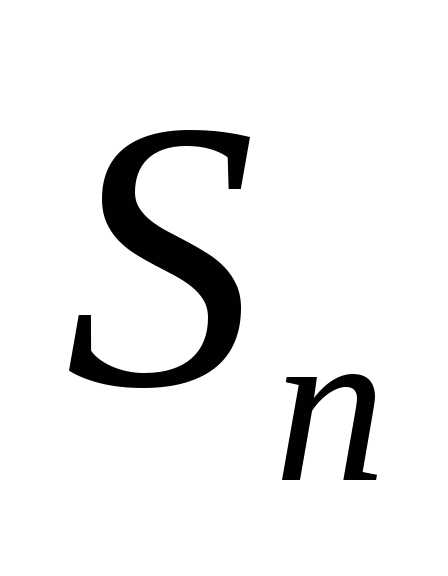от её математического ожидания. Общий смысл накладываемых условий, на величинызаключается в том, что отдельные отклонениядолжны быть равномерно малы по сравнению с суммарным отклонениемТочную формулировку этих условий, при которых справедливо предельное соотношение дал М.А. Ляпунов в 1901 году. Она заключается в следующем.

Пусть для каждой из величин числаконечны, (заметим, что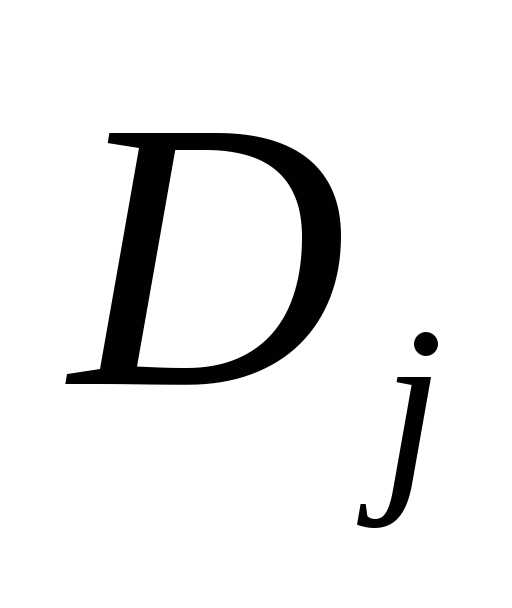есть дисперсия с.в.— «

центральный момент третьего порядка»).

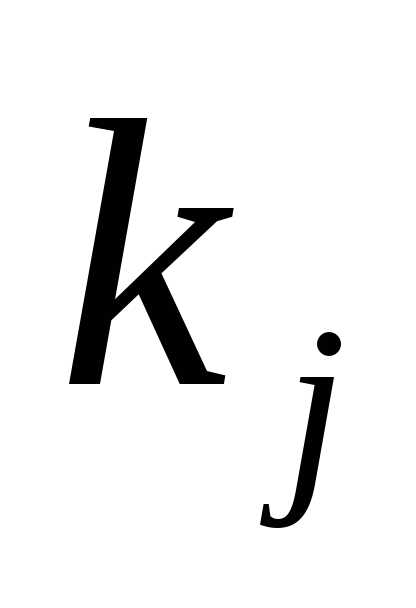Если при

,

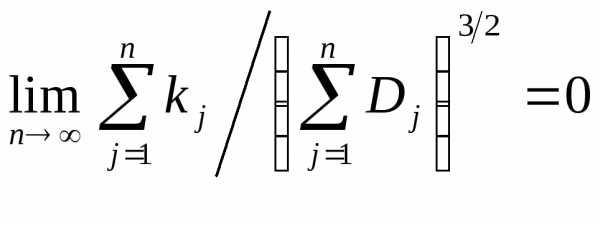то будем говорить, что последовательность 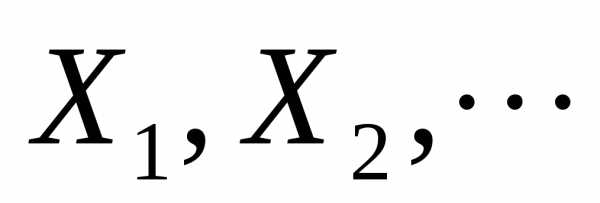удовлетворяетусловию Ляпунова.

В частности, ЦПТ для случаев, когда в сумме случайных величин каждый слагаемый имеет одинаковое распределение, т.е. все ито условие Ляпунова выполняется

Именно, на практике такой случай ЦПТ чаще всего используется. Потому, что в математической статистике любая случайная выборка с.в. имеют одинаковые распределения, поскольку «выборки» получены из одной и той же генеральной совокупности.

Сформулируем этот случай как отдельное утверждение ЦПТ.

Теорема 10.7 (ЦПТ). Пусть случайные величины независимы, одинаковораспределены, имеют конечные математическое ожидание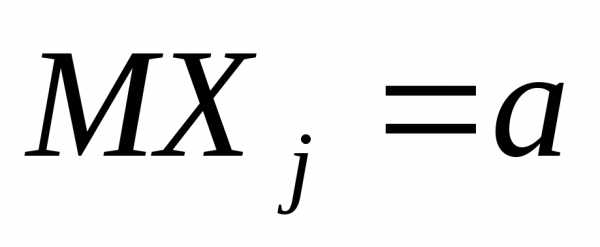

и дисперсию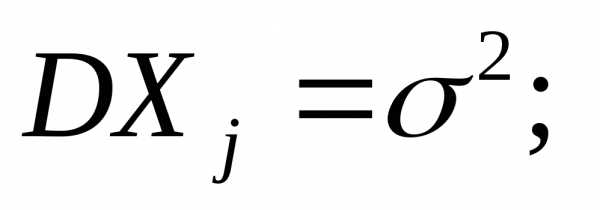

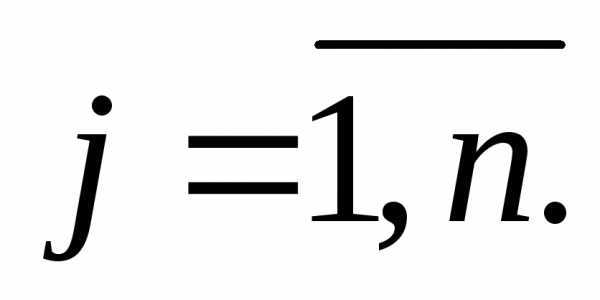
Тогда функция распределения центрированной и нормированной суммы этих с.в. при стремится к функции распределения стандартной нормальной случайной величины:

(27)

где

На этом частном случае хорошо осмыслить, в чем находит своё проявление равномерная «малость» слагаемых, где величина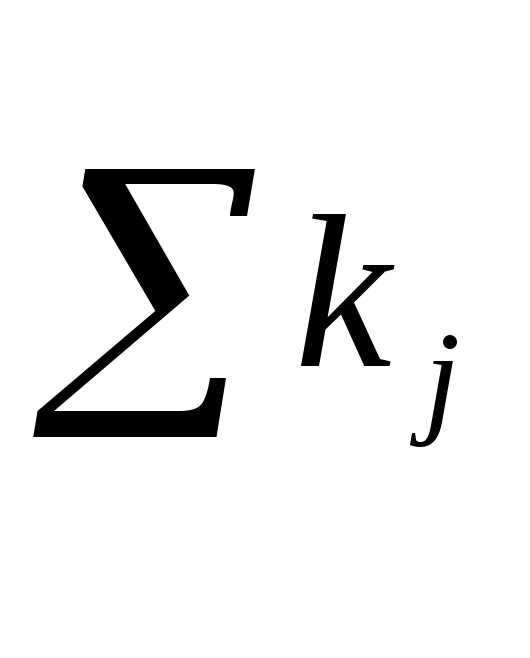имеет порядок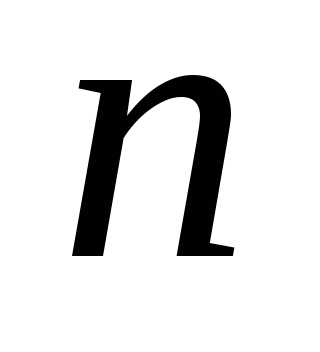, а величина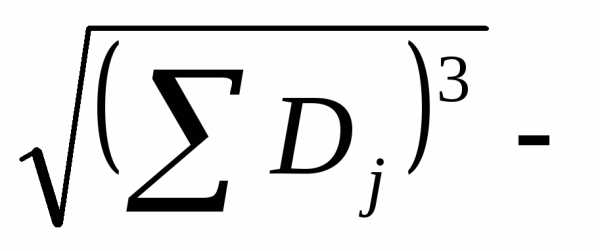порядок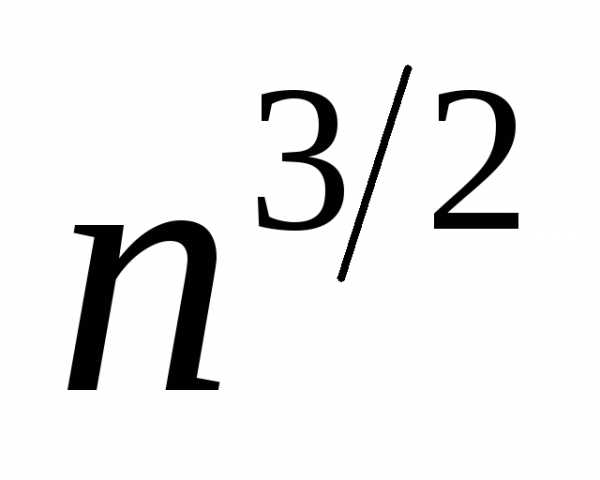, тем самым отношение первой величины ко второй стремится, к 0.

Теперь мы в состоянии сформулировать центральную предельную теорему в форме А.М. Ляпунова.

Теорема 10.8. (Ляпунова). Если последовательность 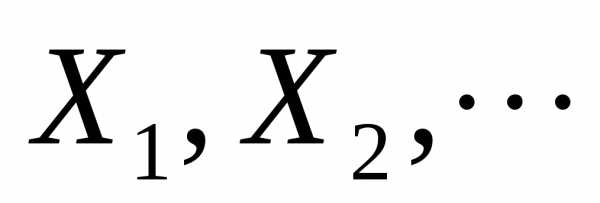независимых случайных величин удовлетворяет условию Ляпунова, то справедливо предельное соотношение

(28) ,

для любых и, при этом (.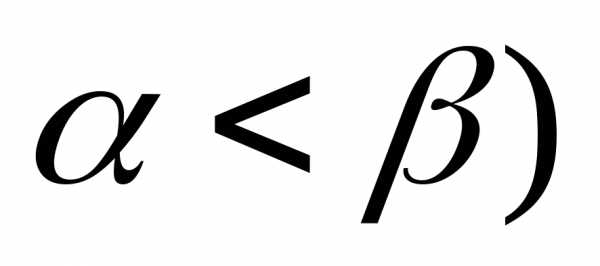

Иными словами, в этом случае закон распределения нормированной суммы 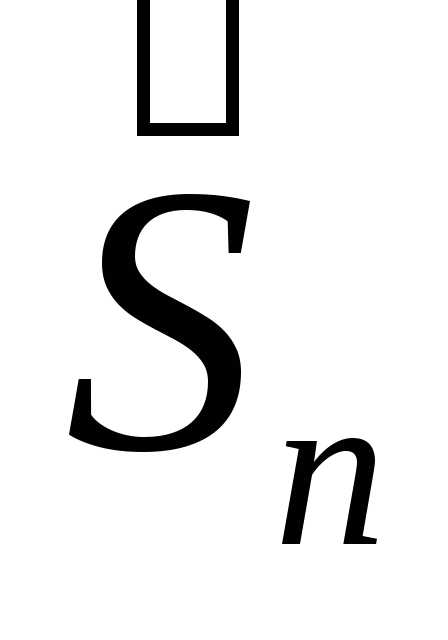сходится к нормальному закону с параметрами

Следует отметить, что для доказательства ЦПТ А.М. Ляпунов разработал специальный метод, основанный на теорию так называемых характеристических функций. Этот метод оказался весьма полезным и в других разделах математики (см. доказательство ЦПТ например в кн. Бородин […] ). В этой книге мы, о производящих функциях будем давать краткую информацию и некоторые применения к подсчёту числовых характеристик случайных величин.

Краткие сведения об ошибке измерений. Известно, что при повторении измерений одного и того же объекта, выполненными одним и тем же измерительным прибором с одинаковой тщательностью (при одинаковых условиях) не всегда достигаются одинаковые результаты. Разброс результатов измерения вызван тем, что на процесс измерения влияют многочисленные факторы, которые не возможно и не целесообразно учитывать. В этой ситуации ошибку, возникающую при измерении интересующей нас величины часто можно рассматривать как сумму большого числа независимых между собой слагаемых, каждое из которых даёт лишь незначительный вклад в образование всей суммы. Но такие случаи приводят нас как раз к условиям применимости теоремы Ляпунова и можно ожидать, что распределение ошибки измеряемой величины мало отличается от нормального распределения.

В более общем случае, ошибка является функцией большого числа случайных аргументов, каждый из которых лишь немного отличается от своего математического ожидания. Линеаризуя эту функцию, то есть, заменяя её линейной, опять приходят к предыдущему случаю. Накопленный опыт по статистической обработке результатов измерений действительно подтверждает этот факт в большинстве практических случаев.

Аналогичные рассуждения объясняют появление нормального распределения в отклонениях параметров, определяющих выпущенную готовую продукцию (изделия), от нормативных значений при массовом производстве.

Рассмотрим следующий пример.

Пример 5. Независимые случайные величины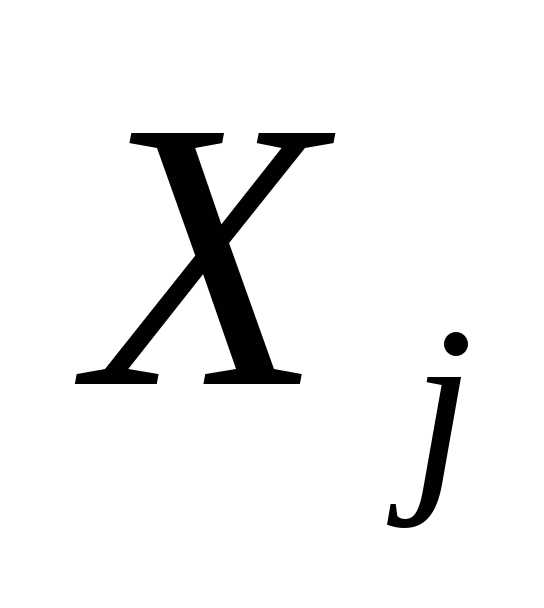распределены равномерно на отрезке [0,1]. Найти закон распределения с.в.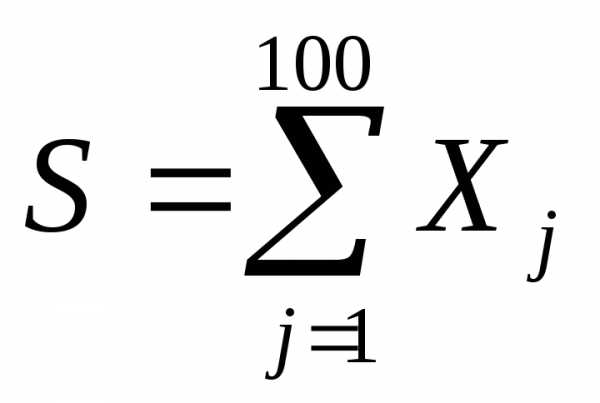, а также вероятность того, что

Решение.Условия ЦПТ соблюдается, поэтому с.в.имеет приближенно плотность распределения

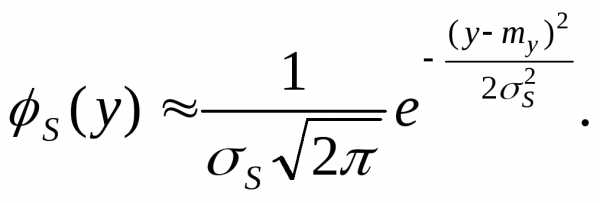
По известным формулам для м.о. и дисперсии в случае равномерного распределения находим: Тогда

.

Поэтому

На основании формулы (26), находим (с учётом табличных значений функции Лапласа)

studfiles.net

ЦПТ — это… Что такое ЦПТ?

ЦПТ — ТЦП ЦТП центральный тепловой пункт; тепловой центральный пункт энерг. ЦТП Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ЦПТ центральная предельная теорема ЦПТ Ц …   Словарь сокращений и аббревиатур

ТЦП — ЦПТ ТЦП ЦТП центральный тепловой пункт; тепловой центральный пункт энерг. ЦТП Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ТЦП Тойота центр Приморский авто, организация, Санкт Петербург… …   Словарь сокращений и аббревиатур

центра и периферии теория — (ЦПТ), создана для описания пространственных отношений между территориями (странами и районами), находящимися на разных стадиях социально экономического развития. По Дж. Фридману, ЦПТ применима для национального и глобального уровней. Для… …   Географическая энциклопедия

Бунин, Игорь Михайлович — Игорь Михайлович Бунин Игорь Бунин в феврале 2012 года Дата рожден …   Википедия

Бунин, Игорь — Игорь Михайлович Бунин (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

Бунин И. М. — Игорь Михайлович Бунин (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

Бунин Игорь — Игорь Михайлович Бунин (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

Бунин Игорь Михайлович — Игорь Михайлович Бунин (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

Игорь Бунин — Игорь Михайлович Бунин (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

Игорь Михайлович Бунин — (лтш. Igors Buņins; родился 25 февраля 1946 в городе Рига)  российский политолог. Содержание 1 Образование 2 Научная деятельность 3 Политтехнолог …   Википедия

abbr_rus.academic.ru

4. Центральная предельная теорема

Центральная предельная теорема (ЦПТ) представляет собой вторую группу предельных теорем, которые устанавливают связь между законом распределения суммы случайных величин и его предельной формой –нормальным законом распределения.

До сих пор мы часто говорили об устойчивости средних характеристик большого числа испытаний, говоря точнее, об устойчивости сумм вида

Однако следует обратить внимание, что величинаслучайная, а значить, она имеет некоторый закон распределения. Оказывается этот замечательный факт, составляет содержание

другой группы теорем, объединяемых под общим названием центральная предельнаятеорема, что при досточно общих условиях закон распределенияблизок к нормальному закону.

Поскольку величина отличается от суммы

лишь постоянным множителем то в общих чертах содержание ЦПТ может быть сформулировано следующим образом.

Распределение суммы большого числа независимых случайных величин при весьма

общих условиях близко к нормальному закону распределению.

Известно, что нормально распределенные случайные величины широко распространены на практике (не только в теории вероятностей, но и в её многочисленных приложениях). Чем такое явление объясняется? Ответ на такой «феномен» впервые был дан выдающимся русским математиком А.М. Ляпуновым в 1901году: «Центральная предельная теорема Ляпунова». Ответ Ляпунова заключается в его условии, при которых справедливо ЦПТ (см. далее).

В целях подготовки точной формулировки ЦПТ, поставим перед собой два вопроса:

1. Какой точный смысл содержит в себе утверждение о том, что «закон распределения суммы «близка» к нормальному закону?».

2. При каких условиях справедлива эта близость?

Чтобы ответить на эти вопросы, рассмотрим бесконечную последовательность случайных величин: Составим «частичные суммы» нашей последовательности с.в.

(23)

От каждой случайных величин перейдём к «нормированной» случайной величине

(24)

Нами было установлено (см.Т.8., п.3, равенства (19)), что .

Ответ на первый вопрос теперь можно сформулировать в виду предельного равенства

(25) , (,

означающего, что закон распределения с.в. с ростомприближается к нормальному закону с. Разумеется, из того факта, что величинаимеет приближенно нормальное распределение, следует, что и величинараспределена приближенно нормально,

или

(26)

— формула для определения вероятности того, что сумма нескольких с.в. окажется в заданных пределах. Часто ЦПТ используют при

По поводу условий, которые следует наложить на величины можно высказать следующие соображения. Рассмотрим разностьПолучим отклонение с.вот её математического ожидания. Общий смысл накладываемых условий, на величинызаключается в том, что отдельные отклонениядолжны быть равномерно малы по сравнению с суммарным отклонениемТочную формулировку этих условий, при которых справедливо предельное соотношение дал М.А. Ляпунов в 1901 году. Она заключается в следующем.

Пусть для каждой из величин числаконечны, (заметим, чтоесть дисперсия с.в.- «центральный момент третьего порядка»).

Если при

,

то будем говорить, что последовательность удовлетворяетусловию Ляпунова.

В частности, ЦПТ для случаев, когда в сумме случайных величин каждый слагаемый имеет одинаковое распределение, т.е. все ито условие Ляпунова выполняется

Именно, на практике такой случай ЦПТ чаще всего используется. Потому, что в математической статистике любая случайная выборка с.в. имеют одинаковые распределения, поскольку «выборки» получены из одной и той же генеральной совокупности.

Сформулируем этот случай как отдельное утверждение ЦПТ.

Теорема 10.7 (ЦПТ). Пусть случайные величины независимы, одинаковораспределены, имеют конечные математическое ожидание и дисперсию

Тогда функция распределения центрированной и нормированной суммы этих с.в. при стремится к функции распределения стандартной нормальной случайной величины:

(27)

где

На этом частном случае хорошо осмыслить, в чем находит своё проявление равномерная «малость» слагаемых, где величинаимеет порядок, а величинапорядок, тем самым отношение первой величины ко второй стремится, к 0.

Теперь мы в состоянии сформулировать центральную предельную теорему в форме А.М. Ляпунова.

Теорема 10.8. (Ляпунова). Если последовательность независимых случайных величин удовлетворяет условию Ляпунова, то справедливо предельное соотношение

(28) ,

для любых и, при этом (.

Иными словами, в этом случае закон распределения нормированной суммы сходится к нормальному закону с параметрами

Следует отметить, что для доказательства ЦПТ А.М. Ляпунов разработал специальный метод, основанный на теорию так называемых характеристических функций. Этот метод оказался весьма полезным и в других разделах математики (см. доказательство ЦПТ например в кн. Бородин […] ). В этой книге мы, о производящих функциях будем давать краткую информацию и некоторые применения к подсчёту числовых характеристик случайных величин.

Краткие сведения об ошибке измерений. Известно, что при повторении измерений одного и того же объекта, выполненными одним и тем же измерительным прибором с одинаковой тщательностью (при одинаковых условиях) не всегда достигаются одинаковые результаты. Разброс результатов измерения вызван тем, что на процесс измерения влияют многочисленные факторы, которые не возможно и не целесообразно учитывать. В этой ситуации ошибку, возникающую при измерении интересующей нас величины часто можно рассматривать как сумму большого числа независимых между собой слагаемых, каждое из которых даёт лишь незначительный вклад в образование всей суммы. Но такие случаи приводят нас как раз к условиям применимости теоремы Ляпунова и можно ожидать, что распределение ошибки измеряемой величины мало отличается от нормального распределения.

В более общем случае, ошибка является функцией большого числа случайных аргументов, каждый из которых лишь немного отличается от своего математического ожидания. Линеаризуя эту функцию, то есть, заменяя её линейной, опять приходят к предыдущему случаю. Накопленный опыт по статистической обработке результатов измерений действительно подтверждает этот факт в большинстве практических случаев.

Аналогичные рассуждения объясняют появление нормального распределения в отклонениях параметров, определяющих выпущенную готовую продукцию (изделия), от нормативных значений при массовом производстве.

Рассмотрим следующий пример.

Пример 5. Независимые случайные величиныраспределены равномерно на отрезке [0,1]. Найти закон распределения с.в., а также вероятность того, что

Решение.Условия ЦПТ соблюдается, поэтому с.в.имеет приближенно плотность распределения

По известным формулам для м.о. и дисперсии в случае равномерного распределения находим: Тогда

.

Поэтому

На основании формулы (26), находим (с учётом табличных значений функции Лапласа)

studfiles.net

Центральная предельная теорема — это… Что такое Центральная предельная теорема?

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 15 мая 2011.

Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что совокупность достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

Так как многие случайные величины в приложениях формируются под влиянием нескольких слабо зависимых случайных факторов, их распределение считают нормальным. При этом должно соблюдаться условие, что ни один из факторов не является доминирующим. Центральные предельные теоремы в этих случаях обосновывают применение нормального распределения.

Классическая формулировка Ц.П.Т.

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние и , соответственно. Пусть также

.

Тогда

по распределению при ,

где — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом выборочное среднее первых величин, то есть , мы можем переписать результат центральной предельной теоремы в следующем виде:

по распределению при .

Скорость сходимости можно оценить с помощью неравенства Берри-Эссеена.

Замечания

Локальная Ц.П.Т.

В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение также абсолютно непрерывно, и более того,

при ,

где — плотность случайной величины , а в правой части стоит плотность стандартного нормального распределения.

Некоторые обобщения

Результат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.

Ц.П.Т. Линдеберга

Пусть независимые случайные величины определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: . Как и прежде построим частичные суммы . Тогда в частности, . Наконец, пусть выполняется условие Линдеберга:

Тогда

по распределению при .

Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины имеют конечный третий момент. Тогда определена последовательность

. Если предел

(условие Ляпунова),

то

по распределению при .

Ц.П.Т. для мартингалов

Пусть процесс является мартингалом с ограниченными приращениями. В частности, допустим, что

и приращения равномерно ограничены, т.е.

п.н.

Введём случайные процессы и следующим образом:

и

.

Тогда

по распределению при .

См. также

Ссылки

dic.academic.ru

Центральная предельная теорема Ляпунова — это… Что такое Центральная предельная теорема Ляпунова?



Центральная предельная теорема Ляпунова

Центра́льные преде́льные теоре́мы (Ц.П.Т.) — класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях являются суммами нескольких случайных факторов, центральные предельные теоремы обосновывают популярность нормального распределения.

Классическая формулировка Ц.П.Т.

Пусть есть бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию. Обозначим последние μ и σ², соответственно. Пусть . Тогда

по распределению при ,

где N(0,1) — нормальное распределение с нулевым математическим ожиданием и стандартным отклонением, равным единице. Обозначив символом выборочное среднее первых n величин, то есть , мы можем переписать результат центральной предельной теоремы в следующем виде:

по распределению при .

Замечания

• Неформально говоря, классическая центральная предельная теорема утверждает, что сумма n независимых одинаково распределённых случайных величин имеет распределение, близкое к N(nμ,nσ²). Эквивалентно, имеет распределение близкое к N(μ,σ² / n).
• Так как функция распределения стандартного нормального распределения непрерывна, сходимость к этому распределению эквивалентна поточечной сходимости функций распределения к функции распределения стандартного нормального распределения. Положив , получаем , где Φ(x) — функция распределения стандартного нормального распределения.
• Центральная предельная теорема в классической формулировке доказывается методом характеристических функций (теорема Леви о непрерывности).
• Вообще говоря, из сходимости функций распределения не вытекает сходимость плотностей. Тем не менее в данном классическом случае имеет место

Локальная Ц.П.Т.

В предположениях классической формулировки, допустим в дополнение, что распределение случайных величин абсолютно непрерывно, то есть оно имеет плотность. Тогда распределение Z_n также абсолютно непрерывно, и более того,

при ,

где — плотность случайной величины Z_n, а в правой части стоит плотность стандартного нормального распределения.

Некоторые обобщения

Результат классической центральной предельной теоремы справедлив для ситуаций гораздо более общих, чем полная независимость и одинаковая распределённость.

Ц.П.Т. Линдеберга

Пусть независимые случайные величины определены на одном и том же вероятностном пространстве и имеют конечные математические ожидания и дисперсии: . Как и прежде построим частичные суммы . Тогда в частности, . Наконец, пусть выполняется условие Линдеберга:

Тогда

по распределению при .

Ц.П.Т. Ляпунова

Пусть выполнены базовые предположения Ц.П.Т. Линдеберга. Пусть случайные величины {X_i} имеют конечный третий момент. Тогда определена последовательность

. Если предел

(условие Ляпунова),

то

по распределению при .

Ц.П.Т. для мартингалов

Пусть процесс является мартингалом. Введём случайные процессы и τ_n следующим образом:

и

.

Тогда

по распределению при .

Wikimedia Foundation. 2010.

• Центральная предельная теорема для мартингалов
• Центральная киностудия детских и юношеских фильмов им. М. Горького

Смотреть что такое «Центральная предельная теорема Ляпунова» в других словарях:

• Центральная предельная теорема — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете …   Википедия

• Центральная предельная теорема для мартингалов — Центральные предельные теоремы (Ц.П.Т.) класс теорем в теории вероятностей, утверждающих, что сумма большого количества независимых случайных величин имеет распределение, близкое к нормальному. Так как многие случайные величины в приложениях… …   Википедия

• ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА — общее название ряда предельных теорем теории вероятностей (см.), указывающих условия, при выполнении к рых суммы или др. функции от большого числа независимых или слабо зависимых величин случайных (см.) имеют распределения вероятностей (см.),… …   Российская социологическая энциклопедия

• Ляпунов, Александр Михайлович — Александр Михайлович Ляпунов А. М. Ляпунов в молодости Дата рождения: 25 мая (6 июня) 1857(1857 06 06) Место рождения: Ярославль …   Википедия

• Ляпунов, Александр — Александр Михайлович Ляпунов А. М. Ляпунов в молодости Дата рождения: 25 мая 1857(18570525) Место рождения: Ярославль Дата смерти …   Википедия

• Ляпунов А. М. — Александр Михайлович Ляпунов А. М. Ляпунов в молодости Дата рождения: 25 мая 1857(18570525) Место рождения: Ярославль Дата смерти …   Википедия

• Ляпунов Александр Михайлович — Александр Михайлович Ляпунов А. М. Ляпунов в молодости Дата рождения: 25 мая 1857(18570525) Место рождения: Ярославль Дата смерти …   Википедия

• Предельные теоремы —         теории вероятностей, общее название ряда теорем вероятностей теории (См. Вероятностей теория), указывающих условия возникновения тех или иных закономерностей в результате действия большого числа случайных факторов. Исторически первые П. т …   Большая советская энциклопедия

• ЭРГОДИЧЕСКАЯ ТЕОРИЯ — Введение Э. т. (метрическая теория динамических систем) раздел теории динамических систем, изучающий их статистич. свойства. Возникновение Э. т. (1 я треть 20 в.) было стимулировано попытками доказать эргодическую гипотезу (термин введён П. и Т.… …   Физическая энциклопедия

• ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ — теории вероятностей общее название ряда теорем теории вероятностей, указывающих условия возникновения тех или иных закономерностей в результате действия большого числа случайных факторов. Первые П. т., установленные Я. Бернулли (J. Bernoulli,… …   Математическая энциклопедия

dic.academic.ru

Центральная предельная теорема | Математика, которая мне нравится

Каков средний вес человека?

Основная идея статистики заключается в том, что о населении в целом можно сказать что-то, выяснив это для меньшей группы людей. Без этой идеи не было бы опросов общественного мнения или предвыборных прогнозов, не было бы возможности испытать новые медицинские препараты или исследовать безопасность мостов и т. д. В значительной степени за факт, что мы можем делать все это и уменьшать неопределенности прогнозов, отвечает центральная предельная теорема.

Чтобы понять, как работает теорема, представим, что нужно узнать средний вес жителя Великобритании. Вы выходите и измеряете вес, скажем, ста случайно выбранных людей, и находите средний вес человека для этой группы — назовем это выборочным средним. Теперь выборочное среднее должно дать достаточно точное представление о среднем по стране. Но что, если вам в выборке попались только полные люди или, наоборот, только очень худые?

Чтобы получить представление о том, насколько типичным будет полученное среднее значение, нужно знать, как средний вес выборки из 100 человек варьируется в зависимости от населения: если вы взяли очень много групп из 100 человек и нашли средний вес для каждой группы, то насколько будут различаться найденные числа? И насколько его среднее (среднее средних) будет совпадать с истинным средним весом человека в популяции?

Например, предположим, что если выбрать очень много групп из 100 человек и записать средний вес каждой группы, получатся бы все значения от 10 кг до 300 кг в равных количествах. Тогда ваш метод оценки общего среднего по одной выборке из 100 человек не очень хороший, потому что слишком большой разброс значений — вы можете получить любое из возможных значений, поэтому нельзя сказать, какое из них ближе всего к истинному среднему весу в популяции.

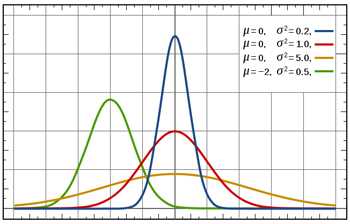
Примеры нормального распределения с различными средними значениями и дисперсиями.

Итак, как мы можем говорить что-либо о распределении средних значений масс 100 человек — называемом распределением выборки — когда мы ничего не знаем о распределении масс всего населения? В этом и заключается центральная предельная теорема: в ней говорится, что для достаточно большой выборки распределение выборки аппроксимируется нормальным распределением — это распределение, имеющее известную форму колокола. (Обычно считается, что размер выборки 30 достаточно хорош.)

Среднее этого нормального распределения (среднее из средних значений, соответствующих вершине колокола) такое же, как среднее по всему населению (средний вес популяции). Дисперсия этого нормального распределения, то есть насколько вес отклоняется от среднего (определяется шириной колокола), зависит от размера выборки: чем больше выборка, тем меньше дисперсия. Существует уравнение, которое дает точное соотношение.

Поэтому, если ваш размер выборки достаточно велик (100, конечно, подойдет, так как это больше 30), то относительно небольшая дисперсия нормального распределения выборки означает, что средний вес, который вы наблюдаете, близок к среднему значению этого нормального распределения (поскольку колокол довольно узкий). И так как среднее этого нормального распределения равно истинному среднему весу во всей популяции, наблюдаемый средний показатель является хорошим приближением к истинному среднему.
Вы можете сделать все это точно, например, вы можете сказать, насколько вы уверены в том, что истинное среднее значение удалено от выборочного среднего, и вы также можете использовать результат для расчета того, насколько большой образец вам нужен, чтобы получить оценку с определенной степенью точности. Именно центральная предельная теорема отвечает за точность статистического вывода, и именно она стоит за широкой распространенностью нормального распределения.
На самом деле, центральная предельная теорема немного более общая, чем здесь представлено. Вот ее точная формулировка.

Теорема. Пусть — бесконечная последовательность независимых одинаково распределённых случайных величин, имеющих конечное математическое ожидание и дисперсию . Пусть . Тогда

   

по распределению при .

Обозначив символом выборочное среднее первых величин, то есть , мы можем переписать результат центральной предельной теоремы в следующем виде:

   

по распределению при .

Замечание. Здесь — нормальное распределение с параметрами .

Источник: https://plus.maths.org/content/maths-three-minutes-central-limit-theorem

hijos.ru