Теория больших чисел простыми словами
В жизни людей широко пользуются понятием среднего арифметического нескольких чисел. Вычисляется оно просто – все числа складываются, и их сумма делится на число слагаемых. Результат деления и есть среднее арифметическое всех чисел. Поясним пример вычисления среднего арифметического, взятый из истории мер и весов. В 16 веке длина английского фута по указу короля была определена как среднее арифметическое длины ступни первых 16 человек, выходящих из церкви от заутрени в воскресенье. Задание эталона фута позволило покончить с произволом в торговле и строительстве.
Знают ли короли теорию больших чисел?
Закона больших чисел, опубликованного в 1713 году (уже после смерти) швейцарским математиком Я. Бернулли, в 16 веке знать не могли, но именно этот закон лежит в обосновании использованного при определении длины фута принципа среднего арифметического. Согласно закону больших чисел, совместное действие множества случайных факторов приводит к результату, почти не зависящему от случая.

Возвращаемся к определению длины фута по 16 прихожанам. Предполагается, что поскольку прихожане не выбирались по какому-то признаку (только высокие, или только в обуви определенного фасона, или еще какому признаку), то отобраны они случайно, и среднее арифметическое 16 индивидуальных «футов» близко к неизвестному нам значению «истинного» фута, к которому можно приблизиться как угодно точно, увеличивая число слагаемых в формуле вычисления среднего арифметического (т.е. число прихожан в рассматриваемом случае).
Закон больших чисел и выборы
Теорема Бернулли, являющаяся частным случаем закона больших чисел, гласит, что относительная частота появления события в независимых экспериментах сходится к вероятности события. Этим частным случаем широко пользуются при проведении социологических исследований. Чтобы выяснить мнение очень большой группы людей, вовсе не обязательно опрашивать всех членов группы – достаточно опросить несколько сотен или тысяч случайных людей, и по их ответам составить представление о мнении всей группы по рассматриваемому вопросу.
Вы обратили внимание, что при подсчете голосов после состоявшихся выборов в масштабе страны после подсчета всего 20% голосов в большинстве случаев (при достаточном разрыве) уже можно поздравлять победителя? Здесь тоже действует закон больших чисел – случайно отобранные 20% избирателей (предполагается, что данные с избирательных участков поступают случайно) по проценту проголосовавших за отдельных кандидатов не отличаются существенно от процента проголосовавших по всей совокупности избирателей.
Куда лететь в отпуск и встречу ли я динозавра?
Неосознанно законом больших чисел люди пользуются в повседневной жизни при принятии решений. Решив лететь в январе из Москвы в Таиланд на отдых, вы имеете ясное представление, какая погода вас там ждет – результаты многолетних метеорологических наблюдений позволят предсказать ожидаемую температуру воздуха и воды, которые не могут сильно отличаться от среднеарифметических значений в это время года.

И в заключение известный вопрос о вероятности встретить на улице динозавра. Вы за жизнь провели 10 тысяч экспериментов – выходили на улицу и динозавра не встретили. Вероятность встретить динозавра, следовательно, близка к нулю, и нет особых оснований предполагать, что сегодня, выйдя на улицу в 10001 раз, вы его встретите. Ваша уверенность основана на законе больших чисел.
it-lenta.ru
БОЛЬШИХ ЧИСЕЛ ЗАКОН • Большая российская энциклопедия
БОЛЬШИ́Х ЧИ́СЕЛ ЗАКО́Н, общий принцип, согласно которому совместное действие большого числа случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа испытаний (т. н. устойчивость частот) может служить примером действия этого принципа.
На рубеже 17 и 18 вв. Я. Бернулли доказал теорему, утверждающую, что в последовательности независимых испытаний, в каждом из которых вероятность наступления некоторого события $A$ имеет одно и то же значение $p$, $0{<}p{<}1$, верно соотношение $$\mathsf P \left \{ \left | \frac {S_n}{n}-p \right | > ε \right \} \to0 \qquad (1)$$ при любом фиксированном $ε>0$ и $n \to \infty$; здесь $S_n$ – число появлений события $A$ в первых $n$ испытаниях, $S_n/n$ – частота появлений, $\mathsf P$ – вероятность события, указанного в скобках. Эта Бернулли теорема была распространена С. Пуассоном на случай последовательности независимых испытаний, где вероятность появления события $A$ может зависеть от номера испытания. Пусть эта вероятность для $k$-го испытания равна $p_k,\ k=1, 2, …,$ и пусть $$p̅_n=\frac{p_1+…p_n}{n}.$$ Тогда Б. ч. з. в форме Пуассона утверждает, что $$\mathsf P \left \{ \left | \frac {S_n}{n}-p̅_n \right | > ε \right \} \to0 \qquad (2)$$ для любого фиксированного $ε>0$ при $n→∞$. Строгое доказательство этого утверждения было дано П. Л. Чебышевым (1846). Термин «закон больших чисел» впервые встречается у Пуассона, так он назвал вышеуказанное обобщение теоремы Бернулли.
Дальнейшие обобщения утверждений Бернулли и Пуассона возникают, если заметить, что случайные величины $S_n$ можно представить в виде суммы $S_n=X_1+…+X_n$ независимых случайных величин, где $X_k=1$, если $A$ появляется в $k$-м испытании, и $X_k=0$ в противном случае, $k=1, .., n$. При этом математическое ожидание $\mathsf E(S_n/n)$ равно $p$ для случая Бернулли и для случая Пуассона. Другими словами, в обоих случаях рассматривается отклонение среднего арифметического величин $X_1, …, X_n$ от среднего арифметического их математич. ожиданий.
В работе П. Л. Чебышева «О средних величинах» (1867) было установлено, что для независимых случайных величин $X_1, X_2, …,$ соотношение $$\mathsf P \left \{ \left | \frac {X_1+…+X_n}{n}- \frac {\mathsf EX_1+…+\mathsf EX_n}{n} \right | > ε \right \} \to0 \qquad (3)$$
P{∣∣∣X1+…+Xnn−EX1+…+EXnn∣∣∣>ε}→0(3)
при $n→∞$ верно для любого фиксированного $ε>0$ при весьма общих предположениях. Чебышев предполагал, что математич. ожидания $\mathsf EX_k^2$ ограничены одной и той же постоянной, хотя из его доказательства видно, что достаточно ограниченности дисперсий $\mathsf DX_k$, или даже выполнения условия $$B_n^2=\mathsf DX_1+…+\mathsf DX_n=o(n^2)$$B2n=DX1+…+DXn=o(n2)
при $n→∞$. Таким образом, Чебышев показал возможность широкого обобщения теоремы Бернулли. А. А. Марков отметил возможность дальнейших обобщений и предложил применять назв. «Б. ч. з.» ко всей совокупности обобщений теоремы Бернулли, и в частности к (3). Метод Чебышева основан на установлении общих свойств математич. ожиданий и на использовании т. н. Чебышева неравенства. Последующие доказательства разл. форм Б. ч. з. в той или иной степени являются развитием метода Чебышева. Применяя надлежащее «урезание» случайных величин $X_k$ (замену их вспомогательными величинами $X_{k,n}$, равными $X_{n,k}=X_k$, если $|X_k-\mathsf EX_k|{⩽}t_n$, и равными нулю в противном случае, где $t_n$ зависят лишь от $n$), Марков распространил Б. ч. з. на случаи, когда дисперсии слагаемых не существуют. Напр., он показал, что (3) имеет место, если для некоторого числа $δ>0$ величины $\mathsf E|X_k-\mathsf EX_k|^{1+δ}$ ограничены одной и той же постоянной.
Аналогично доказывается теорема Хинчина (1929): если $X_1, X_2, …$ имеют одинаковые законы распределения и $\mathsf EX_1$ существует, то Б. ч. з. (3) выполняется.
Существуют примеры, когда Б. ч. з. не выполняется. Так, он не выполняется, если случайные величины $X_1, X_2, …$ имеют Коши распределение, т. е. распределение с плотностью $1/(π(1+x^2))$. Здесь средние арифметические $(X_1+…+X_n)/n$ первых $n$ случайных величин имеют при любом $n$ то же самое распределение, что и отдельные слагаемые. Для распределения Коши математич. ожидание не существует.
Применимость Б. ч. з. к суммам зависимых величин связана в первую очередь с убыванием зависимости между случайными величинами $X_i$ и $X_j$ при увеличении разности их номеров, т. е. при увеличении $|i-j|$. Впервые соответствующие теоремы были доказаны А. А. Марковым (1907) для величин, связанных в Маркова цепь.
Представление об отклонениях $S_n/n$ от $A_n=(\mathsf EX_1+…+\mathsf EX_n)/n$, наряду с неравенством Чебышева и его уточнениями, даёт центральная предельная теорема.
Предыдущие результаты можно обобщать в разл. направлениях. Так, всюду выше рассматривалась т. н. сходимость по вероятности. Рассматривают и др. виды сходимости, напр. сходимость в среднем квадратичном и сходимость с вероятностью 1 (сходимость почти наверное). Обобщения Б. ч. з. на случай сходимости с вероятностью 1 называют усиленными Б. ч. з.
Пусть $X_1, X_2, …$ – последовательность случайных величин и, как и раньше, $S_n=X_1+ …+X_n$. Говорят, что последовательность $X_1, X_2, …$ удовлетворяет усиленному Б. ч. з., если существует такая последовательность постоянных $A_n$, что вероятность соотношения $S_n/n-A_n→0$ при $n→∞$ равна 1. Последовательность $X_1, X_2, …$ удовлетворяет усиленному Б. ч. з. тогда и только тогда, когда при любом фиксированном $ε>0$ вероятность одновременного выполнения неравенств $$\left | \frac {S_n}{n}-A_n \right |{⩽}ε, \ \left | \frac {S_{n+1}}{n+1}-A_{n+1} \right |{⩽}ε, \ …$$ стремится к 1 при $ n→∞$. Т. о., здесь рассматривается поведение всей последовательности сумм в целом, в то время как в обычном Б. ч. з. речь идёт лишь об отд. суммах. Если последовательность $X_1, X_2, …$ удовлетворяет усиленному Б. ч. з., то она удовлетворяет и обычному Б. ч. з. с теми же самыми $A_n$, т. е. $$\mathsf P \left \{ \left | \frac {S_n}{n}-A_n \right |≤ ε \right \} \to1$$ при любом фиксированном $ε>0$ и $n\to\infty$. Обратное, вообще говоря, неверно.
Усиленный Б. ч. з. был впервые сформулирован и доказан Э. Борелем (1909) для схемы Бернулли. Частные случаи схемы Бернулли возникают, напр., при разложении взятого наудачу (т. е. с равномерным распределением) действительного числа из отрезка [0, 1] в бесконечную дробь по к.-л. основанию. Так, в двоичном разложении $$ω=\sum\nolimits_{n=1}^\infty\frac{X_n(ω)}{2^n}$$ случайные величины $X_1(ω), X_2(ω),…$ принимают два значения 0 и 1 с вероятностью 1/2 каждое и являются независимыми. Сумма $S_n(ω)=\sum\nolimits_{k-1}^nX_k(ω)$ равна числу единиц среди первых $n$ знаков двоичного разложения $ω$, а $S_n(ω )/n$ – их доле. В то же время случайную величину $S_n$ можно рассматривать как число «успехов» в схеме Бернулли с вероятностью «успеха» (появления 1), равной 1/2. Борель доказал, что доля единиц $S_n(ω)/n$ стремится к 1/2 при $n→∞$ для почти всех $ω$ из отрезка [0, 1] (т. е. лебегова мера множества тех точек $ω∈$ [0, 1], для которых $\lim\limits_{n\to\infty}S_n(ω )/n=$ 1/2, равна 1). Аналогично, при разложении $ω$ по основанию 10 можно назвать «успехом» появление к.-л. одной из цифр 0, 1, …, 9 (напр., цифры 3). При этом получается схема Бернулли с вероятностью успеха 1/10, и частота появления выбранной цифры среди первых $n$ знаков десятичного разложения $ω$ стремится к 1/10 для почти всех $ω$ из отрезка [0, 1] (такие числа $ω$ иногда называют нормальными). Борель отметил также, что частота появления любой фиксированной группы из $r$ цифр стремится к 1/10 r для почти всех $ω$.
В случае независимых слагаемых наиболее известными являются условия справедливости усиленного Б. ч. з., установленные А. Н. Колмогоровым: достаточное (1930) – для величин с конечными дисперсиями и необходимое и достаточное (1933) – для одинаково распределённых величин (заключающееся в существовании математич. ожидания этих величин). Теорема Колмогорова для независимых случайных величин $X_1, X_2, …$ с конечными дисперсиями утверждает, что из условия $$\sum\nolimits_{n=1}^\infty\frac{\mathsf DX_n}{n^2}<\infty$$ вытекает справедливость усиленного Б. ч. з. с $A_n=\mathsf E(S_n/n)$.
Представление об отклонениях $S_n/n$ от $A_n$ даёт повторного логарифма закон.
bigenc.ru
Закон больших чисел
Слова о больших числах относятся к числу испытаний – рассматривается большое число значений случайной величины или совокупное действие большого числа случайных величин. Суть этого закона состоит в следующем: хотя невозможно предсказать, какое значение в единичном эксперименте примет отдельная случайная величина, однако, суммарный результат действия большого числа независимых случайных величин утрачивает случайный характер и может быть предсказан практически достоверно (т.е. с большой вероятностью). Например, невозможно предсказать, какой стороной упадет одна монета. Однако если подбросить 2 тонны монет, то с большой уверенностью можно утверждать, что вес монет, упавших гербом вверх, равен 1 тонне.
К закону больших чисел прежде всего относится так называемое неравенство Чебышева, которое оценивает в отдельном испытании вероятность принятия случайной величиной значения, уклоняющееся от среднего значения не более, чем на заданное значение.
Неравенство Чебышева. Пусть Х – произвольная случайная величина, а=М(Х), а D(X) – ее дисперсия. Тогда
.
Пример. Номинальное (т.е. требуемое) значение диаметра вытачиваемой на станке втулки равно 5мм , а дисперсия не более 0.01 (таков допуск точности станка). Оценить вероятность того, что при изготовлении одной втулки отклонение ее диаметра от номинального окажется менее 0.5мм .
Решение. Пусть с.в. Х – диаметр изготовленной втулки. По условию ее математическое ожидание равно номинальному диаметру (если нет систематического сбоя в настройке станка) : а=М(Х)=5 , а дисперсия D(Х)≤0.01. Применяя неравенство Чебышева при ε = 0.5, получим:
.
Таким образом, вероятность такого отклонения достаточно велика, а потому можно сделать вывод о том, что при единичном изготовлении детали практически наверняка отклонение диаметра от номинального не превзойдет 0.5мм .
По своему смыслу среднее квадратическое отклонение σ характеризует среднее отклонение случайной величины от своего центра (т.е. от своего математического ожидания). Поскольку это среднее отклонение, то при испытании возможны и большие (ударение на о) отклонения. Насколько же большие отклонения практически возможны? При изучении нормально распределенных случайных величин мы вывели правило «трех сигм»: нормально распределенная случайная величина Х при единичном испытании практически не отклоняется от своего среднего далее, чем на 3σ, где σ= σ(Х) – среднее квадратическое отклонение с.в. Х. Такое правило мы вывели из того, что получили неравенство
.
Оценим теперь вероятность для произвольной случайной величины Х принять значение, отличающееся от среднего не более чем на утроенное среднее квадратическое отклонение. Применяя неравенство Чебышева при ε =3σ и учитывая, что D(Х)= σ2, получаем:
.
Таким образом, в общем случае вероятность отклонения случайной величины от своего среднего не более чем на три средних квадратичных отклонения мы можем оценить числом 0.89, в то время как для именно нормального распределения можно гарантировать это с вероятностью 0.997 .
Неравенство Чебышева может быть обобщено на систему независимых одинаково распределенных случайных величин.
Обобщенное неравенство Чебышева. Если независимые случайные величины Х1, Х2, … , Хn имеют одинаковое распределение с математическими ожиданиями M(Xi)=a и дисперсиями D(Xi)=D, то
.
При n=1 это неравенство переходит в неравенство Чебышева, сформулированное выше.
Неравенство Чебышева, имея самостоятельное значение для решения соответствующих задач, применяется для доказательства так называемой теоремы Чебышева. Мы с начала расскажем о сути этой теоремы, а затем дадим ее формальную формулировку.
Пусть Х1,
Х2,
… , Хn – большое число независимых случайных
величин с математическими ожиданиями М(Х1)=а1,
… , М(Хn)=аn . Хотя каждая из них в результате
эксперимента может принять значение,
далекое от своего среднего (т.е.
математического ожидания), однако,
случайная величина 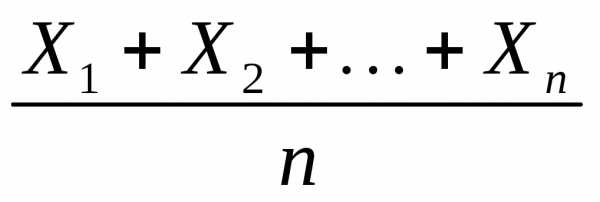 ,
равная их среднему арифметическому, с
большой вероятностью примет значение,
близкое к фиксированному числу
,
равная их среднему арифметическому, с
большой вероятностью примет значение,
близкое к фиксированному числу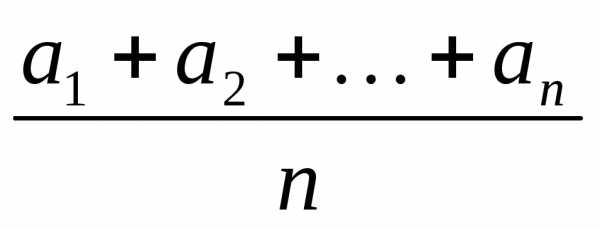 (это среднее всех математических
ожиданий). Это означает следующее. Пусть
в результате испытания независимые
случайные величиныХ1,
Х2,
… , Хn (их много!) приняли значения соответственно х1,
х2,
… , хn соответственно. Тогда если сами эти
значения могут оказаться далекими от
средних значений соответствующих
случайных величин, их среднее значение
(это среднее всех математических
ожиданий). Это означает следующее. Пусть
в результате испытания независимые
случайные величиныХ1,
Х2,
… , Хn (их много!) приняли значения соответственно х1,
х2,
… , хn соответственно. Тогда если сами эти
значения могут оказаться далекими от
средних значений соответствующих
случайных величин, их среднее значение 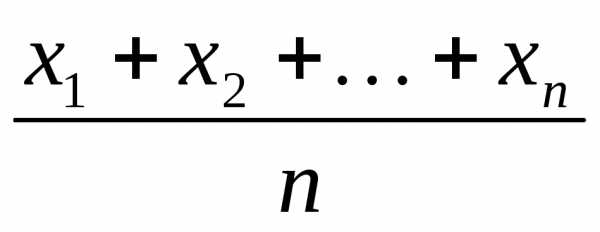 с большой вероятностью окажется близким
к числу
с большой вероятностью окажется близким
к числу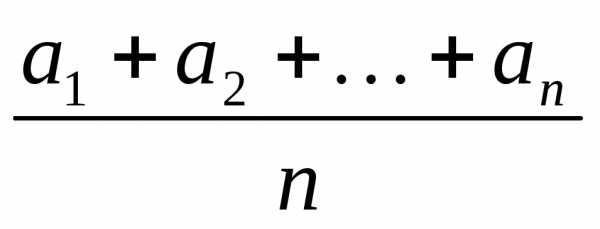 .
Таким образом, среднее арифметическое
большого числа случайных величин уже
теряет случайный характер и может быть
предсказано с большой точностью. Это
можно объяснить тем, что случайные
отклонения значенийХi от ai могут быть разных знаков, а потому в в
сумме эти отклонения с большой вероятностью
компенсируются.
.
Таким образом, среднее арифметическое
большого числа случайных величин уже
теряет случайный характер и может быть
предсказано с большой точностью. Это
можно объяснить тем, что случайные
отклонения значенийХi от ai могут быть разных знаков, а потому в в
сумме эти отклонения с большой вероятностью
компенсируются.
Терема Чебышева (закон больших чисел в форме Чебышева). Пусть Х1, Х2, … , Хn … – последовательность попарно независимых случайных величин, дисперсии которых ограничены одним и тем же числом. Тогда, какое бы малое число ε мы ни взяли, вероятность неравенства
будет как угодно близка к единице, если число n случайных величин взять достаточно большим. Формально это означает, что в условиях теоремы
.
Такой вид сходимости называется сходимостью по вероятности и обозначается:
.
Таким образом, теорема Чебышева говорит о том, что если есть достаточно большое число независимых случайных величин, то их среднее арифметическое при единичным испытании практически достоверно примет значение, близкое к среднему их математических ожиданий.
Чаще всего теорема Чебышева применяется в ситуации, когда случайные величины Х1, Х2, … , Хn … имеют одинаковое распределение (т.е. один и тот же закон распределения или одну и ту же плотность вероятности). Фактически это просто большое число экземпляров одной и той же случайной величины.
Следствие (обобщенного неравенства Чебышева). Если независимые случайные величины Х1, Х2, … , Хn … имеют одинаковое распределение с математическими ожиданиями M(Xi)=a и дисперсиями D(Xi)=D, то
, т.е. .
Доказательство следует из обобщенного неравенства Чебышева переходом к пределу при n→∞ .
Отметим еще раз, что выписанные выше равенства не гарантируют, что значение величины стремится ка при n→∞. Эта величина по-прежнему остается случайной величиной, а ее отдельные значения могут быть достаточно далекими от а. Но вероятность таких (далеких от
Замечание. Заключение следствия, очевидно, справедливо и в более общем случае, когда независимые случайные величины Х1, Х2, … , Хn … имеют различное распределение, но одинаковые математические ожидания (равные а) и ограниченные в совокупности дисперсии. Это позволяет предсказывать точность измерения некоторой величины, даже если эти измерения выполнены разными приборами.
Рассмотрим подробнее применение этого следствия при измерении величин. Проведем некоторым прибором n измерений одной и той же величины, истинное значение которой равно а и нам неизвестно. Результаты таких измерений х1, х2, … , хn могут значительно отличаться друг от друга (и от истинного значения а) в силу различных случайных факторов (перепады давления, температуры, случайная вибрация и т.д.). Рассмотрим с.в. Х – показание прибора при единичном измерении величины, а также набор с.в. Х1, Х2, … , Хn – показание прибора при первом, втором, …, последнем измерении. Таким образом, каждая из величин Х1, Х2, … , Хn есть просто один из экземпляров с.в. Х, а потому все они имеют то же самое распределение, что и с.в. Х. Поскольку результаты измерений не зависят друг от друга, то с.в. Х1, Х2, … , Хn можно считать независимыми. Если прибор не дает систематической ошибки (например, не «сбит» ноль на шкале , не растянута пружина и т.п.), то можно считать, что математическое ожидание М(Х) = а , а потому и М(Х1) = … = М(Х
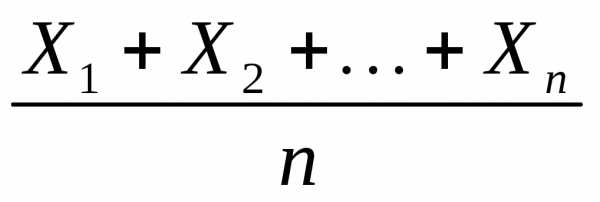 в нашем эксперименте (заключающемся в
проведении серии изn измерений), т.е.
в нашем эксперименте (заключающемся в
проведении серии изn измерений), т.е..
При большом числе измерений практически достоверна хорошая точность вычисления по этой формуле. Это является обоснованием того практического принципа, что при большом числе измерений их среднее арифметическое практически почти не отличается от истинного значения измеряемой величины.
На законе больших чисел основан широко применяемый в математической статистике «выборочный» метод, который позволяет по сравнительно небольшой выборке значений случайной величины получать ее объективные характеристики с приемлемой точностью. Но об этом будет рассказано в следующем разделе.
Пример.
На измерительном приборе, не делающем
систематических искажений, измерена
некоторая величина а один раз (получено значение х1),
а потом еще 99 раз (получены значения х2,
… , х100).
За истинное значение измерения а сначала взят результат первого измерения 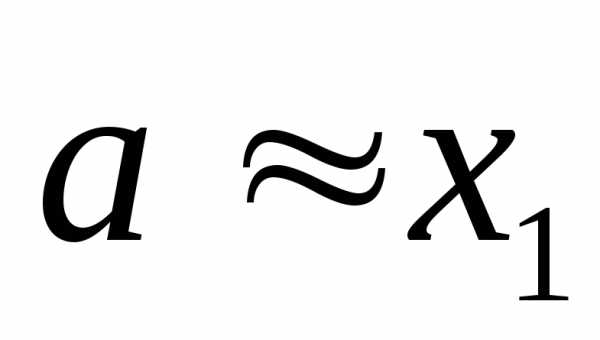 ,
а затем среднее арифметическое всех
измерений.
Точность измерения прибора такова, что
среднее квадратическое отклонение
измерения σ не более 1 (потому дисперсияD=σ2 тоже не превосходит 1). Для каждого из
способов измерения оценить вероятность,
что ошибка измерения не превзойдет 2.
,
а затем среднее арифметическое всех
измерений.
Точность измерения прибора такова, что
среднее квадратическое отклонение
измерения σ не более 1 (потому дисперсияD=σ2 тоже не превосходит 1). Для каждого из
способов измерения оценить вероятность,
что ошибка измерения не превзойдет 2.
Решение. Пусть с.в. Х – показание прибора при единичном измерении. Тогда по условию М(Х)=а. Для ответа на поставленные вопросы применим обобщенное неравенство Чебышева
при ε=2 сначала для n=1, а затем для n=100. В первом случае получим , а во втором. Таким образом, второй случай практически гарантирует задаваемую точность измерения, тогда как первый оставляет в этом смысле большие сомнения.
Применим приведенные выше утверждения к случайным величинам, возникающим в схеме Бернулли. Напомним суть этой схемы. Пусть производится n независимых испытаний, в каждом из которых некоторое событие А может появиться с одной и той же вероятностью р, а q=1–р (по смыслу это вероятность противоположного события – не появления события А) . Проведем некоторое число n таких испытаний. Рассмотрим случайные величины: Х1 – число появлений события А в 1-ом испытании, …, Хn – число появлений события А в n-ом испытании . Все введенные с.в. могут принимать значения 0 или 1 (событие А в испытании может появиться или нет), причем значение 1 по условию принимается в каждом испытании с вероятностью p (вероятность появления события А в каждом испытании), а значение 0 с вероятностью q=1– p . Поэтому эти величины имеют одинаковые законы распределения:
, … ,
Поэтому средние значения этих величин и их дисперсии тоже одинаковы: М(Х1)=0∙q+1∙ р= р , …, М(Хn)= р ; D(X1)=(02∙q+12∙p)−p2=p∙(1−p)= p ∙q, … , D(Xn)=p ∙q . Подставляя эти значения в обобщенное неравенство Чебышева, получим
.
Ясно, что с.в. Х=Х1+…+Хn – это число появлений события А во всех n испытаниях (как говорят – «число успехов» в n испытаниях). Пусть в проведенных n испытаниях событие А появилось в k из них. Тогда предыдущее неравенство может быть записано в виде
.
Но
величина 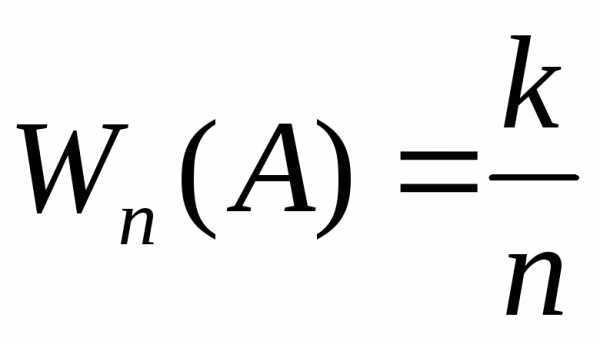 ,
равная отношению числа появлений событияА в n независимых испытаниях, к общему числу
испытаний , ранее была названа относительной
частотой события А в n испытаниях . Поэтому имеет место
неравенство
,
равная отношению числа появлений событияА в n независимых испытаниях, к общему числу
испытаний , ранее была названа относительной
частотой события А в n испытаниях . Поэтому имеет место
неравенство
.
Переходя
теперь к пределу при n→∞,
получим
,
т.е.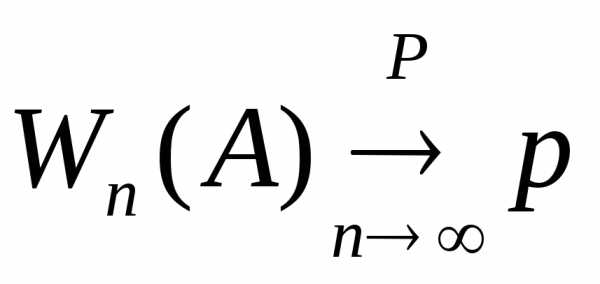 (по вероятности). Это составляет содержание
закона больших чисел в форме Бернулли.
Из него следует, что при достаточно
большом числе испытанийn сколь угодно малые отклонения относительной
частоты
(по вероятности). Это составляет содержание
закона больших чисел в форме Бернулли.
Из него следует, что при достаточно
большом числе испытанийn сколь угодно малые отклонения относительной
частоты  события от его вероятностир − почти достоверные события, а большие
отклонения − почти невозможные.
Полученный вывод о такой устойчивости
относительных частот (о которой мы ранее
говорили как об экспериментальном факте) оправдывает введенное ранее
статистическое определение вероятности
события как числа, около которого
колеблется относительная частота
события.
события от его вероятностир − почти достоверные события, а большие
отклонения − почти невозможные.
Полученный вывод о такой устойчивости
относительных частот (о которой мы ранее
говорили как об экспериментальном факте) оправдывает введенное ранее
статистическое определение вероятности
события как числа, около которого
колеблется относительная частота
события.
Учитывая,
что выражение p∙q=p∙(1−p)=p−p2 не превосходит  на интервале изменения
на интервале изменения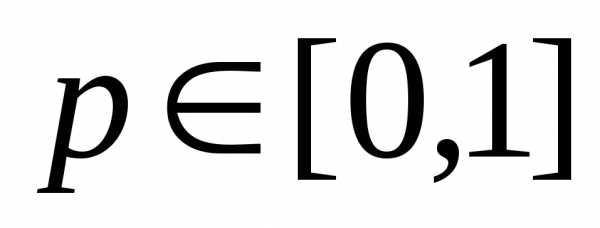 (в этом легко убедиться, найдя минимум
этой функции на этом отрезке), из
приведенного выше неравенствалегко получить, что
(в этом легко убедиться, найдя минимум
этой функции на этом отрезке), из
приведенного выше неравенствалегко получить, что
,
которое применяется при решении соответствующих задач (одна из них будет приведена ниже).
Пример. Монету подбросили 1000 раз. Оценить вероятность того, что отклонение относительной частоты появления герба от его вероятности будет меньше 0.1.
Решение. Применяя неравенство приp=q=1/2, n=1000, ε=0.1, получим .
Пример. Оценить вероятность того, что в условиях предыдущего примера число k выпавших гербов окажется в пределах от 400 до 600.
Решение.
Условие 400<k<600 означает, что 400/1000<k/n<600/1000,
т.е. 0.4<Wn(A)<0.6 или 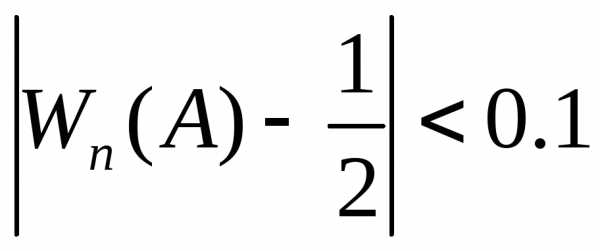 .
Как мы только что убедились из предыдущего
примера, вероятность такого события не
менее0.975.
.
Как мы только что убедились из предыдущего
примера, вероятность такого события не
менее0.975.
Пример. Для вычисления вероятности некоторого события А проведено 1000 экспериментов, в которых событие А появилось 300 раз. Оценить вероятность того, что относительная частота (равная 300/1000=0.3) отстоит от истиной вероятности р не далее, чем на 0.1 .
Решение. Применяя выписанное выше неравенство дляn=1000, ε=0.1 , получим .
79
studfiles.net
Закон больших чисел в Достижение Цели
Позвольте закону больших чисел работать на вас в достижении цели. Позвольте перефразировать знаменитую фразу о гениальности — чтоб добиться успеха нужно: 10 процентов умения и 90 процентов настойчивости. Итак, о всем этом и более, по порядку…
Закон больших чисел в достижении успеха
Если вы читали труды Роберта Кийосаки (миллионер, мастер-тренер по финансовому благополучию, автор «Бедны Папа, Богатый Папа»), то вы, наверное, как и я, удивлялись его упорству, большой мотивации к деланию денег, хорошему трудоголизму (трудоголизм может быть плохим – когда применяешь силу не к месту).
Но, что самое интересное, он никогда не называл себя умным, способным, т.е. как-то уже расположенным к богатству.
Я прочитал около 6-ти его книг, Р. Кийосаки часто рассказывает о себе, о том как он хотел заработать. И главный секрет того, что он смог достигнуть желанной цели – его настойчивость и усердие в этом.
Этот человек на виду, и выше сказанное легко проверить, прочитав его книги. НО, что интересно, все спортсмены, многие мульти миллиардеры, известные авторы бестселлеров достигали успеха согласно такой формуле: 10% умения и 90% настойчивости.
О чем утверждает закон больших чисел? (это математическая модель, но в контексте о успехе можно выделить следующее)
Большое количество определенных действий приводит к необходимому результату, не зависящего от воли случая.
Т.е. чем более вы пытаетесь и что-то делаете, чтоб преуспеть в определенном деле – тем ближе вы к успеху! Это Закон!
Формула достижения цели, согласно закону больших чисел
Достижение цели = 10 процентов знания того, как добиться цели + Nmax произведенных действий.
Nmax — количество попыток, или целенаправленных действий, работы
P.S. Число Nmax хотелось, чтоб было поменьше…На самом деле оно не так уж и велико. Его можно даже подсчитать, хорошо изучив автобиографию великих людей. Но проще воспринять закон – как аксиому, внушить себе, что это ЗАКОН и действовать соответственно ему!

Хоть раз, да попадете в Цель?! Конечно, по закону больших чисел, если Вы стрелять будете много раз!
www.iaim.ru
Тема 7. Закон больших чисел
Заканчивается раздел «Теория вероятностей» темой 7 – «Закон больших чисел» . Под законом больших чисел в широком смысле понимается общий принцип, согласно которому, по формулировке академика А.Н. Колмогорова, совокупное действие большого числа случайных факторов приводит (при некоторых весьма общих условиях) к результату, почти не зависящему от случая. Другими словами, при большом числе случайных величин их средний результат перестает быть случайным и может быть предсказан с большой степенью определенности.
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Так, в теореме Чебышева утверждается, что средняя арифметическая п независимых случайных величин – величина случайная – при приближается (точнее сходится по вероятности) к средней арифметической их математических ожиданий – величине неслучайной, т.е. практически перестает быть случайной. А втеореме Бернулли доказывается, что случайная величина – статистическая вероятность или частость события в п повторных независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью р, при неограниченном увеличении числа п приближается (сходится по вероятности) к вероятности р этого события в отдельном испытании – величине неслучайной. Так, например, если вероятность рождения мальчика нам не известна, то в качестве ее значения на основании теоремы Бернулли мы можем принять частость (статистическую вероятность) этого события, которая, как известно по многолетним статистическим данным, составляет приближенно 0,515.
Обратите внимание на понятиеcxo димости по вероятности , под которой понимается стремление случайной величины к постоянной величине с вероятностью, как угодно близкой к единице при
Прежде чем доказать указанные основные теоремы, в теме рассматриваются неравенство Маркова или лемма Чебышева, (применяемое для неотрицательных случайных величин), и неравенство Чебышева, (применимое для любых случайных величин). При использовании этих неравенств следует учесть, что они дают лишь верхнюю или нижнюю границы вероятности рассматриваемого события.
Завершая обзор учебного материала по разделу «Теория вероятностей» следует отметить, что усвоение этого материала предполагает решение достаточно большого числа задач, в частности, с помощью компьютерной программы «КОПР2».
Раздел 2. Математическая статистика
Второй раздел «Математическая статистика»включает в себя четыре темы:
8. Вариационные ряды
9. Основы выборочного метода
10. Элементы проверки статистических гипотез
11. Элементы теории корреляции
Математическая статистика – раздел математики, изучающий математические методы сбора, систематизации, обработки и интерпретации результатов наблюдений с целью выявления статистических закономерностей.
Тема 8. Вариационные ряды
В теме 8 «Вариационные ряды» Вы познакомитесь с простейшей статистической обработкой опытных данных — построением вариационных рядов и вычислением их числовых характеристик.
Вариационным рядом называется ранжированный (т.е. упорядоченный) ряд значений изучаемого признакаX или вариантов с соответствующими им частотами (или частостями). Частоты (или частости) указывают число (долю) соответствующих вариантов. Обратите внимание на графическое изображение вариационного ряда – на полигон и гистограмму, а также эмпирическую функцию распределения.
Вариационный ряд является статистическим аналогом (реализацией) распределения признака (случайной величиныX ). В этом смысле полигон (гистограмма) вариационного ряда аналогична кривой распределения, эмпирическая функция распределения – функции распределения случайной величины. А числовые характеристики вариационного ряда – средняя арифметическая (обозначается ) и дисперсияs 2являются аналогами соответствующих числовых характеристик случайнойвеличины – математического ожидания М(X ) и дисперсии Г 2. Точно так же понятие частости (относительной частоты)w для вариационного ряда аналогично понятию вероятности р для случайной величины.
Необходимо знать формулы средней арифметической и дисперсииs 2вариационного ряда, их свойства. Учтите, что более сложные формулы их вычисления, используемые в упрощенном способе расчета (учебник [1], §8.4) носят технический, вспомогательный характер, и их сложность объясняется переходом в расчетах от рассматриваемых вариантов к условным.
studfiles.net
Теория больших чисел простыми словамиВ жизни людей широко пользуются понятием среднего арифметического нескольких чисел. Вычисляется оно просто – все числа складываются, и их сумма делится на число слагаемых. Результат деления и есть среднее арифметическое всех чисел. Поясним пример вычисления среднего арифметического, взятый из истории мер и весов. В 16 веке длина английского фута по указу короля была определена как среднее арифметическое длины ступни первых 16 человек, выходящих из церкви от заутрени в воскресенье. Задание эталона фута позволило покончить с произволом в торговле и строительстве. Знают ли короли теорию больших чисел?Закона больших чисел, опубликованного в 1713 году (уже после смерти) швейцарским математиком Я. Бернулли, в 16 веке знать не могли, но именно этот закон лежит в обосновании использованного при определении длины фута принципа среднего арифметического. Согласно закону больших чисел, совместное действие множества случайных факторов приводит к результату, почти не зависящему от случая. Возвращаемся к определению длины фута по 16 прихожанам. Предполагается, что поскольку прихожане не выбирались по какому-то признаку (только высокие, или только в обуви определенного фасона, или еще какому признаку), то отобраны они случайно, и среднее арифметическое 16 индивидуальных «футов» близко к неизвестному нам значению «истинного» фута, к которому можно приблизиться как угодно точно, увеличивая число слагаемых в формуле вычисления среднего арифметического (т.е. число прихожан в рассматриваемом случае).Закон больших чисел и выборыТеорема Бернулли, являющаяся частным случаем закона больших чисел, гласит, что относительная частота появления события в независимых экспериментах сходится к вероятности события. Этим частным случаем широко пользуются при проведении социологических исследований. Чтобы выяснить мнение очень большой группы людей, вовсе не обязательно опрашивать всех членов группы – достаточно опросить несколько сотен или тысяч случайных людей, и по их ответам составить представление о мнении всей группы по рассматриваемому вопросу.Предположим, что в городе Н. предстоят выборы мэра, и число избирателей равно 100 тысячам. Если накануне выборов случайно отобрать 100 человек, и по результатам их опроса выясняется, что за кандидата А отдадут голоса 26 человек, а за Б – 58, нет оснований предполагать, что результат выборов окажется иным – у Б явное преимущество. Более точным предсказание результата окажется при случайном отборе 1000 человек, и т.д.Вы обратили внимание, что при подсчете голосов после состоявшихся выборов в масштабе страны после подсчета всего 20% голосов в большинстве случаев (при достаточном разрыве) уже можно поздравлять победителя? Здесь тоже действует закон больших чисел – случайно отобранные 20% избирателей (предполагается, что данные с избирательных участков поступают случайно) по проценту проголосовавших за отдельных кандидатов не отличаются существенно от процента проголосовавших по всей совокупности избирателей. Куда лететь в отпуск и встречу ли я динозавра?Неосознанно законом больших чисел люди пользуются в повседневной жизни при принятии решений. Решив лететь в январе из Москвы в Таиланд на отдых, вы имеете ясное представление, какая погода вас там ждет – результаты многолетних метеорологических наблюдений позволят предсказать ожидаемую температуру воздуха и воды, которые не могут сильно отличаться от среднеарифметических значений в это время года. И в заключение известный вопрос о вероятности встретить на улице динозавра. Вы за жизнь провели 10 тысяч экспериментов – выходили на улицу и динозавра не встретили. Вероятность встретить динозавра, следовательно, близка к нулю, и нет особых оснований предполагать, что сегодня, выйдя на улицу в 10001 раз, вы его встретите. Ваша уверенность основана на законе больших чисел.it-lenta.ru Божественные числа во вселенной — Новейшая философия жизни 21 векаЧто такое божественные числа во Вселенной?Древние говорили: «Числа как и слова имеют смысл и значение». Если каждый из нас проанализирует любые события и число им сопутствующее, то удивлению вашему не будет предела. ЗАКОН ТЕРНЕРА и понятие божественных цифрВ предыдущих главах нам уже встречались понятия: Монада, дуада (дуализм), триада (троица). Т.е. если обозначить: ½=3. 1 – Член активный (свет) пирамида вершиной вверх. 2 – Член пассивный (тьма) пирамида вершиной вниз. 3 – Член средний (полусвет, полутьма) Вытекающий из действия двух первых друг на друга 9сумма двух пирамид, т.е. пирамидальный кристалл). Данный закон (ЗАКОН ТЕРНЕРА) применяется повсюду. В числах он отражается так: 1+2=3 1 – число активное. 2 – число пассивное. 3 – число среднее (действие активного с пассивным) Как числа связаны с божественной сущностью во Вселенной?Считалось, что БОЖЕСТВЕННУЮ СУЩНОСТЬ можно охарактеризовать «языком разума», а не «языком чувств». Поэтому, единым принципам они дали свои названия: БОГ, ВСЕЛЕННАЯ – 1 – МОНАДА (МОНО-ОДИН, АКТИВНОЕ НАЧАЛО) МАТЕРИИ – 2 – ДИАДА (ДВОЙСТВЕННАЯ, ПАССИВНОЕ НАЧАЛО) МИР – 3 – ТРИАДА (ТРОИЦА, СУММАДЕЙСТВИЯ АКТИВНОЕ НА ПАССИВНОЕ). По мнению древних великих мыслителей Путь, которым следует ПРИРОДА во всех своих проявлениях подвержена числовым взаимосвязям и влияниям, но не по простым математическим вычислениям, а по специальным-тайным: |
greecehist.ru
ЗАКОН БОЛЬШИХ ЧИСЕЛ — это… Что такое ЗАКОН БОЛЬШИХ ЧИСЕЛ?
- ЗАКОН БОЛЬШИХ ЧИСЕЛ
- ЗАКОН БОЛЬШИХ ЧИСЕЛ
(law of large numbers) В том случае, когда поведение отдельных представителей населения отличается большим своеобразием, поведение группы в среднем более предсказуемо, чем поведение любого ее члена. Тенденция, в соответствии с которой группы ведут себя более определенно по сравнению с отдельными индивидами, усиливается с увеличением размера группы. Этот закон подчеркивает способность специалистов страховых компаний прогнозировать коэффициенты смертности, а статистиков – определять воздействие ценовых изменений на спрос.
Экономика. Толковый словарь. — М.: «ИНФРА-М», Издательство «Весь Мир». Дж. Блэк. Общая редакция: д.э.н. Осадчая И.М.. 2000.
- ЗАКОН БОЛЬШИХ ЧИСЕЛ
(англ. law of large numbers)
принцип, согласно которому частота финансовых потерь определенного вида может быть предсказана с высокой точностью тогда, когда есть большое количество потерь аналогичных видов.
Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. — 2-е изд., испр. М.: ИНФРА-М. 479 с.. 1999.
Экономический словарь. 2000.
- ЗАКЛЮЧИТЕЛЬНЫЕ ОБОРОТЫ
- ЗАКОН ГРЭШАМА
Смотреть что такое «ЗАКОН БОЛЬШИХ ЧИСЕЛ» в других словарях:
ЗАКОН БОЛЬШИХ ЧИСЕЛ — см. БОЛЬШИХ ЧИСЕЛ ЗАКОН. Antinazi. Энциклопедия социологии, 2009 … Энциклопедия социологии
Закон Больших Чисел — принцип, согласно которому количественные закономерности, присущие массовым общественным явлениям, наиболее явным образом проявляются при достаточно большом числе наблюдений. Единичные явления в большей степени подвержены воздействию случайных и… … Словарь бизнес-терминов
ЗАКОН БОЛЬШИХ ЧИСЕЛ — утверждает, что с вероятностью, близкой к единице, среднее арифметическое большого числа случайных величин примерно одного порядка будет мало отличаться от константы, равной среднему арифметическому из математических ожиданий этих величин. Разл.… … Геологическая энциклопедия
закон больших чисел — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN law of averageslaw of large numbers … Справочник технического переводчика
Закон больших чисел — в теории вероятностей утверждает, что эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения. В зависимости … Википедия
закон больших чисел — didžiųjų skaičių dėsnis statusas T sritis fizika atitikmenys: angl. law of large numbers vok. Gesetz der großen Zahlen, n rus. закон больших чисел, m pranc. loi des grands nombres, f … Fizikos terminų žodynas
ЗАКОН БОЛЬШИХ ЧИСЕЛ — общий принцип, в силу к рого совместное действие случайных факторов приводит при нек рых весьма общих условиях к рез ту, почти не зависящему от случая. Сближение частоты наступления случайного события с его вероятностью при возрастании числа… … Российская социологическая энциклопедия
Закон больших чисел — закон, гласящий, что совокупное действие большого числа случайных факторов приводит, при некоторых весьма общих условиях, к результату, почти не зависящему от случая … Социология: словарь
ЗАКОН БОЛЬШИХ ЧИСЕЛ — статистический закон, выражающий связь статистических показателей (параметров) выборочной и генеральной совокупности . Фактические значения статистических показателей, полученные по некоторой выборке, всегда отличаются от т.н. теоретических… … Социология: Энциклопедия
ЗАКОН БОЛЬШИХ ЧИСЕЛ — принцип, по которому частота финансовых потерь определенного вида может быть предсказана с высокой точностью тогда, когда есть большое количество потерь аналогичных видов … Энциклопедический словарь экономики и права
dic.academic.ru
