длина радиуса — это… Что такое длина радиуса?
- длина радиуса
radius
Англо-русский словарь технических терминов. 2005.
- длина рабочего зазора
- длина распада
Смотреть что такое «длина радиуса» в других словарях:
ДЛИНА СВОБОДНОГО ПРОБЕГА — (средняя длина свободного пробега, l), средняя длина пути, проходимого ч цей между двумя последоват. соударениями с др. ч цами. Т. к. столкновения могут быть разного типа упругие, неупругие, с возбуждением или ионизацией и т. д. (см. СТОЛКНОВЕНИЯ … Физическая энциклопедия
Длина Дебая — Дебаевская длина (дебаевский радиус) расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса… … Википедия
Длина дебая — Дебаевская длина (дебаевский радиус) расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса… … Википедия
Длина дуги — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
Длина дуги кривой — Дифференциальная геометрия кривых раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами. Содержание 1 Способы задания кривой 1.1 Плоские… … Википедия
Длина окружности
— Длинна окружности = π × диаметр Длина окружности это длина закрытой кривой. Определение окружности в статье Окружность. Длина окружности вычисляется из диаметра по формуле:: Или из половины диаметра, радиуса: где r это радиус, d диаметр круга, а… … ВикипедияДебаевская длина — (дебаевский радиус) расстояние, на которое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса дебаевской длины… … Википедия
ДЕБАЕВСКАЯ ДЛИНА — дебаевский радиус, расстояние, на к рое распространяется действие электрического поля отдельного заряда в нейтральной среде, состоящей из положительно и отрицательно заряженных частиц (плазма, электролиты). Вне сферы радиуса Д. д. электрич. поле… … Математическая энциклопедия
Поступательное движение — … Википедия
Солнечная радиация — Все процессы на поверхности земного шара, каковы бы они ни были, имеют своим источником солнечную энергию. Изучаются ли процессы чисто механические, процессы химические в воздухе, воде, почве, процессы ли физиологические или какие бы то ни было… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ЧИСЛО — Понятие числа в математике может относиться к объектам различной природы: натуральным числам, используемым при счете (положительным целым числам 1, 2, 3 и т.д.), числам, являющимся возможными результатами (идеализированных) измерений (это такие… … Энциклопедия Кольера
dic.academic.ru
Чему равен радиус окружности
Чему равен радиус окружности
Радиус окружности можно найти несколькими способами, в зависимости от того, какие данные уже известны.
Например, если диаметр окружности равен 144 см, то радиус будет равен:
(см).
Рассмотрим вычисление радиуса через длину окружности.
Запишем формулу длины окружности через ее радиус:
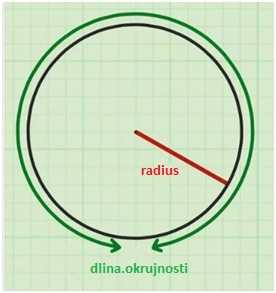
Выразим радиус из этой формулы:
Например, если длина окружности равна 289 см, то ее радиус будет равен:
При решении математических задач можно оставлять число Пи, не подставляя его значение. Но при решении задач по геометрии все же берут приближенное значение числа Пи, равное 3,14:
(см).
Рассмотрим вычисление радиуса через площадь круга.
Запишем формулу площади круга:
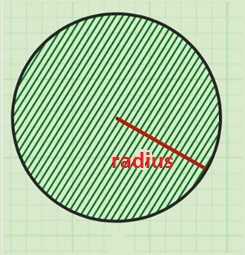
Выразим длину радиуса из этой формулы:
Например, площадь круга равна 378 квадратных сантиметров.
Найдем радиус окружности:
(см).
ru.solverbook.com
Длина окружности [wiki.eduVdom.com]
Наглядное представление о длине окружности получается следующим образом. Представим себе нить в форме окружности. Разрежем ее и растянем за концы. Длина полученного отрезка и есть длина окружности.
Как найти длину окружности, зная ее радиус? При неограниченном увеличении числа сторон вписанного в окружность правильного многоугольника его периметр неограниченно приближается к длине окружности (рис.1). Это используется при доказательстве следующей теоремы.
Рис.1
Теорема 1. Отношение длины окружности к ее диаметру не зависит от окружности, т. е. одно и то оке для любых двух окружностей.
Отношение длины окружности к ее диаметру принято обозначать греческой буквой $\pi$ (читается «пи»): $$ \frac{C}{2R} = \pi \,\,\, (6)$$ где С — длина окружности, R — ее радиус.
Число $\pi$ иррациональное, его приближенное значение $\pi \approx 3,1416$.
Из равенства (6) имеем $$ C = 2\pi R, \,\,\, (7) $$ т. е. длина окружности радиуса R вычисляется по формуле (7). Например, длина окружности радиуса 12 м равна $2\pi \bullet 12 = 24\pi\text{ м.}$
Пример 1. На сколько изменится длина окружности, если радиус увеличится на 1 м?
Решение. Пусть радиус первоначальной окружности был R1 , тогда длина этой окружности $C = 2\pi R_1$ .
По условию радиус первоначальной окружности увеличивается на 1 м, т.е. $R_2 = (R_1 + 1)$ , тогда длина новой окружности $$ C_2 = 2\pi R_2 = 2\pi (R_1 + 1) $$ Найдем разность: $$ C_2 — C_1 = 2\pi (R_1 + 1) — 2\pi R_1 = 2\pi $$ Итак, $ C_2 — C_1 = 2\pi \approx 6,28\text{ (м)}$
Пример 2. Точки М и N делят окружность на две дуги, разность градусных мер которых равна 90°. Чему равны градусные меры каждой из дуг?
Решение. Сумма градусных мер дуг равна 360°, а разность равна 90°. Обозначим градусные меры этих дуг х и у.
Имеем:
$$ \left\{\begin{matrix}
x + y = 360
\\ x — y = 90
\end{matrix}\right.
$$
Решая эту систему, получим х = 225°; у = 135°.
Пример 3. Сторона квадрата равна 4 см. Вычислить длину окружности: 1) вписанной в него; 2) описанной около него.
Решение.
Радиус вписанной в квадрат окружности равен 2 см, тогда длина окружности равна $C = 2\pi R \text{ , т. е. } C = 4\pi\text{ см.}$
Радиус окружности, описанной около квадрата, равен $\frac{a}{ \sqrt{2} }$. Поэтому $R = \frac{4}{ \sqrt{2} } = 2\sqrt{2}$ , а длина окружности равна $C = 4\sqrt{2}\bullet\pi$ см.
www.wiki.eduvdom.com
Таблица. Длина окружности диаметра D. Длина окружности через радиус (радиус=полдиаметра). Диаметр через длину окружности. Диаметр (радиус) через охват. Окружность трубы. Окружность столба.
|
формула, как найти длину круга и разницу между величинами
Очень часто при решении школьных заданий по математике или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы, понятия и определения требуются для этого.
…
Вконтакте
Google+
Мой мир
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку. Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности.
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр. Он обозначается латинской буквой d.
- Окружность — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности. Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!

Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r. Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два.
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r.
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь. В школьной математике она считается заранее известной табличной величиной, равной 3,14!
Теперь перепишем предыдущую формулу, чтобы найти длину окружности через её диаметр, помня, в чём состоит его разница по отношению к радиусу. Получится: l = 2*П*r = 2*r*П = П*d.
Из курса математики известно, что формула, описывающая площадь окружности, имеет вид: s = П*r^2.
Теперь перепишем предыдущую формулу, чтобы найти площадь окружности через её диаметр. Получим,
s = П*r^2 = П*d^2/4.
Одним из самых сложных заданий в данной теме является определение площади круга через длину окружности и наоборот. Воспользуемся тем, что s = П*r^2 и l = 2*П*r. Отсюда получим r = l/(2*П). Подставим полученное выражение для радиуса в формулу для площади, получится: s = l^2/(4П). Абсолютно аналогичным способом определяется и длина окружности через площадь круга.
Определение длины радиуса и диаметра
Важно! Прежде всего узнаем, как измерить диаметр. Это очень просто — проводим любой радиус, продлеваем его в противоположную сторону до пересечения с дугой. Циркулем отмеряем полученное расстояние и с помощью любого метрического инструмента узнаем искомое!
 Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.
Ответим на вопрос, как узнать диаметр окружности, зная её длину. Для этого выразим его из формулы l = П*d. Получим d = l/П.
Мы уже знаем как из длины окружности можно найти её диаметр, точно также найдём и радиус.
l = 2*П*r, отсюда r = l/2*П. Вообще, чтобы узнать радиус, его нужно выражать через диаметр и наоборот.
Пусть теперь требуется определить диаметр, зная площадь окружности. Используем то, что s = П*d^2/4. Выразим отсюда d. Получится d^2 = 4*s/П. Для определения самого диаметра потребуется извлечь корень квадратный из правой части. Получится d = 2*sqrt(s/П).
Это интересно! Первый признак равенства треугольников: доказательство
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга . Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см. Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр. Пусть d = 815 метров. Вспомним формулу, как найти площадь окружности. Подставим сюда данные нам значения, получим s = 3,14*815^2/4 = 521416,625 кв. м.
- Теперь узнаем, как найти площадь круга, зная длину его радиуса. Пусть радиус равняется 38 см. Используем известную нам формулу. Подставим сюда данное нам по условию значение. Получится следующее: s = 3,14*38^2 = 4534,16 кв. см.
- Последним заданием определим площадь круга по известной длине окружности. Пусть l = 47 метров. s = 47^2/(4П) = 2209/12,56 = 175,87 кв. м.
Это интересно! Что такое биссектриса треугольника: свойства, связанные с отношением сторон
Длина окружности
Окружность, диаметр, хорда геометрия 7 класс
Заключение
Исходя из приведённых выше рассуждений, можно прийти к выводу, что никаких сложностей в задачах, связанных с нахождением всевозможных характеристик окружности, нет. Достаточно хорошо выучить понятия и формулы, а также уметь производить арифметические действия, причём все выражения выводятся друг из друга.
Это интересно! Чему равна и как найти площадь равностороннего треугольника
uchim.guru
Радиус окружности
Для начала дадим определение радиуса. В переводе с латинского radius – это «луч, спица колеса». Радиус окружности – это отрезок прямой, соединяющий центр окружности с точкой, которая находится на ней. Длина данного отрезка – это значение радиуса. В математических расчётах для обозначения данной величины используют латинскую букву R.
Советы по нахождению радиуса:
- Диаметр окружности является отрезком прямой, проходящей через ее центр и соединяющей точки, лежащие на окружности, которые максимально удалены друг от друга. Радиус окружности равняется половине её диаметра, следовательно, если вам известен диаметр окружности, то для нахождения её радиуса следует применить формулу: R = D/2, где D – диаметр.
- Длина закрытой кривой, которая образуется на плоскости – это длина окружности. Если вы знаете ее длину, то для нахождения радиуса окружности вы можете применить универсальную в своем роде формулу: R = L/(2*π), где L является длиной окружности, а π – константой, равной 3,14. Константа π представляет собой отношение длины окружности к длине ее диаметра, она одинакова для всех окружностей.
- Круг представляет собой геометрическую фигуру, являющуюся частью плоскости, ограниченной кривой – окружностью. В том случае, если вы знаете площадь какого либо круга, то радиус окружности может быть найден по специальной формуле R = √(S/π), где S является площадью круга.
- Радиус вписаной окружности (в квадрат) находится следующим образом: r = a/2, где а является стороной квадрата.
- Радиус описанной окружности (вокруг прямоугольника) вычисляют по формуле: R = √ (a2 + b 2)/2, где а и b являются сторонами прямоугольника.
- В том случае, если вы не знаете длину окружности, но знаете высоту и длину какого-либо ее сегмента, то вид формулы будет таков:
R = (4*h3 + L2)/8*h, где h является высотой сегмента, а L является его длиной.
Находим радиус окружности, вписанной в треугольник (прямоугольный). В треугольник, какой бы вид он не имел, может быть вписана лишь одна-единственная окружность, центр которой будет одновременно той точкой, где пересекаются биссектрисы его углов. Прямоугольный треугольник имеет множество свойств, которые должны быть учтены, когда вычисляется радиус вписанной окружности. В задаче могут быть приведены различные данные, следовательно, требуется выполнить дополнительные вычисления, необходимые для ее решения.
Советы по нахождению радиуса вписанной окружности:
- Сначала нужно построить треугольник с теми размерами, которые уже были заданы в вашей задаче. Это необходимо делать, зная размеры всех трёх сторон или двух сторон и угла между ними. Так как размер одного угла вам уже известен, то в условии должны быть два катета. Катеты, которые противолежат углам, должны быть обозначены, как а и b, а гипотенуза – как с. Что касается радиуса вписанной окружности, то он обозначается как r.
- Для применения стандартной формулы определения радиуса вписанной окружности требуется найти все три стороны прямоугольного треугольника. Зная размеры всех сторон, вы сможете найти полупериметр треугольника из формулы: p = (a + b+ c)/2.
- Если вы знаете один угол и катет, то вам следует определить, прилежащий он или противолежащий. Если он прилежащий, то гипотенузу можно вычислить, используя теорему косинусов: c = a/cosCBA. Если он противолежащий, то тогда требуется воспользоваться теоремой синусов: c=a/sinCAB.
- Если у вас есть полупериметр, то вы можете определить радиус вписанной окружности. Вид формулы для радиуса будет таким: r=√(p-b)(p-a)(p-c)/p.
- Следует отметить, что найти радиус можно по формуле: r = S/p. Так что если вам известны два катета, то процедура вычисления будет более лёгкой. Гипотенуза, требуемая для полупериметра, может быть найдена по сумме квадратов его катетов. Вычислить площадь вы можете, перемножив все имеющиеся катеты и разделив надвое число, которое вы получили.
fb.ru
