Определение длины дуги
Часть фигуры, которая образует окружность, точки которой равноудалены, называется дугой. Если из точки центра окружности, провести лучи в точки, совпадающие с концами дуги, будет образован её центральный угол.
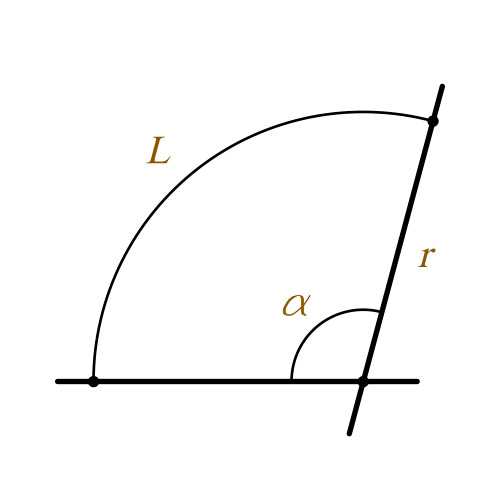
Определение длины дуги
Расчет длины дуги производится по следующей формуле:
r – радиус окружности
α – угол
L – длина дуги
π – 3.14
Расчет длины дуги
Задача:
Нужно определить длину дуги окружности радиусом 10 сантиметров при центральном угле, равном 85°.
Воспользуемся формулой
где L – искомая длина дуги, π = 3,14, r – радиус окружности, α – центральный угол.
| L | = |
3,14 × 10 × 85 180° |
= |
14,82 |
Длина дуги окружности равна 14,82 сантиметра.
В элементарной геометрии под дугой понимается подмножество окружности, расположенной между двумя расположенными на ней точками. На практике решать задачи по определению ее длины инженерам и архитекторам приходится достаточно часто, поскольку этот геометрический элемент широко распространен в самых разнообразных конструкциях.
Пожалуй, первым, перед кем встала эта задача, были древние зодчие, которым так или иначе приходилось определять этот параметр для сооружения сводов, широко используемых для перекрытия промежутков между опорами в круглых, многоугольных или эллиптических зданиях. Если внимательно присмотреться к дошедшим до наших дней шедеврам древнегреческого, древнеримского и особенно арабского зодчества, то можно заметить, что в их конструкциях дуги и своды встречаются чрезвычайно часто. Творения современных архитекторов ими не так богаты, но эти геометрические элементы наличествуют, конечно же, и в них.
Длину различных дуг необходимо рассчитывать при сооружении автомобильных и железных дорог, а также автодромов, причем во многих случаях от правильности и точности вычислений во многом зависит безопасность движения. Дело в том, что многие повороты магистралей с точки зрения геометрии представляют собой именно дуги, и по движению по ним на транспорт воздействуют различные физические силы. Параметры их результирующей во многом определяются длиной дуги, а также ее центральным углом и радиусом.
Конструкторам машин и механизмов приходится вычислить длины различных дуг для правильной и точной компоновки составных частей различных агрегатов. В данном случае ошибки в расчетах чреваты тем, что важные и ответственные детали будут неправильно взаимодействовать друг с другом и механизм просто не сможет функционировать так, как планируют его создатели. В качестве примеров конструкций, изобилующих такими геометрическими элементами, как дуги, можно привести двигатели внутреннего сгорания, коробки переключения передач, дерево- и металлообрабатывающее оборудование, кузовные элементы легковых и грузовых автомобилей и т.д.
Дуги достаточно широко встречаются в медицине, в частности, в стоматологии. Например, они используются для исправления неправильного прикуса. Корректирующие элементы, называемые брекетами (или брекет-системами) и имеющие соответствующую форму, изготавливаются из специальных сплавов, и устанавливаются таким образом, чтобы изменить положение зубов. Само собой разумеется, что для того, чтобы лечение проходило успешно, эти дуги должны быть очень точно рассчитаны. Кроме того, дуги очень широко используются в травматологии, и, пожалуй, самым ярким примером тому является знаменитый аппарат Илизарова, изобретенный российским врачом в 1951 году и чрезвычайно успешно используемый по сей день. Неотъемлемыми его частями являются металлические дуги, снабженные отверстиями, через которые продеваются специальные спицы, и являющиеся основными опорам всей конструкции.
simple-math.ru
Хорды — Длины — Таблицы
Длину хорд можно определить по таблице или по формуле [c.40]В третьей части таблицы приводят диаметр делительной окружности и толщину зуба (если отсутствуют данные для контроля) для косозубых колес — осевой шаг (а, или ход винтовой линии 5, или угол наклона зуба Ро на основном цилиндре для шевингуемых или шлифуемых колес, или при наличии в данных для контроля показателя Ьf — диаметр основной окружности и радиус кривизны в начале рабочего участка зуба (можно указать высоту кр рабочего участка зуба) толщину зуба по хорде или длину общей нормали — при отсутствии этих показателей во второй части сведения о сопряженном колесе и другие справочные данные.
Круг радиуса, равного единице — Длина дуг, хорд, стрелок и площадь сегментов — Таблицы 37, 38 Круги шлифовальные — см. [c.754] Примечание. Радиус г для данной дуги I и стрелки Л определяется из отношения г=—, где /о —длина дуги, которая при радиусе 1 соответствует заданному —, ио-/(I я мещенному в графе 1 таблицы. Если г—радиус круга, а ср —центральный угол в градусах, то 1) длина хорды S = 2г sin [c.95]
Характеристика логарифма 77 Характеристики вероятностные 326 Хорды — Длины — Таблицы 37 Храповые механизмы — см. Механизмы храповые [c.590]
ТАБЛИЦА VI. ЭЛЕМЕНТЫ КРУГА ДЛИНА ДУГИ, СТРЕЛКА, ДЛИНА ХОРДЫ И ПЛОЩАДЬ СЕГМЕНТА КРУГА ДЛЯ РАДИУСА у — — 1 [c.37]
Во второй части таблицы параметров венца приводят данные для контроля взаимного положения разноименных профилей зубьев по одному из следующих вариантов постоянная хорда зуба и высота до постоянной хорды длина общей нормали W толщина по хорде зуба и высота до хорды торцовый [c.472]
Для деления окружности на равное число частей пользуются таблицами хорд (табл. 95). Вычислив длину хорды для данного числа делений, откладывают полученную величину на разделяемой окружности. [c.193]
В таблице против числа делений 12 находим величину хорды, равную 0,5176. Умножив найденную длину хорды на радиус делимой окружности, находим длину хорды, стягивающей Vi2 часть окружности радиусом 100 мм. [c.84]
По таблице находят, что при 15 делениях, т. е. при центральном угле, равном 24°, длина хорды (5) для окружности радиуса, равного единице, есть 0,4158.
Если при заданном подъеме (отношении стрелы к хорде) длина хорды равна а, то помещенное в таблице значение длины дуги должно быть умножено на а, а площадь сегмента — на а . [c.35]
Длину измеренной хорды отсчитывают непосредственно по нониусу 4. Определение номинальной толщины зуба и высоты до постоянной хорды производят по заранее составленным таблицам этих величин или расчетом по формулам, помещенным в справочниках для машиностроителей. [c.134]
Длина хорды, при помощи которой делят окружность на конгруэнтные дуги, зависит от числа делений и величины диаметра d окружности (берется из табл. 4). Например, для деления окружности диаметром 100 мм на девять конгруэнтных дуг в первой графе таблицы находим число делений 9. Во второй графе этому числу соответствует хорда длиной 0,34202 х й — 0,34202 х 100, что составляет приближенно 34,2 мм. При помощи циркуля или циркуля-измерителя этим размером засекают на окружности точки деления. [c.47]
Библиографические указания. Определению сил, действующих на тонкие тела, которые движутся в потоке жидкости или газа, посвящена обширная литература [4, 5, 12, 14, 15, 24, 27, 28, 31, 39, 43, 52, 67, 74]. Изложение этого вопроса применительно к задачам аэроупругости можно найти в книгах [4, 15, 39, 67]. Приближенные формулы для больших сверхзвуковых скоростей приведены в статьях [27, 31, 74] сопоставление этих формул дано в книге [15]. Области применения различных аэродинамических теорий приведены в табл. 1 [39]. В этой таблице к — приведенная частота по выражению (7) 6 — отношение толщины или амплитуды к хорде крыла 1, — удлинение (отношение длины крыла к хорде). [c.473]
Приборы для деления окружностей. Применение простейших приборов для деления окружностей на равные части и отыскания длин хорд, соответствующих заданным центральным углам, освобождает разметчиков от вспомогательных графических построений или расчетов с применением таблиц (см. стр. 51).
Приборы для деления окружностей на равные части и определения хорд по центральным углам (фиг. 200) позволяют по заданному радиусу окружности без вычислений или таблиц определять длины хорд (стороны вписанных многоугольников), делящих окружности на любое число частей, а также определять хорды, соответствующие заданным центральным углам. [c.270]
Нанесение наклонных рисок. Наклонные линии под заданными углами могут быть нанесены тремя способами построением прямоугольного треугольника по его сторонам и углам построением угла наклона прямых по длине хорды, взятой из таблицы (см. стр. 37) при помощи специальных инструментов и приспособлений (см. стр. 303). [c.316]
Пользуясь угловым масштабом, опреде- 8. Постройте, пользуясь таблицей хорд, лите ширину полки А двутавра, изображенного правильный одиннадцатиугольник с диаметром на рис.. 33. Определите диаметр и длину проб- описанной окружности 65 мм. [c.27]Деление окружности на неравные части производят при помощи таблиц [41, в которых длина хорды определяется по углу между соседними лучами. [c.147]
В случае недоступности вершины полного конуса построение развертки ведут иначе. Вначале по формула. определяют R, г и а, а затем по таблице 14] —длины хорд АБ п ВГ и стрелки hi и /ij. Последовательность построения дуги по размерам хорды и стрелки приведена в п. 53 (см. рис. 84, е). [c.152]
| Таблица 7. Длины дуг I, хорд а и стрелок й сегментов круга в зависимости от центрального угла а при г = | 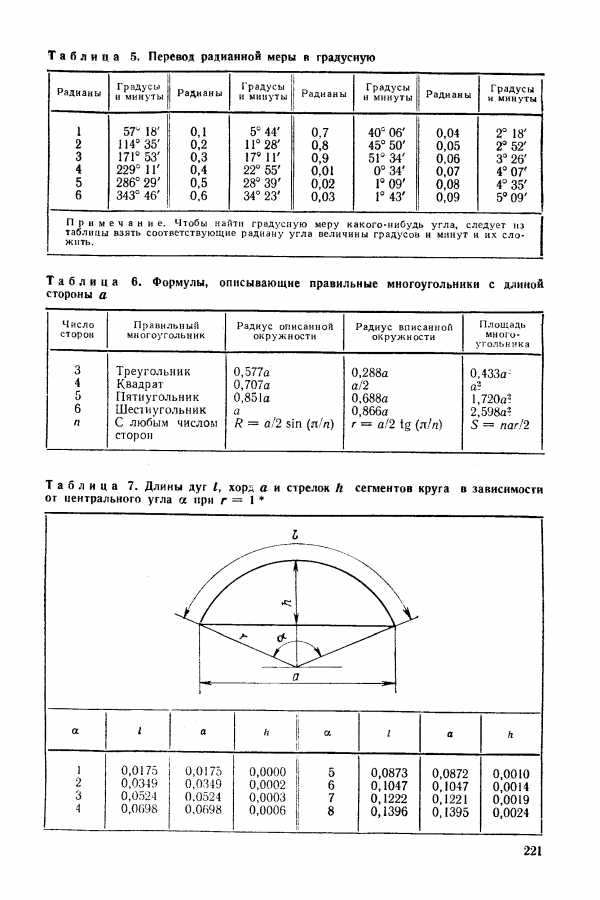 |
При плоскостной разметке приходится выполнять разнообразные построения делить прямые линии на равные части, проводить перпендикулярные и параллельные линии, строить углы, делить углы и окружности на равные части и т. д. Указанные построения слесарь должен делать быстро и точно. Для деления окружности на равное число частей можно пользоваться таблицей хорд (табл. 7). Вычислив длину хорды для данного числа делений, откладывают полученную величину на разделяемой окружности. [c.49]
| Таблица 9.1 Стрелы круговых кривых в середине хорды длиной 20 м |  |
Хорды — Длина — Таблицы 131 [c.602]
Во второй части таблицы приводят данные для контроля взаимного положения разноименных профилей зубьев по одному из следующих вариантов 1) постоянная хорда зуба и высота до постоянной хорды /г 2) длина общей нормали 3) толщина по хорде зуба у и высота до хорды Тг 4) торцовый размер по роликам (шарикам) М и диаметр ролика (шарика) [c.288]
Если радиус/ не равен единице, то для определения длины дуги /, длины стрелки /) и длины хорды з нужно табличные значения умножить на R. Таблица 4 [c.23]
Эйлер указывает, что произведение длины полной кривой на ее хорду равно площади круга радиуса, равного горизонтальному прогибу. При взятых четырехзначных таблицах получается (а — отброшена) по формулам (40), (41) и (26) 2 1,8541 2 0,8471 и я=1,4142 что дает разницу на единицу в третьем знаке после запятой. [c.12]
ТАБЛИЦА КОЭФФИЦИЕНТОВ Кз, и Кь для ПОДСЧЕТА ДЛИН ДУГ /, СТРЕЛОК Л И ДЛИН ХОРД с в ЗАВИСИМОСТИ ОТ УГЛА а° [c.259]
При фрезеровании зубчатых колес на фрезерном станке качество отфрезерованного зубчатого колеса можно определить не только измерением толщины зуба по постоянной хорде с помощью штангензубомера, но и путем измерения длины общей нормали (рис. 9) (длина общей нормали определяется по формулам или по специально подготовленным таблицам) [c.187]
Чтобы разде.шть окружность на любое число равных частей, проще всего пользоваться специальными таблицами (например, табл. 12 на стр. 23), в которых указана длина хорды х для окружности радиусом / =1. [c.154]
Примечание. Делительная толщина по хорде 51 — длина хорды, стягивающей дугу, по которой измеряется толщина зуба по делительной окружности. Делительная высота до хорды зуба ка — крат-чайщее расстояние от вершины зуба до средней точки делительной толщины по хорде. Для определения размеров вг и йо для модулей, отличных от т= . мм, необходимо данны е таблицы умножить на величину модуля. Например, при модуле 3 мм, числе зубьев 30 ка=ЗХ XI,0206 = 3,0618 3,06 мм = ЗХ 1,5700 = 4,71 мм. [c.191]
При заданных силе тяги, радиусе и концевой скорости несущего винта индуктивная и профильная мощности могут быть минимизированы соответствующим выбором крутки и сужения. На внешней части лопасти, где нагрузки самые большие, оптимальные распределения длин хорд и углов установки можно хорошо аппроксимировать линейными функциями. В самом деле, с лопастями, линейно закрученными на углы от —8 до 12°, получается почти весь тот выигрыш (по сравнению с незакру-ченными лопастями), который дают лопасти с идеальной круткой. Лопасти с линейной круткой просты в производстве, так что значительное улучшение аэродинамических характеристик достигается за счет лишь небольшого увеличения стоимости производства. Сужение также улучшает аэродинамические характеристики, но вследствие высокой стоимости производства оправдывается только для очень больших несущих винтов. В приведеной ниже таблице, составленной по данным Гессоу [c.79]
Примечание. Нормальной точностью построений следует считать точность до 0,2 мм исходя из этого, за длину дуги для вычерчивания можно принимать ее хорду при условии, что длина дуги не превышает длину ее хорды на 0,2 мм. На основании сказанного составлена таблица по В. А. Осадченко) для спрямления дуг окружностей [c.62]
Деление на семь п более частей рекомендуется производить построением с исрользованием специальной таблицы. Допустим, окружность диаметром 112,7 мм Фо) (рис. 87) необходимо разделить на п равных частей. Для этого величину Оо умножают на соответствующий коэффициент а, взятый из табл. 5. Это произведение равно длине хорды 5, соответствующей расстоянию между двумя соседними точками данной окружности. Для повышения точности разметки целесообразно расчет длины хорды вести не по [c.146]
Теплоты образования 2 — 304 Химия 2 — 269—315 Хлорметил — Свойства 2 — 97 Ходовые посадки для древесины 5 — 621 Холод искусственный — Производство — Термодинамика 2 — 97 Холодильные агенты 2 — 97, 98 Холодильные машины 2—103—105 Хомутики металлокерамическне 5 — 261 Хорды — Длины — Таблицы 1—37 Хранение моделей 5 — 23 — опок 5 — 19 [c.491]
Деление окружности на произвольное число равных частей. Разделить окрулсность на любое число равных частей можно, пользуясь таблицей хорд (табл. 4), приведенной ниже, в которой дается длина хорды в зависимости от числа сторон правильного многоугольника, вписанного в окружность, диаметр которой с1. [c.36]
В второй части таблицы (данные для контроля) приводятся размеры и от-клонемя для контроля взаимного положения разноименных п(эофилей зубьев по одном з следующих вариантов 1) постоянная хорда зуба с и в ысота до постоянной хомы Ьс й) длина общей нормали 1 3) толщина по хорде зуба и высота до хор ы Ьау 4) торцовый азмер по роликам (шарикам) М и диаметр ролика (шарика) О, и Яс определяется по табл. 5.29. [c.357]
mash-xxl.info
Как определить радиус по длине дуги и хорды?
Мда, че-то школьную задачку с ходу «не осилил» 🙂 Там есть формула дуги: L = a*R. где а — центральный угол, образующий дугу. Теперь смотрим треугольник, образованный центром, концом дуги и серединой хорды. Прямоугольный, гипотенуза = R. катет I/2, противолежащий угол a/2. Для удобства я взял не угол а, а угол b = a/2 тогд система будет такой: L = 2bR I = 2Rsin(b) После подстановки 2R, выраженного из первого уравнения во второе, получим sin(b) / b = I/L Дальше чего-то затупил, как это уравнение решить. Возможно, надо записать так sin(b) = (I/L) * b Слева — синусоида, справа — прямая, проходящая через начало координат с известным углом наклона. Теперь надо найти точку пересечения. ..Ну, хотя бы графически.. . может поможет :)) PS найдем угол b значит будем знать угол а (в радианах) , значт найдем R = L/a
Это задача Архимеда ( по-моему так и называется ) В этих формулах а — половина хорды ; L- » стрела дуги » т. е. расстояние от края до середины ; H — высота сегмента : R =(a^2+H^2)/2H ; P =2L+2/3 (L -a )/Удачи !!!
У matod всё верно. Зря только он искал школьного способа решения полученного уравнения — его нет, такое решается только численно (графически).
В общем случае решается только приближённо L= pi*R * (a/180град) = R * (a) (в радианах) l^2/4 = (2R-h)h => l^2 = 4*(2R-h)h 1/2 R^2*sina = 1/2 l(R-h) => R-h=R^2*sina/l итого 4*(R + (R^2*sina/l) )(R- (R^2*sina/l)) = l^2 (1 + (R*sina/l) )(1- (R*sina/l)) = l^2/(4*R^2) 1- (R*sina/l)^2 = l^2/(4*R^2) 1- (R*sin(L/R)/l)^2 = l^2/(4*R^2) Итого мы получили функцию одной переменной вида 1- (x*sin(L/x)/l)^2 = l^2/(4*x^2) Дальше только с помощью приближённых методов Вот решение этого уравнения <a rel=»nofollow» href=»http://www.wolframalpha.com/input/?i=1-+(x*sin(4/x)/3)^2+=+3^2/(4*x^2)+» target=»_blank» >математическим пакетом</a> при L=4 l=3 Можно, например, разложить функцию 1- (x*sin(L/x)/l)^2 — l^2/(4*x^2) в ряд<img src=»//otvet.imgsmail.ru/download/691332c04f9e8fb7d7066a0dfd404cbd_i-201.gif» >(пример разложения при L=4 l=3 ), взять ограниченное количество членов, приравнять их к нулю и искать приближённое решение Причём взяв разложение до x^8, можно найти точную относительно разложения формулу в радикалах, но она будет такой гигантской, что страшно даже представить. Вот такой (опять же при 4 и 3)<img src=»//otvet.imgsmail.ru/download/691332c04f9e8fb7d7066a0dfd404cbd_i-202.gif» > для первого корня и вот такой для второго <img src=»//otvet.imgsmail.ru/download/691332c04f9e8fb7d7066a0dfd404cbd_i-203.gif» >
Сам на работе часто сталкиваюсь с подобными расчетами, когда приносят деталь и просят сделать на ЧПУ подобный радиус. формула — R=(a^2+c^2)/2c, где а — половина хорды, с — высота дуги. Точно, как и писал выше Владимир Ерёмин 6 лет назад…
touch.otvet.mail.ru
