Решение более сложных задач по комбинаторике. Видеоурок. Алгебра 11 Класс
Из 2 математиков и 10 экономистов надо составить комиссию из 10 человек. Сколько есть способов сделать это при условии, что в комиссии должен участвовать хотя бы 1 математик?
Решение
Рассмотрим два случая:
1. В комиссии будет один математик.
Существует 2 способа выбрать 1 математика из 2. Из 10 экономистов нужно выбрать 9 человек; количество способов выбрать из 10 человек 9 – это . Следовательно, всего способов:
Однако можно посчитать иначе: выбирать не 9 экономистов из 10, а выбрать 1 экономиста из 10, который не попадет в комиссию, то есть:
2. В комиссии будет более одного математика, то есть 2.
Существует 1 способ выбрать 2 математиков из 2. Оставшиеся восемь человек комиссии должны быть экономистами. Количество способов выбрать 10 человек 8 – это . Следовательно, всего способов:
3. Складываем количество способов в первом и во втором случае:
Ответ: 65 способов.
Сколько есть способов составить ожерелье из 5 одинаковых красных бусинок и 2 одинаковых синих бусинок?
Решение
Ожерелье может быть замкнутым и незамкнутым.
1. Если ожерелье замкнутое, то между синими бусинками может находиться или 0, или 1, или 2 красных бусинок (если между синими находятся 3, 4 или 5 красных, то это тоже самое, что и 0, 1, 2, только с другой стороны) (см. Рис. 1). Следовательно, существует три варианта расположения 2 синих и 5 красных бусинок на замкнутом ожерелье.
Рис. 1. Иллюстрация к задаче
2. Если ожерелье незамкнутое (см. Рис. 2), тогда количество вариантов определяется также положением синих бусинок. Количество способов выбрать 2 места из 7 – это .
Рис. 2. Иллюстрация к задаче
Ответ: 1. Если ожерелье замкнутое, то существует три способа составить ожерелье; 2. Если ожерелье незамкнутое, то существует 21 способ составить ожерелье.
План города имеет вид прямоугольника (см. Рис. 3). Его улицы идут строго параллельно сторонам. На каждом перекрестке водитель имеет право ехать либо вправо, либо вверх. Сколько существует различных маршрутов добраться из нижнего левого угла в правый верхний?
Рис. 3. Иллюстрация к задаче
Решение
Движение водителя задается последовательностью движений вправо (П) и вверх (В). Например: если водитель использует схему движения, показанную на рисунке 4, то он 10 раз (10 клеточек) едет вправо (П), а затем 5 раз (5 клеточек) вверх (В):
Если водитель использует схему движения, показанную на рисунке 5, то он едет 1 раз вверх (В), 1 раз вправо (П), 1 раз В, 1 П, 1 В, 1 П, 1 В, 1 П, 1 В, 6 П:
Рис. 5. Иллюстрация к задаче
Таким образом, каждый маршрут водителя задается последовательностью из 15 символов В и П, при этом водитель каждый раз смещается на 10 единиц вправо и на 5 единиц вверх. Следовательно, из 15 символов 5 будут символами В, а 10 будут символами (П). Поэтому для решения задачи необходимо найти количество способов выбрать 5 мест из 15, в которых водитель поедет вверх. Это будет .
Ответ: маршрутов.
Даны 2 слова: «интегрирование» и «суперкомпьютер». Вася посчитал, сколько получается слов из слова «интегрирование», если вычеркнуть в нем 2 произвольные буквы (получившиеся слова не обязательно осмысленные). Маша сделала то же самое для слова «суперкомпьютер». У кого слов получилось больше?
Решение
В данных словах одинаковое количество букв (по 14), поэтому вычеркнуть две буквы из каждого из них можно одинаковым количеством способов. Заметим, что при вычеркивании двух букв из слова «суперкомпьютер» все полученные слова будут различны, а при вычеркивании букв РИ и ИР из слова «интегрирование» получается одно и то же слово «интегрование». Поэтому, у Маши получится на одно слово больше.
Количество способов выбрать 2 буквы из 14 – это , именно столько слов будет у Маши, а у Васи будет слов.
Ответ: больше слов получилось у Маши.
Сколько существует способов рассадить за круглый стол 5 юношей и 5 девушек так, чтобы они чередовались?
Решение
На рисунке 6 изображен стол, на котором для удобства пронумерованы места.
Рис. 6. Иллюстрация к задаче
Предположим, что на месте номер 1 сидит юноша. Тогда все юноши садятся через 1 от этого места (на нечетные места), а девушки – на четные. Количество способов усадить 5 юношей на 5 кресел (количество перестановок) – это , количество способов усадить 5 девушек на 5 кресел – это также . Значит, всего вариантов усадить юношей и девушек – это . Однако на месте номер 1 может сидеть девушка (на четных – юноши, на нечетных – девушки), тогда окончательный ответ будет в два раза больше, то есть .
Ответ: способов.
В стране есть 20 городов, которые соединены между собой 172 авиалиниями. Предположим, что между двумя городами есть только одна авиалиния. Докажите, что из любого города можно попасть в любой город, возможно, с пересадками.
Доказательство
Докажем от противного.
Предположим, что есть города и такие, что из нельзя долететь в . Тогда какой бы мы ни взяли город , одновременно существовать авиалинии и не могут (если существуют обе, можно долететь из в с пересадкой), и так для любого города из оставшихся 17 (см. Рис. 7).
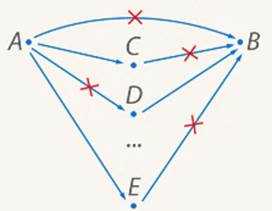
Рис. 7. Иллюстрация к задаче
Следовательно, отсутствует авиалиния и еще 18 авиалиний, которые связывают другие города либо с городом , либо с городом , то есть всего отсутствует 19 авиалиний.
В стране 20 городов, следовательно, всего теоретически возможно провести авиалиний.
Тогда если из 190 возможных авиалиний 19 отсутствуют, то присутствует всего:
авиалиния
Однако это противоречит условию:
Следовательно, исходное предположение неверно, а из любого города можно попасть в любой.
Пример
Задача 7
Дано слово «логарифм». Сколько существует способов поменять местами буквы в этом слове так, чтобы в полученном буквосочетании согласные были упорядочены по алфавиту слева направо?
Решение
Например, нам подойдут следующие буквосочетания: ОАИГЛМРФ или ГОАЛИМРФ, или ГЛМАИРОФ. В каждом буквосочетании согласные идут в определенном порядке по алфавиту (ГЛМРФ), следовательно, общее количество вариантов таких буквосочетаний определяется только 3 гласными. Поэтому достаточно определить 3 места из 8 для гласных, после чего все буквы расставляются однозначно. А это будет способов.
Ответ: 336 способов.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа 10-11 кл. В. 2 ч. Ч. 1: Учебник для общеобразоват. учреждений. – М.: Мнемозина, 2009.2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. Алгебра. Начала математического анализа. Профильный уровень: задачник для 10-11 классов. – М.: БИНОМ. Лаборатория знаний, 2009.
4. Мордкович А.Г. Алгебра и начала анализа 10-11 кл. В. 2 ч. Ч. 2: Задачник для общеобразоват. учреждений. – М.: Мнемозина, 2009.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет-сайт «Математический тандем» (Источник)
2. Интернет-сайт YouTube (Источник)
3. Интернет-сайт «МатБюро» (Источник)
Домашнее задание
1. Глава 20, задания 56, 67, 82 (стр. 382–386) – М.И. Шабунин, А.А. Прокофьев, Т.А. Олейник, Т.В. Соколова. Алгебра. Начала математического анализа. (Источник).
2. У Васи дома живут 4 кота.
а) сколькими способами можно рассадить котов по углам комнаты?
б) сколькими способами можно отпустить гулять котов?
в) сколькими способами Вася может взять на руки двух котов (одного на левую, другого на правую)?
3. Сколько различных буквосочетаний можно получить перестановкой карточек со следующими буквами: К, О, Л, О, К, О, Л, Ь, Ч, И, К?
4. Студенческая группа состоит из 23 человек, среди которых 10 юношей и 13 девушек. Сколькими способами можно выбрать двух человек одного пола?
interneturok.ru
Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний.
ОГАПОУ «Алексеевский агротехнический техникум»
Методическая разработка урока
по учебной дисциплине: «Математика: алгебра и начала математического анализа, геометрия»
Тема: «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний.»
Разработала: Медведенко Юлия Юрьевна,
преподаватель математики
г. Алексеевка
2017 г.
СОДЕРЖАНИЕ
Предисловие
Технологическая карта учебного занятия
Структура и методический инструментарий учебного занятия
Ход урока
Рефлексия
Литература
Предисловие
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций можно составить из заданных объектов, называется комбинаторикой.
Исторический экскурс
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть всевозможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов, называется комбинаторикой.
Комбинаторика возникла в XVI веке. В жизни привилегированных слоев тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и развивавшейся одновременно с ней теорией вероятностей. Одним из первых занялся подсчетом числа различных комбинаций при игре в кости итальянский математик Тарталья. Он составил таблицу, показывавшую, сколькими способами могут выпасть r костей. Однако при этом не учитывалось, что одна и та же сумма очков может быть получена разными способами (например, 1+3+4=4+2+2).
Теоретическое исследование вопросов комбинаторики предприняли в XVII веке французские ученые Паскаль и Ферма. Исходным пунктом их исследований тоже были проблемы азартных игр. Особенно большую роль здесь сыграла задача о разделе ставки, которую предложил Паскалю его друг шевалье де Мере, страстный игрок. Проблема состояла в следующем: «матч» в орлянку ведется до 6 выигранных партий; он был прерван, когда один игрок выиграл 5 партий, а другой – 4; как разделить ставку? Было ясно, что раздел в отношении 5:4 несправедлив. Применив методы комбинаторики, Паскаль решил задачу в общем случае, когда одному игроку остается до выигрыша r партий, а втолрому – s партий. Другое решение задачи дал Ферма.
Дальнейшее развитие комбинаторики связано с именами Якоба Бернулли, Лейбница и Эйлера. Однако и у них основную роль играли приложения к различным играм (лото, солитер и др.). В последнее время комбинаторика переживает период бурного развития, связанного с общим повышением интереса к проблемам дискретной математики. Комбинаторные методы используются для решения транспортных задач (составление расписаний), для составления планов производства и реализации продукции. Установлены связи между комбинаторикой и задачами линейного программирования, статистики и т.д. Комбинаторика используется для составления и декодирования шифров и решения других проблем теории информации.
Основа хорошего понимания комбинаторики умение считать, думать, рассуждать, находить удачные решения задач. Все эти навыки и способности можно выработать, если быть настойчивым, трудолюбивым и внимательным на уроках, самостоятельно и с интересом заниматься.
Урок по теме «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов» знакомит обучающихся с новым разделом математики: «Комбинаторика», основными понятиями и задачами, использованием в практических целях и в жизни человека.
Задачи с использованием элементов комбинаторики входят в состав экзамена по математике. Поэтому у обучающихся должны формироваться первоначальные представления о комбинаторных задачах.
На уроке будут использованы такие виды деятельности, как практические, самостоятельные работы, решение задач, защита докладов и сообщений. Данный урок поможет обучающимся по-другому посмотреть на окружающий мир. После данного урока они смогут объективно оценивать некоторые вещи, опираясь на математические подсчеты.
Они учатся решать комбинаторные задачи на «перестановки», «сочетания», «размещения» по формулам, что развивает логическое мышление.
Тема «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов» является первым уроком в разделе «Комбинаторика, теория вероятностей и математическая статистика» рабочей программы.
При подготовке к уроку трем обучающимся было дано опережающее задание, которое требовало самостоятельно изучить и подготовить материал к уроку по следующим вопросам: какие факторы (причины) способствовали появлению науки комбинаторики, какие ученые стояли у самых истоков возникновения, существует ли комбинаторика в реальной жизни, если да, то в каких отраслях применяется, какие задачи называются комбинаторными и как можно их решить. Рассмотрение данных вопросов в начале урока позволит вызвать интерес у обучающихся к изучаемой теме, создать рабочую атмосферу.
Предварительно была подготовлена презентация по теме «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов», которая наглядно демонстрирует основные шаги объяснения материала. Так же были подготовлены карточки с заданиями для каждого обучающегося, которые должны заполнятся в течении всего урока.
Технологическая карта учебного занятия
Дата:
Учебная дисциплина: «Математика: алгебра и начала математического анализа, геометрия».
Тема занятия: Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний.
Тип занятия: урок изучения и первичного закрепления новых знаний.
Вид занятия: смешанный урок (исследовательская работа, беседа)
Место проведения: кабинет 205.
Продолжительность: 90 минут.
Цели занятия: обеспечить оценку и проверку знаний; создать условия для развития у обучающихся умения формулировать проблемы, предлагать пути их решения, для формирования системы знаний, связанных с понятиями размещений, перестановок и сочетаний, содействовать умению общаться между собой; формировать умения делать обобщения на основе полученных данных в результате исследования, выбирать правильные утверждения из нескольких данных.
По окончанию занятия обучающийся имеет практический опыт:
Знает:
понятие предмета комбинаторика
понятие факториала
понятие размещений, перестановок и сочетаний
Умеет:
организовывать поиск, сбор и получение информации об истории развития комбинаторики, ее применении при решении задач, находить связь комбинаторики с окружающим миром, решать простейшие комбинаторные задачи.
Владеет:
умением анализировать, сравнивать, аргументировать свои ответы.
Дидактические задачи:
Образовательные: ввести понятие предмета комбинаторики, познакомить с историей развития и применения в жизни; рассмотреть различные виды комбинаторных соединений: размещения, перестановки и сочетания; сформировать у обучающихся первичные умения и навыки решения задач.
Воспитательные: формировать научное мировоззрение у обучающихся, культуру математической речи, информационную и коммуникативную культуру студентов; воспитание дружелюбного отношения друг другу, умение работать в коллективе.
Развивающие: развивать познавательный интерес студентов, логическое мышление, умение применять знания в изменённой ситуации, делать выводы и обобщения; развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля.
Методическая цель:
Использовать приемы, активизирующие внимание и память;
Продемонстрировать возможность использования на уроке информационных технологий, организацию фронтальной и индивидуальной работы.
Методы обучения:
Проблемно-поисковый, метод беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности.
Формы организации познавательной деятельности:
Фронтальная, работа в парах, индивидуальная работа.
Средства технологической поддержки учебной работы:
компьютер,
проектор,
презентация по теме «Что такое комбинаторика? Истоки комбинаторики», презентация по теме «Комбинаторика в реальной жизни», презентация по теме «Решение комбинаторных задач», «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов»
экран
5. Рабочая программа, календарно- тематический план, план занятия.
Межпредметные связи:
Обеспечиваемые – информатика, химия, экономика
Обеспечивающие – информатика, реальная математика
Структура и методический инструментарий учебного занятия
Этапы занятия | Методические приемы и методы обучения | Деятельность преподавателя | Деятельность студентов | ||
1.Организационный момент. Задача: Обеспечить нормальную внешнюю обстановку для работы на занятии, нормальный микроклимат, психологическую подготовку студентов к восприятию материала. | Методы формирования внимания долга ответственности, стремление познать новое. | Создание в аудитории рабочей обстановки, проверка отсутствующих. Преподаватель сообщает план работы урока, мотивирует студентов к деятельности. | Обучающиеся настраиваются на урок, приветствуют гостей и друг друга, быстрое включение в деловой ритм, установка внимания всей группы. | ||
2. Мотивация к усвоению нового материала Задача: организовать и целенаправить деятельность студентов, подготовить их к усвоению нового материала. | Осуществляет логический переход к теме занятия, ставит перед обучающимися проблему: решение задачи по новой теме. | Воспринимают информацию, выполняют предложенное задание, готовят себя к предстоящей работе. | |||
3.Изучение и первичное закрепление новых знаний. Задача: Изучить различные виды комбинаторных соединений, сформировать основные понятия и тезисы по теме, применить полученные знания для решения задач. | Метод словесной передачи информации и слухового восприятия информации. Метод наглядности передачи информации и зрительного восприятия информации. Иллюстрация (слайды презентации). | Определяет цели предстоящей работы; знакомит студентов с порядком выполнения работы; знакомит студентов с основными вопросами темы, предлагает задачи для закрепления, комментирует выполняемую работу. | Слушают преподавателя; выполняют работу; комментируют выполненную работу, записывают в сопроводительный лист определения, решение задач. | ||
4. Закрепление нового материала Задача: Установление правильности и осознанности усвоения нового учебного материала, выявление пробелов и неверных представлений и их коррекция. | Метод передачи информации с помощью практической деятельности, метод консультирования и взаимопомощи. | Предлагает решение задач в парах с последующей самопроверкой. | Самостоятельное выполнение заданий, требующих применения новых знаний: решение задач. | ||
5.Подвидение итогов занятия. Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы. | Метод самооценки и оценки знаний. | Кратко напоминает цель урока. Предлагает подвести итоги выставить оценки за урок. Объявляет итоговую оценку. | Высказывают свое мнение о достижении поставленной цели. | ||
6.Рефлексия. Задача: Мобилизация студентов на рефлексию (мотивация способов деятельности, общения). Усвоение принципов саморегуляции и сотрудничества. | Установление логических связей и развитее аналитика – рефлексивных способностей. | Предлагает ответить на вопросы: Достиг ли ты своих целей? Оцени степень усвоения. Продолжи одно из предложений: “Мне понятно… “Я запомнил… “Мне на уроке… “Я думаю… | Открытость студентов в осмыслении своих действий и самооценки. Прогнозирование способов саморегуляции и сотрудничества. | ||
6.Информации о домашнем задании, инструктаж по его выполнению. Задача: Сообщить студентам о домашнем задании, разъяснить методику, его выполнения. | Метод контроля и самоконтроля, метод словесной передачи информации и слухового её восприятия. | Ставит перед обучающимися проблему, разъясняет пути ее решения. | Слушают преподавателя осмысливают, записывают условия выполнения задания. | ||
Подготовительная работа.
За две недели до проведения данного урока студентам дается задание:
Исследовать различные источники, и найти информацию, так или иначе связанную с темой данного урока. (Студентам выдаются темы сообщений, список литературы, возможно, ссылки на Интернет ресурсы.)
Собранная студентами информация изучается учителем, систематизируется. Учитель выясняет, какая тема больше всего интересна каждому студенту, окончательно утверждает темы сообщений и вбираются докладчики.
Темы сообщений:
«Что такое комбинаторика? Истоки комбинаторики»
«Комбинаторика в реальной жизни»
«Решение комбинаторных задач»
Примерный перечень вопросов при работе над темой:
Основные понятия по данной теме;
Исторические комментарии;
Связь рассматриваемых объектов с природой и жизнью человека;
Интегрирование полученных знаний в различные области науки, техники, технологии, в творческие области;
Упражнения и задачи решения.
Ход урока
1. Организационный момент. Постановка цели и задач урока. (2 мин)
Преподаватель проверяет готовность к уроку.
Я рада приветствовать всех Вас на сегодняшнем уроке. Все мы с вами пришли на урок с разным настроением, но я надеюсь, что в конце нашего занятия у нас у всех будут только положительные эмоции.
Девизом нашего занятия я предлагаю взять слова английского математика Д. Сильвестра
«Число, положение и комбинация —
три взаимно пересекающиеся,
но различные сферы мысли,
к которым можно отнести
все математические идеи»
Английский математик
Джеймс Джозеф Сильвестр
(1814-1897)
2. Мотивация к усвоению нового материала. Фронтальная работа с группой. (5 мин)
Давайте здороваться, т.е. все пожмем друг другу руки. Рядом сидящим пожмем руку, а с остальными будем здороваться мысленным рукопожатием.
– В классе нас сколько?
Вопрос: Сколько было всего рукопожатий?
– Итак, какие будут ответы?
Допустим нас 25.
Каждый из 25-и человек пожал руки 24-м. Однако произведение 25 * 24 = 600 дает удвоенное число рукопожатий (так как в этом расчете учтено, что первый пожал руку второму, а затем второй первому, на самом же деле было одно рукопожатие). Итак, число рукопожатий равно: (25 * 24) : 2 = 300.
– Мы с вами столкнулись с комбинаторной задачей.
Поиском ответов на вопросы: сколько всего есть комбинаций в том или другом случае, занят целый раздел математики, и мы познакомимся с ним. Особая примета подобных задач – это вопрос, который можно сформулировать таким образом, что он начинался бы словами:
Итак тема нашего урока: «Основные понятия комбинаторики. Задачи на подсчет числа размещений, перестановок, сочетаний. Решение задач на перебор вариантов»
3. Изучение и первичное усвоение новых знаний.
Выступление учащихся с итогами своей работы:
Представителям самых различных специальностей приходиться решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.
При рассмотрении простейших вероятностных задач нам приходилось подсчитывать число различных исходов (комбинаций). Для небольшого числа элементов такие вычисления сделать несложно. В противном случае такая задача представляет значительную сложность.
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
Комбинаторика — раздел математики, в котором изучаются простейшие «соединения». Перестановки — соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их Размещения — соединения, содержащие по m предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами; число их Сочетания — соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом (в современном толковом словаре изд. «Большая Советская Энциклопедия»).
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы.
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве».
Первоначально комбинаторика возникла в XVI в в связи с распространением различных азартных игр.
Основы комбинаторики и теории вероятностей создали и разработали французские математики XVII века Пьер Ферма и Блез Паскаль.
Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты.
В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.
В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний.
Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей.
Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома.
Ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике.
В этот же период формируется терминология новой науки. Термин «сочетание» впервые встречается у Паскаля. Термин «перестановка» употребил в указанной книге Якоб Бернулли. Бернулли использовал и термин «размещение».
Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики.
Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь большей частью жизненные вопросы являются на самом деле задачами из теории вероятностей.
П. Лаплас
Проведём небольшой эксперимент, вы можете представить себя отцом дочерей-двойняшек, которым вы накупили дюжину платьев. А теперь ответьте на вопрос: сколько же существует разных вариантов одеть ваших девочек? Чтобы получить ответ, достаточно провести подсчеты на обычном листке бумаги. Но представьте на минуту, что вы — этот самый человек, который выдает штрих коды на товары. Но производителю товара уже точно не обойтись одной бумагой и карандашом; для этого необходимо владеть специальной техникой, которая обеспечит гарантированное использование всех возможных вариантов, другими словами, нужна лучшая «техника счета».
В царице наук – математике, все эти техники объединяются в одну отрасль науки, которую называют комбинаторикой. Кроме всего прочего, комбинаторика — это прелюдия к расчету вероятностей.
Области применения комбинаторики:
учебные заведения (составление расписаний)
сфера общественного питания (составление меню)
лингвистика (рассмотрение вариантов комбинаций букв)
география (раскраска карт)
спортивные соревнования (расчёт количества игр между участниками)
производство (распределение нескольких видов работ между рабочими)
агротехника (размещение посевов на нескольких полях)
азартные игры (подсчёт частоты выигрышей)
химия (анализ возможных связей между химическими элементами)
экономика (анализ вариантов купли-продажи акций)
криптография (разработка методов шифрования)
доставка почты (рассмотрение вариантов пересылки)
Решить комбинаторную задачу — это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.
Рассмотрим несколько типичных для комбинаторики задач.
Задача 1. Майор Зимин ежедневно формирует наряд для поддержания общественного порядка в городе. Наряд состоит из двух человек: старшего наряда и дежурного. В расположении майора находится 20 полицейских. На сколько дней подряд майор Зимин составит график?
Решение. Пусть сначала избирается старший наряда. Поскольку каждый полицейский может быть выбран старшим, то, очевидно, есть 20 способов его выбора. Тогда дежурным может стать каждый из оставшихся 19 полицейских. Любой из 20 способов выбора старшего наряда может осуществиться вместе с любыми из 19 способов выбора дежурного. Поэтому всего существует 20 ∙ 19 = 380 способов формирования наряда. Т.о. на 380 дней майор Зимин может составить график.
Задача 2. В отделении сержанта Сбруева проходят службу 4 новобранца: Белкин, Пенкин, Свечкин и Овечкин. В свободное от нарядов время сержант обучает их, как рассчитаться по порядку. По команде «В одну шеренгу становись!» солдаты выстраиваются справа от Сбруева и по команде «По порядку номеров рассчитайсь!» производят расчет: «первый-второй-третий-четвертый-пятый». После этого сержант перестраивает новобранцев по-новому и расчет повторяется. Сколько раз может Сбруев повторить это упражнение, используя только разные способы построения солдат?
Решение. Первого новобранца стоящего в шеренге можно выделить четырьмя способами; второго, очевидно, тремя способами. На третье место будут претендовать только два человека, и, следовательно, есть два способа заполнить третье место. Для четвертого новобранца места уже не остается, и он выступает последним.
Занумеруем новобранцев: 1 – Белкин, 2 – Пенкин, 3 – Свечкин, 4 – Овечкин.
Составим схему.
Каждый способ выбора первого новобранца может быть скомбинирован с шестью случаями выбора остальных, то число способов составляет
4 ∙ 6 = 24.
Задача 3. Сколькими способами можно выбрать из пяти разных книг какие-либо две и подарить их двум полицейским, в день милиции в городе Брюково?
Решение. Обозначим книги буквами A, B, C, D, E, можно выписать все возможные пары книг, а именно: AB, AC, AD, AE, BC, BD, BE, CD, CE, DE. Мы видим, что их число равно десяти.
Введение новых понятий (30 мин)
В практической деятельности юристам часто приходится иметь дело с различными ситуациями. Умение анализировать сложившуюся обстановку, адекватно ее оценивать и делать правильные выводы является важным качеством каждого профессионала. Во многих случаях практика приводит к комбинаторным задачам.
Факториал
Определение. Произведение всех последовательных натуральных чисел от 1 до n обозначается n!
n! = 1 · 2 · 3 · … · n.
Используя знак факториала, можно, например, записать
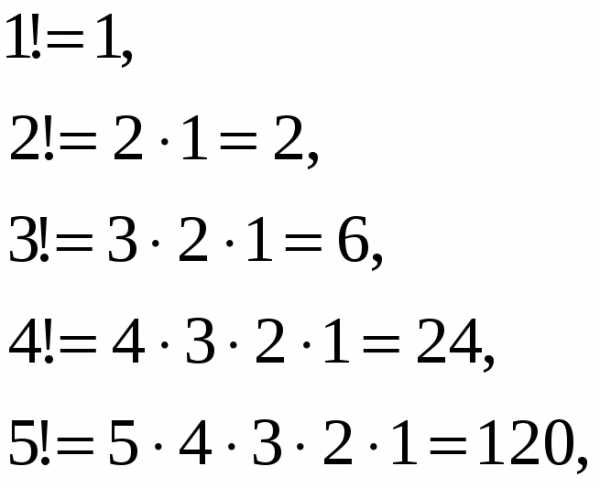
Факториалы растут удивительно быстро.
Точные значения факториалов
Размещения
Определение. Размещениями из n элементов по m называются такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их следования.
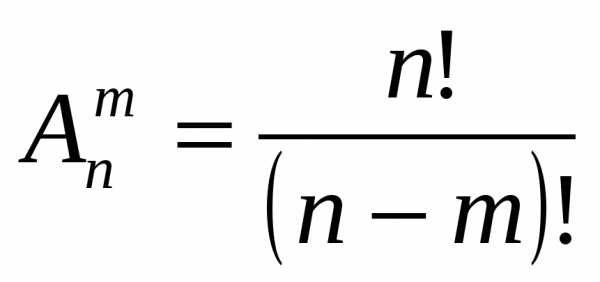
Пример. При расследовании хищения установлено, что у преступника семизначный телефонный номер, в котором ни одна цифра не повторяется и нет нуля. Следователь, полагая, что перебор этих номеров потребует одного-двухчасов, доложил о раскрытии преступления. Прав ли он?
Решение. Число номеров равно числу размещений из 9 элементов по 7, т.е. равно 
По формуле получаем номеров.
Даже если на проверку одного номера тратить 1 минуту, то на все уйдет 3024 часа или 126 суток. Таким образом, следователь – не прав.
Сочетания
Определение. Сочетаниями из n элементов по m называются такие соединения, которые отличаются друг от друга хотя бы одним элементом. (Подмножества, отличающиеся друг от друга только порядком следования элементов, не считаются различными.)
Число сочетаний из n элементов по m обозначается символом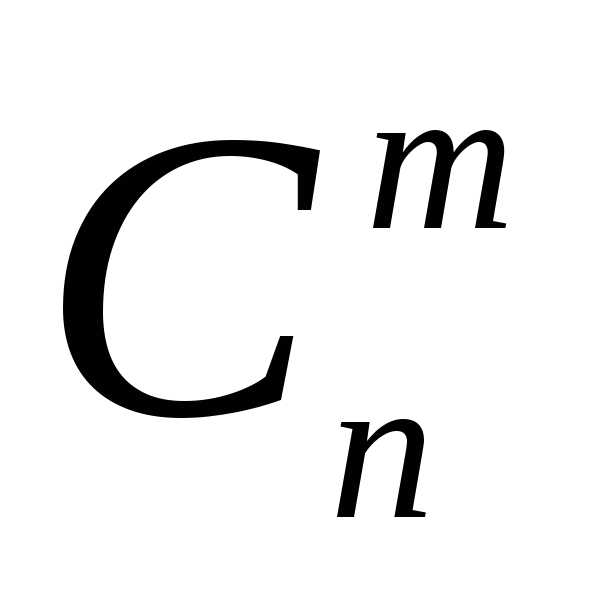 
и вычисляется по формуле:
Пример. В штате прокуратуры областного центра имеется 16 следователей. Сколькими способами можно выбрать 2 из них для проверки оперативной информации о готовящемся преступлении?
Решение. Способов столько, сколько существует двухэлементных подмножеств у множества, состоящего из 16 элементов, т.е. их число равно , т.е. всего 120 способов выбора следователей.
Перестановки
Определение. Перестановками из n элементов называются такие соединения из n элементов, которые отличаются друг от друга лишь порядком следования элементов.
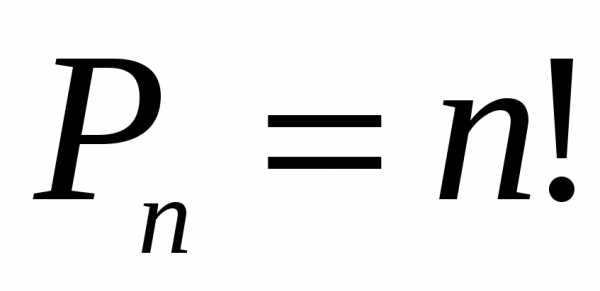
Пример. Замок сейфа открывается, если введена правильная комбинация. Преступник пытается открыть сейф, набирая код наудачу. Он знает, что код состоит из цифр 1, 2, 3, 4, 5, 6 при условии, что все числа не повторяются и последней является 5. Сколько попыток ему придется сделать.
Решение. Так как число пять должно стоять на последнем месте, то остальные пять цифр могут стоять на оставшихся местах в любом порядке. Следовательно, количество кодов из шестизначных чисел, с пятеркой на конце, равно числу перестановок из пяти элементов, т.е. .
4. Закрепление нового материала. (20 мин)
А теперь перейдем к работе в парах. Ваша задача: решить задачи, оформить их в своем конспекте, проверить и оценить свою работу. Задания на столах в ваших конспектах. Помогайте друг другу при решении. (Учитель, в процессе работы учащихся, оказывает помощь каждой паре).
Вариант 1.
1. Сколькими способами можно составить расписание одного учебного дня из 5 различных уроков?
1) 30 2) 100 3) 120 4) 5
2. На 1 курсе 12 учащихся, имеющих по математике оценки «4-5». Сколькими способами можно сформировать команду из 4 человек для участия в математической олимпиаде?
1) 128 2) 495 3) 36 4) 48
3. Сколько существует различных двузначных чисел, в записи которых можно использовать цифры 1, 2, 3, 4, 5, 6, если цифры в числе должны быть различными?
1) 10 2) 60 3) 20 4) 30
№ задания 1 2 3
№ ответа 3 2 4
Вариант 2.
1. Сколько различных пятизначных чисел можно составить из цифр 1, 2, 3, 4, 5?
1) 100 2) 30 3) 5 4) 120
2. Имеются помидоры, огурцы, лук. Сколько различных салатов можно приготовить, если в каждый салат должно входить 2 различных вида овощей?
1) 3 2) 6 3) 2 4) 1
3. Сколькими способами из 8 учебных предметов можно составить расписание учебного дня из 4 различных уроков.
1) 10000 2) 1680 3) 32 4) 1600
№ задания 1 2 3
№ ответа 4 1 2
Вариант 3.
1. Сколькими способами можно расставить 4 различные книги на книжной полке?
1) 24 2) 4 3) 16 4) 20
2. Сколько диагоналей имеет выпуклый семиугольник?
1) 30 2) 21 3) 14 4) 7
3. В футбольной команде 11 человек. Необходимо выбрать капитана и его заместителя. Сколькими способами это можно сделать?
1) 22 2) 11 3) 150 4) 110
№ задания 1 2 3
№ ответа 1 2 4
Вариант 4
1. Сколькими способами могут встать в очередь в билетную кассу 5 человек?
1) 5 2) 120 3) 25 4) 100
2. Сколькими способами из 15 учеников класса можно выбрать трёх для участия в праздничном концерте?
1) 455 2) 45 3) 475 4) 18
3. В теннисном турнире участвуют 10 спортсменов. Сколькими способами теннисисты могут завоевать золото, серебро и бронзу?
1) 600 2) 100 3) 300 4)720
№ задания 1 2 3
№ ответа 2 1 4
Вариант 5
Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
10 2) 20 3) 120 4) 50
Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
35 2) 30 3) 70 4) 45
На соревнованиях по лёгкой атлетике наш техникум представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете на первом, втором, третьем и четвёртом этапах?
120 2) 1560 3) 4800 4) 5040
№ задания 1 2 3
№ ответа 3 1 4
Сейчас каждый из вас выступит в роли учителя. Студент решил задачу. Проверьте, верно, ли решена задача:
Задача. Сколько четырехбуквенных слов можно образовать из букв слова сапфир?
Решение. P4=4! = 1*2*3*4 =24 (неверно)
.
5. Подведение итогов занятия (3мин)
Подведем итоги нашего занятия. Обсуждение и выставление оценок за урок.
6. Рефлексия. (3 мин)
Достиг ли ты своих целей? _____________________
Оцени степень усвоения: ________________________
Продолжи одно из предложений:
“Мне понятно…
“Я запомнил…
“Мне на уроке…
“Я думаю…
7. Домашнее задание (1 мин)
Решить задачу (дифференцированные задачи)
Задача на «3»
Сколько различных четырехзначных чисел можно составить из цифр 2, 3, 5, 7.
Задачи на «4»
Восемь студентов обменялись рукопожатиями. Сколько было рукопожатий?
Сколькими способами можно составить трехцветный полосатый флаг из пяти различных по цвету отрезков материи?
Задача на «5»
Сколько словарей надо издать, чтобы можно было выполнять переводы с любого из шести языков на любой из них?
kopilkaurokov.ru
Комбинаторика
Замечание 1
При решении многих практических задач часто приходится выбирать из некоторой совокупности объектов элементы, которым свойственны те или иные особенности, размещать элементы в некотором порядке, подсчитывать их количества и т.п. Поскольку в таких задачах речь идёт о комбинациях объектов, их называют комбинаторными.
Основные элементы комбинаторики, используемые при решении комбинаторных задач, таковы:
- Правила суммы и произведения;
- Перестановки без повторений;
- Размещения без повторений;
- Сочетания без повторений;
- Перестановки с повторениями;
- Размещения с повторениями;
- Сочетания с повторениями.
Правило произведения
Если элемент a множества $A$ можно выбрать $m$ способами и при каждом из этих выборов элемент $b$ множества $B$ можно выбрать $n$ способами, то упорядоченную пару ($a$;$b$) можно выбрать $m$•$n$ способами.
Правило суммы
Если элемент $a$ из множества $A$ можно выбрать $m$ способами, а элемент $b$ из множества $B$ можно выбрать $n$ способами, то число способов, которыми можно осуществить выбор хотя бы одного элемента $a$ или $b$, равно сумме $m$+$n$.
Предполагается, что выборы $a$ и $b$ взаимно исключительны, то есть ни один из способов выбора элемента a не совпадает со способом выбора элемента $b$. При наличии таких совпадений результат выбора будет равен $m$+$n$-$p$,где $p$-количество совпадений.
Замечание 2
Правила суммы и произведения справедливы не только для двух, но и для любого числа объектов.
При выборе элементов по правилу суммы используется соединитель «или»‘ (выбираем элемент из первого конечного множества, или из второго, или из третьего и т.д.).
При образовании пары (тройки, четверки и т.д.) элементов по правилу произведения используется соединитель «и»‘ (из первого множества выбираем первый элемент и к нему присоединяем второй элемент из второго множества — образуется пара, и к паре присоединяем третий элемент из третьего множества — образуется тройка и т.д.).
Количество перестановок без повторений
Рассмотрим свойства сочетаний без повторений в комбинаторике. Разные последовательности, которые можно построить из элементов данного множества, взятых ровно по одному разу, называются перестановками. Эти последовательности отличаются друг от друга только порядком расположения элементов.
Например, из двухэлементного множества $M2$={$a$,$b$} можно образовать два упорядоченных двухэлементных множества: {$a$,$b$} или {$b$,$a$}.
Формула числа перестановок в комбинаторике: $Pn$ = $n$!
Комбинаторика: правило размещения без повторений
Подмножество, выбираемое из данного множества предметов, называют выборкой. Выборки бывают упорядоченные и неупорядоченные. Для упорядоченной выборки существенен порядок элементов. Иначе говоря, меняя порядок элементов, мы получаем другие выборки. Составим, например, из цифр 1, 2, 3, 4, 5 трехзначные числа: 123, 431, 524 и т.д. Это упорядоченные трехэлементные выборки, отличающиеся составом или порядком элементов.
Размещениями из $n$ элементов по $m$ элементов ($m$≤$n$) называют упорядоченные $m$-элементные выборки из данных $n$ элементов.
Формула размещения без повторений в комбинаторике $n$ по $m$ элементов имеет вид: $A_{n}^{m} =\frac{n!}{\left(n-m\right)!} $.
Сочетания без повторений
Сочетаниями из $n$ элементов по $m$ ($m$≤$n$) в комбинаторике называют неупорядоченные $m$-элементные выборки из данных $n$ элементов. Сочетания отличаются друг от друга хотя бы одним элементом, а порядок элементов не существенен.
Формула cочетания в комбинаторике выглядит следующим образом: $C_{n}^{m} =\frac{n!}{m!\cdot \left(n-m\right)!} $.
Размещения с повторениями
Разные упорядоченные последовательности длиной $m$, составленные из элементов данного множества, содержащего $n$ элементов, так, что эти элементы в последовательности могут повторяться, называются размещениями с повторениями из $n$ по $m$.
Формула числа размещений с повторениями: $\bar{A}_{n}^{m} =n^{m} $.
Комбинаторика: перестановка с повторением
Рассматриваем мультимножество M, то есть множество, которое может содержать одинаковые элементы.
Пусть заданы предметы $m$-типа. Сколько существует перестановок $n_1$ элементов первого типа, $n_2$ — второго типа и так далее, внутри предмета $m$-типа? Такие перестановки в комбинаторике называют перестановками с повторениями.
Формула числа перестановок с повторениями: $P\left(n_{1} ,n_{2} ,\ldots ,n_{m} \right)=\frac{n!}{n_{1} !\cdot n_{2} !\cdot \ldots \cdot n_{m} !} $, где $n=n_{1} +n_{2} +\ldots +n_{m} $ — общее число элементов множества.
Сочетания с повторениями
Имеем множество из $n$ элементов. Разные неупорядоченные наборы, составленные из $m$ элементов этого множества так, что могут повторяться и порядок их несущественен. Иначе говоря, это число способов, которыми можно разложить $m$ одинаковых предметов по $n$ ящикам.
Формула числа сочетаний с повторениями: $\bar{C}_{n}^{m} =\frac{\left(n+m-1\right)!}{m!\cdot \left(n-1\right)!} $.
Рассмотрим теперь как решать задачи на комбинаторику — ниже приведены различные примеры и задачи с сочетаниями, размещениями и перестановками.
Пример 1
Задание: химик использует семь ингредиентов для приготовления нужного состава. Сколькими способами можно осуществить порядок приготовления?
Решение. Давайте применим элементы комбинаторики и осуществим решение. Как известно, перестановками из $n$ элементов называются комбинации, состоящие из $n$ элементов и отличающиеся порядком расположения элементов.
Количество перестановок вычисляется по формуле $P_{n} =n!$.
Количество различных порядков вливания семи ингредиентов в сосуд — это число перестановок из семи элементов: $P_{7} =7!=1\cdot 2\cdot 3\cdot 4\cdot 5\cdot 6\cdot 7=5040$.
Разберём еще один пример задачи на размещение в комбинаторике с решением.
Пример 2
Задание: На собрании присутствуют 20 человек. Сколькими способами из присутствующих можно выбрать председателя, члена президиума и секретаря?
Решение. Как известно, количество размещений вычисляется по формуле $A_{n}^{m} =\frac{n!}{\left(n-m\right)!} $.
Количество различных способов выбора из двадцати присутствующих на собрании председателя, члена президиума и секретаря — это число размещений из двадцати элементов по три: $A_{20}^{3} =\frac{20!}{\left(20-3\right)!} =\frac{20!}{17!} =18\cdot 19\cdot 20=6840$.
Пример 3
Задание. Директор завода заполняет три вакансии из числа 10 претендентов. Сколькими способами директор может заполнить эти вакансии?
Решение. Количество различных способов выбора из десяти выпускников университета троих для заполнения вакансий — это число размещений из десяти элементов по три: $A_{10}^{3} =\frac{10!}{\left(10-3\right)!} =\frac{10!}{7!} =8\cdot 9\cdot 10=720$.
spravochnick.ru
Комбинаторика. Примеры решения задач
Комбинаторика
1. Перестановками из элементов называют соединения, состоящие из одних и тех же различных элементов и отличающихся только порядком их расположения: ,
где Причем по определению .
Пример. Скольким числом способов можно расставить на полке восьмитомник?
Решение. Искомое число перестановок
.
Перестановки с повторениями — видеоурок:
Размещениями из элементов по называются такие соединения, которые отличаются друг от друга либо составом элементов, либо их порядком.
.
Пример. Сколько различных двузначных чисел можно составить из множества цифр , причем так, чтобы цифры числа были различны?
Решение. Искомое число чисел .
Сочетаниями элементов по m называются такие соединения, которые отличаются друг от друга только составом элементов, порядок соединения элементов не важен.
Пример. Скольким числом способов можно в группе из 30 человек распределить три бесплатные путевки?
Решение. Искомое число способов .
Следует отметить, что число размещений, перестановок и сочетаний связаны равенством
www.matem96.ru