Эйлер венн диаграмма – —

Диаграммы Эйлера-Венна Википедия

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества^[1][2].

Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов^[3], для :

• описания функционирования формальных нейронов Мак-Каллока и сетей из них^[4]
• синтеза надежных сетей из не вполне надежных элементов^[5],
• построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств ^[6],
• получения логических следствий из заданной информации, минимизации формул исчислений^[7][8].

Диаграммы Венна при помощи n{\displaystyle n} фигур изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру^[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм ^[10], понятие сети диаграмм, использующей диаграммы Венна как операторы^[11].

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.

ru-wiki.ru

Диаграмма Эйлера — это… Что такое Диаграмма Эйлера?



Диаграмма Эйлера

Пример диаграммы Эйлера. B — живое существо, A — человек, C — неживая вещь.

Круги́ Э́йлера^[1] — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.

Важный частный случай кругов Эйлера — диаграммы Эйлера — Венна, изображающие все 2ⁿ комбинаций n свойств, то есть конечную булеву алгебру. При n = 3 диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

При решении целого ряда задач Леонард Эйлер использовал идею изображения множеств с помощью кругов. Однако, этим методом ещё до Эйлера пользовался выдающийся немецкий философ и математик Готфрид Вильгельм Лейбниц (1646—1716). Лейбниц использовал их для геометрической интерпретации логических связей между понятиями, но при этом всё же предпочитал использовать линейные схемы.

[2]

Но достаточно основательно развил этот метод сам Л. Эйлер. Методом кругов Эйлера пользовался и немецкий математик Эрнст Шрёдер (1841—1902) в книге «Алгебра логики». Особенного расцвета графические методы достигли в сочинениях английского логика Джона Венна (1843—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году. Поэтому такие схемы иногда называют Диаграммы Эйлера — Венна.

Примечания

1. ↑ «Круги…» — это условный термин, вместо кругов могут быть любые многомерные фигуры, иерархически расположенные в пространстве, то есть одни фигуры поглощают либо часть других фигур, либо полностью.
2. ↑ Leibniz G. W. Opuscules et fragments inédits de Leibniz. — Paris, 1903. — p. 293—321.

См. также

Ссылки

Wikimedia Foundation. 2010.

• Диаграмма Смита
• Диаграмма Фейнмана

Смотреть что такое «Диаграмма Эйлера» в других словарях:

• ДИАГРАММА ЭЙЛЕРА — ДИАГРАММА ЭЙЛЕРА, простая диаграмма, используемая в логике для демонстрации силлогизмов. Классы предметов изображаются в виде кругов, и утверждения типа «Некоторое а находится в b» представляется двумя пересекающимися кругами, представляющими а и …   Научно-технический энциклопедический словарь

• Диаграмма Венна — Диаграмма Венна, показывающая все пересечения греческого, русского и латинского алфавитов (буквы заглавные) Диаграмма Венна …   Википедия

• диаграмма Далитца — Область фазового пространства трёх частиц, остающаяся после факторизации его по области изменения углов Эйлера …   Политехнический терминологический толковый словарь

• Круги Эйлера — Пример кругов Эйлера. Буквами обозначены, например, свойства:   живое существо,   человек,   неживая вещь Круги Эйлера[1]  геометрическая схема, с помощью которой можно изобразить отношения …   Википедия

• Диаграммы Эйлера—Венна — Пример диаграммы Эйлера. B  живое существо, A  человек, C  неживая вещь. Круги Эйлера[1]  геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… …   Википедия

• Наркотик/Диаграмма — Приведённые ниже круги Эйлера представляют собой попытку в наглядном виде представить в пересекающихся группах и подгруппах наиболее распространённые психоактивные средства, с использованием и синтезом классификаций, основаных как на их… …   Википедия

• Наркотики/Диаграмма — Приведённые ниже круги Эйлера представляют собой попытку в наглядном виде представить в пересекающихся группах и подгруппах наиболее распространённые психоактивные средства, с использованием и синтезом классификаций, основаных как на их… …   Википедия

• Диаграммы Венна — Пример диаграммы Эйлера. B  живое существо, A  человек, C  неживая вещь. Круги Эйлера[1]  геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Эйлером. Используется в… …   Википедия

• Симметрическая разность — Не следует путать с Разность множеств. Диаграмма Эйлера Венна для симметрической разности Симметрическая разность двух множеств это теоретико множественная операция, р …   Википедия

• Тессеракт — Диаграмма Шлегеля для тессеракта. Изображена проекция (перспектива) четырёхмерного куба на трёхмерное пространство …   Википедия

dic.academic.ru

Диаграмма Эйлера — Венна Википедия

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества^[1][2].

Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов^[3], для :

• описания функционирования формальных нейронов Мак-Каллока и сетей из них^[4]
• синтеза надежных сетей из не вполне надежных элементов^[5],
• построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств^[6],
• получения логических следствий из заданной информации, минимизации формул исчислений^[7][8].

Диаграммы Венна при помощи n{\displaystyle n} фигур изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру^[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм ^[10], понятие сети диаграмм, использующей диаграммы Венна как операторы^[11].

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами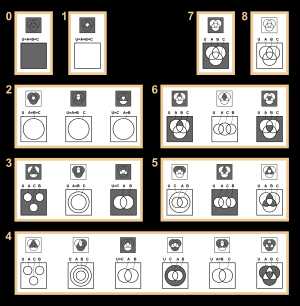 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера в отличие от диаграмм Эйлера — Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.

Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера^[12]. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[12].

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

См. также

Примечания

1. ↑ Столл, 1968, с. 25.
2. ↑ Нефедов, 1992, с. 8.
3. ↑ Кузичев, 1968, с. 106.
4. ↑ Кузичев, 1968, с. 171.
5. ↑ Кузичев, 1968, с. 134.
6. ↑ Кузичев, 1968, с. 9.
7. ↑ Кузичев, 1968, с. 97.
8. ↑ Столл, 1968, с. 26.
9. ↑ Кузичев, 1968, с. 57.
10. ↑ Кузичев, 1968, с. 124.
11. ↑ Кузичев, 1968.
12. ↑ ^{1 2} Кузичев, 1968, с. 25.

Ссылки

Литература

wikiredia.ru

Диаграммы Эйлера-Венна Википедия

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества^[1][2].

Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов^[3], для :

• описания функционирования формальных нейронов Мак-Каллока и сетей из них^[4]
• синтеза надежных сетей из не вполне надежных элементов^[5],
• построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств^[6],
• получения логических следствий из заданной информации, минимизации формул исчислений^[7][8].

Диаграммы Венна при помощи n{\displaystyle n} фигур изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру^[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм ^[10], понятие сети диаграмм, использующей диаграммы Венна как операторы^[11].

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера в отличие от диаграмм Эйлера — Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.

Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера^[12]. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[12].

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

См. также

Примечания

1. ↑ Столл, 1968, с. 25.
2. ↑ Нефедов, 1992, с. 8.
3. ↑ Кузичев, 1968, с. 106.
4. ↑ Кузичев, 1968, с. 171.
5. ↑ Кузичев, 1968, с. 134.
6. ↑ Кузичев, 1968, с. 9.
7. ↑ Кузичев, 1968, с. 97.
8. ↑ Столл, 1968, с. 26.
9. ↑ Кузичев, 1968, с. 57.
10. ↑ Кузичев, 1968, с. 124.
11. ↑ Кузичев, 1968.
12. ↑ ^{1 2} Кузичев, 1968, с. 25.

Ссылки

Литература

wikiredia.ru

Диаграммы Эйлера-Венна — Студопедия.Нет

Чтобы наглядно изображать множества, английский математик Джон Венн (1834-1923) предложил использовать замкнутые фигуры на плоскости. Намного раньше Эйлер (1707-1783) для изображения отношений между множествами использовал круги. Позднее такие изображения получили названия диаграмм Эйлера-Венна.

Диаграммы – очень удобный инструмент, позволяющий изображать множества и иллюстрировать операции над ними. Это геометрические представления множеств.

Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри него – кругов или каких-либо других замкнутых фигур, представляющих множества, входящие в универсальное. Фигуры находятся в определенном положении по отношению друг к другу. В наиболее общем случае они пересекаются. Точки, лежащие внутри различных областей диаграммы, обозначают элементы соответствующих множеств.

Все множества на диаграммах обозначаются, как обычно, заглавными буквами латинского алфавита. Построив диаграмму, обычно штрихуют определенные области для обозначения вновь образованных множеств, или выделяют это множество каким-либо другим способом.

В таблице 1 приведены иллюстрации операций объединения, пересечения, разности, дополнения и симметрической разности двух множеств А и В, входящих в универсальное множество U.

Примеры построения более сложных диаграмм приведены ниже.

 

Пример 3. Представить множество диаграммой Эйлера-Венна.

Решение: 1) Обозначим множества А, В, С и универсальное множество U (см. рис. 1а).

2) Заштрихуем множество В диагональными линиями в одном направлении, а — в другом. Площадь с двойной штриховкой представляет собой их пересечение, т.е. множество . Выделим это вновь полученное множество жирной линией (рис. 1б).

3) Сделаем копию диаграммы, на которой заштрихуем областьлиниями одного направления, а А – другого. Вся заштрихованная область представляет объединение множеств А и , т.е. то, что требовалось по заданию. Обведем искомую область жирной линией. (рис. 1в)

Таблица 1

 

 

а) б) в)

 

Рис. 1

 

Диаграммы Эйлера-Венна также могут использоваться для решения задач, связанных с пересеченными множествами.

При этом для двухпеременных пересеченных множеств используется формула:

|АÈВ| = |А| +|В| — |АÇВ|,

где |А| — число элементов множества А;

|В| — число элементов множества В;

|АÇВ| — число элементов, входящих одновременно и в множество А, и в множество В.

Для трехпеременных пересеченных множеств используется формула:

|АÈВÈС|= |А|+ |В|+ |С| — |АÇВ| — |АÇС| — |ВÇС| + |АÇВÇС|.

Пример 4. Из 100 студентов английский язык изучают 28, немецкий – 30 , французский – 42, английский и немецкий – 8, английский и французский – 10, немецкий и французский – 5, немецкий, английский и французский – 3:

а) сколько студентов не изучают ни одного языка?

б) сколько студентов изучают один английский?

в) один французский?

г) один немецкий?

д) менее двух языков?

Решение. Обозначим: Е – множество всех студентов, А – множество студентов, изучающих английский язык, В – немецкий, С – французский.

Имеем:

|А| = 28, |В| = 30, |С| = 42, |АÇВ| = 8, |АÇС| = 10, |ВÇС| = 5, |АÇВÇС| = 3.

б) один английский изучают:

|А| — |АÇВ| — |АÇС| + |АÇВÇС| = 28 – 8 – 10 + 3 = 13.

в) один французский:

|С| — | ВÇС | — |АÇС| + |АÇВÇС| = 42 – 5 – 10 + 3= 30.

г) один немецкий: |В| — |ВÇС| — |АÇВ| + |АÇВÇС| = 30 – 5 – 8 + 3 = 20.

а) ни одного языка не изучают: , но

|АÈВÈС|= |А|+ |В|+ |С| — |АÇВ| — |ВÇС| — |АÇС| + |АÇВÇС|=

=100 – 8 – 10 – 5 + 3=80.

Тогда = 100 – 80 = 20.

д) |АÇВ| + |АÇС| + |ВÇС| — 2|АÇВÇС| = 8 + 10 + 5 — 2·3 = 23 – 6 = 17.

Решение данной задачи можно произвести с помощью диаграммы Эйлера-Венна.

Рис. 2

studopedia.net

Диаграммы Эйлера — Венна Википедия

Диаграмма Венна (также используется название диаграмма Эйлера — Венна) — схематичное изображение всех возможных отношений (объединение, пересечение, разность, симметрическая разность) нескольких (часто — трёх) подмножеств универсального множества. На диаграммах Венна универсальное множество U{\displaystyle U} изображается множеством точек некоторого прямоугольника, в котором располагаются в виде кругов или других простых фигур все остальные рассматриваемые множества^[1][2].

Диаграммы Венна применяются при решении задач вывода логических следствий из посылок, выразимых на языке формул классического исчисления высказываний и классического исчисления одноместных предикатов

[3], для :

• описания функционирования формальных нейронов Мак-Каллока и сетей из них^[4]
• синтеза надежных сетей из не вполне надежных элементов^[5],
• построения управляющих и самоуправляющихся систем и блочного анализа и синтеза сложных устройств^[6],
• получения логических следствий из заданной информации, минимизации формул исчислений^[7][8].

Диаграммы Венна при помощи n{\displaystyle n} фигур изображают все 2n{\displaystyle 2^{n}} комбинаций n{\displaystyle n} свойств, то есть конечную булеву алгебру^[9]. При n=3{\displaystyle n=3} диаграмма Эйлера — Венна обычно изображается в виде трёх кругов с центрами в вершинах равностороннего треугольника и одинаковым радиусом, приблизительно равным длине стороны треугольника.

Дальнейшим развитием аппарата диаграмм Венна в классическом исчислении высказываний является аппарат вероятностных диаграмм ^[10], понятие сети диаграмм, использующей диаграммы Венна как операторы^[11].

Они появились в сочинениях английского логика Джона Венна (1834—1923), подробно изложившего их в книге «Символическая логика», изданной в Лондоне в 1881 году.

Связь диаграмм Эйлера и Венна

Пример получения произвольных кругов Эйлера из диаграмм Венна с пустыми (чёрными) множествами 22 (из 256) существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу)

Диаграммы Эйлера в отличие от диаграмм Эйлера — Венна изображают отношения между множествами: непересекающиеся множества изображены непересекающимися кругами, а подмножества изображены вложенными кругами.

Диаграммы Венна основаны на существенно иной идее, чем круги Эйлера^[12]. Круги Эйлера возникли на основе идей силлогистики Аристотеля. Диаграммы Венна были созданы для решения задач математической логики. Их основная идея разложения на конституенты возникла на основе алгебры логики^[12].

На рис. ниже даны диаграммы Венна и Эйлера для 3 множеств однозначных натуральных чисел:

• A={1,2,5}{\displaystyle A=\{1,\,2,\,5\}}
• B={1,6}{\displaystyle B=\{1,\,6\}}
• C={4,7}{\displaystyle C=\{4,\,7\}}

• диаграмма Эйлера

• диаграмма Венна

Иногда, если какая-то комбинация свойств соответствует пустому множеству, то эту комбинацию закрашивают. На рисунке справа даны 22 существенно различных диаграмм Венна с 3 кругами (сверху) и соответствующие им диаграммы Эйлера (снизу). Некоторые из диаграмм Эйлера не типичны, а некоторые даже эквивалентны диаграммам Венна. Черные области указывают на то, что в них нет элементов (пустые множества).

См. также

Примечания

1. ↑ Столл, 1968, с. 25.
2. ↑ Нефедов, 1992, с. 8.
3. ↑ Кузичев, 1968, с. 106.
4. ↑ Кузичев, 1968, с. 171.
5. ↑ Кузичев, 1968, с. 134.
6. ↑ Кузичев, 1968, с. 9.
7. ↑ Кузичев, 1968, с. 97.
8. ↑ Столл, 1968, с. 26.
9. ↑ Кузичев, 1968, с. 57.
10. ↑ Кузичев, 1968, с. 124.
11. ↑ Кузичев, 1968.
12. ↑ ^{1 2} Кузичев, 1968, с. 25.

Ссылки

Литература

wikiredia.ru

Диаграммы Венна — Викизнание… Это Вам НЕ Википедия!

Диаграммы Венна (Venn diagrams) — общее название целого ряда методов визуализации и способов графической иллюстрации, широко используемых в различных областях науки и математики: теория множеств, теория вероятностей, эвентология, логика, статистика, компьютерные науки, «формальные нейронные сети» и др.; введены Джоном Венном, британским философом, математиком и логиком в 1881; показывают математические, теоретико-множественные или логические отношения между множествами или событиями; собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства; разновидностями диаграмм Венна служат: диаграммы Эйлера, диаграммы Джонстона, карты Карно, диаграммы Перси, «зубчатые колеса» Эдвардса.

Диаграммы Венна[править]

Диаграмма Венна четырёх множеств.

Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.

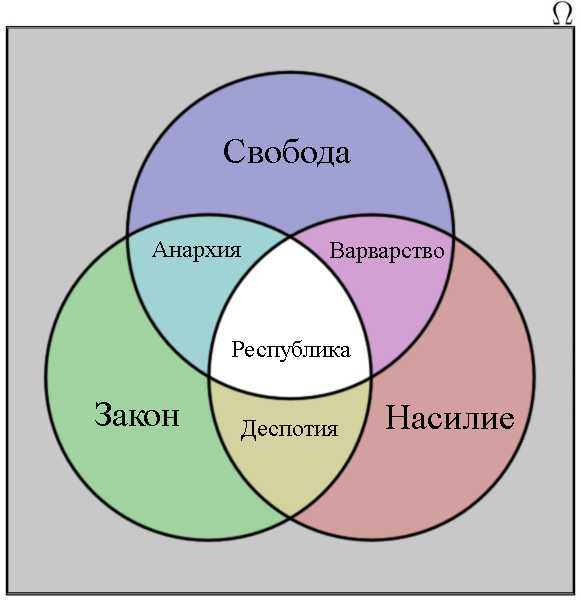Диаграмма Венна, иллюстрирующая представления Канта о формах государства.

Диаграммы Эйлера[править]

Диаграммы Эйлера аналогичны диаграммам Венна, но не обязательно иллюстрируют все возможные отношения между множествами или событиями.

Диаграммы Джонстона[править]

Диаграммы Джонстона используются для иллюстрации высказываний пропозициональной логики, таких как «Ни A или B истинно» и служат способом визуализаций таблиц истинности. Внешне они идентичны диаграммам Венна, но не представляют множеств.

Карты Карно[править]

Карты Карно, или диаграммы Вейча (Veitch), — ещё один способ визуализации выражений булевой алгебры.

Диаграммы Перси[править]

Диаграммы, предложенные Чарльзом Перси (Charles Peirce), — расширение диаграмм Венна, которое включает дополнительную логическую информацию, а также информацию о вероятностях и отношениях.

«Зубчатые колеса» Эдвардса[править]

А.В.Ф.Эдвардс (A.W.F.Edwards) дал красивую конструкцию для большого числа множеств, используя центральную симметрию и изображая множества в виде «зубчатых колес».

Ошибка создания миниатюры: Ошибочный параметр миниатюры

Диаграмма Венна, иллюстрирующая эвентологическое распределение стечения событий на рынке четырёх напитков.

Диаграммы Венна, широко используемые в эвентологии для визуализации эвентологических распределений множеств событий, содержат дополнительную информацию о возможных стечениях событий и их вероятностях.

www.wikiznanie.ru