Расчет средних показателей динамического ряда
Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средние уровни ряда и средние показатели изменения уровней ряда.
Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны.
Для интервальных рядов динамики из абсолютных уровней средний за период времени определяется по формуле средней арифметической:
а) при равных интервалах применяется средняя арифметическая простая:
,
где у1,…,уn – абсолютные уровни ряда;
б) при неравных интервалах – средняя арифметическая взвешенная:
,
где у1,…,уn – уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени, t; t1,…, tn – веса, длительность интервалов времени (дней, месяцев) между смежными датами.
Средний уровень производства электроэнергии за 1989-1994 гг.:
.
Средний уровень моментного ряда динамики с равноотстоящими уровнями определяется по формуле средней хронологической моментного ряда:
,
где у1,…,уn – уровни периода, за который делается расчет; n – число уровней; n–1 – длительность периода времени.
Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний годовой абсолютный прирост как среднюю арифметическую простую: 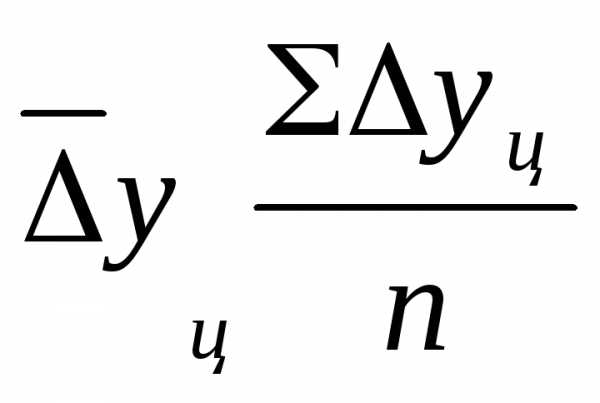 ,
,
где n – число цепных абсолютных приростов 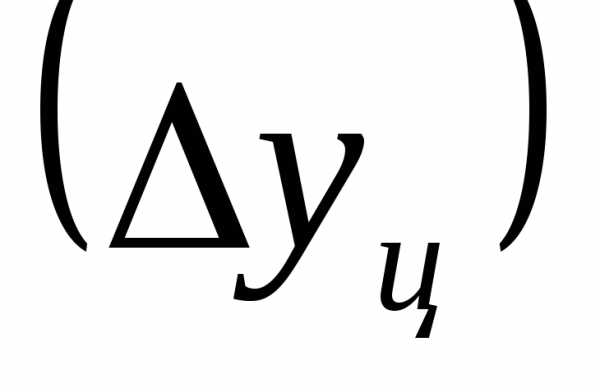 визучаемом
периоде.
визучаемом
периоде.
Используя данные табл. 5 о цепных абсолютных приростах производства электроэнергии, млрд кВт-ч:
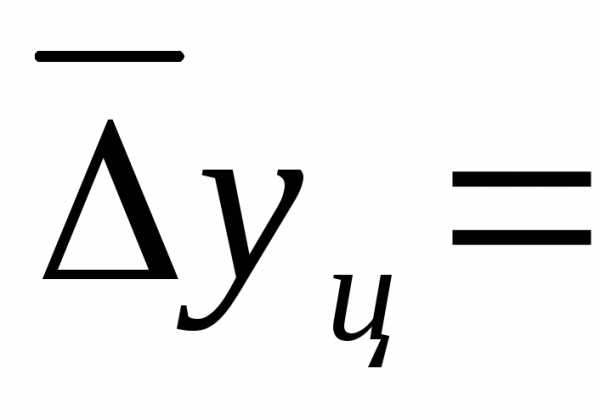 (5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
(5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
Средний
абсолютный прирост определим через
накопленный (базисный)
абсолютный прирост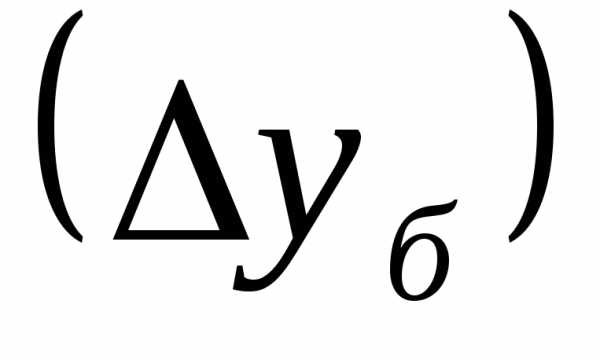
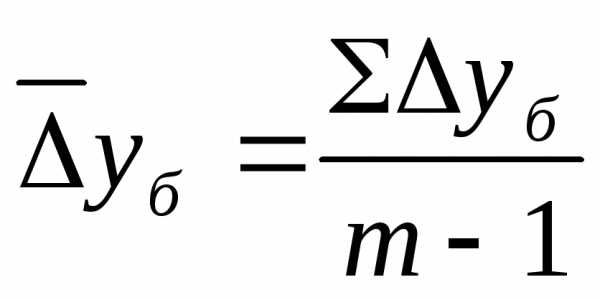 ,
,
где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Для нашего примера, млрд кВт-ч:

т.е. получен тот же результат.
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа (снижения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, , то для равностоящих рядов динамикирасчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по цепному способу):
,
где n – число цепных коэффициентов роста; 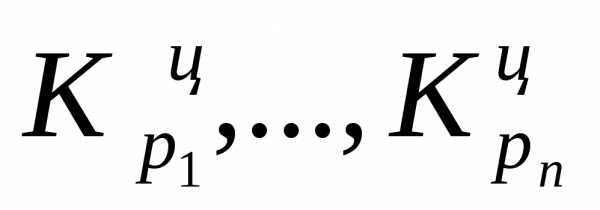 ‑
цепные коэффициенты роста;
‑
цепные коэффициенты роста;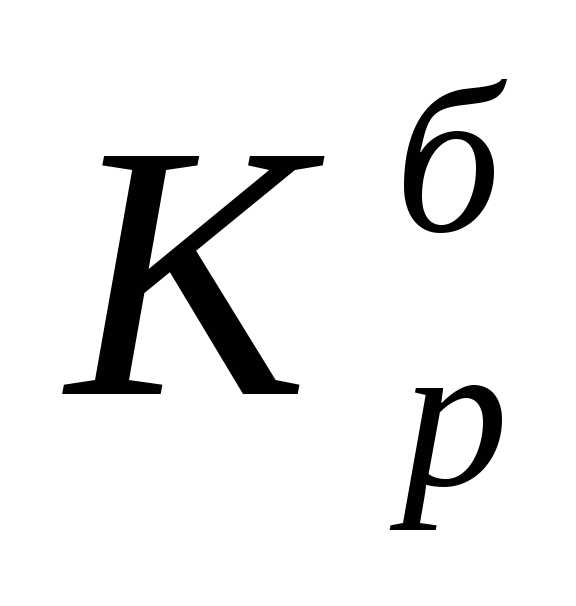 ‑
базисный коэффициент роста за весь
период.
‑
базисный коэффициент роста за весь
период.
В нашем примере среднегодовой темп изменения производства электроэнергии с 1990 по 1994г.:
;
Следовательно, с 1990 по 1994г. производство электроэнергии в России снижалось в среднем на 4 % в год, т.е. (0,96 * 100) – 100.
Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода уп на уровень базисного периода у0.
Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу») выглядит следующим образом:
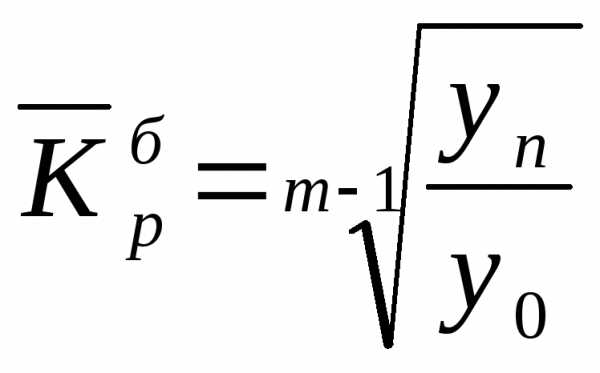 ,
,
где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Для расчета средних коэффициентов роста не нужно знать годовые темпы. Для нашего примера:
Получен тот же результат, расчеты упрощены.
Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100%. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
; 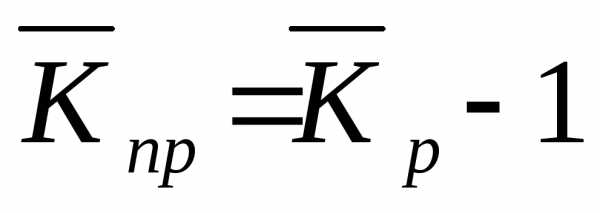 ,
,
где 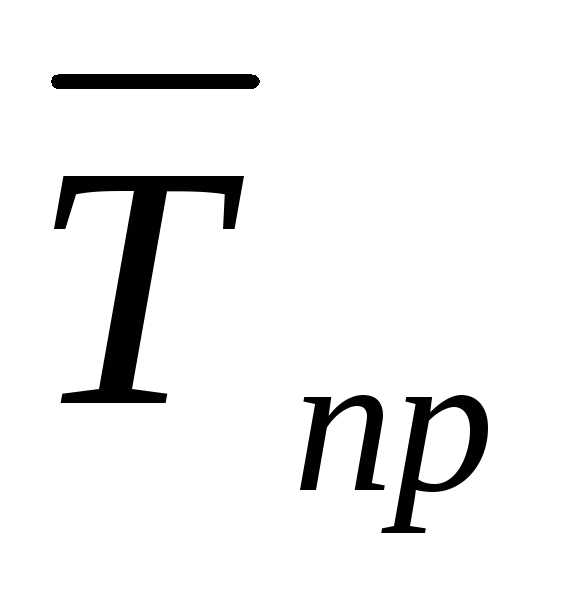 ‑ средний темп прироста.
‑ средний темп прироста.
Если
уровни ряда динамики снижаются, то
средний темп роста будет
меньше 100 %, а средний темп прироста —
отрицательной величиной.
Отрицательный темп прироста 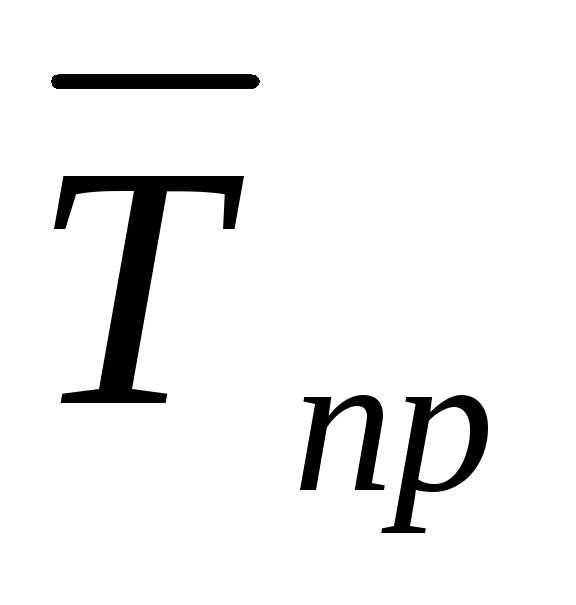 представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
При анализе развития явлений, отражаемых двумя динамическими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамических рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к различным организациям (министерствам, предприятиям, учреждениям), или при сравнении рядов разного содержания, но характеризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах.
Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
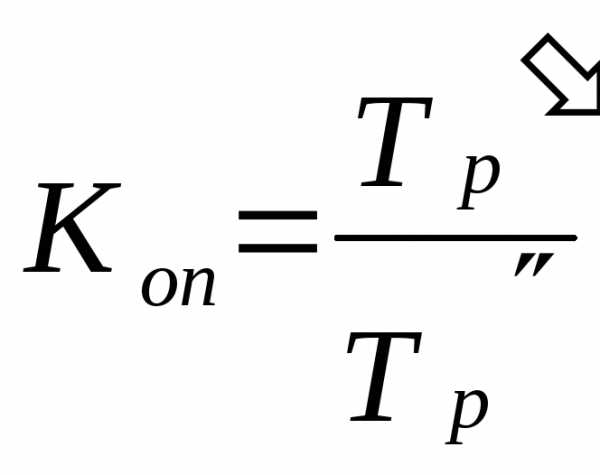 ,
, 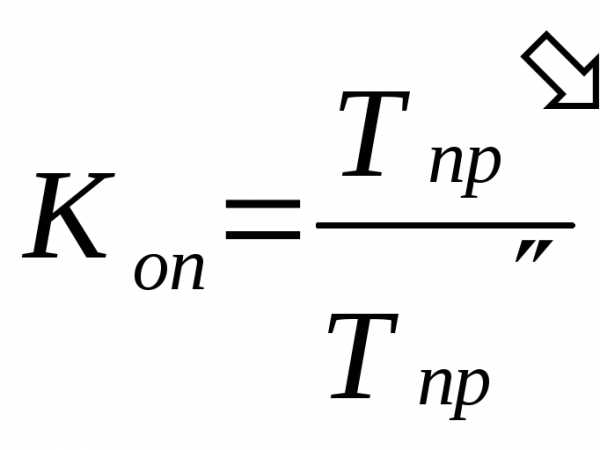 ,
,где ‑базисные темпы роста и прироста первого и второго рядов динамики (соответственно).
Коэффициенты опережения (отставания) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени:
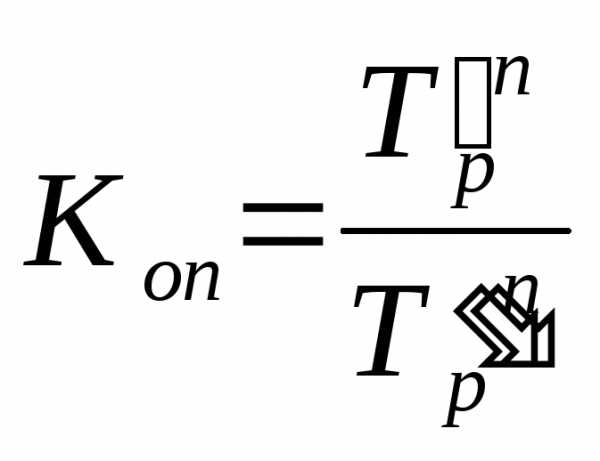 ,
,
где 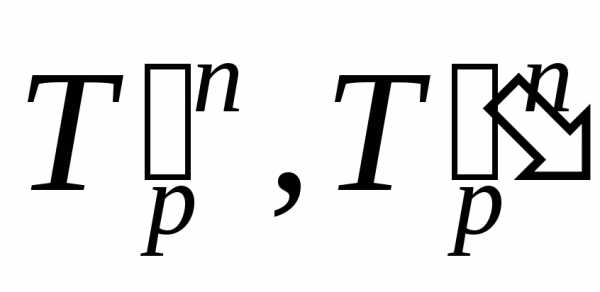 ‑средние
темпы роста первого и второго рядов
динамики
соответственно; n – число лет в периоде.
‑средние
темпы роста первого и второго рядов
динамики
соответственно; n – число лет в периоде.
Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другим. При этом сравнении темпы должны характеризовать тенденцию одного направления.
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Гусаров В.М. Теория статистики: Учебное пособие для вузов. — М.: Аудит, ЮНИТИ, 2001.
2. Елисеева и.и., Юзбашев М.М. Общая теория статистики: Учебник/ Под ред. И.И. Елисеевой. — М.: Финансы и статистика, 2000.
3. Ефимова М.Р., Петрова Е.В., Румянцев В.Н. Общая теория статистики: Учебник. — М.: ИНФРА-М, 2002.
4. Ильина Г.Г. Статистика. Общая теория статистики. Ч. I. — М.: РосНОУ, 1996.
5. Теория статистики: Учебник. / Под ред. Р.А. Шмойловой. — М.: Финансы и статистика, 2002.
6. Общая теория статистики: Статистическая методология в изучении коммерческой деятельности: Учебник / Под ред. О.Э. Башиной, А.А. Спирина. -М.: Финансы и статистика, 2000.
7. Сиденко А.В., Попов Г.И., Матвеева В.М. Статистика: Учебник. — М.: Дело-Сервис, 2000.
8. Российский статистический ежегодник. — М.: Финансы и статистика, 2001.9. Россия в цифрах. Статистический сборник. — М.: Финансы и статистика, 2001.
10. Адамов В.Е., Ильенкова С.Д., Сиротина С.А. и другие. Экономика и статистика фирм: Учебник / Под ред. С.Д. Ильенковой. — М.: Финансы и статистика, 2000.
11. Ильина Г.Г. Статистика. Статистика предприятий. Ч. 2. — М.: РосНОУ, 1998.
12. Курс социально-экономической статистики: Учебник для вузов / Под ред. Проф. М.Г. Назарова. — М.: Финстатинформ, ЮНИТИ-ДАНА, 2000.
13. Салин В.П., Шпаковская Е.П. Социально-экономическая статистика: Учебник. — М.: Юрист, 2001.
14. Экономическая статистика: Учебник / Под ред. Ю.Н. Иванова. — М.: ИНФРА-М, 2002.
studfiles.net
Расчет средних показателей динамического ряда
Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Он рассчитывается по средней хронологической, т.е. по средней исчисленной из значений, изменяющихся во времени.
Методы расчета среднего уровня интервального и моментного рядов динамики различны.
Для интервальных рядов динамики из абсолютных уровней средний за период времени определяется по формуле средней арифметической:
а) при равных интервалах применяется средняя арифметическая простая:
,
где у1,…,уn– абсолютные уровни ряда;n– число уровней ряда.
б) при неравных интервалах – средняя арифметическая взвешенная:
,
где у1,…,уn– уровни ряда динамики, сохраняющиеся без изменения в течение промежутка времени,t;t1,…, tn– веса, длительность интервалов времени (дней, месяцев) между смежными датами.
Средний уровень производства электроэнергии за 1989-1994 гг.:
.
Средний уровень моментного ряда динамики с равноотстоящими уровнями определяется по формуле средней хронологической моментного ряда:
,
где у1,…,уn– уровни периода, за который делается расчет;n– число уровней;n–1 – длительность периода времени.
Обобщающий показатель скорости изменения уровней во времени — средний абсолютный прирост (убыль), представляющий собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики. По цепным данным об абсолютных приростах за ряд лет можно рассчитать средний годовой абсолютный прирост как среднюю арифметическую простую:
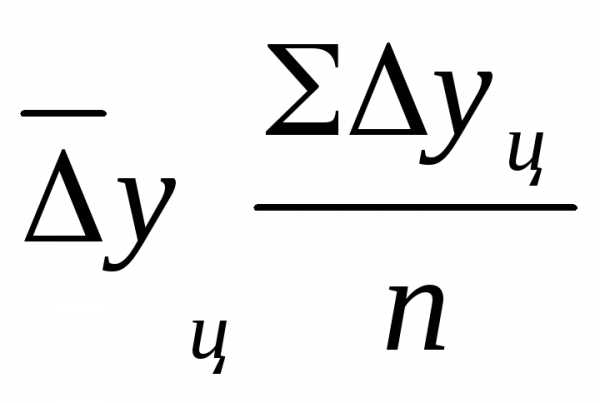 ,
,
где n– число цепных абсолютных приростов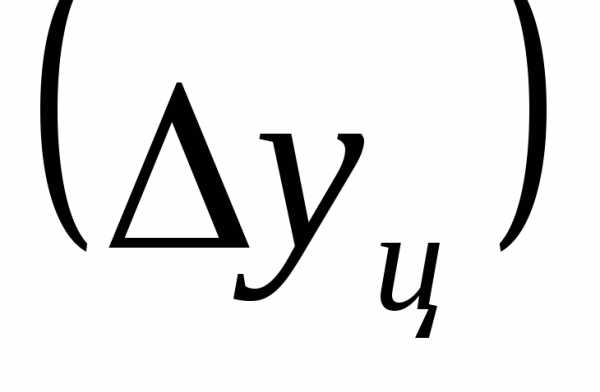 визучаемом
периоде.
визучаемом
периоде.
Используя данные табл. 5 о цепных абсолютных приростах производства электроэнергии, млрд кВт-ч:
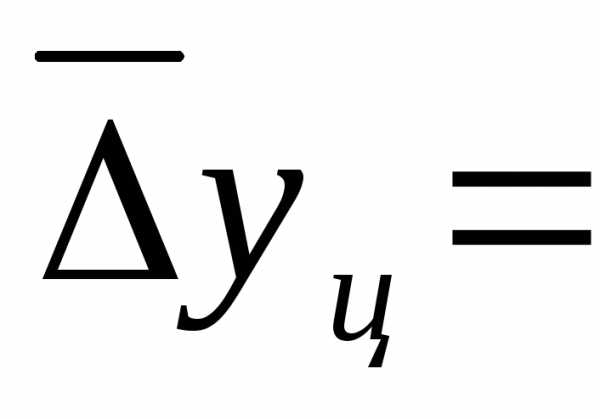 (5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
(5
– 14 – 60 – 51 – 81) : 5 = ‑201 : 5 = ‑40,2
Средний
абсолютный прирост определим через
накопленный (базисный)
абсолютный прирост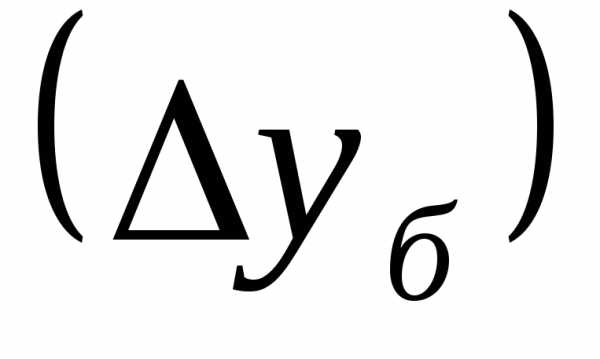 .
Для случая равных интервалов применим
следующую формулу:
.
Для случая равных интервалов применим
следующую формулу:
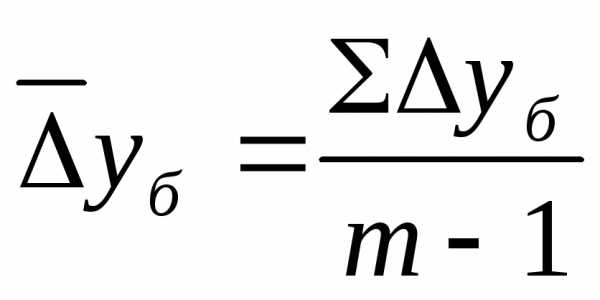 ,
,
где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Для нашего примера, млрд кВт-ч:

т.е. получен тот же результат.
Сводной обобщающей характеристикой интенсивности изменения уровней ряда динамики служит средний темп роста (снижения), показывающий во сколько раз в среднем за единицу времени изменяется уровень ряда динамики.
Средний темп роста (снижения) — обобщенная характеристика индивидуальных темпов роста ряда динамики. В качестве основы и критерия правильности исчисления среднего темпа (снижения) применяется определяющий показатель — произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Следовательно, если значение признака образуется как произведение отдельных вариантов, то нужно применять среднюю геометрическую. Поскольку средний темп роста представляет собой средний коэффициент роста, выраженный в процентах, , то для равностоящих рядов динамикирасчеты по средней геометрической сводятся к исчислению средних коэффициентов роста из цепных коэффициентов роста (по цепному способу):
,
где n– число цепных коэффициентов роста;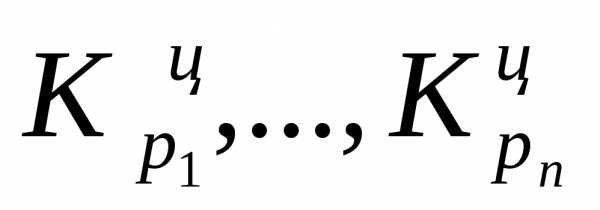 ‑
цепные коэффициенты роста;
‑
цепные коэффициенты роста;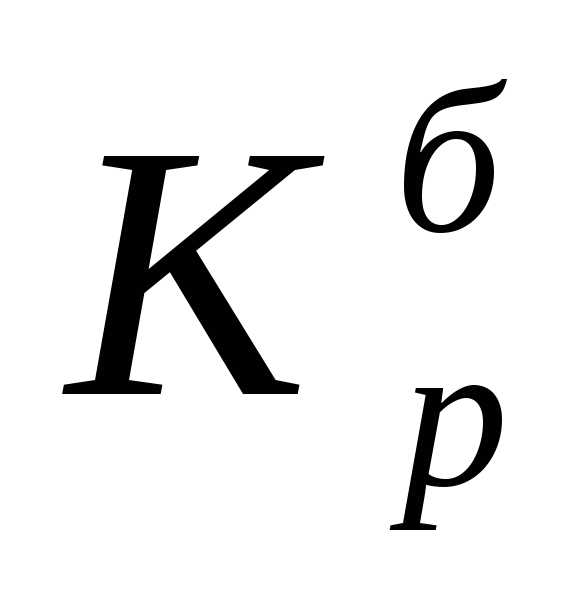 ‑
базисный коэффициент роста за весь
период.
‑
базисный коэффициент роста за весь
период.
В нашем примере среднегодовой темп изменения производства электроэнергии с 1990 по 1994г.:
;
Следовательно, с 1990 по 1994г. производство электроэнергии в России снижалось в среднем на 4 % в год, т.е. (0,96 * 100) – 100.
Если известны уровни динамического ряда, то расчет среднего коэффициента роста упрощается. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляется базисный коэффициент роста. Базисный коэффициент, как известно, получается непосредственно как частное от деления уровня последнего периода уп на уровень базисного периода у0.
Тогда формула для расчета среднего коэффициента роста для равностоящих рядов динамики (по «базисному способу») выглядит следующим образом:
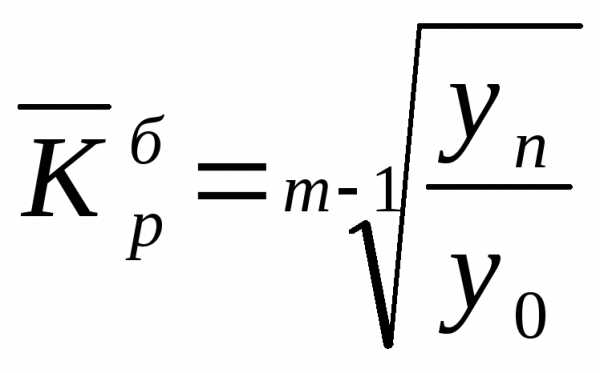 ,
,
где т — число уровней ряда динамики в изучаемом периоде, включая базисный.
Для расчета средних коэффициентов роста не нужно знать годовые темпы. Для нашего примера:
Получен тот же результат, расчеты упрощены.
Средние темпы прироста (сокращения) рассчитываются на основе средних темпов роста, вычитанием из последних 100%. Соответственно при исчислении средних коэффициентов прироста из значений коэффициентов роста вычитается единица:
; 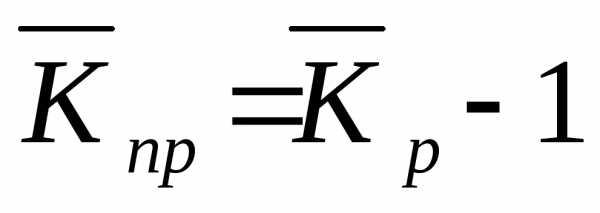 ,
,
где 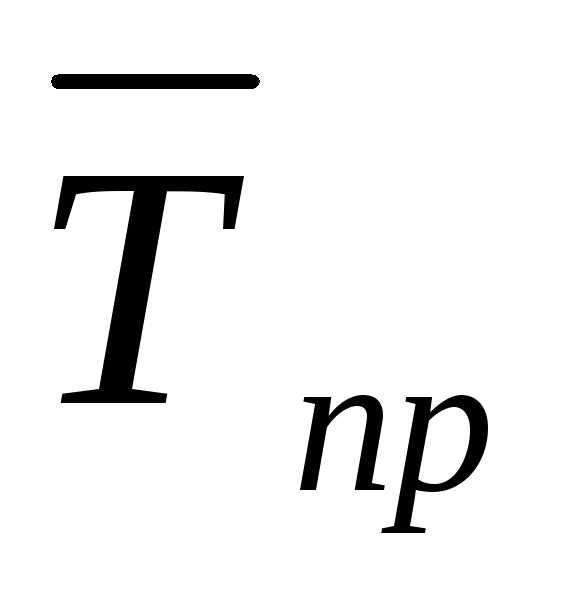 ‑ средний темп прироста.
‑ средний темп прироста.
Если
уровни ряда динамики снижаются, то
средний темп роста будет
меньше 100 %, а средний темп прироста —
отрицательной величиной.
Отрицательный темп прироста 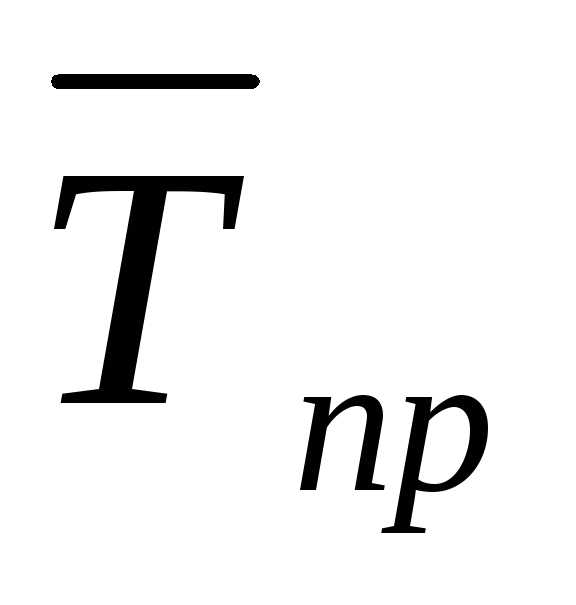 представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
представляет собой средний
темп сокращения и характеризует среднюю
относительную скорость снижения
уровня.
При анализе развития явлений, отражаемых двумя динамическими рядами, представляет интерес сравнение интенсивностей изменения во времени обоих явлений. Такое сопоставление интенсивностей изменения производится при сравнении динамических рядов одинакового содержания, но относящихся к разным территориям (странам, республикам, районам и т.п.), или к различным организациям (министерствам, предприятиям, учреждениям), или при сравнении рядов разного содержания, но характеризующих один и тот же объект. Например, сравнение рядов динамики, характеризующих производство важнейших видов продукции в Российской Федерации и других странах.
Сравнение интенсивности изменений уровней рядов во времени возможно с помощью коэффициентов опережения (отставания), представляющих собой отношение базисных темпов роста (или прироста) двух рядов динамики за одинаковые отрезки времени:
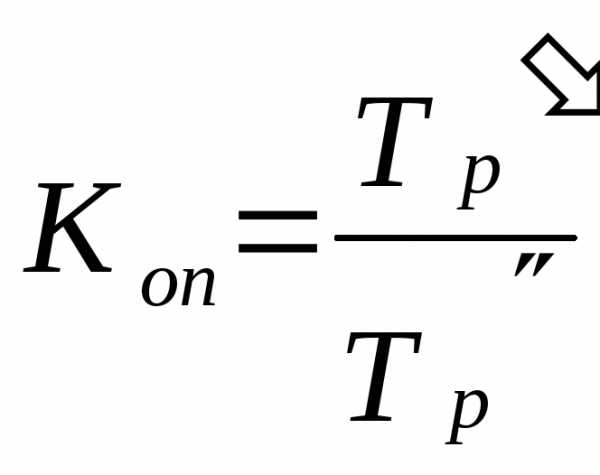 ,
, 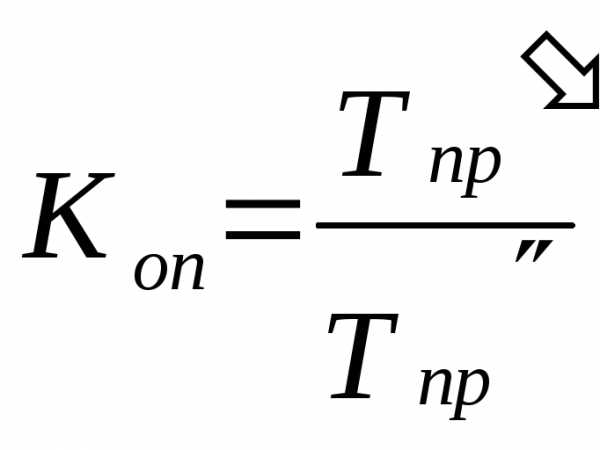 ,
,
где ‑базисные темпы роста и прироста первого и второго рядов динамики (соответственно).
Коэффициенты опережения (отставания) могут быть исчислены на основе сравнения средних темпов роста (или прироста) двух динамических рядов за одинаковый период времени:
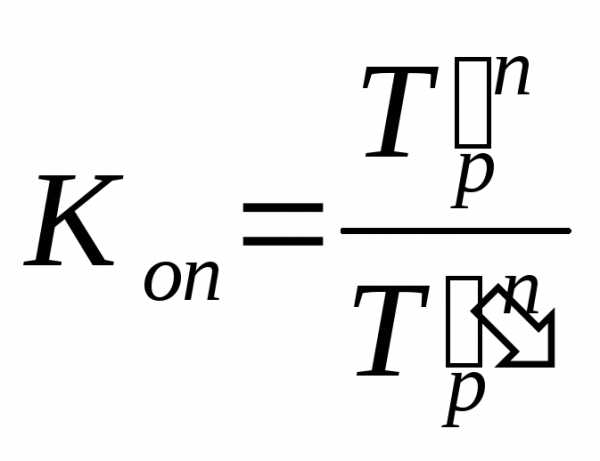 ,
,
где 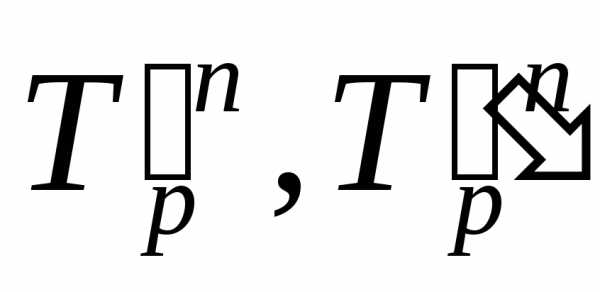 ‑средние
темпы роста первого и второго рядов
динамики
соответственно; n– число лет в периоде.
‑средние
темпы роста первого и второго рядов
динамики
соответственно; n– число лет в периоде.
Коэффициент опережения (отставания) показывает, во сколько раз быстрее растет (отстает) уровень одного ряда динамики по сравнению с другим. При этом сравнении темпы должны характеризовать тенденцию одного направления.
Статистика населения
Понятие статистики населения, ее объект предмет изучения
Население как объект исследования
1. Статистика населения — отрасль статистической науки, изучающая население и процессы, связанные с его динамикой, с количественной стороны в конкретных условиях общественного развития и разрабатывающая методы статистического учета и анализа демографических явлений и процессов.
Объект изучения — население в целом, отдельные группы населения (трудоспособные, инвалиды, мужчины, женщины и др.), молодые семьи, родившиеся (умершие) за определенный промежуток времени.
Предмет статистики населения — население и закономерности его развития.
Основные задачи статистики населения:
определение численности населения;
анализ размещения населения по территории страны;
характеристика состава населения;
изучение процессов воспроизводства населения;
определение перспективной численности и состава населения.
Единица наблюдения — отдельный человек как индивидуум, семья, домохозяйство, населенный пункт.
При этом источниками информации являются: текущий учет; единовременный учет (микропереписи; выборочные переписи; сплошные переписи).
2. Население — совокупность людей, проживающих в пределах определенной территории:
Также это социальная категория, т.е. совокупность лиц, проживающих на определенной территории, и одновременно экономическая категория, т. е. совокупность участников процесса производства и потребителей его результатов.
Различаются следующие группировки населения:
Рис. Возрастно-половая пирамида населения РФ на 01.01.1998
studfiles.net
Пример расчета показателей рядов динамики
Анализ интенсивности изменения во времени осуществляется с помощью показателей, получаемых в результате сравнения уровней, к таким показателям относятся: абсолютный прирост, темп роста, темп прироста.
Система средних показателей включает средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста.
Показатели анализа динамики могут вычисляться на постоянной и переменных базах сравнения. При этом принято называть сравниваемый уровень отчетным, а уровень, с которым производится сравнение, ‑ базисным. Для расчета показателей анализа динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. В качестве базисного выбирается либо начальный уровень в ряду динамики, либо уровень, с которого начинается какой-то новый этап развития явления. Исчисляемые при этом показатели называются базисными.
Для расчета показателей анализа динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим. Вычисленные таким образом показатели анализа динамики называются цепными.
Важнейшим статистическим показателем анализа динамики является абсолютное изменение ‑ абсолютный прирост (сокращение).
Абсолютный прирост характеризует увеличение или уменьшение уровня ряда за определенный промежуток времени. Абсолютный прирост с переменной базой называют скоростью роста.
Абсолютный прирост Абсолютный прирост
(цепной): (базисный):
где уi ‑ уровень сравниваемого периода; уi-1 ‑ уровень предшествующего периода; у0 ‑ уровень базисного периода.
Цепные и базисные абсолютные приросты представлены в табл. 5. Они показывают прирост (сокращение) производства электроэнергии по годам и абсолютное изменение по сравнению с 1989г.
Цепные и базисные абсолютные приросты связаны между собой: сумма последовательных цепных абсолютных приростов равна базисному, т.е. общему приросту за весь промежуток времени:
.
По данным табл. 5 сумма последовательных цепных абсолютных приростов равна базисному приросту за весь период, млрд кВт.ч: Таблица 5
Динамика производства электроэнергии в Российской Федерации
Год | Млрд кВт.ч | Абсолютный прирост, млрд. кВт.ч | Темпы роста | Темпы прироста, % | |||
= | = |
|
| = | = | ||
1 | 2 | 3 | 4 | 5 | 6 | ||
1989 1990 1991 1992 1993 1994 | 1077 1082 1068 1008 957 876 | ‑‑ 5 ‑14 ‑60 ‑51 ‑81 | ‑‑ 5 9 ‑69 ‑120 ‑201 | ‑‑ 100,5 98,7 94,4 94,9 91,5 | ‑‑ 100,5 99,2 93,6 88,9 81,3 | ‑‑ 0,5 ‑1,3 ‑5,6 ‑5,1 ‑8,5 | ‑‑ 0,5 0,1 ‑6,4 ‑11,1 ‑18,7 |
Итого
6068 | |||||||
Примечание: В графе 1 – сравнение с уровнем предшествующего года; в графе 2 – с уровнем 1989г. | |||||||
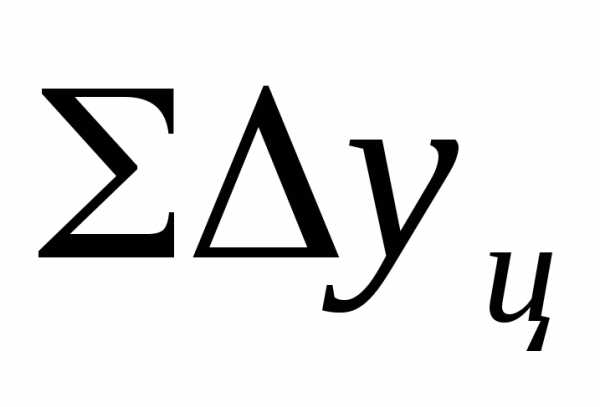 = 5 – 14 – 60 – 51 –
81 = ‑ 201.
= 5 – 14 – 60 – 51 –
81 = ‑ 201.
Для характеристики интенсивности, т.е. относительного изменения уровня динамического ряда за какой-либо период времени исчисляют темпы роста (снижения).
Интенсивность изменения уровня оценивается отношением отчетного уровня к базисному.
Показатель интенсивности изменения уровня ряда, выраженный в долях единицы, называется коэффициентом роста, а в процентах —темпом роста. Эти показатели интенсивности изменения отличаются только единицами измерения.
Коэффициент роста (снижения) показывает, во сколько раз сравниваемый уровень больше уровня, с которым производится сравнение (если этот коэффициент больше единицы) или какую часть уровня, с которым производится сравнение, составляет сравниваемый уровень (если он меньше единицы). Темп роста всегда представляет собой положительное число.
Коэффициент роста Коэффициент роста
(цепной): (базисный):
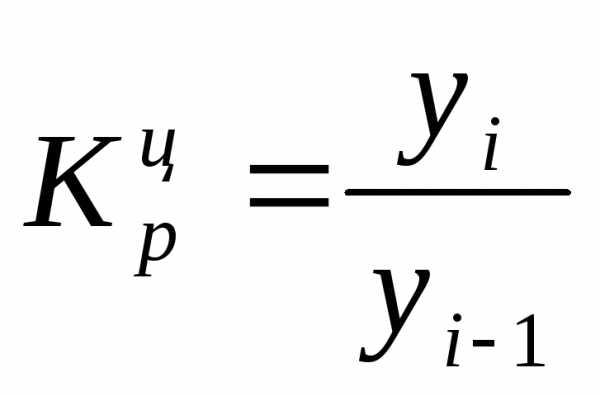
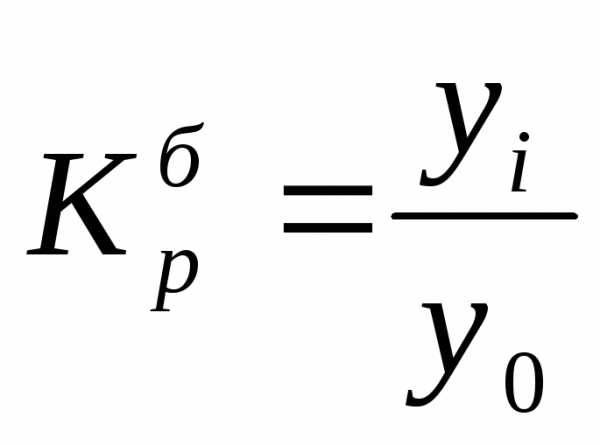
Темп роста Темп роста
(цепной): (базисный):
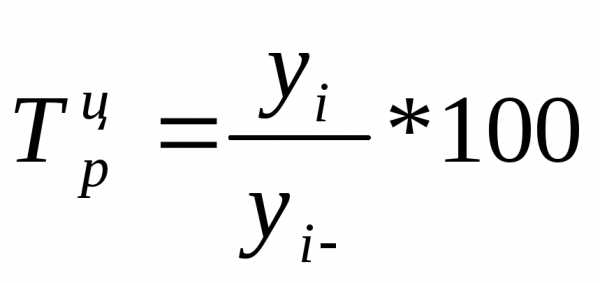
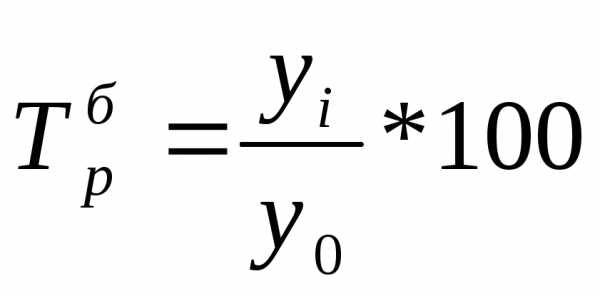
Итак, Тр = Кр * 100.
Цепные и базисные коэффициенты роста, характеризующие интенсивность изменения производства электроэнергии в России по годам, и за весь период исчислены в табл. 5. Между цепными и базисными коэффициентами роста существует взаимосвязь (если базисные коэффициенты исчислены по отношению к начальному уровню ряда динамики): произведение последовательных цепных коэффициентов роста равно базисному коэффициенту роста за весь период, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста.
Взаимосвязь легко проверить:
.
Проверим взаимосвязь цепных и базисных темпов роста на нашем примере: П = 1,005 * 0,987 * 0,944 * 0,949 * 0,915 = 0,813.
Относительную оценку скорости измерения уровня ряда в единицу времени дают показатели темпа прироста (сокращения).
Темп прироста (сокращения) показывает, на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения и вычисляется как отношение абсолютного прироста к абсолютному уровню, принятому за базу сравнения.
Темп прироста может быть положительным, отрицательным или равным нулю, выражается он в процентах и долях единицы (коэффициенты прироста).
Темп прироста Темп прироста
(цепной): (базисный):
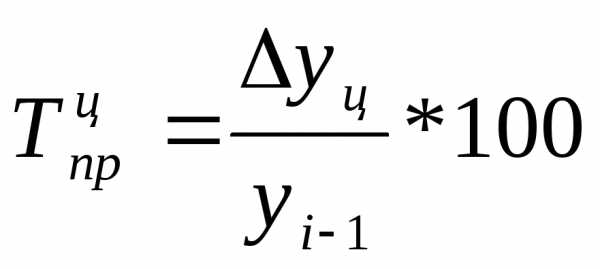 ;
; 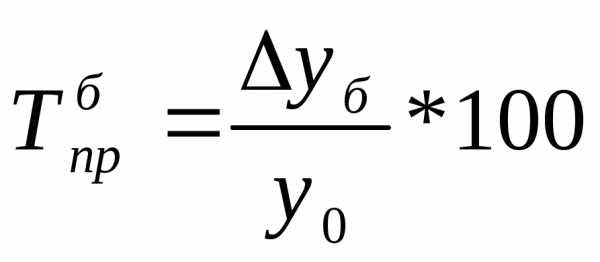 .
.
Темп прироста (сокращения) можно получить и из темпа роста, выраженного в процентах, если из него вычесть 100%. Коэффициент прироста получается вычитанием единицы из коэффициента роста:
Тпр = Тр – 100; Кпр = Кр – 1.
Цепные и базисные темпы прироста (сокращения) производства электроэнергии исчислены в табл. 5.
studfiles.net
Формула среднего темпа роста и примеры
Сущность темпа роста
Математика и статистика, а также экономические науки часто используют в расчетах формулу темпа роста.
Формула среднего темпа роста требует следующих показателей:
- Начальное значение,
- Базисное значение показателя,
- Несколько промежуточных значений, измеренных за равные интервалы.
Для расчета, например среднегодового темпа роста, применяют временной интервал, равный месяцу.
Понятие темп роста используется во многих областях (в экономике, финансовом анализе, статистике, промышленности и др.). Темп роста — статистическая величина, которая дает возможность анализировать:
- Динамику рассматриваемого процесса,
- Скорость развития определенного явления (процесса),
- Интенсивность развития и др.
Формула среднего темпа роста предполагает расчет и сравнение значений, получаемых за выбранные временные промежутки.
Общая формула темпа роста
При определенных базисных и текущих величинах формула темпа роста в общем виде выглядит таким образом:
Тр=Птек/Пбаз
Здесь Тр – темп роста,
Птек – показатель текущего периода,
Пкп – показатель базисного периода.
Для получения более наглядного результата, полученный ответ умножается на 100% для выражения темпа роста в процентном соотношении.
Порядок расчета среднего темпа роста
Для вычисления среднего темпа роста в первую очередь определяется период, за который онрассчитывается. Чаще всего таким периодом может быть календарный год или кратные ему показатель.
Темп роста — относительное понятие,определяющее изменение соответствующих значений по отношению к определенному начальному показателю. Формула среднеготемпа роста за год может определяться исходя из начального значения на 1 января рассматриваемого года. Вычисление среднего темпа роста проводится по следующим величинам:
- Базисные показатели, отражающие отношение изменения величин по отношению к базисному значению;
- Цепные показатели, показывающие интенсивность изменения величин соседних периодов или дат.
Формуласреднего темпа роста выглядит следующим образом:
Тр ср =
Здесь n– количество (лет, месяцев),
yn–текущий показатель,
y0 – базисный показатель (например, на 1 января)
Особенности расчета среднего темпа роста
Формула среднего темпа роста в качестве базисного показателя использует числовую величину, характеризующую исследуемое явление и определяющуюся на конец предыдущего года. Базисная величина может быть показателем на 1 января того года, для которого требуется определить средний темп роста.
Например, в расчете формулы среднего годового темпа роста с помощью коэффициентов, базисный показатель может приниматься за единицу или 100 (в случае процентных расчетов). В ходе вычисления базовых темпов роста за каждый месяц все показатели конца каждого месяца соотносятся с базовым показателем (например, показателем 1 января).
В процессе определенияцепных показателей, базовым показателем может быть показатель предыдущего периода. По этой причине при вычислениях формула среднего темпа роста удобнее рассчитывается посредством цепных показателей.
Формула среднего темпа роста имеет огромное значение, так как при ее расчетах по нескольким годам (месяцам) можно получить результат для последующего учета и анализа сезонных колебаний.
Примеры решения задач
ru.solverbook.com
Средний абсолютный прирост определяется как простая средняя арифметическая величина из цепных абсолютных приростов

Средний абсолютный прирост
показывает, на сколько в среднем изменялся изучаемый показатель при переходе от предыдущего периода времени к смежному последующему периоду времени
|
|
| ΣΔi | Σ(Yi Yi 1 ) | Yn Y1 | , |
|
| |||||
|
|
| s | s | n 1 |
|
где | n – число уровней ряда динамики; |
| ||||
S = n — 1 – количество цепных приростов

Среднегодовой коэффициент роста определяется как средняя геометрическая из цепных коэффициентов роста и
показывает , сколько в среднем составлял рост показателя

Если цепные коэффициенты роста определялись для рядов с равностоящими интервалами, то применяется простая средняя геометрическая величина

Средний коэффициент роста рассчитывается по формуле средней геометрической из цепных коэффициентов роста:
k n 1 kц2 k3ц kц4 … kцn
k 5 1 1,133 1,088 1,027 1,105 1,088
k n 1 yn 4 21 1,088 y1 15
|
| yb |
| 21 |
| |
k b a | 2008 2004 | 1,088 | ||||
ya | 15 | |||||

С неравными интервалами времени
Взвешенная средняя геометрическая
k= ti k1t1*kt22*kt31*…*k1nn
где ki – коэффицент роста;
ti – период времени между двумя соседними значениями
studfiles.net
Расчет абсолютного прироста и темпов роста показателей базисным и цепным способами (стр. 1 из 2)
Задача
Имеются следующие данные:
Определить базисным и цепным способами :
– абсолютный прирост
– темп роста, %
– темп прироста, %
– среднегодовой темп роста, %
Провести расчеты всех показателей, результаты расчетов свести в таблицу. Сделать выводы, описав в них каждый показатель таблицы в сравнении с предыдущим или базисным показателем.
Результатом данной работы является подробный вывод.
Решение
Приведём расчеты.
1. Абсолютный прирост, единиц
Цепной способ:
В 1991 году: 117299–116339=960
В 1992 году: 120500–117299=3201
В 1993 году: 121660–120500=1160
В 1994 году: 119388–121660=-2272
В 1995 году: 119115–119388=-273
В 1996 году: 126388–119115=7273
В 1997 году: 127450–126388=1062
В 1998 году: 129660–127450=2210
В 1999 году: 130720–129660=1060
В 2000 году: 131950–130720=1230
В 2001 году: 132580–131950=630
Базисный способ:
В 1991 году: 117299–116339=960
В 1992 году: 120500–116339=4161
В 1993 году: 121660–116339=5321
В 1994 году: 119388–116339=3049
В 1995 году: 119115–116339=2776
В 1996 году: 126388–116339=10049
В 1997 году: 127450–116339=11111
В 1998 году: 129660–116339=13321
В 1999 году: 130720–116339=14381
В 2000 году: 131950–116339=15611
В 2001 году: 132580–116339=16241
2. Темп роста, %
Цепной способ:
В 1991 году: 117299/116339*100%=100,8%
В 1992 году: 120500/117299*100%=102,7%
В 1993 году: 121660/120500*100%=100,9%
В 1994 году: 119388/121660*100%=98,1%
В 1995 году: 119115/119388*100%=99,7%
В 1996 году: 126388/119115*100%=106,1%
В 1997 году: 127450/126388*100%=100,8%
В 1998 году: 129660/127450*100%=101,7%
В 1999 году: 130720/129660*100%=100,8%
В 2000 году: 131950/130720*100%=100,9%
В 2001 году: 132580/131950*100%=100,4%
Базисный способ:
В 1991 году: 117299/116339*100%=100,8%
В 1992 году: 120500/116339*100%=103,5%
В 1993 году: 121660/116339*100%=104,5%
В 1994 году: 119388/116339*100%=102,6%
В 1995 году: 119115/116339*100%=102,3%
В 1996 году: 126388/116339*100%=108,6%
В 1997 году: 127450/116339*100%=109,5%
В 1998 году: 129660/116339*100%=111,4%
В 1999 году: 130720/116339*100%=112,3%
В 2000 году: 131950/116339*100%=113,4%
В 2001 году: 132580/116339*100%=113,9%
3. Темп прироста, %
Цепной способ:
В 1991 году: (117299–116339)/116339*100%=0,8%
В 1992 году: (120500–117299)/117299*100%=2,7%
В 1993 году: (121660–120500)/120500*100%=0,9%
В 1994 году: (119388–121660)/121660*100%=-1,8%
В 1995 году: (119115–119388)/119388*100%=-0,2%
В 1996 году: (126388–119115)/119115*100%=6,1%
В 1997 году: (127450–126388)/126388*100%=0,8%
В 1998 году: (129660–127450)/127450*100%=1,7%
В 1999 году: (130720–129660)/129660*100%=0,8%
В 2000 году: (131950–130720)/130720*100%=0,9%
В 2001 году: (132580–131950)/131950*100%=0,4%
Базисный способ:
В 1991 году: (117299–116339)/116339*100%=0,8%
В 1992 году: (120500–116339)/116339*100%=3,5%
В 1993 году: (121660–116339)/116339*100%=4,5%
В 1994 году: (119388–116339)/116339*100%=2,6%
В 1995 году: (119115–116339)/116339*100%=2,3%
В 1996 году: (126388–116339)/116339*100%=8,6%
В 1997 году: (127450–116339)/116339*100%=9,5%
В 1998 году: (129660–116339)/116339*100%=11,4%
В 1999 году: (130720–116339)/116339*100%=12,3%
В 2000 году: (131950–116339)/116339*100%=13,4%
В 2001 году: (132580–116339)/116339*100%=13,9%
4. Среднегодовой темп роста, %
Цепной способ:
Тр =100,9%*100,4% = 102,9%
Базисный способ:
Тр =
113,4%*113,9% = 109,9%
Сведём полученные данные в таблицу.
Динамика показателей абсолютного прироста (снижения), темпа роста (снижения), темпа прироста (понижения) наличия мотоциклов в угоне в г. Архангельске в период с 1990 по 2001 годы, исчисленные базисным и цепным способами
Вывод
В 1990 году наличие мотоциклов в угоне в г. Архангельске составило 116339 единиц.
В 1991 году наличие мотоциклов в угоне в г. Архангельске составило 117299 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске цепным и базисным способами в 1991 году по сравнению с 1990 годом составил 960 единиц. Темп роста наличия мотоциклов в угоне в г. Архангельске цепным и базисным способами в 1991 году по сравнению с 1990 годом составил 100,8 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске цепным и базисным способами в 1991 году по сравнению с 1990 годом составил 0,8 процента.
В 1992 году наличие мотоциклов в угоне в г. Архангельске составило 120500 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске цепным способом в 1992 году по сравнению с 1991 годом составило 3201 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске базисным способом в 1992 году по сравнению с 1990 годом составило 4161 единиц. Темп роста наличия мотоциклов в угоне в г. Архангельске цепным способом в 1992 году по сравнению с 1991 годом составило 102,7 процента. Темп роста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1992 году по сравнению с 1990 годом составило 103,5 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске цепным способом в 1992 году по сравнению с 1991 годом составило 2,7 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1992 году по сравнению с 1990 годом составило 3,5 процента.
В 1993 году наличие мотоциклов в угоне в г. Архангельске составило 121660 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске цепным способом в 1993 году по сравнению с 1992 годом составило 1160 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске базисным способом в 1993 году по сравнению с 1990 годом составило 5321 единиц. Темп роста наличия мотоциклов в угоне в г. Архангельске цепным способом в 1993 году по сравнению с 1992 годом составило 100,9 процента. Темп роста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1993 году по сравнению с 1990 годом составило 104,5 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске цепным способом в 1993 году по сравнению с 1992 годом составило 0,9 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1993 году по сравнению с 1990 годом составило 4,5 процента.
В 1994 году наличие мотоциклов в угоне в г. Архангельске составило 119388 единиц. Абсолютное снижение наличия мотоциклов в угоне в г. Архангельске цепным способом в 1994 году по сравнению с 1993 годом составило 2272 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске базисным способом в 1994 году по сравнению с 1990 годом составило 3049 единиц. Темп снижения наличия мотоциклов в угоне в г. Архангельске цепным способом в 1994 году по сравнению с 1993 годом составило 98,1 процента. Темп роста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1994 году по сравнению с 1990 годом составил 102,6 процента. Темп понижения наличия мотоциклов в угоне в г. Архангельске цепным способом в 1994 году по сравнению с 1993 годом составило 1,8 процента. Темп прироста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1994 году по сравнению с 1990 годом составило 2,6 процента.
В 1995 году наличие мотоциклов в угоне в г. Архангельске составило 119115 единиц. Абсолютное снижение наличия мотоциклов в угоне в г. Архангельске цепным способом в 1995 году по сравнению с 1995 годом составило 273 единиц. Абсолютный прирост наличия мотоциклов в угоне в г. Архангельске базисным способом в 1995 году по сравнению с 1990 годом составило 2776 единиц. Темп снижения наличия мотоциклов в угоне в г. Архангельске цепным способом в 1995 году по сравнению с 1994 годом составило 99,7 процента. Темп роста наличия мотоциклов в угоне в г. Архангельске базисным способом в 1995 году по сравнению с 1990 годом составил 102,3 проце
mirznanii.com

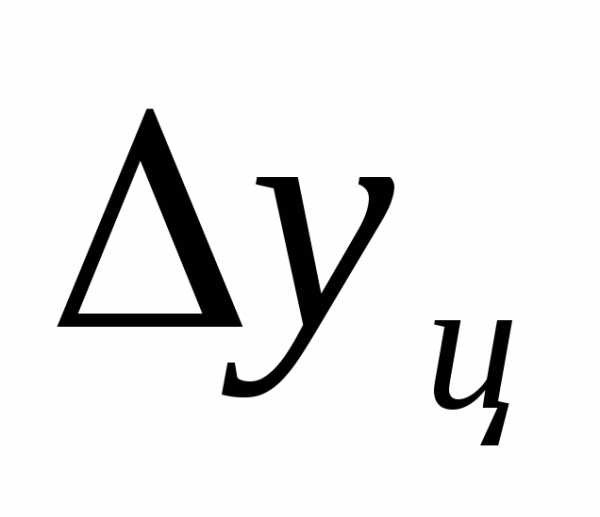 =
=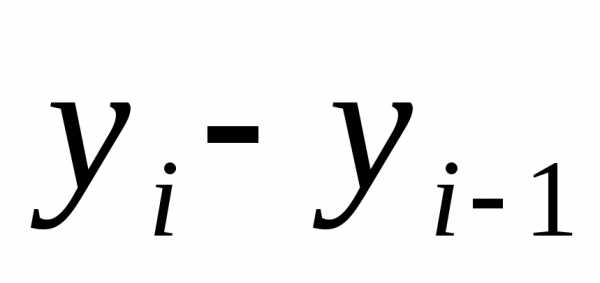
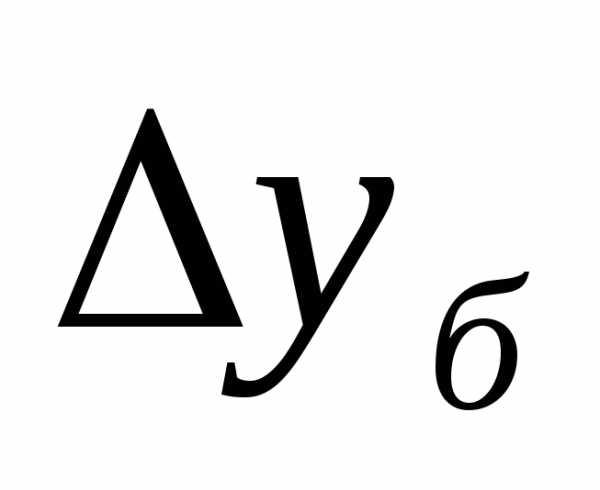 =
=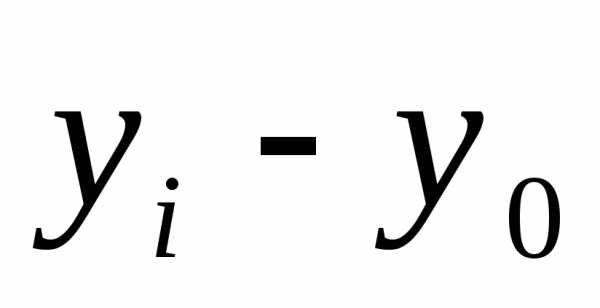
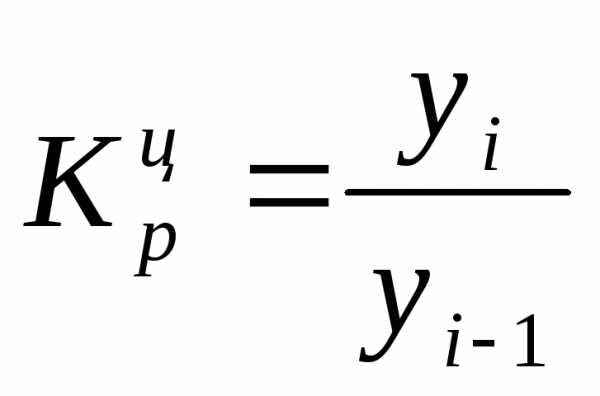
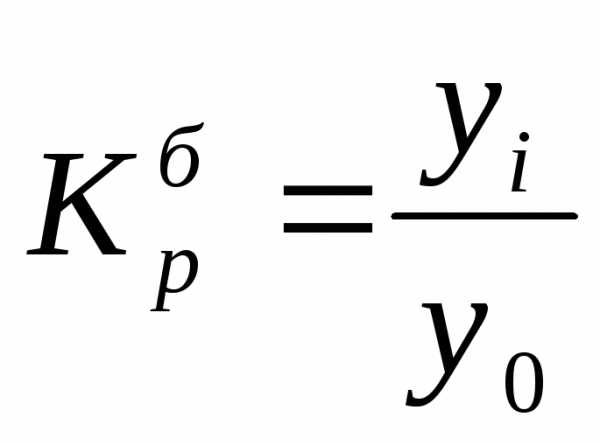
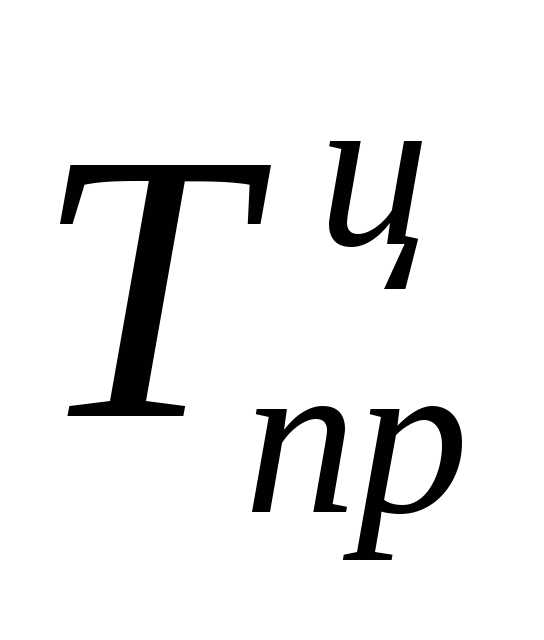 =
=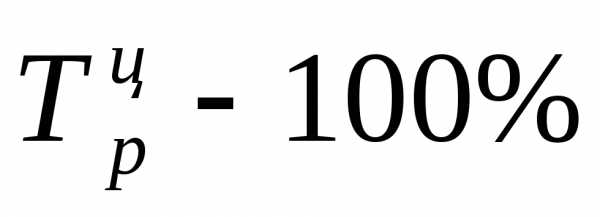
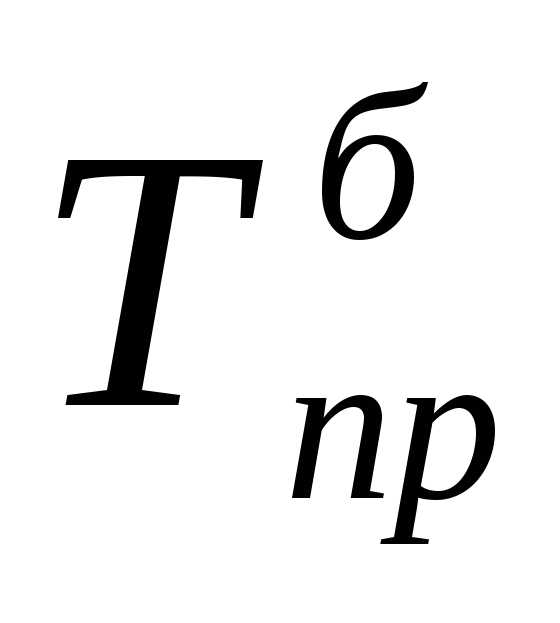 =
=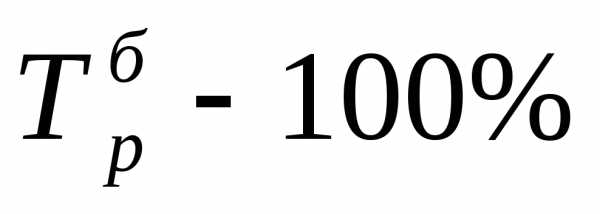
 =‑201
‑ П=0,813 ‑ ‑
‑
=‑201
‑ П=0,813 ‑ ‑
‑