Свойства определителя матрицы | Мозган калькулятор онлайн
Свойства определителя матрицы | Мозган калькулятор онлайн- Определитель единичной матрицы равен единице: det(E) = 1. Единичная матрица — это квадратная матрица, элементы главной диагонали которой равны единице, а все остальные элементы равны 0.
- Определитель матрицы с двумя равными строками или столбцами равен нулю.
- Определитель матрицы с двумя пропорциональными строками или столбцами равен нулю.
- Определитель матрицы, содержащий нулевую строку или столбец, равен нулю.
- Определитель матрицы равен нулю, если две или несколько строк или столбцов матрицы линейно зависимы.
- При транспонировании значение определителя матрицы не меняется:
- Определитель обратной матрицы: det(A-1) = det(A)-1.
- Определитель матрицы не изменится, если к какой-то его строке или столбцу прибавить другую строку или столбец, умноженную на некоторое число.
- Определитель матрицы не изменится, если к какой-то его строке или столбцу прибавить линейную комбинации других строк или столбцов.
- Если поменять местами две строки или два столбца матрицы, то определитель матрицы поменяет знак.
- Общий множитель в строке или столбце можно выносить за знак определителя:
- Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n -той степени:
B = k·A => det(B) = kn·det(A), где A матрица n×n, k — число.
- Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
- Определитель верхней или нижней треугольной матрицы равен произведению его диагональных элементов.
- Определитель произведения матриц равен произведению определителей этих матриц: det(A·B) = det(A)·det(B).
Другой материал по теме
www.mozgan.ru
Находим определитель исходной матрицы.
2.Если │А│=0, то матрица А вырожденная и обратной матрицы А-1 не существует.
Если определитель матрицы А не равен нулю, то обратная матрица существует.
3. Находим АT, транспонированную к А.
4. Находим алгебраические дополнения элементов транспонированной матрицы и составляем из них присоединенную матрицу . 5. Вычисляем обратную матрицу по формуле: 6. Проверяем правильность вычисления обратной матрицы, исходя из её определения А-1∙А = А ∙А-1 = Е.
· №28
· В матрице размера m x n вычеркиванием каких-либо строк и столбцов можно выделить квадратные подматрицы k-го порядка, где k≤min(m; n). Определители таких подматриц называются минорами k-го порядка матрицы А.
· Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы.
· Ранг матрицы А обозначается rang A или r(A).
· Из определения следует:
· 1) ранг матрицы размера m x n не превосходит меньшего из её размеров, т.е. r(A) ≤ min (m; n).
· 2) r(A)=0 тогда и только тогда, когда все элементы матрицы равны нулю, т.е. А=0.
· 3) Для квадратной матрицы n-го порядка r(A) = n тогда и только тогда, когда матрица А – невырожденная.
· В общем случае определение ранга матрицы перебором всех миноров достаточно трудоемко. Для облегчения этой задачи используются элементарные преобразования, сохраняющие ранг матрицы:
· 1) Отбрасывание нулевой строки (столбца).
· 2) Умножение всех элементов строки (столбца) матрицы на число, не равное нулю.
· 3) Изменение порядка строк (столбцов) матрицы.
· 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.
· 5) Транспонирование матрицы.
· Теорема. Ранг матрицы не изменится при элементарных преобразованиях матрицы.
№31
Пусть число уравнений системы (1) равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а её определитель Δ=│А│называется определителем системы.
Предположим, что │А│не равен нулю, тогда существует обратная матрица А-1.
Умножая слева обе части матричного равенства на обратную матрицу А -1 получим:
А-1 (АХ)= А-1 В.
Решением системы уравнений методом обратной матрицы будет матрица-столбец:
Х= А-1В.
(А-1 А)Х =ЕХ =Х
Теорема Крамера. Пусть Δ – определитель матрицы системы А, а Δj – определитель матрицы, полученный из матрицы заменой j-го столбца столбцом свободных членов. Тогда если Δ не равен нулю, то система имеет единственное решение, определённое по формулам Крамера:
где j=1..n.
№33
Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого или треугольного вида.
Рассмотрим матрицу:
эта матрица называется расширенной матрицей системы (1), так как в нее кроме матрицы системы А, дополнительно включен столбец свободных членов.
№26
N-мерным вектором называется упорядоченная совокупность n действительных чисел, записываемых в виде Х=(х1,х2,…хn) , где хi – i-я компонента вектора Х.
Два n-мерных вектора равны тогда и только тогда, когда равны их соответствующие компоненты, т.е. Х=У, если xi=yi, i=1…n.
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющие приведённым выше свойствам, называется векторным пространством.
Векторное пространство R, называется n-мерным, если в нем существует n линейно независимых векторов, а любые n+1 векторов уже являются зависимыми. Число n называется размерностью векторного пространство R и обозначается dim(R).
№29
Линейные операторы
Определение. Если задан закон (правило), по которому каждому вектору x пространства ставится в соответствие единственный вектор y пространства
то говорят: что задан оператор (преобразование, отображение) A(x), действующий из в и
записывают y=A(x).
Оператор называется линейным, если для любого вектора x и y пространства
и любого числа λ выполняются следующие соотношения:
№37
Пустъ А – множество, состоящее из конечного числа элементов a1, a2, a3…an. Из различных элементов множества А можно образовывать группы. Если в каждую группу входит одно и то же число элементов m (m из n), то говорят, что они образуют соединения из n элементов пo m в каждом. Различают три вида соединений: размещения, сочетания и перестановки.
Соединения, в каждое из которых входят все n элементов множества А и которые, следовательно, отличаются друг от друга только порядком элементов называются перестановками из n элементов. Число таких перестановок обозначается символом Рn.
№35
Классическое определение вероятности основано на понятии равновозможности событий.
Равновозможность событий означает, что нет оснований предпочесть какое-либо одно из них другим.
Рассмотрим испытание, в результате которого может произойти событие A. Каждый исход, при котором осуществляется событие A, называется благоприятным событию A.
Вероятностью события A (обозначают P(A)) называется отношение числа исходов, благоприятных событию A (обозначают k), к числу всех исходов испытания – N т.е. P(A)= k/ N.
Из классического определения вероятности вытекают следующие ее свойства:
Вероятность любого события заключена между нулем и единицей.
Вероятность достоверного события равна единице.
Вероятность невозможного события равна нулю
№39, 40
Теорема сложения. Если А и В несовместны, то Р(А + В) = Р(А) +Р(В)
Рекомендуемые страницы:
lektsia.com
Что если определитель матрицы равен 0. Если определитель матрицы равен нулю, то обратная к ней не существует. Продолжаем решать системы методом Крамера вместе
Задана система N линейных алгебраических уравнений (СЛАУ) с неизвестными, коэффициентами при которых являются элементы матрицы , а свободными членами — числа
Первый индекс возле коэффициентов указывает в каком уравнении находится коэффициент, а второй — при котором из неизвестным он находится.
Если определитель матрицы не равен нулю
то система линейных алгебраических уравнений имеет единственное решение.
Решением системы линейных алгебраических уравнений называется такая упорядоченная совокупность чисел , которая при превращает каждое из уравнений системы в правильную равенство.
Если правые части всех уравнений системы равны нулю, то систему уравнений называют однородной. В случае, когда некоторые из них отличны от нуля – неоднородной
Если система линейных алгебраических уравнений имеет хоть одно решение, то она называется совместной, в противном случае — несовместимой.
Если решение системы единственное, то система линейных уравнений называется определенной. В случае, когда решение совместной системы не единственный, систему уравнений называют неопределенной.
Две системы линейных уравнений называются эквивалентными (или равносильными), если все решения одной системы является решениями второй, и наоборот. Эквивалентны (или равносильны) системы получаем с помощью эквивалентных преобразований.
Эквивалентные преобразования СЛАУ
1) перестановка местами уравнений;
2) умножение (или деление) уравнений на отличное от нуля число;
3) добавление к некоторого уравнения другого уравнения, умноженного на произвольное, отличное от нуля число.
Решение СЛАУ можно найти разными способами.
МЕТОД КРАМЕРА
ТЕОРЕМА КРАМЕРА. Если определитель системы линейных алгебраических уравнений с неизвестными отличен от нуля то эта система имеет единственное решение, которое находится по формулам Крамера:
— определители, образованные с заменой -го столбца, столбцом из свободных членов.
Если , а хотя бы один из отличен от нуля, то СЛАУ решений не имеет. Если же , то СЛАУ имеет множество решений. Рассмотрим примеры с применением метода Крамера.
—————————————————————
Дана система трех линейных уравнений с тремя неизвестными. Решить систему методом Крамера
Найдем определитель матрицы коэффициентов при неизвестных
Так как , то заданная система уравнений совместная и имеет единственное решение. Вычислим определители:
По формулам Крамера находим неизвестные
Итак единственное решение системы.
Дана система четырех линейных алгебраических уравнений. Решить систему методом Крамера.
Найдем определитель матрицы коэффициентов при неизвестных. Для этого разложим его по первой строке.
Найдем составляющие определителя:
Подставим найденные значения в определитель
Детерминант , следовательно система уравнений совместная и имеет единственное решение. Вычислим определители по формулам Крамера:
Разложим каждый из определителей по столбцу в котором есть больше нулей.
По формулам Крамера находим
Решение системы
Данный пример можно решить математическим калькулятором YukhymCALC . Фрагмент программы и результаты вычислений наведены ниже.
——————————
МЕТОД К Р А М Е Р А
|1,1,1,1|
D=|5,-3,2,-8|
|3,5,1,4|
|4,2,3,1|
D=1*(-3*1*1+2*4*2+(-8)*5*3-((-8)*1*2+2*5*1+(-3)*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))+1*(5*5*1+(-3)*4*4+(-8)*3*2-((-8)*5*4+(-3)*3*1+5*4*2))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(-3+16-120+16-10+36)-1*(5+32-72+32-6-60)+1*(25-48-48+160+9-40)-1*(75-12+12-40+27-10)=1*(-65)-1*(-69)+1*58-1*52=-65+69+58-52=10
|0,1,1,1|
Dx1=|1,-3,2,-8|
|0,5,1,4|
|3,2,3,1|
Dx1=-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(1*5*1+(-3)*4*3+(-8)*0*2-((-8)*5*3+(-3)*0*1+1*4*2))-1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))= -1*(1+24+0+24+0-12)+1*(5-36+0+120+0-8)-1*(15-9+0-30+0-2)= -1*(37)+1*81-1*(-26)=-37+81+26=70
|1,0,1,1|
Dx2=|5,1,2,-8|
|3,0,1,4|
|4,3,3,1|
Dx2=1*(1*1*1+2*4*3+(-8)*0*3-((-8)*1*3+2*0*1+1*4*3))+1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*1*1+2*4*4+(-8)*3*3-((-8)*1*4+2*3*1+5*4*3))= 1*(1+24+0+24+0-12)+1*(0+16-72+0-3-60)-1*(0+4+18+0-9-15)= 1*37+1*(-119)-1*(-2)=37-119+2=-80
|1,1,0,1|
Dx3=|5,-3,1,-8|
|3,5,0,4|
|4,2,3,1|
Dx3=1*(-3*0*1+1*4*2+(-8)*5*3-((-8)*0*2+1*5*1+(-3)*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))-1*(5*0*1+1*4*4+(-8)*3*3-((-8)*0*4+1*3*1+5*4*3))= 1*(0+8-120+0-5+36)-1*(0+16-72+0-3-60)-1*(75+0+6-20+27+0)= 1*(-81)-1*(-119)-1*88=-81+119-88=-50
|1,1,1,0|
Dx4=|5,-3,2,1|
|3,5,1,0|
|4,2,3,3|
Dx4=1*(-3*1*3+2*0*2+1*5*3-(1*1*2+2*5*3+(-3)*0*3))-1*(5*1*3+2*0*4+1*3*3-(1*1*4+2*3*3+5*0*3))+1*(5*5*3+(-3)*0*4+1*3*2-(1*5*4+(-3)*3*3+5*0*2))= 1*(-9+0+15-2-30+0)-1*(15+0+9-4-18+0)+1*(75+0+6-20+27+0)= 1*(-26)-1*(2)+1*88=-26-2+88=60
x1=Dx1/D=70,0000/10,0000=7,0000
x2=Dx2/D=-80,0000/10,0000=-8,0000
x3=Dx3/D=-50,0000/10,0000=-5,0000
x4=Dx4/D=60,0000/10,0000=6,0000
Посмотреть материалы:
{jcomments on}
В общем случае правило вычисления определителей-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
Пример
Задание. Вычислить определитель второго порядка
Решение.
Ответ.
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
Пример
Задание. Вычислить определитель методом треугольников.
Решение.
Ответ.
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
Пример
Задание. Вычислить определитель с помощью правила Саррюса.
Решение.
1kingvape.ru
Определитель матрицы
Определителем
квадратной матрицы 
называется число, которое обозначается
как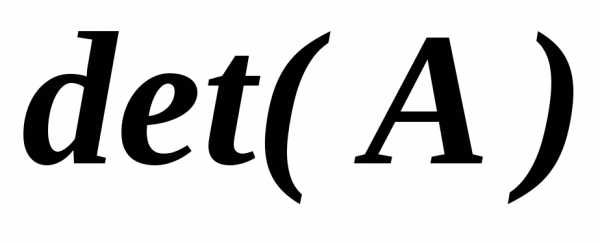
или
и вычисляется при помощи следующих трех
правил.
Правило 1. Определитель диагональной матрицы равен произведению элементов, стоящих на главной диагонали.
Замечание: Определитель одноэлементной матрицы равен самому элементу.
Правило 2. Общий множитель элементов любой строки или столбца матрицы можно вынести за знак определителя.
Замечание:
Определитель матрицы, у которой строка
или столбец состоит только из нулей,
равен 
.
Правило 3. Определитель матрицы не изменится, если к одной из строк (столбцов) матрицы прибавить другую строку (столбец) этой матрицы.
Свойства определителя матрицы.
1. Определитель не меняется при транспонировании.
2. Если в определителе переставить две строки, определитель поменяет знак.
3. Определитель, содержащий две одинаковые строки, равен нулю.
4. Определитель, содержащий две пропорциональные строки, равен нулю.
5. Если
все элементы 
строки определителя представлены в
виде суммы двух слагаемых,
то определитель равен сумме определителей,
у которых все строки, кроме
,
— такие же, как в заданном определителе,
а
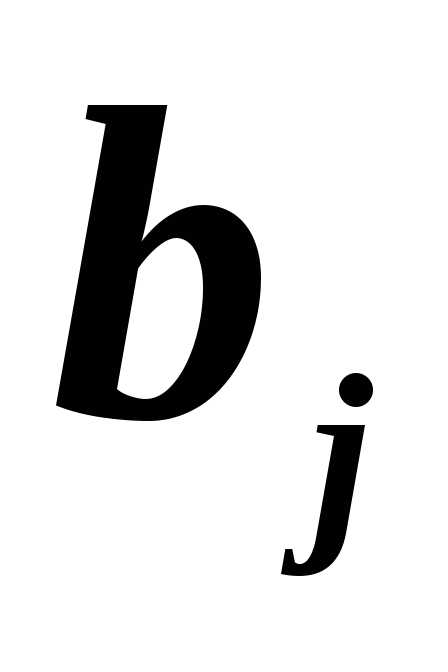строка в одном из слагаемых состоит из
элементов
,
в другом — из элементов
.
Замечание. Все свойства остаются справедливыми, если вместо строк взять столбцы.
Миноры и алгебраические дополнения
Обозначим
через 
матрицу, которая остается при вычеркивании
из матрицы
строки и
столбца. Тогда
называется минором элемента
.
Величинаназывается алгебраическим дополнением
элемента
.
Разложение определителя матрицы по элементам строки или столбца.
Теорема.
Определитель каждой матрицы равен сумме
произведений элементов любой ее строки
(столбца) на их алгебраические дополнения,
т. е. при разложении по элементам 
строки
Для вычисления значений определителей матриц второго порядка пользуются формулой:
Для вычисления значений определителей матриц третьего порядка можно воспользоваться формулой разложения определителя по первой строке:
Пример
7. Не
вычисляя определителя 
,
показать, что он равен нулю.
Решение. Вычтем из второй строки первую, получим определитель
,
равный исходному. Если из третьей
строки также вычесть первую, то получится
определитель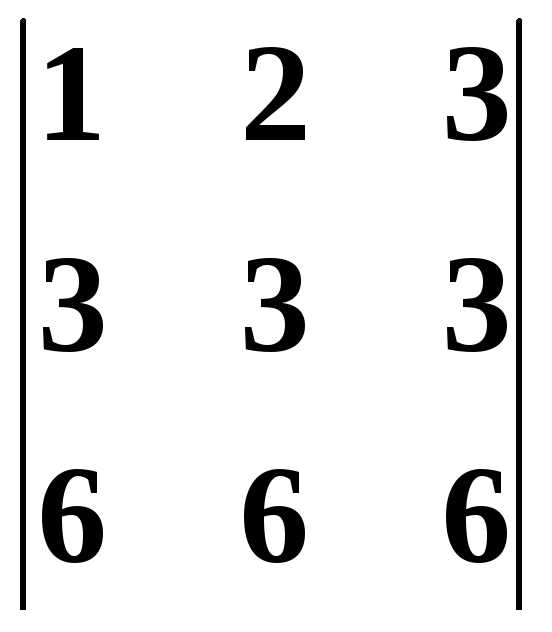 
,
в котором две строки пропорциональны.
Такой определитель равен нулю.
Пример
8. Вычислить
определитель 
,
разложив его по элементам второго
столбца.
Решение. Разложим определитель по элементам второго столбца:
4. Ранг матрицы
Рассмотрим
прямоугольную матрицу 
.
Если в этой матрице выделить произвольно
строк и
столбцов, то элементы, стоящие на
пересечении выделенных строк и столбцов,
образуют квадратную матрицу
порядка. Определитель этой матрицы
называетсяминором
k-го порядка матрицы 
.
Очевидно, что матрица
обладает минорами любого порядка от
до наименьшего из чисел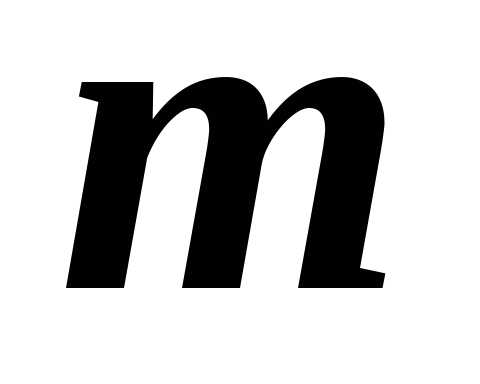
и
.
Некоторые среди них будут равны нулю.
Среди всех отличных от нуля миноров
матрицы
найдется, по крайней мере, один минор,
порядок которого будет наибольшим.
Наибольший из порядков миноров данной
матрицы, отличных от нуля, называется рангом матрицы. Если ранг
матрицы 
равен
,
то это означает, что в матрице
имеется отличный от нуля минор порядка
,
но всякий минор порядка, большего чем
,
равен нулю. Ранг матрицы
обозначается через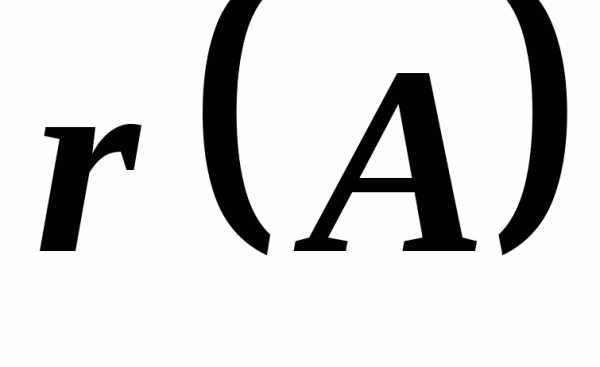
.
Очевидно, что выполняется соотношение
Ранг
матрицы находится либо методом окаймления
миноров, либо методом элементарных
преобразований. При вычислении ранга
матрицы первым способом следует
переходить от миноров низших порядков
к минорам более высокого порядка. Если
уже найден минор 
порядка матрицы
,
отличный от нуля, то требуют вычисления
лишь минорыпорядка, окаймляющие минор
,
т.е. содержащие его в качестве минора.
Если все они равны нулю, то ранг матрицы
равен
.
Элементарными называются следующие преобразования матрицы:
перестановка двух любых строк (или столбцов),
умножение строки (или столбца) на отличное от нуля число,
прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные
матрицы не являются, вообще говоря,
равными, но их ранги равны. Если матрицы 
и 
эквивалентны, то это записывается так: 
.
Каноническойматрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,
.
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
Пример 11. Найти методом окаймления миноров ранг матрицы
Решение. Начинаем
с миноров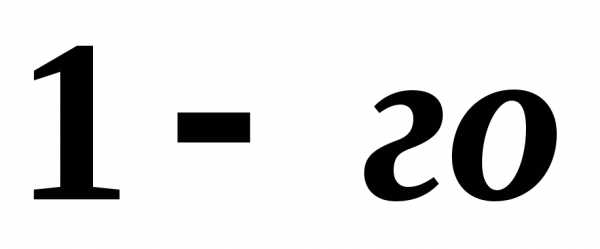 
порядка, (т.е. с элементов матрицы
).
Выберем, например, минор (элемент)
,
расположенный в первой строке и первом
столбце. Окаймляя при помощи второй
строки и третьего столбца, получаем
минор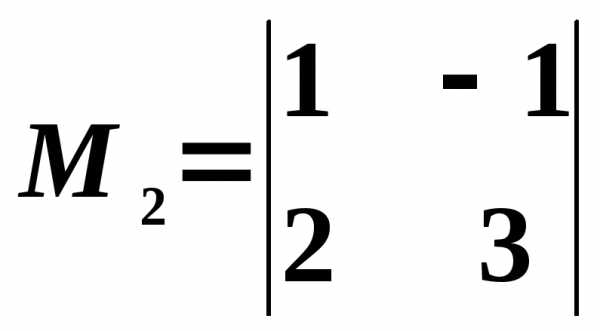
,
отличный от нуля. Переходим теперь к
минорам
порядка, окаймляющим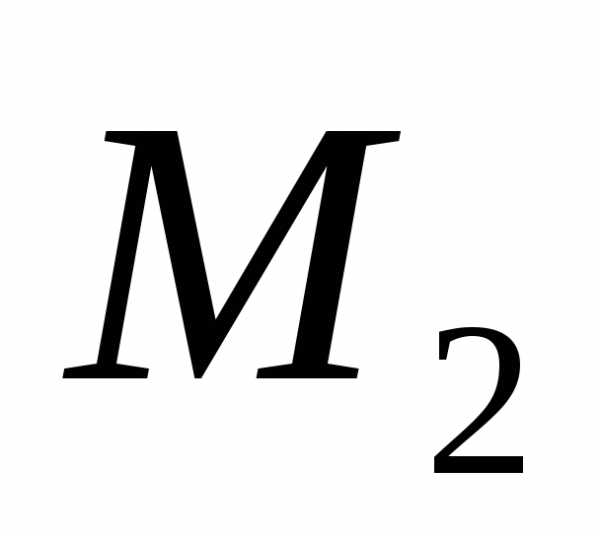
.
Их всего два (можно добавить второй
столбец или четвертый). Вычисляем их:
, 
.
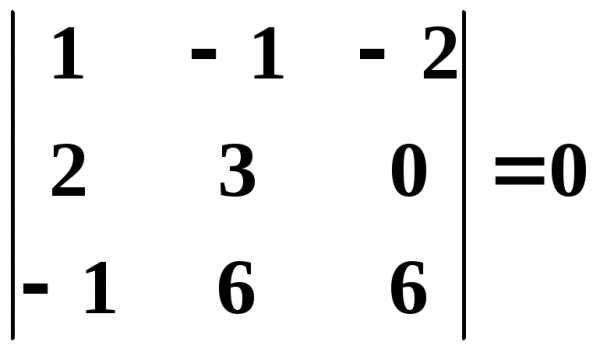Таким
образом, все окаймляющие миноры третьего
порядка оказались равными нулю. Ранг
матрицы 
равен двум.
Пример 12. Найти ранг матрицы
и привести ее к каноническому виду.
Решение. Из второй строки вычтем первую и переставим эти строки:
.
Теперь из второй и третьей
строк вычтем первую, умноженную
соответственно на 
и
:
;
из третьей строки вычтем вторую, при этом получим матрицу
,
которая эквивалентна матрице 
,
так как получена из нее с помощью
конечного множества элементарных
преобразований. Очевидно, что ранг
матрицы
равен
,
а следовательно, и
.
Матрицу 
легко привести к канонической.
Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются.
Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
. 
studfiles.net
Если определитель матрицы равен нулю, то обратная к ней не существует.
Количество просмотров публикации Если определитель матрицы равен нулю, то обратная к ней не существует. — 274
Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.
Определение 14.9 Квадратную матрицу назовем вырожденной или особенной матрицей, в случае если , и невырожденной или неособенной матрицей, в случае если .
Предложение 14.21 В случае если обратная матрица существует, то она единственна.
Доказательство. Пусть две матрицы и являются обратными для матрицы . Тогда
и
Следовательно, .
Предложение 14.22 В случае если квадратная матрица является невырожденной, то обратная для нее существует и
| (14.14) |
где — алгебраические дополнения к элементам .
Доказательство. Так как для невырожденной матрицы правая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы . Обозначим правую часть равенства (14.14) буквой . Тогда нужно проверить, что и что . Докажем первое из этих равенств, второе доказывается аналогично.
Пусть . Найдем элементы матрицы , учитывая, что :
В случае если , то по предложению 14.17 сумма справа равна нулю, то есть при .
В случае если , то
Сумма справа представляет собой разложение определителя матрицы по -ой строке (предложение 14.16). Таким образом,
Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть .
Результаты предложений 14.20, 14.21, 14.22 соберем в одну теорему.
Теорема 14.1 Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица — невырожденная, обратная матрица единственна, и справедлива формула (14.14).
Замечание 14.12 Следует обратить особое внимание на места͵ занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номер столбца, а второй — номер строки, в которые нужно записать вычисленное алгебраическое дополнение.
Пример 14.7 Найдите обратную матрицу для матрицы .
Решение. Находим определитель
Так как , то матрица — невырожденная, и обратная для нее существует.
Находим алгебраические дополнения:
Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй — строке:
| (14.15) |
Полученная матрица и служит ответом к задаче.
Замечание 14.13 В предыдущем примере было бы точнее ответ записать так:
| (14.16) |
При этом запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, в случае если таковые потребуются. По этой причине запись ответа в виде (14.15) предпочтительнее, в случае если элементы матриц — целые числа. И наоборот, в случае если элементы матрицы — десятичные дроби, то обратную матрицу лучше записать без множителя впереди.
Замечание 14.14 При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. По этой причине велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. В случае если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.
Пример 14.8 Найдите обратную матрицу для матрицы .
referatwork.ru
Свойства определителей
Определитель не меняется при транспонировании.
Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен 0.
Если две строки (два столбца) поменять местами, то определитель меняет знак.
Если элементы какой-либо строки (столбца) содержат общий множитель, то его можно вынести за знак определителя.
Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен 0.
Справедливо равенство
.
Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.
Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю.
Сумма произведений элементов любой строки (столбца) определителя на алгебраические дополнения другой строки (столбца) равна 0.
Теорема
1. Если 
и
– квадратные матрицы
-го
порядка, то
.
Следствие. .
Пример
5. (Образец
решения задачи 2 из контрольной работы).
Даны матрицы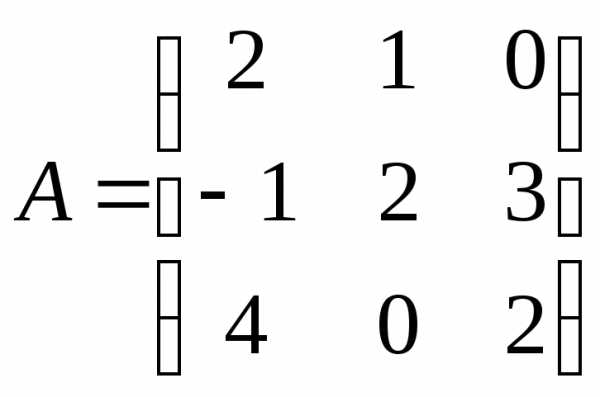
и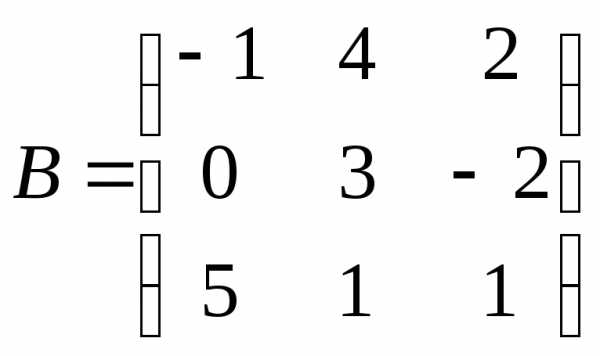
.
Проверить справедливость равенства .
Решение.
Таким образом,
=–1650. n
1.1.5. Обратные матрицы
Матрица 
называется обратной к квадратной матрице
,
если
.
Матрица 
называетсявырожденной,
если 
;
в противном случае
–невырожденная матрица.
Для
того, чтобы матрица 
имела обратную, необходимо и достаточно,
чтобы она была невырожденной, т.е.
.
В таком случае,
,
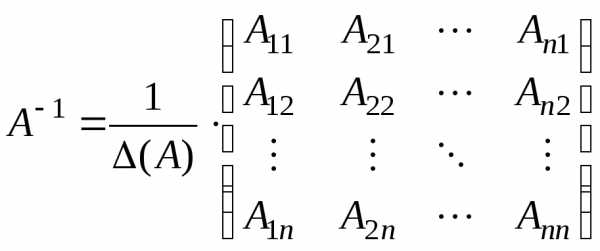т.е.
обратная матрица есть разделенная на 
транспонированная матрица алгебраических
дополнений элементов матрицы
.
Пример
6. Дана
матрица 
.
Найти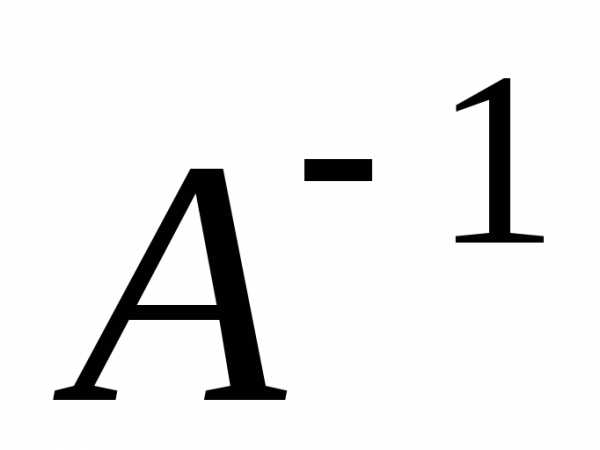
.
Решение.
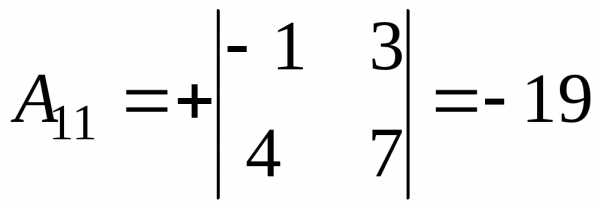
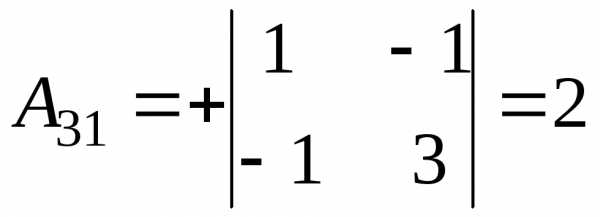
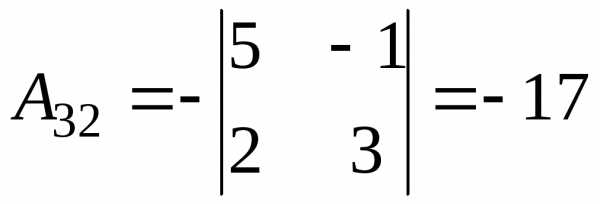
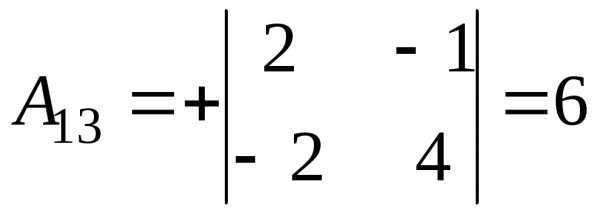
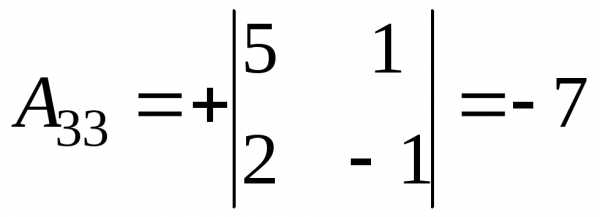
и тогда, .
Проверка.
.
Аналогично
убеждаемся, что
.
Значит, матрица
найдена верно.n
Справедлива следующая теорема:
Теорема
2. Если 
и
невырожденные квадратные матрицы
одинакового порядка, то
.
1.2. Системы линейных алгебраических уравнений
Рассмотрим систему из 3-х алгебраических уравнений с 3-мя неизвестными:
| (1.1) |
1.2.1. Метод Крамера
Теорема 3. Если определитель матрицы системы (1.1)
отличен
от нуля (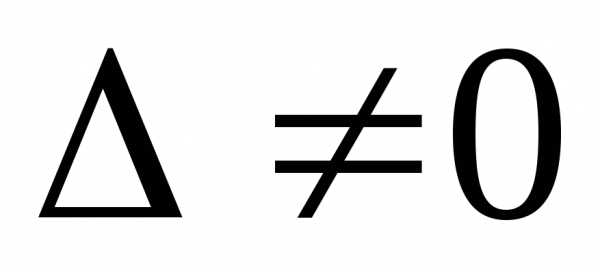
),
то система имеет единственное решение,
определяемое формулами Крамера:
где
, 
,
.
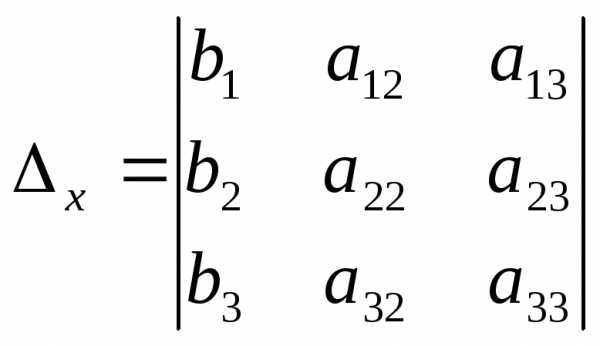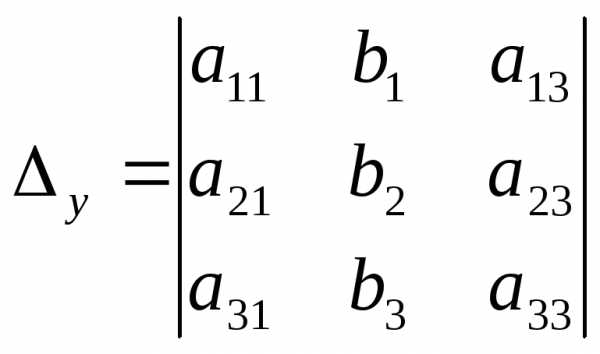1.2.2. Матричный метод
Обозначим
через 
матрицу системы (1.1), т.е. матрицу,
составленную из коэффициентов при
неизвестных:
,
через 
– матрицу-столбец из неизвестных и
через
–
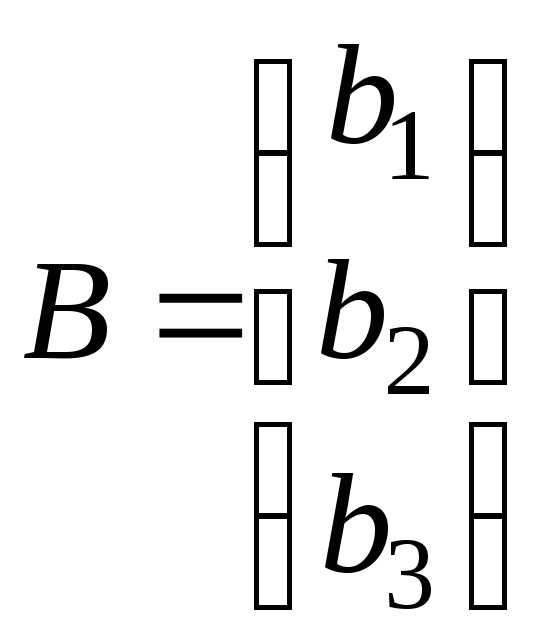матрицу-столбец правых частей.
Принимая во внимание правило умножения матриц, можно систему линейных уравнений (1.1) записать в виде матричного уравнения:
,
решение которого имеет вид
.
Пример 7. (Образец выполнения задачи 1 из контрольной работы) Решить систему уравнений двумя способами:
.
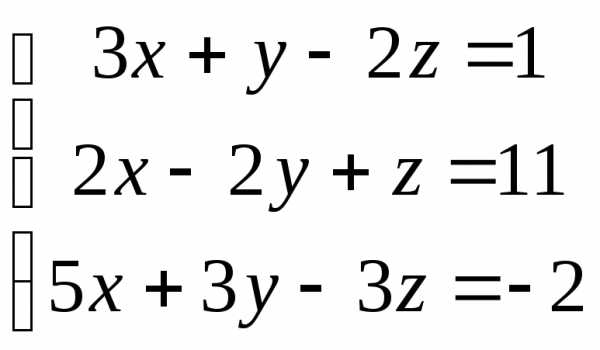Решение. Используем метод Крамера:
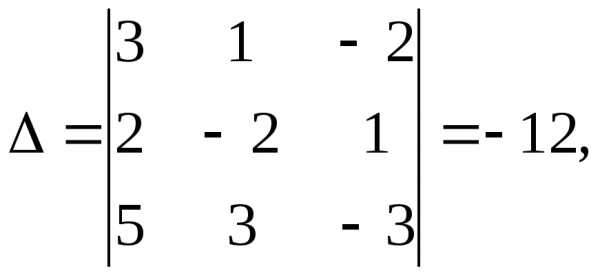
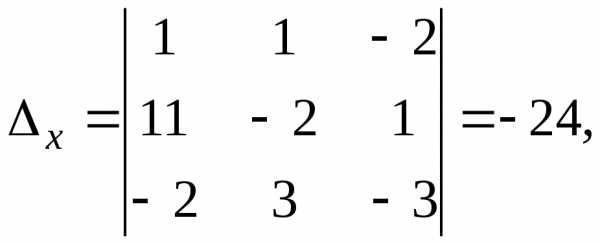
Тогда
Проверим правильность полученных решений, для чего подставим их в условие:
Теперь решим ту же
систему матричным методом. Найдем
обратную матрицу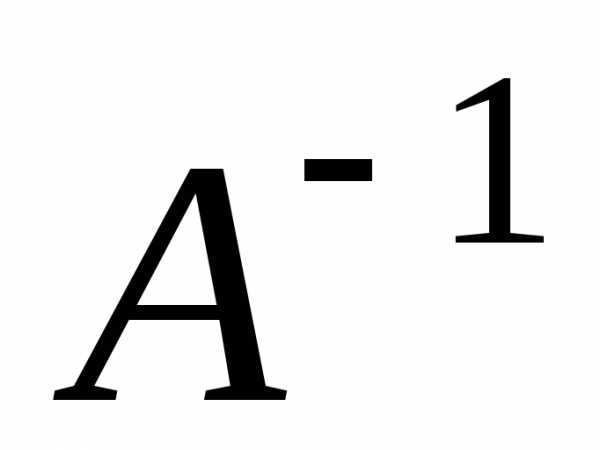 
к матрице системы
.
Вычислим все алгебраические дополнения:
; 
;;
; 
;
;
; 
;
.
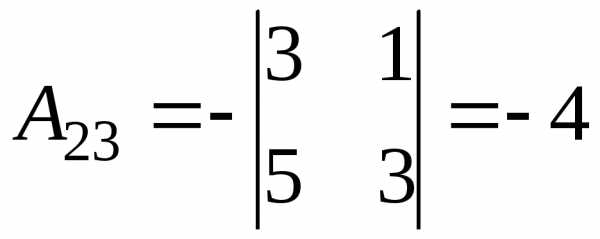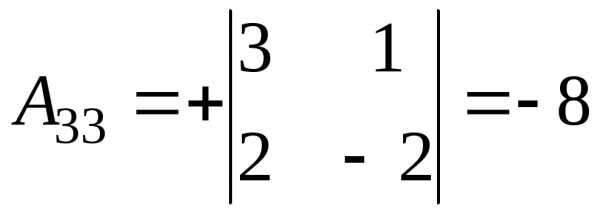Определитель
матрицы найден выше (фактически это 
)
и равен -12.
Следовательно, 
.
Тогда
.
Ответ: .n
Замечание 1.Метод Крамера и матричный метод применимы для систем любого конечного порядка при двух условиях: количество уравнений совпадает с количеством неизвестных и определитель системы отличен от нуля.
Замечание 2.Если определитель системы равен нулю, то система либо не имеет решений вообще, либо имеет бесконечное множество решений.
studfiles.net
Определитель матрицы
Рассмотрим систему двух линейных уравнений с двумя неизвестными:
| (1) |
Умножим обе части первого уравнения на a22 а второе на —a12 и сложим. Получим следующее уравнение
Далее, первое уравнение умножим на —a21 а второе на a11 и сложим:
Пусть Тогда решение системы (1) примет следующий вид:
Выражение называется определителем матрицы
и обозначается:
Нетрудно заметить, что
Таким образом, решение системы линейных уравнений можно представить в виде:
Рассмотрим случай из трех неизвестных и трех уравнений. Пусть дана система линейных уравнений
| (2) |
Исключим неизвестные x2 и x3. Для этого умножим первое уравнение на a22a33—a32a23, второе на —(a12a33—a13a32), третье на a12a23—a22a13, и сложим:
Сделаем следующие обозначения:
Учитывая, что выражения перед элементами x2 и x3 равны нулю, имеем:
Выражение называется определителем матрицы
| (3) |
и обозначается:
| (3a) |
Элементы Mij называются минорами элементов aij, и являются определителями матрицы (3), полученные вычеркиванием i-ой строки и j-го столбца.
Заметим, что выражение
является определителем матрицы
Если определитель (3a) неравен нулю, то x1 вычисляется из следующего выражения:
Аналогично вычисляются x2 и x3, умножая уравнения системы (2) на соответствующие выражения и суммируя:
Распространяя вышеизложенное на системы линейных уравнений с n неизвестными и n уравнениями можно сформулировать понятие определителя для квадратной матрицы порядка n.
Пусть задана матрица
| (4) |
Определителем порядка n, соответствующим матрице (4), называется число равное
| (5) |
Сделаем следующее обозначение:
Тогда выражение (5) можно переписать в следующем виде:
| (6) |
Aij называется алгебраическим дополнением элемента aij.
В вышеизложенном выражении определитель вычисляется суммируя произведения всех элементов первого столбца на соответствующие им алгебраические дополнения. Аналогично можно показать, что определитель равна сумме произведений всех элементов какой либо строки (или столбца) на соответствующие алгебраические дополнения:
| (7) |
Однако, для вычисления определителя матрицы большой размерности, такой подход требует больших усилий. Ниже мы представим более оптимальный метод вычисления определителя. Для этого сначала изложим некоторые важные свойства определителей.
Свойства определителей
- Перестановка строк меняет знак определителя на обратное.
- Общий для всех элементов множитель какой либо строки, можно выносить за знак определителя.
- При сложении двух определителей, различающихся только одной строкой, соответствующие элементы этой строки складываются.
- Прибавление одной строки к другой строке, умноженной на число, не изменяет значение определителя.
- При замене местами строк и столбцов (при транспонировании) определитель не изменит своего значения.
Вычисление определителя матрицы с помощью исключения Гаусса
Для вычисления определителя приведем матрицу к верхнему треугольному виду с помощью исключения Гаусса. Тогда выражение (7) примет следующий вид:
| (8) |
где Z— общее количество перестановок. При каждой перестановке строк, изменяется знак определителя на обратное (свойство 1). Если общее число перестановок нечетное, то нужно поменять знак произведения элементов главной диагонали на обратное.
Онлайн нахождение определителя матрицы
Для нахождения определителя матрицы вы можете использовать матричный онлайн калькулятор. Для подробного решения используйте онлайн калькулятор для вычисления определителя матрицы.
matworld.ru