Формула косинусов для сферического треугольника – Сферические треугольники решение и формулы (Таблица)

Содержание

Сферические теоремы косинусов — Howling Pixel

Первая и вторая сферические теоремы косинусов устанавливают соотношения между сторонами и противолежащими им углами сферического треугольника.

Формулировка

Теоремы косинусов для сферического треугольника со сторонами a, b, c и углами A, B, C имеют следующий вид:

cos⁡c=cos⁡acos⁡b+sin⁡asin⁡bcos⁡C,{\displaystyle \cos c=\cos a\cos b+\sin a\sin b\cos C,}

cos⁡A=−cos⁡Bcos⁡C+sin⁡Bsin⁡Ccos⁡a.{\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cos a.}

Эти две теоремы двойственны по отношению друг к другу, поскольку углы и стороны всякого сферического треугольника дополняются до развёрнутого угла сторонами и углами соответствующего полярного треугольника. Поэтому достаточно доказать одну из них.

Следствия и применение

Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:

cos⁡c=cos⁡acos⁡b.{\displaystyle \cos c=\cos a\cos b.}

Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек φA{\displaystyle \varphi _{A}} и φB{\displaystyle \varphi _{B}}, разность долгот — ΔλAB{\displaystyle \Delta \lambda _{AB}}, кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии^[2]:

cos⁡(da)=sin⁡φA⋅sin⁡φB+cos⁡φA⋅cos⁡φB⋅cos⁡ΔλAB{\displaystyle \cos \left({\frac {d}{a}}\right)=\sin \varphi _{A}\cdot \sin \varphi _{B}+\cos \varphi _{A}\cdot \cos \varphi _{B}\cdot \cos \Delta \lambda _{AB}}

Эта формула сразу получается применением теоремы косинусов к стороне AB сферического треугольника P_nAB. Подобная формула справедлива для любой сферической поверхности и поэтому её можно применять также для определения углового расстояния между звёздами по известным их экваториальным координатам

[3].

Теорема косинусов в её втором виде (соотношение между тремя углами и стороной) может быть применена для вычисления взаимного наклонения двух орбит при известном наклонении каждой орбиты к какой-то другой плоскости. Например, по этой формуле можно вычислить наклонение орбиты Плутона к орбите Нептуна, используя наклонения их орбит к эклиптике и долготы их восходящих узлов.

История

Теорема косинусов для сферического треугольника математиками средневекового Востока в общем виде сформулирована не была, хотя при решении конкретных астрономических задач они иногда пользовались соотношениями, равносильными этой теореме. Эти соотношения, используемые при определении высоты Солнца, встречаются в сочинениях Сабита ибн Корры, ал-Махани, ал-Баттани, Ибн Юниса, ал-Бируни.

Впервые теорему косинусов в явном виде сформулировал в XV веке Региомонтан, назвав её «теоремой Альбатегния» (по латинизированному имени ал-Баттани).

См. также

Примечания

↑ Приводится по изданию: Степанов Н.Н. Формулы косинуса стороны // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 24—28. — 154 с.
↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы её задания // Навигация и лоция. — Киев, 2009.
↑ Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир, 1988. — С. 44—46. — 168 с. — ISBN 5030009361.
↑ Lee Kai Ming. PHYS 2021 — The Physical Universe. — 2010. — С. 6.

Литература

Вентцель М. К. Сферическая тригонометрия. 2-е изд., ИГКЛ, 1948, 115с.
Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.
Степанов Н. Н. Сферическая тригонометрия. — Л.-М., 1948.

Решение треугольников

Решение треугольников (лат. solutio triangulorum) — исторический термин, означающий решение главной тригонометрической задачи: по известным данным о треугольнике (стороны, углы и т. д.) найти остальные его характеристики. Существуют также обобщения этой задачи на случай, когда заданы другие элементы треугольника (например, медианы, биссектрисы, высоты, площадь и т. д.). Треугольник может располагаться на плоскости или на сфере. Данная задача часто встречается в тригонометрических приложениях, например, в геодезии, астрономии, строительстве, навигации.

Сферическая теорема синусов

Сферическая теорема синусов устанавливает пропорциональность между синусами сторон a, b, c и синусами противолежащих этим сторонам углов A, B, C сферического треугольника:

sin⁡asin⁡A=sin⁡bsin⁡B=sin⁡csin⁡C.{\displaystyle {\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}}.}

Сферическая теорема синусов является аналогом плоской теоремы синусов и переходит в последнюю в пределе малости сторон треугольников по сравнению с радиусом сферы.

Сферическая тригонометрия

Сферическая тригонометрия — раздел тригонометрии, в котором изучаются зависимости между величинами углов и длинами сторон сферических треугольников. Применяется для решения различных геодезических и астрономических задач.

This page is based on a Wikipedia article written by authors (here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.

howlingpixel.com

Основные формулы сферической тригонометрии — КиберПедия

Задачей сферической тригонометрии является решение сферического треугольника, то есть вычисление его неизвестных элементов через заданные (известные).

Известно, что для нахождения какого-либо угла или стороны треугольника необходимо, чтобы три любых других его элемента были известны (заданы).

Рассмотрим (без вывода) четыре основные теоремы сферической тригонометрии, устанавливающие необходимую аналитическую зависимость между элементами сферического треугольника.

I. Формула косинуса стороны.

Эта формула связывает между собой все три стороны и один из углов сферического треугольника. Для любого сочетания таких четырех элементов установлена зависимость, что …

«… косинус стороны сферического треугольника равняется произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…».

Рис. 2.2. Сферический треугольник

Применительно к стороне а (рис. 2.2) сферического треугольника АВМ, руководствуясь теоремой косинуса стороны, можем записать:

cos a = cos b · cos m + sin b · sin m · cos A

Для сторон b и m зависимость между элементами треугольника выразится формулами:

(2.1)

II. Формула синусов связывает между собой противолежащие элементы сферического треугольника → углы и стороны.

«… во всяком сферическом треугольнике синусы сторон относятся как синусы противолежащих углов…».

Для сферического треугольника АВМ (рис. 2.2) можем записать соотношения:

Формула синусов применяется для вычисления одного из элементов, входящих в записанные равенства, если известны три других элемента.

III. Формула котангенсов связывает между собой четыре элемента сферического треугольника, лежащие рядом.

«… котангенс крайнего угла, умноженный на синус среднего, равняется произведению котангенса крайней стороны на синус средней без произведения косинусов средних элементов…».

Если в сферическом треугольнике АВМ (рис. 2.2) устанавливается зависимость между элементами А, m, В и а, то угол А и сторона а являются крайними, а угол В и сторона m – средними элементами, и тогда:

ctg A · sin B = ctg a · sin m — cos B · cos m

Всего для треугольника можно написать шесть таких соотношений, а именно:

(2.3)

Формула котангенсов применяется для вычисления стороны или угла сферического треугольника, если они лежат рядом с тремя заданными элементами.

IV. Формула косинуса угла связывает между собой три угла и одну из сторон сферического треугольника.

«… косинус угла сферического треугольника равняется произведению синусов двух других углов на косинус стороны между ними без произведения косинусов тех же углов…».

Для каждого из углов сферического треугольника АВМ можно написать формулы:

(2.4)

Эти формулы удобны при вычислении угла по двум другим углам и стороне между ними, а также служат для нахождения стороны по трем заданным углам.

Рис. 2.3. Прямоугольный сферический треугольник

Решение прямоугольных треугольников проще, чем косоугольных, так как один из их элементов (угол 90°) всегда известен и для решения треугольника достаточно знать только два элемента.

То же самое относится и к четвертным треугольникам, в которых один из элементов (сторона 90°) всегда известен.

Если в сферическом треугольнике АВМ (рис. 2.3) заданы угол В = 90°, катет а и угол М, то для вычисления неизвестного угла А можно применить формулу косинуса угла (6.4) → cos A = sin B · sin M · cos a — cos B · cos M.

Если теперь заменить все функции угла В = 90° их значениями (sin B = 1, cos B = 0), то получим

cos A = sin M · cos a

(2.5)

2.3. Вычисление горизонтных координат светил по таблицам логарифмических функций мореходных таблиц «МТ-75»

При вычислении счислимой высоты (h

С) и азимута (А_С) светила по формулам сферической тригонометрии, как по натуральным значениям тригонометрических функций, так и по логарифмам, наиболее удобными являются формулы:

(2.6)

В формуле знак «~» означает, что при φ_С и δ одноименных из большей величины вычитается меньшая, а при разноименных → величины φ_С и δ складываются.

Значения , и табулированы так, что при вычислениях не нужно делить аргументы Z_C, φ_С~δ и t_M, а значения тригонометрических функций возводить в квадрат, → все эти действия выполнены в таблицах 5а (5б) «МТ-75» (в «МТ-2000» таких таблиц нет).

Производить исследование формулы на знаки тригонометрических функций не требуется, так как оба члена ее правой части всегда положительны.

Методику вычисления горизонтных координат светил с помощью «МТ-75» рассмотрим на примере решения конкретной задачи.

Задача: Вычислить значения счислимых высоты (h_C) и азимута (А_С) светила, если:

φ_С = 43°20,6′N; δ = 17°36,7′N; t_M = 17°12,4′W.

Решение:

→ Составляем схему вычислений:

cyberpedia.su

Теоремы косинусов в плоской и сферической тригонометрии

Как уже говорилось, тригонометрии как таковой (и вообще каких-либо измерений) в «Началах» Евклида нет. Тем не менее, в них сформулировано утверждение, необходимое для решения плоских треугольников – а именно, теорема косинусов, позволяющая по двум сторонам и углу между ними найти третью сторону. Как известно, в современных обозначениях, теорема косинусов записывается так:

c² = a² + b² – 2ab cos A.

Эта теорема является обобщением теоремы Пифагора на непрямоугольные треугольники. У Евклида теорема косинусов распадается на два утверждения – о тупоугольном и остроугольном треугольнике. Первая сформулирована так:

В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше суммы квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключенный между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле:

BC² = AB² + AC² + 2AC ∙ AD.

Рис. 1. Теорема косинусов для тупоугольного треугольника, Евклид

Поскольку

AD = AB cos BAD, а

cos BAD = –cos BAС,

данное утверждение действительно эквивалентно теореме косинусов для тупого угла.

Доказательство в современных обозначениях сводится к цепочке равенств:

BC² = BD² + CD² = BD² + (AC + AD)² = BD² + AC² + AD² + 2AC ∙ AD = (BD² + AD²) + AC² + 2AC ∙ AD = AB² + AC² + 2AC ∙ AD.

Здесь дважды применена теорема Пифагора – в первом и в последнем равенствах.

Теорема косинусов для остроугольного треугольника звучит у Евклида так:

В остроугольных треугольниках квадрат на стороне, стягивающей острый угол, меньше суммы квадратов на заключающих острый угол сторонах на дважды взятый прямоугольник, заключенный между одной из сторон при остром угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром внутрь отрезком при остром угле:

BC² = AB² + AC² – 2AC ∙ AD.

Рис. 2. Теорема косинусов для остроугольного треугольника, высота лежит внутри треугольника, Евклид

Опять-таки, поскольку AD равно AB cos BAC, данное утверждение эквивалентно теореме косинусов для острого угла:

BC² = BD² + CD² = BD² + (AC – AD)² = BD² + AC² + AD² – 2AC ∙ AD = (BD² + AD²) + AC² – 2AC ∙ AD = AB² + AC² – 2AC ∙ AD.

Следует отметить, что эта теорема верна не только для остроугольных треугольников, но и для любых треугольников – а именно, для квадрата той ее стороны, которая лежит против острого угла. В том числе она остается верной для случая, когда основание перпендикуляра BD лежит вне стороны AC.

Рис. 3. Теорема косинусов для остроугольного треугольника, высота не лежит в треугольнике, Евклид

Нужно ли что-либо изменить в доказательстве для этого случая?

Ответ

Если раньше выполнялось CD = AC – AD, то теперь выполняется CD = AD – AC, однако это ничего не меняет в равенствах в доказательстве теоремы.

Современные школьники изучают лишь плоскую тригонометрию, в то время как математиков древности, средневековья и нового времени больше всего интересовала сферическая тригонометрия, рассматривающая треугольники на сфере и позволяющая находить одни элементы этих треугольников по другим их элементам. Под сферическим треугольником подразумевается треугольник на поверхности сферы, составленный из дуг больших кругов – т. е. таких окружностей, центром которых является центр сферы.

Рис. 4. Сферический треугольник

Такое обобщение понятия треугольника естественно: подобно тому, что на плоскости линия кратчайшей длины между двумя точками – это прямая, на сфере линией кратчайшей длины является большой круг. Длина дуги AB пропорциональна центральному углу AOB, опирающемуся на нее; если мы пользуемся радианной мерой углов, то длина дуги просто равна произведению радиуса сферы на величину угла AOB. Для простоты будем рассматривать сферу, радиус которой равен 1. Стороны треугольников на такой сфере просто будут равны соответствующим центральным углам, а значит, можно будет измерять синусы и косинусы сторон, а не только углов, треугольников.

Углы сферического треугольника – это углы между касательными к его сторонам, проведенными в его вершинах. Как и углы обычного треугольника, они меняются от 0 до 180°. В отличие от плоского треугольника, у сферического сумма углов не равна 180°, а больше: в этом нетрудно убедиться, рассмотрев, например, треугольник, образованный дугами двух меридианов и экватора на глобусе: хотя меридианы сходятся в полюсе, оба они перпендикулярны экватору, а значит, у этого треугольника два прямых угла!

Рис. 5. У сферического треугольника может быть два прямых угла

Уже у индийца Варахамихиры (V–VI вв.), у арабских математиков и астрономов начиная с IX в. (Сабит ибн Корра, ал-Баттани), а у западных математиков начиная с Региомонтана (XV в.) встречается в различных формулировках замечательная теорема о сферических треугольниках. Вот как она может быть сформулирована в современных обозначениях:

cos a = cos b cos c + sin b sin c cos A.

Рис. 6. Теорема о сферических треугольниках

Казалось бы, эта формула внешне нисколько не походит на привычную нам теорему косинусов для плоского случая, но она тоже позволяет по двум сторонам и углу между ними находить третью сторону и в этом смысле аналогична теореме косинусов.

Сферическая теорема косинусов очень важна и для астрономии, и для географии. Эта теорема позволяет по координатам двух городов A и B находить расстояние между ними. В самом деле, рассмотрим сферический треугольник ABN, где N – северный полюс (предположим для простоты, что обе точки находятся в северном полушарии).

Рис. 7. Нахождение расстояния между двумя точками на сфере

Тогда, если широта и долгота точки A равны φ_A и λ_A, а точки B – φ_B и λ_B, то угловые величины сторон треугольника таковы:

AN = π/2 – φ_A, BN = π/2 – φ_B,

угол при вершине N равен (λ_A – λ_B),

и, по сферической теореме косинусов,

cos AB = cos (π/2 – φ_A) cos (π/2 – φ_B) + sin (π/2 – φ_A) sin (π/2 – φ_B) cos (λ_A – λ_B) = sin φ_A sin φ_B + cos φ_A cos φ_B cos (λ_A – λ_B).

Попробуйте, пользуясь этой формулой, узнать расстояние от Москвы (56° с. ш., 38° в. д.) до Санкт-Петербурга (60° с. ш., 30° в. д.).

Кроме того, математикам стран ислама сферическая теорема косинусов помогала в решении другой практической задачи: в городе с данными координатами находить направление на священный город Мекку (всякий правоверный мусульманин должен пять раз день молится в направлении Мекки). При решении этой задачи, считая город B Меккой, требовалось найти угол A того же треугольника.

Рис. 8. Страница из «Собрания правил науки астрономии», XI в., автор неизвестен

В астрономии сферическая теорема косинусов позволяет переходить из одной системы координат на небесной сфере в другую. Чаще всего используются три такие системы: у одной экватором служит небесный экватор, а полюсами – полюсы мира, вокруг которых происходит видимое суточное вращение светил; у другой экватором является эклиптика – круг, по которому в течение года совершается видимое движение Солнца на фоне звезд; у третьей роль экватора выполняет горизонт, а роль полюсов – зенит и надир. В частности, благодаря сферической теореме косинусов можно вычислять высоту Солнца над горизонтом в разные моменты времени и в разные дни в году.

Арабские математики сформулировали и теоремы синусов – плоскую и сферическую. Эта последняя выглядит очень похоже на плоскую:

sin a / sin A = sin b / sin B = sin c / sin C.

files.school-collection.edu.ru

Теоремы косинусов (сферическая геометрия) — это… Что такое Теоремы косинусов (сферическая геометрия)?

Сферический треугольник.

Формулировка

Теоремы косинусов для сферического треугольника со сторонами a, b, c и углами A, B, C имеют следующий вид:

Доказательство

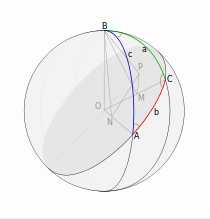Рисунок к доказательству теоремы косинусов с помощью проекций.

Доказательство проведём с помощью проекций^[1]. На рисунке показан сферический треугольник ABC на сфере радиуса R с центром в точке O. BP — перпендикуляр к плоскости большого круга, проходящего через сторону b, BM — перпендикуляр к OC, BN — перпендикуляр к OA. По утверждению, обратному теореме о трёх перпендикулярах, PM — перпендикуляр к OC, PN — перпендикуляр к OA. Заметим, что угол PMB равен π — C, кроме того, ON = R cos c и OM = R cos a. Далее, проецируем ломаную OMPN на прямую, содержащую ON.

Подставляем три последних выражения и указанное выше выражение ON = R cos c в первое выражение и получаем:

Теоремы косинусов для двух других сторон, то есть теорему для cos a и теорему для cos b, получаем аналогично, их также можно получить сразу из формулы для стороны c при помощи круговой перестановки букв:

Сферический треугольник для определения кратчайшего расстояния между точками на Земле.

Следствия и применение

Если угол C — прямой, первая теорема косинусов переходит в сферическую теорему Пифагора:

Хотя для решения косоугольных сферических треугольников обычно используются более удобные формулы, с помощью теоремы косинусов выводится важная для геодезии формула длины ортодромии — кратчайшего расстояния между точками на земной поверхности с известными координатами (в предположении сферичности Земли). Обозначим географические широты двух данных точек и , разность долгот — , кратчайшее расстояние между ними обозначим d, длину дуги в 1 градус — a. Тогда формула длины ортодромии^[2]:

Пример 1: определение углового расстояния между двумя светилами на небесной сфере

Определим угловое расстояние (x) между звездой δ Цефея (экваториальные координаты: α₁=22ч 29м, δ₁=+58° 25′) и галактикой Туманность Андромеды (α₂=0ч 43м, δ₂=+41° 16′) на небесной сфере. Выражаем α₁ в градусах и долях градуса:

Аналогично получаем, что α₂=10°,75. Выражаем δ₁ в градусах и долях градуса:

Аналогично δ₂=41°,27. Применяем теорему косинусов^[4]:

Отсюда x=27°,11.

Пример 2: определение взаимного наклонения орбит небесных тел

Определим взаимное наклонение (x) орбит Плутона (наклонение орбиты к эклиптике — 17°,14, долгота восходящего узла — 110°,30) и Нептуна (наклонение орбиты к эклиптике — 1°,77, долгота восходящего узла — 131°,79). В соответствующем сферическом треугольнике известны два угла: один равен наклонению орбиты Плутона к эклиптике, другой — дополнению наклонения орбиты Нептуна к эклиптике до 180 градусов. Известна также прилегающая к этим углам сторона, равная разности долгот восходящих узлов Плутона и Нептуна. Осталось применить второй вариант теоремы косинусов — для углов:

Отсюда x≈15°,51.

История

См. также

Примечания

↑ Приводится по изданию: Степанов Н.Н. Формулы косинуса стороны // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 24—28. — 154 с.
↑ Михайлов В.С., Кудрявцев В.Г., Давыдов В.С. 26.2. Основные формулы ортодромии. Способы ее задания // Навигация и лоция. — Киев, 2009.
↑ Меёс Ж. 9. Угловое расстояние между объектами // Астрономические формулы для калькуляторов. — Мир, 1988. — С. 44—46. — 168 с. — ISBN 5030009361
↑ Lee Kai Ming PHYS 2021 — The Physical Universe. — 2010. — С. 6.

Литература

Матвиевская Г. П. Очерки истории тригонометрии. Ташкент: Фан, 1990.

dic.academic.ru

3)Элементы сферической тригонометрии

Приближенные вычисления. Соотношение между угловой и радиальной мерами измерения углов и длинами дуг.

Приближённые вычисления, вычисления, в которых данные и результат (или по крайней мере только результат) являются числами, лишь приближённо представляющими истинные значения соответствующих величин. П. в. возникают в связи с численным решением задач и обусловлены неточностями, которые присущи формулировке задачи и способам её решения. Общие правила и теорию методов П. в. принято называть численными методами.Обозначение единиц измерения плоского угла:

градус- «°»;минута — «’»;секунда — «»».

Соотношение между угловыми единицами:

1° = 1/360 полного оборота = 2Π/З60 рад = 0,017453 рад;

1’ = 1/60° = Π/108*10^-2 рад = 0,000 291 рад;1’’ = 1/60’’ = Π/648*10^-3 рад = 0,000 005 рад.

2)Тригонометрические функции малых углов.

Пусть a будет какой-нибудь острый угол. Возьмём на одной из его сторон произвольную точку и опустим из неё перпендикуляр на другую сторону угла. Тогда мы получим прямоугольный треугольник. Возьмём отношения сторон этого треугольника попарно, а именно:1) отношение катета, противолежащего углу, к гипотенузе,

2) отношение катета, прилежащего углу, к гипотенузе,

3) отношение катета, противолежащего углу, к катету прилежащему,и обратные им отношения.

Величина каждого из этих отношений не зависит от положения точки на стороне угла.Все указанные отношения называются тригонометрическими функциями. Чаще других отношений берутся следующие четыре:

1) отношение катета, противолежащего углу a, к гипотенузе называется синусом угла a и обозначается sin(a),2) отношение катета, прилежащего углу a, к гипотенузе называется косинусом угла a и обозначается соs(a),3) отношение катета, противолежащего углу a, к катету прилежащему называется тангенсом угла a и обозначается tg(a),4) отношение катета, прилежащего углу a, к катету противолежащему называется котангенсом угла a и обозначается сtg(a).Так как каждый из двух катетов меньше гипотенузы, то синус и косинус каждого угла есть число меньшее единицы. Зависимости между тригонометрическими функциями одного и того же угла. Простейшие из этих зависимостей следующие четыре:

;;;

Сферическая тригонометрия занимается изучением соотношений между сторонами и углами сферических треугольников (например, на поверхности Земли и на небесной сфере).Сферические треугольники. На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара и сферической поверхности. Сторонами a, b, c сферического треугольника называют те углы между лучами, которые меньше 180 (если один из этих углов равен 180, то сферический треугольник вырождается в полуокружность большого круга). Каждой стороне треугольника соответствует дуга большого круга на поверхности шара (см. рисунок).

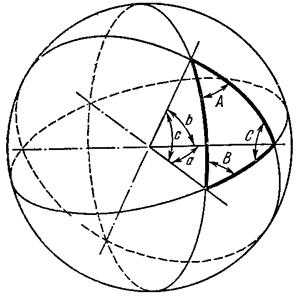
Углы A, B, C сферического треугольника, противолежащие сторонам a, b, c соответственно, представляют собой, по определению, меньшие, чем 180, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лучами.Геометрия на поверхности шара является неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360, сумма углов заключена между 180 и 540. В каждом сферическом треугольнике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180 плюс третий угол.Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):1) тремя сторонами, 2) тремя углами, 3) двумя сторонами и заключенным между ними углом, 4) стороной и двумя прилежащими к ней углами.

4)Формула косинуса стороны.

Формула косинуса стороны связывает три стороны и один из углов сферического треугольника. Удобна для нахождения неизвестного угла или стороны, противолежащей этому углу, и читается следующим образом: «в сферическом треугольнике косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов этих сторон на косинус угла между ними»

5)Формула косинуса угла и синусов

Формула косинуса угла связывает три угла и сторону сферического треугольника, удобна для нахождения неизвестной стороны или угла, противолежащего этой стороне, и читается так: «косинус угла сферического треугольника равен отрицательному произведению косинусов двух других углов плюс произведение синусов этих углов на косинус стороны между ними».;

С*sinA=a*sinc;

6)Формулы пяти элементов и котангенсов.

Формула котангенсов (4-х рядом лежащих элементов) связывает 4 рядом лежащих элемента, используется для нахождения крайних элементов и читается следующим образом: «произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних элементов «.

; SINb*COSА=cosa*sinc-sina*cosc*cosB

Синус сторон х на косинус прилежащего угла равен произведению косинуса стороны на синус 3-ей стороны минус произведению синуса противолежащей стороны на косинус 3-ей стороны и на косинус угла между ними.

7) Решение прямоугольных сферических треугольников. Правило Модюи-Непера. Дополнительные формулы для решение косоугольных сферических треугольников.

Прямоугольным называется такой сферический треугольник, у которого один из углов равен 90°. Прямоугольные сферические треугольники более рационально решать по правилам Модюи-Непера:в прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов; косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов. Примечание: в обоих правилах принято, что катеты лежат рядом друг с другом и что вместо катетов надо брать их дополнения до 90°, изменяя соответственно наименования тригонометрических функций.

8)Фигура и размеры Земли.

Земля представляет собой неправильной формы шар. Длина его экваториального радиуса равна 6 378 245 м. а полярного—6 356 863 м. Как видно, экваториальный диаметр Земли длиннее полярного примерно на 42,8 км. Если изобразить отклонение формы Земли от шара на глобусе с поперечником в 1 м по экватору, то его полярная ось будет короче экваториальной на 3,35 мм. Фигура Земли имеет форму геоида, что переводится как «землеподобный». Геоидом называется фигура, ограничивающая невозмущённую поверхность уровня мирового океана, мысленно проходит под материками и островами, таким образом, что она в каждой своей точке перпендикулярна отвесной линии и имеющая неправильную геометрическую форму. Геометрия геоида очень сложна, поэтому вместо геоида при решении штурманских задач используют более простые модели Земли: эллипсоид вращения, сферу, карту. Размеры референц-эллипсоида Красовского: большая полуось а=6378245 м; в=6356863 м; полярное сжатие а=(а-в)/а=1/298,3; эксцентриситет е=0,0818;R=6371110м.

9)Основные элементы на поверхности небесной сферы и земного сфероида.

Плоскость истинного меридиана наблюдателя пересекается с плоскостью истинного горизонта по линии N — S, которая называется полуденной линией, так как в этой плоскости Солнце бывает точно в полдень.

Вертикальную плоскость, проходящую через глаз наблюдателя перпендикулярно плоскости истинного меридиана наблюдателя, называют плоскостью первого вертикала (плоскость 3). Она пересекается с плоскостью истинного горизонта наблюдателя по линии Ost—W. Таким образом, пересечение взаимно перпендикулярных плоскостей истинного меридиана наблюдателя и первого вертикала дает четыре главные линии на плоскости истинного горизонта наблюдателя, которые указывают на главные точки горизонта: N, S, Ost и W. Если наблюдатель станет лицом к северу, то за спиной у него будет юг, справа—восток, слева—запад. Линии N—S, Ost—W в любой точке земной поверхности (кроме полюсов) занимают вполне определенное положение. Направления N, S, Ost и W называют главными направлениями, или главными румбами, которые делят истинный горизонт на четыре четверти: NOst— северо-восточную, SOst — юго-восточную, SW—юго-западную и NW—северозападную. Каждая четверть делится на 8 румбов, а весь горизонт—на 32 румба.Основные географические точки, линии и круги на земном шаре.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.Земля непрерывно вращается в направлении с запада на восток. Диаметр, вокруг которого происходит это вращение, называется осью вращения Земли.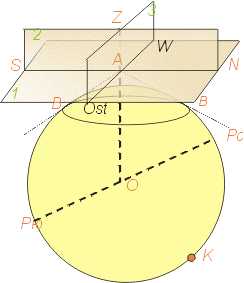

Эта ось пересекается с поверхностью Земли в двух точках, которые называются географическими полюсами: один Северным (С), а другой Южным (Ю). Северным называется тот полюс, в котором, если смотреть на него сверху, вращение Земли направлено против хода часовой стрелки. Противоположный полюс называется Южным.

Через любую точку на земном шаре можно провести бесчисленное множество больших и малых кругов.Большим называется круг, образованный на земной поверхности плоскостью сечения, проходящей через центр Земли. Малым называется круг, образованный на земной поверхности плоскостью сечения, не проходящей через центр Земли. Большой круг, плоскость которого перпендикулярна оси вращения Земли, называется экватором. Экватор делит земной шар на Северное и Южное полушария. Малый круг, плоскость которого параллельна плоскости экватора, называется параллелью. Через каждую точку на земной поверхности можно провести только, одну параллель, которая называется параллелью места. Большой круг, проходящий через полюсы Земли, называется географическим, или истинным меридианом. Через каждую точку на земной поверхности, кроме полюсов, можно провести только один меридиан, который называется меридианом места. Меридиан, проходящий через Гринвичскую астрономическую обсерваторию, находящуюся в Англии вблизи Лондона, принят по международному соглашению в качестве начального меридиана.Начальный меридиан делит земной шар на Восточное и Западное полушария. Плоскость экватора и плоскость начального меридиана являются основными плоскостями, от которых производится отсчет географических координат.

studfiles.net

Сферические теоремы косинусов Википедия

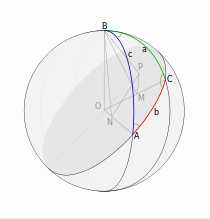Рисунок к доказательству теоремы косинусов с помощью проекций.

pr ON=pr OM+pr MP+pr PN{\displaystyle {\mbox{pr }}ON={\mbox{pr }}OM+{\mbox{pr }}MP+{\mbox{pr }}PN},

PN⊥OA⇒pr PN=0{\displaystyle PN\perp OA\Rightarrow {\mbox{pr }}PN=0},

pr OM=OMcos⁡b=Rcos⁡acos⁡b{\displaystyle {\mbox{pr }}OM=OM\cos b=R\cos a\cos b},

pr MP=PMcos⁡(π−(π2−∠MPN))=PM(−sin⁡∠MPN){\displaystyle {\mbox{pr }}MP=PM\cos(\pi -({\frac {\pi }{2}}-\angle MPN))=PM(-\sin \angle MPN)}

ruwikiorg.ru

Сферические теоремы косинусов Википедия

Рисунок к доказательству теоремы косинусов с помощью проекций.

pr ON=pr OM+pr MP+pr PN{\displaystyle {\mbox{pr }}ON={\mbox{pr }}OM+{\mbox{pr }}MP+{\mbox{pr }}PN},

PN⊥OA⇒pr PN=0{\displaystyle PN\perp OA\Rightarrow {\mbox{pr }}PN=0},

pr OM=OMcos⁡b=Rcos⁡acos⁡b{\displaystyle {\mbox{pr }}OM=OM\cos b=R\cos a\cos b},

pr MP=PMcos⁡(π−(π2−∠MPN)

ru-wiki.ru

Сферические теоремы косинусов — Howling Pixel

Формулировка

Следствия и применение

История

См. также

Примечания

Литература

Основные формулы сферической тригонометрии — КиберПедия

Теоремы косинусов в плоской и сферической тригонометрии

Теоремы косинусов (сферическая геометрия) — это… Что такое Теоремы косинусов (сферическая геометрия)?

Формулировка

Следствия и применение

История

См. также

Примечания

Литература

3)Элементы сферической тригонометрии

5)Формула косинуса угла и синусов

Сферические теоремы косинусов Википедия

Сферические теоремы косинусов Википедия

Добавить комментарий Отменить ответ