Умножение дробей примеры 8 класс – Умножение и деление алгебраических дробей. Видеоурок. Алгебра 8 Класс

Умножение и деление алгебраических дробей. Видеоурок. Алгебра 8 Класс

На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил. Умножение и деление алгебраических дробей не отличается от умножения и деления обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение и деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении. 

Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями

Урок: Умножение и деление алгебраических дробей

Правила умножения и деления алгебраических дробей абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:

То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).

Деление на дробь – это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).

Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:

Во всех этих правилах мы пользовались следующим фактом: .

Решим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.

Пример 1

Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что

простыми числами называются такие натуральные числа, которые делятся только на  и на само себя. Остальные числа называются составными. Число  не относится ни к простым, ни к составным. Примеры простых чисел: .

Пример 2

Рассмотрим теперь один из частных случаев с обыкновенными дробями.

Пример 3

Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.

Рассмотрим умножение и деление алгебраических дробей.

Пример 4

Пример 5

Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.

Пример 6

Пример 7

Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.

Пример 8

Пример 9

Пример 10

Пример 11

Пример 12

Пример 13

До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.

Пример 14

Пример 15

Пример 16

Пример 17

Пример 18

На данном уроке мы рассмотрели правила умножения и деления алгебраических дробей, а также применение этих правил для конкретных примеров.

 

Список литературы

1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал для всей семьи (Источник).

2. Фестиваль педагогических идей «Открытый урок» (Источник).

3. Вся элементарная математика (Источник).

 

Домашнее задание

1. №№73-77, 80. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Выполнить умножение: а), б)

3. Выполнить деление: а) , б)

4. Упростить выражение:

interneturok.ru

Умножение и деление рациональных дробей — 8 класс

16 сентября 2015

Прежде всего, чтобы научиться работать с рациональными дробями без ошибок, необходимо выучить формулы сокращённого умножения. И не просто выучить — их необходимо распознавать даже тогда, когда в роли слагаемых выступают синусы, логарифмы и корни.

Однако основным инструментом остаётся разложение числителя и знаменателя рациональной дроби на множители. Этого можно добиться тремя различными способами:

1. Собственно, по формула сокращённого умножения: они позволяют свернуть многочлен в один или несколько множителей;
2. С помощью разложения квадратного трёхчлена на множители через дискриминант. Этот же способ позволяет убедиться, что какой-либо трёхчлен на множители вообще не раскладывается;
3. Метод группировки — самый сложный инструмент, но это единственный способ, который работает, если не сработали два предыдущих.

Как вы уже, наверное, догадались из названия этого видео, мы вновь поговорим о рациональных дробях. Буквально несколько минут назад у меня закончилось занятие с одним десятиклассником, и там мы разбирали именно эти выражения. Поэтому данный урок будет предназначен именно для старшеклассников.

Наверняка у многих сейчас возникнет вопрос: «Зачем ученикам 10-11 классов изучать такие простые вещи как рациональные дроби, ведь это проходится в 8 классе?». Но в том то и беда, что большинство людей эту тему именно «проходят». Они в 10-11 классе уже не помнят, как делается умножение, деление, вычитание и сложение рациональных дробей из 8-го класса, а ведь именно на этих простых знаниях строятся дальнейшие, более сложные конструкции, как решение логарифмических, тригонометрических уравнений и многих других сложных выражений, поэтому без рациональных дробей делать в старших классах практически нечего.

Формулы для решения задач

Давайте перейдем к делу. Прежде всего, нам потребуется два факта — два комплекта формул. Прежде всего, необходимо знать формулы сокращенного умножения:

• ${{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$ — разность квадратов;
• ${{a}^{2}}\pm 2ab+{{b}^{2}}={{\left( a\pm b \right)}^{2}}$ — квадрат суммы или разности;
• ${{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)$ — сумма кубов;
• ${{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)$ — разность кубов.

В чистом виде они ни в каких примерах и в реальных серьезных выражениях не встречаются. Поэтому наша задача состоит в том, чтобы научиться видеть под буквами $a$ и $b$ гораздо более сложные конструкции, например, логарифмы, корни, синусы и т.д. Научиться видеть это можно лишь при помощи постоянной практики. Именно поэтому решать рациональные дроби совершенно необходимо.

Вторая, совершенно очевидная формула — это разложение квадратного трехчлена на множители:

\[a{{x}^{2}}+bx+c=0\to a\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)=0\]

${{x}_{1}}$; ${{x}_{2}}$ — корни.

С теоретической частью мы разобрались. Но как решать реальные рациональные дроби, которые рассматриваются в 8 классе? Сейчас мы и потренируемся.

Задача № 1

\[\frac{27{{a}^{3}}-64{{b}^{3}}}{{{b}^{3}}-4}:\frac{9{{a}^{2}}+12ab+16{{b}^{2}}}{{{b}^{2}}+4b+4}\]

Давайте попробуем применить вышеописанные формулы к решению рациональных дробей. Прежде всего, хочу объяснить, зачем вообще нужно разложение на множители. Дело в том, что при первом взгляде на первую часть задания хочется сократить куб с квадратом, но делать этого категорически нельзя, потому что они являются слагаемыми в числителе и в знаменателе, но ни в коем случае не множителями.

Вообще, что такое сокращение? Сокращение — это использование основного правила работы с такими выражениями. Основное свойство дроби заключается в том, что мы можем числитель и знаменатель можем умножить на одно и то же число, отличное от «нуля». В данном случае, когда мы сокращаем, то, наоборот, делим на одно и то же число, отличное от «нуля». Однако мы должны все слагаемые, стоящие в знаменателе, разделить на одно и то же число. Делать так нельзя. И сокращать числитель со знаменателем мы вправе лишь тогда, когда оба они разложены на множители. Давайте это и сделаем.

Теперь необходимо посмотреть, сколько слагаемых находится в том или ином элементе, в соответствии с этим узнать, какую формулу необходимо использовать.

Преобразуем каждое выражение в точный куб:

\[27{{a}^{3}}={{3}^{3}}\cdot {{a}^{3}}={{\left( 3a \right)}^{3}}\]

\[64{{b}^{3}}={{4}^{3}}\cdot {{b}^{3}}={{\left( 4b \right)}^{3}}\]

Перепишем числитель:

\[{{\left( 3a \right)}^{3}}-{{\left( 4b \right)}^{3}}=\left( 3a-4b \right)\left( {{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}} \right)\]

Давайте посмотрим на знаменатель. Разложим его по формуле разности квадратов:

\[{{b}^{2}}-4={{b}^{2}}-{{2}^{2}}=\left( b-2 \right)\left( b+2 \right)\]

Теперь посмотрим на вторую часть выражения:

Числитель:

\[9{{a}^{2}}+12ab+16{{b}^{2}}={{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}}\]

Осталось разобраться со знаменателем:

\[{{b}^{2}}+2\cdot 2b+{{2}^{2}}={{\left( b+2 \right)}^{2}}\]

Давайте перепишем всю конструкцию с учетом вышеперечисленных фактов:

\[\frac{\left( 3a-4b \right)\left( {{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}} \right)}{\left( b-2 \right)\left( b+2 \right)}\cdot \frac{{{\left( b+2 \right)}^{2}}}{{{\left( 3a \right)}^{2}}+3a\cdot 4b+{{\left( 4b \right)}^{2}}}=\]

\[=\frac{\left( 3a-4b \right)\left( b+2 \right)}{\left( b-2 \right)}\]

Нюансы умножения рациональных дробей

Ключевой вывод из этих построений следующий:

• Далеко не каждый многочлен раскладывается на множители.
• Даже если он и раскладывается, необходимо внимательно смотреть, по какой именно формуле сокращенного умножения.

Для этого, во-первых, нужно оценить, сколько всего слагаемых (если их два, то все, что мы можем сделать, то это разложить их либо по сумме разности квадратов, либо по сумме или разности кубов; а если их три, то это, однозначно, либо квадрат суммы, либо квадрат разности). Очень часто бывает так, что или числитель, или знаменатель вообще не требует разложения на множители, он может быть линейным, либо дискриминант его будет отрицательным.

Задача № 2

\[\frac{3-6x}{2{{x}^{2}}+4x+8}\cdot \frac{2x+1}{{{x}^{2}}+4-4x}\cdot \frac{8-{{x}^{3}}}{4{{x}^{2}}-1}\]

В целом, схема решения этой задачи ничем не отличается от предыдущей — просто действий будет больше, и они станут разнообразнее.

Начнем с первой дроби: посмотрим на ее числитель и сделаем возможные преобразования:

\[3-6x=3\left( 1-2x \right)\]

Теперь посмотрим на знаменатель:

\[2{{x}^{2}}+4x+8=2\left( {{x}^{2}}+2x+4 \right)\]

Со второй дробью: в числителе вообще ничего нельзя сделать, потому что это линейное выражение, и вынести из него какой-либо множитель нельзя. Посмотрим на знаменатель:

\[{{x}^{2}}-4x+4={{x}^{2}}-2\cdot 2x+{{2}^{2}}={{\left( x-2 \right)}^{2}}\]

Идем к третьей дроби. Числитель:

\[8-{{x}^{3}}={{2}^{3}}-{{x}^{3}}=\left( 2-x \right)\left( {{2}^{2}}+2\cdot x+{{x}^{2}} \right)\]

Разберемся со знаменателем последней дроби:

\[4{{x}^{2}}-1={{\left( 2x \right)}^{2}}-{{1}^{2}}=\left( 2x-1 \right)\left( 2x+1 \right)\]

Перепишем выражение с учетом вышеописанных фактов:

\[\frac{3\left( 1-2x \right)}{2\left( {{x}^{2}}+2x+4 \right)}\cdot \frac{2x+1}{{{\left( x-2 \right)}^{2}}}\cdot \frac{\left( 2-x \right)\left( {{2}^{2}}+2x+{{x}^{2}} \right)}{\left( 2x-1 \right)\left( 2x+1 \right)}=\]

\[=\frac{-3}{2\left( 2-x \right)}=-\frac{3}{2\left( 2-x \right)}=\frac{3}{2\left( x-2 \right)}\]

Нюансы решения

Как видите, далеко не все и не всегда упирается в формулы сокращенного умножения — иногда просто достаточно вынести за скобки константу или переменную. Однако бывает и обратная ситуация, когда слагаемых настолько много или они так построены, что формулы сокращенного умножения к ним вообще невозможно. В этом случае к нам на помощь приходит универсальный инструмент, а именно, метод группировки. Именно это мы сейчас и применим в следующей задаче.

Задача № 3

\[\frac{{{a}^{2}}+ab}{5a-{{a}^{2}}+{{b}^{2}}-5b}\cdot \frac{{{a}^{2}}-{{b}^{2}}+25-10a}{{{a}^{2}}-{{b}^{2}}}\]

Разберем первую часть:

\[{{a}^{2}}+ab=a\left( a+b \right)\]

\[5a-{{a}^{2}}+{{b}^{2}}-5b=5\left( a-b \right)-\left( {{a}^{2}}-{{b}^{2}} \right)=\]

\[=5\left( a-b \right)-\left( a-b \right)\left( a+b \right)=\left( a-b \right)\left( 5-1\left( a+b \right) \right)=\]

\[=\left( a-b \right)\left( 5-a-b \right)\]

Давайте перепишем исходное выражение:

\[\frac{a\left( a+b \right)}{\left( a-b \right)\left( 5-a-b \right)}\cdot \frac{{{a}^{2}}-{{b}^{2}}+25-10a}{{{a}^{2}}-{{b}^{2}}}\]

Теперь разберемся со второй скобкой:

\[{{a}^{2}}-{{b}^{2}}+25-10a={{a}^{2}}-10a+25-{{b}^{2}}=\left( {{a}^{2}}-2\cdot 5a+{{5}^{2}} \right)-{{b}^{2}}=\]

\[={{\left( a-5 \right)}^{2}}-{{b}^{2}}=\left( a-5-b \right)\left( a-5+b \right)\]

Так как два элемента не получилось сгруппировать, то мы сгруппировали три. Осталось разобраться лишь со знаменателем последней дроби:

\[{{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)\]

Теперь перепишем всю нашу конструкцию:

\[\frac{a\left( a+b \right)}{\left( a-b \right)\left( 5-a-b \right)}\cdot \frac{\left( a-5-b \right)\left( a-5+b \right)}{\left( a-b \right)\left( a+b \right)}=\frac{a\left( b-a+5 \right)}{{{\left( a-b \right)}^{2}}}\]

Задача решена, и больше ничего упростить здесь нельзя.

Нюансы решения

С группировкой мы разобрались и получили еще один очень мощный инструмент, который расширяет возможности по разложению на множители. Но проблема в том, что в реальной жизни нам никто не будет давать вот такие рафинированные примеры, где есть несколько дробей, у которых нужно лишь разложить на множитель числитель и знаменатель, а потом по возможности их сократить. Реальные выражения будут гораздо сложнее.

Скорее всего, помимо умножения и деления там будут присутствовать вычитания и сложения, всевозможные скобки — вообщем, придется учитывать порядок действий. Но самое страшное, что при вычитании и сложении дробей с разными знаменателями их придется приводить к одному общему. Для этого каждый из них нужно будет раскладывать на множители, а потом преобразовывать эти дроби: приводить подобные и многое другое. Как это сделать правильно, быстро, и при этом получить однозначно правильный ответ? Именно об этом мы и поговорим сейчас на примере следующей конструкции.

Задача № 4

\[\left( {{x}^{2}}+\frac{27}{x} \right)\cdot \left( \frac{1}{x+3}+\frac{1}{{{x}^{2}}-3x+9} \right)\]

Давайте выпишем первую дробь и попытаемся разобраться с ней отдельно:

\[{{x}^{2}}+\frac{27}{x}=\frac{{{x}^{2}}}{1}+\frac{27}{x}=\frac{{{x}^{3}}}{x}+\frac{27}{x}=\frac{{{x}^{3}}+27}{x}=\frac{{{x}^{3}}+{{3}^{3}}}{x}=\]

\[=\frac{\left( x+3 \right)\left( {{x}^{2}}-3x+9 \right)}{x}\]

Переходим ко второй. Сразу посчитаем дискриминант знаменателя:

\[D=9-4\cdot 9<0\]

Он на множители не раскладывается, поэтому запишем следующее:

\[\frac{1}{x+3}+\frac{1}{{{x}^{2}}-3x+9}=\frac{{{x}^{2}}-3x+9+x+3}{\left( x+3 \right)\left( {{x}^{2}}-3x+9 \right)}=\]

\[=\frac{{{x}^{2}}-2x+12}{\left( x+3 \right)\left( {{x}^{2}}-3x+9 \right)}\]

Числитель выпишем отдельно:

\[{{x}^{2}}-2x+12=0\]

\[D=4-4\cdot 12<0\]

Следовательно, этот многочлен на множители не раскладывается.

Максимум, что мы могли сделать и разложить, мы уже сделали.

Итого переписываем нашу исходную конструкцию и получаем:

\[\frac{\left( x+3 \right)\left( {{x}^{2}}-3x+9 \right)}{x}\cdot \frac{{{x}^{2}}-2x+12}{\left( x+3 \right)\left( {{x}^{2}}-3x+9 \right)}=\frac{{{x}^{2}}-2x+12}{x}\]

Все, задача решена.

Если честно, это была не такая уж и сложная задача: там все легко раскладывалось на множители, быстро приводились подобные слагаемые, и все красиво сокращалось. Поэтому сейчас давайте попробуем решить задачку посерьезней.

Задача № 5

\[\left( \frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{{{x}^{3}}-8}-\frac{1}{x-2} \right)\cdot \left( \frac{{{x}^{2}}}{{{x}^{2}}-4}-\frac{2}{2-x} \right)\]

Сначала давайте разберемся с первой скобкой. С самого начала разложим на множители знаменатель второй дроби отдельно:

\[{{x}^{3}}-8={{x}^{3}}-{{2}^{3}}=\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)\]

\[\frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{{{x}^{3}}-8}-\frac{1}{{{x}^{2}}}=\]

\[=\frac{x}{{{x}^{2}}+2x+4}+\frac{{{x}^{2}}+8}{\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)}-\frac{1}{x-2}=\]

\[=\frac{x\left( x-2 \right)+{{x}^{2}}+8-\left( {{x}^{2}}+2x+4 \right)}{\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)}=\]

\[=\frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)}=\]

\[=\frac{{{x}^{2}}-4x+4}{\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)}=\frac{{{\left( x-2 \right)}^{2}}}{\left( x-2 \right)\left( {{x}^{2}}+2x+4 \right)}=\frac{x-2}{{{x}^{2}}+2x+4}\]

Теперь поработаем со второй дробью:

\[\frac{{{x}^{2}}}{{{x}^{2}}-4}-\frac{2}{2-x}=\frac{{{x}^{2}}}{\left( x-2 \right)\left( x+2 \right)}-\frac{2}{2-x}=\frac{{{x}^{2}}+2\left( x-2 \right)}{\left( x-2 \right)\left( x+2 \right)}=\]

\[=\frac{{{x}^{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}\]

Возвращаемся к нашей исходной конструкции и записываем:

\[\frac{x-2}{{{x}^{2}}+2x+4}\cdot \frac{{{x}^{2}}+2x+4}{\left( x-2 \right)\left( x+2 \right)}=\frac{1}{x+2}\]

Ключевые моменты

Еще раз ключевые факты сегодняшнего видеоурока:

1. Необходимо знать «назубок» формулы сокращенного умножения — и не просто знать, а уметь видеть в тех выражениях, которые будут вам встречаться в реальных задачах. Помочь нам в этом может замечательное правило: если слагаемых два, то это либо разность квадратов, либо разность или сумма кубов; если три — это может быть только квадрат суммы или разности.
2. Если какая-либо конструкция не раскладывается при помощи формул сокращенного умножения, то нам на помощь приходит либо стандартная формула разложения трехчленов на множители, либо метод группировки.
3. Если что-то не получается, внимательно посмотрите на исходное выражение — а требуются ли вообще какие-то преобразования с ним. Возможно, достаточно будет просто вынести множитель за скобку, а это очень часто бывает просто константа.
4. В сложных выражениях, где требуется выполнить несколько действий подряд, не забывайте приводить к общему знаменателю, и лишь после этого, когда все дроби приведены к нему, обязательно приведите подобное в новом числителе, а потом новый числитель еще раз разложите на множители — возможно, что-то сократится.

Вот и все, что я хотел вам рассказать сегодня о рациональных дробях. Если что-то непонятно — на сайте еще куча видеоуроков, а также куча задач для самостоятельного решения. Поэтому оставайтесь с нами! 

Смотрите также:

1. Учимся упрощать рациональные выражения и дроби с помощью формул сокращённого умножения.
2. Дробно-рациональные выражения
3. Умножение и деление дробей
4. Пробный ЕГЭ 2012 от 7 декабря. Вариант 1 (без логарифмов)
5. Как быстро извлекать квадратные корни
6. Задача B2: Сложный процент и метод коэффициентов

www.berdov.com

Урок «Умножение дробей» 8 класс

Тема урока: «Умножение алгебраических дробей» 8 класс

Цель урока: научиться умножать дроби.

Задачи урока:

• Обучающая: Формирование знаний и умений правил умножения дробей. Умение выполнять указанные действия. Повторить и обобщить полученные знания об обыкновенных дробях.

• Развивающая: Развитие кругозора, мышления, любознательности, внимания, культуры математической речи, привитие интереса к изучению математики.

• Воспитывающая: Воспитание аккуратности, чувство коллективизма, самоконтроля.

Ход урока

1. Организационный момент

2. Мотивация урока.

Эпиграф нашего урока “О, сколько нам открытий чудных готовит просвещенья дух…”. А были ли открытия в вашей жизни? Что значат слова “Я сделал открытие”? Если человек своим трудолюбием, упорством достигает истины в чем-либо, то это и есть его открытие. По этому поводу Борис Пастернак сказал:

Во всем мне хочется дойти

До самой сути.

В работе, в поисках пути,

В сердечной смуте.

До сущности истекших дней

До их причины,

До оснований, до корней,

До сердцевины

Всё время схватывая нить

Судеб, событий,

Жить, думать, чувствовать, любить

Свершать открытья.

На сегодняшнем уроке мы тоже попытаемся совершить маленькое, но самостоятельное открытие. Для этого надо быть настойчивым и внимательным.

3. Считай скорей:

а) Сократить дроби:

Каким правилом пользовались? (Основное свойство дроби)

б) Разложить на множители многочлен:

=

=

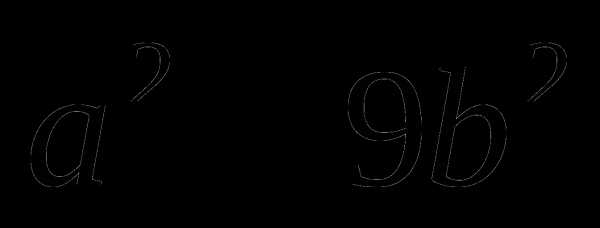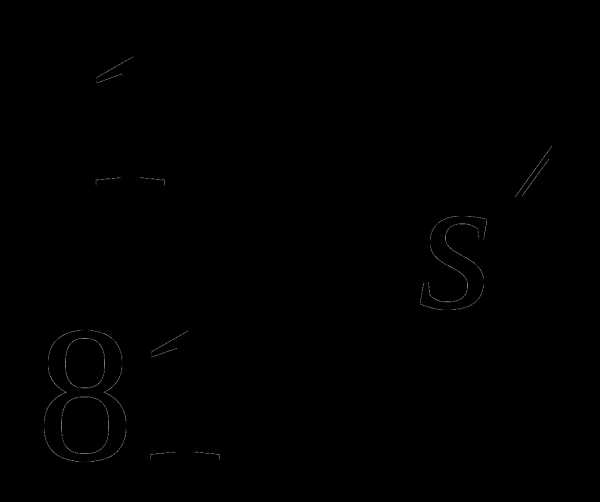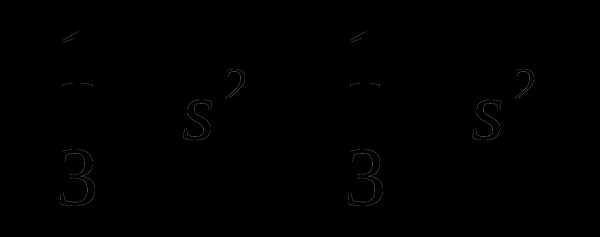
Как называются формулы, которые мы здесь применили? (Формулы сокращенного умножения).

в) Умножить дроби:

1.

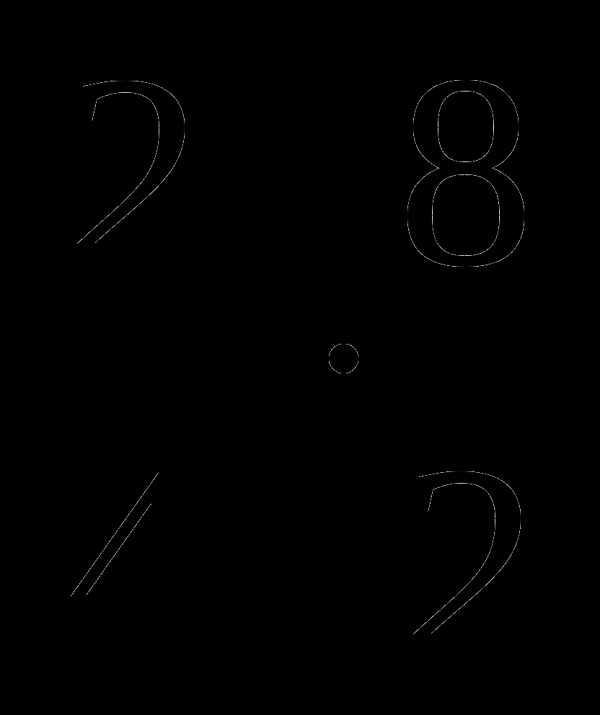
2.

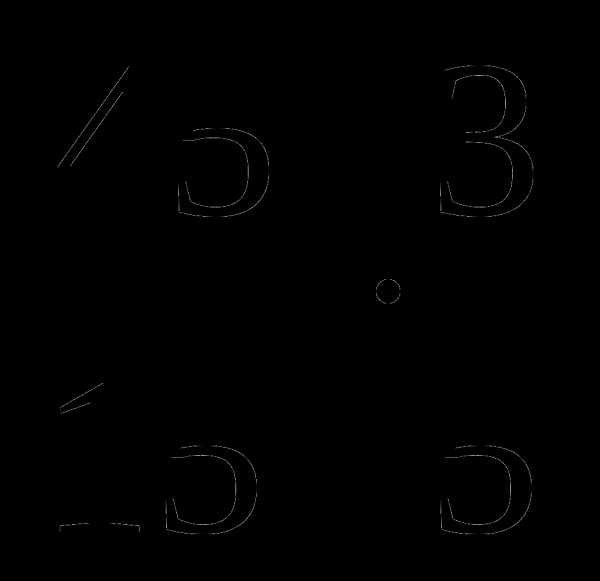
3.

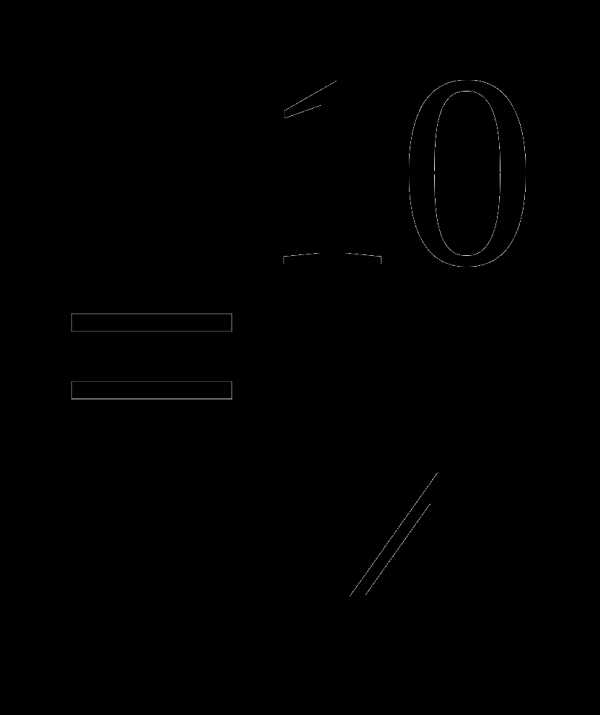
Как вы нашли произведение данных дробей? (дети высказывают свои предложения).

Давайте сформулируем правило умножения дробей:

Чтобы умножить дробь на дробь, надо:

1) найти произведение числителей и произведение знаменателей этих дробей;

2) первое произведение записать числителем, а второе – знаменателем.

При умножении и трёх и более дробей:

Удобнее сначала в числителе записать произведение всех числителей, в знаменателе – произведение всех знаменателей.

Сократить получившуюся дробь. Что значит сократить дробь? (Деление числителя и знаменателя дроби на одно и то же число)

Выполнить умножение оставшихся множителей.

Если надо, выделить целую часть.

Теперь мы соберем в корзину, все то, что мы знаем о дроби:

А как вы думаете, что сегодня на уроке мы будем изучать? И какова тема нашего урока?

Выслушать мнения детей.

4. На доске записывается тема урока. «Умножение алгебраических дробей». А цель нашего урока? Как вы считаете? (Научиться находить произведение дробей).

Эти же правила выполняются и при умножении алгебраических дробей.

Привожу пример произведения дробей:

1.

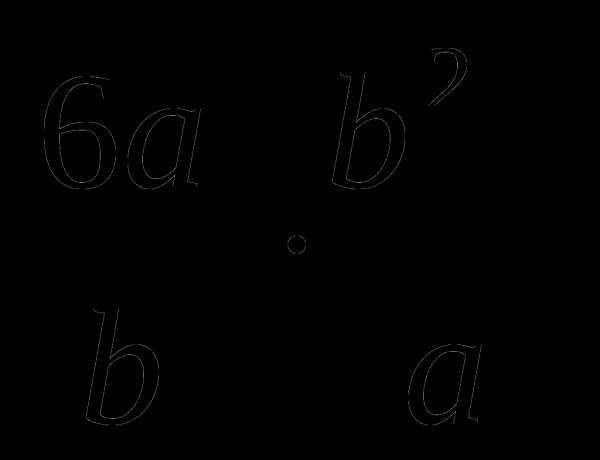
2.

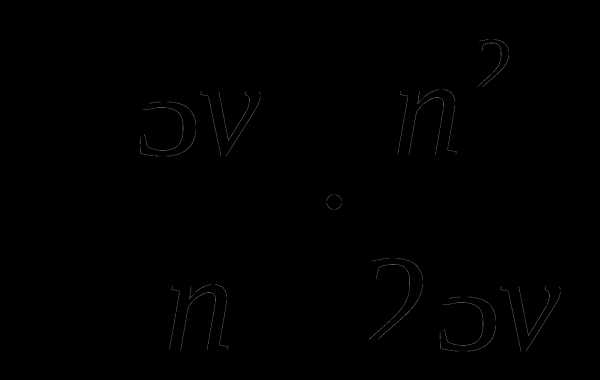
3.

4. Физкультминутка.

Дополнительно возле доски по одному

1.

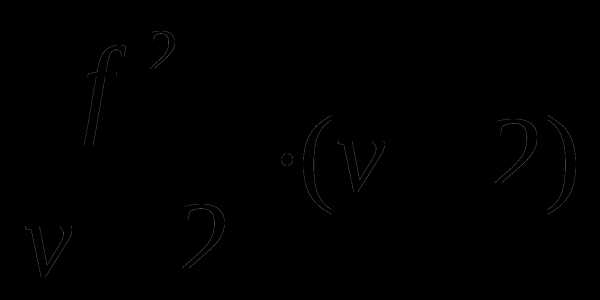
2.

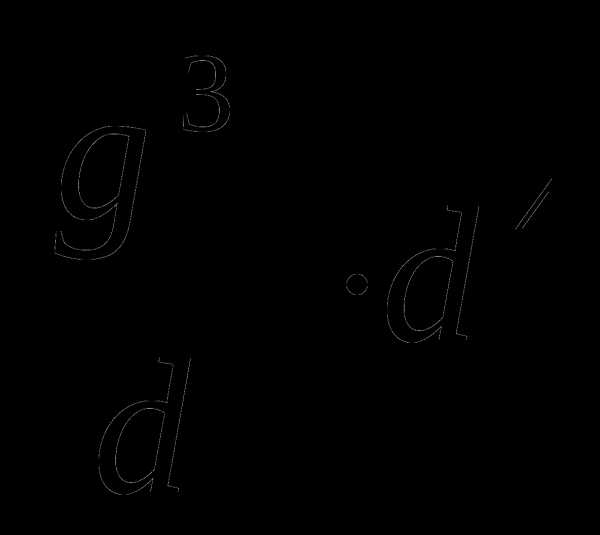
3.

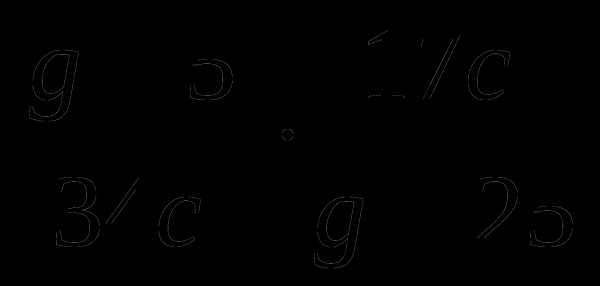
4.

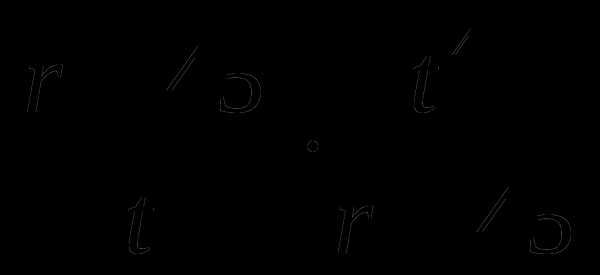
5.

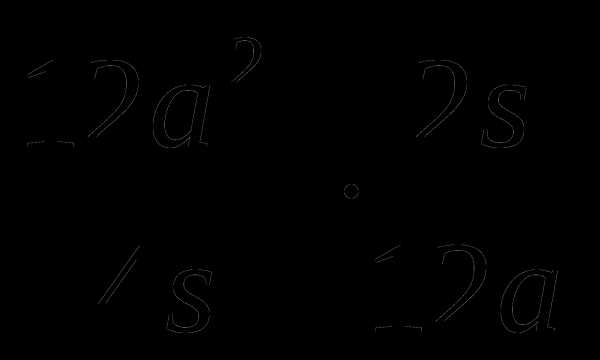
6.

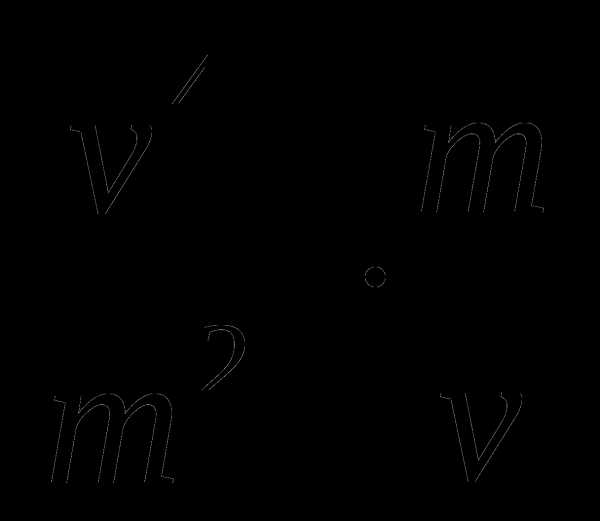
7.

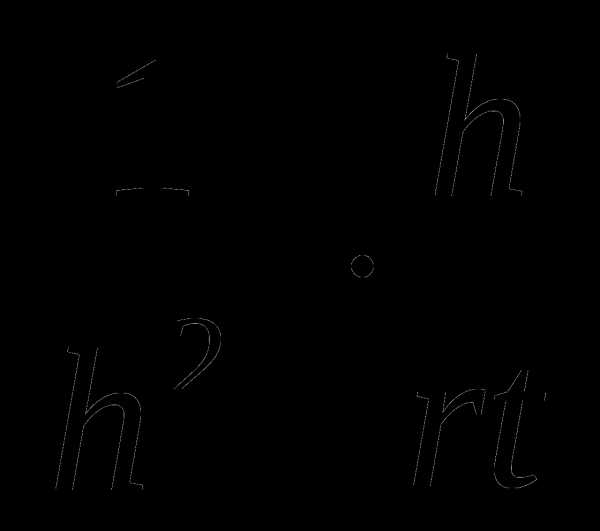
8.

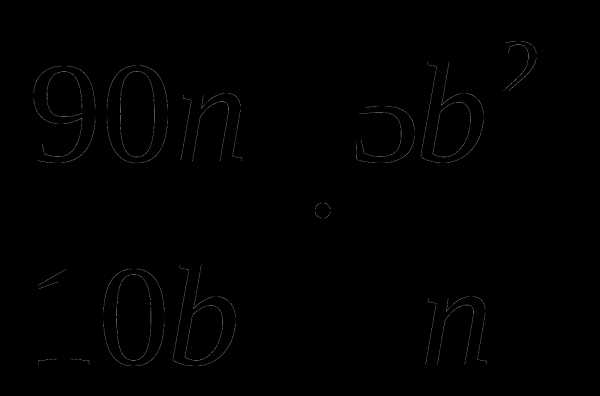
5. Самостоятельная работа

Проведем небольшое исследование. Мы сейчас будем работать группами, т е по 3 человека. Выполним задание № 108, 110 на стр. 27-28 учебника.

6. Закрепление нового материала.

Решить с комментированием на месте №112, 115

Д\З № 109, 114, 116

7. Рефрексия. Итог урока. Оценки за урок

infourok.ru

Урок математики для 8 класса школы VIII вида «Решение задач на умножение и деление обыкновенных дробей. Работа с калькулятором»

Урок математики в школе VIII вида

Класс: 8

Тема: Решение задач на умножение и деление обыкновенных дробей. Работа с калькулятором.

Цель:Выработка умений решения задач на умножение и деление обыкновенных дробей.

Задачи:

Образовательные:

Отрабатывать приемы вычислений с обыкновенными дробями, учить решать задачи.

Коррекционно- развивающие:

Развивать внимание, память, речь, логическое мышление, умение анализировать, делать выводы.

Воспитывающие:

Воспитание мотивации к учению.

План.

1.Оргмомент.

Сегодня на уроке мы повторим действия с дробями (умножение и деление) через решение примеров и задач. На уроке вам предстоит хорошо потрудиться, быть внимательными, активными и усердными.

1) Упражнение на развитие внимания и памяти.

13542

689107

21495

31154

791088

36101

23548

106978

82594

1 табличка

— сколько

троек

(3)

2 табличка

— сколько восьмерок

(4)

3 табличка

— сколько

единиц

(3)

2) Упражнение на классификацию целых чисел и дробей.
Расставить числа в два столбика и объяснить.

(3; 1/8; 3/4; 8; 1; 5/12; 6/6; 5; 2/7)

3) Упражнение на внимание.
Найдите, где допущена ошибка.

2. Проверка домашнего задания.

3. Устный счёт.

50, 100, 150, …20, 40, 60, …1/2,1/4,1/6,1/8, …., …, … Назови самую большую дробь(1/2), самую маленькую (1/8).

На доске записаны дроби: 5/3 , 1/4 , 8/8 , 3/12 , 7/12.

—         Назовите правильные дроби.

—         Назовите неправильные дроби.

—         Выделите целую часть неправильной дроби.

—         Назовите равные дроби.

Вспомним правило умножения и деления дроби на число.

4. Работа по теме урока.

А) Работа в тетрадях.

Используя правила умножения дроби на число, выполните действие:

5/6*8;

8/9:4;

23/20*10;

3/4:6;

Б) Работа по учебнику.

Открываем учебники на стр. 111, найдите №310.Решаем задачу под номером 1 (Резерв 3,4).

1. Чтение задачи.

2. Разбор задачи.

3. Запись схемы краткой записи.

4. Определение количества действий.

5. Составление вопросов и решение задачи по действиям.

1)Условие задачи:

3п.- 3/5кг

10п.-?

Решение:

1) 3/5: 3=3/15=1/5

2) 10*1/5=10/5=2

Ответ: 2 кг.

3) 2/5*10=4

4) 24/25:40=24/1000 (работа с калькулятором)

Физминутка (для глаз)

Работа с калькулятором: стр. 112 №313 (3)

Задание на смекалку.

Расшифруйте слово, решив примеры и используя ключ к разгадке.

5х5

54: 9

7 х 8

42 : 7

2+3: 3

45 — 16

91-27

Ключ к разгадке:

3

6

25

29

56

64

д

о

м

е

л

ц

Ответ: Молодец.

5. Домашнее задание.

Решить задачу из №312 (1) на стр.111, подобная задача.

6. Итог урока.

Выставление оценок.

Какое задание было самым трудным? Какое самым легким? Все ли вам на уроке было понятно? Какие встретились трудности?

Спасибо за работу на уроке!!!

  

infourok.ru

Умножение, деление и возведение в степень алгебраических дробей. Алгебра, 8 класс: уроки, тесты, задания.

1.	Произведение алгебраических дробей Сложность: лёгкое
2.	Частное алгебраической дроби и переменной Сложность: лёгкое
3.	Частное алгебраических дробей (одночлены) Сложность: лёгкое
4.	Произведение алгебраических дробей (одночлены, знаки) Сложность: лёгкое
5.	Частное алгебраических дробей (одночлены, знаки) Сложность: лёгкое
6.	Произведение алгебраических дробей (степени, числа) Сложность: лёгкое
7.	Возведение в степень алгебраической дроби (одночлены, числа) Сложность: лёгкое
8.	Частное алгебраических дробей (степени, буквы) Сложность: лёгкое
9.	Произведение одночлена и алгебраической дроби Сложность: лёгкое
10.	Произведение алгебраических дробей (биномы и одночлены) Сложность: лёгкое
11.	Частное алгебраических дробей (общий множитель) Сложность: среднее
12.	Возведение в степень отрицательной алгебраической дроби Сложность: среднее
13.	Произведение степеней алгебраических дробей (буквы) Сложность: среднее
14.	Произведение алгебраических дробей, разложение на множители Сложность: среднее
15.	Частное алгебраических дробей Сложность: среднее
16.	Произведение алгебраических дробей со степенями, возведение дроби в степень Сложность: среднее
17.	Произведение алгебраических дробей (общий множитель, противоположные биномы) Сложность: среднее
18.	Частное алгебраических дробей (разность квадратов) Сложность: среднее
19.	Произведение алгебраических дробей (сумма или разность кубов) Сложность: среднее
20.	Частное алгебраических дробей (формулы сокращённого умножения, общий множитель) Сложность: среднее
21.	Значение выражения Сложность: среднее
22.	Частное алгебраических дробей (сумма или разность кубов, разность квадратов) Сложность: сложное
23.	Частное степеней алгебраических дробей Сложность: сложное

www.yaklass.ru

«Умножение и деление алгебраических дробей» (8 класс)

И г р а «Дешифровщик».

Когда астрономы начали исследование Вселенной с помощью радиотелескопов, они обнаружили, что многие звёзды меняют интенсивность и частоту излучаемых ими волн.

Однако некоторые из звёзд испускают постоянный поток волн, который меняется только в зависимости от времени. Долгое время ученые не могли объяснить природу этого явления.

Говорили, например, что это – радиостанции, с помощью которых неизвестные нам разумные существа ищут во Вселенной собратьев по разуму.

Но исследования, проведенные с помощью искусственных спутников Земли, показали, что эти звёзды являются просто звёздами огромной величины и состоят из раскаленной материи.

Вы узнаете, как называются эти необычные звёзды, если правильно выполните все задания и составите слово из полученных букв.

Учащиеся выполняют задания по вариантам: первый вариант получает первую, третью, пятую и седьмую буквы данного слова, а второй – вторую, четвёртую, шестую и восьмую.

З а д а н и е: выполните действия.

В а р и а н т 1

1) .

Д. ; Н. ;

К. ; П. .

2) .

З. ; М. ;

Л. ; Р. .

3) .

К. ; С. ;

М. ; Т. .

4) .

Н. ; Т. ;

Р. ; Х. .

В а р и а н т 2

1) .

А. ; О. ;

Е. ; У. .

2) .

И. ; Ь. ;

У. ; Ю. .

3) .

А. ; О. ;

И. ; У. .

4) .

И. ; С. ;

Т. ; Ы. .

О т в е т: ПУЛЬСАРЫ.

infourok.ru

Конспект урока по алгебре «Умножение и деление алгебраических дробей» 8 класс

Тема: « Умножение и деление алгебраических дробей»

Цель урока: сформировать комплекс ЗУН по теме «Умножение и деление алгебраических дробей»

Задачи:

Образовательные:

1. Познакомить учащихся с правилами умножения и деления алгебраических дробей

2. Научить решать задачи обязательного уровня

3. Повторить формулы сокращённого умножения. правило вынесения общего множителя

4. Совершенствовать общеучебные У и Н учащихся: извлекать информацию при слушании, работать в быстром темпе, компактно и логически последовательно излагать мысли.

5. Совершенствовать предметные У и Н учащихся: задавать вопросы по условию задания, Н использования математических терминов.

Развивающие:

1. Совершенствовать аналитические способности учащихся: У анализировать, сравнивать, делать выводы.

2. Используя различные формы работы, развивать познавательную активность учащихся и интерес к предмету.

Воспитательные:

1. Формирование ценностного отношения ко времени.

2. Воспитывать аккуратность при записи деления и умножения дробей.

Тип урока (по Поташнику): изучение нового материала.

Структура урока:

1. Орг. момент – 1 мин.

2. Проверка д/з – 3 мин.

3. Актуализация опорных знаний –4.

4. Изучение нового материала, включая сообщения учащихся по теме урока –6 мин.

5. Закрепление (решение примеров, написанных на доске ) – 15 мин.

6. Физ. минутка (гимнастика для глазных и шейных мышц) – 2 мин.

7. Первичный контроль уровня усвоения материала с последующей взаимопроверкой – 6 мин.

8. Подведение итогов, рефлексия, д\з – 3 мин.

Ход урока:

1. Орг. момент

2. Проверка д/з: на доске учащимися написаны решения заданий д/р, ученики сравнивают свое решение с написанным на доске, учитель обращает внимание на наиболее трудные моменты.

3. Актуализация опорных знаний

Фронтальная устная работа

1) Разложить на множители

5х-15 на отдельном листе: 5х-15=5( )

7а-21 7а-21=7( )

6в-12 6в-12=6( )

2) Сократить дробь

(3х-9)÷(х-3) (3х-9)÷(х-3)=3(

(6х-3)÷(2х-1) (6х-3)÷(2х-1) =3(

(5х-25)÷(х-5) (5х-25)÷(х-5)=5(

3) Как называются дроби:

2\3 и 3\2, 4\7 и 7\4

Проговариваем правила умножения и деления обыкновенных дробей. Формулы записываем на доске и в рабочих тетрадях.

4. Изучение нового материала, включая сообщения учащихся по теме урока –6мин.

Первый и второй пример самостоятельно, с последующей записью решения учащимися на доске. Решение третьего примера учитель показывает на доске.

5. Закрепление (15 мин.)

1)Работа по задачнику: № 5.2 (а,б), №5.8-№ 5.11 (а, б). Стр.32

6. Физ. минутка (гимнастика для глазных и шейных мышц) – 2 мин.

5. Закрепление

2) Работа в парах

У слабоуспевающих учащихся смотрю в это время классную работу, вношу коррективы в его записи.

7. Первичный контроль уровня усвоения материала с последующей взаимопроверкой – 6 мин.

Ι Вариант

 

ΙΙ Вариант

 

8. Подведение итогов, рефлексия, д\з – 3 мин.

9 Домашняя работа: № 5.8; № 5.10; № 5.13(а, б)

infourok.ru