Основные формулы по геометрии и их свойства.
Основные формулы по геометрии и свойства
Радиус описанной окружности трапеции по сторонам и диагонали
a — боковые стороны трапеции
c — нижнее основание
b — верхнее основание d — диагональ
h – высота p = (a+d+c)/2
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Найти радиус описанной окружности треугольника, формула
a, b, c — стороны треугольника
p — полупериметр, p= (a+b+c)/2
Найти радиус описанной окружности равностороннего треугольника по стороне
a — сторона треугольника
Формулы вычисления площади треугольника (если даны все стороны треугольника):
I формула Герона
p — полупериметр p=(a+b+c)|2
II формула Герона.
Формула расчета площади треугольника
h — высота треугольника
a — основание
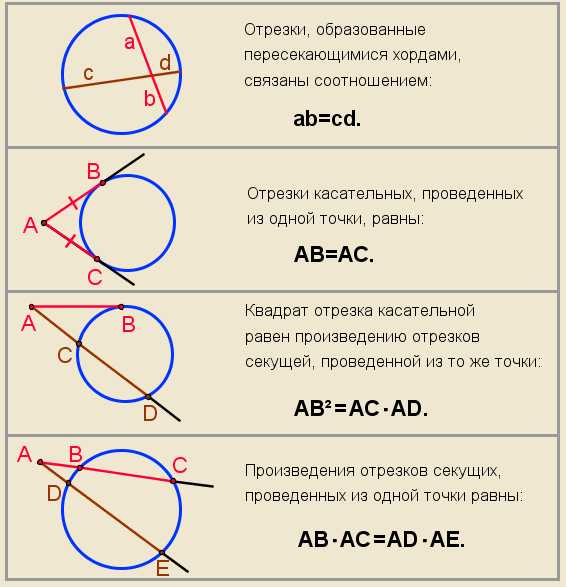
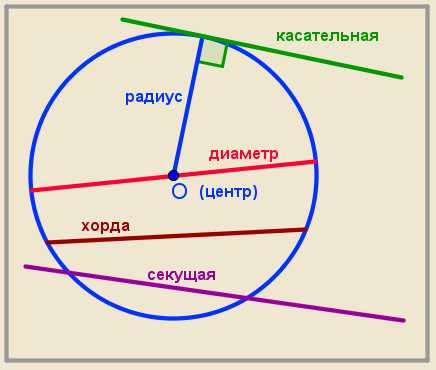
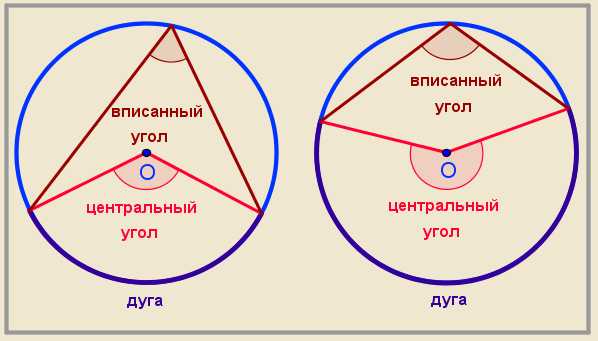
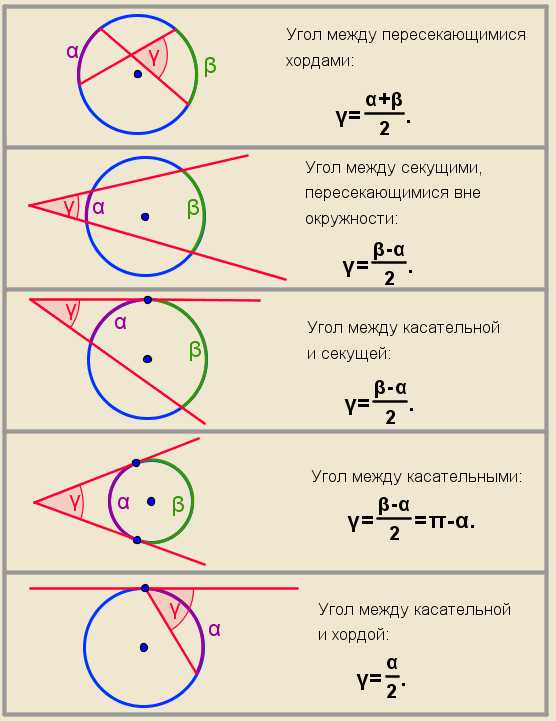
Центральным называется угол с вершиной в центре окружности.
Центральный угол равен градусной мере дуги, на которую опирается. Поэтому углом в один радиан называется центральный угол, который опирается на дугу в один радиан.
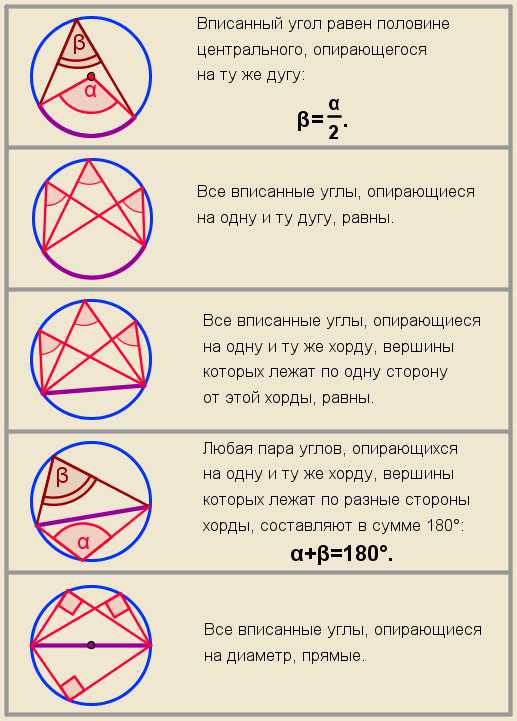
Вписанным называется угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.
Вписанный угол равен половине градусной меры дуги, на которую опирается.
Две различные точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности.
Дугою в один градус называется дуга окружности, длина которой равняется части его длины. Дугою в один радиан (1 рад) называется дуга окружности, длина которой равняется радиусу этой окружности.
Переход от градусной меры углов и дуг к радианной, и наоборот, осуществляется по формулам:
рад.
В частности:
рад.
рад.
Формула площади параллелограмма через сторону и высоту
a, b — стороны параллелограмма
Hb — высота на сторону b
Ha — высота на сторону a
Формула площади трапеции через основания и высоту
a — нижнее основание
b — верхнее основание
m — средняя линия
h — высота трапеции
2. Формула площади трапеции через четыре стороны
a — нижнее основание
b — верхнее основание
c , d — боковые стороны
Формула площади трапеции, (S ):
Вычислить площадь ромба
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
Формулы площади ромба через диагонали и углы между сторонами ( S ):
a — сторона ромба h — высота
r — радиус вписанной окружности
Радиус вписанной окружности в шестиугольник
a — сторона шестиугольника
Радиус вписанной окружности в равнобедренный треугольник
a, b — стороны треугольника
Радиус вписанной окружности в равносторонний треугольник
a — сторона треугольника
Радиус вписанной окружности в треугольник
a, b, c — стороны треугольника
p — полупериметр, p=(a+b+c)/2
Радиус вписанной окружности в прямоугольный треугольник
Радиус вписанной окружности в ромб
r — радиус вписанной окружности
a — сторона ромба
D, d — диагонали
h — высота ромба
Радиус вписанной окружности в квадрат
a — сторона квадрата
Радиус вписанной окружности в равнобочную трапецию
с — нижнее основание
b — верхнее основание
a — боковые стороны
h — высота
Радиусы описанной окружности
Радиус описанной окружности правильного шестиугольника
a — сторона шестиугольника
d — диагональ шестиугольника
Найти радиус описанной окружности треугольника, формула
p= (a+b+c)/2
Найти радиус описанной окружности прямоугольного треугольника по катетам
Радиус описанной окружности прямоугольника по стороне
a, b — стороны прямоугольника
d — диагональ
Найти радиус описанной окружности около квадрата
Найти радиус описанной окружности равностороннего треугольника по стороне
найти радиус описанной окружности равнобедренного треугольника по сторонам
Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.
infourok.ru
Геометрия. Основные понятия. Видеоурок. Геометрия 7 Класс
С геометрией мы встречались в пятом и шестом классе, если выразиться обобщенно, это наука, которая изучает фигуры, их свойства. Сейчас, приступая к более глубокому изучению геометрии, нужно выйти на новый уровень этой науки, более строгий и более четкий, разобрать ее базовые понятия и аксиомы. Это нужно для того, чтобы начать изучать базовые объекты, которые необходимо определять, т. е. доказывать, и на которых мы будем строить дальнейшие определения.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Основы геометрии»
Базовые понятия геометрии, которые не нужно определять: точка, прямая, плоскость.
На этих базовых понятиях строятся другие понятия. Рассмотрим это на определении луча. Луч – это часть прямой, ограниченная с одной стороны точкой. Из базовых понятий
Рис. 1. Точка, прямая, луч
Аналогично, зная определение луча, можно дать определение угла. Угол – это геометрическая фигура, образованная двумя лучами, имеющими общую вершину (рис. 2).
Рис. 2. Точка, прямая, угол
Так можно поэтапно дать определение треугольнику, четырехугольнику, равенству треугольников и т. д.
Также нужно, кроме определений, уметь доказывать различные утверждения. Например, мы знаем, что сумма углов треугольника равна 180о, чтобы это доказать, нужно построить цепь верных определений, которые приведут к тому, что сумма углов треугольника равна 180о.
Аксиома – это заведомо истинное утверждение, принимаемое без доказательств.
Пример аксиомы:
Через любые две точки можно провести прямую и только одну (рис. 3).
Рис. 3. Иллюстрация к аксиоме
Дальнейшие утверждения могут быть выведены из аксиом, их называют теоремами (утверждения которые можно доказать), а уже из теорем получают следствия теорем.
Геометрия построена так, что в основании лежат базовые понятия (которые не нужно доказывать) и аксиомы, из них выводятся следующие понятия (первичные теоремы) и так по цепочке, сложнее и сложнее, это все развивается в науку.
Из программы геометрии пятого, шестого класса мы знаем, что площадь квадрата равна квадрату его стороны, но почему это именно так, можно будет разобрать в процессе изучения геометрии седьмого класса. Мы введем понятия площади, квадрата, угла, градуса, треугольника и т. д., докажем соответствующие теоремы, чтобы потом ими можно было пользоваться, объясняя более сложные теоремы и следствия теорем по цепочке, от фундамента базовых понятий и аксиом.
На сегодняшнем уроке мы узнали структуру геометрии, разобрали, на каких понятиях она базируется.
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. – 5-е изд. – М.: Просвещение.
- Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
- Чупин В.Д. От Пифагора до наших дней. – Пермь, 1992.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Festival.1september.ru (Источник).
- Festival.1september.ru (Источник).
- Festival.1september.ru (Источник).
Домашнее задание
- Ознакомьтесь самостоятельно с аксиомами геометрии (планиметрии)
- Если две прямые имеют общую точку, то как они находятся относительно друг друга на плоскости?
- Докажите теорему: через каждую точку прямой можно провести перпендикулярную ей прямую, и притом только одну.
interneturok.ru
Основные формулы геометрия 7-11 класс
Сумма площадей боковых граней
Призма прямая
Пирамида
Сумма площадей боковых граней
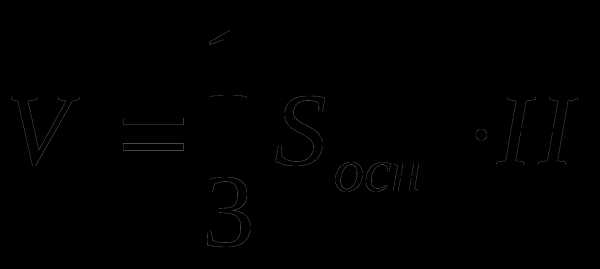
Цилиндр
Конус

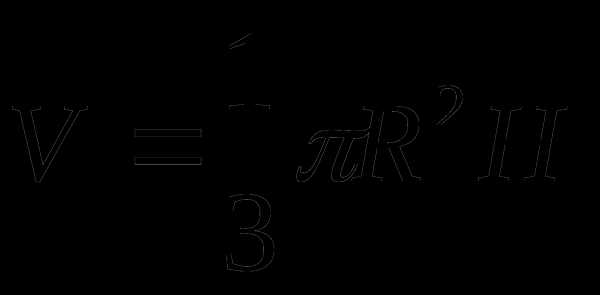
Шар, сфера
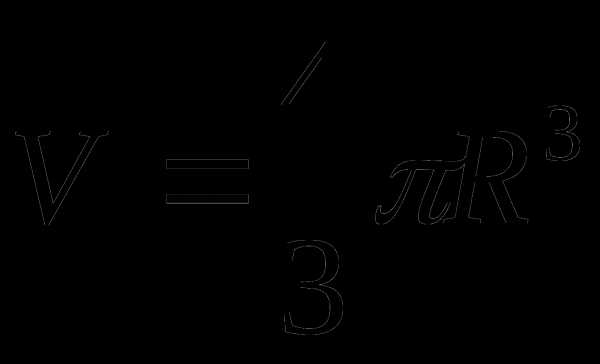
Тетраэдр
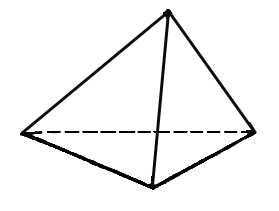

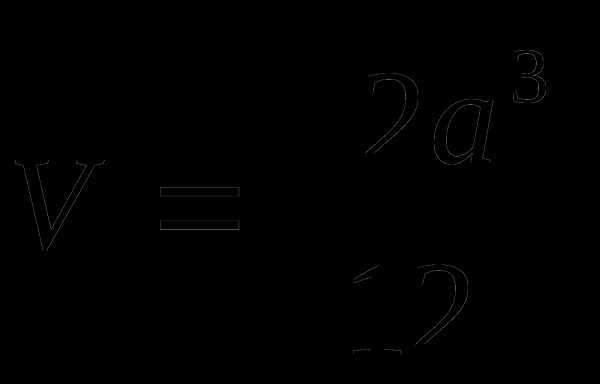
d – длина диагонали
Прямоугольник
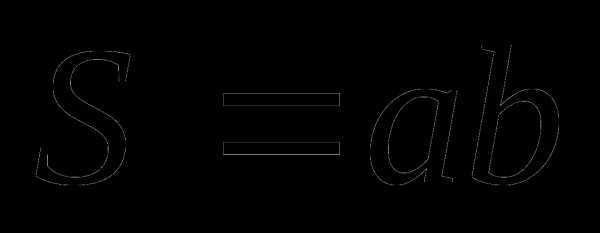
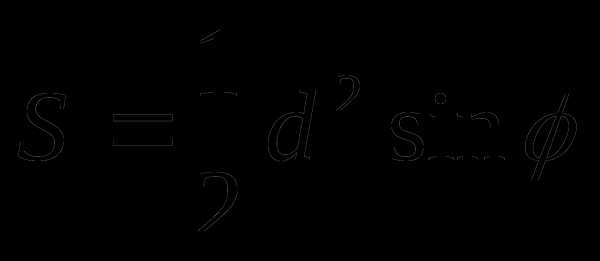
a,b – длина стороны
d – длина диагонали
Параллелограмм
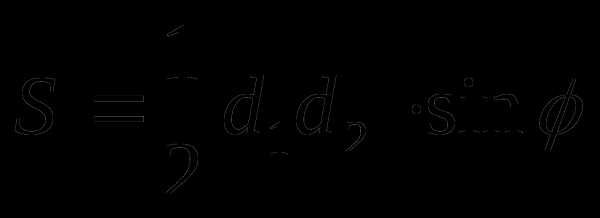
a, b – длина стороны
h – высота
d – диагональ
Ромб
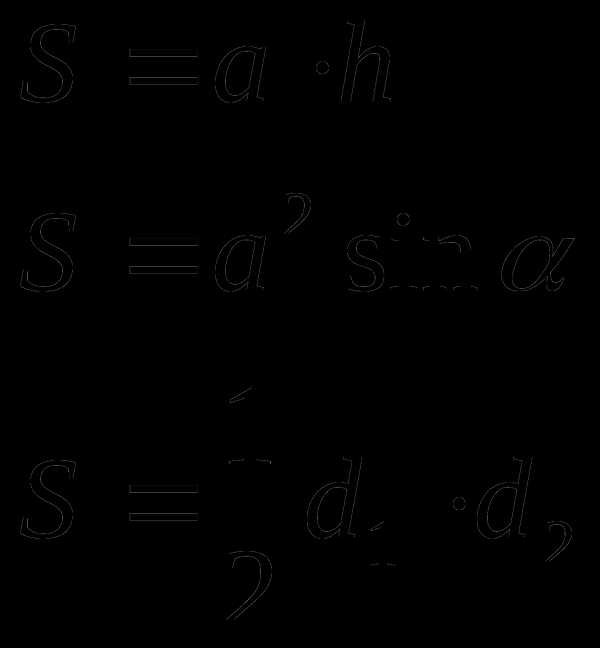
а – сторона
h – высота
d — диагональ
Треугольник
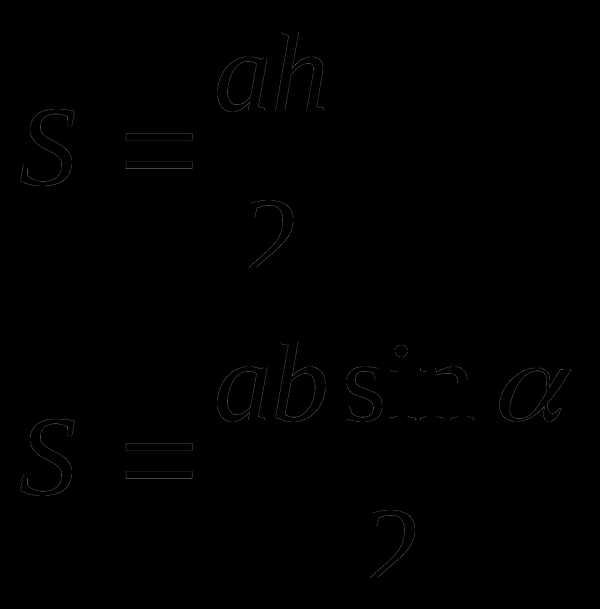
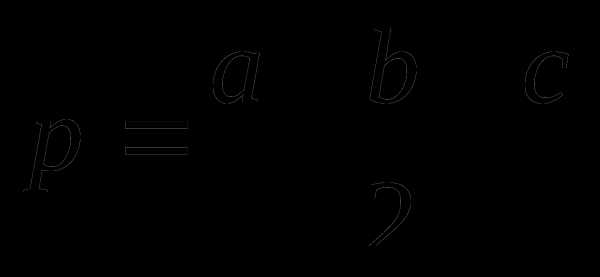
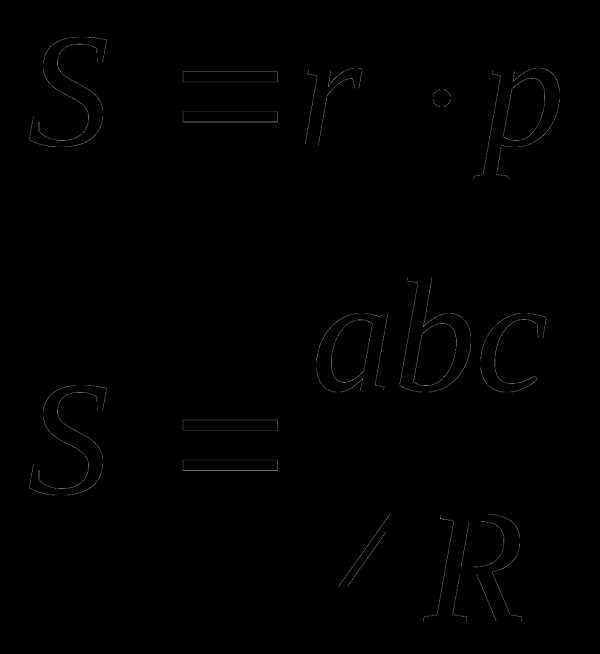
a, b, c – стороны треугольника
h – высота треугольника
p – полупериметр
R – радиус вписанной окружности
R – радиус описанной окружности
Прямоугольный треугольник
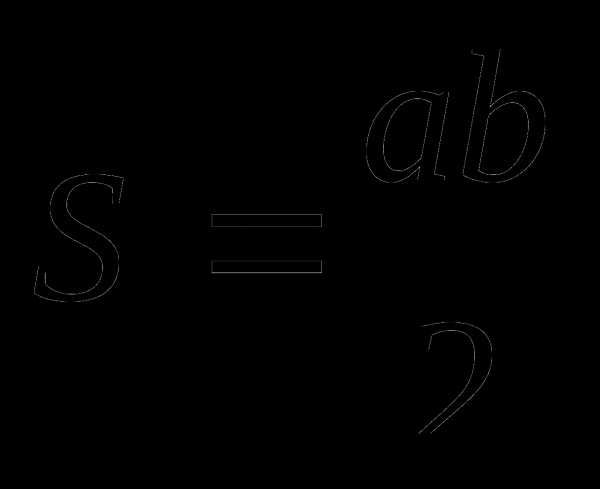
Теорема Пифагора
a, b – катеты
c – гипотенуза
Трапеция
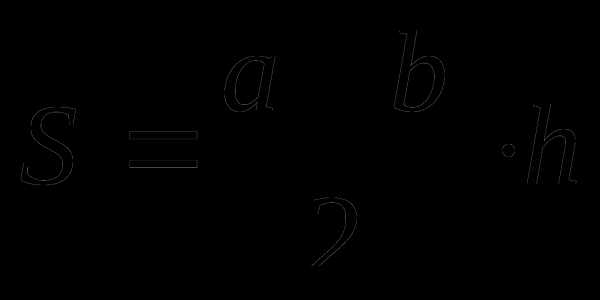
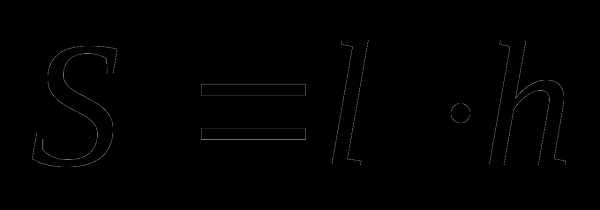
a,b – основания трапеции
h – высота трапеции
l – средняя линия трапеции
Круг
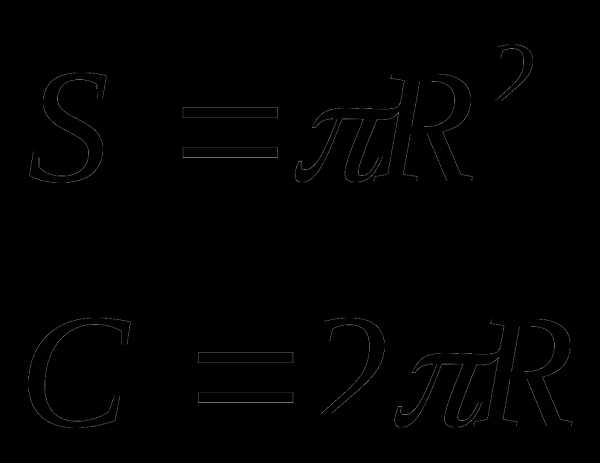
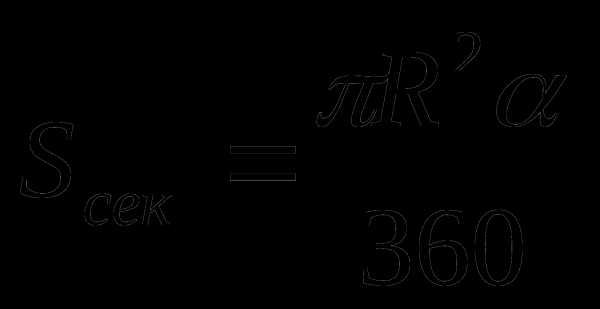
R – радиус окружности
C – длина окружности
Правильные многоугольники
infourok.ru
Основные геометрические понятия | Математика
Тела отличаются друг от друга весом, цветом, плотностью, твердостью, занимаемым ими местом и т. д.
Эти признаки называются свойствами тел.
Тела, обладающие этими свойствами, называются физическими телами.
Между этими свойствами особенного внимания заслуживает свойство тела, называемое протяженностью.
Протяженность есть свойство тела занимать в пространстве определенное место.
Его называют геометрическим свойством тела. Этим свойством определяется форма и величина тела.
Тело, обладающее только одним свойством протяженности, называется геометрическим телом. Рассматривая геометрическое тело, обращают внимание только на его форму и величину.
Остальные свойства тела называются физическими.
Геометрическое тело есть место, занимаемое физическим телом.
Геометрическое тело ограничено со всех сторон. Оно отделяется от остального пространства поверхностью тела. Чтобы выразить это, говорят, что
Поверхность есть предел тела.
Линия есть предел поверхности.
Конец линии называется точкой. Точка ограничивает и отделяет одну линию от другой, поэтому точку называют границей линии.
Точка есть предел линии.
На чертеже 1 изображено тело, имеющее форму закрытого со всех сторон ящика. Оно ограничено шестью сторонами, образующими поверхность ящика. На каждую из сторон ящика можно смотреть как на отдельную поверхность. Эти стороны отделяются друг от друга 12 линиями, образующими ребра ящика. Линии же отделяются друг от друга 8 точками, составляющими углы ящика.
Тела, поверхности и линии бывают неодинаковой величины. Это значит, что они занимают неодинаковое пространство, или неодинаковое протяжение.
Объем тела. Величина геометрического тела называется объемом или вместимостью тела.
Площадь поверхности.
Величина поверхности называется площадью.Длина линии. Величина линии называется длиною.
Длина, площадь и объем являются разнородными величинами. Они измеряются различными единицами и употребляются для различных целей. Чтобы найти расстояние двух предметов, ширину руки, глубину колодца, высоту башни, определяют длину линии. Для этого делают только одно измерение, то есть производят измерение в одном направлении. При измерении прибегают к единицам длины. Эти единицы длины называются верстами, саженями, аршинами, футами, метрами и т. д. Единица длины имеет одно измерение, поэтому и говорят, что
Линии имеют одно измерение. Линии не имеют ни ширины, ни толщины. Они имеют одну длину.
Чтобы иметь понятие о размерах картины, нужно знать ее длину и ширину. Длина и ширина дают понятие о площади картины. Для определения площади нужно стало быть сделать два измерения, или измерить картину в двух направлениях. Для определения величины площади прибегают к единицам площадей. За единицу площадей принимают квадрат, стороны которого имеют определенную единицу длины. Единицы площадей называются квадратными милями, квадратными верстами, квадратными футами и т. д. Квадратная верста есть площадь квадрата, у которого каждая сторона равна версте, и т. д. Единица площадей имеет два измерения: длину и ширину. Так как поверхности измеряются единицами площадей, то в этом смысле и говорят, что
Поверхности имеют два измерения. Поверхности не имеют толщины. Они могут иметь только длину и ширину.
Чтобы иметь понятие о вместимости комнаты или ящика, нужно знать их объемы. Для этого нужно знать длину, ширину и высоту комнаты, то есть сделать три измерения или измерить ее в трех направлениях. Объемы измеряются единицами объема. За единицу объема принимают куб, каждая сторона которого равна единице. Единицы объема имеют три измерения: длину, ширину и высоту. Так как объемы измеряются единицами объемов, то и говорят, что
Тела имеют три измерения.
Единицы объемов называются кубическими верстами, кубическими футами и т. д. Смотря по длине стороны куба.
Точка не имеет ни длины, ни ширины, ни вышины, или точка не имеет измерения.
Геометрические протяжения. Линии, поверхности и тела называются геометрических протяжениями.
Геометрия есть наука о свойствах и измерении геометрических протяжений.
Геометрия есть наука о пространстве. В ней излагается совокупность необходимых отношений, связанных с природой пространства.
Образование геометрических протяжений движением
На линию можно смотреть так же, как на след, оставляемый движением точки, на поверхность как на след, оставляемый движением лини и на тело как на след, оставляемый движением поверхности. На этих соображениях основаны другие определения линии, поверхности и тела.
Линия есть геометрическое место движущейся точки.
Поверхность есть геометрическое место движущейся линии.
Тело есть геометрическое место движущейся поверхности.
Все предметы, рассматриваемые в природе, имеют три измерения. В ней нет ни точек, ни линий, ни поверхностей, а существуют только тела. Однако в геометрии рассматривают точки, линии и поверхности отдельно от тел. При этом некоторое приближенное наглядное представление о поверхности дает нам очень тонкая оболочка тела, наглядное представление о линии дает очень тонкая нить или волосок и о точке конец нити.
Линии
Линии разделяются на прямые, ломаные и кривые.
Прямая линия есть кратчайшее расстояние между двумя точками.
Сильно натянутая тонкая нить дает некоторое наглядное представление о прямой линии.
Всякую линию обозначают буквами, поставленными при ее точках. Чертеж 2 изображает прямую линию AB. Во всякой прямой линии обращают внимание на ее направление и величину.
Направление прямой линии определяется ее положением.
Ломаная линия есть последовательное и непрерывное соединение нескольких прямых, имеющих неодинаковое направление.
Ломаная линия ABCD (черт. 3) составлена из прямых AB, BC, CD, имеющих неодинаковое направление.
Кривая линия есть такая, которая не может быть составлена из прямых.
Линия, изображенная на черт. 4, будет кривой линией.
Линия, составленная из прямых и кривых, называется иногда составной линией.
Чертеж (4, а) представляет такую составную линию.
Поверхности
Поверхности разделяются на прямые или плоские и кривые. Плоская поверхность называется плоскостью.
Плоскость. Поверхность называется плоскостью в том случае, когда всякая прямая линия, проведенная через каждые две точки поверхности, лежит на ней всеми своими точками.
Кривая поверхность есть такая, которая не может быть составлен из плоскостей.
Прямая линия, проведенная между всякими двумя точками кривой поверхности, не помещается на ней всеми своими промежуточными точками.
Некоторое наглядное представление о плоскости дает поверхность хорошо полированного зеркала или поверхность стоячей воды. Примером кривых поверхностей может послужить поверхность бильярдного шара.
Разделы геометрии
Геометрия делится на планиметрию и стереометрию.
Планиметрия изучает свойство геометрических протяжений, рассматриваемых на плоскости.
Стереометрия изучает свойства таких геометрических протяжений, которые не могут быть представлены в одной плоскости.
Планиметрия называется геометрией на плоскости, стереометрия — геометрией в пространстве.
Геометрия разделяется еще на начальную и высшую. В настоящем сочинении предлагается изложение только начальной геометрии.
Различные формы выражения геометрических истин
Геометрические истины выражаются в форме аксиом, теорем, лемм и проблем или задач.
Аксиома есть истина, но своей очевидности не требующая доказательства.
Примерами истин, не требующих доказательства, могут послужить следующие аксиомы:
Целое равно сумме своих частей.
Целое больше своей части. Части меньше целого.
Две величины, равные одной и той же третьей, равны между собой.
Прибавив или вычтя из равных величин поровну, получим величины равные.
Прибавив или вычтя из равных величин не поровну, получим величины неравные.
Прибавив или вычтя из неравных величин поровну, получим величины неравные.
Сумма больших больше суммы меньших величин.
Однородная величина, которая не больше и не меньше другой, равна ей и т. д.
Теорема. Теоремой или предположением называется истина, требующая доказательства.
Доказательство есть совокупность рассуждений, делающих теорему очевидной.
Теорема доказывается при помощи аксиом.
Состав теоремы. Всякая теорема состоит из условия и заключения.
Условие называется иногда предположением, допущением, а заключение называют иногда следствием. Условие дано и потому получает иногда название данного.
Теорема называется обратной, если заключение делается условием, а условие или предположение заключением. В таком случае данная теорема называется прямою. Не всякая теорема имеет свою обратную.
Проблема или задача есть вопрос, разрешаемый при помощи теорем.
Лемма есть вспомогательная истина, облегчающая доказательство теоремы.
maths-public.ru
Основные понятия геометрии
Основные геометрические понятия возникли еще в доисторические времена. Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий. Одним из первых достижений абстрактного мышления древнего человека стало понимание прямой линии.
Дальнейшая практическая деятельность человека послужила началом длительного процесса выработки основных отвлеченных понятий геометрии, открытия элементарных зависимостей и соотношений.

Муза геометрии, Лувр
По мере того, как накапливались знания о мире, человек стремительно расширял геометрическую терминологию, обобщая, анализирую и синтезируя известные факты. Логические связи, попытки объяснить явления и доказать правоту своих предположений положили начало геометрической науки.
Величайших историк древнего мира Геродот, выдающийся математик Демокрит, философ и ученый Аристотель были едины во мнении, что колыбелью Геометрии был Египет. Действительно, именно в Египте зародилась это сложная и важная наука. Около 5 — 6 вв. до нашей эры в Древней Греции начался новый этап развития геометрии как науки. Научное сочинение Герона Александрийского было в то время своего рода энциклопедией по прикладной механике и практической геометрии. «Геометрика» Герона на протяжении нескольких веков была главным справочником и учебником по геометрической науке. Позднее «геометрика» Герона была вытеснена гениальным сочинением выдающегося ученого Евклида «Начала».
Геометрические формулы были найдены на древних египетских папирусах, а вот доказательства их не было. Возникает вопрос: А когда же появились первые доказательства?
Историки геометрической науки едины во мнении: первые доказательства теорем о вертикальных углах, свойстве равнобедренного треугольника и др. принадлежат философу и математику Фалесу Милетскому (даты жизни которого 625 — 527 г.г. до н.э.).
Однако уже в те далекие времена, ученые заметили, что некоторые теоремы не нуждаются в доказательстве.
Кстати, Омар Хайям в девятом веке заметил, что Евклид в своих сочинениях доказал многое из того, что не нуждалось в доказательстве. Так появились аксиомы.
Все основные геометрические знания, приблизительно в объеме современного курса средней школы были изложены более двух тысяч лет назад в «Началах» Евклида.
В семнадцатом веке Рене Декарт занялся изучением свойств фигур и алгебраических методов применительно к геометрии. Им были созданы новые разделы геометрической науки — аналитическая геометрия, начертательная геометрия и другие. Но это все были разные методы изучения одного и того же пространства, заданного аксиомами.
В восемнадцатом веке возникла неевклидова геометрия выдающегося русского математика Н. И. Лобачевского.
Далее мы дадим определения некоторым простейшим понятиям геометрии таким, как точка, прямая и плоскость. Эти понятия являются отправным пунктом при изложении геометрии.
Прямая бесконечна. Однако на рисунках мы изображаем лишь часть прямой, при этом не забываем, что она бесконечна.
Точки (пункты) на геометрических чертежах и рисунках обозначают прописными буквами латинского алфавита, а прямые — строчными.
Наряду с прямыми также изучают кривые линии, к примеру, окружность.
Следует напомнить, что линия будь то прямая или кривая состоит из бесчисленного множества точек. Поэтому справедливы выражения: «Точка А лежит на линии а» или «линия а проходит через точку А».
К основным свойствам прямой относятся:
- Черед две различные точки проходит одна единственная прямая. Следовательно две прямые не могут иметь более одной общей точки.
- Две разные прямые, имеющие общую точку, пересекаются в ней. В связи с тем, что две точки определяют прямую, проходящую через них, прямую обозначают сочетанием букв, к примеру, прямая АВ, прямая PQ.
- Точка М, лежащая на прямой а, разбивает её на две части. Каждая из которых называется полупрямой или лучом. Точка М служит началом каждого их этих лучей. Две точки М и N разбивают прямую на три части: два луча МР и NQ и отрезок MN.
Итак, сформулируем определения понятий луча, отрезка и фигуры:
- Лучом называется часть прямой, ограниченная одной из её точек.
- Отрезком называется часть прямой, заключенная между двумя её точками.
- Под фигурой понимают некоторое сочетание определенным образом расположенных в одной плоскости (а иногда и в пространстве) элементов: точек, прямых, лучей, отрезков (иногда и плоскостей).
Поделиться ссылкой
sitekid.ru
| Главная > Учебные материалы > Математика: Формулы геометрии | ||
     
|
||
|
1.Признаки параллельности прямых.
|
||
| 1 2 3 4 5 6 7 8 | ||
Признаки параллельности прямых |
||
Признаки равенства треугольников |
||
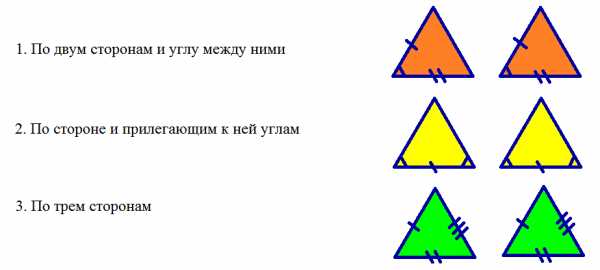 |
||
Теорема Пифагора |
||
 |
||
Рассчитать стороны прямоугольного треугольникаКатет a Катет b Гипотенуза c =
|
||
| Гипотенуза c Катет a Катет b = | ||
 |
||
Радиус вписанной и описанной окружностей правильных многоугольников |
||
 |
||
Рассчитать радиус вписанной и описанной окружностейСторона a Число углов n Радиус R = Радиус r = |
||
Теорема синусов |
||
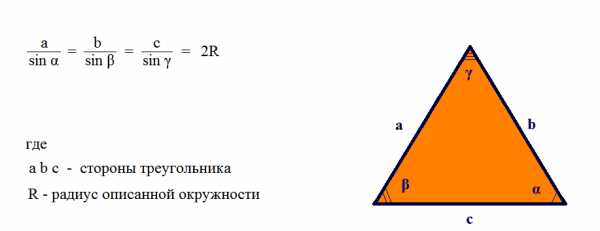 |
||
Рассчитать сторону треугольникаСторона а sin (α= °) sin (β= °) Сторона b =Рассчитать угол треугольникаСторона а sin (α= °) Сторона b Угол β = °
|
||
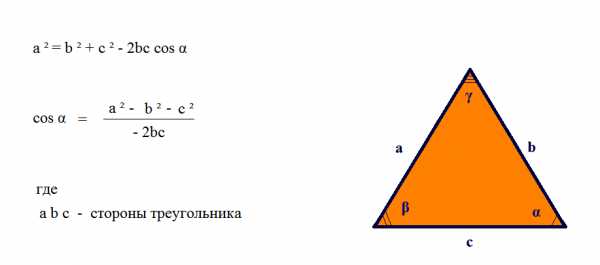
Теорема косинусов |
||
 |
||
Рассчитать сторону треугольникаСторона b Сторона с cos (α= °) Сторона a =Рассчитать угол треугольникаСторона а Сторона b Сторона c Угол α = ° |
||
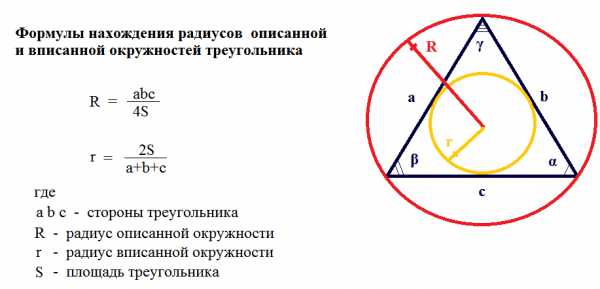
Радиус вписанной и описанной окружностей |
||
 |
||
|
Рассчитать радиус описанной и вписанной окружности Сторона а Сторона b Сторона c
Площадь S = Радиус R = Радиус r = |
||
| 1 2 3 4 5 6 7 8 | ||
www.mathtask.ru
Формулы стереометрии
Формулы стереометрии. В этой статье общий обзор формул для решения задач по стереометрии. Нужно сказать, что задачи по стереометрии довольно разнообразны, но они несложны. Это задания на нахождение геометрических величин: длин, углов, площадей, объёмов.
Рассматриваются: куб, прямоугольный параллелепипед, призма, пирамида, составной многогранник, цилиндр, конус, шар. Печалит тот факт, что некоторые выпускники на самом экзамене за такие задачи даже не берутся., хотя более 80% таких задач решаются элементарно, практически устно.
Остальные требуют небольших усилий, наличия знаний и специальных приёмов. В будущих статьях мы с вами будем рассматривать все эти задачи, не пропустите!
Для решения необходимо знать формулы площадей поверхности и объёмов параллелепипеда, пирамиды, призмы, цилиндра, конуса и шара. Ещё раз подчеркну, что сложных задач нет, все они решаются в 2-3 действия (максимум). Важно «увидеть» какую формулу необходимо применить, только и всего.
Все необходимые формулы представлены ниже:
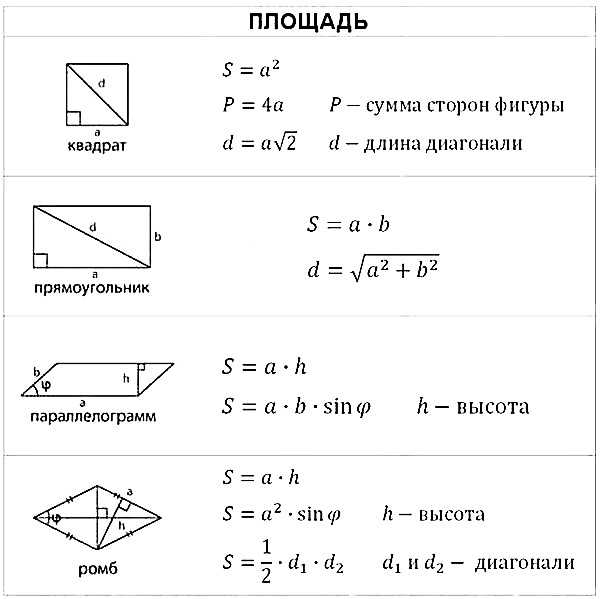
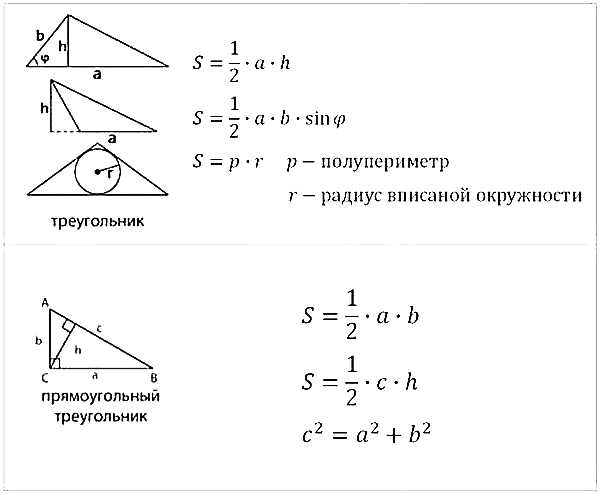
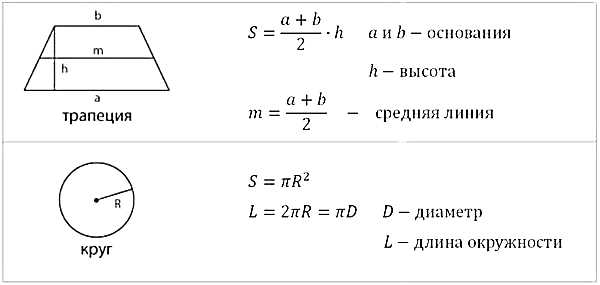
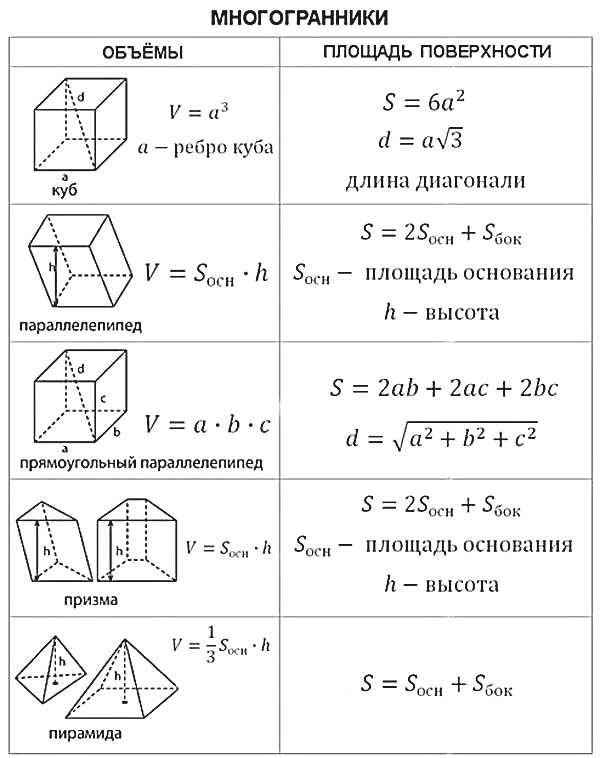
 Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.
Конечно, кроме указанных формул необходимо знать теорему Пифагора, определения тригонометрических функций, понятие средней линии треугольника и ещё немного теоретических фактов, о которых мы поговорим в следующей статье.С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
