Геометрические векторы
Дисциплина: Высшая математика
Тема: Геометрические векторы
1. Геометрические векторы. Основные определения
В математике, физике, теоретической механике приходится иметь дело с величинами двух типов: одни имеют чисто числовой характер; другие же имеют не только числовую характеристику, но и связаны с понятием о направлении в пространстве. Рассмотрим, например, температуру, массу, энергию, скорость, ускорение, силу. Отличие последних трех величин от первых трех состоит в том, что с ними должно быть связано понятие о направлении. Первые три величины, не связанные с понятием о направлении, называются скалярами. Остальные три величины, имеющие определенное направление, называются векторами.
Так, при измерении температуры, мы получим положительное или отрицательное число, характеризующее ее величину в градусах. Точно так же можно измерить массу, энергию.
Определение 1. Скаляром называется величина, характеризующаяся только числом.
Следовательно, скаляры — это обычные числа, и различие между двумя одинаковыми числами может заключаться лишь в их размерности (м и см, м и кг).
Если необходимо измерить такую величину, как скорость точки, то для этого знать два числа (путь и время) недостаточно. Необходимо еще знать, куда двигается точка, то есть ее направление движения.
Определение 2. Вектором называется величина, характеризующаяся не только численным значением, но и направлением в пространстве.
Следовательно, утверждать, что если обе точки движутся со скоростью 2
, то их скорости равны, нет никакого основания. Необходимо знать в какие стороны они двигаются.Из сказанного следует, что для описания скаляра достаточно написать число и указать его размерность. Для описания векторной величины используют направленные отрезки, длина которых при выбранном масштабе соответствует величине вектора, а направление — совпадает с направлением векторной величины. В дальнейшем эти отрезки и будем называть геометрическими векторами.
При изображении вектора одна точка, ограничивающая вектор, называется началом, а вторая — концом вектора. В конце вектора ставится стрелка. Для краткой записи вектор можно обозначить с помощью двух букв
(первая соответствует началу, вторая — концу) или же одной буквы (здесь начало и конец не обозначены).Определение 3. Расстояние между началом и концом вектора называется его длиной или модулем и обозначается
или .Определение 4. Вектор, у которого конец совпадает с началом, называется ноль вектором и обозначается
.Определение 5. Векторы называются коллинеарными, если они расположены на одной прямой или параллельных прямых. Векторы называются коллинеарными, если они расположены в одной плоскости или в параллельных плоскостях.
Определение 6. Два вектора
и называются равными, если они коллинеарные, одинаково направлены и равны по длине.Записывается это так
.Из определения 6 следует, что вектор можно переносить параллельно самому себе, помещая его начало в любую точку пространства. При этом каждый новый вектор будет равен исходному.
Однако следует отметить, что все сказанное выше связано с так называемыми свободными векторами. Кроме них существуют еще передвижные и определенные векторы. У свободных векторов точку приложения можно выбирать где угодно. У передвижных — точку приложения можно перемещать вдоль самого вектора (например, сила, приложенная к твердому телу). У определенных векторов точка приложения должна быть зафиксирована (например, сила, действующая на жидкость). Но изучение всех векторов можно, в конечном счете, свести к изучению свободных векторов, поэтому в дальнейшем мы будем заниматься только ими.
2. Простейшие операции над векторами
К простейшим операциям над векторами относится сложение и вычитание векторов и умножение вектора на скаляр. Все эти операции называются линейными.
1) Сложение векторов.
Определение 1. Чтобы найти сумму двух векторов
и , необходимо конец вектора совместить с началом . Вектор , соединяющий точки и , будет их суммой.Обозначается сума следующим образом:
. Величину ее можно найти и другим способом. Начала векторов и совмещаются и на них как на сторонах строится параллелограмм. Диагональ параллелограмма и будет суммой векторов.Из правила параллелограмма видно, что сумма векторов обладает переместительным свойством
.Если слагаемых больше, например, три:
, поступают следующим образом. Строят вначале сумму , а затем, прибавляя , получают вектор .Из рисунка видно, что тот же результат будет, если сложить вначале
, а затем прибавить , то есть сумма векторов обладает сочетательным свойством: .Если при сложении нескольких векторов конец последнего совпадает с началом первого, то сумма равна ноль вектору
. Очевидно, .2) Разность векторов.
Определение 2. Разностью двух векторов
и называется такой вектор , сумма которого с вычитаемым дает вектор .Значит, если
, то .Из определения суммы двух векторов вытекает правило построения разности. Откладываем из общей точки векторы
Видно, что если на векторах
и построить параллелограмм, то одна его диагональ соответствует их сумме, а вторая — разности.mirznanii.com
Лекция 1 Пространство геометрических векторов
Линейные операции над геометрическими векторами. Коллинеарные и компланарные векторы. Базис, координаты вектора, их свойства. Проекция вектора на ось. Декартов базис и декартовы координаты вектора. Декартовы координаты точки. |
1.1. Понятие геометрического вектора. Линейные операции над векторами, их свойства
Определение 1.
Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке (т. е. указано, какая из его граничных точек является началом, а какая — концом). Е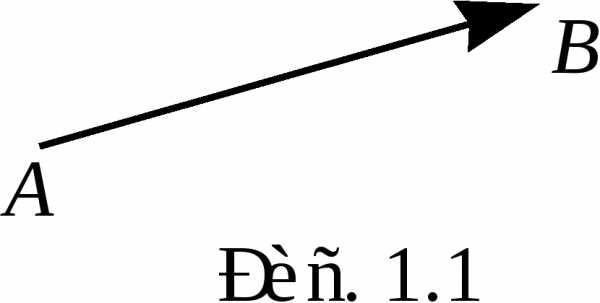 сли
за начало отрезка
сли
за начало отрезка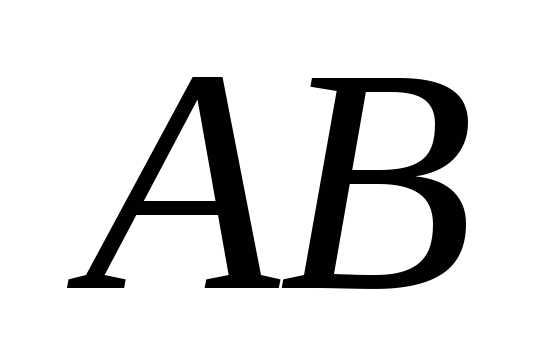 принята точка
принята точка ,
вектор будем обозначать символом
,
вектор будем обозначать символом (либо одной малой латинской буквой,
например,
(либо одной малой латинской буквой,
например, ),
а точку
),
а точку называтьточкой приложениявектора.
называтьточкой приложениявектора.
На чертеже вектор  будем изображать отрезком со стрелкой
в конечной точке (рис. 1.1).
будем изображать отрезком со стрелкой
в конечной точке (рис. 1.1).
Длинойвектора назовем длину отрезка
назовем длину отрезка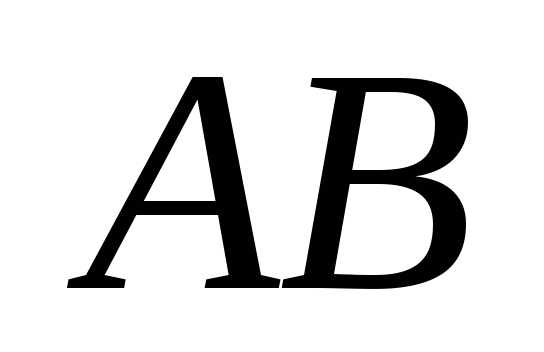 и
в записи используем знак абсолютной
величины:
и
в записи используем знак абсолютной
величины: (либо
(либо ).
).
Вектор  называетсянулевымвектором, если
его конечная точка
называетсянулевымвектором, если
его конечная точка совпадает
с начальной
совпадает
с начальной .
.
Нулевой вектор в силу его определения не имеет направления, а длина его равна нулю.
Векторы  и
и
Два вектора  и
и называютравными, если они коллинеарны,
имеют общее направление и равные длины
(рис. 1.4).
называютравными, если они коллинеарны,
имеют общее направление и равные длины
(рис. 1.4).
Из определения следует, что два вектора, порознь равные третьему, равны между собой. Именно поэтому в аналитической геометрии не различают равные векторы, имеющие разные точки приложения. Векторы, изучаемые в аналитической геометрии, называются свободными.
О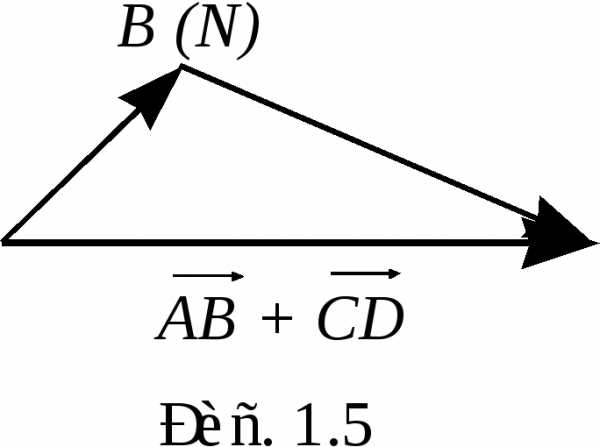 пределение
2.Суммой векторов
пределение
2.Суммой векторов  и
и  называется вектор, идущий из начала
первого вектора
называется вектор, идущий из начала
первого вектора
 )в конец второго (
)в конец второго ( ),
при условии, что
),
при условии, что  приложен к концу вектора
приложен к концу вектора  (рис. 1.5).
(рис. 1.5). Обозначать сумму в тексте будем 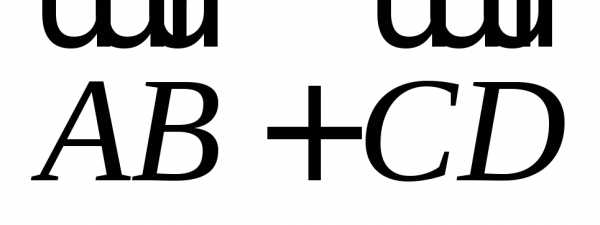 (либо
(либо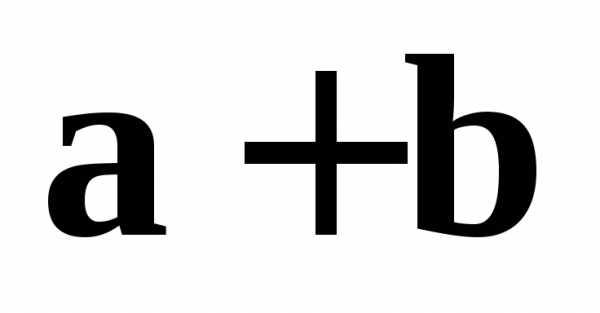 ,
если
,
если ,
, ).
).
Замечание 1.Из определения 2 следует так называемое
«правило параллелограмма»: если векторы и
и
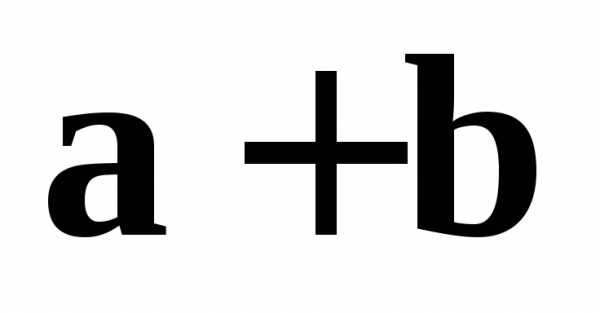 представляет собой диагональ
параллелограмма, построенного на
векторах
представляет собой диагональ
параллелограмма, построенного на
векторах и
и как на сторонах.
как на сторонах. Д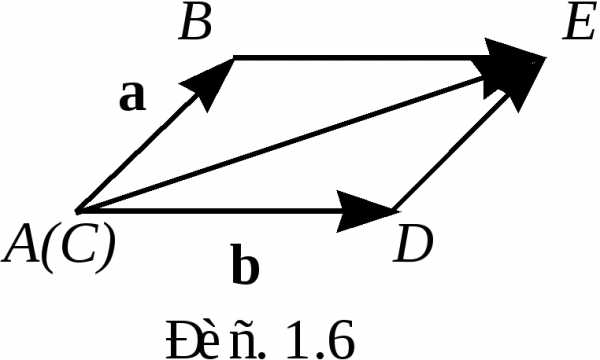 ействительно,
в параллелограмме
ействительно,
в параллелограмме (рис. 1.6) векторы
(рис. 1.6) векторы и
и равны:,
а тогда по определению 2 диагональили.
равны:,
а тогда по определению 2 диагональили.
Докажем два свойства операции сложениягеометрических векторов:
1) для любых двух геометрических векторов 
 :
:;
2) для любых трех геометрических векторов  ,
, и
и :
:
.
Д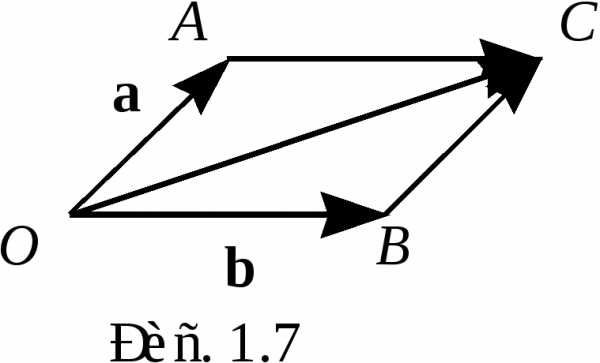 оказательство
свойства 1.
оказательство
свойства 1.
Приложим векторы  и
и к одному началу – произвольной точке
к одному началу – произвольной точке ,
концевые точки обозначим так, как
показано на рис. 1.7 и рассмотрим
треугольники
,
концевые точки обозначим так, как
показано на рис. 1.7 и рассмотрим
треугольники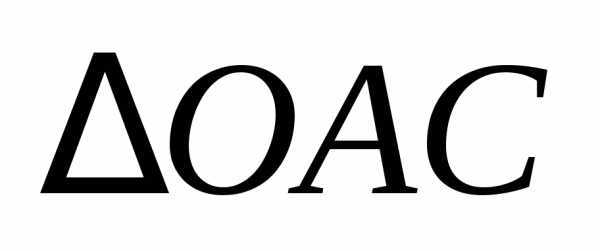 и
и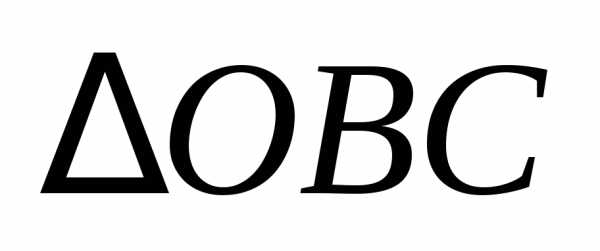 .
.
Из  вектор,
так как по определению равных векторов.
вектор,
так как по определению равных векторов.
С другой стороны, из 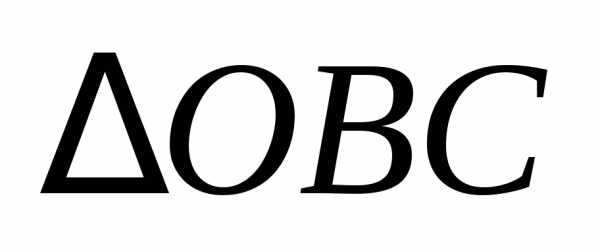 тот же самый вектор,
так как.
тот же самый вектор,
так как.
Таким образом, , и свойство 1 доказано.
Доказательство свойства 2.
П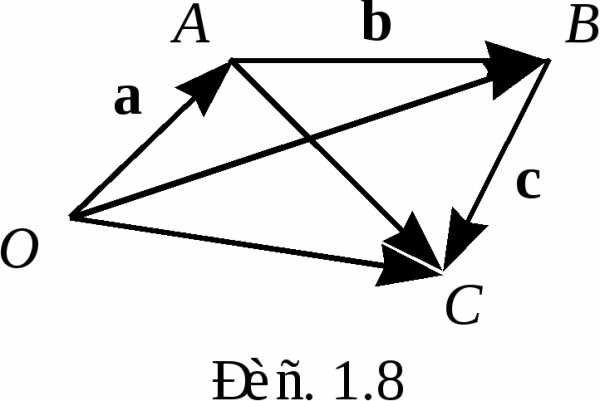 риложим
вектор
риложим
вектор к произвольной точке
к произвольной точке ,
к концу вектора
,
к концу вектора приложим вектор,
к концу
приложим вектор,
к концу — вектор
— вектор .
Концевые точки обозначим так, как
показано на рис. 1.8, и рассмотрим вектор
.
Концевые точки обозначим так, как
показано на рис. 1.8, и рассмотрим вектор ,
идущий из начала
,
идущий из начала в конец вектора
в конец вектора .
.
Из 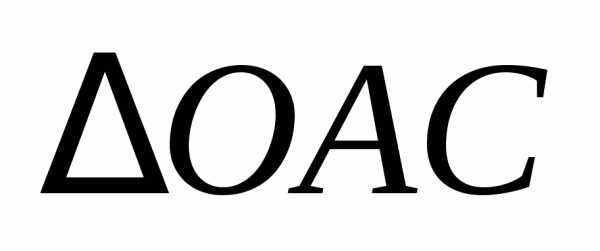 имеем:
имеем:
, (1.1)
но вектор  из
из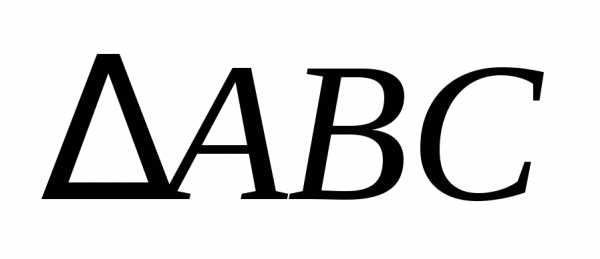 равен
равен
. (1.2)
Из (1.1) и (1.2) получим
. (1.3)
С другой стороны, тот же самый вектор  из треугольника
из треугольника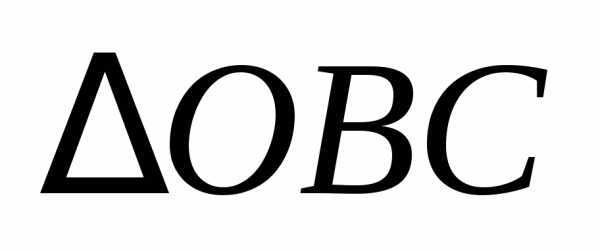 можно записать в виде
можно записать в виде
, (1.4)
но из 
. (1.5)
Равенства (1.4) и (1.5) дают следующее:
.
Сравнив последнее равенство с (1.3), получим
,
и свойство 2 доказано.
Замечание 2.Свойство 2 означает, что мы можем далее
не различать векторы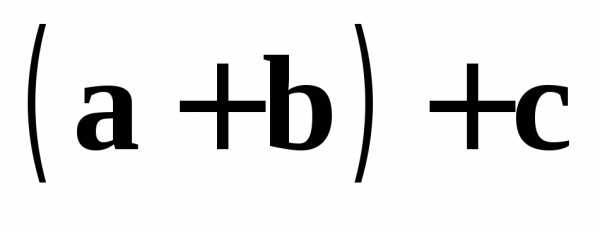 и
и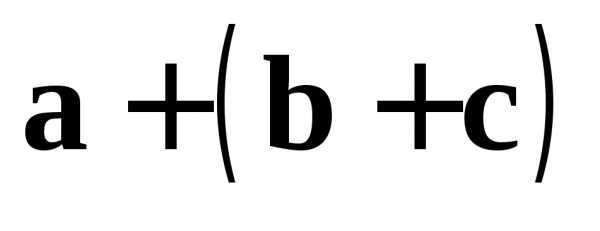 ,
а рассматривать их как один и тот же
вектор.
,
а рассматривать их как один и тот же
вектор.
С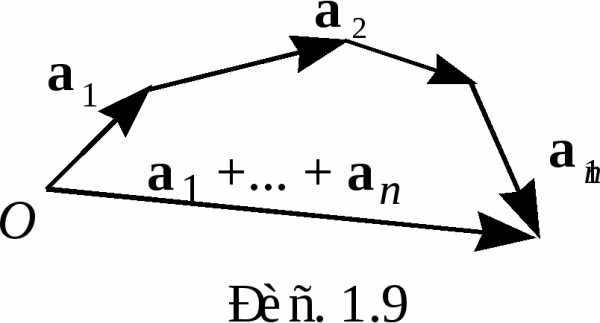 умма
произвольного числа векторовможет быть получена по следующему
правилу: к произвольной точке
умма
произвольного числа векторовможет быть получена по следующему
правилу: к произвольной точке приложим вектор
приложим вектор ,
к его концу – вектор
,
к его концу – вектор и так далее, к концу вектора
и так далее, к концу вектора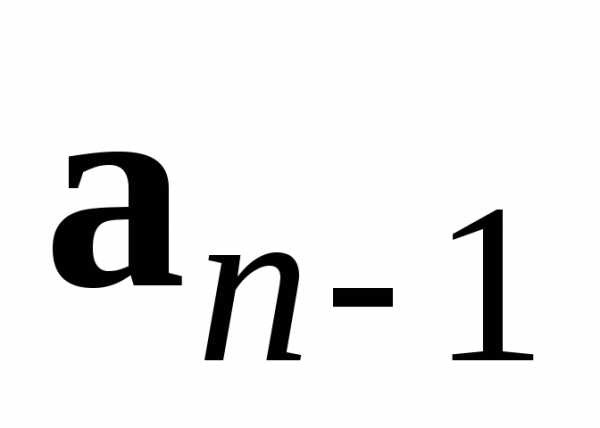 приложим вектор
приложим вектор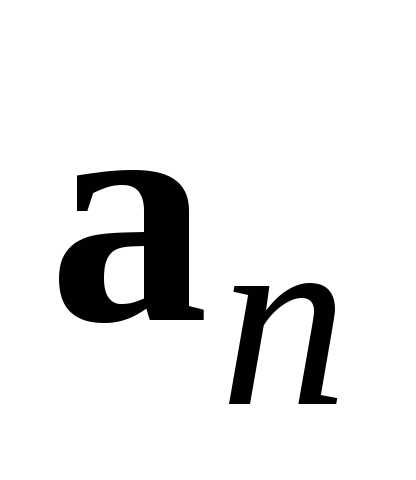 ,
тогда вектор, начало которого совпадет
с началом,
а конец – с концом
,
тогда вектор, начало которого совпадет
с началом,
а конец – с концом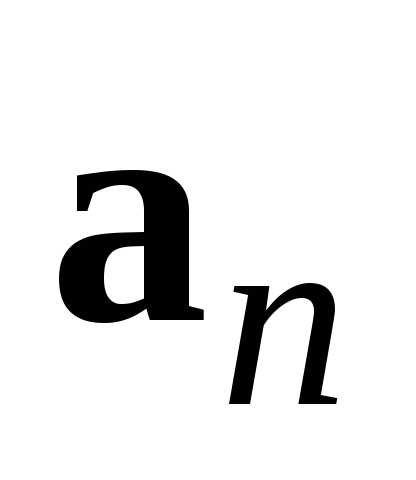 ,
и будет вектором(рис. 1.9).
,
и будет вектором(рис. 1.9).
Замечание 3.Существует такой вектор ,
что для любого геометрического вектора
,
что для любого геометрического вектора справедливо равенство
справедливо равенство
.
Действительно, в качестве вектора  можно взять введенный ранее нулевой
вектор.
можно взять введенный ранее нулевой
вектор.
Если  – произвольный геометрический вектор,
то по определению суммы вектор
– произвольный геометрический вектор,
то по определению суммы вектор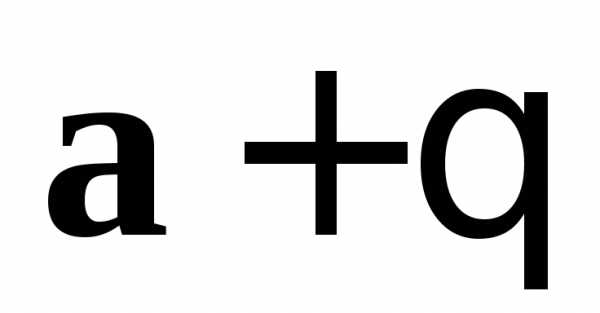 имеет начало в начале
имеет начало в начале ,
а конец – в конце второго слагаемого,
т. е.
,
а конец – в конце второго слагаемого,
т. е. ,
но у
,
но у начало и конец совпадают и, таким образом,
у вектора
начало и конец совпадают и, таким образом,
у вектора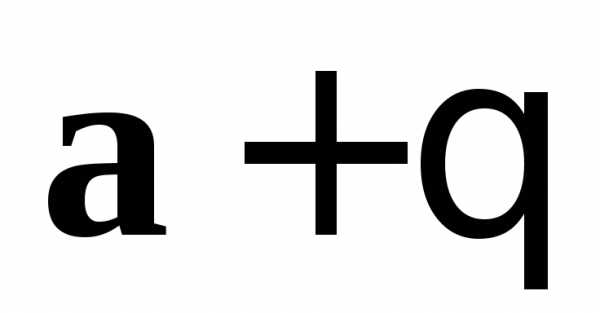 начало совпадает с началом вектора
начало совпадает с началом вектора ,
а конец – с концом вектора
,
а конец – с концом вектора и.
и.
Аналогично устанавливаем, что .
Определение 3. Разностью векторов  и
и называется такой вектор
называется такой вектор  ,
что.
,
что.
Запись: .
И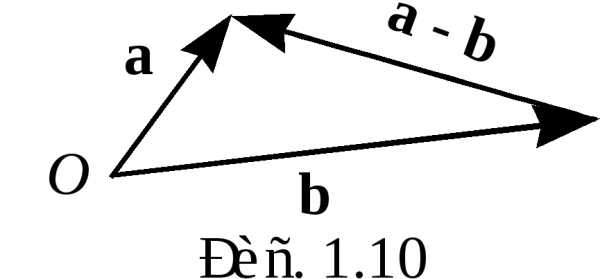 з
определения 3 следует, что если привести
векторы
з
определения 3 следует, что если привести
векторы и
и к одному началу, тоизображается вектором, идущим из конца
к одному началу, тоизображается вектором, идущим из конца в конец
в конец (рис. 1.10).
(рис. 1.10).
Определение 4.Произведением
вектора  на число
на число 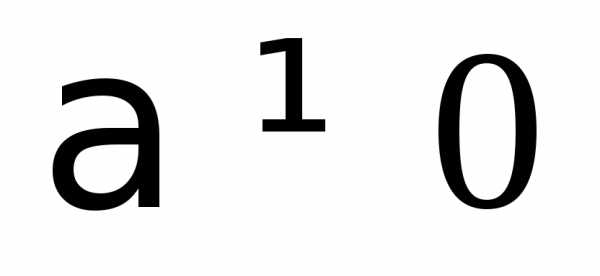 назовем вектор
назовем вектор  ,
удовлетворяющий следующим трем условиям:
,
удовлетворяющий следующим трем условиям:
 коллинеарен
коллинеарен  ;
; ;
;направление
 совпадает с направлением
совпадает с направлением  ,
если
,
если ,
и противоположно ему, если
,
и противоположно ему, если .
.
Под произведением вектора  на
на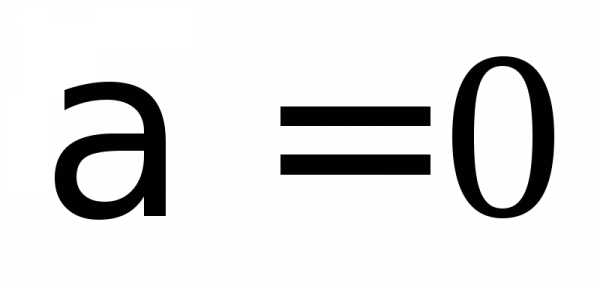 будем понимать нулевой вектор
будем понимать нулевой вектор .
.
Запись: 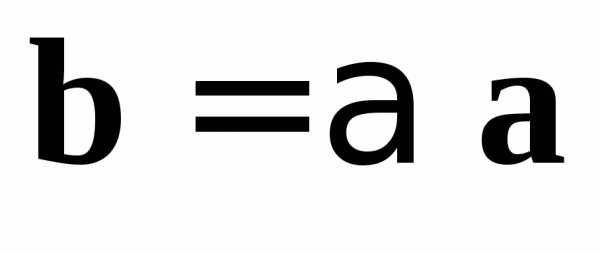 .
.
З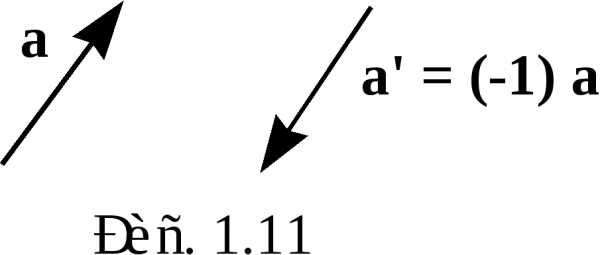 амечание
4.Вектор
амечание
4.Вектор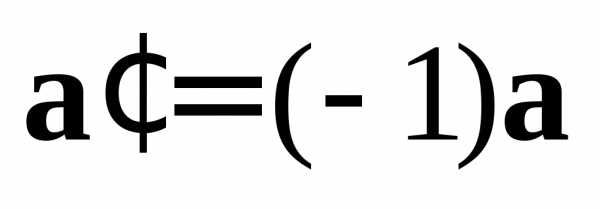 имеет длину такую же, как вектор
имеет длину такую же, как вектор (),
и направление, противоположное направлению
(),
и направление, противоположное направлению (так как число
(так как число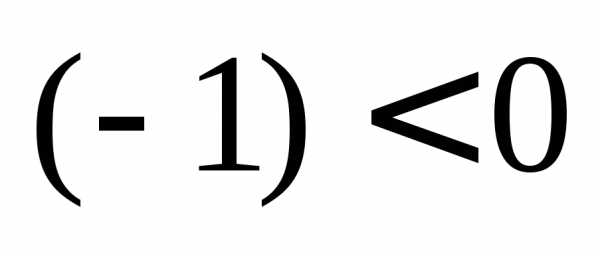 ).
).
Вектор  называется противоположным для вектора
называется противоположным для вектора (рис. 1.11).
(рис. 1.11).
Замечание 5.Для любых векторов и
и ,
если
,
если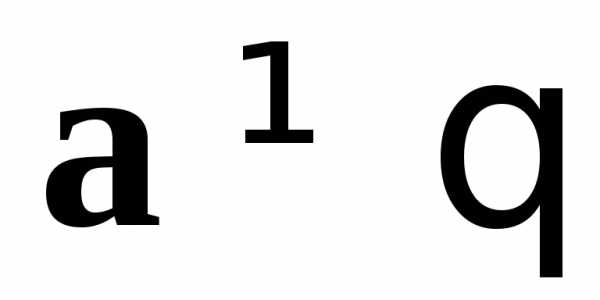 ,
,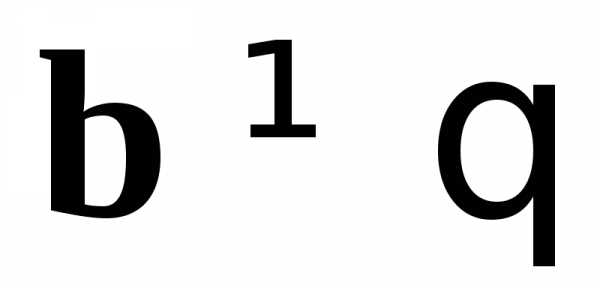 ,
равенство
,
равенство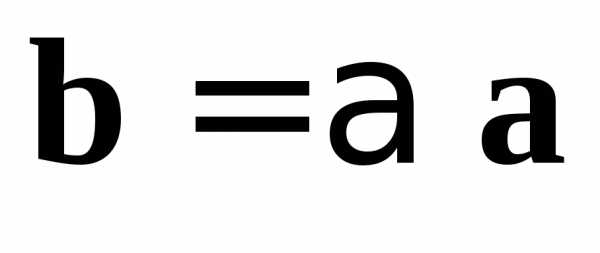 есть необходимое и достаточное условие
коллинеарности векторов
есть необходимое и достаточное условие
коллинеарности векторов и
и .
.
В самом деле, пусть 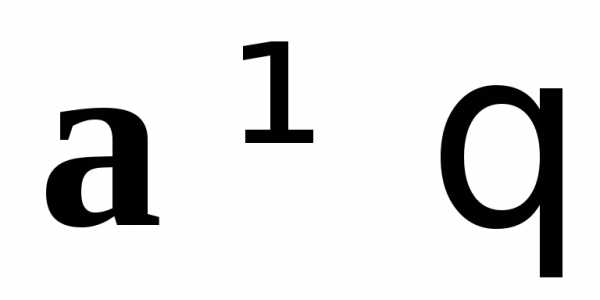 ,
,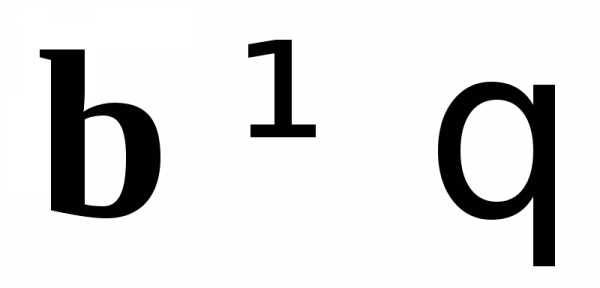 и
и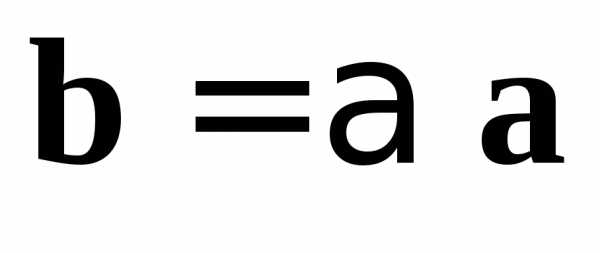 .
Тогда в соответствии с определением 4
.
Тогда в соответствии с определением 4 и
и коллинеарны.
коллинеарны.
Обратно. Пусть  и
и коллинеарны. Так как
коллинеарны. Так как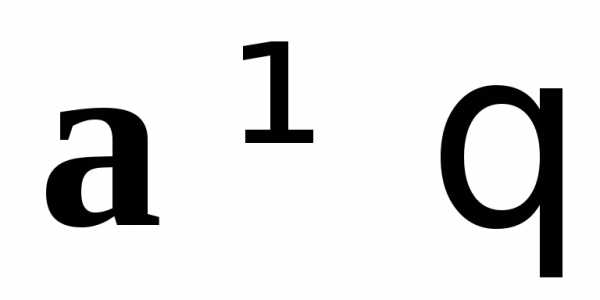 ,
, ,
можно рассмотреть векторы
,
можно рассмотреть векторы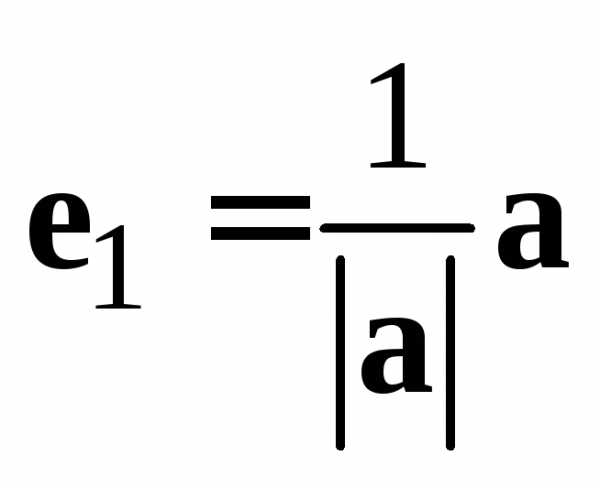 и
и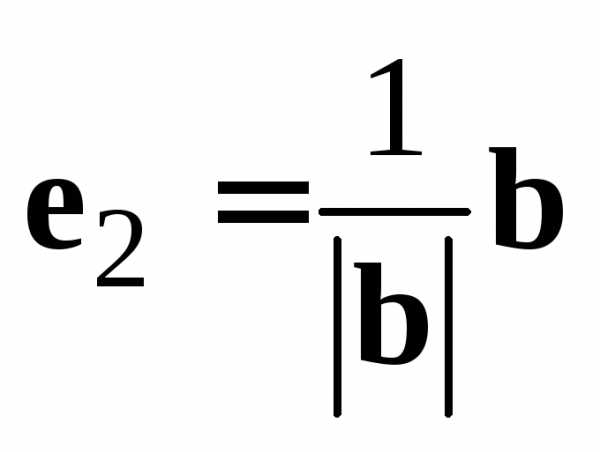 .
.
В соответствии с определением 4  и
и коллинеарны, аналогично
коллинеарны, аналогично и
и коллинеарны, но тогда
коллинеарны, но тогда и
и тоже коллинеарны.
тоже коллинеарны.
Имеем 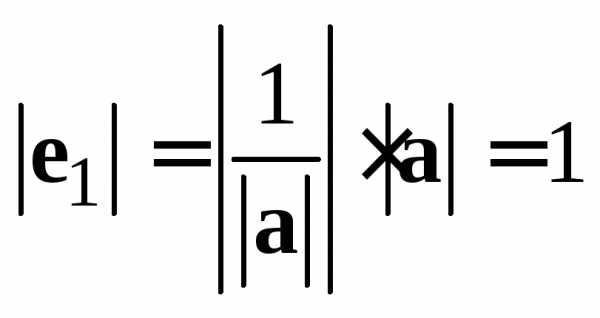 и
и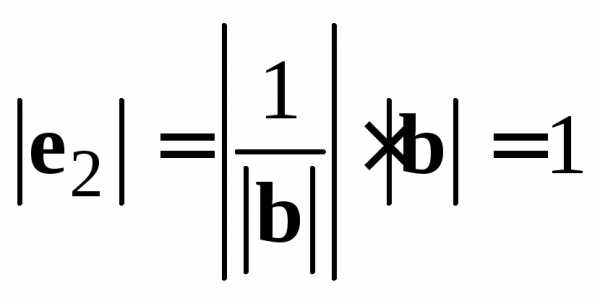 .
.
Таким образом, 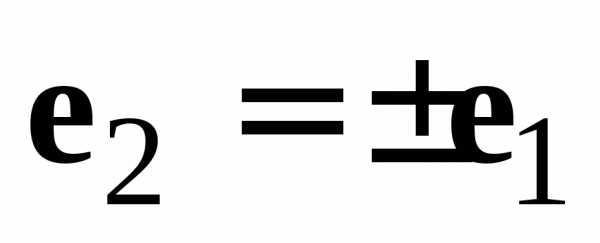 ,
т.е.
,
т.е.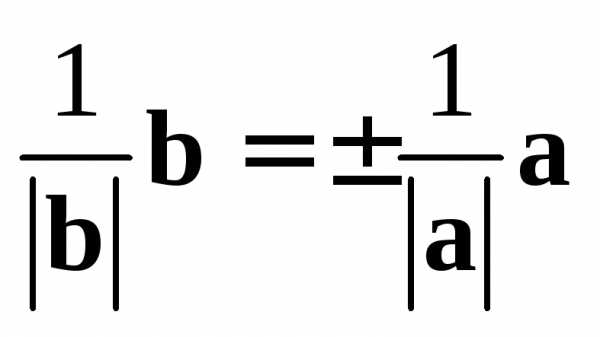 ,
или
,
или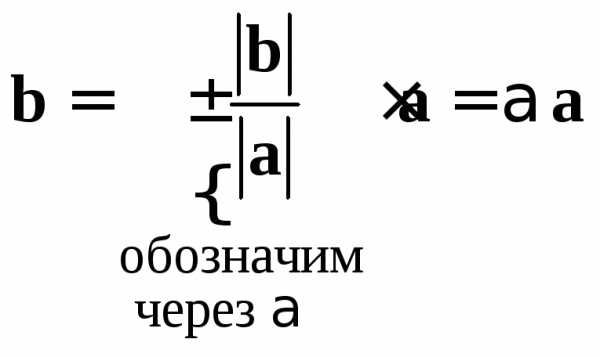 и
и оказывается равным вектору
оказывается равным вектору ,
умноженному на число
,
умноженному на число .
.
Отметим следующие свойства умножения вектора на число:
3) ;
4) ;
5) .
Доказательство свойства 3.
Приложим векторы  и
и к общему началу – произвольной точке
к общему началу – произвольной точке и построим на них как на сторонах
параллелограмм (рис. 1.12).
и построим на них как на сторонах
параллелограмм (рис. 1.12).
И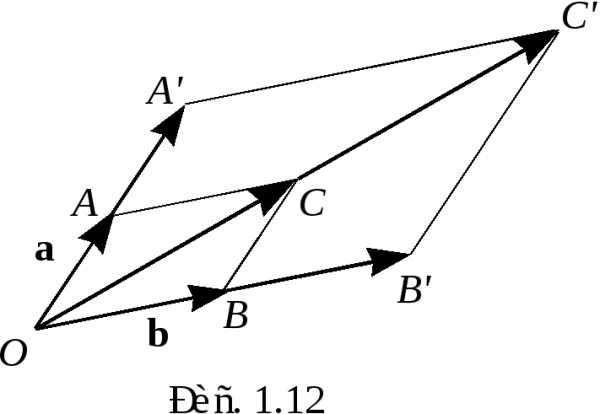 з
подобия треугольников
з
подобия треугольников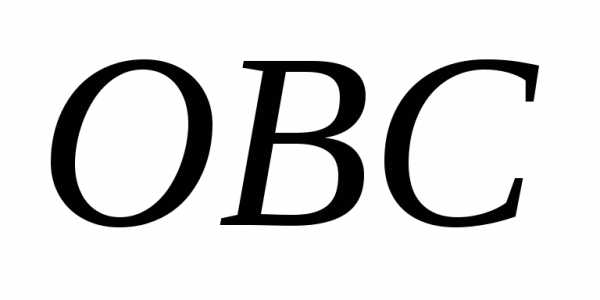 и
и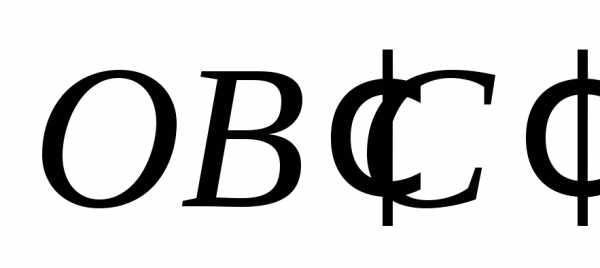 найдем
найдем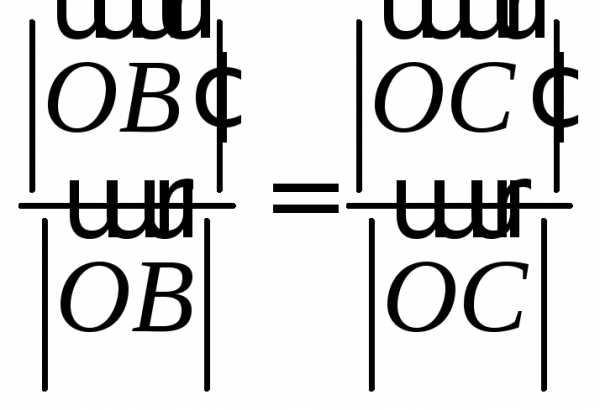 ,
но,
а тогда.
,
но,
а тогда.
С другой стороны, , и свойство 3 доказано.
Свойства 4 и 5 очевидны из наглядных геометрических соображений, и доказательство их опустим.
Совокупность всех геометрических
векторов с операциями сложения и
умножения на число будем называть пространством геометрических векторови обозначать .
.
studfiles.net
Векторы на плоскости и в пространстве: основные определения
Определение вектора
В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.
Для начала дадим определение:
Определение 1Вектор – это направленный отрезок прямой.
Yandex.RTB R-A-339285-1Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.
В математике для обозначения вектора обычно используют строчные латинские буквы, однако над вектором всегда ставится небольшая стрелочка, например a→. Если известны граничные точки вектора – его начало и конец, к примеру A и B, то вектор обозначается так AB→.
Нулевой вектор
Определение 2Под нулевым вектором 0→ будем понимать любую точку плоскости или пространства.
Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.
Длина вектора
Определение 3Под длиной вектора AB→ понимается число, большее либо равное 0, и равное длине отрезка АВ.
Длину вектораAB→ принято обозначать так AB→.
Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.
Коллинеарность векторов
Определение 4Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.
Определение 5Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.
zaochnik.com
Семинар 9
Операции над векторами, скалярное, векторное и смешанное произведения векторов.
Вводная информация
I. Геометрический вектор.
Определение. Вектором (геометрическим
вектором)
называется направленный прямолинейный
отрезок, т.е. отрезок, имеющий определенную
длину и определенное направление. Если  — начало вектора, а
— начало вектора, а — его конец, то вектор обозначается
символом
— его конец, то вектор обозначается
символом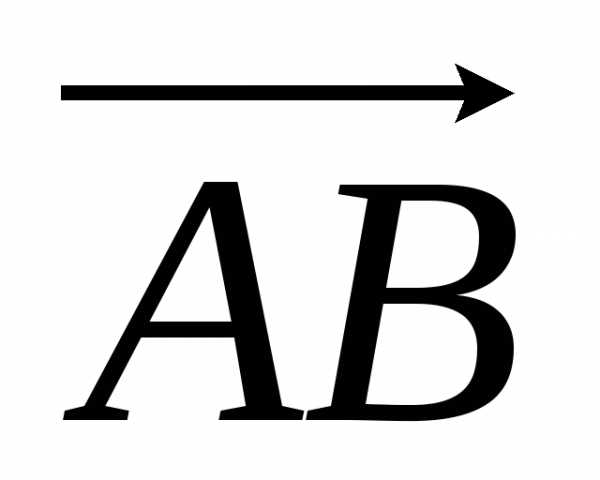 или
или .
Вектор
.
Вектор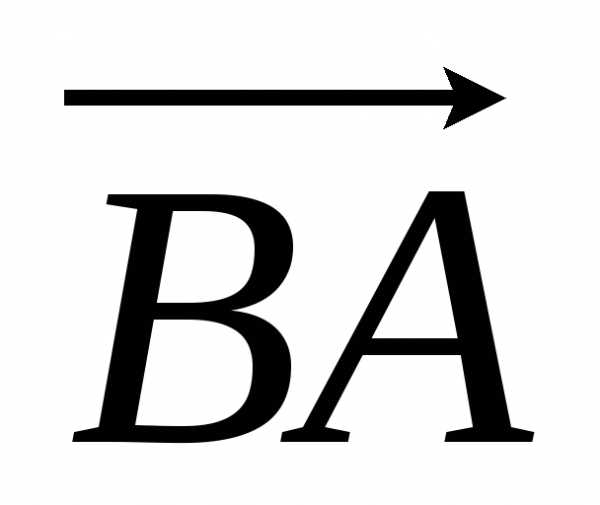 (
(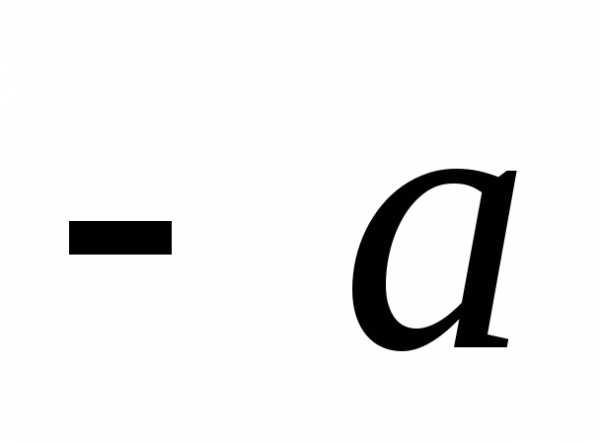 )
называетсяпротивоположным вектору
)
называетсяпротивоположным вектору 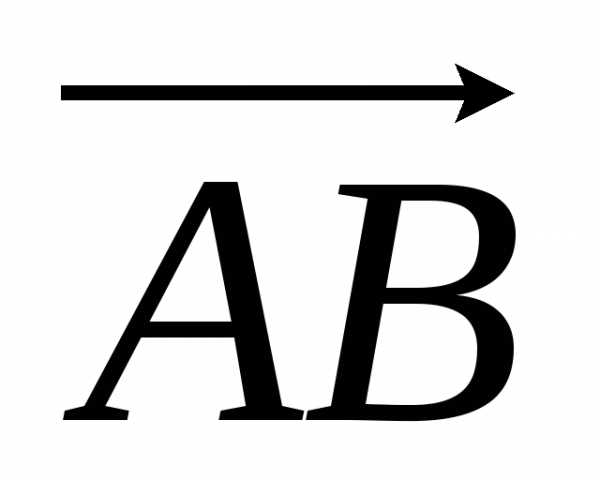 .
.
Длиной вектора
или его модулем называется длина отрезка и обозначается 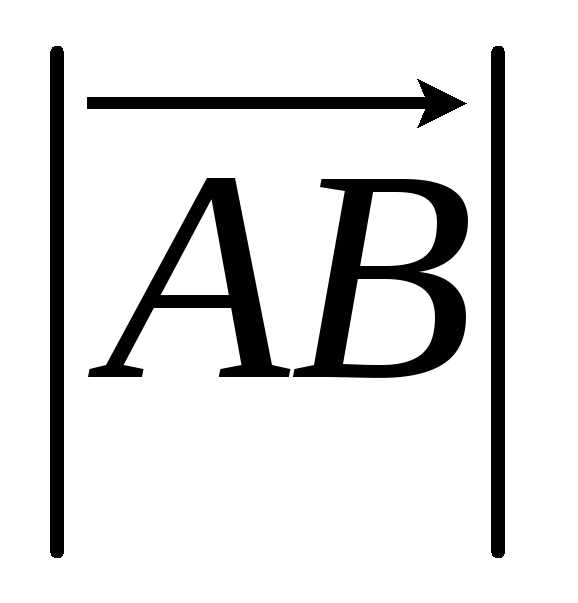 .
Вектор, длина которого равна нулю,
называетсянулевым
вектором и
обозначается
.
Вектор, длина которого равна нулю,
называетсянулевым
вектором и
обозначается 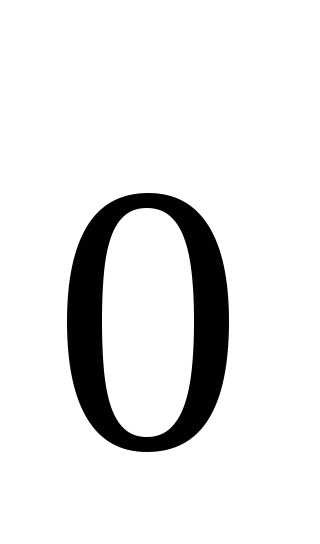 .
Вектор, длина которого равна единице,
называетсяединичным
вектором.
Единичный вектор, направление которого
совпадает с направлением вектора
.
Вектор, длина которого равна единице,
называетсяединичным
вектором.
Единичный вектор, направление которого
совпадает с направлением вектора  ,
называетсяортом этого
вектора и обозначается
,
называетсяортом этого
вектора и обозначается 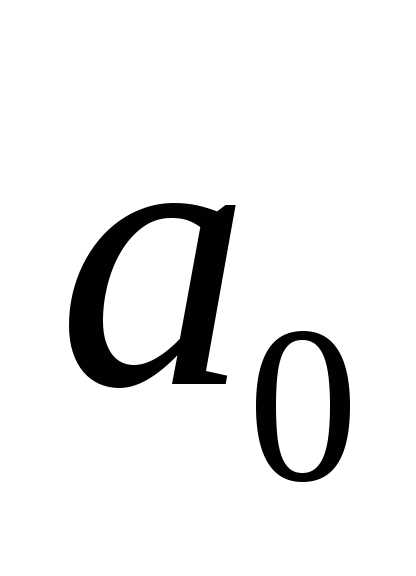 .
.
Векторы  и
и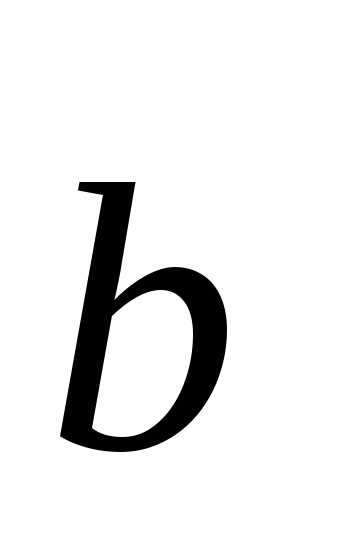 называютсяколлинеарными, если они
лежат на одной прямой или на параллельных
прямых. Для
коллинеарных векторов принято обозначение
называютсяколлинеарными, если они
лежат на одной прямой или на параллельных
прямых. Для
коллинеарных векторов принято обозначение 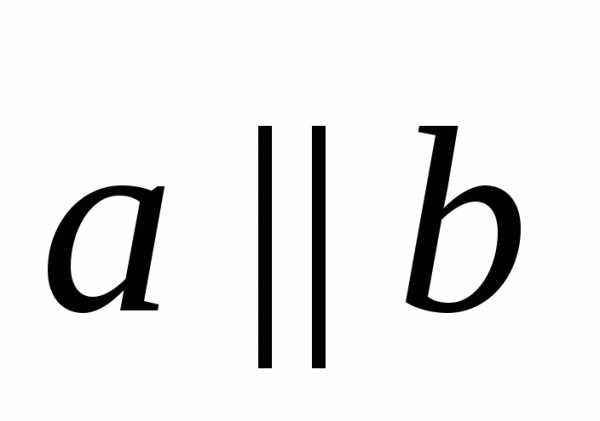 .
Два вектора называютсяравными (
.
Два вектора называютсяравными (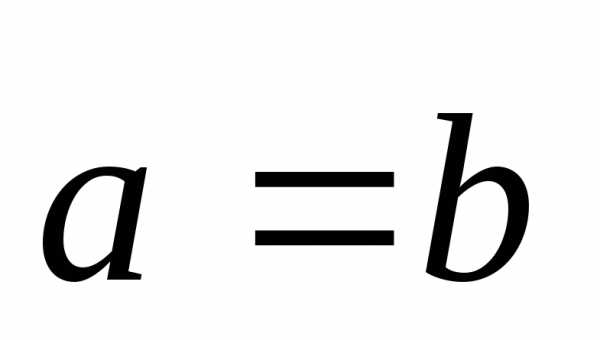 ),
если они одинаково направлены и имеют
одинаковые длины. Три вектора в
пространстве называютсякомпланарными,
если они лежат в одной плоскости или в
параллельных плоскостях.
),
если они одинаково направлены и имеют
одинаковые длины. Три вектора в
пространстве называютсякомпланарными,
если они лежат в одной плоскости или в
параллельных плоскостях.
II. Операции над векторами.
На множестве
векторов вводится бинарная операция,
которая называется сложением векторов. Эту операцию можно определить
либо правилом
параллелограмма (если
векторы 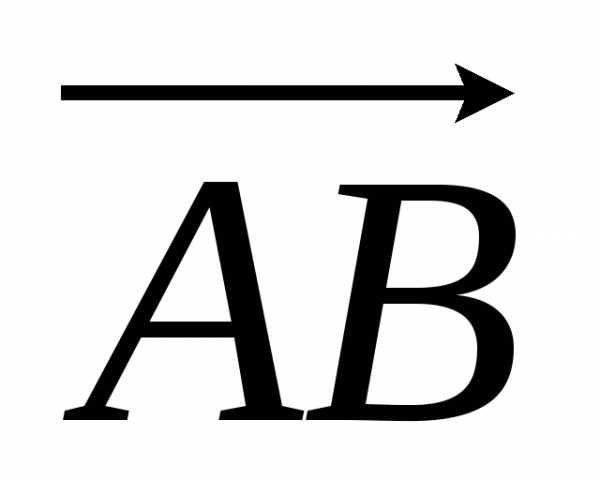 и
и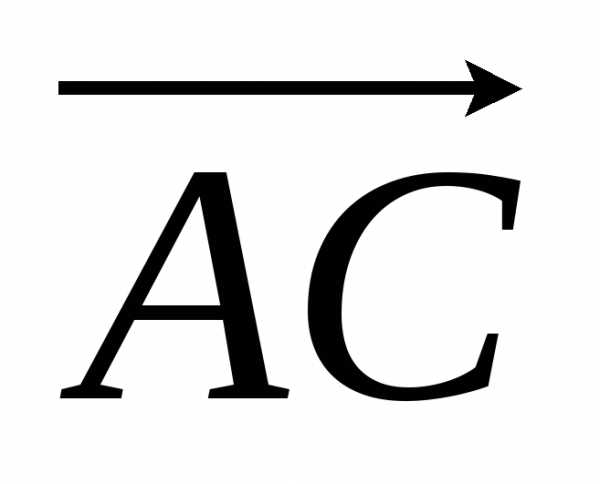 ,
являются сторонами параллелограмма,
то их суммой будет вектор
,
являются сторонами параллелограмма,
то их суммой будет вектор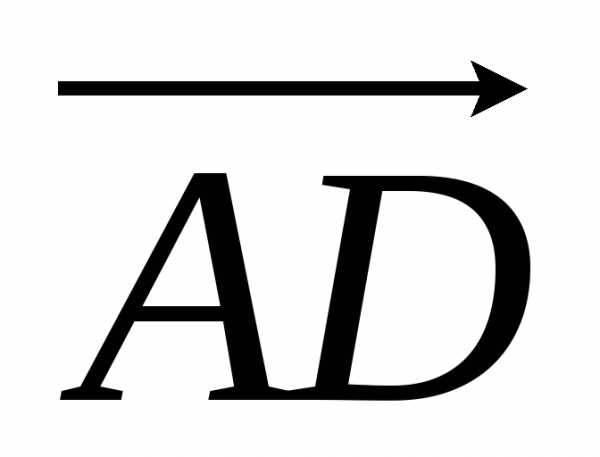 ,
где
,
где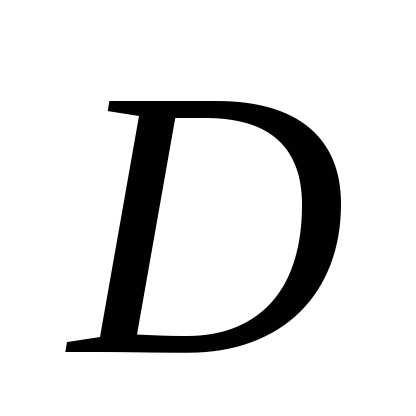 — четвертая вершина параллелограмма),
либо правиломтреугольника (если
векторы
— четвертая вершина параллелограмма),
либо правиломтреугольника (если
векторы 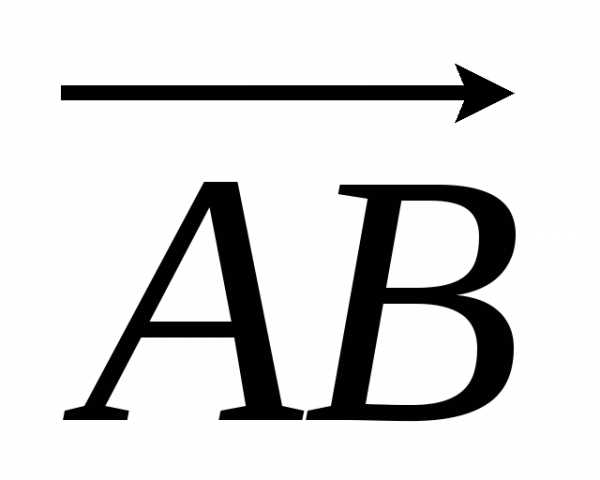 и
и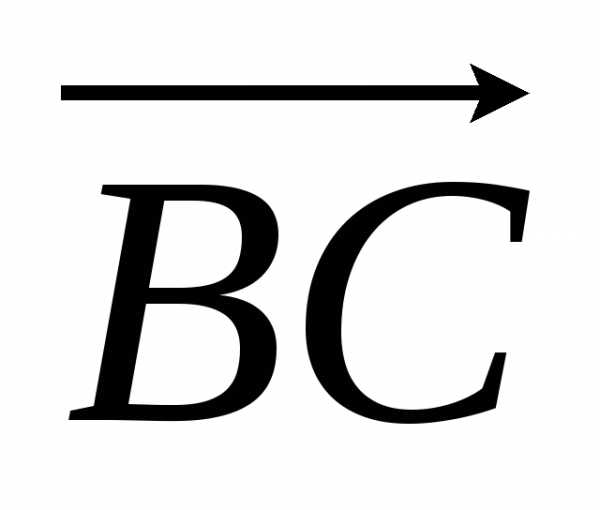 являются сторонами треугольника, то их
суммой называют вектор
являются сторонами треугольника, то их
суммой называют вектор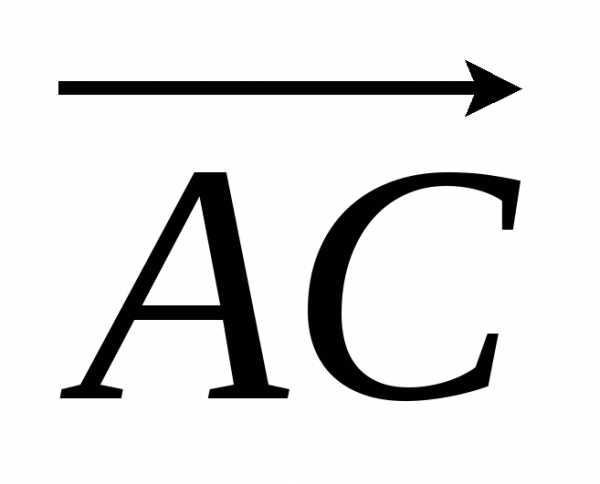 ).
).
Легко убедиться в следующих свойствах этой бинарной операции на множестве векторов:
1) ;
2) ; 3);
4) .
Следовательно, относительно сложения множество векторов образует абелеву группу.
Произведением
вектора  на число
на число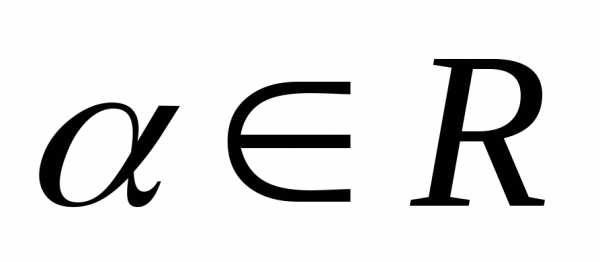 называется вектор
называется вектор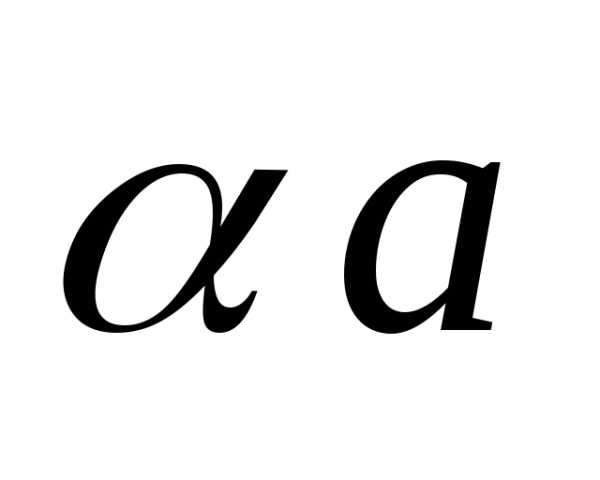 ,
который имеет длинуи направление вектора
,
который имеет длинуи направление вектора ,
если
,
если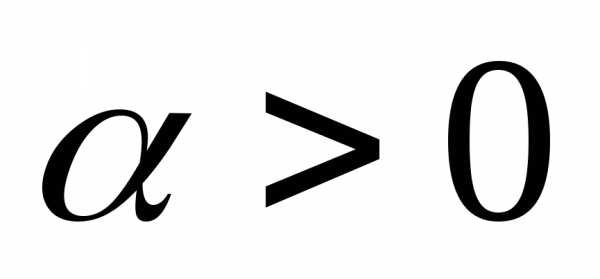 ;
направление противоположного вектора
к
;
направление противоположного вектора
к ,
если
,
если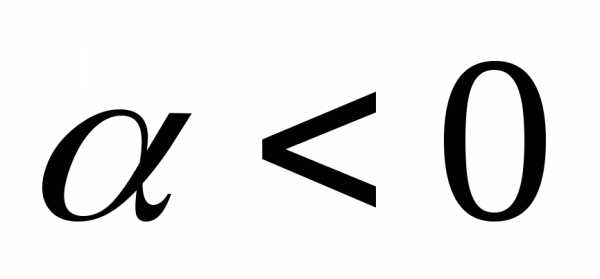 .
Отметим, что
.
Отметим, что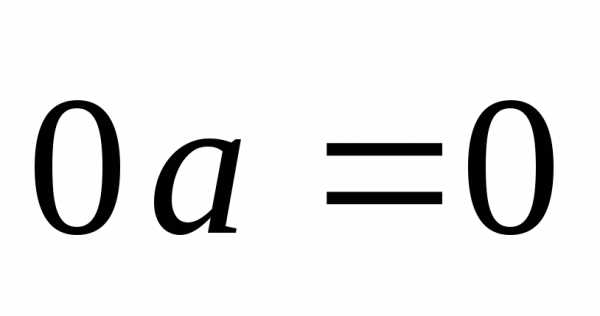 .
.
Произведение вектора на число обладает свойствами:
1) ;
2) ;
3) .
Множество
геометрических векторов  с
введенными на нем операциями называетсявекторным
пространством.
с
введенными на нем операциями называетсявекторным
пространством.
III. Координаты вектора.
Рассмотрим
пространство  с введенной на нем декартовой системой
координат. Пусть
с введенной на нем декартовой системой
координат. Пусть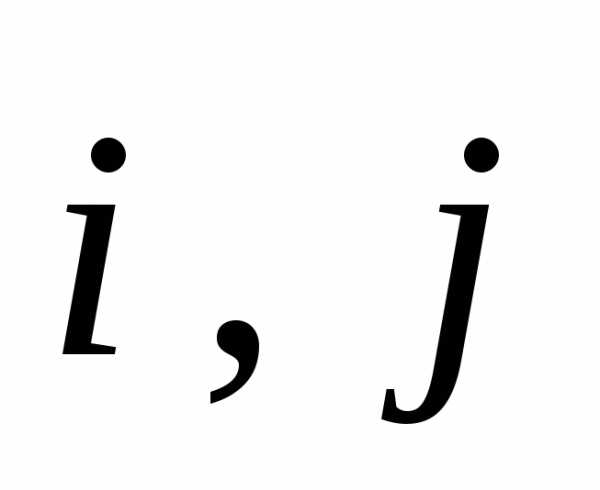 и
и —
три единичных вектора, исходящих из
начала координат в направлениях
соответственно декартовых осей
—
три единичных вектора, исходящих из
начала координат в направлениях
соответственно декартовых осей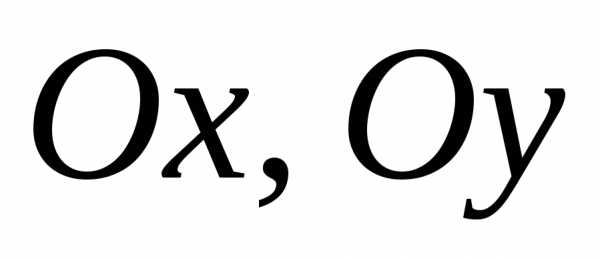 и
и .
Эти векторы называютсяортами
координатных осей. Пусть вектор
.
Эти векторы называютсяортами
координатных осей. Пусть вектор  имеет начало также в точке(начале координат). Спроектируем конец
вектора
имеет начало также в точке(начале координат). Спроектируем конец
вектора на координатные оси. Полученные проекции
можно записать в видеи,
где
на координатные оси. Полученные проекции
можно записать в видеи,
где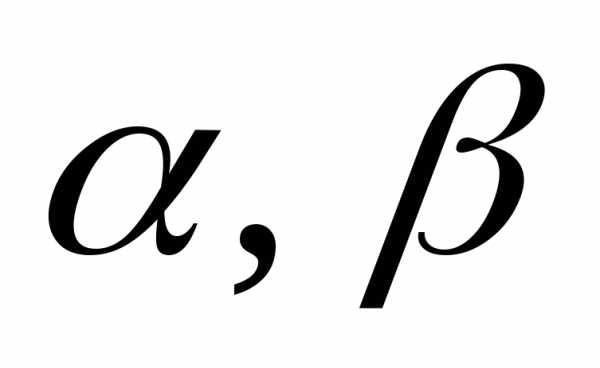 и
и — углы, которые образует вектор
— углы, которые образует вектор соответственно с координатными осями
соответственно с координатными осями и
и .
Числаи
.
Числаи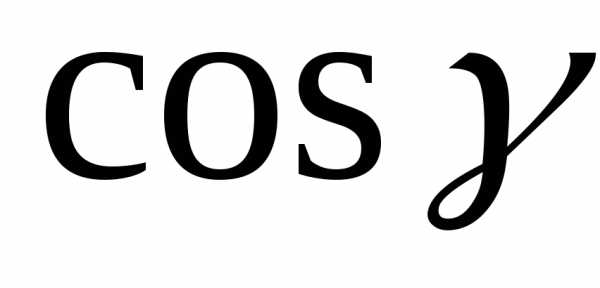 называютсянаправляющими
косинусами вектора
называютсянаправляющими
косинусами вектора  .
Вектор
.
Вектор и его проекции на координатные оси
удовлетворяют равенству
и его проекции на координатные оси
удовлетворяют равенству
.
Тройка векторов 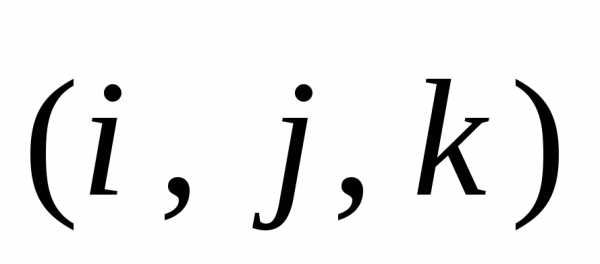 называетсябазисом
векторного пространства
называетсябазисом
векторного пространства  ,
а написанное выше равенство – разложением
вектора
,
а написанное выше равенство – разложением
вектора  по базису
по базису .
При этом числа
.
При этом числа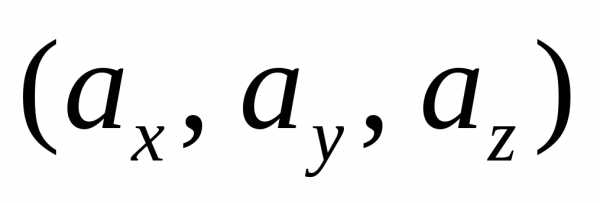 носят названиекоординат вектора
носят названиекоординат вектора  относительно базиса
относительно базиса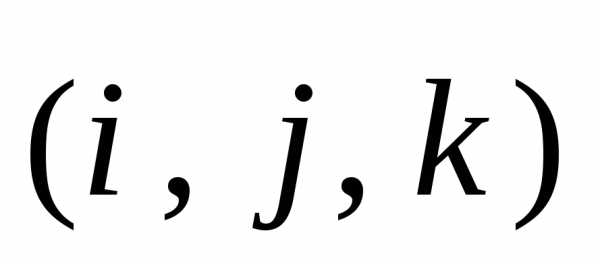 .
Поскольку координаты вектора
.
Поскольку координаты вектора относительно данного базиса являются
проекциями этого вектора на координатные
оси, длина вектора и его координаты
связаны формулой
относительно данного базиса являются
проекциями этого вектора на координатные
оси, длина вектора и его координаты
связаны формулой
.
Подставляя в эту формулу координаты вектора, выраженные через направляющие косинусы, легко получить равенство
,
которому удовлетворяют
направляющие косинусы любого вектора.
Заметим, что направляющие косинусы
являются координатами орта вектора 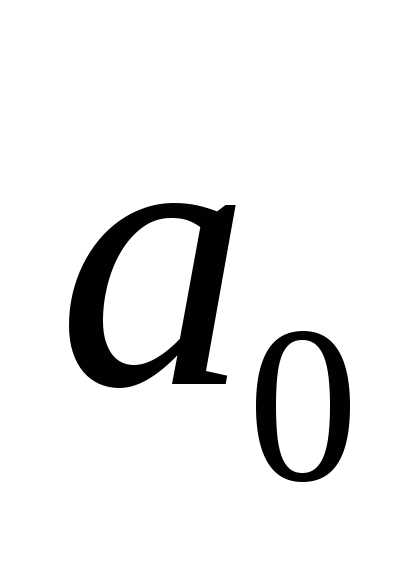 .
.
Поскольку
координаты вектора 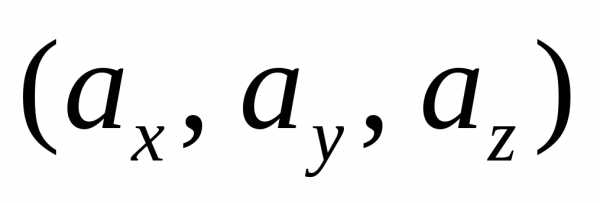 полностью его определяют, можно ввести
обозначениеи заменить введенные операции над
векторами операциями над их координатами.
Так сложение векторов
полностью его определяют, можно ввести
обозначениеи заменить введенные операции над
векторами операциями над их координатами.
Так сложение векторов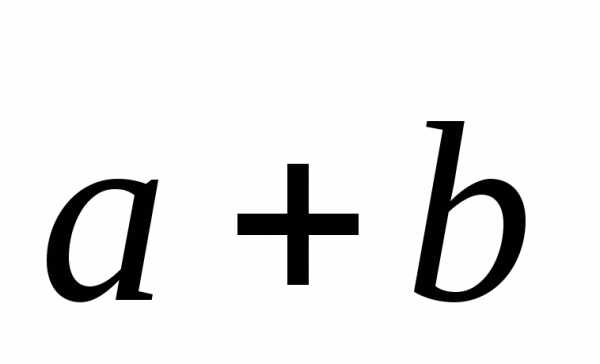 можно заменить сложением их координат:,
т.е.,
можно заменить сложением их координат:,
т.е.,
а умножение вектора
на число 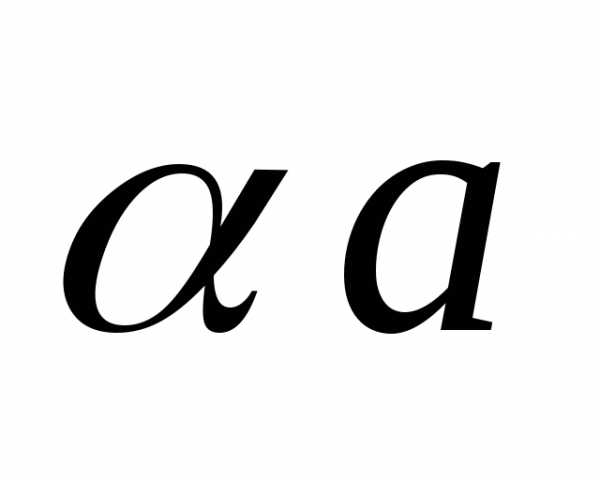 — умножением координат на это число:или.
— умножением координат на это число:или.
Равенство векторов 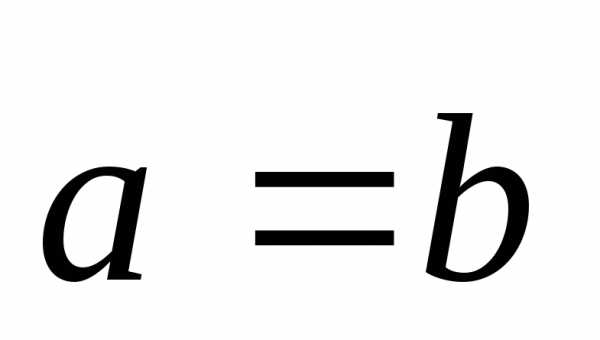 на координатном языке предполагает
равенство их координат,
а коллинеарность
на координатном языке предполагает
равенство их координат,
а коллинеарность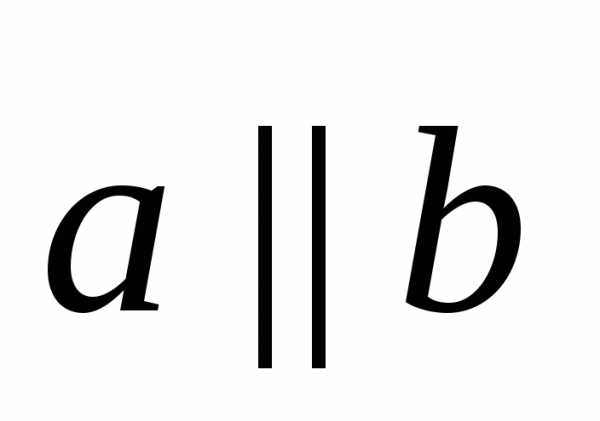 — пропорциональность их координат
— пропорциональность их координат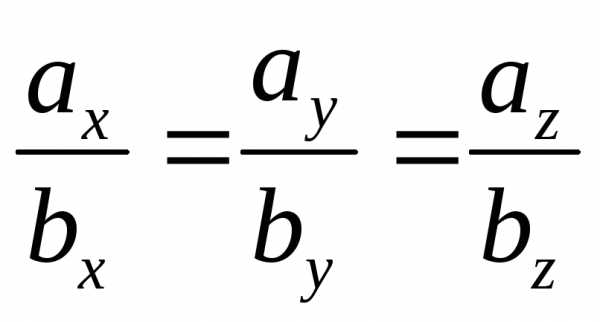 .
.
Пусть имеются
две точки
и.
Тогда вектор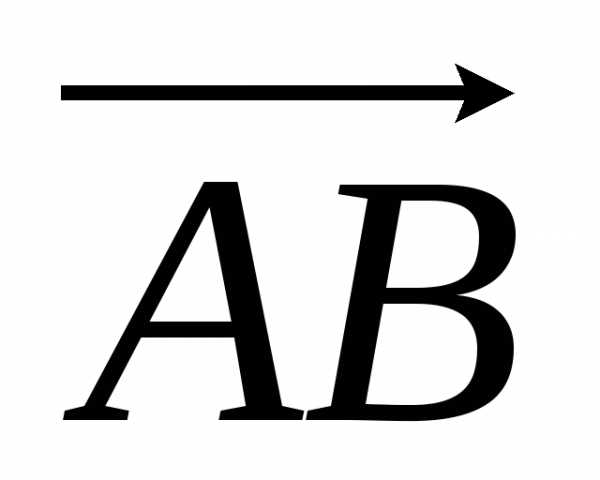 можно записать в видеили.
В частности, длярадиус-вектора точки
имеем формулыили.
можно записать в видеили.
В частности, длярадиус-вектора точки
имеем формулыили.
studfiles.net
2.1. Начальные сведения о векторах. Понятие геометрического вектора
Определение 5. Геометрический вектор — это направленный отрезок прямой на плоскости или в пространстве, у которого один конец (точка ) называется началом вектора, другой конец (точка ) концом вектора.
Обозначения вектора: или . Вектор характеризуется Длиной (или Модулем) и направлением: от к . Модуль вектора равен длине отрезка и обозначается или .
Определение 6. Вектор называется вектором, Противоположным Вектору . Вектор называется Нулевым, если он имеет нулевую длину.
Очевидно, модули противоположного и исходного векторов равны. У нулевого вектора начало и конец совпадают. Нулевому вектору приписывают любое направление.
Определение 7. Два вектора называются Коллинеарными, если они лежат на одной прямой или на параллельных прямых. Два коллинеарных вектора называются Одинаково (Противоположно) Направленными, если их концы лежат по одну сторону (по разные стороны) от прямой, соединяющей их начала, или от общего начала. Если вектора и одинаково (противоположно) направлены, мы будем писать: (). Если вектора и коллинеарны, мы будем писать: .
Определение 8. Два вектора называются Равными, если они имеют равные длины и одинаково направлены (т. е. , если и ). Все нулевые векторы считаются равными.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Компланарные векторы — урок. Геометрия, 10 класс.
Одно из определений компланарных векторов гласит:
векторы, которые параллельны одной плоскости или лежат на одной плоскости, называются компланарными векторами.
Тот же смысл имеет и другое определение:три вектора называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.
Обрати внимание!
Всегда возможно найти плоскость, параллельную двум произвольным векторам, поэтому любые два вектора всегда компланарные.
Eсли из трёх векторов два коллинеарны, то очевидно, что эти три вектора компланарны.
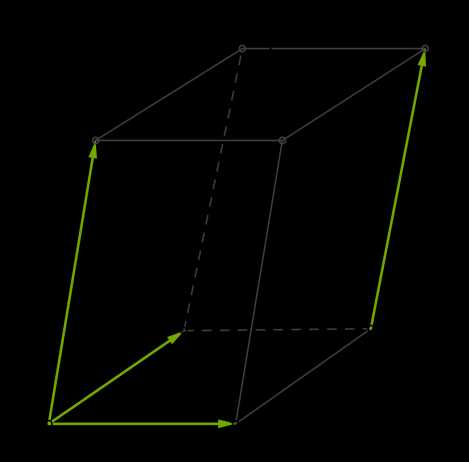
Все вышеупомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда.
1. Любые два вектора находятся в одной плоскости, но в одной плоскости можно разместить и векторы AA1→, CC1→ и AD→, то есть, эти векторы компланарны. Также компланарны векторы AA1→, AB→ и CC1→, так как два из этих векторов параллельны. Легко представить, что если привести их к общему началу, то вектор CC1→ совпадёт с вектором AA1→.
2. Например, векторы AB→, AD→ и AA1→ не компланарны, так как их нельзя разместить в одной и той же плоскости.
Признак компланарности трёх векторов:
пусть векторы a→ и b→ не коллинеарны. Если для вектора c→ существует единственная пара реальных чисел \(x\) и \(y\), такая, что c→=x⋅a→+y⋅b→, то векторы a→, b→ и c→ компланарны.
Справедливо и обратное утверждение:
если три вектора a→, b→ и c→ компланарны и векторы a→ и b→ не коллинеарны, то вектор c→ можно разложить по векторам a→ и b→ одним-единственным образом.
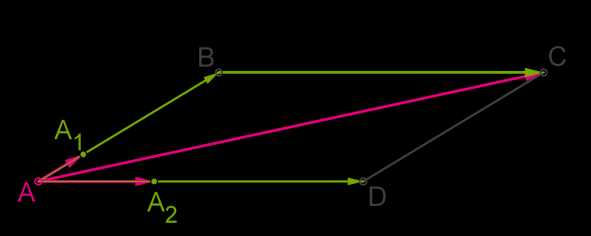
Если разложить вектор AC→ по векторам AA1→ и AA2→, то это можно сделать одним-единственным образом: AC→=AB→+AD→=x⋅AA1→+y⋅AA2→.
Закон параллелепипеда
Если три вектора не компланарны, то для их сложения в пространстве применяет закон параллелепипеда.
1. Векторы приводят к общему началу \(A\).
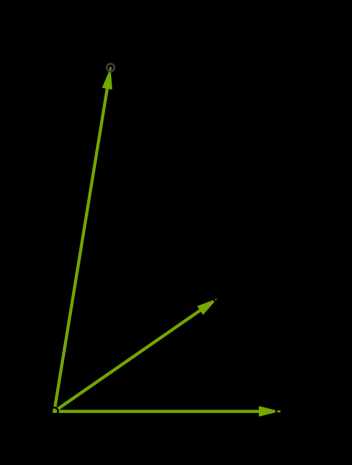
2. На этих трёх рёбрах строит параллелепипед.
3. Диагональ параллелепипеда, которая выходит из этой же точки, изображает суммы векторов AB→, AD→ и AA1→.
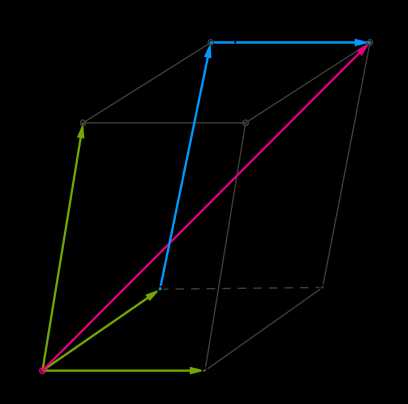
Разложение вектора по трем не компланарным векторам
Теорема о разложении по базису в пространстве
Любой вектор d→ можно разложить по трём данным не компланарным векторам a→, b→ и c→, причём реальные коэффициенты разложения \(x\), \(y\) и \(z\) определяются единственным образом: AC1→=AD→+AB→+AA1→=x⋅AA2→+y⋅AA3→+z⋅AA4→.
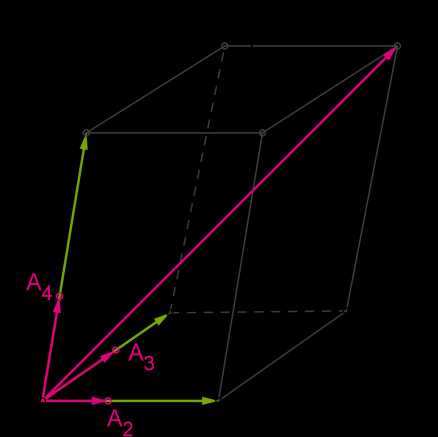
www.yaklass.ru
Векторы, графическое изображение векторов, величина вектора, направление вектора
Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.
Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.
Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,
В контексте векторов мы применяем = чтобы обозначить их равность.
Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.
Решение Сначала мы находим длину каждого вектора с использованием формулы расстояния:
|u| = √[2 — (-1)]2 + (4 — 3)2 = √9 + 1 = √10,
|| = √[0 — (-3)]2 + [0 — (-1)]2 = √9 + 1 = √10,
|w| = √(4 — 1)2 + [-1 — (-2)]2 = √9 + 1 = √10.
Отсюда
|u| = | = |w|.
Векторы u, , и w, как видно из рисунка, вроде бы имеют одно и то же направление, но мы проверим их наклон. Если прямые, на которых они находятся, имеют одинаковые наклоны, то векторы имеют одно и то же направление. Рассчитываем наклоны:
Так как u, , и w имеют равные величины и одно и то же напраывление,
u = = w.
Имейте в виду, что равность векторов требует только одинаковой величины и одинакового направления, а не расположения в одном месте. На самом верхнем рисунке — пример равности векторов.
Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.
В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.
Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =
Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.
Если две силы F1 и F2 действуют на один объект, результирующая сила есть сумма F1 + F2 этих двух отдельных сил.
Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.
Решение Нарисуем условие задачи, в этом случае — прямоугольник, используя v или для представления результирующей. Чтобы найти ее величину, используем теорему Пифагора:
|v|2 = 152 + 252 Здесь |v| обозначает длину или величину v.
|v| = √152 + 252
|v| ≈ 29,2.
Чтобы найти направление, отметим, что так как OAB есть прямым углом,
tanθ = 15/25 = 0,6.
Используя калькулятор, мы находим θ, угол, который большая сила образует с результирующей силой:
θ = tan— 1(0,6) ≈ 31°
Результирующая имеет величину 29,2 и угол 31° с большей силой.
Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть
www.math10.com

 коллинеарен
коллинеарен  ;
;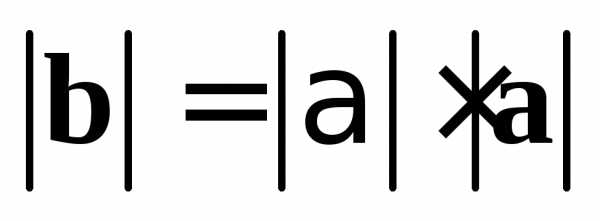 ;
; совпадает с направлением
совпадает с направлением  ,
если
,
если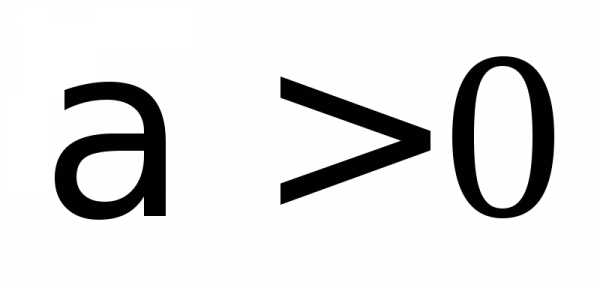 ,
и противоположно ему, если
,
и противоположно ему, если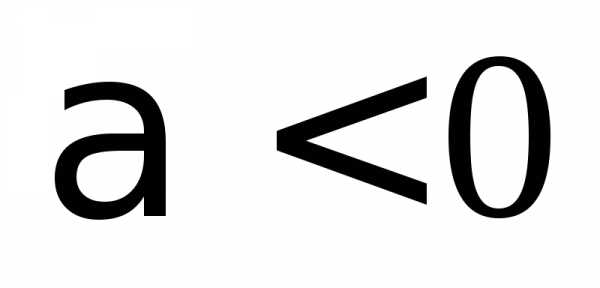 .
.