| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | Найти точное значение | sin(60 град. ) | |
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
Обратные тригонометрические функции, их свойства и графики.
Обратные тригонометрические функции (арксинус, арккосинус, арктангенс и арккотангенс) являются основным элементарным функциями. Часто из-за приставки «арк» обратные тригонометрические функции называют аркфункциями. Сейчас мы рассмотрим их графики и перечислим свойства.
Функция арксинус y = arcsin(x).
Изобразим график функции арксинус:
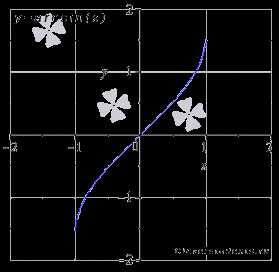
Свойства функции арксинус y = arcsin(x).
Областью определения функции арксинус является интервал от минус единицы до единицы включительно: .
Область значений функции y = arcsin(x): .
Функция арксинус — нечетная, так как .
Функция y = arcsin(x) возрастает на всей области определения, то есть, при .
Функция вогнутая при , выпуклая при .
Точка перегиба (0; 0), она же ноль функции.
Асимптот нет.
Функция арккосинус y = arccos(x).
График функции арккосинус имеет вид:
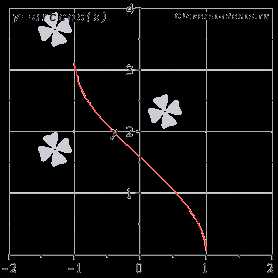
Свойства функции арккосинус y = arccos(x).
Область определения функции арккосинус: .
Область значений функции y = arccos(x): .
Функция не является ни четной ни нечетной, то есть, она общего вида.
Функция арккосинус убывает на всей области определения, то есть, при .
Функция вогнутая при , выпуклая при .
Точка перегиба .
Асимптот нет.
Функция арктангенс y = arctg(x).
График функции арктангенс имеет вид:
Свойства функции арктангенс y = arctg(x).
Функция арккотангенс y = arcctg(x).
Изобразим график функции арккотангенс:
Свойства функции арккотангенс y = arcctg(x).
studfiles.net
Обратные тригонометрические функции
Определение обратных тригонометрических функций
Поскольку тригонометрические функции периодичны, то обратные к ним функции не однозначны. Так, уравнение y = sin x, при заданном , имеет бесконечно много корней. Действительно, в силу периодичности синуса, если x такой корень, то и x + 2πn (где n целое) тоже будет корнем уравнения. Таким образом, обратные тригонометрические функции многозначны. Чтобы с ними было проще работать, вводят понятие их главных значений. Рассмотрим, например, синус: y = sin x. Если ограничить аргумент x интервалом , то на нем функция y = sin x монотонно возрастает. Поэтому она имеет однозначную обратную функцию, которую называют арксинусом: x = arcsin y.
Если особо не оговорено, то под обратными тригонометрическими функциями имеют в виду их главные значения, которые определяются следующими определениями.
Арксинус ( y = arcsin x ) – это функция, обратная к синусу ( x = sin y ), имеющая область определения и множество значений .
Арккосинус ( y = arccos x ) – это функция, обратная к косинусу ( x = cos y ), имеющая область определения и множество значений .
Арктангенс ( y = arctg x ) – это функция, обратная к тангенсу ( x = tg y ), имеющая область определения и множество значений .
Арккотангенс ( y = arcctg x ) – это функция, обратная к котангенсу ( x = ctg y ), имеющая область определения и множество значений .
Графики обратных тригонометрических функций
Графики обратных тригонометрических функций получаются из графиков тригонометрических функций зеркальным отражением относительно прямой y = x. См. разделы Синус, косинус, Тангенс, котангенс.
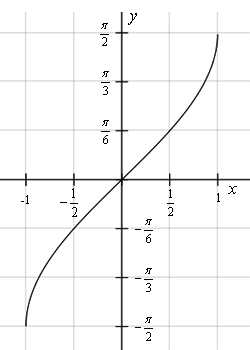
y = arcsin x
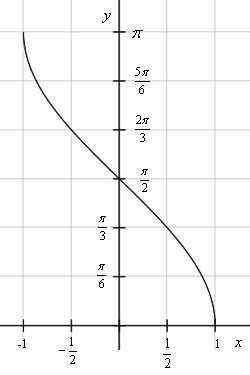
y = arccos x
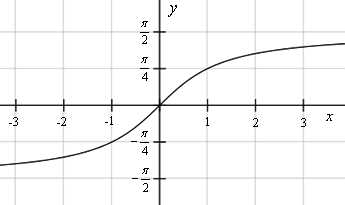
y = arctg x
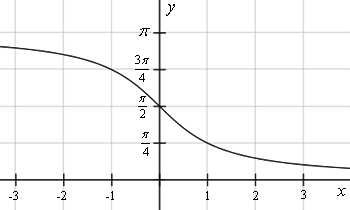
y = arcctg x
Основные формулы
Здесь следует особо обратить внимание на интервалы, для которых справедливы формулы.
arcsin(sin x) = x при
sin(arcsin x) = x
arccos(cos x) = x при
cos(arccos x) = x
arctg(tg x) = x при
tg(arctg x) = x
arcctg(ctg x) = x при
ctg(arcctg x) = x
Формулы, связывающие обратные тригонометрические функции
Формулы суммы и разности
при или
при и
при и
при или
при и
при и
при
при
при
при
при
при
при
при
при
при
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Методические разработки по теме: «Обратные тригонометрические функции»
Разделы: Математика
Тема: Обратные тригонометрические функции.
1. Функции. Определения. Графики и свойства
1.1 Функция у=arcsin x
Для тригонометрической функции Y = sin x, рассматриваемой в интервале , переход к однозначной обратной функции невозможен, так как одному значению у соответствует множество значений аргумента х. Поэтому обратная функция у = arcsin x при каждом значении х, лежащем на отрезке , имеет бесчисленное множество значений. При изучении функции, обратной синусу, выбирают отрезок , на котором функция Y= sin x возрастает, и рассматривают соответствующую этому отрезку обратную функцию у = аrcsin x, которую называют главным значением у = Arcsin x.
Определение 1. Обратной тригонометрической функцией у=arcsin x. называют дугу (угол) у, взятую на отрезке , синус которой равен х. ( Равенства у=Arcsin x и Х= sin у - эквивалентны).
Основные свойства функции у = аrcsin x.
1. Функция у = аrcsin x определена на отрезке, D(у).
2. На отрезке функция у = аrcsin x возрастает, E(у).
4. Функция у= аrcsin x называется главным значением у = arcsin x. Все значения дуг (углов) синус которых равен х, определяются формулой
Аrcsin x =(-1), где n . (1.1)
1.2. Функция у= arccos x.
Определение 2. Обратной тригонометрической функцией у=arccos x называют дугу (угол) у, взятую на отрезке , косинус которой равен х. (Равенство у=arccos x и cos y=x эквивалентны).
Основные свойства функции у=аrccos x.
1. Функция у=аrccos x определена на отрезке, D(у).
2. На отрезке функция у=аrccos x возрастает, E(у).
3. Функция у=аrccos x свойством нечетности и четности не обладает, справедливо равентсво arccos (-x) =
4. Функция у= аrccos x называется главным значением у= Аrccos x. Все значения дуг(углов)косинус которых равен х, определяются формулой
Аrcсos x =, где n . (1.2)
1.3 Функция у= arctg x
Определение 3. Обратной тригонометрической функцией у=arctg x. называют дугу (угол) у, взятую на отрезке , тангенс которой равен х. ( Равенства у=arctg x и Х= tg у - эквивалентны).
Основные свойства функции у = аrctg x.
1. Функция у=аrctg x определена на отрезке , D(у)= .
2. На отрезке функция у=аrctg x возрастает, E(у).
3. Функция у = аrctg x нечетная, аrctg (-x) = -аrctg (x).
4.Функция у = аrctg x называется главным значением функции у = Аrctg x. Все значения дуг (углов) синус которых равен х, определяются формулой x
Аrctg x =, где n . (1.3)
1.4 Функция у= arcctg x
Определение 4. Обратной тригонометрической функцией у=arcctg x называют дугу (угол) у, взятую на отрезке x, котангенс которой равен х. (Равенства у=arcсtg x и Х= сtg у – эквивалентны).
Основные свойства функции у=аrcсtg x.
1. Функция у = аrcctg x определена на отрезке , D(у)= .
2. На отрезке функция у = аrcсtg x убывает, E(у)=
3. Функция у = аrсctg x не обладает ни свойством четности, ни свойством нечетности, но для нее справедливо arcctg (-x)=
4.Функция у = аrcctg x называется главным значением у = Аrcctg x. Все значения дуг (углов) котангенс которых равен х, определяются формулой x
Аrcсtg x =, где n . (1.4)
2. Основные соотношения для обратных тригонометрических функций:
sin(arcsinx)=x, если (2.1)
cos(arccosx)=x, если (2.2)
tg(arctgx)=x, если (2.3)
ctg(arcctgx)=x, если (2.4)
arcsin(sinx)=x, если (2.5)
arcos(cosx)=x, если (2.6)
arctg(tgx)=x, если (2.7)
arcctg(ctgx)=x, если (2.8)
3. Применение свойств обратных тригонометрических функций.
1) Вычисление значений обратных тригонометрических функций разными способами: применяя свойства функций, тригонометрические формулы и графический способ. (Эти вопросы я рассматриваю в данной статье).
2) Решение уравнений, неравенств и систем, содержащих обратные тригонометрические функции.
3) Построение графиков, содержащих обратные тригонометрические функции.
4) Решение уравнений, систем, неравенств с параметром.
3.1 Вычислите:
1).
Дополнительно:
6).
7).
9)
3.1. Учитывая область значений аркфункций и формулы 2.5-2.8 , вычислите:
График фигуры Y=Arccos(cosx) .
главный- arccos(cosx)=x, если
y(10)= 4?-10 12,56-10=2,56, 2,56.(При условии, что )
12) arcsin(sin6)=
График фигуры Y=Arcsin(sin(x)) в приложении №1.
Учитывая, что главный арксинус имеет область значений тогда
arcsin(sinx)=x, если
Ответ: arcsin(sin6)=.
13) arctg(tg. Учитывая, что y=tgx имеет период , то
Ответ:.
Дополнительно:
14) ,
15) arcos(cos8)=3-8
16) arctg(tg4)=4-.
Для вычисления значений некоторых обратных тригонометрических функций удобно пользоваться следующими формулами
Докажем, данные формулы.
1) , .
2) arcsin z=, arccos z=.
4) Учитывая пункт 2), получим :
.
Аналогично доказывается и второе равенство.
3.2 Вычислить:
17)
Решение: ,
?-3 + arcos(sin3) = ,
Ответ: arcos(sin3) =3- .
18) Решение: arctg(tg)+arcctg(ctg)=,
arctg(tg)+ =,
Ответ: arctg(tg)= — .
Дополнительно:
19);
20);
21);
22) .
3.3. Вычислить, используя формулы двойного, тройного и половинного аргумента.
Дополнительно:
28) sin(2arctg3)=
29)
13.03.2006
xn--i1abbnckbmcl9fb.xn--p1ai
Функция arccos График функции y = arccosx
Функция arccos
График функции y = arccosx.
Арккосинусом числа m называется такой угол x, для которого
Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.
cos(arccosx) = x при
arccos(cosy) = y при
D(arccosx) = [ − 1;1], (область определения),
E(arccosx) = [0;π]. (область значений).
Свойства функции arccos
arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
arccosx > 0 при
arccosx = 0 при x = 1.
Получение функции arccos
Дана функция y = cosx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccosx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cosx строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccosx, график которой симметричен графику y = cosx на отрезке [0;π] относительно прямой y = x.
Функция arctg
График функции .
Арктангенсом числа m называется такой угол α, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
Получение функции arctg
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой y = x.
Функция arcctg
График функции y=arcctg x
Арккотангенсом числа m называется такой угол x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
Свойства функции arcctg
(график функции центрально-симметричен относительно точки
при любых x.
Получение функции arcctg
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция , график которой симметричен графику на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу
Функция arcsec
arcsec(x) = arccos(1/x)
Функция arccosec
arccosec(X) = arcsin(1/x)
Производные от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x≥1:
Разложение в бесконечные ряды
Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:
(член в сумме при n= 0 принимается равным 1).
Использование в геометрии
Прямоугольный треугольник ABC
Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например с помощью теоремы косинусов.
В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
МОУ Балабановская школа № 4
Т Р И Г О Н О М Е Т Р И Я
Выполнила: Баширова Вероника
Преподаватель: Заречкова Л.И.
2009 г.
Список литературы:
Большая советская энциклопедия
Энциклопедия Брокгауз и Ефрон
www.wikipedia.ru
bigpo.ru
Функция arccos График функции y = arccosx
Функция arccos
График функции y = arccosx.
Арккосинусом числа m называется такой угол x, для которого
Функция y = cosx непрерывна и ограничена на всей своей числовой прямой. Функция y = arccosx является строго убывающей.
cos(arccosx) = x при
arccos(cosy) = y при
D(arccosx) = [ − 1;1], (область определения),
E(arccosx) = [0;π]. (область значений).
Свойства функции arccos
arccos( − x) = π − arccosx (функция центрально-симметрична относительно точки
arccosx > 0 при
arccosx = 0 при x = 1.
Получение функции arccos
Дана функция y = cosx. На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y = arccosx функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения — [0;π]. На этом отрезке y = cosx строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π] существует обратная функция y = arccosx, график которой симметричен графику y = cosx на отрезке [0;π] относительно прямой y = x.Функция arctg
График функции .
Арктангенсом числа m называется такой угол α, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго возрастающей.
Получение функции arctg
Дана функция На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — На этом отрезке строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале существует обратная функция , график которой симметричен графику на отрезке относительно прямой y = x.Функция arcctg
График функции y=arcctg x
Арккотангенсом числа m называется такой угол x, для которого
Функция непрерывна и ограничена на всей своей числовой прямой. Функция является строго убывающей.
Свойства функции arcctg
(график функции центрально-симметричен относительно точки
при любых x.
Получение функции arcctg
Дана функция . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (0;π). На этом отрезке строго возрастает и принимает все свои значения только один раз, следовательно, на интервале (0;π) существует обратная функция , график которой симметричен графику на отрезке (0;π) относительно прямой y = x. График симметричен к арктангенсу
Функция arcsec
arcsec(x) = arccos(1/x)
Функция arccosec
arccosec(X) = arcsin(1/x)
Производные от обратных тригонометрических функций
Интегралы от обратных тригонометрических функций
Неопределённые интегралы
Для действительных и комплексных x:
Для действительных x≥1:
Разложение в бесконечные ряды
Для арктангенса используется также более быстро сходящийся ряд, открытый Леонардом Эйлером:
(член в сумме при n= 0 принимается равным 1).
Использование в геометрии
Прямоугольный треугольник ABC
В прямоугольном треугольнике, эти функции от отношений сторон сразу дают угол:
α = arcsin (a/c) = arccos (b/c) = arctg (a/b) = arccosec (c/a) = arcsec (c/b) = arcctg (b/a)
МОУ Балабановская школа № 4
Т Р И Г О Н О М Е Т Р И Я
Выполнила: Баширова Вероника
Преподаватель: Заречкова Л.И.
2009 г.
Список литературы:
Большая советская энциклопедия
Энциклопедия Брокгауз и Ефрон
www.wikipedia.ru
www.birmaga.ru
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Свойства функций
arcsin x + arccos x = /2
arctg x + arcctg x = /2 |
fgraphiks.narod.ru
