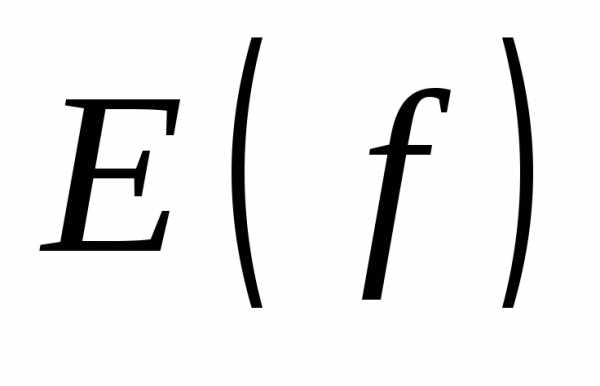Алгебра. Урок 5. Графики функций
Содержание страницы:
Система координат – это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчета для каждой из них.
Координатные оси – прямые, образующие систему координат.
Ось абсцисс (ось x ) — горизонтальная ось.
Ось ординат (ось y ) — вертикальная ось.

Функция — это отображение элементов множества X на множество Y. При этом каждому элементу x множества X соответствует одно единственное значение y множества Y.
Линейная функция – функция вида y=ax+b где a и b — любые числа.
Графиком линейной функции является прямая линия.
Рассмотрим, как будет выглядеть график в зависимости от коэффициентов a и b:
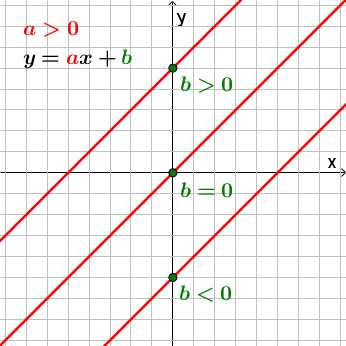
Если a>0, прямая будет проходить через I и III координатные четверти.
b — точка пересечения прямой с осью y.
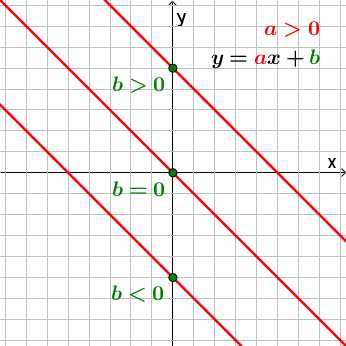
Если a<0, прямая будет проходить через II и IV координатные четверти.
b — точка пересечения прямой с осью y.
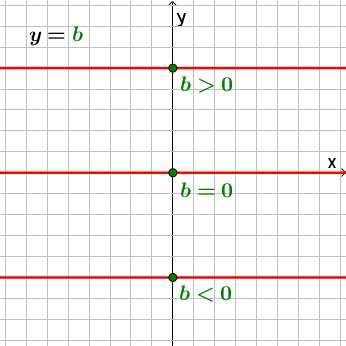
Если a=0, фукция принимает вид y=b.
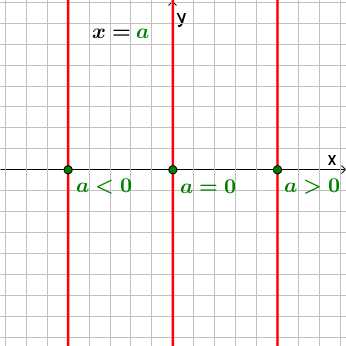
Отдельно выделим график уравнения x=a.
Важно: это уравнение не является функцией так как нарушается определение функции (функция ставит в соответствие каждому элементу x множества X одно единственно значение y множества Y). Данное уравнение ставит в соответствие одному элементу x бесконечное множества элементов y. Тем не менее, график данного уравнения построить можно. Просто не будем называть его гордым словом «Функция».
Графиком функции y=ax2+bx+c является парабола.
Для того, чтобы однозначно определить, как располагается график параболы на плоскости, нужно знать, на что влияют коэффициенты a,b,c:
- Коэффициент a указывает на то, куда направлены ветки параболы.
- Если a>0 , ветки параболы направлены вверх.
- Если a<0 , ветки параболы направлены вниз.
- Коэффициент c указывает, в какой точке парабола пересекает ось y.
- Коэффициент b помогает найти xв — координату вершины параболы.
xв=−b2a
- Дискриминант позволяет определить, сколько точек пересечения у параболы с осью .
- Если D>0 — две точки пересечения.
- Если D=0 — одна точка пересечения.
- Если D<0 — нет точек пересечения.
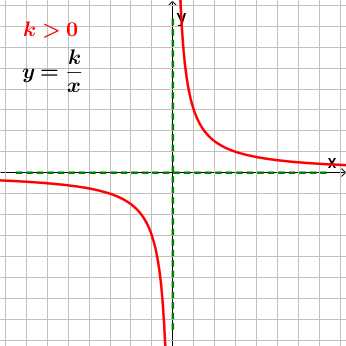
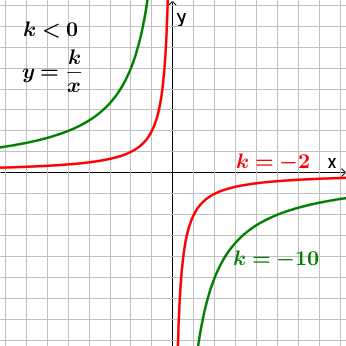
Графиком функции y=kx является гипербола.
Характерная особенность гиперболы в том, что у неё есть асимптоты.
Асимптоты гиперболы – прямые, к которым она стремится, уходя в бесконечность.
Ось x – горизонтальная асимптота гиперболы
Ось y – вертикальная асимптота гиперболы.
На графике асимптоты отмечены зелёной пунктирной линией.
Если коэффициент k>0, то ветви гиперолы проходят через I и III четверти.
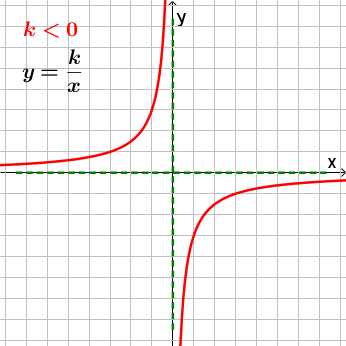
Если k < 0, ветви гиперболы проходят через II и IV четверти.
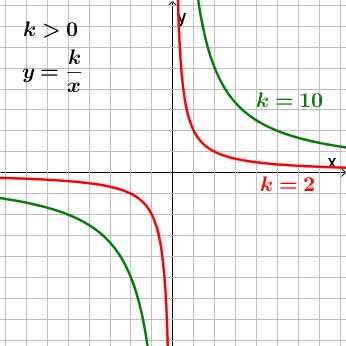
Чем меньше абсолютная величина коэффиента k (коэффициент k без учета знака), тем ближе ветви гиперболы к осям x и y.
Функция y = x имеет следующий график:
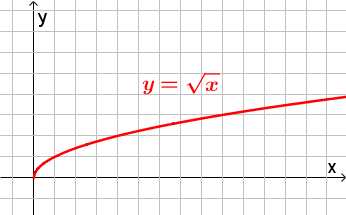
Функция y = f(x)возрастает на интервале, если большему значению аргумента (большему значению x) соответствует большее значение функции (большее значение y).
То есть чем больше (правее) икс, тем больше (выше) игрек. График поднимается вверх (смотрим слева направо)
Примеры возрастающих функций:
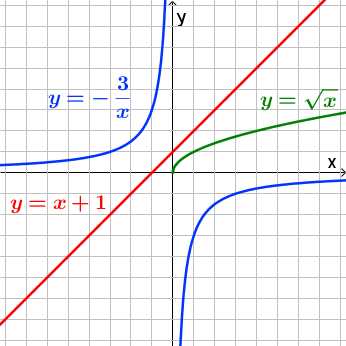
Функция y = f(x)убывает на интервале, если большему значению аргумента (большему значению x) соответствует меньшее значение функции (большее значение y).
То есть чем больше (правее) икс, тем меньше (ниже) игрек. График опускается вниз (смотрим слева направо).
Примеры убывающих функций:
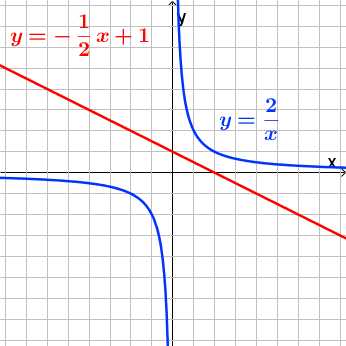
Для того, чтобы найти наибольшее значение функции, находим самую высокую точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наибольшим значением функции.
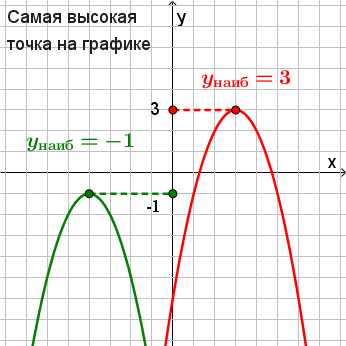
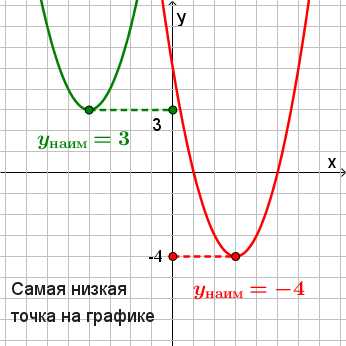
Для того, чтобы найти наименьшее значение функции, находим самую нижнюю точку на графике и смотрим, какая у нее координата по оси ординат (по оси y). Это значение и будет являться наименьшим значением функции.
Скачать домашнее задание к уроку 5.
epmat.ru
Общие свойства функций и построение графиков
График функции и его построение
Определение 1
Графиком функции $f(x)$ будет называться множество точек координатной плоскости, которые имеют вид $(x,\ f\left(x\right))$.
Схема для построения графиков функций:
- Найти $D(f)$ и $E(f)$.
- Исследовать на свойство четности и нечетности, а также на свойство периодичности.
- Найти пересечение с координатными осями и промежутки, на которых $f\left(x\right) >0$ и $f\left(x\right)
- Найти промежутки где функция возрастает и убывает, найти экстремумы.
- Найти интервалы выпуклости $и$ вогнутости функции.
- Вычислить пределы на границах $D(f)$.
- Найти дополнительные точках при необходимости.
- Изобразить график.
Четность и нечетность функции
Определение 2
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть четной, если для всех точек из множества $X$ будет выполняться
\[f\left(x\right)=f(-x)\]График этих функции будет подчиняться закону осевой симметрии по отношению к оси ординат (рис. 1).

Рисунок 1.
Определение 3
Функцию $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть нечетной, если для всех точек из множества $X$ будет выполняться
\[f\left(-x\right)=-f(x)\]График этих функции будет подчиняться закону центральной симметрии по отношению к началу координат (рис. 2).
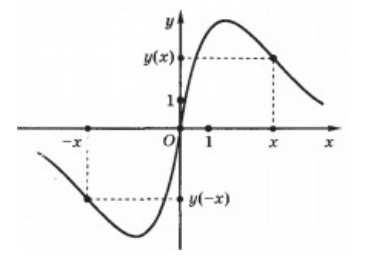
Рисунок 2.
Для исследования функции в её аналитической записи заменяют переменную $x$ на переменную $-x$, производят, при необходимости элементарные преобразования, и проверяют условия определений 2 и 3.
Возрастание и убывание функции
Определение 4
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть возрастающей, если подставив любые две точки получим, что$»$ будет верно $f(x’)
Определение 5
Функция $y=f(x)$, которая имеет своей областью определения множество $X$, будем называть убывающей, если подставив любые две точки получим, что будет верно $f\left(x’\right) >f(x»)$.
Чаще всего функции исследуют на возрастание и убывание с помощью средств математического анализа, а именно производной.
Приведем схему для такого исследования.
- Найти $D(f)$;
- Найти $f'(x)$;
- точки, когда $f’\left(x\right)=0$;
- точки, когда $f'(x)$ не будет существовать;
- Отметить на координатной прямой $D(f)$ и все найденные выше точки;
- знак $f'(x)$ на всех получившихся промежутках;
Выпуклость и вогнутость функции
Определение 6
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться выпуклой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\le \frac{f(x’)+f(x»)}{2}\]верно.
Определение 7
Функция $y=f(x)$, которая имеет своей областью определения множество $X$ будет называться вогнутой, если подставив любые две точки получим, что неравенство
\[f\left(\frac{x’+x»}{2}\right)\ge \frac{f(x’)+f(x»)}{2}\]верно.
Схема исследования:
Найти
- $D(f)$;
- $f»(x)$;
- точки, когда $f»\left(x\right)=0$;
- точки, когда $f»(x)$ не будет существовать;
- знак $f»(x)$ на каждом из найденных промежутков;
- если $f»\left(x\right)0$ то вогнутой.
Пример исследования и построения функции
Пример 1
Исследовать данную функцию и построить график:
\[f\left(x\right)=sinx-cosx\]$D\left(f\right)=R$
\[\ E\left(f\right)=\left(-\infty ,0\right)\cup (0,+\infty ).\]- \[f\left(-x\right)=-cosx-sinx\]
Следовательно, данная функция — общего вида.
- \[sinx-cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
Пересечение с осью $Ox$: $\left(\frac{\pi }{4}+\pi n,0\right)$
Пересечение с осью $Oy$: $\left(0,-1\right)$
На интервале $x\in \left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция будет принимать положительные значения, на интервале $x\in \left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция будет принимать отрицательные значения.
- \[y’=sinx+cosx\] \[sinx+cosx=0\] \[x=-\frac{\pi }{4}+\pi n,n\in Z\]
Функция возрастает на $\left(-\frac{\pi }{4}+2\pi n,\frac{3\pi }{4}+2\pi n\right)$ и убывает на$\left(\frac{3\pi }{4}+2\pi n,\frac{7\pi }{4}+2\pi n\right)$.
- \[y^{»}=cosx-sinx\] \[-sinx+cosx=0\] \[x=\frac{\pi }{4}+\pi n,n\in Z\]
На интервале $\left(\frac{\pi }{4}+2\pi n,\frac{5\pi }{4}+2\pi n\right)$ функция вогнута, на интервале $\left(-\frac{3\pi }{4}+2\pi n,\frac{\pi }{4}+2\pi n\right)$ функция выпукла.

Рисунок 3.
spravochnick.ru
Графики функций. Построение графиков функций
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны отношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
Следовательно, график функции – это множество точек (x; y), где x – это аргумент, а y – значение функции, соответствующее данному аргументу. Координаты каждой точки можно ещё изобразить так:
(x; f(x)) или (x; y(x))
Для примера возьмём самую простую функцию, где аргумент равен значению функции:
y = x
В этом случае нам не придётся для каждого аргумента вычислять значение функции, так как они равны, значит и у всех точек нашего графика абсцисса будет равна ординате. Отметим три точки на координатной плоскости, например L(-2; -2), M(0; 0) и N(1; 1):

Если мы последовательно (от наименьшего значения аргумента к большему) соединим отмеченные точки, то у нас получится прямая линия, значит графиком функции y = x является прямая:
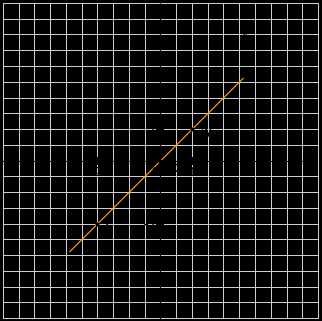
Надпись на чертеже y = x – это уравнение графика. На многих чертежах с графиками можно увидеть надпись с уравнением, к которому относится данный график.
Обратите внимание, что прямая линия бесконечна в обе стороны, поэтому, хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика. Поэтому большинство чертежей изображает только часть графика, обычно расположенную около начала координат.
naobumium.info
График функции — это… Что такое График функции?
- График функции
Wikimedia Foundation. 2010.
Смотреть что такое «График функции» в других словарях:
график функции — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] график функции 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами, где x… … Справочник технического переводчика
График функции — [ graph of a function ] — 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами., где x — любая точка области определения этой функции,… … Экономико-математический словарь
график функции — ▲ изображение ↑ графический, функция (математическая) график изображение функции при помощи линии на плоскости. … грамма. номограмма. кардиограмма. эхограмма. диаграмма наглядное графическое изображение соотношения каких л. величин. круговая… … Идеографический словарь русского языка
график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых … Энциклопедический словарь
Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции … Большой Энциклопедический словарь
График — геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и… … Большая советская энциклопедия
График — График: График функции множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты соответствующими значениями функции . График деятель искусств, занимающийся графикой. График базальной… … Википедия
График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
dic.academic.ru
Свойства функции и её график
О. Функция
вида 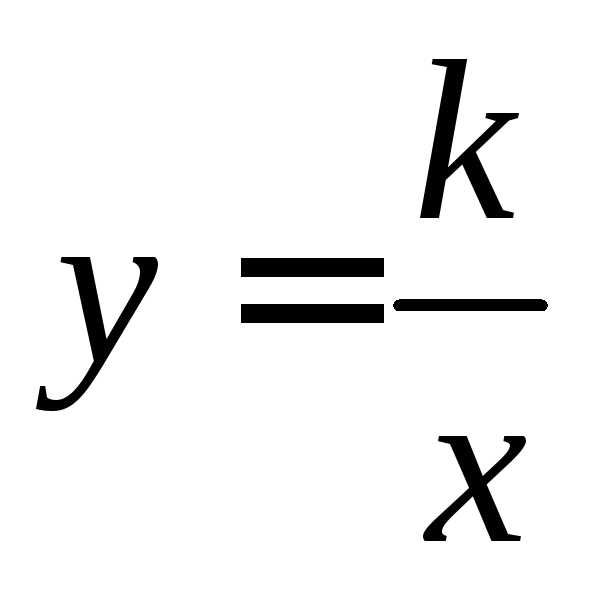 ,
где
,
где ,
,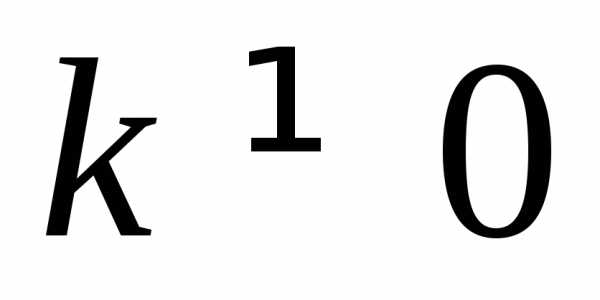 называетсяобратной
пропорциональностью.
называетсяобратной
пропорциональностью.
Свойства:
Область определения функции

Выражение  однозначно вычисляется,
при
однозначно вычисляется,
при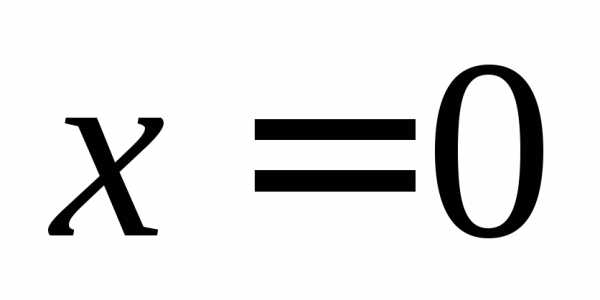 это выражение не определено(почему?),
значит
это выражение не определено(почему?),
значит
Множество значений функции

Уравнение 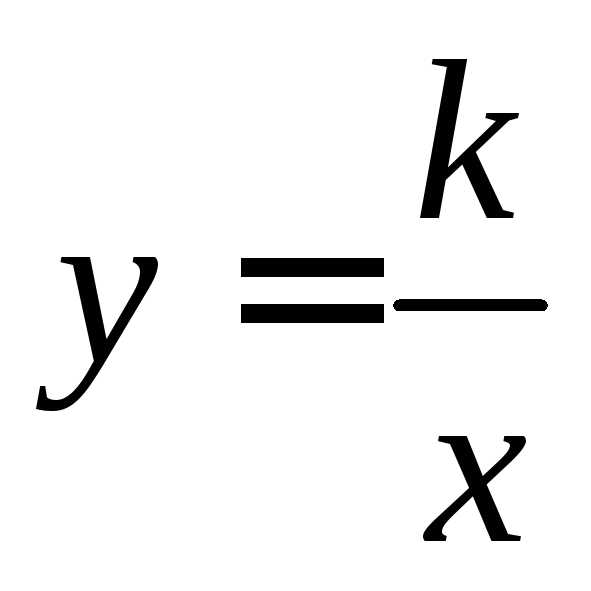 при всех значенияхимеет единственный корень, равный
при всех значенияхимеет единственный корень, равный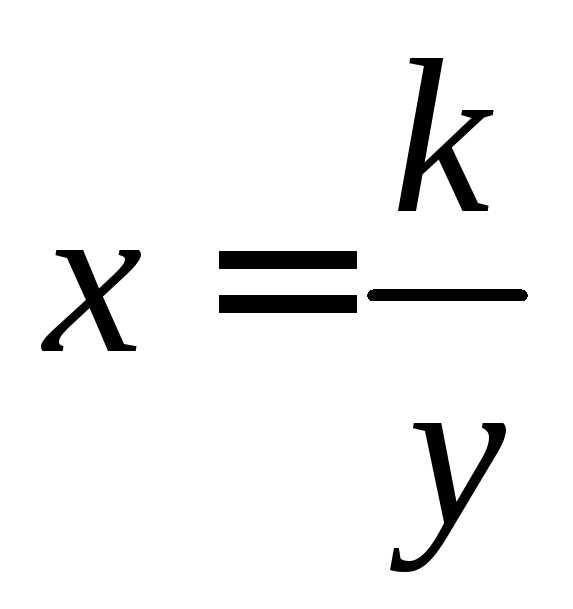
Если 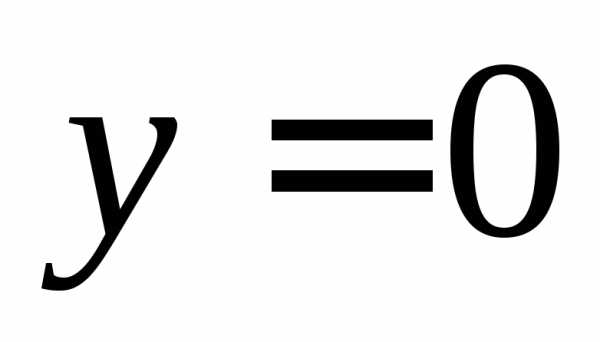 ,
то уравнение корней не имеет, значит
,
то уравнение корней не имеет, значит
Периодичность.
Теорема.
Функция 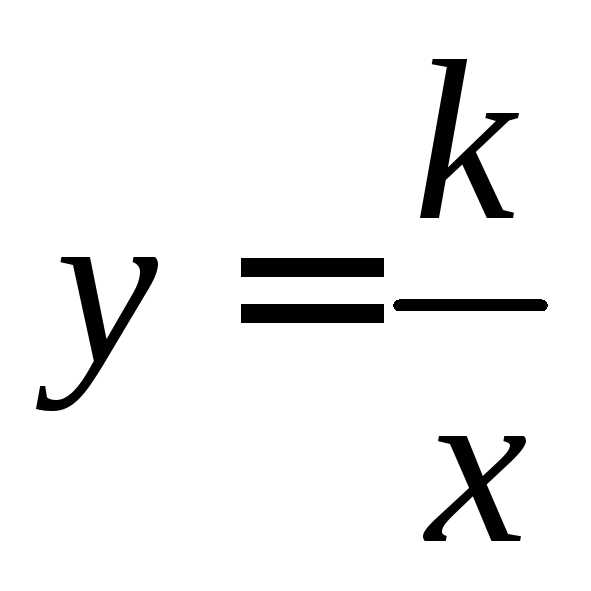 не является периодической.
не является периодической.
Доказательство:
Пусть
функция 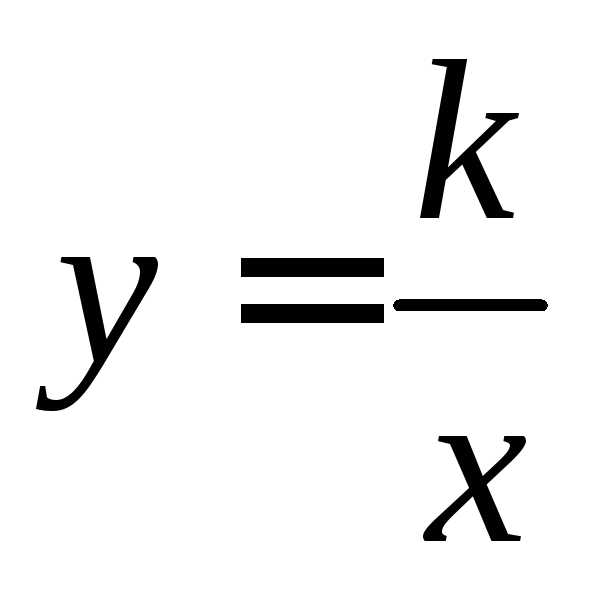 является периодической с периодом
является периодической с периодом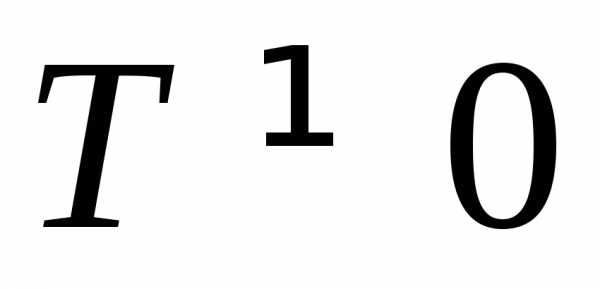 .
Это значит, что.
.
Это значит, что.
Рассмотрим разность:
,
значит
предположение о том, что функция обратная
пропорциональность имеет период 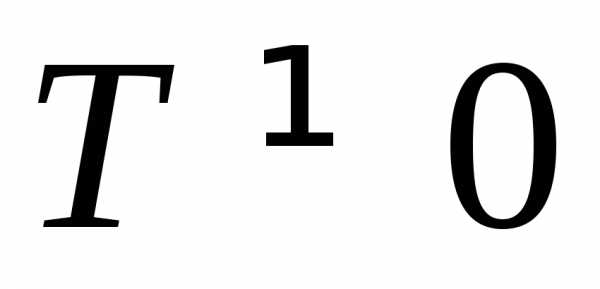 не верно, и функция обратная
пропорциональность не является
периодической.
не верно, и функция обратная
пропорциональность не является
периодической.
Чётность/нечётность.
Функция 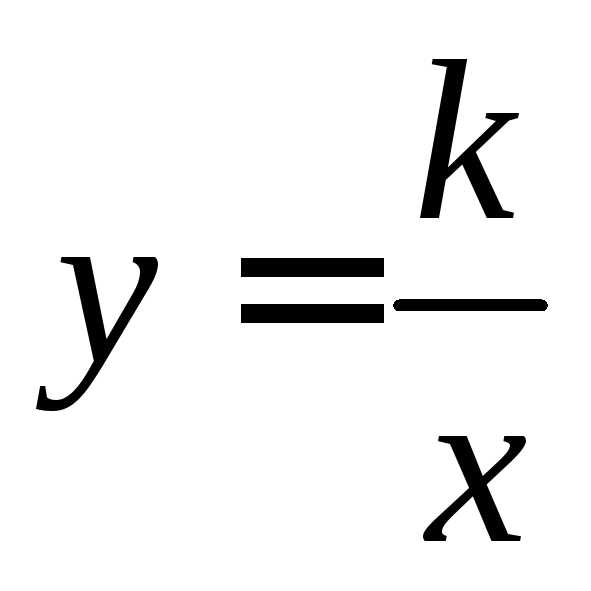 нечётная, т.к. область определения
является симметричной относительно
нуля и
нечётная, т.к. область определения
является симметричной относительно
нуля и
Точки пересечения графика с осями координат.
Т.к.
уравнение 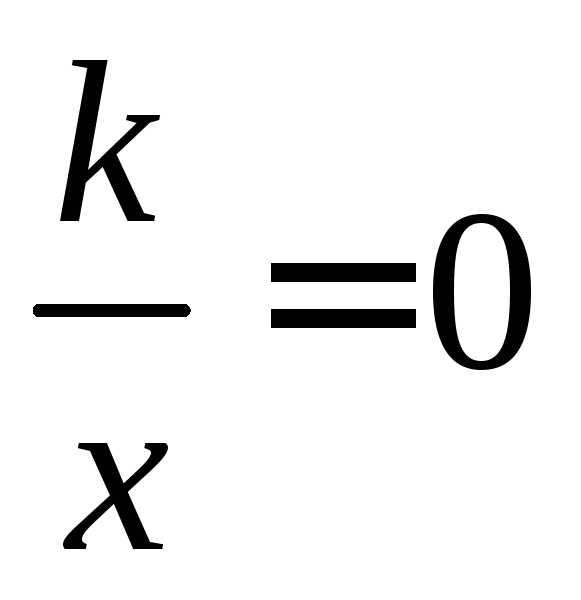 не имеет корней, то график функции
не имеет корней, то график функции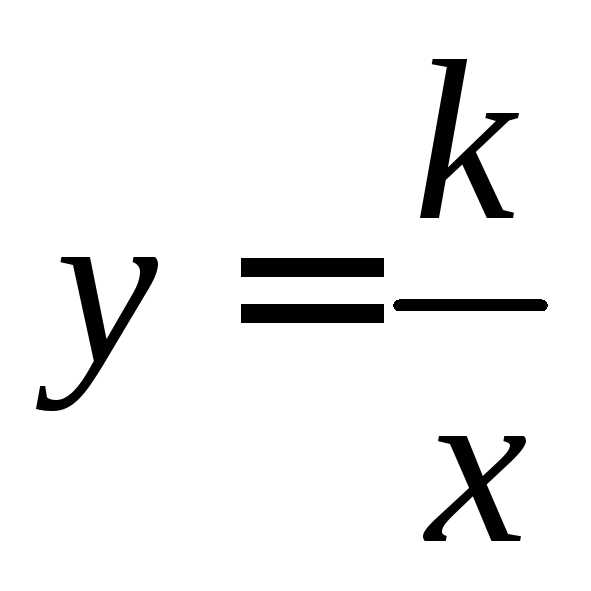 не имеет точек пересечения с осью
абсцисс.
не имеет точек пересечения с осью
абсцисс.
Так
как 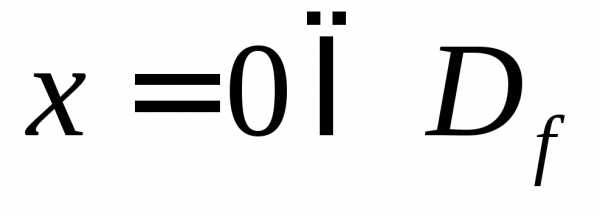 ,
то график функции точек пересечения с
осью ординат не имеет.
,
то график функции точек пересечения с
осью ординат не имеет.
Промежутки знакопостоянства функции.
Интервалы возрастания/убывания функции.
Теорема.
Если 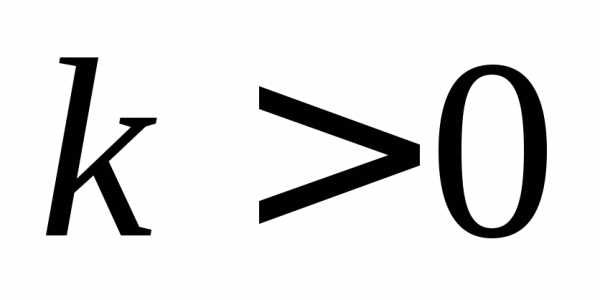 то функция убывает при
то функция убывает при и при
и при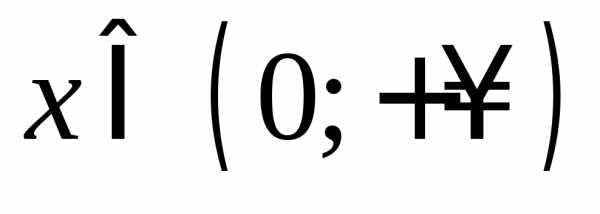
Если 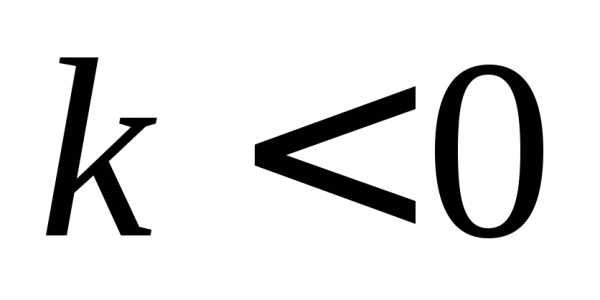 ,
то функция возрастает при
,
то функция возрастает при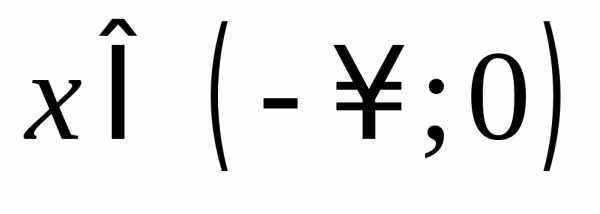 и при
и при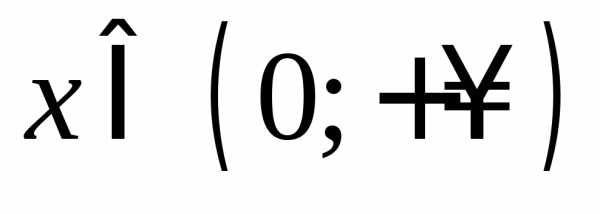
Доказательство:
Пусть 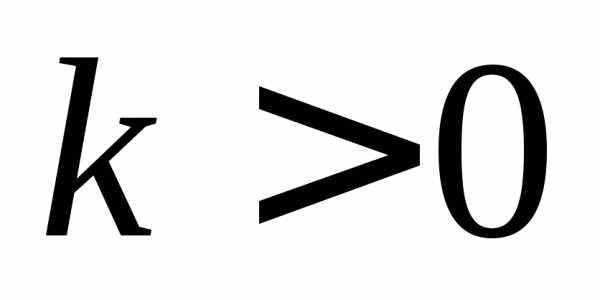 ,
тогда возьмем произвольные,
пусть для определенности
,
тогда возьмем произвольные,
пусть для определенности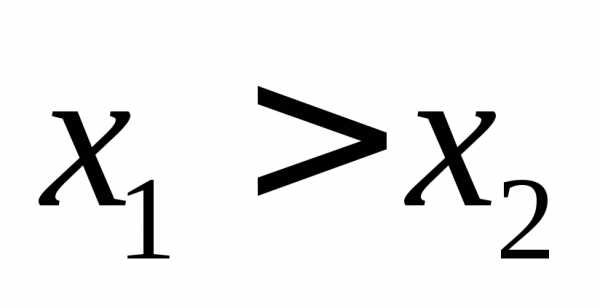 ,
тогда,
то есть,
значит функция убывает при
,
тогда,
то есть,
значит функция убывает при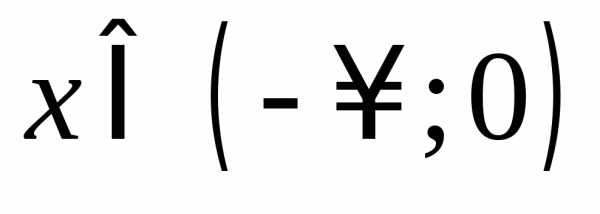 .
.
Теперь
возьмем произвольные
,
и так же для определенности пусть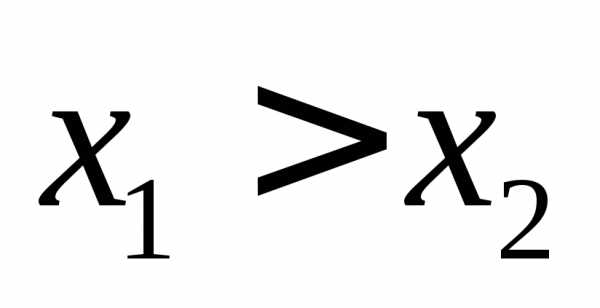 ,
,
тогда рассмотрим разность (почему?),
то
есть
,
значит функция убывает при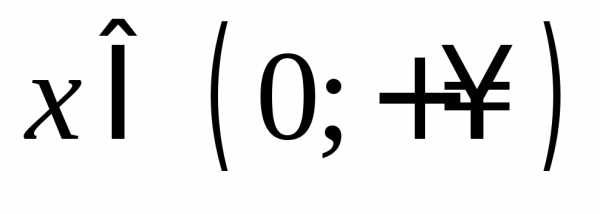 .
.
Аналогично
при 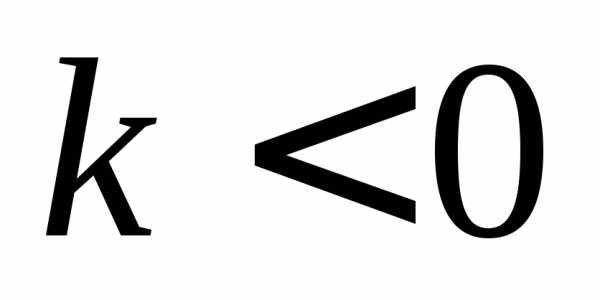
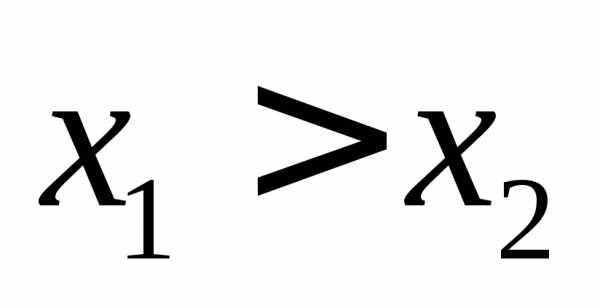 ,
тогда,
то есть,
значит функция возрастает при
,
тогда,
то есть,
значит функция возрастает при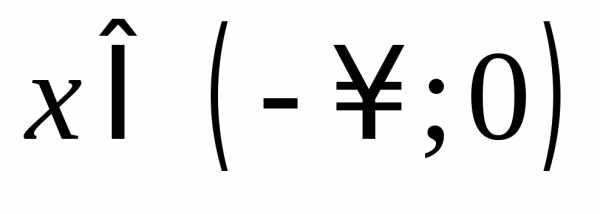 .
.Теперь
возьмем произвольные
,
и так же для определенности пусть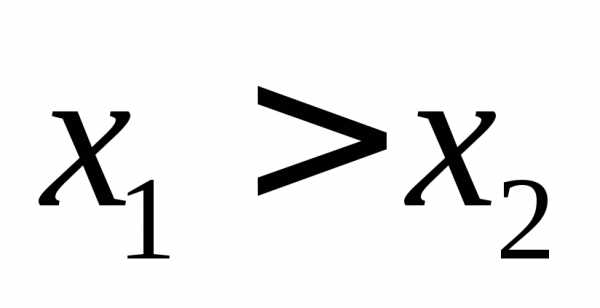 ,
тогда,
то есть,
значит функция возрастает при
,
тогда,
то есть,
значит функция возрастает при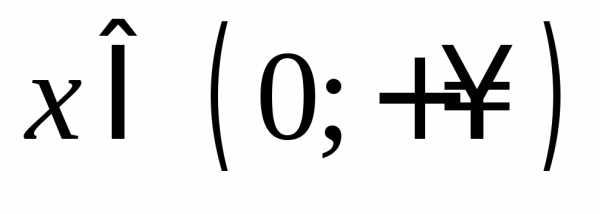 .
.
Замечание: Функция 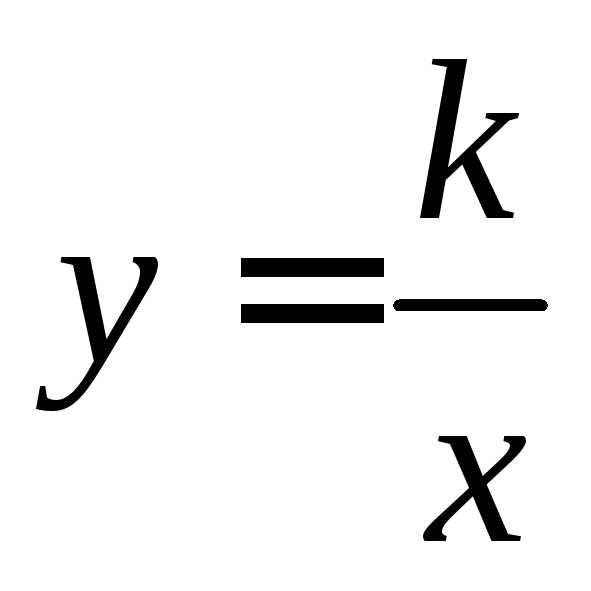 не является монотонной на всей своей
области определения !!!!!!!
не является монотонной на всей своей
области определения !!!!!!!
Действительно,
например,
,
если
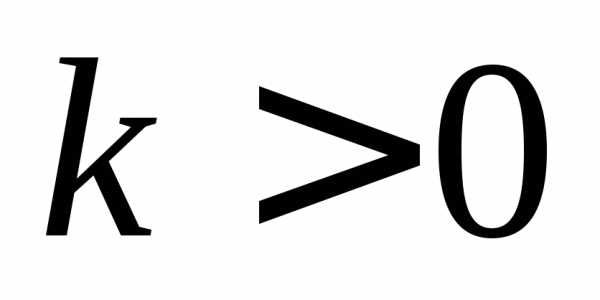 ,
то
,
то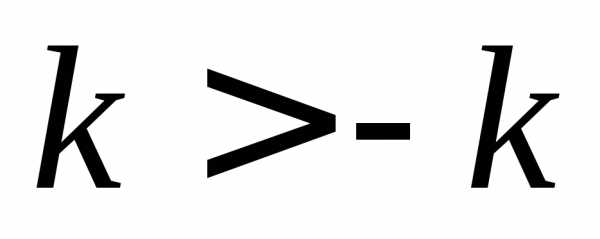 ,
что не верно, т.к. при
,
что не верно, т.к. при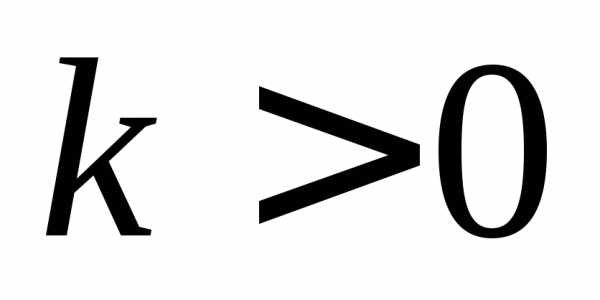 функция является убывающей и по
определению большему значению аргумента
соответствует меньшее значение функции.
функция является убывающей и по
определению большему значению аргумента
соответствует меньшее значение функции.
Наибольшее/наименьшее значение функции.
Функция не имеет наибольшего и наименьшего значения, т.к. её
График функции.
График
функции имеет две асимптоты – вертикальную 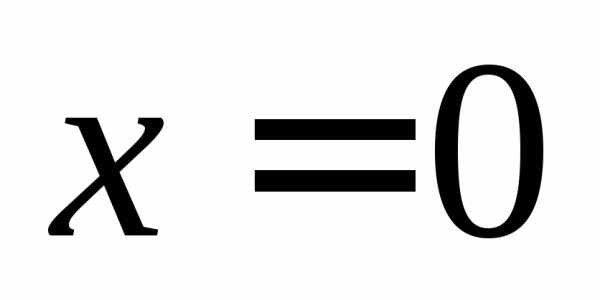 и горизонтальную
и горизонтальную .
.
О. График функции называется гиперболой и расположен в первой и третьей
координатных четвертях, если 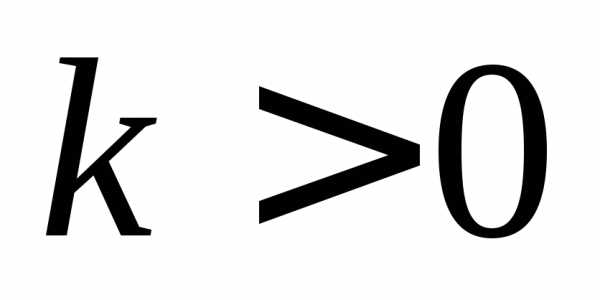 ;
и во второй и четвертой, если
;
и во второй и четвертой, если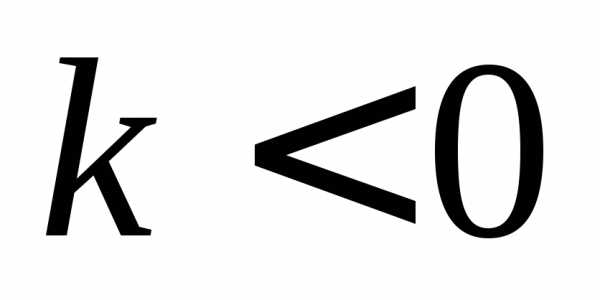 .
(рис.2).
.
(рис.2).
Свойства функции и её график. Взаимное расположение графика квадратичной функции и оси абсцисс.
О. Функция, задаваемая формулой называетсяквадратичной функцией.
Свойства:
Область определения функции:
 .
.
, т.к. значение квадратного трехчлена однозначно определено для любого действительного числа (почему?).
Множество значений функции:

Преобразуем квадратный трехчлен, задающий квадратичную функцию, выделив полный квадрат:
Введем обозначения: тогда.
Выражение 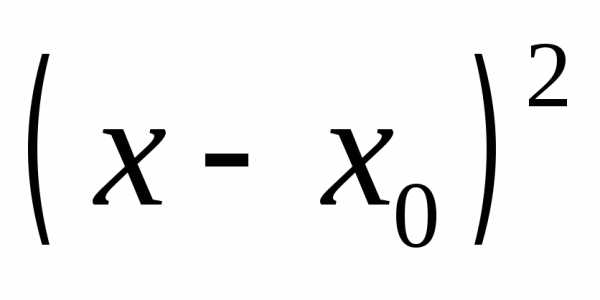 может принимать любые неотрицательные
значения в зависимости отx.
Поэтому, при
может принимать любые неотрицательные
значения в зависимости отx.
Поэтому, при 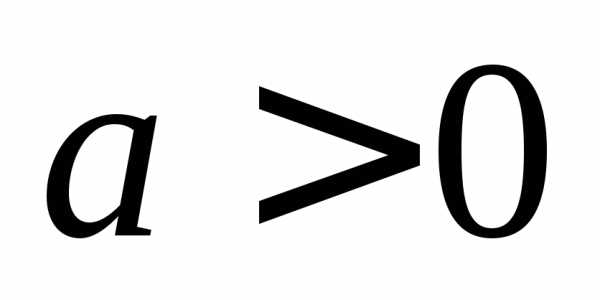 ,
а при
,
а при
Периодичность:
Квадратичная
функция не может быть периодической,
т. к., например, свое значение 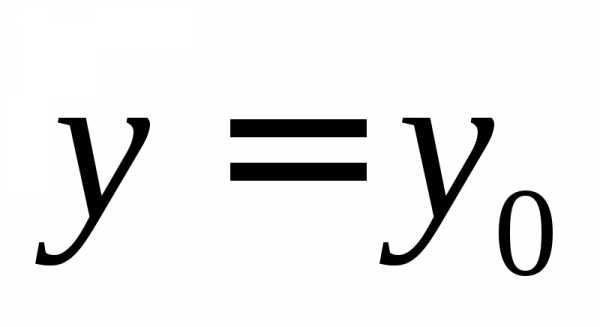 она
она
принимает
только в одной точке 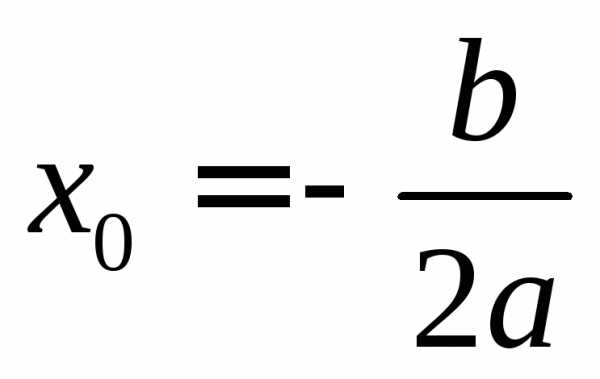 .
.
Чётность/нечётность
Если 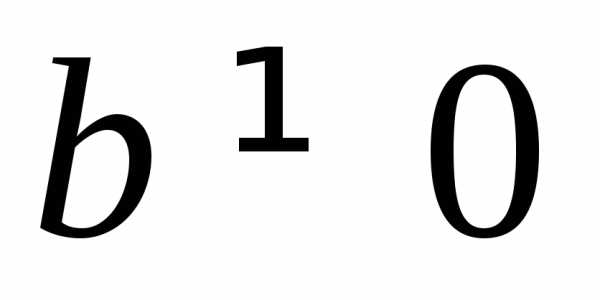 ,
то функция является функцией общего
вида (не является ни четной, ни нечетной),
т.к.,
то естьи
,
то функция является функцией общего
вида (не является ни четной, ни нечетной),
т.к.,
то естьи
Если 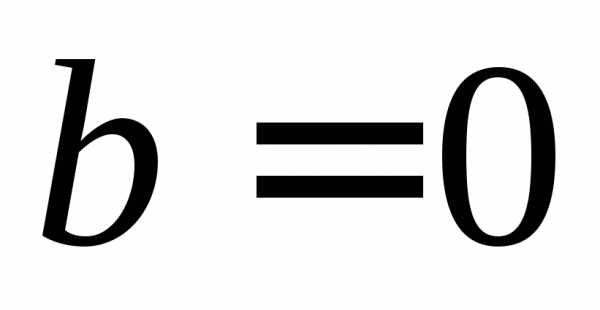 ,
то функция имеет вид
,
то функция имеет вид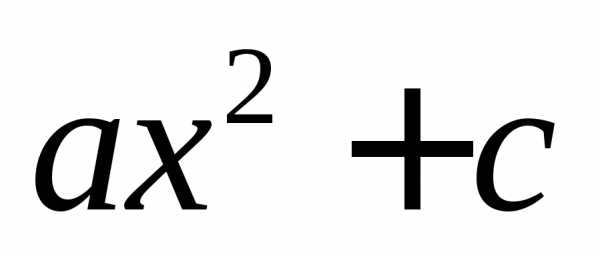 и,
значит функция четная.
и,
значит функция четная.
Точки пересечения графика с осями координат.
Точки
пересечения с осью 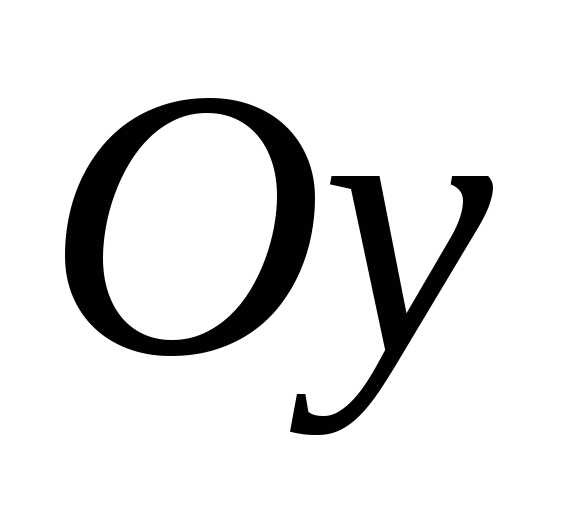 :
:
Точки
пересечения с осью 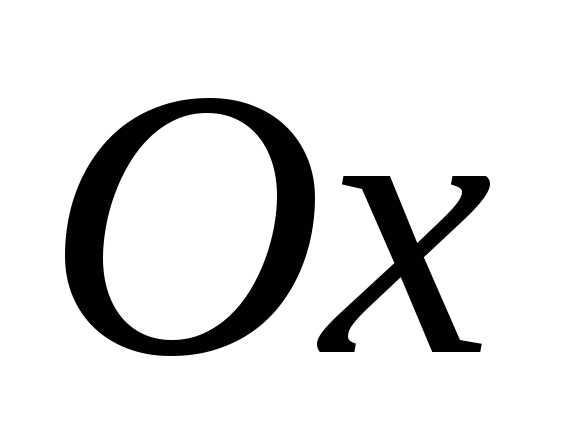 :,
корни этого уравнения существуют, если,
в противном случае точек пересечения
с осью абсцисс нет.
:,
корни этого уравнения существуют, если,
в противном случае точек пересечения
с осью абсцисс нет.
Если 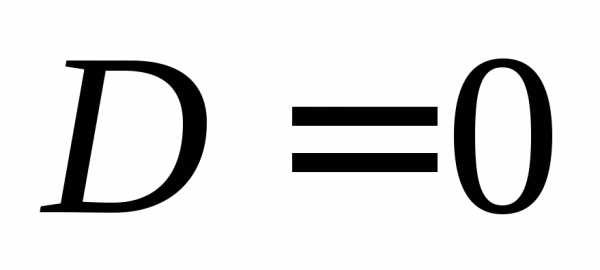 ,
то точка пересечения одна и имеет
координаты
,
то точка пересечения одна и имеет
координаты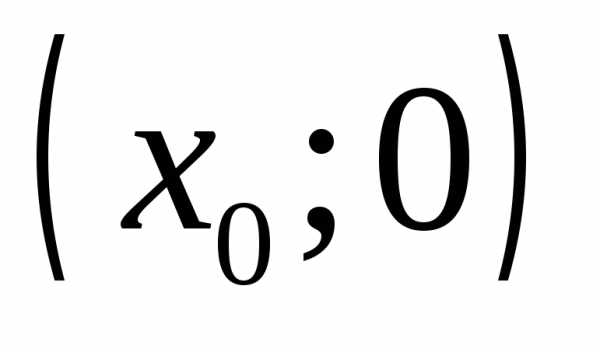
Если  ,
то квадратное уравнение имеет два корня,
которые вычисляются по формулам:
,
то квадратное уравнение имеет два корня,
которые вычисляются по формулам: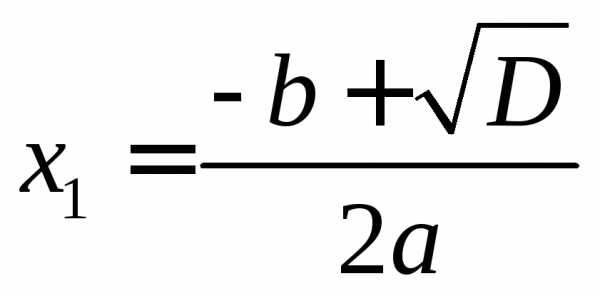 ,
,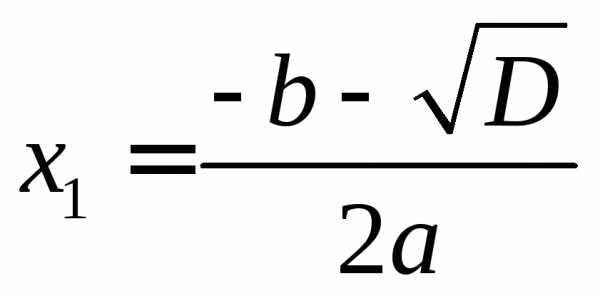
Поэтому
точек пересечения с осью 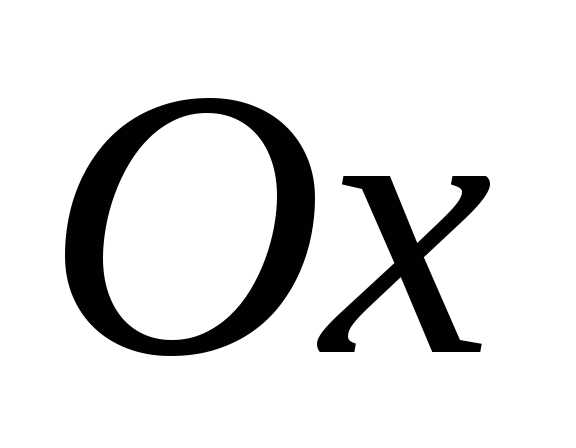 две, и они имеют координаты
две, и они имеют координаты и
и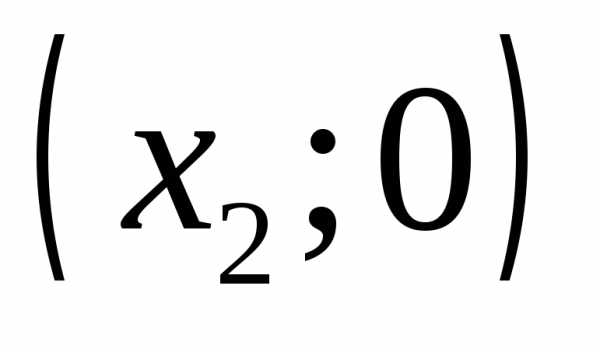
Промежутки знакопостоянства функции:
Если 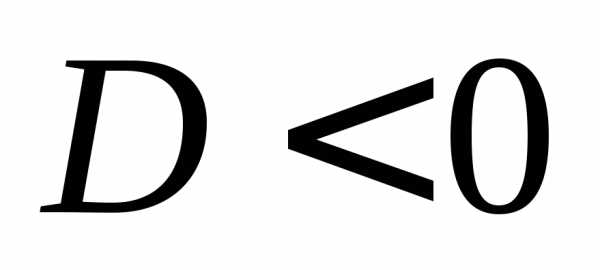 :,
то выражение вида
:,
то выражение вида для всех
для всех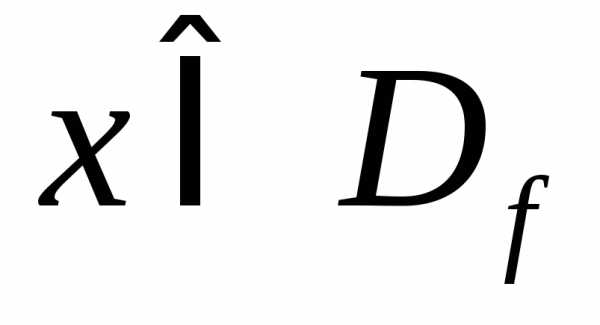 .
Значит,,.
.
Значит,,.
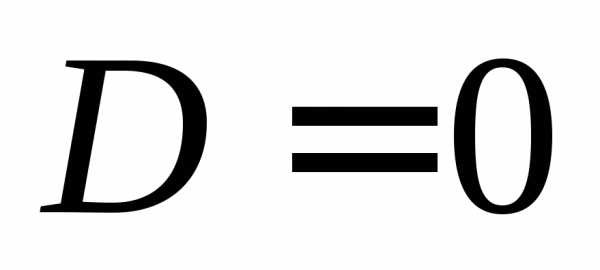 :
,
тогда,
:
,
тогда,
 :
,
где
:
,
где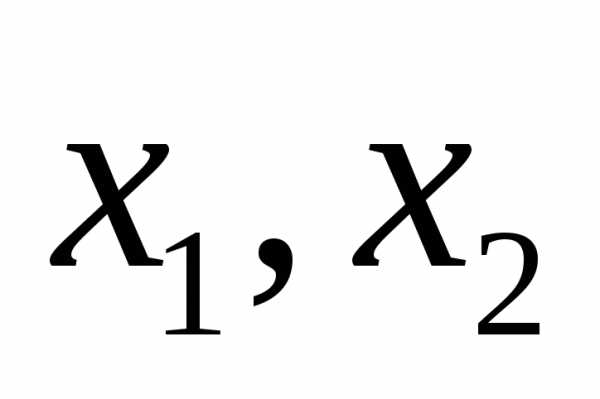 — корни уравнения.
— корни уравнения.
Тогда
при
значения выражений, стоящих в скобках,
будут иметь одинаковые знаки, значит,
их произведение будет положительным,
и при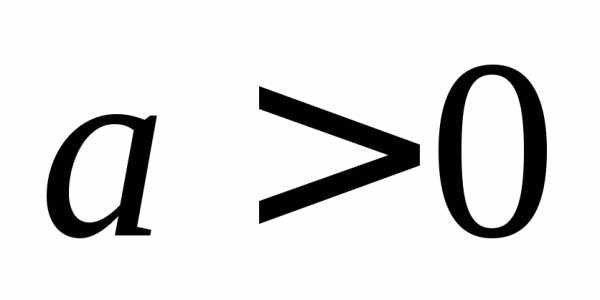 на данных промежутках квадратичная
функция будет принимать положительные
значения, а при
на данных промежутках квадратичная
функция будет принимать положительные
значения, а при — отрицательные.
— отрицательные.
Если 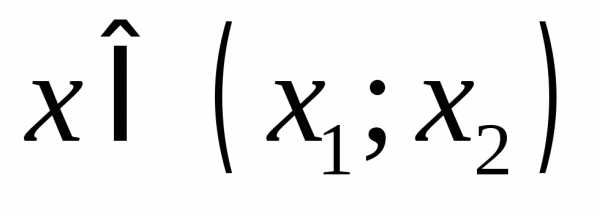 ,
то наоборот, знаки выражений в скобках
будут разными и, следовательно, из
произведение будет отрицательным.
,
то наоборот, знаки выражений в скобках
будут разными и, следовательно, из
произведение будет отрицательным.
Тогда
при 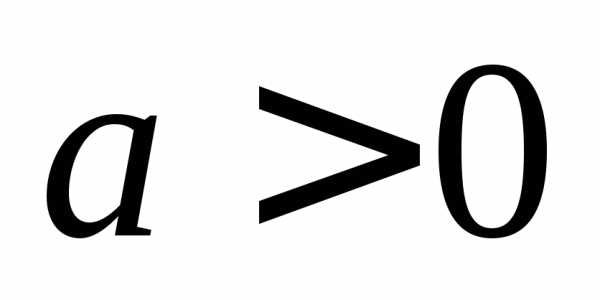 на данном промежутке функция принимает
отрицательные значения, а при
на данном промежутке функция принимает
отрицательные значения, а при — положительные.
— положительные.
Интервалы возрастания/убывания
Теорема.
Если 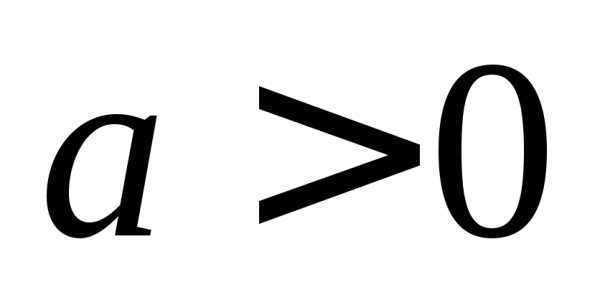 ,
то функция является возрастающей при
,
то функция является возрастающей при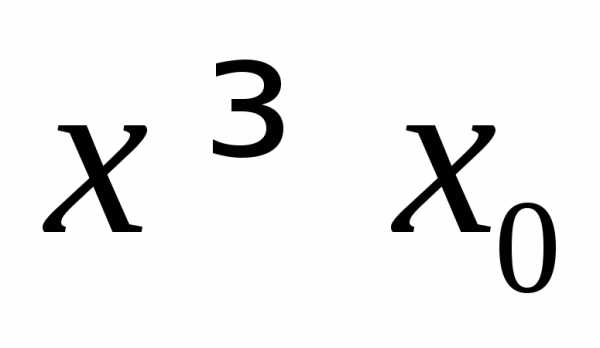 и убывающей при
и убывающей при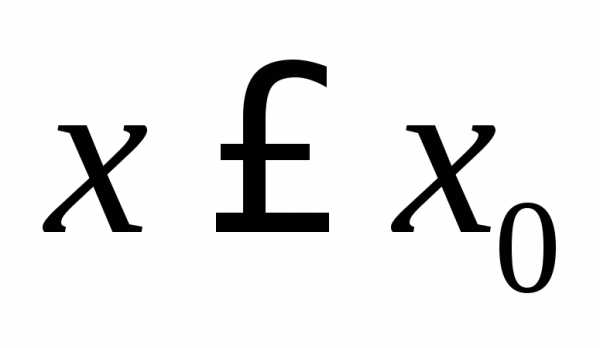
Если  ,
то функция является возрастающей при
,
то функция является возрастающей при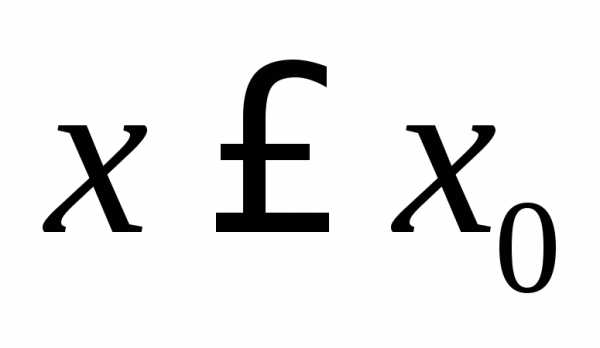 и убывающей при
и убывающей при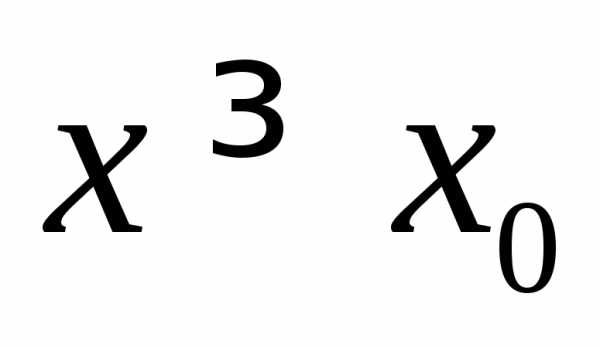
Доказательство:
Пусть 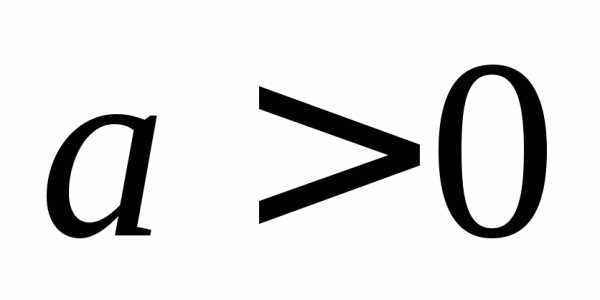 .
.
Рассмотрим
разность значений квадратичной функции
в точках 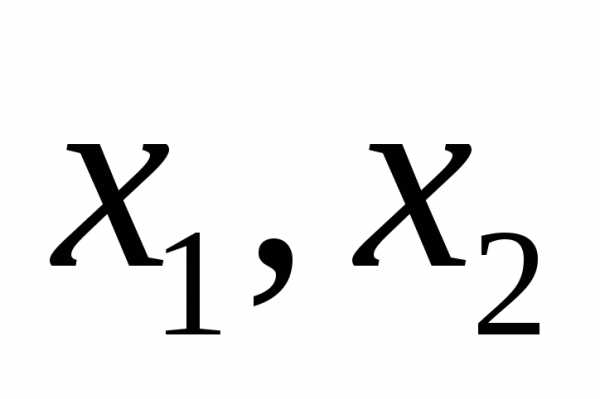 ,
таких, что
,
таких, что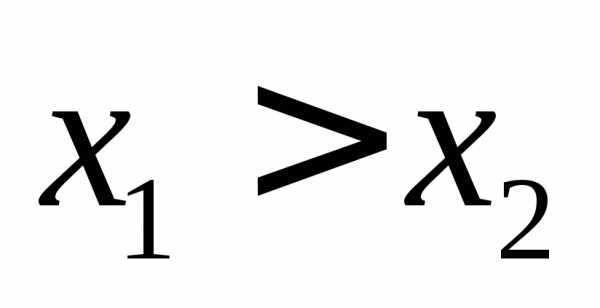
при
чем,  .
Тогда все три сомножителя в полученном
выражении положительны. Это означает,
что,
т.е.,
значит, если
.
Тогда все три сомножителя в полученном
выражении положительны. Это означает,
что,
т.е.,
значит, если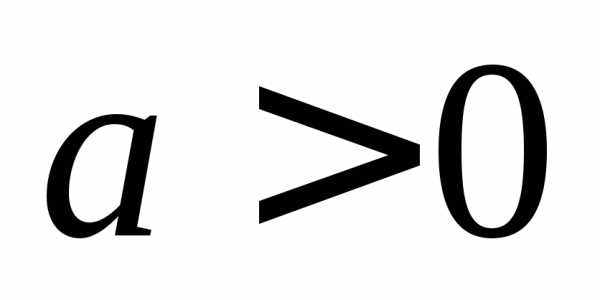 ,
то функция является возрастающей при
,
то функция является возрастающей при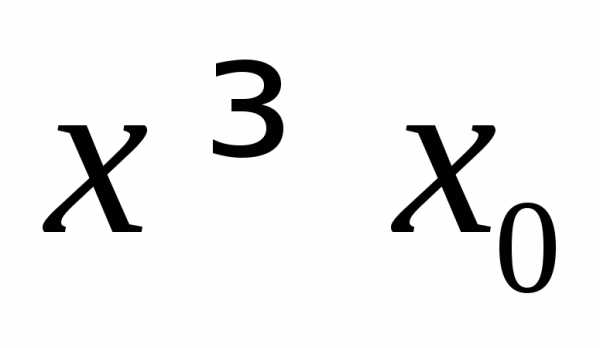 .
.
Если , тогда последний сомножитель отрицателен (как сумма двух отрицательных чисел), а первые два положительны, тогда их произведение – отрицательно.
Таким
образом,,
и функция убывает при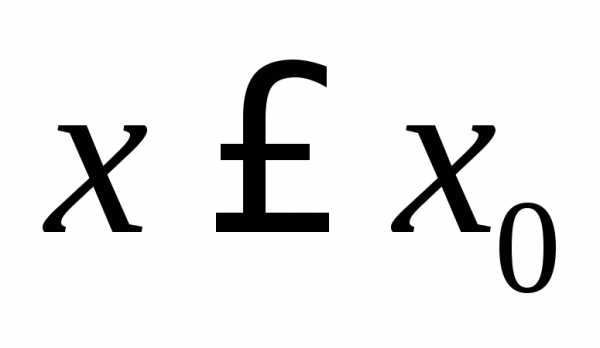 .
.
Случай  рассматривается аналогично(рассмотрите
его самостоятельно).
рассматривается аналогично(рассмотрите
его самостоятельно).
Наибольшее/наименьшее значение функции
Так
как при 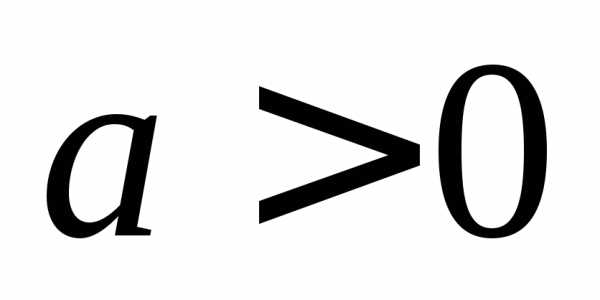 функция возрастает на
функция возрастает на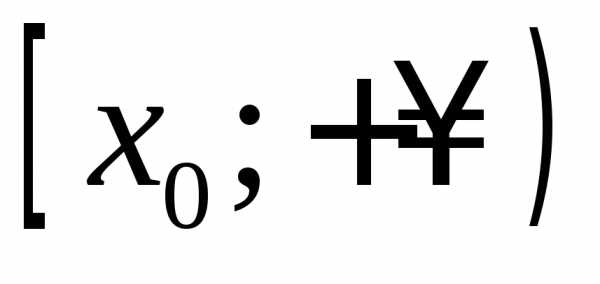 и убывает на
и убывает на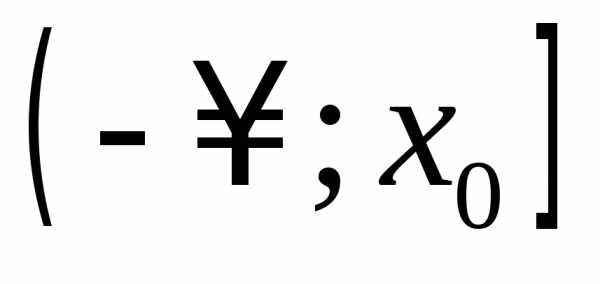 ,
то при
,
то при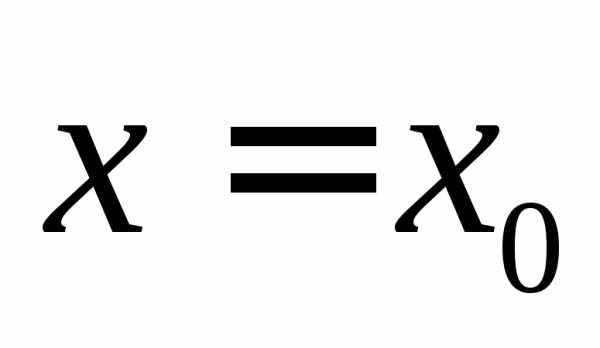 функция принимает наименьшее значение,
и оно равно
функция принимает наименьшее значение,
и оно равно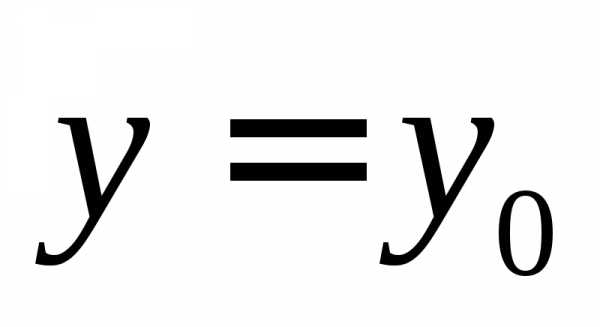 .
.
При  функция возрастает на
функция возрастает на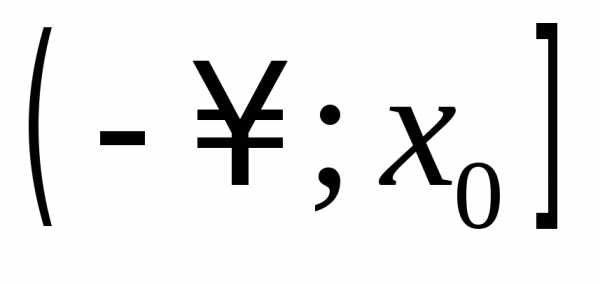 и убывает на
и убывает на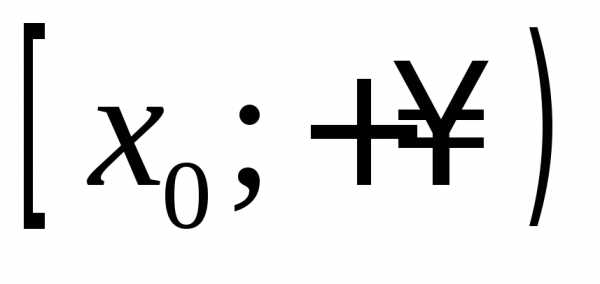 ,
поэтому при
,
поэтому при функция принимает наибольшее значение
и оно равно
функция принимает наибольшее значение
и оно равно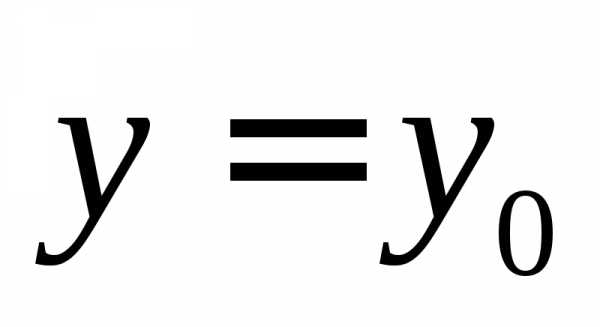 .
.
График функции.
О. Графиком квадратичной функции является кривая, называемая параболой (рис.3).
О. Точка с координатами 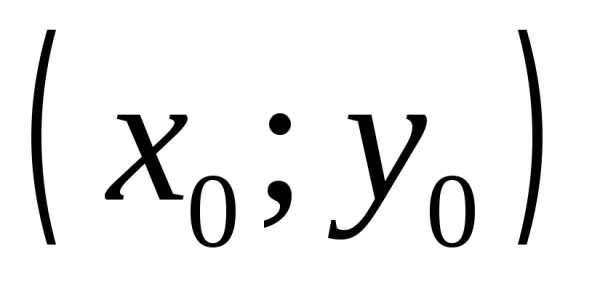 называетсявершиной
параболы.
называетсявершиной
параболы.
studfiles.net
График функции — это… Что такое График функции?
- График функции
Wikimedia Foundation. 2010.
Смотреть что такое «График функции» в других словарях:
график функции — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] график функции 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами, где x… … Справочник технического переводчика
График функции — [ graph of a function ] — 1. Один из основных (наряду с таблицей, формулой, алгоритмом) способов задания функции: множество точек (x,y) плоскости с прямоугольными координатами., где x — любая точка области определения этой функции,… … Экономико-математический словарь
график функции — ▲ изображение ↑ графический, функция (математическая) график изображение функции при помощи линии на плоскости. … грамма. номограмма. кардиограмма. эхограмма. диаграмма наглядное графическое изображение соотношения каких л. величин. круговая… … Идеографический словарь русского языка
график — 1. ГРАФИК, а; м. [от греч. graphikos начерченный] 1. Чертёж, диаграмма и т.п., изображающие с помощью линий количественные показатели развития, состояния и т.п. чего л. Г. изменения атмосферного давления. Г. заболеваемости гриппом. Г. проведённых … Энциклопедический словарь
Функции Бесселя — в математике семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя: где произвольное вещественное число, называемое порядком. Наиболее часто используемые функции Бесселя функции целых… … Википедия
ГРАФИК — (от греч. graphikos начертанный) 1) чертеж, применяемый для наглядного изображения зависимости какой либо величины (напр., пути) от другой (напр., времени), т. е. линия, дающая наглядное представление о характере изменения функции. График функции … Большой Энциклопедический словарь
График — геометрическое изображение функциональной зависимости при помощи линии на плоскости. Например, на рис. 1 изображен Г. изменения атмосферного давления со временем. Г. применяют как для наглядного изображения функциональных зависимостей и… … Большая советская энциклопедия
График — График: График функции множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты соответствующими значениями функции . График деятель искусств, занимающийся графикой. График базальной… … Википедия
График (значения) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
График (знач.) — График График функции График Деятель искусств, занимающийся графикой График базальной температуры График ганта он же Диаграмма Ганта График Найквиста АФЧХ Сетевой график График движения поездов … Википедия
dik.academic.ru
Функция и график функции
В ближайшее время все школы должны будут работать по ФГОС ООО. И учителю математики уже сегодня необходимо строить свою работу так, чтобы она соответствовала требованиям, которые предъявляет ФГОС к современному математическому образованию.
Одним из предметных результатов изучения предметной области «Математика и информатика» ФГОС определяет « овладение системой функциональных понятий, развитие умения использовать функционально-графические представления для решения различных математических задач, для описания и анализа реальных зависимостей».
Понятие функции в математике является основополагающим. К сожалению, даже успешные ученики не всегда могут дать определение функции. А уж «гуманитарии» и подавно не могут объяснить это важное понятие. Но функция это ещё и важное межпредметное понятие, используемое во всех без исключения предметах от алгебры и физики до экономики и литературы.
При изучении курса алгебры понятие графика функции можно использовать не только при изучении в рамках темы «Функция», но и во многих других разделах. А наличие в кабинете компьютера, мультимедиа и навыки работы с графопостроителями позволяют применять графики в исследовательской работе на уроке и вне его.
В своей работе я постоянно обращаюсь к понятию графика функции, чтобы к окончанию обучения (в 9 или 11 классе) ученик имел четкое представление о функции и способах применения функции и графика как при изучении предметной области «Математика и информатика», так и метапредметной (умение применять графический метод при самостоятельном решении проблем в других предметных областях).
Научное понятие функции и графика функции даётся в 7 классе на уроках алгебры. Но уже в 6 классе при изучении понятия «Координатная плоскость» и «График функции» необходимо сформировать у учеников начальные понятие по данной теме. Для этого в 6 классе я уже не первый год использую метод построения рисунков на координатной плоскости по готовым данным. А так же самостоятельное составление рисунков учениками. Такая форма работы очень нравится детям. Они с удовольствием сначала строят рисунки по готовым координатам. Но со временем у них появляется потребность придумывать и создавать свои рисунки. В 6 классе мы организуем проект-конкурс лучших работ. Ученики обмениваются своими работами и с удовольствием угадывают, что зашифровал координатами одноклассник. Результатом такой деятельности является прочное закрепление алгоритма построения точек на координатной плоскости, что немаловажно для дальнейшего изучения в курсе алгебры. Также в 6 классе я знакомлю учеников с компьютерной программой, строящей по координатам рисунки. Детям очень нравится такая работа, так как она похожа на компьютерную игру. Освоение работы с программой – первый шаг к освоению работы с графопостроителями на дальнейшей ступени обучения.
Также в 6 классе мы проводим практическую работу совместно с учителем географии по измерению температуры воздуха и построению на миллиметровой бумаге графиков зависимости температуры от времени суток. Благо весной, когда мы проводим эту работу, температура может значительно меняться в течение суток, что характерно отражается на графиках. Такая работа соответствует требованиям ФГОС (метапредметным, включающим освоенные обучающимися межпредметные понятия и универсальные учебные действия (регулятивные, познавательные, коммуникативные), способность их использования в учебной, познавательной и социальной практике, самостоятельность планирования и осуществления учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, построение индивидуальной образовательной траектории). Таким образом, проводится пропедевтическая работа. К началу изучения алгебры в 7 классе ученики владеют необходимой минимальной базой и начальными навыками исследовательской деятельности с применением средств ИКТ.
Рассмотрим примеры применения в курсе алгебры графиков функций при изучении различного учебного материала.
В 7 классе при изучении темы «Взаимное расположение графиков линейной функции» на уроке мы проводим исследование с целью выяснения от чего зависит взаимное расположение графиков. Составляем таблицу.
|
формула |
Угловой коэффициент |
Взаимное расположение |
|
Y=3x+2 и y=-3x-3 |
3 и 4 |
Пересекаются |
|
Y=3x+2 и y=3x-3 |
3 и 3 |
Не пересекаются |
|
Y=3x и y=3 |
3 и 0 |
пересекаются |
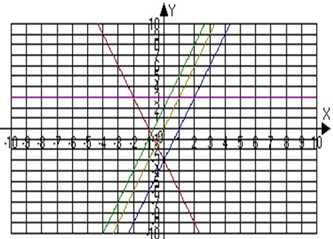
Затем предлагаю решить уравнения 3x+2=-3x-3 и т.п. и убедится в отсутствии или наличии корней. В итоге делам вывод и записываем свойство. В данной статье я привожу только примеры. На самом деле мы строим большое количество графиков до получения нужного результата.
Похожую работу мы проделываем при изучении темы «Решение систем линейных уравнений с двумя неизвестными». В рамках этой темы проводится урок-исследование «Графический способ решения систем уравнений с двумя неизвестными» где ученики на основании построений при помощи графопостроителя делают вывод о количестве решений системы.
В 8 классе при изучении темы «График функции y=k/x» ученики исследуют расположение гиперболы в зависимости от коэффициента k.
|
формула |
Значение k |
Расположение по четвертям |
|
Y=3/x |
3 |
1 и3 |
|
Y=-3/x |
-3 |
2 и 4 |
Выполняем достаточное количество построений и делаем вывод.
Неоценимую помощь оказывает графопостроитель при изучении темы «Графическое решение уравнений». При изучении этого способа программа позволяет приводить большое количество примеров и научить верно, указывать ответ уравнения. А так же позволяет показать ученикам, что графически можно решить уравнения, решение которых им недоступно аналитическим способом.
В 9 классе при изучении темы «Квадратичная функция» с помощью графопостроителя экономится время на построения при отработке умения определять расположение параболы в зависимости от параметров. В последних вариантах ГИА мы видим задания вида: по графику квадратичной функции определить знаки параметров a, b и c.
При изучении темы «График квадратичной функции» проводим урок исследование. На котором учимся строить графики вида: y=ax²+n и y=a(x-m)².
Задание: 1) построить график y=x²; 2) y=x²-2; 3)y=x²+2.
На основании построений даем понятие параллельного переноса и делаем выводы о способах построения графиков при помощи параллельного переноса.
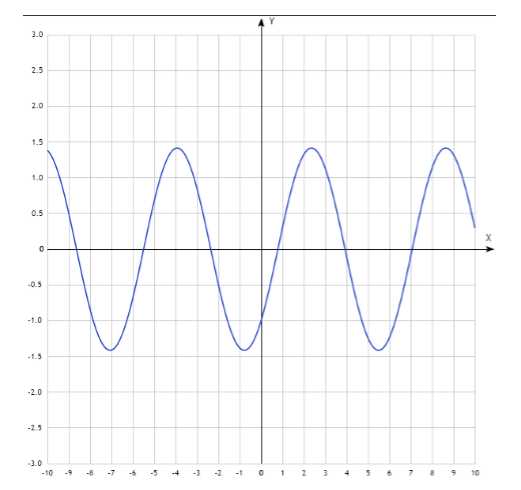
В 10 классе удобно применять графопостроитель при изучении темы «Графики тригонометрических функций». Здесь мы также проводим урок-исследование «Построение графиков вида y=sin(kx+n), cos(kx+n) и т.п.
При изучении темы «Применение производной» при помощи графиков можно наглядно показать взаимосвязь производной и функции, демонстрируя такие иллюстрации.
На рисунке дан график функции y=x² и график её производной y=2x. Ответьте на вопросы:
1) По графику функции: а) промежутки возрастания, убывания функции; б) точки экстремума.
2) По графику производной : а) промежутки знакопостоянства; б) нули.
Предлагаю большое количество таких иллюстраций. Анализируя и сопоставляя, ученики выдвигают гипотезу. Затем формулируем необходимые правила.
Также полезно применять иллюстрации при изучении темы «Касательная». Ученикам необходимо показать наглядно геометрический смысл производной.
В заданиях ЕГЭ в 11 классе необходимо по готовым рисункам определить значения производной. Выработке этого умения способствуют такие задания, которые можно предлагать на устном счете в 10 и 11 классах. Анализ работ ЕГЭ показывает, что ученики часто путают график функции с графиком производной. Поэтому необходимо сформировать умения по различным графикам считывать нужные данные. Приведу примеры задач, формирующих такие умения.
1) По графику функции определить значения x, при которых а) производная равна нулю, б) положительна, в) отрицательна.
2) По графику производной определите: значения x, при которых функция: а) возрастает, б) убывает, в) точки экстремума, г) угловой коэффициент касательной положителен, отрицателен, равен нулю.
Затем приводим рисунок, на котором изображены график функции и график производной.
Таким образом, последовательная и логично построенная на протяжении всего курса работа над понятием функция и график функции позволяет формировать необходимые предметные и метапредметные умения при подготовке к работе по ФГОС ООО.
videouroki.net

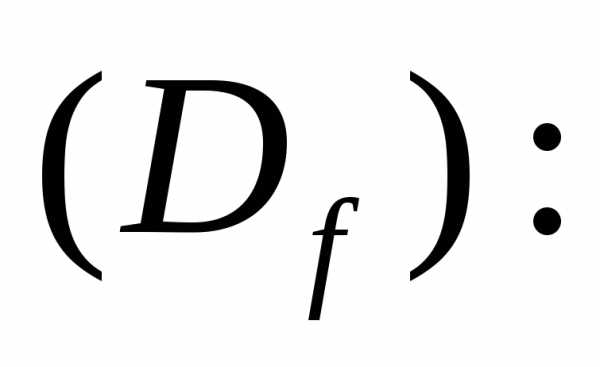

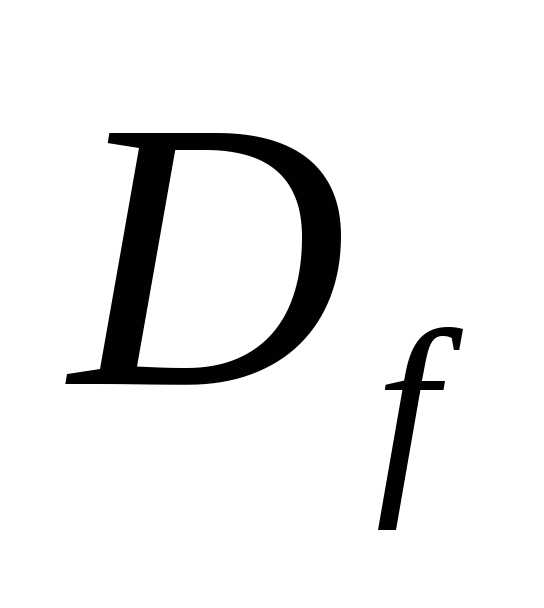 .
.