|
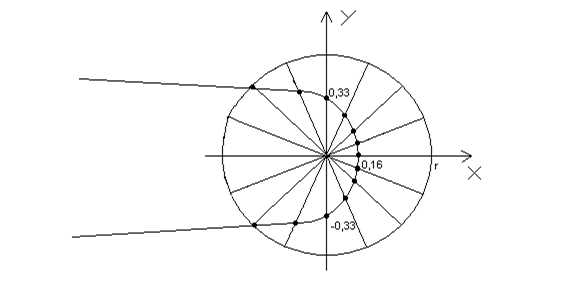
Говорят, что на плоскости введена Полярная система координат, если заданы: 1) некоторая точка 0, называемая Полюсом; 2) некоторый луч, исходящий из точки 0 И называемый Полярной осью. Полярными координатами точки M называются два числа: Полярный радиус и Полярный угол — угол между полярной осью и вектором . Пусть на плоскости введены декартова и полярная системы координат, причем начало декартовой системы совпадает с полюсом, а полярная ось — с положительной полуосью абсцисс. Тогда прямоугольные координаты X, Y точки М и ее полярные координаты ρ, φ связаны следующими формулами: , , Задание 4. Линия задана уравнением в полярной системе координат. Требуется: 1. Построить линию по точкам, придавая φ значения от до через промежуток . 2. Найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью. 3. По уравнению в декартовой прямоугольной системе координат определить тип линии. Решение. 1) Совместим декартову и полярную системы координат и рассмотрим окружность произвольного, достаточно большого радиуса С центром в полюсе. Построим радиусы, образующие углы с полярной осью, где принимает значения от до с шагом . Вычислим косинусы этих углов и по этим значениям найдем . Результаты вычислений занесем в таблицу:
Построим точки () и по полученным точкам построим искомую линию:
2) Найдем уравнение данной линии в декартовой системе координат. Для этого воспользуемся формулами: . Отсюда , . Тогда имеем: Или после упрощения . 3) Чтобы определить тип линии, определяемой полученным уравнением, Преобразуем его к каноническому виду: Или . Окончательно получим: , Где ,. Таким образом, данное уравнение определяет параболу.
|
matica.org.ua
Полярная система координат задана, если задана точка , называемая полюсом, и исходящий из полюса луч , который называется полярной осью. Положение любой точки в полярной системе координат однозначно определяется ее
полярными координатами: полярным радиусом — расстоянием от полюса до точки и полярным углом — углом поворота полярной оси до совпадения с вектором
(рис.31). В полюсе полярный радиус , а полярный угол не определен. Для всех точек плоскости, не
совпадающих с полюсом . Полярный угол измеряется в радианах и считается положительным, если
отсчитывается от полярной оси против часовой стрелки. Полярный угол определяется
с точностью до , где — целое число. Это означает, что точки с полярными координатами
и при целом совпадают. Если задана полярная система координат, то каждой паре чисел , из которых , соответствует точка плоскости, для которой эти числа являются
ее полярными координатами. Если , то эта точка расположена на луче, составляющим угол с полярной осью , и на расстоянии от полюса. Если , то эта точка совпадает с полюсом. Из определения полярных координат следует, что уравнение задает на плоскости окружность с центром в полюсе и
радиусом , а уравнение задает на плоскости луч, проходящий через полюс и
составляющий с полярной осью угол , в частности уравнения полярной оси .
Если задать на плоскости прямоугольную декартову систему координат, поместив
ее начало в полюс и совместив ось абсцисс с полярной осью, то, как легко видеть
из рис. 32, декартовы координаты и выражаются через полярные координаты из
соотношений Если каждое уравнение системы возвести в квадрат и сложить их, то получим
уравнение , из которого по заданным декартовым координатам можно
определить полярный радиус.
|
||||||
nww13.narod.ru
Полярная система координат.
Поиск ЛекцийФункций при помощи электронных
Таблиц Excel.»
Автор работы: Белкин Алексей Васильевич,
ученик 10 класса МБОУ «Многопрофильная гимназия г. Лагани»
Научный руководитель: Никифоров Евгений Алексеевич,
учитель математики МБОУ «Многопрофильная гимназия г. Лагани»
Г. Лагань — 2013
ОГЛАВЛЕНИЕ
| Введение | |
| 1.1.Инструкция по построению кривых с помощью программы Microsoft Excel. | 3-5 |
| 1.2. Полярная система координат | 5-6 |
| 1.3. Инструкция по построению кривых в полярных координатах с помощью программы Microsoft Excel | 6-10 |
| 1.4. Построение кусочно-заданной функции на примере построения эскиза национального орнамента | 11-12 |
| Заключение | 13 — 14 |
| Список литературы |
ВВЕДЕНИЕ
Актуальность работы.При изучении, темы преобразования графиков функций возникла необходимость построения графиков элементарных функций и уравнений выше второй степени. Для изучения свойств этих функций Microsoft Excel предлагает широкие возможности, которые в школьных учебниках по информатике не оговариваются.
Вопрос (мотивация): Как построить график с изменяющимся параметром, для дальнейшего его изучения?
Проблема: необходимо найти удобный (сравнительно простой, наглядный, доступный) способ построения графиков элементарных функций и уравнений степеней выше второй с двумя переменными.
Гипотеза: для решения поставленной проблемы, возможно использовать инструменты прикладной программы Microsoft Excel, а для построения графиков уравнений высших порядков ввести новые переменные, или новую систему координат, или и то и другое одновременно.
Поэтому, объект нашего исследования —прикладная программа Microsoft Excel, ее возможности для построений графиков функцийи исследования их.
Исходя из этого, предметом нашего исследования стали уравнения элементарных функций и кривых высших порядков.
Цель работы – показать алгоритм построение графиков функций в Excel, принцип построения линий высших порядков в полярной системе координат с помощью формул перехода от декартовых координат к полярным координатам. Результаты исследования:
Ø Научился строить графики функций, с дальнейшей возможностью изучения их свойств
Ø изучил переход от декартовой системы координат к полярной и обратно;
Ø исследовал изменения вида графиков функций и кривых, в зависимости от параметров входящих в её уравнение;
Ø познакомились с некоторыми замечательными кривыми известных математиков.
Планы и перспективы: продолжить изучение плоских кривых.
Инструкция по построению кривых с помощью программы
Microsoft Excel.
Пусть задана функция y= f(x), где х – независимая переменная , а y – переменная зависящая от х.
Для начала нам необходимо задать значения независимой переменной с заданным шагом (шаг лучше выбрать дробным значением). Чем меньше шаг вычисления независимой переменной тем точнее построенный график.
Задаем формулу по которой определяется зависимая переменная. Вычисляем для каждого значения независимой переменной ее соответствующее значение функции.
По построенным данным строим график функции.
Следовательно, математическая модель у нас уже есть. Рассмотрим пример построения уравнения графика и ее исследования
. Рассмотрим в качестве примера тригонометрическую функцию
Построим компьютерную модель исследования.
Для дальнейших исследований будем одновременно строить график исходной элементарной функции y= sinx и преобразованной функции и сравнивать полученные результаты.
Формулы будут записаны в терминах электронных таблиц следующим образом:
| А3= -7 А4 =А3+0,1 (шаг можно уменьшить например до 0,001) B3 =sin(a3) у меня независимая переменна изменяется на интервале (-7;7), что примерно соответствует интервалу ( ) | d3= -7 d4 =d3+0,1 E3 =sin($f$1*d3) В ячейке F1 будем задавать значение параметра k, и рассматривать полученные изменения графика функции |
Фрагмент произведенных расчетов из электронной таблицы приведен ниже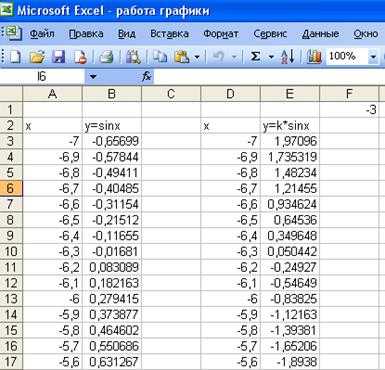
В приложенном к работе файле Microsoft Excel работа графики можно увидеть полные вычисления и полученные результаты
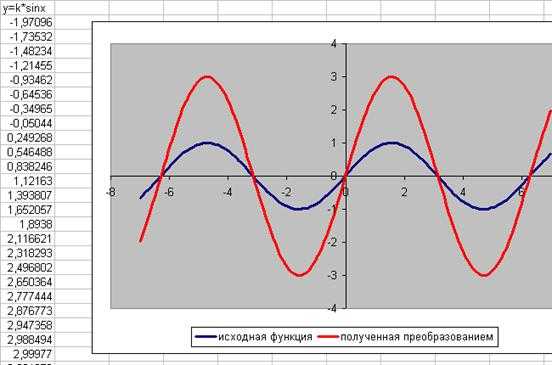
Для детального изучения преобразований графики построил в одной системе координат, что дает возможность сравнить полученные результаты.
Для дальнейших исследований достаточно теперь изменить значение в ячейке f1, и получим иную картину. Например f1=-4
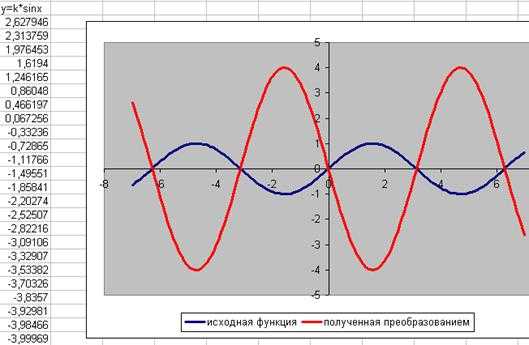
Как видно значения функции автоматически пересчитаны, и построен уже другой график. Данные возможности мною были продемонстрированы одноклассникам на уроке математики. В дальнейшем мои товарищи на уроки изучили свойства полученных графиков функций и наглядно изучили преобразования графиков следующих функций
( и др.)
Полярная система координат.
Мои исследования, на этом не закончились, возник вопрос в построении более сложных графиков. В качестве примера мною рассмотрено уравнение
В полярной системе координат положение точки определяется полярным радиусом R и углом , образуемым полярным радиусом с полярной осью. Следовательно, полярная система координат — система координат, ставящая в соответствие каждой точке на плоскости пару чисел . Основными понятиями этой системы являются точка отсчёта (полюс) и луч, начинающийся в этой точке (полярная ось).
Если в декартовой системе координат предельно простое выражение определяет прямую линию, то это же выражение, переписанное в форме , уже превращается в спираль. Фигуры в полярных координатах образуются как след конца бегающего по кругу полярного радиуса переменной длины. Длина полярного радиуса определяется величиной угла, который в данный момент времени он образует с полярной осью. Координата берётся со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «-» в противоположном случае. Любая точка в этой системе имеет бесконечное число координат вида , которым соответствует одна и та же точка при любых натуральных . Для полюса , угол произвольный.
Связь между полярной и декартовой системами координат.
Точка О — полярный полюс, луч ОЕ будем называть полярной осью, отрезок ОМ — называют длиной полярного радиуса R, положительный угол от луча ОЕ до луча F — полярный угол.
Если известны полярные координаты R и , точки М, то можно уставить связь с её декартовыми координатами.
Построим прямоугольный ОМЕ. В этом треугольнике гипотенуза ОМ=R, ЕОМ = , катет ЕМ = у, катет ОЕ = х координаты точки М.
Для того, чтобы перейти от полярных координат к декартовой системе, используют формулы: , , . Обратно, чтобы, имея прямоугольные координаты, получить расстояние нужное для задания полярных координат, надо воспользоваться теоремой Пифагора: , затем , .
Некоторые замечательные кривые.На протяжении многих лет ученые собирали информацию о формулах, рисующих разные фигуры. Многие фигуры получили свои названия. Список таких названий внушителен: спираль Архимеда, Ферма, Галлилея, Фибоначчи, кардиоида, овалы Кассини, лемниската Бернулли, фигуры Лиссажу, розы Гвидо Гранди, кривые Маклорена, верзьера (локон Марии Аньези) и т.д.
Рекомендуемые страницы:
Поиск по сайту
poisk-ru.ru