Несобственный интеграл cos(x)/x, признаки Абеля и Дирихле.
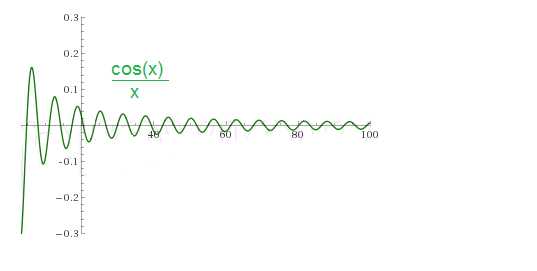
В данной заметке рассмотрим сходимость несобственного интеграла .
Утверждение Функция f(x) непрерывна и ограничена , функция g(x) интегрируема , тогда
Доказательство
Для произвольного ε>0 подберём такое N, что
Следовательно
По критерию сходимости Коши несобственный интеграл сходится.
Замечание Из доказательства видно, что условие неотрицательности g(x) можно заменить на абсолютную интегрируемость .
Теорема (Признак Дирихле) Если выполнены следующие условия:
- Функция f(x) имеет первообразную , такую что найдётся M
- Функция
Тогда сходится .
Доказательство
Интеграл сходится согласно утверждению, поэтому .
, так как g(x) сходится , то и
По критерию сходимости Коши несобственный интеграл сходится.
Теорема (Признак Абеля)
- Функция f(x) интегрируема на [a,∞)
- Функция g(x) непрерывно дифференцируема.
- Функция g(x) ограничена и монотонна.
Тогда сходится .
Доказательство Умножая если надо g(x) на (-1) и прибавляя или отнимая некоторую константу C, можно получить новую функцию g~(x)=(-1?)g(x)+C, которая будет удовлетворять условиям признака Дирихле.
Замечание Условия признаков можно ослабить сказав, что g(x) необязательно имеет непрерывную производную, а просто монотонна и ограничена, монотонна и неотрицательна (неположительна).
Согласно признаку Дирихле интеграл сходится, обозначили .
Однако интеграл расходится, что означает условную сходимость несобственного интеграла от функции cos(x)/x. Докажем расходимость.
Лемма Справедливо неравенство при .
Доказательство
Перепишем
Потенцируем
Определим , тогда неравенство перепишется .
Подставим
Лемма доказана.
Докажем по индукции тождество
База индукции очевидно выполняется.
Пусть тождество справедливо для , докажем для
К N-m=k применим индукционное предположение
Доказали неравенство
Так как натуральный логарифм стремится к бесконечности при стремлении к бесконечности его аргумента, то расходимость интеграла доказана.
Пример Доказать, что функция на отрезке не имеет ограниченную вариацию.
Определение Вариация функции на отрезке есть , точная верхняя грань по всем разбиениям T отрезка [a,b].
Доказательство
Вариация
Сделаем замену
Слагаемые с нечётным k оценим снизу нулём, останутся только чётные слагаемые.
Докажем расходимость ряда
Пришли к пункту доказательства расходимости , что уже было сделано.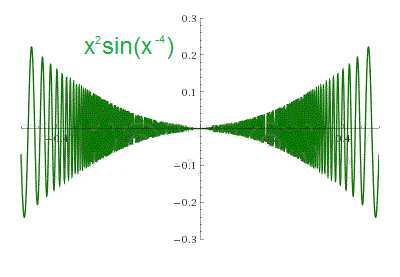
Из бесконечности вариации следует отсутствие длины у кривой, заданной формулой
vipetroff.livejournal.com
Вычислить интеграл от Х*cosX dX
Задание.
Вычислить интеграл от x*cosx dx.
Решение.
Часто при вычислении интегралов, под знаком которых стоит выражение, которое состоит из произведения двух функций (в данном случае функция х и cosx), используют метод интегрирования частями.
Используем этот метод для решения заданного интеграла:
Выполним замену:
Тогда вычислим остальные необходимые компоненты формулы:
Подставим полученные выражения в формулу для вычисления интеграла методом интегрирования частями:
Поскольку интеграл от синуса равен минус косинусу, не забываем о неопределенном постоянном числе, запишем:
Знак неопределенной постоянной С при вынесении ее за скобки не изменился, поскольку она и так является неопределенной, так какая тогда разница со знаком минус она или со знаком плюс.
Примером решения интегралов этим же способом (интегрирования по частям) является также интеграл .
Причем обратим внимание, что за переменную dv всегда берут то выражение, от которого легче найти интеграл, чтобы получить значение переменной v. В нашем случае это было выражение cos x dx, а в этом будет .
ru.solverbook.com
| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |
www.mathway.com
∫ Найти интеграл от y = f(x) = cos(x)/e^x dx (косинус от (х) делить на e в степени х)
Решение
1 / | | cos(x) | ------ dx | x | E | / 0
$$\int_{0}^{1} \frac{1}{e^{x}} \cos{\left (x \right )}\, dx$$
Подробное решение[LaTeX]
Перепишите подынтегральное выражение:
Есть несколько способов вычислить этот интеграл.
Метод #1
пусть .
Тогда пусть и подставим :
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
Используем интегрирование по частям:
пусть и пусть dx.
Затем dx.
Чтобы найти :
Интеграл от экспоненты есть он же сам.
Теперь решаем под-интеграл.
Интеграл от произведения функции на константу есть эта константа на интеграл от данной функции:
Используем интегрирование по частям, отметим, что в конечном итоге подынтегральное выражение повторяется.
Для подинтегрального выражения :
пусть и пусть .
Затем .
Для подинтегрального выражения :
пусть и пусть .
Затем .
Обратите внимание, что подынтегральное выражение повторилось, поэтому переместим его в сторону:
Поэтому,
Таким образом, результат будет:
Таким образом, результат будет:
Если сейчас заменить ещё в:
Метод #2
Используем интегрирование по частям, отметим, что в конечном итоге подынтегральное выражение повторяется.
Для подинтегрального выражения :
пусть и пусть .
Затем .
Для подинтегрального выражения :
пусть и пусть .
Затем .
Обратите внимание, что подынтегральное выражение повторилось, поэтому переместим его в сторону:
Поэтому,
Теперь упростить:
Добавляем постоянную интегрирования:
Ответ:
1 / | -1 -1 | cos(x) 1 e *sin(1) cos(1)*e | ------ dx = - + ---------- - ---------- | x 2 2 2 | E | / 0
$${{\log E}\over{\left(\log E\right)^2+1}}-{{\cos 1\,\log E-\sin 1 }\over{E\,\left(\log E\right)^2+E}}$$
Численный ответ[LaTeX]
Ответ (Неопределённый)[LaTeX]
/ | -x -x | cos(x) e *sin(x) cos(x)*e | ------ dx = C + ---------- - ---------- | x 2 2 | E | /
$${{e^ {- \log E\,x }\,\left(\sin x-\log E\,\cos x\right)}\over{ \left(\log E\right)^2+1}}$$
www.kontrolnaya-rabota.ru
Интеграл косинуса
Неопределенный интеграл от косинуса cos (x) равен синусу. Для первоначальной косинуса к правой стороне добавляем постоянную Постоянную определяют с дополнительного условия на первоначальную.
График косинуса имеет вид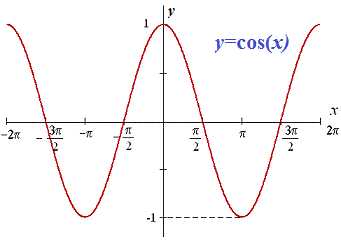 
Само по себе определение интеграла косинуса достаточно простое. Но как только задают вычислить интеграл косинуса двойного угла, тройного или половины угла, сразу возникают трудности в половины студентов. Выведем формулу интегрирования для функции cos (k*x). Для применения табличной формулы интегрирования надо внести коэффициент под дифференциал, что может привести к изменению самого интеграл. Поэтому одновременно необходимо разделить на этот коэффициент.
.
Зная приведенную формулу, проинтегрировать косинус двойного угла сможет каждый школьник 10, 11 класса. Все что необходимо это подставить 2 или 3 в интеграл
и по индукции следующие интегралы
int(sin(k*x)=-1/k*cos(k*x).
Приведенная формула позволяет вычислить интеграл от косинуса половины угла
и интеграл от косинуса одной трети угла
В этих случаях коэффициент, стоящий при переменной в косинусе при интегрировании становится обратным значением перед синусом.
Распространенные примеры интегрирования косинуса
Пример 1. Найти интеграл от cos(5*x).
Решение: По формуле интегрируем косинус
Пример 2. Вычислить интеграл от cos(7*x).
Решение: Выполняем интегрирование
Пример 3. Проинтегрировать выражение cos (11*x).
Решение: Вычисляем неопределенный интеграл
Пример 4. Найти интеграл функции y= cos (x/5).
Решение: Записываем неопределенный интеграл
Пример 5. Найти интеграл функции y= cos (x/6).
Решение: Проинтегрируем по приведенной выше формуле
Как только Вы освоите методику интегрирования на простых примерах, смело можете переходить к определенным интегралам и первообразным. Для отискания определенного интеграла проводим интегрирование, а дальше подставляем пределы интегрирования и находим изменение первообразной функции.
Пример 6. Проинтегрировать косинус двойного угла y = cos (2 * x) от 0 до 45 градусов.
Решение: Находим указанный интеграл от косинуса
Пример 7. Найти интеграл от косинуса y = cos (x) от 0 до 60 градусов.
Решение: Вычисляем интеграл и подставляем пределы интегрирования
Пример 8. Найти первоначальную от cos (x), которая при 30 градусах равна 1.
Решение: Находим первоначальную
С наложенного условия на первоначальную вычисляем постоянную
sin(Pi/6)+C=1; C=1-
sin(Pi/6)=1-0,5=0,5.
На этом задача решена. На таких простых примерах Вы четко должны знать, чему равный интеграл от косинуса.
Далее полученные знания можно применять для вычисления площадей криволинейных трапеций. Это достаточно абстрактное понятие, но с помощью интегрирования находить площадь фигур достаточно просто и быстро. Следует только помнить, что площадь всегда принимает положительное значение, в то время как определенный интеграл может принимать отрицательное значение.
Например вычислим площадь и интеграл от косинуса, если переменная принадлежит интервалу от 0 до 2*Pi.
По физическому содержанию площадь равна заштрихованным поверхностям.
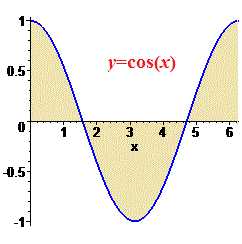Находим определенный интеграл в указанных пределахОн равен нулю. Что касается площади, то сначала следует найти точки пересечения с осью абсцисс на этом интервале
Таким образом площадь необходимо искать на трех промежутках
Ось абсцисс можем записать функцией y = 0. Таким образом на первом промежутке площадь равна интегралу от косинуса,
на втором 0-cos (x) = — cos (x) от минус косинуса и на третьем от косинуса. Все при вычислении площади зависит от того, какая функция принимает большее значение по оси ординат (Oy). Вычисляем площадь интегрированием в указаных пределах
Таким образом искомая площадь равна 4. Если иметь график функции перед глазами, то данное значение можно получить как 4 площади косинус функции, которые периодически повторяются
На этом знакомство с интегрированием косинуса завершается. Приведенная методика интегрирования позволяет вычислить 80% основных задач на интегрирование косинуса. Остальные 20% Вы научитесь после изучения способов нахождения интегралов от функций вида
Мы научим Вас, какие свертки и замены переменных следует использовать, в каких случаях целесообразно интегрировать по частям.
Интегралы от других тригонометрических и обратных к ним функций Вы найдете в категории «Интегрирование функций».
yukhym.com
| 1 | Найти производную — d/dx | квадратный корень x | |
| 2 | Найти производную — d/dx | натуральный логарифм x | |
| 3 | Вычислить | интеграл натурального логарифма x по x | |
| 4 | Найти производную — d/dx | e^x | |
| 5 | Вычислить | интеграл e^(2x) относительно x | |
| 6 | Найти производную — d/dx | 1/x | |
| 7 | Найти производную — d/dx | x^2 | |
| 8 | Вычислить | интеграл e^(-x) относительно x | |
| 9 | Найти производную — d/dx | 1/(x^2) | |
| 10 | Найти производную — d/dx | sin(x)^2 | |
| 11 | Найти производную — d/dx | sec(x) | |
| 12 | Вычислить | интеграл e^x относительно x | |
| 13 | Вычислить | интеграл x^2 относительно x | |
| 14 | Вычислить | интеграл квадратного корня x по x | |
| 15 | Вычислить | натуральный логарифм 1 | |
| 16 | Вычислить | e^0 | |
| 17 | Вычислить | sin(0) | |
| 18 | Найти производную — d/dx | cos(x)^2 | |
| 19 | Вычислить | интеграл 1/x относительно x | |
| 20 | Вычислить | cos(0) | |
| 21 | Вычислить | интеграл sin(x)^2 относительно x | |
| 22 | Найти производную — d/dx | x^3 | |
| 23 | Найти производную — d/dx | sec(x)^2 | |
| 24 | Найти производную — d/dx | 1/(x^2) | |
| 25 | Вычислить | интеграл arcsin(x) относительно x | |
| 26 | Вычислить | интеграл cos(x)^2 относительно x | |
| 27 | Вычислить | интеграл sec(x)^2 относительно x | |
| 28 | Найти производную — d/dx | e^(x^2) | |
| 29 | Вычислить | интеграл в пределах от 0 до 1 кубического корня 1+7x по x | |
| 30 | Найти производную — d/dx | sin(2x) | |
| 31 | Вычислить | интеграл натурального логарифма x по x | |
| 32 | Найти производную — d/dx | tan(x)^2 | |
| 33 | Вычислить | интеграл e^(2x) относительно x | |
| 34 | Вычислить | интеграл 1/(x^2) относительно x | |
| 35 | Найти производную — d/dx | 2^x | |
| 36 | График | натуральный логарифм a | |
| 37 | Вычислить | e^1 | |
| 38 | Вычислить | интеграл 1/(x^2) относительно x | |
| 39 | Вычислить | натуральный логарифм 0 | |
| 40 | Найти производную — d/dx | cos(2x) | |
| 41 | Найти производную — d/dx | xe^x | |
| 42 | Вычислить | интеграл 1/x относительно x | |
| 43 | Вычислить | интеграл 2x относительно x | |
| 44 | Найти производную — d/dx | ( натуральный логарифм x)^2 | |
| 45 | Найти производную — d/dx | натуральный логарифм (x)^2 | |
| 46 | Найти производную — d/dx | 3x^2 | |
| 47 | Вычислить | натуральный логарифм 2 | |
| 48 | Вычислить | интеграл xe^(2x) относительно x | |
| 49 | Найти производную — d/dx | 2e^x | |
| 50 | Найти производную — d/dx | натуральный логарифм 2x | |
| 51 | Найти производную — d/dx | -sin(x) | |
| 52 | Вычислить | tan(0) | |
| 53 | Найти производную — d/dx | 4x^2-x+5 | |
| 54 | Найти производную — d/dx | y=16 корень четвертой степени 4x^4+4 | |
| 55 | Найти производную — d/dx | 2x^2 | |
| 56 | Вычислить | интеграл e^(3x) относительно x | |
| 57 | Вычислить | интеграл cos(2x) относительно x | |
| 58 | Вычислить | интеграл cos(x)^2 относительно x | |
| 59 | Найти производную — d/dx | 1/( квадратный корень x) | |
| 60 | Вычислить | интеграл e^(x^2) относительно x | |
| 61 | Вычислить | sec(0) | |
| 62 | Вычислить | e^infinity | |
| 63 | Вычислить | 2^4 | |
| 64 | Найти производную — d/dx | x/2 | |
| 65 | Вычислить | 4^3 | |
| 66 | Найти производную — d/dx | -cos(x) | |
| 67 | Найти производную — d/dx | sin(3x) | |
| 68 | Вычислить | натуральный логарифм 1/e | |
| 69 | Вычислить | интеграл x^2 относительно x | |
| 70 | Упростить | 1/( кубический корень от x^4) | |
| 71 | Найти производную — d/dx | 1/(x^3) | |
| 72 | Вычислить | интеграл e^x относительно x | |
| 73 | Вычислить | интеграл tan(x)^2 относительно x | |
| 74 | Вычислить | интеграл 1 относительно x | |
| 75 | Найти производную — d/dx | x^x | |
| 76 | Найти производную — d/dx | x натуральный логарифм x | |
| 77 | Вычислить | интеграл sin(x)^2 относительно x | |
| 78 | Найти производную — d/dx | x^4 | |
| 79 | Вычислить | предел (3x-5)/(x-3), если x стремится к 3 | |
| 80 | Вычислить | интеграл от x^2 натуральный логарифм x по x | |
| 81 | Найти производную — d/dx | f(x) = square root of x | |
| 82 | Найти производную — d/dx | x^2sin(x) | |
| 83 | Вычислить | интеграл sin(2x) относительно x | |
| 84 | Найти производную — d/dx | 3e^x | |
| 85 | Вычислить | интеграл xe^x относительно x | |
| 86 | Найти производную — d/dx | y=x^2 | |
| 87 | Найти производную — d/dx | квадратный корень x^2+1 | |
| 88 | Найти производную — d/dx | sin(x^2) | |
| 89 | Вычислить | интеграл e^(-2x) относительно x | |
| 90 | Вычислить | интеграл натурального логарифма квадратного корня x по x | |
| 91 | Вычислить | 2^5 | |
| 92 | Найти производную — d/dx | e^2 | |
| 93 | Найти производную — d/dx | x^2+1 | |
| 94 | Вычислить | интеграл sin(x) относительно x | |
| 95 | Вычислить | 2^3 | |
| 96 | Найти производную — d/dx | arcsin(x) | |
| 97 | Вычислить | предел (sin(x))/x, если x стремится к 0 | |
| 98 | Вычислить | e^2 | |
| 99 | Вычислить | интеграл e^(-x) относительно x | |
| 100 | Вычислить | интеграл 1/x относительно x |
www.mathway.com